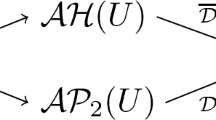Abstract
Harmonic and polyanalytic functional calculi have been recently defined for bounded commuting operators. Their definitions are based on the Cauchy formula of slice hyperholomorphic functions and on the factorization of the Laplace operator in terms of the Cauchy–Fueter operator \({\mathcal{D}}\) and of its conjugate \(\overline{{\mathcal{D}}}.\) Thanks to the Fueter extension theorem, when we apply the operator \({\mathcal{D}}\) to slice hyperholomorphic functions, we obtain harmonic functions and via the Cauchy formula of slice hyperholomorphic functions, we establish an integral representation for harmonic functions. This integral formula is used to define the harmonic functional calculus on the S-spectrum. Another possibility is to apply the conjugate of the Cauchy–Fueter operator to slice hyperholomorphic functions. In this case, with a similar procedure we obtain the class of polyanalytic functions, their integral representation, and the associated polyanalytic functional calculus. The aim of this paper is to extend the harmonic and the polyanalytic functional calculi to the case of unbounded operators and to prove some of the most important properties. These two functional calculi belong to so called fine structures on the S-spectrum in the quaternionic setting. Fine structures on the S-spectrum associated with Clifford algebras constitute a new research area that deeply connects different research fields such as operator theory, harmonic analysis, and hypercomplex analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the main motivations to investigate quaternionic spectral theory can be found in the paper of Birkhoff and Von Neumann, see [10], where the authors show that quantum mechanics can also be formulated using quaternions, but they do not specify the definition of spectrum for quaternionic linear operator. The spectral theory on the S-spectrum for quaternionic linear operators began in 2006 with the discovery of the S-spectrum. This notion of spectrum was identified using only methods in hypercomplex analysis even though its existence was suggested by quaternionic quantum mechanics; for more details, see the introduction of the book [22]. The notion of S-spectrum extends also to operators in the Clifford algebra setting, see [31, 32], but recently it has been shown that the quaternionic and the Clifford settings are just particular cases of a more general framework in which the spectral theory on the S-spectrum can be developed, see [23, 25]. Using the notion of S-spectrum, it was possible to prove the spectral theorem for quaternionic linear operators, see [1], that is a central theorem for the formulation of quantum mechanics, and more recently, the spectral theorem was extended to Clifford operators, see [24].
The spectral theory based on the S-spectrum is systematically organized in the books [21, 22, 31]. Nowadays, this theory has several research directions, without claiming completeness we mention: The slice hyperholomorphic Schur analysis, see [2], new classes of fractional diffusion problems based on fractional powers of quaternionic linear operators, see [17, 18, 22, 26]. The results on the fractional powers are based on the \(H^{\infty }\)-functional calculus, see [6, 20]. Other interesting research directions are the study of the characteristic operator function, see [3], and the quaternionic perturbation theory and invariant subspaces, see [12].
In recent times, a new branch of the spectral theory on the S-spectrum has been developed that is called fine structures on the S-spectrum. It consists of the function spaces arising from the Fueter–Sce theorem with their integral representations that are used to define various functional calculi, see [13, 16, 34, 35].
The function spaces of a given fine structure are determined by the factorizations of the second operator \(T_{FS2}\) in the Fueter–Sce (extension) theorem and on the Cauchy formula of slice hyperholomorphic functions. In the sequel, we will work just in the quaternionic setting and the map \(T_{FS2}\) will be denoted by \(T_{F2}\) because it was introduced by Fueter, while the map \(T_{FS2}\) was introduced by Sce for the Clifford algebra setting. The integral representations of the spaces of the fine structures are crucial to define the associated functional calculi for bounded operators on the S-spectrum. Among these functional calculi, we have the harmonic, the polyharmonic, the polyanalytic ones, and several others. In this paper, we concentrate on the quaternionic setting that contains two important fine structures. In fact, in the quaternionic setting, the second mapping \(T_{F2}\) in the Fueter extension theorem is equal to the Laplace operator \(\Delta\) in dimension 4 and the most important factorizations of \(\Delta\) lead to the harmonic fine structure and to the polyanalytic one.
The goal of this paper is to extend the harmonic and the polyanalytic functional calculi to unbounded operators and to prove some of their properties.
To present our results, we need to explain more about the setting in which we work, so we will quote some results that we will need in the sequel and whose proofs can be found in [22]. We start by fixing the notation of the quaternions, that are defined as
where for the imaginary units holds the following relations
and
We denote by \({\textrm{Re}}(q)=q_0\) the real part of a quaternion and by \({\underline{q}}\,{:}{=}\, q_1e_1+q_2e_2+q_3e_3\) its imaginary part. The conjugate of a quaternion \(q \in {\mathbb{H}}\) is defined as \({\bar{q}}=q_0- {\underline{q}}\) and the modulus of \(q \in {\mathbb{H}}\) is given by \(|q|= \sqrt{q {\bar{q}}}= \sqrt{q_0^2+q_1^2+q_2^2+q_3^2}.\) The unit sphere of purely imaginary quaternions is defined as
We observe that if \(J \in {\mathbb{S}}\) then \(J^2=-1.\) This means that J behaves like an imaginary unit, and we denote by
an isomorphic copy of the complex numbers. If we consider a non-real quaternion \(q=q_0+ {\underline{q}}=q_0+ J_q |{\underline{q}}|,\) where \(J_q\,{:}{=}\, {\underline{q}}/ |{\underline{q}}|.\) We can associate to q the two-sphere defined by
Let \(U\subseteq {\mathbb{H}}\) and \(I\in {\mathbb{S}}.\) Whenever \(u+Iv\in U\) and, for any \(J\in {\mathbb{S}},\) \(u+Jv\in U\), we say that U is axially symmetric.
Axially symmetric sets are suitable domains of the following class of functions.
Definition 1.1
(Slice hyperholomorphic functions) Let us consider \(U \subset {\mathbb{H}}\) an axially symmetric open set and we set
A function \(f:U \rightarrow {\mathbb{H}}\) of the form
is called left (resp. right) slice hyperholomorphic if \(\alpha\) and \(\beta\) are quaternionic-valued functions such that for all \((u,v) \in {\mathcal{U}}\), we have
Moreover, the functions \(\alpha\) and \(\beta\) have to fulfill the Cauchy–Riemann system
The class of left (resp. right) slice hyperholomorphic functions on U is denoted by \({\mathcal{S}\mathcal{H}}_L(U)\) (resp. \({\mathcal{S}\mathcal{H}}_R(U)\)). If the functions \(\alpha\) and \(\beta\) are real valued, then we are dealing with the subset of intrinsic slice hyperholomorphic functions. This set of functions is denoted by \({\mathcal{N}}(U).\)
By means of the left (resp. right) slice hyperholomorphic Cauchy kernel defined by
for \(s\not \in [q],\) it is possible to give slice hyperholomorphic functions an integral representation. First, we recall the definition of slice Cauchy domains that will be often used in the integral representations of functions.
Definition 1.2
(Slice Cauchy domain) We say that \(U\subseteq {\mathbb{H}}\) is a slice Cauchy domain if it is an axially symmetric open set and if, for any \(J\in {\mathbb{S}},\) \(U\cap {\mathbb{C}}_J\) is a Cauchy domain in \({\mathbb{C}}_J.\) In particular, this is equivalent to requiring that \(\partial (U\cap {\mathbb{C}}_J)\) is the union of a finite number of non-intersecting piecewise continuously differentiable Jordan curves in \({\mathbb{C}}_{J}.\)
Theorem 1.3
(The Cauchy formulas of slice hyperholomorphic functions) We assume that \(U \subset {\mathbb{H}}\) is a bounded slice Cauchy domain. Let us considerer \(J \in {\mathbb{S}}\) and set \({\textrm{d}}s_J={\textrm{d}}s(-J).\) For any \(q \in U\) a left (reps. right) slice hyperholomorphic function f, defined on a set contained in \({\bar{U}},\) can be written as
Similar formulas hold for unbounded domains. Another class of hyperholomorphic functions that we will use are the so-called axially monogenic functions, see [36].
Definition 1.4
(Axially monogenic functions) Let \(U \subset {\mathbb{H}}\) be a slice Cauchy domain. A function \(f: U \rightarrow {\mathbb{H}}\) of class \({\mathcal{C}}^1\) is said to be (left) axially monogenic if it is monogenic, i.e.,
and it has the form
where the functions A and B satisfy the even–odd conditions (1.1). We denote by \({\mathcal{A}\mathcal{M}}(U)\) the set of (left) axially monogenic functions. A similar definition can be given for right axially monogenic functions and we use the notation
The classes of slice hyperholomorphic and axially monogenic functions are connected by the well-known Fueter mapping theorem, see [39].
Theorem 1.5
(Fueter mapping theorem) Let us assume that \(f_0:D\rightarrow {\mathbb{C}}\) is a holomorphic function where D is an open and connected subset of the upper-half complex plane. Suppose that
is the open set associated with D in \({\mathbb{H}}.\) Let
where \(z=u+iv.\) We have that the function
is an intrinsic slice hyperholomorphic function. In particular, the operator
is a map between the set of holomorphic functions and the set of intrinsic slice hyperholomorphic functions. Moreover, the function
is an axially monogenic function where \(\Delta\) is the Laplacian in four variables. In particular, the operator \(T_{F_2}\,{:}{=}\,\Delta\) can be viewed as a map between the set of slice hyperholomorphic functions and the set of axially monogenic functions.
Remark 1.6
In the Fueter mapping theorem, the restriction that the holomorphic function has to be defined in the upper-half complex plane can be removed when we impose the even–odd conditions (1.1).
Remark 1.7
We can summarize the Fueter construction by the following diagram

where \({\mathcal{O}}(D)\) is the set of holomorphic functions defined on D.
Remark 1.8
In the Clifford algebra setting, the operator \(T_{F2}\) is equal to \(\Delta _{n+1}^{\frac{n-1}{2}},\) where \(\Delta _{n+1}\) is the Laplace operator in \(n+1\) variables. If n is odd, then the \(T_{F2}\) is a pointwise differential operator, see [30, 44]. If n is even, we are dealing with the fractional powers of the Laplace operator, see [43].
The Cauchy formula of slice hyperholomorphic function allows to prove the Fueter mapping theorem in integral form, see [29].
Theorem 1.9
(Fueter mapping theorem in integral form) Let us assume that f is a left (resp. right) slice hyperholomorphic function on a set \(W\subseteq {\mathbb{H}}\) which contains a slice Cauchy domain U. We have that
where \(\breve{f}(q)=\Delta f(q),\) \(J\in {\mathbb{S}},\) \({\textrm{d}}s_J={\textrm{d}}s(-J),\) the kernel is given by
and the pseudo Cauchy kernel is defined by
The kernel \(F_L(s,q)\) (resp. \(F_R(s,q))\) is right slice hyperholomorphic in the variable s (resp. left slice hyperholomorphic) and it is left axially monogenic in the variable q (resp. right axially monogenic). In particular, different choices of the domain U and of the imaginary unit J do not change the result of the previous integral representation formulas.
It is possible to factorize the Laplace operator appearing in the diagram (1.3) in the following two different ways. Precisely, if \({{\mathcal{D}}}\,{:}{=}\,\partial _{q_0}+ \sum _{i=1}^3 e_i \partial _{q_i}\) and \({{\overline{{\mathcal{D}}}}}\,{:}{=}\,\partial _{q_0}- \sum _{i=1}^3 e_i \partial _{q_i}\) are the Cauchy–Fueter operator and its conjugate, respectively, then we have
Even though the operators \({{\mathcal{D}}}\) and \(\overline{{{\mathcal{D}}}}\) commute the factorizations, \({{\mathcal{D}}}\overline{{{\mathcal{D}}}}\) and \(\overline{{{\mathcal{D}}}}{{\mathcal{D}}}\) give rise to different functions spaces according to the order \({{\mathcal{D}}}\) and \(\overline{{{\mathcal{D}}}}\) applied to a slice hyperholomorphic function. In fact, if we first apply operator \({{\mathcal{D}}}\) to functions in \({\mathcal{S}\mathcal{H}}(\Omega _D)\), we have:

where \({\mathcal{A}\mathcal{H}}(\Omega _D)\) is the class of axially harmonic function, i.e., functions of the form (1.2) and in the kernel of the Laplace operator in four real variables. In the case we apply \(\overline{{{\mathcal{D}}}}\) to functions in \({\mathcal{S}\mathcal{H}}(\Omega _D)\), we obtain

where \({\mathcal{A}\mathcal{P}}_2(\Omega _D)\) is the class of axially polyanalytic functions of order 2, i.e., functions of the form (1.2) and in the kernel of the operator \({{\mathcal{D}}}^2.\) The above cases lead us to the following definition.
Definition 1.10
(Fine structures of the spectral theory on the S-spectrum) All the set of functions spaces and the associated functional calculi induced by a factorization of the Fueter map, i.e., the Laplace operator in Four real variables, are called fine structures of the spectral theory on the S-spectrum.
In [13, 34], we give an integral representation for axially harmonic functions and axially polyanalytic functions of order 2, we now recall such integral representations. Let \(W \subset {\mathbb{H}}\) be an open set. Let U be a slice Cauchy domain such that \({\bar{U}} \subset W.\) For \(J \in {\mathbb{S}}\) and \({\textrm{d}}s_J={\textrm{d}}s(-J)\) we have that:
\(\bullet\) given a left (resp. right) slice hyperholomorphic function f in W, the function \({\tilde{f}}(q)\,{:}{=}\, {{\mathcal{D}}} f(q)\) (resp. \({\tilde{f}}(q)\,{:}{=}\, f(q){{\mathcal{D}}}\)) is harmonic and it can be written in the following integral form
\(\bullet\) given a left (resp. right) slice hyperholomorphic function f in W, the function \(\breve{f}^{0}(q)= {{\overline{{\mathcal{D}}}}}f(q)\) (resp. \(\breve{f}^{0}(q)\,{:}{=}\, f(q) {{\overline{{\mathcal{D}}}}}\)) is polyanalytic of order 2 and it can be written in the following integral form
Our main results are an extension of the Riesz–Dunford functional calculus, see [37] for the classes of functions of the quaternionic fine structures. Precisely, let f be a holomorphic function defined on an open set containing \({\overline{\Omega }},\) where \(\Omega \subset {\mathbb{C}}\) is an open set that contains the spectrum of the bounded operator B on a complex Banach space \(X_{\mathbb{C}}.\) The holomorphic functional calculus f(B) is defined as
To define the functional calculus for an unbounded operator A, we assume that the function f is holomorphic at infinity and on the spectrum \(\sigma (A)\) of the closed linear operator A whose domain is contained in \(X_{\mathbb{C}}.\)
Let us assume that the resolvent \(\rho (A)\) is non-empty. We set \(\Phi (\lambda )\,{:}{=}\, (\lambda - \alpha )^{-1},\) \(\Phi (\infty )=0\) and \(\Phi (\alpha )=\infty ,\) for \(\alpha \in \rho (A).\) We define the functional calculus for unbounded operators as \(f(A)\,{:}{=}\,\phi (B)\) where \(\phi (\mu )= f(\Phi ^{-1}(\mu ))\) and \(B\,{:}{=}\, (A- \alpha {\mathcal{I}})^{-1}.\) For this functional calculus, we have the following integral representation
where \(\Gamma\) consists of a finite numbers of Jordan arcs, that surround the spectrum \(\sigma (A)\) and the point at infinity. We recall that the function f has to be holomorphic in an open set that contains \(\Gamma\) and its interior. Moreover, formula (1.6) implies that f(A) is independent from the parameter \(\alpha .\)
The harmonic and polyanalytic functional calculi for bounded quaternionic operators with commuting components were introduced in [13, 34] where operators of the form \(T=T_0+e_1T_1+e_2T_2+e_3T_3\) are considered. The operator \({\bar{T}}=T_0-e_1T_1-e_2T_2-e_3T_3\) is called the conjugate of T. The harmonic resolvent operator is defined as
and it tuned out to be the well-known commutative pseudo S-resolvent operator. The polyanalytic (left) resolvent operator is defined as
where \(F_L(s,T)=-4(s- {\bar{T}}) {\mathcal{Q}}_{c,s}(T)^{-2}.\) Similarly, we defined the polyanalytic right resolvent operator. In [13, 34], we proved that the harmonic functional calculus (also called Q-functional) for \(f \in {\mathcal{S}\mathcal{H}}_L(U),\) given by
and the \(P_2\)-functional calculus, defined as
are well defined since the integrals do not depend on the open set U nor on \(J \in {\mathbb{S}}.\) Here U denotes a suitable open set that has smooth boundary and contains the S-spectrum of T.
The goal of this paper is to define the harmonic functional calculus and the \(P_2\)-functional calculus for commuting unbounded operators in the spirit of the holomorphic functional calculus for closed operators mentioned above. Let us consider f to be a suitable slice hyperholomorphic function and let \({\tilde{\psi }}\) be defined as:
where \(\phi (q)\,{:}{=}\,(f \circ \phi _{\alpha }^{-1})(q),\) \(q\,{:}{=}\, \phi _{\alpha }(s)= (s- \alpha )^{-1},\) \(\phi _{\alpha }(\infty )=0,\) \(\phi _{\alpha }(\alpha )=\infty .\) We assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and we set \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Then it is \(\alpha \in \rho _S \cap {\mathbb{R}} \ne \emptyset .\) For the case of unbounded operators, we will always assume that \(T_0=0.\) Then the Q-functional calculus for closed quaternionic operators is defined as
Using the same notations, we define
and, by means of this function, we define the \(P_2\)-functional calculus for closed operators
Moreover, we show integral representations for \(\tilde{f}(T)\) and \(\breve{f}^0(T),\) which are the counter part of formula (1.6) for the Riesz–Dunford functional calculus.
This fact is not necessarily expected because the Q-functional and \(P_2\)-functional calculi are defined through integral transforms, whereas the Riesz–Dunford functional calculus is based on the Cauchy formula of holomorphic functions.
Outline of the paper. The paper consists of five sections, the first one being this introduction. In Sect. 2, we briefly revise the S-functional calculus and the F-functional calculus, both for bounded and unbounded operators with commuting components with some new insight to this calculus. In Sect. 3, we establish and prove the main properties for the harmonic functional calculus for closed operators. In Sect. 4, we define the \(P_2\)-functional calculus for closed operators and we prove its main properties. Section 5 contains some concluding remarks.
2 Preliminary results on quaternionic operators
In this section, we recall some results on the S-functional calculus and F-functional calculus for bounded and unbounded operators, see for more details [22], to give a complete picture of the fine structures on the S-spectrum.
Bounded quaternionic linear operators We denote by \({\mathcal{B}}(X)\) the set of all bounded right linear operators defined on a two-sided quaternionic Banach module \(X=X_{{\mathbb{R}}}\otimes {\mathbb{H}}\) where \(X_{{\mathbb{R}}}\) is a real Banach space. The S-resolvent set and the S-spectrum of \(T\in {\mathcal{B}}(X)\) are defined via the operator
Definition 2.1
The S-resolvent set of \(T\in {\mathcal{B}}(X)\) is denoted by \(\rho _S(T)\) and it is defined as
where the operator
is called the pseudo S-resolvent operator of T at s. Moreover, the S-spectrum of T is defined as
Due to the lack of commutativity, there exist two different resolvent operators.
Definition 2.2
Let \(T \in {\mathcal{B}}(X)\) and \(s \in \rho _S(T).\) Then the left (resp. right) S-resolvent operator is defined as
Definition 2.3
Let \(T\in {\mathcal{B}}(X),\) we define \({\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. \({\mathcal{S}\mathcal{H}}_R(\sigma _S(T)),\) resp. \({\mathcal{N}}(\sigma _S(T))\)) as the set of left (resp. right, resp. intrinsic) slice hyperholomorphic functions whose domains contain \(\sigma _S(T).\)
For these classes of functions, we introduce the S-functional calculus for bounded operators.
Definition 2.4
(S-functional calculus for bounded operators) For \(T\in {\mathcal{B}}(X)\) and \(f\in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. \(f\in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T))\)) we define
where \({\textrm{d}}s_J\,{:}{=}\,(-J){\textrm{d}}s\) and U is a bounded slice Cauchy domain such that \(\sigma _S(T)\subseteq U\subseteq {{\overline{U}}}\subseteq {\text{dom}}(f).\)
The integrals in (2.1) do not depend on the choice of U on the choice of the imaginary unit \(J \in {\mathbb{S}}.\) The definition and the properties of the S-functional calculus can be found in the books [21, 22, 31].
Now, we recall the F-functional calculus, which was introduced for the first time in [29] and further developed in [14, 15, 19]. This is a monogenic functional calculus in the same spirit of McIntosh and collaborators, see [40, 41], but it is based on the theory of the S-spectrum. The F-functional calculus arises by the Fueter theorem in integral form (see Theorem 1.9) by formally replacing the quaternion q with a suitable quaternionic operator T.
The \(F-\)functional calculus is defined for operators \(T\in {\mathcal{B}}(X)\) whose components commute with each other. More precisely, any right linear operator \(T\in {\mathcal{B}}(X)\) can be written as \(T=T_0+e_1T_1+e_2T_2+e_3T_3\) where the operators \(T_i\) for \(i=0,\, 1,\, 2,\, 3\) are called components of T and they are bounded linear operators from \(X_{{\mathbb{R}}}\) to \(X_{{\mathbb{R}}}\) (see [22, Paragraph 4.5]). We set
We are going to define the F-functional calculus for any operators \(T\in {\mathcal{B}\mathcal{C}}(X).\) As a first step in this direction, in the next definition we introduce, for any \(T\in {\mathcal{B}\mathcal{C}}(X),\) the notion of the \(F-\)spectrum which turns out to be equivalent to the notion of the S-spectrum but it will be more appropriate for our aim.
Definition 2.5
The \(F-\)resolvent set of \(T\in {\mathcal{B}\mathcal{C}}(X)\) is given by
where, for any \(s\in {\mathbb{H}},\) we set
and \({{\overline{T}}}\,{:}{=}\,T_0-e_1T_1-e_2T_2-e_3T_3.\) Moreover, the F-spectrum of T is defined as
In [27], it is proved that the F-spectrum is the commutative version of the S-spectrum, i.e., for \(T \in {\mathcal{B}\mathcal{C}}(X)\), we have
The operator \({\mathcal{Q}}_{c,s}(T)^{-1},\) for \(s\in \rho _F(T),\) is called the commutative pseudo S-resolvent operator of T at s. In [27], a commutative version of the S-functional calculus for bounded operators is established and in this case, we have to deal with the following resolvent operators.
Definition 2.6
Let us assume that T belongs to \({\mathcal{B}\mathcal{C}}(X)\) and \(s \in \rho _S(T).\) The left (resp. right) commutative S-resolvent operator is defined as
Remark 2.7
Since no ambiguity will arise in the sequel, we write the commutative version of the S-resolvent operators using the same symbol adopted for the non-commutative ones
A commutative S-functional calculus can be also defined by means of the above resolvent operators, as in Definition 2.4. Now, we have all the tools to give the definition for the F-functional calculus.
Definition 2.8
(F-resolvent operators) Let us assume that T belongs to \({\mathcal{B}\mathcal{C}}(X).\) For \(s \in \rho _S(T),\) the left (resp. right) F-resolvent operator is defined as
Definition 2.9
(F-functional calculus for bounded operators) Let us assume that U is a slice Cauchy domain that contains \(\sigma _S(T).\) Moreover, we assume that \({\overline{U}}\) is contained in the domain of f. We consider an operator \(T=T_1e_1+T_2e_2+T_3e_3\) that belongs to \({\mathcal{B}\mathcal{C}}(X),\) where the operators \(T_{\ell },\) \(\ell =1,2,3\) have real spectrum. For \(J \in {\mathbb{S}}\), we set \({\textrm{d}}s_J={\textrm{d}}s(-J).\) For \(\breve{f}= \Delta f(q)\) with \(f \in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. \(f \in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T)))\), we define
The S-functional calculus as well as the F-functional calculus are well defined,, since the integrals in (2.3) depend neither on U and nor on the imaginary unit \(J \in {\mathbb{S}}.\)
Remark 2.10
Since \(\breve{f}= \Delta f(q)\), we observe that \(\Delta\) has a kernel and the independence on the kernel is discussed in Remark 7.1.13 in [22]. The independence of the F-functional calculus from the \({\textrm{ker}}(\Delta )\) is obtained by an application of the monogenic functional calculus of McIntosh that requires that operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum and one of the \(T_{\ell }\) has to be the zero operator. This requirement is enforced in order not to disconnect the monogenic resolvent set and it usually takes \(T_0\) to be zero.
Unbounded quaternionic linear operators. Now we recall the main notions for the S-functional calculus and F-functional calculus for unbounded operators, introduced in [27, 28]. These functional calculi are defined for a peculiar class of operators, that are defined as follows.
Definition 2.11
We assume that X is a two-sided Banach space \(T: {{\textrm{dom}}}(T) \subset X \rightarrow X\) a right linear operator. The operator T is called closed if its graph is closed in the Cartesian product \(X \times X.\)
Definition 2.12
Let \(T_{\ell }: {{\textrm{dom}}}(T_\ell ) \subset X \rightarrow X\) be a linear closed operators for \(\ell =0,\ldots ,3\) such that
\(T_{\ell }T_kv=T_kT_{\ell }v\) for all \(v\in \bigcap _{k=0}^3{{\textrm{dom}}}( T^2_k).\) Then \({{\textrm{dom}}}(T)= \cap _{\ell =0}^3 {{\textrm{dom}}}(T_{\ell })\) is the domain of the quaternionic right linear operators \(T=T_0+ \sum _{\ell =1}^3 e_{\ell } T_{\ell }: \, {{\textrm{dom}}}(T) \subset X \rightarrow X,\) and \({\bar{T}}=T_0- \sum _{\ell =1}^3 e_{\ell } T_{\ell }: \, {{\textrm{dom}}}(T) \subset X \rightarrow X,\) since \({{\textrm{dom}}}(T)={{\textrm{dom}}}({\bar{T}}).\) We denote this set of closed right linear operators with commuting components by \({\mathcal{K}\mathcal{C}}(X).\)
Now, we give the notion of S-spectrum in this setting.
Definition 2.13
Let \(T \in {\mathcal{K}\mathcal{C}}(X).\) We denote by \(\rho _S(T)\) the S-resolvent set of T defined as
with
We define the S-spectrum \(\sigma _S(T)\) of T as
The extended S-spectrum is defined as
Remark 2.14
In the sequel, we will always assume that the S-resolvent is non-empty.
Definition 2.15
Let \(T \in {\mathcal{K}\mathcal{C}}(X).\) For \(s \in \rho _S(T)\) we define
the commutative pseudo S-resolvent operator of T at s, where \({\mathcal{Q}}_{c,s}(T)^{-1}\) maps X to \({{\textrm{dom}}}(T^2)\) for \(s\in \rho _S(T).\)
Definition 2.16
(The (commutative) S-resolvent operators in the unbounded case) Let \(T \in {\mathcal{K}\mathcal{C}}(X).\) For \(s \in \rho _S(T),\) we define the left (resp. right) S-resolvent operator of T at s as
Observe that because of how \(S^{-1}_L(s,T)\) and \(S^{-1}_R(s,T)\) are defined they map X to \({{\textrm{dom}}}(T).\)
Definition 2.17
Let \(T \in {\mathcal{K}\mathcal{C}}(X).\) A function f is left slice hyperholomorphic in \({\overline{\sigma }}_S(T)\) if and only if f is left slice hyperholomorphic with \(\sigma _S(T)\subset {{\textrm{dom}}}(f).\) Moreover, we have to request that \({\mathbb{H}} {\setminus } B_r(0)\subset {{\textrm{dom}}}(f)\) for some \(r >0\) and \(f( \infty )= \lim _{q \rightarrow \infty } f(q)\) exists. This set of functions is denoted by \({\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T)).\)
Similarly, we can define the functions in \({\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \({\mathcal{N}}({\overline{\sigma }}_S(T)).\)
Definition 2.18
For \(\alpha \in \rho _S(T) \cap {\mathbb{R}}\not =\emptyset ,\) we define the mapping \(\phi _{\alpha }: \overline{{\mathbb{H}}} \rightarrow \overline{{\mathbb{H}}}\) as
Proposition 2.19
We assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and we set \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Then it is \(\alpha \in \rho _S(T) \cap {\mathbb{R}} \ne \emptyset .\) Let \(\phi _{\alpha }\) defined as above, then the mapping \(f \mapsto f \circ \phi _{\alpha }^{-1}\) is a one-to-one correspondences between \({\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) (resp. \({\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \({\mathcal{S}\mathcal{H}}_L(\sigma _S(A))\) (resp. \({\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T)),\) and between \({\mathcal{N}}({\overline{\sigma }}_S(T))\) and \({\mathcal{N}}(\sigma _S(A)).\) To be precise we have
Proof
It is a consequence of [22, Cor. 5.2.4]. \(\square\)
Definition 2.20
(S-functional for unbounded operators) Let \(T \in {\mathcal{K}\mathcal{C}}(X).\) We assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and we set \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) We suppose that \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) and we consider \(\phi (p)=f(\phi _{\alpha }^{-1}(p))\) as above. We define
We observe that the S-functional calculus for commuting unbounded operators is well defined. This is based on the fact that \(f(T)=\phi ((T-\alpha {\mathcal{I}})^{-1})\) does not depend on \(\alpha ,\) thanks to the following theorem.
Theorem 2.21
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse. Let suppose that \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) and f(T) is the operator defined in (2.5). Let us assume that U is an unbounded slice Cauchy domain such that \(\sigma _S(T) \subset U\) and \({\overline{U}}\) is contained in \({{\textrm{dom}}}(f).\) Then every \(J \in {\mathbb{S}}\) we have
Similarly, if \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T)),\) f(T) is the operator defined in (2.5), and the set U satisfies the same properties as above, we have
To prove the above theorem, it is crucial to recall the relation between the resolvents \(S^{-1}_L(s,T)\) and \(S^{-1}_L(p,A)\) given by the following result, see [27, Thm. 6.12].
Theorem 2.22
Assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse. If \(\phi _{\alpha }\) is defined as (2.4), then \(\phi _{\alpha }({\overline{\sigma }}_S(T))=\sigma _S(A),\) and we have the following identities
where \(S^{-1}_L(p,A)\) is the commutative S-resolvent operator in the unbounded case in Definition 2.16.
Now, we recall the properties of the S-functional calculus for unbounded operators that we need in this paper, see [27, Theorem 6.14].
Theorem 2.23
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse.
-
Let us suppose that f, \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T)).\) For \(a \in {\mathbb{H}}\) we have
$$\begin{aligned} (fa+g)(T)=f(T)a+g(T), \end{aligned}$$ -
Let us assume that \(f \in {\mathcal{N}}({\overline{\sigma }}_S(T))\) and \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) or \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \(g \in {\mathcal{N}}({\overline{\sigma }}_S(T),\) then we have
$$\begin{aligned} (fg)(T)=f(T)g(T). \end{aligned}$$ -
If s, \(q \in \rho _S(T)\) with \(s \notin [q]\) then
$$\begin{aligned} S^{-1}_R(s,T)S^{-1}_L(q,T)= & {} [(S^{-1}_R(s,T)-S^{-1}_L(q,T))q\\{} & {} -{\bar{s}}(S^{-1}_R(s,T)-S^{-1}_L(q,T))](q^2-2s_0q+|s|^2)^{-1}. \end{aligned}$$
The following result puts in relation the commutative pseudo S-resolvent of T with the one of A, see [22, Theorem 8.1.1].
Theorem 2.24
Let us assume that \(T\in {\mathcal{K}\mathcal{C}}(X)\) and that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse. We set \(A\,{:}{=}\,(T-\alpha {\mathcal{I}})^{-1}.\) Then for \(p =\phi _{\alpha }(s)=(s - \alpha )^{-1},\) we have
and
Now, we revise the F-functional calculus for unbounded operators.
Definition 2.25
Let us assume that T belongs to \({\mathcal{K}\mathcal{C}}(X).\) Then for \(s \in \rho _S(T)\), left F-resolvent operator is defined as
and the right F-resolvent operator as
The F-functional calculus for unbounded operators considered in this paper will be based on the following relation between the F-resolvent operators \(F_L(p,A)\) and \(F_{L}(s,T).\) The difference with the definition in [28] is in the powers of the operator \(A {\bar{A}}.\)
Theorem 2.26
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A=(T- \alpha {\mathcal{I}})^{-1}.\) For \(s \in \rho _S(T)\) and \(p=\phi _{\alpha }(s)=(s- \alpha )^{-1},\) we have
Proof
We start by observing that we can write the F-resolvent operator \(F_L(p,A)\) as
By using formula (2.6) and Theorem 2.24 we get
Thanks to the hypothesis on T and consequently on A the operator
does not contain imaginary units as well as
This implies that we can commute \((A{\overline{A}})^{-1}\) with \(p^{-1}\) and its powers since \(p=(s- \alpha )^{-1}.\) Moreover, \((A{\overline{A}})^{-1}\) commutes also with the commutative version of the S-resolvent
Regarding the domains of the operators, we recall that
and
so we have
for all for \(s\in \rho _S(T).\)Then we obtain
This fact is justified by observing that
so the range of \(-4{\mathcal{Q}}_{c,s}(T)^{-1}p^{-3}-F_L(s,T)p^{-4}\) is contained in the domain of \((A {\bar{A}})^{-1}.\) Moreover, the range of \(F_{L}(p,A)\) is contained in the domain of \(A {\bar{A}}.\) With these observations, we can multiply on the left-hand side by \(A {\bar{A}}\) and on the right-hand side by \(p^{4} {\mathcal{I}}\) to get the statement. \(\square\)
Formula (2.7) is suitable to define the F-functional calculus for unbounded operators. It is worth noticing that the above formula gives a definition for the F-functional calculus, slightly different from the customary definition used in the literature, see [22].
Keeping in mind the definition of \(\phi _\alpha\) and its property, see Definition 2.18 and Proposition 2.19, we are in the position to define the F-functional calculus for unbounded operators.
Definition 2.27
(F-functional calculus for unbounded operators) Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A=(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell },\) \(\ell =1,2,3\) have real spectrum. Consider \(\phi _{\alpha }\) as in (2.4). Let f be in \({\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) with \(f(\alpha )=0,\) then we take into account the functions
and the operator \(\breve{f}(T),\) for \(\breve{f}=\Delta f,\) is defined as
where \(\breve{\phi }(A)\) is defined by means of the bounded F-functional calculus. A similar definition holds for \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) with \(f(\alpha )=0.\)
Theorem 2.28
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A=(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell },\) \(\ell =1,2,3\) have real spectrum. Consider \(\phi _{\alpha }\) as in (2.4). Let us assume that \(\breve{f}= \Delta f\) with \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) and \(f(\alpha )=0.\) Then for any unbounded slice Cauchy domain U that contains \(\sigma _S(T),\) \({\overline{U}} \subset {{\textrm{dom}}}(f)\) and \(J \in {\mathbb{S}}.\) The operator \(\breve{f}(T)\) defined in (2.8) satisfies the following integral representation
A similar integral representation holds for \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) with \(f(\alpha )=0.\)
Proof
Taking into account the relation (2.7), the proof follows exactly the same lines of [22, Thm 8.2.3]. \(\square\)
We observe that, like what happens in the S-functional calculus for unbounded operators, even the F-functional calculus for unbounded operators does not depend on the parameter \(\alpha ,\) and the considerations of Remark 2.10 have to be done in the unbounded case as well.
3 Harmonic functional calculus for unbounded operators
It is well known that we can factorize the Laplace operator in terms of the Cauchy–Fueter operator \({{\mathcal{D}}}\) and we have \(\Delta = {{\mathcal{D}}} {{\overline{{\mathcal{D}}}}}= {{\overline{{\mathcal{D}}}}} {{\mathcal{D}}}.\) When we apply the operator \({{\mathcal{D}}}\) or its conjugate \({{\overline{{\mathcal{D}}}}}\) to a slice hyperholomorphic function, we obtain different classes of functions. In this section, we consider the harmonic fine structure in the sense of Definition 1.10, see also [13].
Definition 3.1
(Axially harmonic functions) Let \(U \subset {\mathbb{H}}\) be a slice Cauchy domain. A function \(f: \Omega \rightarrow {\mathbb{H}},\) with \(f \in {\mathcal{C}}^2(\Omega ),\) is said to be axially harmonic if
and if it has the form (1.2) where the functions A and B satisfy the even–odd conditions (1.1), we will denote this function space with the symbol \({\mathcal{A}\mathcal{H}}(\Omega ).\)
When we apply the operator \({{\mathcal{D}}}\) to a slice hyperholomorphic function f(q), as a direct consequence of the Fueter theorem, we get that
This means that the function \({{\mathcal{D}}}f(q)\) is axially harmonic in the sense of Definition 3.1, and therefore the function spaces of the harmonic fine structure are given by the diagram

The aim of this section is to define the unbounded functional calculus for the fine structure (3.1). Before we need to recall the definition of the harmonic functional calculus (or Q-functional calculus) for bounded operators based on the S-spectrum, see [13].
Definition 3.2
Let \(T \in {\mathcal{B}\mathcal{C}}(X),\) assume that the operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum, where one of the \(T_{\ell }\) is the zero operator and set \({\textrm{d}}s_J={\textrm{d}}s(-J)\) for \(J \in {\mathbb{S}}.\) Let U be an arbitrary bounded slice Cauchy domain that contains the S-spectrum, with \({\overline{U}} \subset {{\textrm{dom}}}(f)\) and \(J \in {\mathbb{S}}.\) Let \(f \in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. \(f \in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T))\)), then for any function \(\tilde{f}= {{\mathcal{D}}}f\) (resp. \(\tilde{f}= f {{\mathcal{D}}}\)), we set
Remark 3.3
The independence of the Q-functional calculus from the \(\text{ker}({{\mathcal{D}}})\) is obtained using the monogenic functional calculus of McIntosh. This needs that the operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum and one of the \(T_{\ell }\) has to be zero (see also the proof of Proposition 3.12 for the case of the unbounded operators).
The Q-functional calculus for left (resp. right) slice hyperholomorphic functions is quaternionic right (resp. left) linear. This means that if we consider \(\tilde{f}= {{\mathcal{D}}}f\) and \(\tilde{g}={{\mathcal{D}}}g\) (resp. \(\tilde{f}= f{{\mathcal{D}}}\) and \(\tilde{g}=g{{\mathcal{D}}}\)) with f, \(g \in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. f, \(g \in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T))\) and \(a \in {\mathbb{H}},\) for \(T \in {\mathcal{B}\mathcal{C}}(X)\) we have
In [13], the Q-functional calculus is introduced to get a product rule for the F-functional calculus. Moreover, we study a resolvent equation for this functional calculus suitable to generate the Riesz projectors in this setting and to get the following product rule, see [35].
Theorem 3.4
Let \(T \in {\mathcal{B}\mathcal{C}}(X),\) assume that the operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum, where one of the \(T_{\ell }\) is the zero operator. We assume that \(f \in {\mathcal{N}}(\sigma _S(T))\) and \(g \in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) or \(f \in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T))\) and \(g \in {\mathcal{N}}(\sigma _S(T)),\) then
where \({\underline{T}}\,{:}{=}\, T_1e_1+T_2e_2+T_3e_3\) and where we have written \({{\mathcal{D}}}f\) instead of \(\tilde{f}\) and \({{\mathcal{D}}}g\) instead of \(\tilde{g}\) for the sake of clarity in the product rule.
To introduce the harmonic functional calculus for unbounded operators, we need to use the homeomorphism \(\phi _{\alpha }\) introduced in Definition 2.18 and its properties in Proposition 2.19.
Remark 3.5
Let \(T=T_0+T_1e_1+T_2e_2+T_3e_3\) with commuting components in the sense of Definition 2.12 and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) and \({\overline{T}}- \alpha {\mathcal{I}}\) have bounded inverses and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Then we can write A in terms of its components because it is a bounded operator
and we have
because
so the components are
where we have set
Definition 3.6
(Harmonic functional calculus for unbounded operators) Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero.
For \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\), we define the functions
where \({{\mathcal{D}}}\) is the Cauchy–Fueter operator and \(\phi _{\alpha }\) is as in (2.4). The harmonic functional calculus \(\tilde{f}(T)\) is defined as
where \(\tilde{f}={{\mathcal{D}}}f.\) A similar definition holds for \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T)).\)
We now use the relation between the two commutative pseudo S-resolvent \({\mathcal{Q}}_{c,p}(A)^{-1}\) and \({\mathcal{Q}}_{c,s}(T)^{-1}\) to provide the harmonic functional calculus for unbounded operators an integral formulation.
We can prove that the harmonic functional calculus for unbounded operators is well defined because it does not depend on the point \(\alpha \in \rho _S(T).\) Moreover, we also have to prove that the functional calculus is independent from the kernel of \({{\mathcal{D}}}\) taking slice hyperholomorphic functions.
Theorem 3.7
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero.
For \(\tilde{f}= {{\mathcal{D}}}f\) with \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T)),\) the operator \(\tilde{f}(T)\) defined in (3.5) satisfies
where U is any unbounded slice Cauchy domain with \(\sigma _S(T) \subset U\) and \({\bar{U}} \subset {{\textrm{dom}}}(f)\) and \(J \in {\mathbb{S}}.\) A similar integral representation holds for \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T)).\)
Proof
We assume that \(\alpha \notin U.\) If this is not the case, we can replace the set U with the axially symmetric slice Cauchy domain \(U {\setminus } \overline{B(\alpha )}\) with \(\varepsilon >0\) small enough, without altering the value of the integral (3.6) by the Cauchy integral formula.
We set \(V= \phi _{\alpha }(U).\) This is a bounded slice Cauchy domain that contains \(\sigma _S(A)\) and \({\overline{V}} \subset {{\textrm{dom}}}(f \circ \phi _{\alpha }^{-1}).\) From the relation among \({\mathcal{Q}}_{c,s}(T)^{-1}\) and \({\mathcal{Q}}_{c,p}(A)^{-1},\) see Theorem 2.24, and the changing of variables \(p= \phi _{\alpha }(s)\) we get
\(\square\)
Remark 3.8
Unlike to what happens for the F-functional calculus, we do not require that \(f(\alpha )=0.\)
Before we prove that the Q-functional calculus is well posed, we need the following lemma.
Lemma 3.9
Let assume that f, \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T)).\) Then we have
where c is a constant.
Proof
We observe that since f, \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\), then \(f-g\in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\), so in particular they are of class \({\mathcal{C}}^1.\) By hypothesis, we have that \(f-g\) is a monogenic function that is
where \(P_k(J)\) are suitable polynomials that depend on the angular part \(J\in {\mathbb{S}}\) and A and B are \({\mathbb{H}}\)-valued continuously differentiable functions in \({\mathbb{R}}^2\) in polar coordinates and they are characterized by the Vekua-type system
Monogenic functions of the form (3.7) are called axial monogenic of degree k, see [36]. We observe that the coefficient A of a slice hyperholomorphic function does not depend on \(P_k(J),\) this implies \(k=0\) and so that \(P_0(J)=1.\) Since f, \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\)
also \(A(x_0,r)+J\,B(x_0,r)\) must satisfy the Cauchy–Riemann system. Hence we get \(B=0,\) \(\partial _{x_0}A=0\) and \(\partial _rA=0.\) This implies that A is constant on each connected components. \(\square\)
Remark 3.10
In the sequel, we will always consider the constant c to be different in each connected components of \({\overline{\sigma }}_S(T).\)
Remark 3.11
By similar arguments of Lemma 3.9, it is possible to show, for f, \(g \in {\mathcal{S}\mathcal{H}}_L(\sigma _{S}(T)),\) that
where c is a constant.
Let us consider f, \(f_* \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) such that \({{\mathcal{D}}}(f)= {{\mathcal{D}}}(f_*).\) By Lemma 3.9 we have that \(f_*=f+c.\) In the next result, we show that the harmonic functional calculus is equivalent for f and \(f_*.\)
Proposition 3.12
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero. For every function \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T)),\) the operator \(\tilde{f}(T)\) defined in (3.5) does not depend on the choice of \(\alpha \in {\mathbb{R}}.\) Moreover, if we replace f by \(f+c\) where c is a quaternionic constant, then the Q-functional calculus does not depend on c. A similar consideration holds for the integral representation when \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T)).\)
Proof
The operator defined in (3.5) is independent from the parameter \(\alpha \in {\mathbb{R}}\) since the integral in (3.6) does not depend on \(\alpha .\) For the second part of the statement, let \(f_*=f+c\) and we consider
where we have used the definition of the harmonic functional calculus for bounded operators, see Definition 3.2, and the fact that
The last equality is a consequence of two properties of the F-resolvent operator and Q-resolvent operator. The first property is expressed by the left F-resolvent equation [22, Thm. 7.3.1]
which implies
The second property is that the following integrals are zero:
where \(U_i\)’s, for some \(q\in {\mathbb{N}}\) and \(i=1,\dots , q,\) are the connected components of U. This fact is a consequence of the monogenic functional calculus developed by McIntosh and collaborators (see [41] and [22, Remark 7.1.13 and Lemma 7.4.1]). We can apply this calculus since we are assuming that the operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum and one of the \(T_{\ell }\) is the zero operator. \(\square\)
Remark 3.13
In the hypothesis of the previous theorem, if we consider the constant c the same in all the connected components of U, we can delete the request that one of the \(T_{\ell }\) is the zero operator. Indeed, in this case to prove that
it is sufficient to apply the Cauchy integral theorem for the left slice hyperholomorphic vector-valued function \({\mathcal{Q}}_{c,s}(T)^{-1}.\)
We conclude this section by proving a linearity property and a product rule for the Q-functional calculus for unbounded operators. These arise naturally as consequences of the respective properties of the Q-functional calculus for bounded operators.
Theorem 3.14
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero.
-
(Linearity) If f, \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) and \(a \in {\mathbb{H}},\) then
$$\begin{aligned} (\tilde{f}a+\tilde{g})(T)=\tilde{f}(T)a+\tilde{g}(T). \end{aligned}$$Similarly, if f, \(g \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \(a \in {\mathbb{H}},\) then
$$\begin{aligned} (a\tilde{f}+\tilde{g})(T)=a\tilde{f}(T)+\tilde{g}(T). \end{aligned}$$ -
(Product rule) If \(f \in {\mathcal{N}}({\overline{\sigma }}_S(T))\) and \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) or \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \(g \in {\mathcal{N}}({\overline{\sigma }}_S(T)),\) then
$$\begin{aligned} {{\mathcal{D}}}(fg)(T)= f(T)({{\mathcal{D}}}g)(T)+({{\mathcal{D}}}f)(T) g(T)+ (A {\bar{A}})^{-1}({{\mathcal{D}}}f)(T) {\underline{A}} ({{\mathcal{D}}}g)(T), \end{aligned}$$where \({\underline{A}}\,{:}{=}\, A_1e_1+A_2e_2+A_3e_3.\)
Proof
Let \(\alpha \in \rho _S(T) \cap {\mathbb{R}},\) set \(A= (T- \alpha {\mathcal{I}})^{-1},\) and define \(\phi _{\alpha }\) as in (2.4). By (3.5) and (3.2) we have
The statement for right slice hyperholomorphic functions follows from the second equation of (3.2) and similar arguments.
To show the product rule, we have to use (3.5), (3.3) and (2.5). Since the operator \(A{{\bar{A}}}\) is scalar valued, we get
\(\square\)
Remark 3.15
To obtain polyharmonic functional calculus for unbounded operators, we need to consider the Fueter–Sce’s theorem in the Clifford algebra setting in dimension at least five. In this case, we have factorizations of the Fueter extension that take into account polyharmonic functions of any order.
We conclude this section with a relation among the operators \({\mathcal{Q}}_{c,p}(A)^{-1},\) \({\mathcal{Q}}_{c,s}(T)^{-1}\) and \(S^{-1}_L(s,T)\) that is of independent interest and shows a link between the resolvent operators of the harmonic fine structure.
Proposition 3.16
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) For \(s \in \rho _S(T)\) and \(p=\phi _{\alpha }(s)=(s- \alpha )^{-1},\) we have
Proof
By Theorem 2.24, since we assumed that \(T\in {\mathcal{K}\mathcal{C}}(X)\) and that there exists a point \(\alpha \in \rho _{S}(T)\cap {\mathbb{R}}\not =\emptyset ,\) for \(A\,{:}{=}\,(T-\alpha {\mathcal{I}})^{-1}\) and \(p =\phi _{\alpha }(s),\) we have
So, we have the chain of equalities
and also
Recalling the left S-resolvent operator
and multiplying on the right for \(p^{2}\), we obtain
Taking into account the relation \(p =\phi _{\alpha }(s)\), we get
Multiplying one more time on the right by p, we finally get
The manipulation on A is justified by the fact that it is a bounded operator and the above relation holds for every \(v\in X.\) \(\square\)
4 Polyanalytic functional calculus for unbounded operators
As we have discussed in Sect. 3, although \(\Delta = {{\mathcal{D}}} {{\overline{{\mathcal{D}}}}}={{\overline{{\mathcal{D}}}}} {{\mathcal{D}}} ,\) if we apply the conjugate Cauchy–Fueter operator \({{\overline{{\mathcal{D}}}}}\) to a slice hyperholomorphic function f(q), we get a different set of functions with respect to the harmonic case. In fact, as a direct consequence of the Fueter mapping theorem, we have
So, we obtain a second sequence of function spaces for the quaternionic fine structure

where \({\mathcal{A}\mathcal{P}}_2(\Omega _D)\) is the set of axially polyanalytic functions of order 2.
Definition 4.1
(Axially polyanalytic functions of order 2) Let \(\Omega \subset {\mathbb{H}}\) be an axially symmetric slice domain. A function \(f: \Omega \rightarrow {\mathbb{H}}\) is said to be (left) axially polyanalytic of order 2 if \(f \in {\mathcal{C}}^2(\Omega )\) and
moreover, f has the form (1.2) and the functions A and B satisfy the even–odd conditions (1.1).
We now focus our attention on the polyanalytic functional calculus for unbounded operators of this fine structure. To do this, we need the basic notions for this functional calculus for bounded operators, see [34] for more details.
Definition 4.2
(\(P_2\)-resolvents) Let \(T=T_0+ \sum _{i=1}^3 e_i T_i \in {\mathcal{B}\mathcal{C}}(X),\) \(s \in {\mathbb{H}},\) we define the left (resp. right) \(P_2\)-resolvent operator as
We recall that the polyanalytic functional calculus for bounded operators is also called \(P_2\)-functional calculus.
Definition 4.3
(Polyanalytic functional calculus for bounded operators) Let \(T \in {\mathcal{B}\mathcal{C}}(X),\) assume that the operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum, where one of the \(T_{\ell }\) is the zero operator, and set \({\textrm{d}}s_J={\textrm{d}}s(-J)\) for \(J \in {\mathbb{S}}.\) For every function \(\breve{f}^\circ = {{\overline{{\mathcal{D}}}}} f\) (resp. \(\breve{f}^{\circ }= f {{\overline{{\mathcal{D}}}}}\)) with \(f \in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. \(f \in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T))\)), we define
where \(F_L(s,T)\) (resp. \(F_R(s,T)\)) is the left (resp. right) resolvent operator defined in (2.2).
Remark 4.4
Similarly to the Q-functional calculus and F-functional calculus, the independence of the polyanalytic functional calculus from the \(\text{ker}({{\overline{{\mathcal{D}}}}})\) follows by the monogenic functional calculus of McIntosh. This requires that the operators \(T_{\ell },\) \(\ell =0,1,2,3\) have real spectrum and one of the \(T_{\ell }\) has to be zero.
Remark 4.5
As it happens for other functional calculi based on the S-spectrum, also the polyanalytic functional calculus enjoys a linearity property. If \(\breve{f}^{\circ }= {{\overline{{\mathcal{D}}}}}f\) and \(\breve{g}^{\circ }= {{\overline{{\mathcal{D}}}}} g\) (resp. \(\breve{f}^{\circ }= f{{\overline{{\mathcal{D}}}}}\) and \(\breve{g}^{\circ }=g {{\overline{{\mathcal{D}}}}}\)) with f, \(g \in {\mathcal{S}\mathcal{H}}_L(\sigma _S(T))\) (resp. f, \(g \in {\mathcal{S}\mathcal{H}}_R(\sigma _S(T))\)) and \(a \in {\mathbb{H}}\) then
Considering the transformation from unbounded operators \(T \in {\mathcal{K}\mathcal{C}}(X)\) to bounded operators A defined as \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1},\) we now show a relation between the resolvents \(P_2^L(p,A)\) and \(P_2^{L}(s,T)\) that will lead us to the suitable definition of the \(P_2\)-functional calculus.
Theorem 4.6
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Assume that \(s\in \rho _S(T)\) and \(p=(s-\alpha )^{-1},\) then we have
where (4.3) holds on X.
Proof
By Theorem 2.24 we know that
and from the definition of the left \(P_2\)-resolvent and of the F-resolvent operators, we get
We observe that
Moreover, we recall that \({{\textrm{dom}}}(T)={{\textrm{dom}}}({\overline{T}})\) so
Therefore, for \(s\in \rho _S(T)\), we have
and
Furthermore, we have that
Hence, for \(s\in \rho _S(T)\) and for all\(v\in X\), we get
On \({{\textrm{dom}}}(T^2)\), it is \((A{{\bar{A}}})^{-1}(p{\mathcal{I}}-{{\bar{A}}})=(p{\mathcal{I}}-{{\bar{A}}})(A{{\bar{A}}})^{-1},\) so from the assumption \(p=\Phi _\alpha (s),\) we have \(\alpha =s-p^{-1}\) and
so for all \(v\in {{\textrm{dom}}}(T^2)\), we have
With some computations, we have
which holds on \({{\textrm{dom}}}(T^2).\) By formula (4.5), (4.4) and (4.6), we have
Now, since \((-s{\mathcal{I}}+p{\mathcal{Q}}_{c,s}(T)+T_0)\) and \({\mathcal{Q}}_{c,s}(T)^{-2}\) commute, we have
By multiplying on the right-hand side by \(p^4\), we get the statement. \(\square\)
Remark 4.7
It is possible to prove Theorem 4.6 starting from other two different ways to write the resolvent operator \(P^L_2(p,A).\) The first one is the following
and, the other one is this
To obtain the desired formula, in the first case, it is sufficient to use the relation
while, in the second case, it is sufficient to use the relations: \(S^{-1}_L(p,A)=p^{-1}{\mathcal{I}}-S^{-1}_L(s,T)p^{-2}\) and \({\mathcal{Q}}_{c,p}(A)^{-1}=(A{{\bar{A}}})^{-1}{\mathcal{Q}}_{c,s}(T)^{-1}p^{-2}.\)
Now, we are ready to give a definition for a polyanalytic functional calculus of order 2 for unbounded operators.
Definition 4.8
(Polyanalytic functional calculus of order 2 for unbounded operators) Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero. Assume that \(\phi _\alpha\) is as in (2.4). For \(f\in {\mathcal{S}\mathcal{H}}_L({{\bar{\sigma }}}_S(T))\) with \(f(\alpha )=0\) and \(\partial _{\alpha } f(\alpha )=0,\) we consider the functions
and we define the operator \(\breve{f}^0(T),\) for \(\breve{f}^0= {{\overline{{\mathcal{D}}}}}f,\) as
where \(\breve{\psi }^0(A)\) is defined via the bounded polyanalytic functional calculus. A similar definition holds for \(f\in {\mathcal{S}\mathcal{H}}_R({{\bar{\sigma }}}_S(T))\) with \(f(\alpha )=0\) and \(\partial _{\alpha } f(\alpha )=0.\) It is enough to interchange f with \(\phi _{\alpha }^{-1}.\)
Even for the polyanalytic functional calculus for unbounded operators, we can have an integral representation.
Theorem 4.9
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero. For \(\breve{f}^0={{\overline{{\mathcal{D}}}}}f\) with \(f\in {\mathcal{S}\mathcal{H}}_L({{\bar{\sigma }}}(T))\) with \(f(\alpha )=0\) and \(\partial _{\alpha }f(\alpha )=0,\) the operator defined in (4.7) satisfies
where U is any unbounded slice Cauchy domain with \({{\bar{\sigma }}}_S(T)\subset U\) and \({{\bar{U}}} \subset {{\textrm{dom}}}(f)\) and J is any imaginary unit in \({\mathbb{S}}.\) A similar integral representation holds for \(f\in {\mathcal{S}\mathcal{H}}_R({{\bar{\sigma }}}_S(T))\) with \(f(\alpha )=0\) and \(\partial _{\alpha } f(\alpha )=0.\) It is enough to consider the right resolvent operator and interchange it with the function f.
Proof
We assume that \(\alpha \notin {{\bar{U}}}.\) If this is not the case, we can replace U by the axially symmetric slice Cauchy domain \(U{\setminus } {{\overline{B}}}_{\epsilon }(\alpha )\) with an \(\epsilon >0\) small enough, without altering the value of the integral by the Cauchy integral formula.
The set \(V=\phi _\alpha (U)\) is a bounded slice Cauchy domain with \({{\bar{\sigma }}}_S(T)\subset V\) and \({{\bar{V}}}\subset {\text{dom}}(f\circ \phi _\alpha ^{-1}).\) Using the relation between \(P^L_2(p,A)\) and \(P^L_2(s,T)\) (see formula (4.3)), we have
where we recall that s and p are related by \(p=\phi _{\alpha }(s)=(s- \alpha )^{-1}.\) Now we focus on the left-hand side of the previous equation, we have
We consider the last three terms in the left-hand side of the previous equation. Using the fact that \(p=(s-\alpha )^{-1}\), we get
since the operator \({\bar{T}}\) is closed, it commutes with the integral. Observe that the functions \(s\mapsto s{\mathcal{Q}}_{c,s}(T)^{-1}\) and \(s\mapsto {\mathcal{Q}}_{c,s}(T)^{-1}\) are operator-valued left slice hyperholomorphic, by the vector-valued Cauchy formula [22, see Theorem 2.3.19] we get
By following similar arguments, we get
To work with the last term of (4.10), we need slightly different manipulations
The identity (4.9) turns into
Since by assumption, we have \(f(\alpha )=0\) and \(\partial _{\alpha } f(\alpha )=0,\) we get
and so we get the statement. \(\square\)
Let us consider f, \(f_* \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) such that \({{\overline{{\mathcal{D}}}}}(f)= {{\overline{{\mathcal{D}}}}}(f_{*}).\) Then by Remark 3.11 we have that there exists a constant c such that \(f_*=f+c.\) In the next result, we show that the polyanalytic functional calculus for f and \(f_{*}\) is equivalent.
Proposition 4.10
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero.
For every function \(f \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) with \(f(\alpha )=0\) and \(\partial _{\alpha }f(\alpha )=0,\) the operator \(\breve{f}^0(T)\) defined in (4.7) does not depend on the choice of \(\alpha \in {\mathbb{R}}.\) Moreover, if we replace f by \(f_*=f+c,\) where c is a quaternionic constant, such that \(f_*(\beta )=0\) and \(\partial _{\beta } f_*(\beta )=0,\) for \(\beta \in {\mathbb{R}}.\) Then the \(P_2\)-functional calculus does not depend on c. Similar considerations hold for \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) with \(f(\alpha )=0\) and \(\partial _{\alpha }f(\alpha )=0.\)
Proof
The operator defined in (4.7) is independent from the parameter \(\alpha \in \rho _S(T) \cap {\mathbb{R}}\) since the integral in (4.8) does not depend on \(\alpha .\)
Let us consider \(f_*\,{:}{=}\,f+c,\) where c is a generic quaternion. We suppose that for some \(\beta \in {\mathbb{R}}\), we have \(f_{*}(\beta )=0\) and \(\partial _{\beta }f_{*}(\beta )=0.\) We observe that \(\breve{f}_*^0= \breve{f}^0.\) From the integral representation (4.8), we have
Since \(P_2^L(s,T)=-F_L(s,T)s+T_0 F_{L}(s,T),\) we can prove that:
using the same argument that we considered at the end of Proposition 3.12 to prove equation (3.10). Then we get
This means that we can define \(\breve{f}^0(T)\) by means of \(\beta\) instead of \(\alpha .\) \(\square\)
Remark 4.11
As we observed in Remark 3.13, in the hypothesis of the previous theorem, if the constant c is the same in all the connected components of U, we can delete the request that one of the \(T_{\ell }\) is the zero operator. Indeed, in this case to prove that
it is sufficient to apply the Cauchy integral theorem for the left slice hyperholomorphic vector-valued function \(P^L_2(s,T).\)
Now, we show two important properties for the \(P_2\)-functional calculus for unbounded operators.
Theorem 4.12
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero.
-
(Linearity) If f, \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) and \(a \in {\mathbb{H}},\) then
$$\begin{aligned} (\breve{f}^0a+\breve{g}^0)(T)= \breve{f}^0(T)a+ \breve{g}^0(T). \end{aligned}$$Similarly, if f, \(g \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \(a \in {\mathbb{H}},\) then
$$\begin{aligned} (a\breve{f}^0+\breve{g}^0)(T)= a\breve{f}^0(T)+ \breve{g}^0(T). \end{aligned}$$
Proof
Let us consider \(A= (T- \alpha {\mathcal{I}})^{-1}.\) We recall that \(\phi _{\alpha }\) is defined in (2.4). By (4.7) and (4.2) we have
By similar arguments, it is possible to show the statement for right slice hyperholomorphic functions. \(\square\)
To show the product rule for the unbounded \(P_2\)-functional calculus, we need the following preliminary result.
Proposition 4.13
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) with \(\rho _S(T) \cap {\mathbb{R}} \ne \emptyset .\) Then if s, \(p \in \rho _S(T)\) with \(s \notin [p]\) we have
where \({\underline{T}}\,{:}{=}\,T_1e_1+T_2e_2+T_3e_3.\)
Proof
The result follows by suitably multiplying the S-resolvent equation with the commutative pseudo Cauchy kernel, like in [35, Thm 4.2]. \(\square\)
We need also the following technical result.
Lemma 4.14
Let \(B \in {\mathcal{K}\mathcal{C}}(X).\) If we consider G being an unbounded slice Cauchy domain and \(f \in {\mathcal{N}}({\overline{\sigma }}_S(T))\) with \(f(\infty )=0,\) for \(p \in G\) we have
Proof
The result follows by following similar arguments of [22, Lemma 4.2.1]. \(\square\)
Theorem 4.15
Let \(T \in {\mathcal{K}\mathcal{C}}(X)\) and assume that there exists \(\alpha \in {\mathbb{R}}\) such that \(T- \alpha {\mathcal{I}}\) has bounded inverse and define \(A\,{:}{=}\,(T- \alpha {\mathcal{I}})^{-1}.\) Moreover, suppose that \(T_0=0\) and let the operators \(T_{\ell }\) for \(\ell =1,2,3\) and \(B_j\) for \(j=0,1,2,3\) defined in (3.4), have real spectrum and one of the \(B_j\) is zero. We assume that \(f(\alpha )=0\) and \(\partial _{\alpha }f(\alpha )=0.\) Moreover, we suppose that \(f(\infty )=0.\) If \(f \in {\mathcal{N}}({\overline{\sigma }}_S(T))\) and \(g \in {\mathcal{S}\mathcal{H}}_L({\overline{\sigma }}_S(T))\) or \(f \in {\mathcal{S}\mathcal{H}}_R({\overline{\sigma }}_S(T))\) and \(g \in {\mathcal{N}}({\overline{\sigma }}_S(T)),\) then
Proof
Let \(G_1\) and \(G_2\) be two unbounded slice Cauchy domains such that they contain the S-spectrum. We suppose also that \({\overline{G}}_1 \subset G_2\) and \({\overline{G}}_2 \subset {{\textrm{dom}}}(f) \cap {{\textrm{dom}}}(g).\) We pick \(p \in \partial (G_1 \cap {\mathbb{C}}_J)\) and \(s \in \partial (G_1 \cap {\mathbb{C}}_J).\) From the integral representations of the unbounded \(P_2\) functional calculus, unbounded S -functional calculus and unbounded Q functional calculus, see Theorems 2.21, 3.7 and 4.9, respectively, we have
Now, from the fact that f is intrinsic, formula (4.11), and the Cauchy integral formula, we have
Finally by Lemma 4.14 and Theorem 4.9, we get
\(\square\)
The definition and the properties of the polyanalytic functional calculus can be extended to the case of n-tuples of unbounded operators and for polyanalytic function of greater order. To do this, we need to work with the Fueter’s theorem in the Clifford algebra setting in dimension at least five, because we will have more involved factorizations than the ones considered in (3.1) and (4.1).
5 Concluding remarks
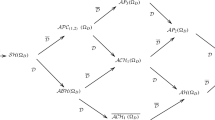
In [13, 34], based on the factorizations (3.1) and (4.1), the authors have studied harmonic and polyanalytic functional calculi based on the S-spectrum. These are based on the integral transforms given in (1.4) and (1.5). The quaternionic fine structures in the cases of bounded and unbounded operators induced by the factorization of the Laplace operator in terms of the Cauchy–Fueter operator and of its conjugate can be globally summarized in the following diagram

We observe that the previous diagram in the Clifford setting is much more involved. Since the Fueter–Sce map is \(T_{F2}= \Delta _{n+1}^{\frac{n-1}{2}},\) with n being an odd number, there are different ways of factorizing \(T_{F2}\) and these give rise to a more complicated fine structures, see [16].
In literature, there is also another way to study a functional calculus for unbounded operators: the so-called direct approach. This is directly based on the Cauchy formula for unbounded domains. For the S-functional calculus and the Riesz–Dunford functional calculus, this is consistent with the approach recalled in this paper in Sects. 1 and 2, see [21, 37]. In a forthcoming paper, we aim to study the unbounded versions of the F-functional calculus, the Q-functional calculus, and the \(P_2\)-functional calculus with the direct approach. Moreover, we aim to show that these approaches are consistent with the ones presented in this paper.
The class of polyanalytic functions is widely studied in literature both in the complex case, see [9], and in the non-commutative setting, see [5, 7, 8, 11]. The motivations to consider this class of functions come from some elasticity problems studied by Kolossov and Muskhelishvili, see [42]. Recently, this class of functions has been also related to the study of some time–frequency problems, see [33, 38]. Moreover, some famous spaces of holomorphic functions have been expanded in the polyanalytic setting, see [4, 45].
In the following table, we summarize the conditions on the slice hyperholomorphic functions given to define the unbounded functional calculi of the quaternionic fine structures:
Functional calculus | Condition |
|---|---|
S-functional | None |
Q-functional | None |
\(P_2\)-functional | \(f(\alpha )=0\) and \(\partial _{\alpha } f(\alpha )=0\) |
F-functional | \(f(\alpha )=0\) |
Data availability
There are no data in our manuscript.
References
Alpay, D., Colombo, F., Kimsey, D.P.: The spectral theorem for quaternionic unbounded normal operators based on the \(S\)-spectrum. J. Math. Phys. 57(2), 023503, 27 (2016)
Alpay, D., Colombo, F., Sabadini, I.: Slice Hyperholomorphic Schur Analysis. Operator Theory: Advances and Applications, vol. 256. Birkhäuser/Springer, Basel (2016)
Alpay, D., Colombo, F., Sabadini, I.: Quaternionic de Branges Spaces and Characteristic Operator Function. SpringerBriefs in Mathematics. Springer, Cham (2020)
Alpay, D., Colombo, F., Diki, K., Sabadini, I.: On a polyanalytic approach to noncommutative de Branges–Rovnyak spaces and Schur analysis. Integral Equ. Oper. Theory 93(4), Paper No. 38, 63 (2021)
Alpay, D., Colombo, F., Diki, K., Sabadini, I.: Poly slice monogenic functions, Cauchy formulas and the PS-functional calculus. J. Oper. Theory 88(8), 309–364 (2022)
Alpay, D., Colombo, F., Qian, T., Sabadini, I.: The \(H^\infty\) functional calculus based on the \(S\)-spectrum for quaternionic operators and for \(n\)-tuples of noncommuting operators. J. Funct. Anal. 271(6), 1544–1584 (2016)
Alpay, D., Diki, K., Sabadini, I.: Correction to: On slice polyanalytic functions of a quaternionic variable. Results Math. 76(2), Paper No. 84, 4 (2021)
Alpay, D., Diki, K., Sabadini, I.: On slice polyanalytic functions of a quaternionic variable. Results Math. 74(1), Paper No. 17, 25 (2019)
Balk, M.B.: Polyanalytic Functions. Mathematical Research, vol. 63. Akademie-Verlag, Berlin (1991)
Birkhoff, G., von Neumann, J.: The logic of quantum mechanics. Ann. Math. (2) 37(4), 823–843 (1936)
Brackx, F.: On \((k)\)-monogenic functions of a quaternion variable. In: Research Notes in Mathematics, vol. 8 pp. 22–44. Pitman Publishing, London-San Francisco, Calif.-Melbourne (1976)
Cerejeiras, P., Colombo, F., Kähler, U., Sabadini, I.: Perturbation of normal quaternionic operators. Trans. Am. Math. Soc. 372(5), 3257–3281 (2019)
Colombo, F., De Martino, A., Pinton, S., Sabadini, I.: Axially harmonic functions and the harmonic functional calculus on the \(S\)-spectrum. J. Geom. Anal. 33(2), 52 (2023)
Colombo, F., De Martino, A., Sabadini, I.: The \({\cal{F}}\)-resolvent equation and Riesz projectors for the \({\cal{F}}\)-functional calculus. Complex Anal. Oper. Theory 17(2), 42 (2023)
Colombo, F., De Martino, A., Sabadini, I.: Towards a general \(F\)-resolvent equation and Riesz projectors. J. Math. Anal. Appl. 517(2), 126652 (2023)
Colombo, F., De Martino, A., Pinton, S., Sabadini, I.: The fine structure of the spectral theory on the \(S\)-spectrum in dimension five. J. Geom. Anal. 33(9), 300 (2023)
Colombo, F., González, D. Deniz, Pinton, S.: Fractional powers of vector operators with first order boundary conditions. J. Geom. Phys. 151, 103618, 18 (2020)
Colombo, F., González, D. Deniz, Pinton, S.: The noncommutative fractional Fourier law in bounded and unbounded domains. Complex Anal. Oper. Theory 15(7), Paper No. 114, 27 (2021)
Colombo, F., Gantner, J.: Formulations of the \({F}\)-functional calculus and some consequences. Proc. R. Soc. Edinb. Sect. A 146(3), 509–545 (2016)
Colombo, F., Gantner, J.: An application of the \(S\)-functional calculus to fractional diffusion processes. Milan J. Math. 86(2), 225–303 (2018)
Colombo, F., Gantner, J.: Quaternionic Closed Operators, Fractional Powers and Fractional Diffusion Processes. Operator Theory: Advances and Applications, vol. 274. Birkhäuser/Springer, Cham (2019)
Colombo, F., Gantner, J., Kimsey, D.P.: Spectral Theory on the S-Spectrum for Quaternionic Operators. Operator Theory: Advances and Applications, vol. 270. Birkhäuser/Springer, Cham (2018)
Colombo, F., Gantner, J., Kimsey, D. P., Sabadini, I.: Universality property of the S-functional calculus, noncommuting matrix variables and Clifford operators. Adv. Math. 410, 39 (2022)
Colombo, F., Kimsey, D.P.: The spectral theorem for normal operators on a Clifford module. Anal. Math. Phys. 12(1), Paper No. 25, 92 (2022)
Colombo, F., Kimsey, D.P., Pinton, S., Sabadini, I.: Slice monogenic functions of a Clifford variable via the S-functional calculus. Proc. Am. Math. Soc. Ser. B 8, 281–296 (2021)
Colombo, F., Peloso, M.M., Pinton, S.: The structure of the fractional powers of the noncommutative Fourier law. Math. Methods Appl. Sci. 42(18), 6259–6276 (2019)
Colombo, F., Sabadini, I.: The \({\cal{F} }\)-spectrum and the \({\cal{SC}}\)-functional calculus. Proc. R. Soc. Edinb. Sect. A 142(3), 479–500 (2012)
Colombo, F., Sabadini, I.: The \(F\)-functional calculus for unbounded operators. J. Geom. Phys. 86, 392–407 (2014)
Colombo, F., Sabadini, I., Sommen, F.: The Fueter mapping theorem in integral form and the \(F\)-functional calculus. Math. Methods Appl. Sci. 33(17), 2050–2066 (2010)
Colombo, F., Sabadini, I., Struppa, D.C.: Michele Sce’s Works in Hypercomplex Analysis—A Translation with Commentaries. Birkhäuser/Springer, Cham (2020)
Colombo, F., Sabadini, I., Struppa, D.C.: Noncommutative Functional Calculus: Theory and Applications of Slice Hyperholomorphic Functions. Progress in Mathematics, vol. 289. Birkhäuser/Springer Basel AG, Basel (2011)
Colombo, F., Sabadini, I., Struppa, D.C.: A new functional calculus for noncommuting operators. J. Funct. Anal. 254(8), 2255–2274 (2008)
De Martino, A., Diki, K.: On the polyanalytic short-time Fourier transform in the quaternionic setting. Commun. Pure Appl. Anal. 21(11), 3629–3665 (2022)
De Martino, A., Pinton, S.: A polyanalytic functional calculus of order 2 on the \(S\)-spectrum. Proc. Am. Math. Soc. 151(6), 2471–2488 (2023)
De Martino, A., Pinton, S.: Properties of a polyanalytic functional calculus on the \(S\)-spectrum. Math. Nachr. (2023). https://doi.org/10.1002/mana.202200318
Delanghe, R., Sommen, F., Souček, V.: Clifford Algebra and Spinor-Valued Functions. Mathematics and Its Applications, vol. 53. Kluwer Academic Publishers Group, Dordrecht (1992)
Dunford, N., Schwartz, J.: Linear Operators, Part I: General Theory. Wiley, Hoboken (1988)
Feichtinger, H.G., Abreu, L.D.: Function spaces of polyanalytic functions. In: Harmonic and Complex Analysis and Its Applications. Trends in Mathematics, pp. 1–38. Birkhäuser/Springer, Cham (2014)
Fueter, R.: Die Funktionentheorie der Differentialgleichungen \(\Delta u=0\) und \(\Delta \Delta u=0\) mit vier reellen Variablen. Comment. Math. Helv. 7(1), 307–330 (1934)
Jefferies, B.: Spectral Properties of Noncommuting Operators. Lecture Notes in Mathematics, vol. 1843. Springer, Berlin (2004)
Jefferies, B., McIntosh, A., Picton-Warlow, J.: The monogenic functional calculus. Stud. Math. 136, 99–119 (1999)
Muskhelishvili, N.I.: Some Basic Problems of the Mathematical Theory of Elasticity, English edn. Noordhoff International Publishing, Leiden (1977). Fundamental equations, plane theory of elasticity, torsion and bending, Translated from the fourth, corrected and augmented Russian edition by J. R. M. Radok
Qian, T.: Generalization of Fueter’s result to \({ R}^{n+1}\). Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 8(2), 111–117 (1997)
Sce, M.: Osservazioni sulle serie di potenze nei moduli quadratici. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. (8) 23, 220–225 (1957)
Vasilevski, N.L.: On the structure of Bergman and poly-Bergman spaces. Integral Equ. Oper. Theory 33(4), 471–488 (1999)
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Communicated by Raul Curto.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Colombo, F., De Martino, A. & Pinton, S. Harmonic and polyanalytic functional calculi on the S-spectrum for unbounded operators. Banach J. Math. Anal. 17, 84 (2023). https://doi.org/10.1007/s43037-023-00304-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43037-023-00304-y