A System of Hamilton-Jacobi Equations Characterizing Geodesic Centroidal Tessellations

Abstract

We introduce a class of systems of Hamilton-Jacobi equations characterizing geodesic centroidal tessellations, i.e., tessellations of domains with respect to geodesic distances where generators and centroids coincide. Typical examples are given by geodesic centroidal Voronoi tessellations and geodesic centroidal power diagrams. An appropriate version of the Fast Marching method on unstructured grids allows computing the solution of the Hamilton-Jacobi system and, therefore, the associated tessellations. We propose various numerical examples to illustrate the features of the technique.

1 Introduction

A partition, or tessellation, of a set $\varOmega$ is a collection of mutually disjoint subsets $\varOmega _k\subset \varOmega$, $k=1,\cdots ,K$, such that $\cup _{k=1}^K \varOmega _k=\varOmega$. A classical model is the Voronoi tessellation and, in this case, the sets $\varOmega _k$ are called Voronoi diagrams. Tessellations and other similar families of geometric objects arise in several applications, ranging from graphic design, astronomy, clustering, geometric modelling, data analysis, resource optimization, quadrature formulas and discrete integration, sensor networks, numerical methods for partial differential equations (PDEs) (see [6, 23]).

Partitions and tessellations are frequently associated with objective functionals, defining desired additional properties to be satisfied. A well-known example is the K-means problem in cluster analysis (see [9, 25]), which aims to subdivide a data set into K clusters such that each data point belongs to the cluster with the nearest cluster center. Minima of the K-means functional result in a partitioning of the data in centroidal Voronoi diagrams, i.e., Voronoi diagrams for which generators and centroids coincide (see [14]). In other applications, the size of the cells is prescribed (capacity-constrained problem), and the partition of $\varOmega$ is given by another generalization of Voronoi diagrams, called power diagrams [5, 10].

Algorithms for the computation of centroidal Voronoi tessellations in the Euclidean case, such as the Lloyd algorithm, exploit geometric properties of the problem to rapidly converge to a solution [1, 28]. The case of geodesic Voronoi tessellation, i.e., tessellation with respect to a general convex metric, presents additional difficulties both in the computation of Voronoi diagrams and in that of the corresponding centroids [21, 22, 24].

In this work, we introduce a PDE method for the computation of the geodesic Voronoi tessellation. Given a density function $\rho$ supported in a bounded set $\varOmega$, representing the distribution of a data set, the aim is to subdivide the data points into K clusters defined by a convex metric $d_C$. As a prototype of the approach, shown in the simple case of the Euclidean distance, we consider the system of first-order Hamilton-Jacobi (HJ) equations

$$\begin{aligned} \left\{ \begin{array}{ll} \vert Du_k\vert = 1,\quad x\in \mathbb {R}^d,\, k=1,\cdots ,K, \\ u_k( \mu _k)=0,\\ S_u^k= \left\{x\in \mathbb {R}^d{:}\,u_k(x)=\min\limits_{j=1,\cdots ,K} u_{j}(x)\right\}, \\ \mu _{k}=\frac{\int _{S_u^k }x \rho (x){\text{d}}x}{\int _{S_u^k}\rho (x){\text{d}}x}. \end{array} \right. \end{aligned}$$

(1)

We show that the family $\{S_u^k\}_{k=1}^K$ defined by (1) corresponds to a critical point of the K-means functional, hence to a centroidal Voronoi tessellation of $\varOmega$ with centroids $\mu _k$; vice versa, each critical point of the K-means functional corresponds to a solution $u=(u_1,\cdots ,u_K)$ of the previous system. Moreover, a system of HJ equations similar to (1) provides a way to compute the optimal weights for the capacity-constrained problem, which aims to find a geodesic centroidal tessellation of the domain with regions of a given area. This problem arises in several applications in economy, and it is connected with the so-called semi-discrete Optimal Transport problem [20].

It is well known that the hard clustering K-means problem can be seen as the limit of the soft clustering Gaussian mixture model when the variance parameter goes to 0 (see [8]). Relying on this observation, we provide an interpretation of system (1) as the vanishing viscosity limit of a multi-population Mean Field Games (MFGs) system introduced in [3] to characterize the parameters of a Gaussian mixture model maximizing a log-likelihood functional. To solve the system (1) we consider an iterative method similar to the Lloyd algorithm [9]. At each step, given the generators of the tessellation computed in the previous step, we compute the Voronoi diagrams solving the HJ equations via a Fast Marching technique. Then, we compute the new generators and we iterate. As we discuss later, smart management of the data and the use of acceleration techniques may considerably speed up the process.

The paper is organized as follows. In Sect. 2, we introduce an HJ system approach to the hard-clustering problem and geodesic centroidal Voronoi tessellations. In Sect. 3, we consider a system of HJ equations to characterize centroidal power diagrams, a generalization of centroidal Voronoi tessellations where the measure of the cells is prescribed. In Sect. 4, we provide an interpretation of the HJ system in terms of the MFG theory. In Sect. 5, we discuss the numerical approximation of the HJ systems introduced in the previous sections and we provide several examples. In Sect. 6, we summarize the results presented in the paper and we outline some prospects for future research.

2 Geodesic Voronoi Tessellations and HJ Equations

In this section, we introduce a class of geodesic distance, the corresponding K-means problem and its characterization via a system of HJ equations. Consider a set-valued map $x\mapsto C(x)\subset \mathbb {R}^d$ and assume that

• (i) for each $x\in \mathbb {R}^d$, C(x) is a compact, convex set and $0\in C(x)$;

• (ii) there exists $L>0$ such that $d_{{{\mathcal {H}}}}(C(x),C(y))\leqslant L\vert x-y\vert$ for all $x,y\in \mathbb {R}^d$;

• (iii) there exists $\delta >0$ such $B(0,\delta )\subset C(x)$ for any $x\in \mathbb {R}^d$,

where $d_{{{\mathcal {H}}}}$ denotes the Hausdorff distance, i.e., for two sets A, $B\subset \mathbb {R}^d,$

$$\begin{aligned} d_{{{\mathcal {H}}}}(A,B)=\max \left\{ \sup _{x\in B}d(x,A), \sup _{y\in A}d(y,B)\right\} . \end{aligned}$$

For $x,y\in \mathbb {R}^d$, let ${{\mathcal {F}}}_{x,y}$ be the set of all the trajectories $X(\cdot )$ defined by the differential inclusion

$$\dot{X}(t)\in C(X(t)), \, X(0)=x,\,X(T)=y$$

for some $T=T(X(\cdot ))>0$. Note that, because of the assumptions on the map C(x), ${{\mathcal {F}}}_{x,y}$ is not empty. The function $d_C{:}\,\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}$, defined by

$$\begin{aligned} d_C(x,y)=\inf _{{{\mathcal {F}}}_{x,y}} T(X(\cdot )), \end{aligned}$$

(2)

is a distance function, equivalent to the Euclidean distance (see [11]). Some examples of distance $d_C$ are provided at the end of this section, see Remark 3.

We introduce the K-means problem for the geodesic distance $d_C$. Let $\varOmega$ be a bounded subset of $\mathbb {R}^d$ and $\rho$ a density function supported in $\varOmega$, i.e., $\rho \geqslant 0$ and $\int _{\varOmega } \rho {\text{d}}x=1$, representing the distribution of the points of a given data set ${\mathcal {X}}$. The K-means problem for the distance $d_C$ aims to minimize the functional

$$\begin{aligned} \begin{aligned}&{{\mathcal {I}}}_{C}(y_1,\cdots ,y_k)=\sum _{k=1}^K\int _{V(y_k)}d_C(x,y_k)^2\rho (x){\text{d}}x,\\&\text {where }\quad V(y_k)=\left\{x\in \mathbb {R}^d{:}\,d_C( y_k,x)=\min _{j=1,\cdots ,K}d_C( y_j,x)\right\}. \end{aligned} \end{aligned}$$

(3)

A minimum of the functional ${{\mathcal {I}}}_{C}$ provides a clusterization of the data set, i.e., a repartition of ${\mathcal {X}}$ into K disjoint clusters $V(y_k)$ such that each data point belongs to the cluster with the smallest distance from centroid $y_k$. This property can be expressed in the elegant terminology of the geodesic centroidal Voronoi tessellations (see [13, 14, 22]). Given a set of generators $\{y_k\}_{k=1}^K$, $y_k\in \overline{\varOmega }$, we define a geodesic Voronoi tessellation of $\varOmega$ as the union of the geodesic Voronoi diagrams

$$\begin{aligned} V(y_k)=\left\{x\in \varOmega {:} \,d_C(x,y_k)=\min _{j=1,\cdots ,K} d_C(x,y_j)\right\} \end{aligned}$$

(4)

(a point of $V(y_k)\cap V(y_j)$ is assigned to the diagram with the smaller index).

Definition 1

A geodesic Voronoi tessellation $\{V(y_k)\}_{k=1}^K$ of $\varOmega$ is said to be a geodesic centroidal Voronoi tessellation (GCVT) if, for each $k=1,\cdots ,K$, the generator $y_k$ of $V(y_k)$ coincides with the centroid of $V(y_k)$, i.e.,

$$\begin{aligned} \int _{V(y_k)}\rho (x)d_C(y_k,x){\text{d}}x=\min _{z\in V(y_k)}\int _{V(y_k)}\rho (x)d_C(z,x){\text{d}}x. \end{aligned}$$

(5)

Remark 1

If $C(x)=B(0,1)$ for each $x\in \mathbb {R}^d$, then $d_C$ coincides with the Euclidean distance and (3) is the classical K-means problem (see [13]). In this case, $\{V(y_k)\}_k$ is called a centroidal Voronoi tessellation (CVT) and the centroids are given by

$$\begin{aligned} y_k=\frac{\int _{V(y_k)} s\rho (s){\text{d}}s}{\int _{V(y_k)} \rho (s){\text{d}}s}. \end{aligned}$$

(6)

Since $\varOmega$ is bounded and ${{\mathcal {I}}}_{C}$ is continuous, a global minimum of the functional (3) exists; but, since ${{\mathcal {I}}}_{C}$ is in general nonconvex, local minimums may also exist. In [22, Theorem 1], it is proved that the previous functional is continuous and

$$\begin{aligned} \text {critical points of } {{\mathcal {I}}}_{C} \text { correspond to GCVTs of } \varOmega . \end{aligned}$$

(7)

Critical points of ${{\mathcal {I}}}_{C}$ can be computed via the Lloyd algorithm, a simple two steps iterative procedure. Starting from an arbitrary initial set of generators, at each iteration the following two steps are performed:

• given the set of generators $\{y_k\}_{k=1}^K$ at the previous step, construct the Geodesic Voronoi tessellation $\{V(y_k)\}_{k=1}^K$ as in (4);

• take the centroids of $\{V(y_k)\}_{k=1}^K$ as the new set of generators and iterate.

The procedure is repeated until an appropriate stopping criterion is met. At each iteration, the objective function ${{\mathcal {I}}}_{C}$ decreases and the algorithm converges to a (local) minimum of (3) (see [13, Theorem 2.3] in the Euclidean case and [22] in the general case).

In order to introduce a PDE characterization of GCVT, we associate to the distance $d_C$ a Hamiltonian $H{:}\,\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}$ defined as the support function of the convex set C, i.e.,

$$\begin{aligned} H(x,p)=\sup _{q\in C(x)}p\cdot q. \end{aligned}$$

(8)

Then, $H{:}\,\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}$ is a continuous function and satisfies the following properties:

• (i) $H(x,0)=0$, $H(x,p)\geqslant 0$ for $p\in \mathbb {R}^d$;

• (ii) H(x, p) is convex and is positive homogeneous in p, i.e., for $\lambda >0$, $H(x,\lambda p)=\lambda H(x,p);$

• (iii) $\vert H(x,p)-H(y,p)\vert \leqslant L\vert x-y\vert (1+\vert p\vert )$ for $x,y\in \mathbb {R}^d$.

Moreover, for any $y\in \mathbb {R}^d$, the function $u{:} \, \mathbb {R}^d\rightarrow \mathbb {R}$, defined by $u(x)=d_C(y,x)$, is the unique viscosity solution (see [7] for the definition) of the problem

$$\begin{aligned} \left\{ \begin{array}{ll} H(x,Du)= 1,\quad x\in \mathbb {R}^d, \\ u(y)=0.\\ \end{array} \right. \end{aligned}$$

(9)

We characterize GCVTs of $\varOmega$ via the following system of HJ equations:

$$\begin{aligned} \left\{ \begin{array}{ll} H(x,Du_k)=1, \\ u_k( \mu _k)=0,\\ S_u^k= \left\{x\in \mathbb {R}^d{:}\,u_k(x)=\min\limits_{j=1,\cdots ,K} u_{j}(x)\right\}, \\ \int _{S^k_u}\rho (x)u_k(x){\text{d}}x=\min \left\{\int _{S^k_u}\rho (x)u_y(x){\text{d}}x{:}\,u_y \text { solution of }(9) \text { with }y\in S^k_u\right\} \end{array} \right. \end{aligned}$$

(10)

for $k=1,\cdots , K$. Recall that the unique solution of (9) is given by $u(x)=d_C( y,x)$, hence $u_k(x)=d_C(\mu _k,x)$. Furthermore, the last condition in (10), see also (5), implies that the points $\mu _k$ are the centroids of the sets $S^k_u$ with respect to the metric $d_C$. On the other hand, the HJ equations are coupled via the points $\mu _1,\cdots ,\mu _k$ which are the centroids of the sets $S^k_u$, $k=1,\cdots ,K$ and therefore, they are unknown. Indeed, the true unknowns in system (10) are the points $\mu _k$, $k=1,\cdots ,K$, since they determine the functions $u_k$ as viscosity solutions of the corresponding HJ equations and consequently the diagrams $S^k_u$.

Remark 2

If $C(x)=B(0,1)$, then $d_C$ is the Euclidean distance, see Remark 1. In this case, $H(x,p)= \vert p\vert$ and (10) coincides with (1). In Sect. 4, we will explain that the latter system can be deduced by passing to the vanishing viscosity limit in a second order system characterizing the optimal parameters for a Gaussian mixtures model in soft clustering analysis.

We now show that system (10) characterizes critical points of the functional (3) or, equivalently, GCVTs of the set $\varOmega$.

Theorem 1

The following conditions are equivalent.

• (i) Let $(y_1,\cdots ,y_K)$ be a critical point of the functional ${{\mathcal {I}}}_{C}$ in (3) with geodesic Voronoi diagrams $V(y_k)$. Then, there exists a solution of (10) such that $\mu _k=y_k$ and $S_u^k=V(y_k).$

• (ii) Given a solution $u=(u_1,\cdots ,u_K)$ of (10), then $(\mu _1,\cdots ,\mu _K)$ is a critical point of ${{\mathcal {I}}}_{C}$ with geodesic Voronoi diagrams $V(y_k)=S_u^k$.

Proof

Assume that $(y_1,\cdots ,y_K)$ is a critical point of the functional ${{\mathcal {I}}}_{C}$, hence $V(y_k)$ defined as in (4) is a GCVT and

$$\begin{aligned} \int _{V(y_k)}\rho (x)d_C(y_k,x){\text{d}}x=\min _{z\in V(y_k)}\int _{V(y_k)}\rho (x)d_C(z,x){\text{d}}x, \qquad \forall k=1, \cdots , K. \end{aligned}$$

(11)

Define $u=(u_1,\cdots ,u_K)$, $\mu =(\mu _1,\cdots , \mu _k)$ by

$$\begin{aligned} u_{k}(x)= d_C(y_k,x), \qquad \mu _k=y_k, \quad k=1,\cdots ,K. \end{aligned}$$

(12)

Then, $u=(u_1,\cdots ,u_K)$ is a solution of the HJ equations in (10) with $\mu _k=y_k$. Moreover, by (3), we have that $S_u^k=V(y_k)$ and therefore (11) is equivalent to

$$\begin{aligned} \int _{S^k_u}\rho (x)u_k(x){\text{d}}x=\min \left\{ \int _{S^k_u}\rho (x)u_z(x){\text{d}}x{:} \, u_z \text { solution of }(9) \text { with }z\in S^k_u\right\} . \end{aligned}$$

We conclude that $u=(u_1,\cdots ,u_K)$ and $\mu =(\mu _1,\cdots , \mu _k)$ in (12) give a solution of (10).

Now assume that $u=(u_1,\cdots ,u_K)$, $\mu =(\mu _1,\cdots , \mu _k)$ is a solution of (10) and set $y_k=\mu _k$, $k=1,\cdots , K$. Then, defined $V(y_k)$ as in (3), we have $V(y_k)=S_u^k$. Moreover, taking into account that $u_{k}(x)= d_C(\mu _k,x)$ and $\mu _k$ are characterized by

$$\begin{aligned} \int _{S^k_u}\rho (x)u_k(x){\text{d}}x=\min \left\{ \int _{S^k_u}\rho (x)u_y(x){\text{d}}x{:} \, u_y \text { solution of }(9) \text { with }y\in S^k_u\right\}, \end{aligned}$$

we also have that $y_k$ satisfies (5). Therefore, $V_k$, $k=1,\cdots , K$, is a GCVT and, by (7), $y_k$, $k=1,\cdots , K$, a minimum of ${{\mathcal {I}}}_{C}$.

The previous result can be restated in the terminology of the Voronoi tessellation, saying that a solution of the system (10) determine a GCVT and vice versa. We have the following existence result for (10).

Corollary 1

Let $\rho$ be a positive and smooth density function defined on a smooth bounded set $\varOmega$. Then, there exists a solution to (10).

Proof

The statement is an immediate consequence of existence of critical points for the functional ${{\mathcal {I}}}_{C}$ and the equivalence result provided by Theorem 1.

Remark 3

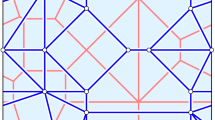
We give some examples of the geodesic distance $d_C$ and the corresponding Hamiltonian H (see also Fig. 1):

• (i) if $C(x)=\{p\in \mathbb {R}^d{:}\,\Vert p\Vert _s:=(\sum _{i=1}^d\vert p_i\vert ^s)^{1/s}\leqslant 1\}$ for $s>1$, then $d_C$ is the Minkowski distance $d_C(x,y)= \Vert x-y\Vert _s$ and $H(x,p)=\vert p\vert ^2/\Vert p\Vert _s$;

• (ii) if $C(x)=a(x)B(0,1)$, where $a(x)\geqslant \delta >0$, then $H(x,p)=a(x)\vert p\vert$. In particular, the Euclidean case corresponds to $a(x)\equiv 1$;

• (iii) if $C(x)=A(x)^{1/2}B(0,1)$, where A is a positive definite matrix such that $A(x)\xi \cdot \xi \geqslant \delta >0$ for $\xi \in \mathbb {R}^d$, then $d_C$ is the Riemannian distance induced by the matrix A on $\mathbb {R}^d$ and $H(x,p)=\sqrt{A(x)p\cdot p}$.

Moreover, it is possible to consider the distance function corresponding to a Hamiltonian H defined by

$$\begin{aligned}H(x,p)=\max \{H_1(x,p),\cdots ,H_N(x,p)\},\end{aligned}$$

where $H_n$, $n=1,\cdots ,N$ are Hamiltonians of the types above.

Fig. 1

Unitary balls for the Minkowski distance for various values of s (left) and a Riemann distance induced by $A(x,y)=\left( (R+r\cos y)^2, 0; \, 0, r^2 \right)$ for $R=1$, $r=0.5$, corresponding to parametrization of a unitary torus in $\mathbb {R}^3$ (cf. Test 4)

3 A System of HJ Equations for Geodesic Centroidal Power Diagrams

In this section, we consider a generalization of centroidal Voronoi diagrams, called centroidal power diagrams. We first introduce the definition of power diagrams, or weighted Voronoi diagrams, then describe centroidal power diagrams and a system of HJ equations that can be used to compute them. Consider the distance $d_C$ defined as in (2). Given a set of K distinct points $\{y_i\}_{i=1}^K$ in $\varOmega$ and K real numbers $\{w_i\}_{i=1}^K$, the geodesic power diagrams generated by the couples $(y_i,w_i)$ are defined by

$$\begin{aligned} V(y_k,w_k)=\left\{x\in \varOmega {:} \,d_C(x,y_k)-w_k=\min _{j=1,\cdots ,K}(d_C(x,y_j)-w_j)\right\}. \end{aligned}$$

(13)

As Voronoi diagrams, power diagrams provide a tessellation of the domain $\varOmega$, i.e., ${V(y_i,w_i)}^{\mathrm {o}}\cap {V(y_j,w_j)}^{\mathrm {o}}=\varnothing$ for $i\ne j$ and ${\bigcup\limits_{i=1}^K} V(y_i,w_i) =\overline{\varOmega }$. Note that, whereas Voronoi diagrams are always nonempty, some of the power diagrams may be empty and the corresponding generators belong to another diagram. Power diagrams reduce to Voronoi diagrams if the weights $w_i$ coincide, but they have an additional tuning parameter, the weights vector $w=(w_1,\cdots ,w_k)$, which allows to impose additional constraints on the resulting tessellation. A typical application of power diagrams is the problem of partitioning a given set in a capacity constrained manner (see [5]). Given a density function $\rho$ supported in $\varOmega$ and K distinct points $\{y_i\}_{i=1}^K$ in $\varOmega$, consider the measure $\pi ({\text{d}}x)=\rho (x){\text{d}}x$ and, to each point $y_i$, associate a cost $c_i>0$ with the property that $\sum _{i=1}^Kc_i=\pi (\varOmega )$. For a partition of $\varOmega$ in a family of K subsets $R_i$, define the cost of each subset as $\pi (R_i)=:\int _{R_i}d_C(x,y_i)\,\pi ({\text{d}}x)$. The aim is to find a partition $\{R_i\}_{i=1}^K$ of $\varOmega$ such that the total cost

$$\begin{aligned} Q(R_1,\cdots ,R_K)=\sum _{i=1}^K\int _{R_i}d_C(x,y_i)\pi ({\text{d}}x) \end{aligned}$$

is minimized under the constraint $\pi (R_i)=c_i$. In [29, Theorem 1], it is shown that the minimum of the previous functional exists and it is reached by a geodesic power diagram generated by the couples $(y_k,w_k)$, $k=1,\cdots ,K$, where the unknown weights $w_k$ can be found by maximizing the concave functional

$$\begin{aligned} {{\mathcal {F}}}(w_1,\cdots ,w_k)=\sum _{i=1}^K\int _{V(y_i,w_i)}d_C(x,y_k)\rho (x){\text{d}}x-\sum _{i=1}^kw_i( \pi (V(y_i,w_i))-c_i). \end{aligned}$$

(14)

The gradient of ${{\mathcal {F}}}$ is given by

$$\begin{aligned} \frac{\partial {{\mathcal {F}}}}{\partial w_i}=c_i- \pi (V(y_i,w_i)) \end{aligned}$$

and, if $(w_1,\cdots ,w_k)$ is a critical point of ${{\mathcal {F}}}$, then the power diagram generated by the couples $(y_i,w_i)$ satisfies the capacity constraint $\pi (V(y_i,w_i))=c_i$. Algorithms to compute critical points of (14) are described in [12, 20].

We consider geodesic centroidal power diagrams, i.e., geodesic power diagram for which generators coincide with the corresponding centroids. Indeed, it has been observed that the use of centroidal power diagrams in the capacity constrained partitioning problem avoid generating irregular or elongated cells (see [10, 29]).

Definition 2

A geodesic power diagram tessellation $\{V(y_i,w_i)\}_{i=1}^K$ of $\varOmega$ is said to be a geodesic centroidal power diagram tessellation if, for each $i=1,\cdots ,K$, the generator $y_i$ of $V(y_i,w_i)$ coincides with the centroid of $V(y_i,w_i)$, i.e.,

$$\begin{aligned}\int _{V(y_k,w_k)}\rho (x)d_C(y_k,x){\text{d}}x=\min _{z\in V(y_k,w_k)}\int _{V(y_k,w_k)}\rho (x)d_C(z,x){\text{d}}x.\end{aligned}$$

In [29], geodesic centroidal power diagrams satisfying the capacity constraints $\pi (V(y_k,w_k))=c_k$ are characterized as a saddle point of the functional

$$\begin{aligned} {{\mathcal {G}}}(y_1,\cdots ,y_k,w_1,\cdots ,w_k)=&\sum _{i=1}^K\int _{V(y_i,w_i)}d_C(x,y_i)\rho (x){\text{d}}x\\&-\sum _{i=1}^kw_i( \pi (V(y_i,w_i))-c_i). \end{aligned}$$

Note that the previous functional is similar to one defined in (14), but it depends also on the generators $(y_1,\cdots ,y_k)$. For $(y_1,\cdots ,y_k)$ fixed, ${{\mathcal {G}}}$ is concave with respect to $w=(w_1,\cdots ,w_K)$ and therefore it admits a maximizer which determine a power diagram $\{V(y_i,w_i)\}_{i=1}^K$. For $(w_1,\cdots ,w_k)$ realizing the capacity constraints $\pi (V(y_i,w_i))=c_i$, ${{\mathcal {G}}}$ coincides with the functional ${{\mathcal {I}}}_{C}$ in (3), hence it is minimized by the centroids of sets $\{V(y_i,w_i)\}_{i=1}^K$. We propose the following HJ system for the characterization of the saddle points of ${{\mathcal {G}}}$:

$$\begin{aligned} \left\{ \begin{array}{ll} H(x,Du_k)=1,\qquad x\in \varOmega , \\ u_k( \mu _k)=-\omega _k,\\ S_u^k= \left\{x\in \mathbb {R}^d{:}\,u_k(x)=\min \limits_{{j=1},\cdots ,{K}} u_{j}(x)\right\},\\ \int _{S^k_u}\rho (x)u_k(x){\text{d}}x=\min \left\{\int _{S^k_u}\rho (x)u_y(x){\text{d}}x{:}\, u_y \text { solution of }(9) \text { with }y\in S^k_u\right\},\\ \pi (S_u^k)=c_k. \end{array} \right. \end{aligned}$$

(15̇)

The previous system is obtained by (10), which characterize GCVT, adding the constraints on the measure of the cell, i.e., $\pi (S_u^k)=c_k$. It depends on the 2K parameters $(\mu _k,\omega _k)$. Recall that a solution of

$$\begin{aligned} \left\{ \begin{array}{ll} H(x,Du) =1, \\ u( y)=-\omega \end{array} \right. \end{aligned}$$

is given by $u_y(x)=-\omega +d_C(y,x)$. Hence, if there exists a solution $u=(u_1,\cdots ,u_k)$ to (15), then $u_k(x)=-\omega _k+d_C(\mu _k,x)$. Moreover

$$\begin{aligned} S_u^k= \left\{ x\in \mathbb {R}^d{:}\,-\omega _k+ d_C(\mu _k,x)=\min _{j=1,\cdots ,K}\{-\omega _j+ d_C(\mu _j,x)\}\right\} \end{aligned}$$

and $\mu _k$ is the centroid of $S_u^k$. It follows that the set $S_u^k$ coincides $V(y_k,w_k)$ defined in (13), and $\pi (S_u^k)=c_k$. We conclude that a solution of (15) gives a centroidal power diagram $\{S_u^k\}_{k=1}^K$ of $\varOmega$ realizing the capacity constraint.

4 A Mean Field Games Interpretation of the HJ System

In this section, we establish a link between the HJ system introduced in Sect. 2 and the theory of MFGs (see [17, 19] for an introduction). We show that the HJ system (1) can be obtained in the vanishing viscosity limit of a second order multi-population MFG system characterizing the extremes of a maximal likelihood functional.

Finite mixture models, given by a convex combination of probability density functions, are a powerful tool for statistical modeling of data, with applications to pattern recognition, computer vision, signal and image analysis, machine learning, etc. (see [8]). Consider a Gaussian mixture model

$$\begin{aligned} m(x)=\sum _{k=1}^K \alpha _k {{\mathcal {N}}}(x; \, \mu _k,\Sigma _k) \quad \text {with }\alpha _k\in (0,1), \; \sum _{k=1}^K\alpha _k=1, \end{aligned}$$

(16)

where $\mu _k$ and $\Sigma _k$ denote the mean and the covariance matrix of the Gaussian distribution ${{\mathcal {N}}}(x; \, \mu _k,\Sigma _k)$. The aim is to determine the parameters $\alpha =(\alpha _1,\cdots ,\alpha _K)$, $\mu =(\mu _1,\cdots ,\mu _K)$, $\Sigma =(\Sigma _1,\cdots ,\Sigma _K)$ of the mixture (16) in such a way that they optimally fit a given data set ${\mathcal {X}}$ described by the density function $\rho$. This can obtained by maximizing the log-likelihood functional

$$\begin{aligned} {{\mathcal {L}}}(\alpha ,\mu ,\Sigma ; \,{\mathcal {X}})=\int _{\mathbb {R}^d}\sum _{k=1}^{K}\gamma _k(x)\{\ln (\alpha _k)+ \ln ({{\mathcal {N}}}(x; \, \mu _k,\Sigma _k))\} \rho (x){\text{d}}x, \end{aligned}$$

(17)

where

$$\begin{aligned} \gamma _k(x)= \dfrac{\alpha _k \mathcal {N}(x; \, \mu _k, \Sigma _k)}{\sum\limits _{j=1}^{K}\alpha _j \mathcal {N}(x; \, \mu _j, \Sigma _j)} \end{aligned}$$

are the responsibilities, or posterior probabilities (see [8, Cap. 7] for more details). In [3], we proposed an approach to parameter optimization for mixture models based on the MFG theory. It can shown that the critical points of the log-likelihood functional (17) can be characterized by means of the multi-population MFG system

$$\begin{aligned} \left\{ \begin{array}{ll} -\varepsilon \Delta u_{k,\varepsilon } + \frac{1}{2} \vert D u_{k,\varepsilon } \vert ^2+\lambda _{k,\varepsilon }= \frac{\varepsilon ^2}{2} (x-\mu _{k,\varepsilon })^t(\Sigma _{k,\varepsilon }^{-1})^t\Sigma _{k,\varepsilon }^{-1}(x-\mu _{k,\varepsilon }),\quad &{} x\in \mathbb {R}^d, \\ \varepsilon \Delta m_{k,\varepsilon } + \mathrm{div}(m_{k,\varepsilon } D u_{k,\varepsilon } )=0,&{}x\in \mathbb {R}^d, \\ \alpha _{k,\varepsilon }=\int _{\mathbb {R}^d }\gamma _{k,\varepsilon }(x) \rho (x){\text{d}}x,\\ m_{k,\varepsilon }\geqslant 0,\,\int _{\mathbb {R}^d} m_{k,\varepsilon } {\text{d}}x=1, u_{k,\varepsilon }( \mu _{k,\varepsilon })=0 \end{array} \right. \end{aligned}$$

(18)

for $k=1, \cdots , K$, where

$$\begin{aligned} \left\{ \begin{array}{ll}&\gamma _{k,\varepsilon }(x)=\dfrac{\alpha _{k,\varepsilon } m_{k,\varepsilon }(x)}{\sum _{j=1}^K\alpha _{j,\varepsilon } m_{j,\varepsilon }(x)},\nonumber \\&\mu _{k,\varepsilon }=\frac{\int _{\mathbb {R}^d}x\gamma _{k,\varepsilon }(x)\rho (x){\text{d}}x}{\int _{\mathbb {R}^d} \gamma _{k,\varepsilon }(x)\rho (x){\text{d}}x}, \nonumber \\&\Sigma _{k,\varepsilon }=\frac{\int _{\mathbb {R}^d}(x-\mu _{k,\varepsilon })(x-\mu _{k,\varepsilon })^t\gamma _{k,\varepsilon }(x)\rho (x){\text{d}}x}{\int _{\mathbb {R}^d} \gamma _{k,\varepsilon }(x)\rho (x){\text{d}}x} \end{array} \right.\end{aligned}$$

(19)

are unknown variables which depend on the solution of the system (18). More precisely, a solution of (18) is given by a family of quadruples $(u_{k,\varepsilon }, \lambda _{k,\varepsilon }, m_{k,\varepsilon }, \alpha _{k,\varepsilon })$, $k=1,\cdots ,K$, with

$$\begin{aligned} \begin{aligned}\left\{ \begin{array}{ll}&u_{k,\varepsilon }(x)=\frac{\varepsilon }{2}(x-\mu _{k,\varepsilon })^t\Sigma ^{-1}_{k,\varepsilon }(x-\mu _{k,\varepsilon }),\quad \lambda _{k,\varepsilon }=\varepsilon ^2 \text {Tr}(\Sigma _{k,\varepsilon }^{-1}),\\&m_{k,\varepsilon }(x)={{\mathcal {N}}}(x; \, \mu _{k,\varepsilon },\Sigma _{k,\varepsilon })=C_k{\text{e}}^{-\frac{u_k(x)}{\varepsilon }},\\&\alpha _{k,\varepsilon }=\int _{\mathbb {R}^d}\gamma _{k,\varepsilon }(x)\rho (x){\text{d}}x, \end{array} \right.\end{aligned} \end{aligned}$$

(20)

and the corresponding parameters $(\alpha _{k,\varepsilon }, \mu _{k,\varepsilon }, \Sigma _{k,\varepsilon })$, $k=1,\cdots ,K$, are a critical point of the log-likelihood functional (17). Note that in general the solution of (18) is not unique. In soft-clustering analysis, the responsibilities can be used to assign a point to the cluster with the highest $\gamma _{k,\varepsilon }$, i.e., the set $\varOmega$ is divided into the disjoint subsets

$$\begin{aligned} S^k_{u,\varepsilon }=\left\{x\in \varOmega{:}\,\gamma _{k,\varepsilon }(x)=\max _{j=1,\cdots ,K}\gamma _{j,\varepsilon }(x)\right\}. \end{aligned}$$

Taking into account (19) and the definition of $m_{k,\varepsilon }$ in (20), we see that the clusters $S^k_{u,\varepsilon }$ can be equivalently defined as

$$\begin{aligned} S^k_{u,\varepsilon }=\left\{x\in \varOmega {:} \,u_{k,\varepsilon }(x)=\min _{j=1,\cdots ,K} u_{j,\varepsilon }(x)\right\}. \end{aligned}$$

It is well known, in cluster analysis, that the K-means functional (3) can be seen as the limit of the maximum likelihood functional (17) when the variance parameter of the Gaussian mixture model is sent to 0 (see [8, Chapter 7]). In order to deduce a PDE characterization for centroidal Voronoi tessellations, we follow a similar idea. Assuming that $\Sigma _k=\sigma I$ and passing to the limit in (18) for $\varepsilon ,\sigma \rightarrow 0^+$ in such a way that $\varepsilon /\sigma ^2\rightarrow 1$, we observe that the responsibility $\gamma _{k,\varepsilon }$ in (19) converges to the characteristic function of the set where $\alpha _k m_k$ is maximum with respect to $\alpha _j m_j$, $j=1,\cdots ,K$ or, equivalently, where $u_k$ is minimum with respect to $u_j$. Hence, we formally obtain that (18) converges to the first order multi-population MFG system

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{2}\vert D u_k \vert ^2+\lambda _k= \frac{1}{2}\vert x-\mu _k\vert ^2,\quad &{} x\in \mathbb {R}^d, \\ \mathrm{div}(m_k D u_k(x) )=0,&{}x\in \mathbb {R}^d, \\ \alpha _k=\int _{\mathbb {R}^d }\mathbbm {1}_{S_u^k}(x) \rho (x){\text{d}}x,\\ m_k\geqslant 0,\,\int _{\mathbb {R}^d} m_k(x){\text{d}}x=1, u_k( \mu _k)=0 \end{array} \right. \end{aligned}$$

(21)

for $k=1,\cdots ,K$, with

$$\begin{aligned}&S_u^k= \left\{x\in \mathbb {R}^d{:}\,u_k(x)=\min _{j=1,\cdots ,K} u_{j}(x)\right\},\end{aligned}$$

(22)

$$\begin{aligned}&\mu _{k}=\frac{\int _{\mathbb {R}^d}x \mathbbm {1}_{S_u^k}(x)\rho (x){\text{d}}x}{\int _{\mathbb {R}^d} \mathbbm {1}_{S_u^k}(x)\rho (x){\text{d}}x}. \end{aligned}$$

(23)

The coupling among the K systems in (21) is in the definition of the subsets $S_u^k$ and the coefficient $\alpha _k$ represents the fraction of the data set contained in the cluster $S_u^k$.

In order to write a simplified version of (21), we observe that the ergodic constant $\lambda _k$ in the HJ equation, which can be characterized as the supremum of the real number $\lambda$ for which the equation admits a subsolution (see [7]), is always equal to 0. Moreover, since the solution $u_k$ is defined up to a constant, we set $u_k(\mu _k)=0$ and we obtain $u_k(x)=\vert x-\mu _k\vert ^2/2$. The solution, in the sense of distribution, of the second PDE in (21) is given by $m_k=\delta _{\mu _k}(\cdot )$, where $\delta _{\mu _k}$ denotes the Dirac function in $\mu _k$. It follows that the HJ equations are independent of $m_k$ and $\alpha _k$. Recalling that the unique viscosity solution of the problem

$$\begin{aligned} \left\{ \begin{array}{ll} \vert Du\vert =1,\quad x\in \mathbb {R}^d, \\ u ( \mu )=0\\ \end{array} \right. \end{aligned}$$

is given by $u(x)=\vert x-\mu \vert$, we can write the equivalent version of (21)

$$\begin{aligned} \left\{ \begin{array}{ll} \vert Du_k\vert =1,\quad x\in \mathbb {R}^d, \\ u_k( \mu _k)=0,\\ S_u^k= \left\{x\in \mathbb {R}^d{:}\,u_k(x)=\min\limits _{j=1,\cdots ,K} u_{j}(x)\right\}, \\ \mu _{k}=\frac{\int _{\mathbb {R}^d}x \mathbbm {1}_{S_u^k}(x)\rho (x){\text{d}}x}{\int _{\mathbb {R}^d} \mathbbm {1}_{S_u^k}(x)\rho (x){\text{d}}x} \end{array} \right. \end{aligned}$$

for $k=1,\cdots ,K$, which is a system of HJ equations coupled through the sets $S_u^k$. Taking into account (23), we see that the previous system coincides with (10) when $d_C$ is given by the Euclidean distance.

5 Numerical Tests

In this section, we study an iterative procedure to solve the HJ systems characterizing centroidal tessellations.

5.1 Tests for the Geodesic K-means Problem

For the K-means problem in Sect. 2 and the associated system (10), we consider the PDE version of the Lloyd algorithm reported in Algorithm 1.

In the first step of the iterative procedure, it is sufficient to solve problem (24) in the set $\varOmega$, the support of the density $\rho$.

Proposition 1

The sequence $u^{(n)}=(u^{(n),1}, \cdots , u^{(n),K})$, $n\in \mathbb {N}$, given by Algorithm 1 converges to a solution $u=(u^{1}, \cdots , u^{K})$ of (10).

Proof

It is sufficient to observe that the PDE Lloyd algorithm is equivalent to the classical one. Indeed, in the first step, by (9) we have that $u^{(n),k}(x)=d_C(\mu ^{(n),k},x)$ and therefore $S^{(n),k}_u$ gives a Voronoi tessellation of the generator $\mu ^{(n),k}$, $k=1,\cdots , K$. Then, in the second step, the centroids of $S^{(n),k}_u$ are updated as in the classical algorithm. Convergence results for the Lloyd algorithm (see [13, 22]) imply that $\mu ^{(n),k}$ converges to a critical point $\mu ^{k}$ of ${{\mathcal {I}}}_{C}$. It follows that $u^{(n),k}$ converges uniformly in $\varOmega$ to $u_k(x)=d_C(\mu ^{k},x)$, which, by Theorem 1, is a solution of (10).

To solve problem (24), we introduce a regular triangulation of $\varOmega$, the support of $\rho$, given by a collection of N disjoint triangles ${\mathcal {T}}:=\{T_i\}_{i=1,\cdots,N}$. We denote with $\Delta x$ the maximal area of the triangles, i.e., $\max _{i=1,\cdots,N}\vert T_i\vert <\Delta x$, and we assume that $\varOmega \subseteq \bigcup _1^NT_i\approx \varOmega$. We denotes with ${\mathcal {G}}:=\{X_i\}_{i=1,\cdots,N}$ the set of the centroids of the triangles $T_i$ and, for a piecewise linear function $U{:}\,\mathcal G\rightarrow \mathbb {R}$, we set $U_i:=U(X_i)$.

To test our method, we start with the classical K-means problem, i.e., the case where the distance $d_C$ coincides with the Euclidean one. In this case, the Hamiltonian in (10) is given by $H(x,p) =\vert p\vert$ and the centroids of the Voronoi diagrams $V(y_k)$ are given by (6). For the approximation of the HJ equation, we consider the semi-Lagrangian monotone scheme

$$\begin{aligned} G_i(U)= \min _{a\in B(0,1)}\left\{ \mathbb {I}\left[ U\right] (X_{i}-ha)+h \right\} , \end{aligned}$$

where h is a fictitious-time parameter (generally taken of order $O(\sqrt{\Delta x})$, see [15] for details), and $\mathbb {I}$ a standard linear interpolation operator on the simplices of the triangulation.

Algorithm 2 is obtained by a discretization of Algorithm 1.

Remark 4

By Proposition 1, we know that, given $u^{(n)}$ as in (24), then there exists a solution of (10) such that $\Vert u-u^{(n)}\Vert _\infty \rightarrow 0$ for $n\rightarrow \infty$. Moreover, by classical results for semi-Lagrangian schemes (see [7, Appendix A, Thm 1.4]), given $U^{(n)}$ as in (26) we have the estimate

$$\begin{aligned}\max _{k=1,\cdots ,K}\Vert u^{(n),k}-U^{(n),k}\Vert _\infty \leqslant C\left( h^\frac{1}{2}+\frac{\Delta x}{h}\right) \end{aligned}$$

with C independent of n. Hence $U^{(n)}$, for n large, gives an approximation of u and of the corresponding centroidal tessellation.

Fig. 2

Three Voronoi tessellations with $K=6$ computed with different initial centroids and $\Delta x=0.004$, top/left: $\mu ^{(0)}=( [0.4, 0.6], [0.6, 0.4], [0.6, -0.4], [-0.4, -0.6], [-0.6, -0.4], [-0.6, 0.4])$; top/right: $\mu ^{(0)}=( [0.4, 0.6], [0.6, 0.4], [0.6, -0.4],[-0.6, -0.4], [-0.4, 0.6], [0.1, 0.1])$; bottom/left: $\mu ^{(0)}=( [0.4, 0.6], [0.6, 0.4], [-0.4, 0.6],[-0.4, -0.6], [-0.6, -0.4], [0.1, 0.1])$; bottom/right: evolution of the $K$-means functional for iteration step of the algorithm

Test 1.

The first test is a simple problem to check the basic features of the technique. We consider a circular domain $\varOmega{:=}\,B(0,1)$ and a CVT composed of 6 cells. The density function $\rho$ is chosen uniformly distributed on $\varOmega$, i.e., $\rho (x)= 1/\vert \varOmega \vert$, where $\vert \varOmega \vert =\uppi$. We set the approximation parameter $\Delta x=0.004$. Moreover, we iterate the algorithm steps till meeting the stopping criterion

$$\begin{aligned} \max _k\{\vert \mu ^{(n+1),k}-\mu ^{(n),k}\vert \}<\varepsilon \end{aligned}$$

and we fix $\varepsilon =\Delta x/10$. Figure 2 shows tessellations computed by the algorithm starting from different sets of initial centroids. The evolution of the centroids is marked in red with a sequential number related to the iteration number. We can observe that in all the cases, the centroids move from the initial guess toward an optimal tessellation of the domain, where the optimality is intended referred to the functional (3). The convergence toward optimality is highlighted in the last picture in Fig. 2, where the value of the K-means functional is evaluated at the end of every iteration for the previous three cases.

Remark 5

(Dependency on K and Fast-Marching method (FMM)) The previous numerical procedure may be computationally expansive, with the bottleneck given by the resolution of K-eikonal equations on the whole domain of interest, see (26). In some cases, the first step of the Lloyd algorithm may turn out to be very expansive, in particular, if we use, to solve (26), a value iteration method, i.e., a fixed point iteration on the whole computational domain (see for details [15]). The following numerical steps are generally much easier since they can benefit from a good initialization of the solution coming from the previous iteration of the algorithm. We observe, anyway, that the dependency on K w.r.t. the computational time is only linear: therefore, to solve the same problem with 2K subdomains we only need double CPU time w.r.t. the original K problem. The latter means that a K (reasonably) large does not pose problems to our algorithm. In addition, the use of parallel computing (the problem is naturally parallelizable w.r.t. K), may constitute a valid strategy if we are in presence of a very high value of K.

The CPU time needed, especially for the first step of the algorithm, is considerably mitigated with the use of a more rational way to process the various parts of the domain, in our case the use of FMM (see [26]). In those methods, the nodes of the discrete grid are processed ideally only once, thanks to the information about the characteristics of the problem that may be derived by the same updating procedure. In our case of unstructured grids, the computational process is slightly more complicated than the standard one, and it requires an updating procedure that includes the geometry of the triangles of the grid. The choice of FMM with respect to other techniques (e.g., Fast Sweeping) comes exactly from the choice (in general not necessary) of using unstructured grids. Refer to [27] for a precise description of the algorithm.

Remark 6

(Performances, CPU time and comparison with sampled-based standard algorithms.) Our PDE-based CVT Algorithm 2 has the undeniable drawback of needing the approximation of K PDEs equations. This is relatively complex and sometimes, computationally expensive. For example, in Test 1, with $\Delta x=0.004$, we reached the approximated solution after 6, 13, and 10 iterations, with the use of the CPU time of 78, 89, and 82 seconds depending on the initial guess of the centroids. The results, in terms of efficiency, are not unacceptable in our opinion, especially since we used a standard portable laptop (specs. Processor 1.4 GHz Quad-Core Intel Core i5 Memory 8 GB 2 133 MHz) while the algorithm, by construction completely parallel, would largely benefit of running on a cluster computer. We must underline, for sake of completeness, that we have been able to mitigate the computational cost with the use of FMM.

To compare our results with other clustering techniques we show the results obtained by the k-means++ algorithm (see [4]) which is, as our proposal, based on the Lloyd algorithm. As it is pretty standard in these techniques, the algorithm works with a sample of the density distribution while in our proposal, we use directly the density function representing the data set. The latter means that the performances of the solver will be strongly dependent on the dimension of the sample set. In Fig. 3 we show the results of the K-means++ algorithm with a sample set of $10^4$, $5\cdot 10^6$, and $10^7$ points for which we obtain the solution after 0.085, 28.7, and 214 seconds. We observe that, as our algorithm, also K-means++ finds various configurations depending on the initialization of the centroids. The accuracy of the technique depends on the dimension of the sample set and comparing the results in the case of the most regular configuration (center in Fig. 3) we may approximately evaluate that our test (Test 1) is equivalent, in terms of accuracy, to K-means++ with a sample set of $5\cdot 10^6$ points. Finally, the latter means that the technique that we propose is less efficient than K-means++ (approx. 80 s vs. 28 s), but it shares with it the same order of CPU time.

Fig. 3

The same problem solved with a standard soft-clustering technique (k-means++ algorithm, see [4]). The density function is sampled, respectively, from left to right, by $10^4$, $10^6$, and $10^7$ points

Test 2.

We consider a bounded domain $\varOmega$ given by the union of two squares $[0,1]\times [0,1]$, $[-1,0]\times [-1, 0]$ and a section of a circle $B(0,1)\cap [-1,0]\times [0,1]$ and we remove by the domain the circle $B([-0.4,0.4], 0.2)$, as displayed in Fig. 4. Then, a CVT of $\varOmega$ given by three cells, i.e., $K=3$, is computed.

At first, the density function $\rho$ is given by a uniform distribution on $\varOmega$, i.e., $\rho (x)= 1/\vert \varOmega \vert$, where $\vert \varOmega \vert = (2+\uppi /4)-\uppi (1/5)^2\approx 2.66$.

Fig. 4

Top: uniformly distributed $\rho$, left: $\Delta x =0.01$; right: $\Delta x=0.001$. Bottom: $\rho$ is a multivariate normal distribution around [0.5, 0.5], left: $\Delta x =0.01$; right: $\Delta x=0.001$

In Fig. 4 we see the evolution of the centroids $\mu ^{(n)}$ starting from the initial position

$$\begin{aligned} \mu ^{(0)}=([-0.6,-0.6], [-0.4,-0.6], [-0.4, 0]). \end{aligned}$$

The two images in the top panels of Fig. 4 are relative to different discretization parameters $\Delta x:=\max \vert T_i\vert$ and $\varepsilon =\Delta x/10$. We underline how the number of iterations does not increase much for a smaller stopping parameter, e.g., setting $\varepsilon$ to $10^{-6}$ we obtained numerical convergence for $n=11$. Moreover, the approximation of the position of the centroids $\mu ^{(n)}$, once reached convergence, is sufficiently accurate even in the presence of a discretization parameter $\Delta x$ relatively coarse. This suggests, at least in this example, avoiding excessive refinement of $\Delta x$ to prevent increasing computational cost for the algorithm.

Even in this easy case, we can observe an additional feature of the method: the approximation of the critical points is monotone with respect to the functional ${{\mathcal {I}}}_{C}$ while a point may have a non-monotone migration toward the correct approximation. This is because the evolution of ${{\mathcal {I}}}_{C}$ in the algorithm is monotone (cf. Fig 2 of the previous test) at any iteration, but not for a single centroid.

We complete this test with a case where $\rho$ is not constant. Consider a multivariate normal distribution around the point [0.5, 0.5] and covariance matrix I, i.e.,

$$\begin{aligned} \rho (x)= \frac{1}{2\uppi \vert \varOmega \vert }{\text{e}}^\frac{{-(x_1-0.5)^2-(x_2-0.5)^2}}{2}. \end{aligned}$$

The results are shown in the bottom panels of Fig. 4, with the same choice of the parameters as in the previous test. We observe, as expected, a reduction of the dimension of the sets ${{\mathcal {S}}}^{(n),k}$ in correspondence to higher values of the density function $\rho$. Even if we need few more steps to reach the numerical convergence, the algorithm shows similar performances and stops for $n=13$.

We now consider the general case of a geodesic distance $d_C$. To approximate the HJ equation in (10), we consider the semi-Lagrangian scheme

$$\begin{aligned} G_i(U)= \min _{\alpha \in C(X_{i})}\left\{ \mathbb {I}\left[ U\right] (X_{i}-ha)+h \right\} , \end{aligned}$$

(28)

since in $C(X_{i})$ are contained all the points of the unitary distance from $X_i$ w.r.t. the distance $d_C$ (see (8)). To compute the new centroids, since $u_y(x)=d_C(y,x)$, the optimization problem in (10) has its discrete version as

$$\begin{aligned}&\sum _{X_j\in {{\mathcal {S}}}^{(n+1),k} }\rho (X_j)d_C(\mu _k^{(n+1)},X_j)\\&\quad = \min \left\{ \sum _{X_j\in {{\mathcal {S}}}^{(n+1),k}}\rho (X_j)d_C(Y,X_j):\, Y\in {{\mathcal {S}}}^{(n+1),k}\right\} , \end{aligned}$$

and, called $\mathcal {H}(Y)=\sum _{X_j\in {{\mathcal {S}}}^{(n+1),k}}\rho (X_j)d_C(Y,X_j)$, the maximal growth direction is (see [24])

$$\begin{aligned}\delta _k:=D\mathcal {H}(Y)=\frac{1}{2}\sum _{X_j\in {{\mathcal {S}}}^{(n+1),k}}\rho (X_j)Dd_C(Y,X_j)n_Y(X_j),\end{aligned}$$

where $n_Y(x)$ is the unit vector tangent at Y to the geodesic path joining $X_i$ to Y.

For the numerical tests, we consider the case of the Minkowski distance on $\mathbb {R}^2$, see Remark 3. We remind that such a distance generalizes the Manhattan distance (case $s=1$) and the Chebyshev distance (case $s\rightarrow \infty$, $d_C(x,y)=\max _i(\vert x_i-y_i\vert )$). In Fig. 1 are shown the balls B(0, 1) in the Minkowski distance for various values of s.

Test 3.

We first consider the problem on a simple L-shaped bounded domain $\varOmega =[0,1]\times [0,1]\cup [-1,0]\times [-1, 1]$ as displayed in Fig. 5. In this case, the Chebyshev distance (i.e., $s\rightarrow \infty$) provides an optimal tessellation which is trivially guessed: due to the geometrical characteristics of the domain and the distance (the contour lines of the distance from a point are squares, see Fig. 1) the solution, for $K=3$ and uniform density function ($\rho (x)= 1/\vert \varOmega \vert$, where $\vert \varOmega \vert = 3$), is simply composed by the three squares $\{[0,1]^2,[-1,0]\times [-1,0],[-1,0]\times [0,1]\}$, with the centroids ${\bar{\mu }}=([0.5,0.5],[-0.5,-0.5],[-0.5,0.5])$.

Fig. 5

Top: left panel $\Delta x =0.01$; right panel: $\Delta x=0.001$ starting from $\mu ^{(0)}=([-0.6,-0.6], [-0.4,-0.6], [-0.4, 0])$. Bottom: left panel $\mu ^{(0)}=([-0.6,0.6], [-0.4,0.6], [-0.5, 0.4])$, $\Delta x=0.001$; right panel, convergence of the error on the centroids for iterations on the Euclidean norm

In Fig. 5, top panels, we see the evolution of the centroids $\mu ^{(n)}$ starting from the initial position $\mu ^{(0)}=([-0.6,-0.6], [-0.4,-0.6], [-0.4, 0])$ for two different values of $\Delta x$. Also in this case we can observe as the position of the centroids and the rough structure of the tessellation is correctly reconstructed even in the presence of a larger grid. This is also highlighted by the evolution of the Euclidean norm of the error $\mu ^{(n)}-{\bar{\mu }}$ reported in Fig. 5 (bottom right). The evolution of the error and the total number of iterations necessary to converge to the correct approximation are barely affected by $\Delta x$. On the other hand, the final approximation apparently converges to ${\bar{\mu }}$ with order $\Delta x$.

We perform the same test with a different initial position $\mu ^{(0)}$ equal to $([-0.6,0.6], [-0.4,0.6], [-0.5, 0.4])$, see Fig. 5, bottom left panel. Since in this case the optimal tessellation is unique, the algorithm converges to the same configuration. The number of iterations necessary is clearly affected by the initial guess of $\mu$.

Test 4.

The flexibility of the technique allows us to solve the problem on more complex domains, in particular on manifolds: in fact, we need to consider an appropriate Riemann metric and to address the periodicity of the manifold, solving the HJ equations on a periodic domain. This allow us to solve the problem on a cylinder: considering the standard parametrization

$$\begin{aligned} \left\{ \begin{array}{l} X=r\cos x,\\ Y=r\sin x, \\ Z=y, \end{array} \right. \end{aligned}$$

(29)

we have the induced metric ${\text{d}}X^2+{\text{d}}Y^2+{\text{d}}Z^2=r^2 {\text{d}} x^2+{\text{d}} y^2,$ therefore, using the notation of Remark 3, $A(x,y)=\left( \begin{array}{cc} r^2 &{} 0\\ 0 &{} 1 \end{array}\right)$. Solving the problem on $[-\uppi ,\uppi ]\times [-1, 1]$ and considering the periodicity $(-\uppi ,y)\sim (\uppi ,y)$ (therefore, $r=1$), we obtain, for the discretization parameters $K=6$, $\Delta x=0.01$, the results shown in Fig. 6, left.

If we want to solve the same problem on a torus (periodicity $(x,y)\sim (x+2\uppi ,y)\sim (x,y+2\uppi )$) we start from the standard parametrization

$$\begin{aligned} \left\{ \begin{array}{l} X=(r\cos x +R)\cos y,\\ Y=(r\cos x +R)\sin y,\\ Z=r\sin x, \end{array} \right. \end{aligned}$$

(30)

where R is the distance from the center of the tube to the center of the torus, and r is the radius of the tube,

$$\begin{aligned} A(x,y)=\left( \begin{array}{cc} (R+r\cos y)^2 &{} 0 \\ 0 &{} r^2 \end{array}\right), \end{aligned}$$

(31)

so we obtain, solving the problem in $[-\uppi ,\uppi ]^2$ for $K=6$, $\Delta x=0.004$ the tesselation represented in Fig. 6.

Finally, considering the same problem on a hyperbolic paraboloid $Z-XY=0$ in $\mathbb {R}^3$ of parametrization $(X,Y,Z)=(x,y,xy)$, we have the induced metric

$$\begin{aligned} A(x,y)=\left( \begin{array}{cc} 1+y^2 &{} xy \\ xy &{} 1+x^2 \end{array}\right). \end{aligned}$$

(32)

The result for $K=6$, $\Delta x=0.004$ is, again, in Fig. 6.

Fig. 6

Three tessellations on two-dimensional manifolds, respectively, a cylinder, a torus, a hyperbolic paraboloid. The parameters are set $K=6$, $\Delta x=0.01, 0.004, 0.004$. The position of the centroids in marked with red dots

5.2 Tests for Geodesic Centroidal Power Diagrams

The procedure to obtain an approximation of centroidal power diagrams contains all the tools already described in the previous sections and it includes a three-step procedure: resolution of K HJ equations, update of the centroids points, and optimization step for the weights.

Test 5.

We consider the Minkowski distance with $s=1$. Since contour lines of the distance assumes a rhombus shape, we expect to be able to see this in the tessellation that we obtain. In addition, we want to show as our technique, with the help of an acceleration method, can successfully address the GCVT problem with a larger K. This is not intended to be an accurate performance evaluation (which is not the main goal of this paper), but only a display of the possibilities give by the techniques proposed. We consider tesselations of $\varOmega =B(0,1)$ with $K=20$ and of $\varOmega =[-1,1]^2$ with $K=30$. In the first case (the circle), the function $\rho$ is given by a uniform distribution, while, in the second case, by multivariate normal distribution around the point [0, 0] and covariance matrix I, i.e.,

$$\begin{aligned} \rho (x)=\rho ([x_1,x_2])= \frac{1}{2\uppi \vert \varOmega \vert }{\text{e}}^\frac{{-(x_1)^2-(x_2)^2}}{2}, \end{aligned}$$

where $\vert \varOmega \vert =4$. The resulting tessellations are shown in Fig. 7.

Fig. 7

Two tessellations with a larger number of sets. On the left: $\Delta x =0.04$, uniform $\rho$, $K=20$. On the right: $\Delta x =0.04$, multivariate $\rho$ around the origin, $K=30$. In this figure, the numbers are merely to identify the k-centroid of the tessellation

We see that our technique can address without too much troubles a problem with a higher K (cf. Remark 5): as observed, this parameter enters in the first step of the Lloyd algorithm linearly. Since we did not observe a substantial change of the number of iterations of the algorithm for a larger K, the technique remains computationally feasible, even performed on a standard laptop computer.

Test 6.

We test the centroidal power diagram procedure, Fig. 8, in a simple case given by the unitary square $\varOmega =[0,1]^2$ for $K=6,8$ and capacity constraint given, respectively, by

$$\begin{aligned}&c=(0.3,0.25, 0.18, 0.12, 0.1, 0.05),\\&c=(0.3, 0.24, 0.15, 0.1, 0.08, 0.06, 0.05, 0.02). \end{aligned}$$

Clearly we have $\bigcup _k {{\mathcal {S}}}^{(n),k}=\varOmega$, for any n and therefore we $\sum _k c_k=\vert \varOmega \vert =1$.

Fig. 8

Left panel: $K=6$, $\Delta x =0.015$, $\mu ^{(0)}=\{0.4, 0.5, 0.6\}\times \{0.4, 0.6\}$; right panel: $\Delta x=0.001,$ $\mu ^{(0)}=\{0.4, 0.45, 0.55, 0.6\}\times \{0.4, 0.6\}$, $c=(0.3, 0.24, 0.15, 0.1, 0.08, 0.06, 0.05, 0.02)$ (in this image some points of the evolution of the centroids are omitted for a better clarity)

Test 7.

The same technique is used to generate some power diagrams of more complex domains: in Fig. 9 we show the optimal tessellation of a text and a rabbit-shaped domain. In the first case, the algorithm parameters are set to $K=8$, $c=(0.33, 0.22, 0.1, 0.1, 0.1, 0.05, 0.05, 0.05)$, $\Delta x=0.002$. In the second one, $K=6$, $c=(0.3, 0.15, 0.15, 0.15, 0.15, 0.10)$, $\Delta x=0.002$.

Fig. 9

Optimal power diagrams of a text and a rabbit shaped domain. The parameters are set $K=8$, $c=(0.33, 0.22, 0.1, 0.1, 0.1, 0.05, 0.05, 0.05)$, $\Delta x=0.002$ (left), $K=6$, $c=(0.25, 0.15, 0.15, 0.15, 0.15, 0.10)$, $\Delta x=0.002$ (right)

6 Conclusion

In this work, we described a PDE method for the computation of centroidal geodesic Voronoi tessellation and power diagrams. The PDE theory is a robust framework to solve classic (and less traditional) tessellation problems. The main advantage of this approach is the high adaptability of the framework to specific variations of the problem (presence of constraints, non-conventional distance functions, periodicity, etc.). This increased adaptability comes with a precise cost: a PDE approach is more computationally demanding than other methods available in the literature. However, the recent developments of numerical methods for nonlinear PDEs, and the increment of the accessibility to more powerful computational resources at any level, make these techniques progressively more appealing in many applicative contexts [2, 16, 18].