An Algorithm of Nonparametric Quantile Regression

Abstract

Extreme events, such as earthquakes, tsunamis, and market crashes, can have substantial impact on social and ecological systems. Quantile regression can be used for predicting these extreme events, making it an important problem that has applications in many fields. Estimating high conditional quantiles is a difficult problem. Regular linear quantile regression uses an L₁ loss function [Koenker in Quantile regression, Cambridge University Press, Cambridge, 2005], and the optimal solution of linear programming for estimating coefficients of regression. A problem with linear quantile regression is that the estimated curves for different quantiles can cross, a result that is logically inconsistent. To overcome the curves crossing problem, and to improve high quantile estimation in the nonlinear case, this paper proposes a nonparametric quantile regression method to estimate high conditional quantiles. A three-step computational algorithm is given, and the asymptotic properties of the proposed estimator are derived. Monte Carlo simulations show that the proposed method is more efficient than linear quantile regression method. Furthermore, this paper investigates COVID-19 and blood pressure real-world examples of extreme events by using the proposed method.

1 Introduction

Extreme events are rare, unusual occurrences such as earthquakes, tsunamis, and market crashes. These events usually have the potential to substantially impact social, and ecological systems. Therefore, understanding and predicting extreme events is of interest in many fields such as earth sciences, traffic prediction, survival analysis and financial markets. To estimating such events’ probability requires a model that focuses on the high conditional quantile of heavy-tailed distribution [7]. Therefore, more sophisticated quantile regression methods are used instead of traditional mean regression. Linear quantile regression uses the least absolute deviation (${L}_{1}$) loss function, and optimization of this loss function is done using linear programming methods. With quantile regression, we can obtain the relationship between variables in high conditional quantiles.

The linear mean regression model is used to estimate the conditional mean of random variable $y$ based on given $\varvec{x} = (1,x_{1} ,x_{2} ,...,x_{k} )^{T} .$

$$ \mu_{{(y|\varvec{x})}} = E(y|x_{1} ,x_{2} ,...,x_{k} ) = \varvec{x}^{T} {\varvec{\beta}} = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + ... + \beta_{k} x_{k}, $$

(1)

where ${\varvec{\beta}} = \left( {\beta_{0} ,\beta_{1} ,\beta_{2} ,...,\beta_{k} } \right) \in R^{p} , \, p = k + 1$.

Let $y_{i} {, }i = 1,2,...,n$, be the response variable from a continuous distribution, which is explained by p-dimensional design vector ${\mathbf{x}}_{i}$. Then ${\varvec{\beta}}$ can be estimated from a random sample $\left\{ {\left( {y_{i} ,\varvec{x}_{i} } \right), \, i = 1,2,...,n} \right\}$ by applying the method of least squares. By minimizing its ${L}_{2}$-squared distance, we can obtain the least-square (LS) estimators $\widehat{{\varvec{\beta}}}_{LS}$. This can be represented by the following equation

$$ \widehat{{\varvec{\beta}}}_{LS} = \arg \mathop {\min }\limits_{{\beta \in R^{p} }} \sum\limits_{i = 1}^{n} {(y_{i} - \varvec{x}_{i}^{T} {\varvec{\beta}})^{2} }. $$

(2)

When the response variable is normally distributed, this model has appealing attributes such as computational tractability and accurate conditional mean estimation. However, the measurement of the central location would be significantly affected if there are outliers in the data. Moreover, for extreme events, the response variable usually has a heavy-tailed distribution such as the extreme value distribution [6], and the focus is on the high quantile curves rather than central location. In this circumstance, the mean regression model is inefficient at capturing the critical information required to predict extreme events. Research results show that quantile regression methods are better to apply.

A real-valued random variable y has right-continuous cumulative distribution function (CDF) $F_{y} \left( y \right)$. The $\tau^{{{\text{th}}}}$ quantile of such y is given by

$$Q\left( \tau \right) = F^{ - 1} \left( \tau \right) = \inf \left\{ {y:F\left( y \right) \ge \tau } \right\}, \, 0 < \tau < 1.$$

If a random univariate y can be explained by ${\mathbf{x}} = \left( {1,x_{1} ,x_{2} , \ldots ,x_{k} } \right)^{T} \in R^{p} .$ The conditional $\tau^{{{\text{th}}}}$ quantile of y given x is defined as

$$ Q_{y} \left( {\tau |{\mathbf{x}}} \right) = F^{ - 1} \left( {\tau |{\mathbf{x}}} \right) = \inf \left\{ {y:F\left( {y|{\mathbf{x}}} \right) \ge \tau } \right\}. $$

(3)

Then the regular $\tau^{{{\text{th}}}}$ quantile linear regression (QR) of y is defined as [20].

$$ Q_{R} \left( {\tau |x} \right) = \beta_{0} \left( \tau \right) + \beta_{1} \left( \tau \right)x_{1} + \beta_{2} \left( \tau \right)x_{2} + ... + \beta_{k} \left( \tau \right)x_{k} , \, 0 < \tau < 1, $$

(4)

where ${\varvec{\beta}}\left( \tau \right) = \left( {\beta_{0} \left( \tau \right),\beta_{1} \left( \tau \right),\beta_{2} \left( \tau \right),...,\beta_{k} \left( \tau \right)} \right)^{T}$. Its estimator $\widehat{{\varvec{\beta}}}\left( \tau \right)$ is obtained by solving the following equation

$$ \widehat{{\varvec{\beta}}}\left( \tau \right) = \arg \mathop {\min }\limits_{{{\varvec{\beta}}\left( \tau \right) \in R^{p} }} \sum\limits_{i = 1}^{n} {\rho_{\tau } \left( {y_{i} - {\mathbf{x}}_{i}^{T} {\varvec{\beta}}\left( \tau \right)} \right), \, 0 < \tau < 1}, $$

(5)

where $\rho_{\tau }$ is a quantile-weighted ${L}_{1}$-loss function which is not differentiable,

$$ \rho_{\tau } \left( u \right) = u\left( {\tau - I\left( {u < 0} \right)} \right) = \left\{ {\begin{array}{*{20}c} {u\left( {\tau - 1} \right),} & {{\text{ if }}u < 0;} \\ {u\tau ,} & {{\text{ if }}u \ge {0}{\text{.}}} \\ \end{array} } \right. $$

(6)

In other words, minimizing the expected loss to obtain estimator $\widehat{{\varvec{\beta}}}\left( \tau \right)$. Furthermore, the quantile regression problem can be reformulated as a linear program

$$ \mathop {\min }\limits_{{\left( {{\varvec{\beta}}\left( \varvec{\tau } \right),\varvec{u,v}} \right) \in R \times R_{ + }^{2n} }} \left\{ {\tau 1_{n}^{T} \varvec{u }+\left( {1 - \tau } \right)1_{n}^{T} \varvec{v}|\varvec{X}{\varvec{\beta}}\left( \tau \right) + {\varvec{u}} - {\varvec{v}} = {\varvec{y}}} \right\}, $$

(7)

where X is an $n \times p$ regression design matrix and ${\mathbf{u}}, \, {\mathbf{v}}$ are two $n \times 1$ vectors with elements of $u_{i} ,v_{i}$ respectively.

In the literature, there are other quantile regression methods. Bayesian approaches provide convenient alternative inference tools for quantile regression. A working likelihood is needed to carry out Bayesian analysis [21]. It is interesting to explore the Bayesian quantile regression methods. In Sect. 7.2, we compare a type of Bayesian quantile regression with this paper which proposes direct nonparametric quantile regression.

In this paper, two real-world datasets are analyzed using linear mean regression, linear quantile regression and nonparametric quantile regression. The first dataset is a tri-variate example based on the status of COVID-19 cases in Ontario that comes from the Ontario Government. The second example’s data comes from National Health and Nutrition Examination Survey (NHANES) about systolic blood pressures.

1.1 Example 1. Number of Hospitalized COVID-19 Patients in Ontario, Canada (April 19, 2020–June 30, 2021)

COVID-19, the coronavirus is a contagious disease spread worldwide and causing the current ongoing pandemic. Based on United States Centers for Disease Control and Prevention (CDC)’s report in March 2020, COVID-19 has already done more damage to the world than the SARS pandemic [4], which appeared in 2002. COVID-19’s average mortality rate is estimated to be around 3.4% by the WHO. However, in Washington State USA, 67% of critically ill patients died [25]. Furthermore, since there are no specific coronavirus treatments right now [16]. People with severe COVID-19 symptoms must be hospitalized. Ensuring sufficient human and physical resources is essential to minimize the mortality rate.

The virus was confirmed in Canada on January 27, 2020, and in March 2020, as cases of community transmission were confirmed, all of Canada's provinces and territories declared states of emergency. Provinces and territories have, to varying degrees, implemented school and daycare closures, prohibitions on gatherings, closures of non-essential businesses and restrictions on entry. By mid to late summer of 2020, the country saw a steady decline in active cases until the beginning of late summer. Through autumn, the country saw a resurgence of cases in all provinces and territories. On September 23, 2020, Canada declared a “second wave” of the virus. Nation-wide cases, hospitalizations and deaths spiked preceding and following December 2020 and January 2021. Following Health Canada's approval of the Pfizer–BioNTech, mRNA-1273 and the Oxford–AstraZeneca vaccine for use, and on March 5, 2021, they additionally approved the Janssen COVID-19 vaccine for a total of four approved vaccines in the nation [14].

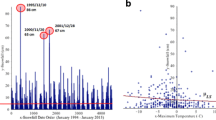
Ontario Canada, in late summer 2021, the province began preparing for a fourth wave of the virus, which was largely affecting unvaccinated individuals. In January 2022, there were changes in the policy regarding testing, such that the reported number of new positive cases no longer reflects the true number of new positive cases. In this paper, we focus on data from April 19, 2020–June 30, 2021, Ontario COVID-19 cases daily data collected for $n^{*} = 438$ days [13]. We focus on high numbers of hospitalized COVID-19 patient’s relationship with percent positive tests last day and the number of new cases. Percent positive tests last day is the percent of COVID-19 tests that were positive in the last day. The response variable is the number of hospitalized COVID-19 patients. To focus on high numbers of hospitalized COVID-19 patients, its upper quartile (75%) 1010 patients, will be used as a threshold. After applying the threshold of 1010, the data was reduced to $n = 103$ days. Figure 1 is a chart plot shows $n^{*} = 438$ days of number of hospitalized COVID-19 patients. Table 1 shows the top 5 daily number of hospitalized COVID-19 patients in Ontario, Canada.

Fig. 1

The number of hospitalized COVID-19 patients in 438 days ($n^{*} = 438$) between April 19, 2020 and June 30, 2021, with a threshold of 1010 hospitalized COVID-19 patients. The number of days with data value above 1010 threshold is 103 days. ($n = 103$)

Table 1 Top 5 daily data of the number hospitalized of COVID-19 patients in Ontario, Canada (April 19, 2020–June 30, 2021)

We also note that there were three waves of COVID-19 during April 19, 2020–June 30, 2021. The top three values are 1043 patients on May-04-2020, 1674 patients on Jan-13-2021, and 2360 patients on April 20, 2021. Our goal is to create a statistical model to analyze the current Ontario hospitalized COVID-19 patients’ number and predict future extreme events.

We are interested in the relationship between the response variable y (the number of hospitalize COVID-19 patients) with $x_{1}$ (percent positive test last day) and $x_{2}$ (the number of new cases). By employing a least-square mean regression model in (1), we can model it using

$$ \mu_{{(y|\varvec{x})}} = E(y|x_{1} ,x_{2} ) = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} . $$

Using the least-square method to estimate ${\varvec{\beta}} = \left( {\beta_{0} ,\beta_{1} ,\beta_{2} } \right)^{T}$. The least-square plane function is

$$\widehat{\mu }_{LS} (x_{1} ,x_{2} ) = {650}{\text{.2139}} + 67.9667x_{1} + 0.1731x_{2}.$$

The 0.95th quantile plane by the regular linear quantile regression (QR) in (5) is given by

$$\begin{aligned} \widehat{{Q_{R} }}\left( {0.95|x_{1} ,x_{2} } \right) &= \widehat{\beta }_{0} \left( {0.95} \right) + \widehat{\beta }_{1} \left( {0.95} \right)x_{1} + \widehat{\beta }_{2} \left( {0.95} \right)x_{2}\\ &= \, 640.5811 + 89.8649x_{1} + 0.2539x_{2}. \end{aligned} $$

Figure 2 is a 3D plot of the LS mean regression plane (in Green) and a linear quantile regression plane (in blue) which shows that there is a strong positive relation between number of hospitalize COVID-19 patients and its regressors. The average number of hospitalized patients increases as percent positive test last day increase. Similarly, the average number of hospitalized patients increases as the number of new cases per day increases.

Fig. 2

A 3D LS mean regression plane $\widehat{\mu }_{LS} (x_{1} ,x_{2} )$ (in green) and the 0.95th linear quantile regression plane $\widehat{{Q_{R} }}\left( {0.95|x_{1} ,x_{2} } \right)$ (in blue) of the number of hospitalized COVID-19 patients y with a threshold of 1010 vs the percent positive test last day $x_{1}$ and the number of new cases $x_{2}$ ($n = 103$). Data are in black dots. We note that about 95% data below the $\widehat{{Q_{R} }}\left( {0.95|x_{1} ,x_{2} } \right)$ plane

For building a 2D relationship of y—the number of hospitalized COVID-19 patients and $x_{1}$—the percent positive test last day. We fix $x_{2}$—the number of new cases. Let $x_{2}$ = 3442 which is the 0.75th quantile of $x_{2}$. Then the least square mean regression line and the 0.95th linear quantile regression line of y and $x_{1}$ are

$$ \widehat{\mu }_{LS} (x_{1} )\left| {_{{x_{2} = 3442}} } \right. = 1246.1294 + 67.9667x_{1} ,\;{\text{when}}\;x_{2} = 3442\,\left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{2} } \right). $$

$$ \widehat{{Q_{R} }}\left( {0.95|x_{1} } \right)\left| {_{{x_{2} = 3442}} } \right. = 1514.521 + 89.8649x_{1} ,\;{\text{when}}\;x_{2} = 3442\,\left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{2} } \right). $$

Figure 3a provides a scatter plot of $x_{1}$—percent positive test last day versus y—the number of hospitalized COVID-19 patients with its least-squares mean regression line (in green) and 0.95th linear quantile regression line (in blue).

Fig. 3

Data are black dots, n = 103. a A 2D LS mean regression line $\widehat{\mu }_{LS} (x_{1} )$ (in green) and a 0.95th linear quantile regression line $\widehat{{Q_{R} }}\left( {0.95|x_{1} } \right)$ (in blue) of the number of hospitalized COVID-19 patients y versus percent positive test last day $x_{1}$ when $x_{2}$ = 3442; b A 2D LS mean regression line $\widehat{\mu }_{LS} (x_{2} )$ (in green) and a 0.95th linear quantile regression line $\widehat{{Q_{R} }}\left( {0.95|x_{2} } \right)$ (in blue) of the number of hospitalized COVID-19 patients y versus the number of new cases $x_{2}$ when $x_{1}$ = 7.8

Similarly, for building a 2D relationship of y—the number of hospitalized COVID-19 patients and $x_{2}$—the number of new cases. We fix $x_{1}$—the percent positive test last day. Let $x_{1}$ = 7.8(%) which is the 0.75th quantile of $x_{1}$. We have the least square mean regression line and the 0.95th linear quantile regression line of line of y and $x_{2}$ are

$$ \widehat{\mu }_{LS} (x_{2} )\left| {_{{x_{1} = 7.8}} } \right. = 1180.3541 + 0.1731x_{2} ,\;{\text{when}}\;x_{1} = 7.8\,\left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{1} } \right). $$

$$ \widehat{{Q_{R} }}\left( {0.95|x_{2} } \right)\left| {_{{x_{1} = 7.8}} } \right. = 1341.5277 + 0.2539x_{2} ,\;{\text{when}}\;x_{1} = 7.8\,\left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{1} } \right). $$

Figure 3b provides a 2D plots of scatter plot of x₂—the number of new cases versus the y—number of hospitalized COVID-19 patients with its least-squares mean regression lines (in green) and 0.95th linear quantile regression lines (in blue).

From Figs. 2 and 3, we observed that the least-squares mean estimator $\widehat{\mu }_{LS}$ estimates the average number of hospitalized COVID-19 patients in Ontario, but it does not represent the extreme high values of the patients in hospital data pattern. It can not estimate the critical situation when the hospitals are crowded with patients. The 0.95th linear Quantile regression $\widehat{{Q_{R} }}\left( {0.95|x_{1} ,x_{2} } \right)$ indicates the 95% number of hospitalized COVID-19 patients in Ontario under the plane or lines. But we note that this model does not capture nonlinear patterns in the high quantiles. In this paper, we proposed a new quantile regression estimator to improve estimating the high quantile plane for extreme values of numbers of hospitalized COVID-19 patients. We will use new quantile regression model to analysis this example in Sect. 6.

1.2 Example 2: Systolic Blood Pressures (January 2017–December 2018)

Blood pressure is expressed as a measurement with two numbers: systolic blood pressure and diastolic blood pressure. The systolic blood pressure refers to the amount of pressure the blood exerts against the artery walls during the heart contraction. The diastolic blood pressure represents the pressure when the heart rests between beats. High blood pressure, also referred to as hypertension, is blood pressure that is higher than normal. Hypertension may cause complications such as heart attack, stroke, and aneurysm [5, 23].

Based on existing studies, high systolic pressures pose a greater risk of heart disease than elevated diastolic pressure. As a result, the response variable of this example is systolic blood pressure (SBP). The CDC is the national public agency of the United States. The CDC categorizes blood pressure in adults into 4 groups: normal, elevated (prehypertension), hypertension stage 1, and hypertension stage 2 [15]. These classifications are given in Table 2. A millimeter of mercury is a manometric unit of pressure, formerly defined as the extra pressure generated by a column of mercury one millimeter high and currently defined as exactly 133.322387415 pascals. It is denoted mmHg.

Table 2 Classification of blood pressure, Centers for Disease Control and Prevention, 2020, USA

NHANES or the National Health and Nutrition Examination Survey, is a program by the CDC that aims to assess the health and nutritional status of adults and children in the USA. We will examine NHANES’s 2017–2018 data which consists of n^* = 6240 subjects between weights 18.6 kg to 219.6 kg [5]. For this study, a threshold of 160 mmHg is applied since people with SBP higher than 160 mmHg are at high risk for coronary heart disease, which can lead to a heart attack or stroke [3]. After omitting subjects with SBP less than 160 mmHg, the data is reduced to $n** = 261$ subjects.

One common cause of hypertension is obesity. Being overweight increases the chance of developing high blood pressure [29]. We set response variable y – SBP (mmHg) vs regressor x – weight (kg). We treat 12 subjects whose weight x > 215 kg as outliers, leaving the n = 249 subjects with weight between 18.6–125 kg, Table 3 shows the top 5 data of SBP. Figure 4 presents the SBP for the n = 249 subjects, and a threshold of 160 mmHg is indicated. Let the response variable y be SPB and explanatory variable x be the subject’s weight. Then, we can employ a least-squares mean regression model to estimate the conditional mean of SBP mmHg (y) given subject’s weight kg (x).

Table 3 Top 5 data for SBP of subjects in USA (January 2017–December 2018) with weight between 18.6 and 125 kg

Fig. 4

Systolic blood pressures (SBP mmHg) of subjects (n^* = 6240) tested by the Centers for Disease Control and Prevention between Month, United States of American, January 2017—December 2018. The number of subjects who have SBP over 160 mmHg is n** = 261

Similar as Example 1, we obtained the least-squares liner regression line and the 0.95th liner quantile regression line as (see Fig. 5)

Fig. 5

Data are black dotes, n = 249. The $\widehat{\mu }_{LS} (x)$ line and the $\widehat{{Q_{R} }}\left( {0.95|x} \right)$ line for Systolic blood pressures (SBP mmHg) y versus weight x for subject with SBP greater than 160 mmHg and weight between 18.6 and 125 kg

$$\widehat{\mu }_{LS} (x) = {173}{\text{.9923}} + {0}{\text{.0191}}x \quad {\text{and}} \quad \widehat{Q}_{R} \left( {0.95|x} \right) = \, 188.2925 + 0.1791x.$$

Figure 5 shows that the least-squares mean line $\widehat{\mu }_{LS} (x)$ can only estimate the mean values of systolic blood pressure relate to the weight. Also, Fig. 5 also shows about 95% subjects with systolic blood pressure data under line of the 0.95th quantile regression $\widehat{{Q_{R} }}\left( {0.95|x} \right)$. However, both $\widehat{\mu }_{LS} (x)$ and $\widehat{{Q_{R} }}\left( {0.95|x} \right)$ lines do not catch the relation well between very high values of systolic blood pressures related to weight. This paper, we propose a new direct nonparametric quantile regression method with 3 steps computational algorithm in Sect. 3, and we will discuss Example 2 by using the proposed new quantile regression method in Sect. 6.

In this paper, notation is introduced in Sect. 2. We propose a direct nonparametric quantile regression method with a three-step computer algorithm in Sect. 3. Section 4 gives asymptotic properties of proposed direct nonparametric quantile regression. The results of Monte Carlo simulation are in Sect. 5. Section 6 compares the proposed direct nonparametric quantile regression with the regular quantile regression and mean regression for two examples. Finally, Sect. 7 gives conclusions and discussions..

2 Notation

2.1 Extreme Value Distribution

Extreme value theory (EVT) is used to study the probability of extreme observations especially from heavy-tailed probability distributions. It helps us find possible limit distribution for sample maxima/minima of independent and identically distributed (i.i.d.) random variables. [7] de Haan & Ferreira (2006) and [24] etc. developed theory; experts also applied extreme value models to many fields, i.e. [6, 9, 17] and [19].

Let ${X}_{1},{X}_{2} ,...,{X}_{n}$ be i.i.d. random variables. Extreme value theory finds the possible limiting distribution of the sample extreme $\max \left( {X_{1} ,X_{2} ,...,X_{n} } \right)$ or $\min \left( {X_{1} ,X_{2} ,...,X_{n} } \right)$ as $n \to \infty$.

Definition 1

(Fisher & Tippett, 1928; Gnedenko, 1943) The c.d.f. of any extreme value distribution is denoted by G $_{\gamma }$(ax + b) for any constants a > 0, b $\in$ R,

$$ G_{\gamma } \left( x \right) = \left\{ {\begin{array}{*{20}c} {\exp \left( { - \left( {1 + \gamma x} \right)^{{ - \frac{1}{\gamma }}} } \right),} & {1 + \gamma x > 0{\text{ and }}\gamma \ne 0:} \\ {\exp \left( { - e^{ - x} } \right),} & {\gamma = 0, x>0. } \\ \end{array} } \right. $$

(8)

where the real parameter $\gamma$ is called the extreme value index.

In this work, we are interested in predicting extreme events by estimating the high conditional quantile curves of heavy-tailed distributions ($\gamma$ > 0).

2.2 Generalized Pareto Distribution

A conditional extreme value distribution exceeding a threshold has a generalized Pareto distribution (GPD) ([24] Pickands, 1975, and [8]).

Definition 2

The c.d.f. $H{}_{\gamma }(x)$ of the two parameter GPD($\gamma ,\sigma$) with shape parameter $\gamma$, location parameter $\mu$ and scale parameter $\sigma$ for random variable X is given by

$$ H{}_{\gamma }(x) = 1 - \left( {1 + \gamma \frac{(x - \mu )}{\sigma }} \right)^{ - 1/\gamma } , \, \gamma \ne 0,{ 0} < \mu < \infty , \, \sigma > 0, \, \mu < x < \infty . $$

(9)

3 New Estimation Method Proposed: A Direct Nonparametric Quantile Regression

This paper proposes a new direct nonparametric quantile regression method. We will ignore the idea of the linear model (4) for generality. Instead, a direct estimator of the true conditional quantile

$$\widehat{Q}_{y} \left( {\tau |{\varvec{x}}} \right) = \widehat{Q}_{y} \left( {\tau |x_{1} ,x_{2} ,...,x_{k} } \right) = \widehat{F}^{ - 1} \left( {\tau |{\varvec{x}}} \right),$$

will be obtained by using local conditional quantile estimator $\xi_{i} (\tau |{\varvec{x}}) = \widehat{Q}_{y} \left( {\tau |{\varvec{x}}_{i} } \right)$ based on the $i{\text{th}}$ point of given random sample, $\left\{ {\left( {y_{i} ,{\varvec{x}}_{i} } \right), \, i = 1,...,n} \right\}$, for ${\varvec{x}}_{i} = \left( {x_{1i} ,x_{2i} ,...,x_{di} } \right)^{T}$, i = 1,2,…,n..

This direct nonparametric quantile regression algorithm has three steps shown as follows:

• Step 1 Estimate Conditional c.d.f.

First estimate the conditional c.d.f. $F(y|{\varvec{x}})$ of y for given $\varvec{x = }(x_{1} ,x_{2} ,...,x_{d} )$ using kernel estimation method [26, 27]

$$ \widehat{F}\left( {y|{\varvec{x}}} \right) = \frac{{\frac{1}{n}\sum\nolimits_{i = 1}^{n} {I\left( {Y_{i} \le y} \right)K\left\{ {\frac{{{\varvec{x}} - {\varvec{X}}_{i} }}{h}} \right\}} }}{{\widehat{g}\left( {\varvec{x}} \right)}}, $$

(10)

where the $I\left( {Y_{i} \le y} \right)$ is an indicator function and $\hat{g}(\varvec{x})$ is an estimator of the marginal density of x.

To estimate the marginal density of x, we use a kernel density estimator. Consider a d-dimensional random sample ${\varvec{X}}_{i} = \left( {x_{1i} ,x_{2i} ,...,x_{di} } \right),\, \, i = 1,2,...,n \,$ from a population $\varvec{x} = (x_{1} ,x_{2} ,...,x_{d} )$ with density g(x). The kernel density estimator for $g(x)$ is given by

$$\widehat{g}({\varvec{x}}) = \frac{1}{{nh^{d} }}\sum\limits_{i = 1}^{n} {K\left\{ {\frac{{\varvec{x}} - {\varvec {X}}_{i} }{h}} \right\}},$$

where $h > 0$ is the bandwidth and the kernel function $K({\varvec{x}})$ is a function defined for d-dimensional $\varvec{x = }(x_{1} ,x_{2} ,...,x_{d} )$ which satisfies $\int_{{R^{d} }} {K({\varvec{x}})dx = 1},$ [11] suggested using

$$\widehat{g}({\varvec{x}}) = \frac{{(\det {\varvec{S}})^{ - 1/2} }}{{nh^{d} }}\sum\limits_{i = 1}^{n} {k\left\{ {\frac{{\left( {\varvec{x}} - {\varvec {X}}_{i} \right)^{T} {\varvec{S}}^{ - 1} \left( {\varvec{x}} - {{\varvec {X}}_{i} } \right)}}{{h^{2} }}} \right\}},$$

where S is the sample covariance matrix of the data, and the function k is

$$k(u) = \left( {\frac{1}{2\pi }} \right)^{d/2} \exp \left( { - \frac{u}{2}} \right), \, k({\varvec{x}}^{T} {\varvec{x}}) = K({\varvec{x}}) = (2\pi )^{ - d/2} \exp \left( { - \frac{1}{2}{\varvec{x}}^{T} {\varvec{x}}} \right).$$

An estimator for the bandwidth $h > 0$ will be given by [27, p. 85].

$$\widehat{h}_{opt} = A(K)n^{ - 1/(d + 4)},$$

where $A(K) = \left( {\frac{4}{d + 1}} \right)^{1/(d + 4)}$ if a multivariate normal kernel is used for smoothing the normal distribution data with unit variance.

• Step 2 Estimate the Local Conditional Quantile Function

Ideally, one would like to estimate the conditional quantile function $\xi \left( {\tau |{\varvec{x}}} \right)$ of y given x by inverting the estimated conditional c.d.f. in (10) from step 1

$$\widehat{\xi }\left( {\tau |{\varvec{x}}} \right) = \widehat{Q}_{y} \left( {\tau |{\varvec{x}}} \right) = \inf \left\{ {y:\widehat{F}\left( {y|{\varvec{x}}} \right) \ge \tau } \right\} = \widehat{F}^{ - 1} \left( {\tau |{\varvec{x}}} \right).$$

However, since the kernel estimated conditional c.d.f. $\hat{F}\left( {y|{\varvec{x}}} \right)$ has many terms, it is challenging to compute its global inverse function $\hat{\xi }\left( {\tau |{\varvec{x}}} \right)$. To bypass the computational difficulties, we invert the estimated conditional c.d.f. (10) at the $i{{{\text{th}}}}$ data point estimates the local conditional quantile point $\widehat{\xi }_{i} \left( {\tau |{\varvec{x}}_{i} } \right)$

$$\widehat{\xi }_{i} \left( {\tau |{\varvec{x}}_{i} } \right) = \widehat{Q}_{y} \left( {\tau |{\varvec{x}}_{i} } \right) = \inf \left\{ {y:\widehat{F}\left( {y|{\varvec{x}}_{i} } \right) \ge \tau } \right\} = \widehat{F}^{ - 1} \left( {\tau |{\varvec{x}}_{i} } \right),\, \, i = 1,2,...,n.$$

• Step 3 Propose a Nonparametric Direct Quantile Regression

This paper proposes a direct nonparametric quantile regression estimator for the $\tau^{{{\text{th}}}}$ conditional quantile curve of x using Nadaraya-Watson (NW) nonparametric regression estimator [28] on $\left( {{\varvec{x}}_{i} ,\widehat{\xi }_{i} \left( {\tau |{\varvec{x}}_{i} } \right)} \right)$ for $i = 1,2,...,n$. The proposed direct nonparametric quantile regression is given by

$$ \widehat{{Q_{N} }}\left( {\tau |{\varvec{x}}} \right) = \widehat{\xi }\left( {\tau |{\varvec{x}}} \right) = \frac{{\sum\nolimits_{i = 1}^{n} {K_{{\varvec{h}}} \left\{ {{\varvec{x}} - {\varvec{X}}_{i} } \right\}} \widehat{\xi }_{i} \left( {\tau |{\varvec{x}}_{i} } \right)}}{{\sum\nolimits_{j = 1}^{n} {K\left\{ {{\varvec{x}} - {\varvec{X}}_{j} } \right\}} }} = \sum\limits_{i = 1}^{n} {W_{{h_{x} }} \left( {{\varvec{x}},{\varvec{X}}_{i} } \right)} \widehat{\xi }_{i} \left( {\tau |{\varvec{x}}_{i} } \right), \, 0 < \tau < 1 $$

(11)

where the equivalent kernel $W_{{h_{x} }} \left( {{\varvec{x}},{\varvec{X}}_{i} } \right)$ is

$$W_{{h_{x} }} \left( {{\varvec{x}},{\varvec{X}}_{i} } \right) = \frac{{K_{{\varvec{h}}} \left\{ {{\varvec{x}} - {\varvec{X}}_{i} } \right\}}}{{\sum\limits_{j = 1}^{n} {K\left\{ {{\varvec{x}} - {\varvec{X}}_{j} } \right\}} }}, \, i = 1,2,...,n,$$

where

$$K_{{\varvec{h}}} \left\{ {{\varvec{x}} - {\varvec{X}}_{i} } \right\} = \frac{1}{{nh_{1} ...h_{d} }}\prod\limits_{j = 1}^{d} {K\left( {\frac{{x - x_{ij} }}{{h_{j} }}} \right)} , \, i = 1,2,...,n,$$

where K is the kernel function and $h_{j} > 0$ is the bandwidth for the $j{\text{th}}$ dimension, and $\varvec{h} = \left( {h_{1} ,h_{2} ,...,h_{d} } \right)$.

We will use the standard normal kernel K for the kernel estimation. The optional bandwidth will also be considered [27],

$$ h_{j,opt} = \left\{ {\int {t^{2} K\left( t \right)dt} } \right\}^{ - 2/5} \left\{ {\int {K\left( t \right)^{2} dt} } \right\}^{1/5} \left\{ {\int {\left( {\nabla^{2} \left( {\varvec{x}} \right)} \right)^{2} d{\varvec{x}}} } \right\}^{ - 1/5} n^{ - 1/5} , \, j = 1,2,...,d, $$

where n is the sample size of the random sample.

4 Asymptotic Properties of the Propose Direct Nonparametric Quantile Regression

In this section, we derive the asymptotic distribution of the proposed direct nonparametric quantile regression estimator $\widehat{\xi }\left( {\tau |\varvec{x}} \right)$ in (11). Let the following conditions hold:

• Condition 1 (C1). In (10both the estimated conditional c.d.f. $\widehat{F}\left( {y|\varvec{x}} \right)$ of $y$ given ${\varvec{x}} = \left( {x_{1} ,x_{2} ,...,x_{d} } \right)^{T}$ and p.d.f. $g\left( \varvec{x} \right)$ of ${\varvec{x}}$ have continuous second-order derivatives with respect to ${\varvec{x}}$. Also, $K\left( \bullet \right)$ is a symmetric, bounded, and compactly supported probability density function.

• Condition 2 (C2). In (11), the product $nh_{1} ...h_{d} \to \infty$ as $h_{j} \to \infty$ for all $j = 1,2,...,d.$

• Condition 3 (C3). The estimated conditional c.d.f. $\widehat{F}\left( {y|\varvec{x}} \right)$ of $y$ given ${\varvec{x}} = \left( {x_{1} ,x_{2} ,...,x_{d} } \right)^{T}$ in (8) has a conditional p.d.f. $f\left( {y|\varvec{x}} \right)$ of $y$ given $\varvec{x}$ that is continuous in ${\mathbb{R}}^{d}$ and $f\left( {\xi \left( {\tau |\varvec{x}} \right)} \right) > 0$.

The main asymptotic result for $\widehat{\xi }\left( {\tau |\varvec{x}} \right)$ given in Theorem 1.

Theorem 1

Asymptotic properties of proposed direct nonparametric quantile regression, under Conditions C1, C2, and C3,

$$ \left( {nh_{1} ,h_{2} ,...,h_{d} } \right)^{1/2} \left( {\widehat{\xi }\left( {\tau |{\varvec{x}}} \right) - \xi \left( {\tau |{\varvec{x}}} \right) - \sum\limits_{j = 1}^{d} {h_{j}^{2} B_{\tau ,j} \left( x \right)} } \right)\mathop{\longrightarrow}\limits^{D}N\left( {0,V_{\tau } \left( {\varvec{x}} \right)} \right),{\text{ as }}n \to \infty $$

(12)

where $\widehat{\xi }\left( {\tau |{\varvec{x}}} \right)$ is defined in (9), $\xi \left( {\tau |{\varvec{x}}} \right)$ is the true conditional quantile, and

$$ B_{\tau ,j} = \frac{{B_{j} \left( {y,\varvec{x}} \right)}}{{f\left( {\xi \left( {\tau |\varvec{x}} \right)} \right)}}, $$

where

$$ B_{\tau ,j} \left( x \right) = \frac{1}{2}\int {v^{2} K\left( v \right)dv\left[ {F^{\prime\prime}_{jj} \left( {y|\varvec{x}} \right) + \frac{{2g^{\prime}_{j} F^{\prime}_{j} \left( {y|\varvec{x}} \right)}}{{g\left( \varvec{x} \right)}}} \right]} , \, j = 1,2...,d. $$

Here, for a real function $H\left( {y,\varvec{x}} \right), \, j = 1,2...,d,$ $H^{\prime}_{j} \left( {y,\varvec{x}} \right)$ and $H^{\prime\prime}_{jj} \left( {y,\varvec{x}} \right)$ are the first and second derivatives of $H\left( {y,\varvec{x}} \right)$ with respect to $x_{j}$ , respectively. For $j = 0, \, H^{\prime}_{0} \left( {y,\varvec{x}} \right)$ and $H^{\prime\prime}_{00} \left( {y,\varvec{x}} \right)$ are the first and second derivatives of $H\left( {y,\varvec{x}} \right)$ with respect to y, respectively. Also,

$$ V_{\tau } \left( \varvec{x} \right) = \frac{{\tau \left( {1 - \tau \prod\limits_{j = 1}^{d} {\left[ {\int {K^{2} \left( {v_{j} } \right)} dv_{j} } \right]} } \right)}}{{f^{2} \left( {\xi \left( {\tau |\varvec{x}} \right)} \right)g\left( {\xi \left( {\tau |\varvec{x}} \right)} \right)}}. $$

Proof. It is similar to Theorem 2 in [18].

5 Computer Simulations

Monte Carlo Simulation is used in this Section to compare efficiencies of the new proposed direct nonparametric quantile regression estimator $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ (QN) in (11) against the regular linear quantile regression estimator $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ (QR) by using (4) and (5). We generate m = 1000 random samples of size n = 200 from the Fisk distribution (the Burr XII distribution) [10] for this simulation.

The Fisk distribution has the c.d.f. with $\gamma$ as the tail index.

$$ F\left( {y,\gamma } \right) = \frac{1}{{1 + y^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} \gamma }} \right. \kern-0pt} \gamma }}} }}, \, \gamma > 0,\;y \, > \, 0. $$

(13)

Let X be a one-dimensional and uniformly distributed on [0, 1], and Y given $X = x$ has the Fisk distribution with the conditional c.d.f.

$$ F_{Fisk} \left( {y|x,\gamma \left( x \right)} \right) = \frac{1}{{1 + y^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} \gamma }} \right. \kern-0pt} \gamma }\left( x \right)}} }}, \, \gamma \left( x \right) > 0, \, 0 \le x \le 1,\;y \, > \, 0 $$

(14)

and a conditional tail index given by

$$ \gamma_{Fisk} \left( x \right) = \frac{3}{100}\left( {\frac{{120x^{2} - 90x + 17}}{{15x^{2} - 15x + 4}}} \right), \, 0 \le x \le 1. $$

(15)

The joint distribution of Fisk y and uniform x is given in Fig. 6. The true $\tau^{{{\text{th}}}}$ conditional quantile function of y for given x is

$$ Q_{YFisk} \left( {\tau |x} \right) = Q_{y} \left( {\tau |x} \right) = \left( {\frac{\tau }{1 - \tau }} \right)^{\gamma \left( x \right)} , \, 0 \le x \le 1, \, \gamma \left( x \right) > 0, \, 0 < \tau < 1. $$

(16)

Fig. 6

a The joint distribution of Fisk y and uniform x. b Fisk distributed y’s conditional quantile given x at $\tau = 0.95$, $\tau = 0.97$ and $\tau = 0.99$

Figure 6 shows the true conditional quantiles of Fisk distributed y given Uniform x is not linear. We note that the traditional quantile regression has the assumption of linear model, We expect that the proposed direct nonparametric quantile regression estimator $\widehat{{Q_{N} }}\left( {\tau |x} \right)$(QN) should outperform the regular quantile linear regression estimator $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ (QR) because $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ does not have the linear model limitation. For comparison, we will examine the average simulation plots, box plots, simulation mean squared errors, and simulation efficiencies in the following section.

We use two quantile regression methods are going to be used to estimate the true conditional quantile of the Fisk distribution,

• 1. The regular linear quantile regression method (QR) $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ based on (4),

  $$ \widehat{{Q_{R} }}\left( {\tau |x} \right) = \widehat{\beta }_{0} \left( \tau \right) + \widehat{\beta }_{1} \left( \tau \right)x, \, 0 < \tau < 1. $$

• 2. The proposed direct nonparametric quantile regression method (QN) $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ based on (11)

  $$\widehat{{Q_{N} }}\left( {\tau |x} \right) = \sum\limits_{i = 1}^{n} {W_{{h_{x} }} \left( {{{x}},{{X}}_{i} } \right)} \widehat{\xi }_{i} \left( {\tau |{{x}}_{i} } \right), \, 0 < \tau < 1.$$

For each method, we generate size n = 200, m = 1000 samples, $\widehat{{Q_{R} }}_{,i} \left( {\tau |x} \right)$ and $\widehat{{Q_{N} }}_{,i} \left( {\tau |x} \right)$ are estimated from the $i{{{\text{th}}}}$ sample, where $i = 1,2,...,n$. Then we compare the $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ with the true quantile computed base on function (16) $Q_{YFisk} \left( {\tau |x} \right)$ quantiles for $\tau = 0.95, \, 0.97,{\text{ and }}0.99$.

5.1 Average Simulation Plots

The average of $m = 1000, \, n = 200$ estimated curves obtained by QR and QN methods are compared with the true $\tau^{{{\text{th}}}}$ conditional quantile $Q_{y} \left( {\tau |x} \right)$ at $\tau = 0.95, \, 0.97,{\text{ and }}0.99$ in Fig. 7. It shows that the proposed direct nonparametric quantile regression estimator $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ in red curves follow the true $Q_{YFisk} \left( {\tau |x} \right)$ in (16) in black dash closer than the regular linear quantile regression estimator $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ straight lines at high quantiles.

Fig. 7

Plots of simulation average $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ (blue) and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ (red) for m = 1000 samples with size n = 200 versus the true conditional quantile $Q_{YFisk} \left( {\tau |x} \right)$ (black dash) at a $\tau = 0.95$, b $\tau = 0.97$, c $\tau = 0.99$

Figure 8 compares the box plots for the estimates for y given x = 0.4 of $\widehat{{Q_{R} }}\left( {\tau |{x}} \right)$ and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ at (a) $\tau = 0.95,$ (b) $\tau = 0.97$ and (c) $\tau = 0.99$. The result shows that the $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ are more concentrated expected values and smaller variance to the true conditional quantile values $Q_{y} \left( {\tau |x} \right)$ in red straight lines. The proposed $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ has a better performance than the regular linear quantile regression $\widehat{{Q_{R} }}\left( {\tau |{x}} \right)$.

Fig. 8

Box plots of the estimates $\widehat{{Q_{R} }}\left( {\tau |{\varvec{x}}} \right)$ (blue) and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ (green) when $x = 0.4$. The true $Q_{y} \left( {\tau |x} \right)$ values are the red lines, with $m = 1000$ samples at a $\tau = 0.95$, b $\tau = 0.97$, c $\tau = 0.99$

5.2 Simulation Mean Squared Errors and Simulation Efficiencies

The simulation mean squared error (SMSE) of the QR estimator and QN estimator are defined as follows

$$ {\text{SMSE}}\left( {\widehat{{Q_{R} }}\left( \tau \right)} \right) = \frac{1}{m}\sum\limits_{i = 1}^{m} {\int_{0}^{1} {\left( {\widehat{{Q_{R} }}_{,i} \left( {\tau |x} \right) - Q_{YFisk} \left( {\tau |x} \right)} \right)} }^{2} dx; $$

(17)

$$ {\text{SMSE}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right) = \frac{1}{m}\sum\limits_{i = 1}^{m} {\int_{0}^{1} {\left( {\widehat{Q}_{N,i} \left( {\tau |x} \right) - Q_{YFisk} \left( {\tau |x} \right)} \right)} }^{2} dx, $$

(18)

where the true $\tau^{{{\text{th}}}}$ conditional quantile $Q_{YFisk} \left( {\tau |x} \right)$ is computed base on function (16), the $\widehat{{Q_{R} }}_{,i} \left( {\tau |x} \right)$ and $\widehat{{Q_{N} }}_{,i} \left( {\tau |x} \right)$ are estimated from the $i{{{\text{th}}}}$ sample, i = 1,2,…,n. from (4) and (11) respectively.

Then the simulation efficiency (SEFF) of QN estimator relative to QR estimator is defined as

$$ {\text{SEFF}}_{{Q_{R} }} \left( {\widehat{{Q_{N} }}\left( \tau \right)} \right) = \frac{{{\text{SMSE}}\left( {\widehat{{Q_{R} }}\left( \tau \right)} \right)}}{{{\text{SMSE}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)}} $$

(19)

where the ${\text{SMSE}}\left( {\widehat{{Q_{R} }}\left( \tau \right)} \right)$ and ${\text{SMSE}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)$ of the QR and QN estimator is given above.

A summary of the SMSEs and SEFFs for the two estimation methods is provided in Table 4.

Table 4 Simulation mean squared errors (SMSE) and simulation efficiencies (SEFF) for estimating $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ using m = 1000 samples of size n = 200

The SMSE of $\widehat{Q}_{R} \left( {\tau |x} \right)$ and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ are in Table 4. At each $\tau$ levels, the ${\text{SMSE}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)$ value is smaller than ${\text{SMSE}}\left( {\widehat{Q}_{R} \left( \tau \right)} \right)$ value, then the SEFF of $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ estimator relative to $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ estimator is greater than 1 at every $\tau$ levels. This indicates that the proposed direct nonparametric quantile regression is more efficient than the regular quantile regression for estimating high conditional quantiles of the Fisk distribution $Q_{YFisk} \left( {\tau |x} \right)$ in (16).

The ${\text{SMSE}}$ for $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ and proposed $\widehat{Q}_{N} \left( {\tau |x} \right)$ at different $\tau$ levels are plotted in Fig. 9a, which shows ${\text{SMSE}}\left( {\widehat{{Q_{R} }}\left( \tau \right)} \right)$ > ${\text{SMSE}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)$. Figure 9b shows that ${\text{SEFF}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)$ > 1 relative to $\widehat{{Q_{R} }}\left( {\tau} \right)$.

Fig. 9

a Simulation mean squared errors ${\text{SMSE}}\left( {\widehat{{Q_{R} }}\left( \tau \right)} \right)$ (green line) and ${\text{SMSE}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)$ (red line); b (blue) ${\text{SEFF}}\left( {\widehat{{Q_{N} }}\left( \tau \right)} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau} \right)$ (blue line)

6 Applications

In this Section, we apply the proposed nonparametric QN methods in (11) and regular QR method in (4) to two real-world examples in Sect. 1.

Example 1. Hospitalized COVID-19 Patients in Ontario, Canada (April 19, 2020–June 30, 2021)

Let us recall the Example 1 in Sect. 1, the Ontario, Canada Hospitalized COVID-19 patients’ example. The purpose of this example is to predict the high conditional quantile curves of the number of hospitalized COVID-19 patients, extreme values of which may cause significant strain on the health system. A threshold of 1010 (hospitalized patients) is applied. After the threshold is applied, $n = 103$ data are retained.

Goodness-of-fit Tests for Heavy Tailed Distribution

We will determine if the reduced data set, n = 103, with greater than 1010 hospitalized COVID-19 patients is from a generalized Pareto distribution (GPD) [8], with probability density function (pdf.)

$$ f_{\gamma ,\mu ,\sigma } \left( x \right) = \frac{1}{\sigma }\left( {1 + \gamma \frac{x - \mu }{\sigma }} \right)^{{ - \frac{1}{\gamma } - 1}} , \, \gamma \ne 0, \, \sigma > 0{, }0 < \mu < \infty , \, \mu \le x < \infty , \, $$

(20)

where $\gamma$ is the shape parameter, $\mu$ is a location parameter (this example takes $\mu$ = threshold 1010 patients), and $\sigma$ $\left( {\sigma > 0} \right)$ is a scale parameter. When $\gamma > 0$, the GPD describes a heavy tailed distribution which is what we are interested in. We would like to fit the GPD given in (20) to the $n = 103$ data and the maximum likelihood estimates are $\widehat{\gamma }_{MLE} = - 0.6456$, $\widehat{\sigma }_{MLE} = 912.7147$.

Table 5 shows three Goodness-of-fit tests. the Kolmogorov–Smirnov test (K–S) [22], Anderson–Darling (A-D) test [2], and Cramer-von-Mises test (C-v-M) [1], are verified how well the estimated GPD model fits the data. All three tests showed no evidence to reject hypothesis that the data is from a generalized Pareto distribution at $\alpha =$ 0.01 significance level. This paper emphasizes that high conditional quantiles estimation is important for heavy-tailed distribution since they are related to extremes. In general, quantile regression method applies data with any distribution.

Table 5 Test statistic values and p-values of three goodness-of-fit tests using MLE for the y—number of hospitalized COVID-19 patients

Proposed Nonparametric Quantile Regression

In Sect. 1, we applied the least-squares mean regression and linear quantile regression method to the COVID-19 data. In this section, we will use proposed quantile regression method to estimate the high quantile planes of the extreme number of hospitalized COVID-19 patients and compare with previous two models.

The QN method in (11) does not need the linear model assumption. Following the steps in Sect. 3 to apply this method, we first use Gaussian kernel and obtain bandwidths of $h_{1} = {0}{\text{.8744}}$ and $h_{2} = {498}{\text{.5987}}$ to estimate the conditional c.d.f. of y given x. Then, we compute the estimated local conditional quantile function. Lastly, we use a Gaussian kernel and bandwidth $h_{1} ,h_{2}$ in the Nadaraya-Watson estimator to estimate the quantile surfaces. The proposed nonparametric $Q_{N}$ quantile regression surfaces at $\tau = 0.95{\text{ and }}0.99$ are provided in Fig. 10.

Fig. 10

The 3D plots of $\widehat{\mu }_{LS}$($x_{1} ,x_{2}$) (green), $\widehat{{Q_{R} }}\left( {\tau |x_{1} ,x_{2} } \right)$(blue) and $\widehat{{Q_{N} }}\left( {\tau |x_{1} ,x_{2} } \right)$ (red) surfaces at a $\tau = 0.95{\text{ and }}$ b $0.99$ for the $x_{1}$- percent positive test last day and the $x_{2}$- number of new cases vs. the y—number of hospitalized COVID-19 patients greater than 1010 and the n = 103, data is in black dots

Next, we will check the estimation quantile regression curves with the number of new case number fixed at 3442 and then percent positive test last day fixed at 7.8%.

Regression of y on x ₁ when x ₂ = 3442 (the th Quantile of x ₂ )

We substitute $x_{2} = 3442$ into $\widehat{{Q_{R} }}\left( {\tau |x_{1} } \right){\text{ and }}\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ surfaces to explore the high conditional quantile curves. Figure 11 gives a scatter plot of the $x_{1}$- percent positive test last day vs. the y—number of hospitalized COVID-19 patients with $\widehat{\mu }_{LS} (x_{1} ), \, \widehat{{Q_{R} }}\left( {\tau |x_{1} } \right){\text{ and }}\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ curves for $\tau = 0.95{\text{ and 0}}{.99}$. Table 6 gives the mean and the conditional quantile estimates.

Fig. 11

The 2D plots of the $\widehat{\mu }_{LS} (x_{1} ){\text{ (green)}}, \, \widehat{{Q_{R} }}\left( {\tau |x_{1} } \right){\text{ (blue) and }}\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right){\text{ (red)}}$ quantile curves at a $\tau = 0.95{\text{ and }}$ b $\tau = 0.99$ for the $x_{1}$- percent positive test last day versus the y—number of hospitalized COVID-19 patients. Data is in black dots, $n = 103$

Table 6 The number of hospitalized COVID-19 patients (y) related to the % positive test last day ($x_{1}$) when the number of new cases $x_{2}$ = 3442

Figure 11 suggested that the $\widehat{{Q_{R} }}\left( {\tau |x_{1} } \right)$ predicts the y—number of hospitalized COVID-19 patients will increase indefinitely as the $x_{1}$ percent positive test last day increases. Conversely, the $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ curve shows that there is maximum value of number of hospitalized COVID-19 patients can reach. The $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ predicts reveal the reality that the available space in hospitals has a limit. Furthermore, the $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ curves seem to fit the data better than the $\widehat{{Q_{R} }}\left( {\tau |x_{1} } \right)$ lines. Especially, at lower values of $x_{1}$.

From Table 6 we can see that $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ predictions fit the data better than $\widehat{{Q_{R} }}\left( {\tau |x_{1} } \right)$ predictions. $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ predictions can capture when $x_{1}$ < 7% the data y—number of hospitalized COVID-19 patients slowly increases from a relative low value of $x_{1}$. $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ predicts also capture when $x_{1}$ = 8%, the data y—number of hospitalized patients is high. Also, since the $\widehat{{Q_{R} }}\left( {\tau |x_{1} } \right)$ model is linear, it is over predicting the y values, where resulted in the predictions made by $\widehat{{Q_{R} }}\left( {\tau |x_{1} } \right)$ predicts are higher than $\widehat{{Q_{N} }}\left( {\tau |x_{1} } \right)$ predictions at $x_{1}$ = 4 ~ 6%. On the other hand, the $\widehat{\mu }_{LS} (x_{1} )$ predicts can only represent the mean value of the y—number of hospitalized COVID-19 patients.

Regression of y on x ₁ when x ₂ = 7.8 (the 0.75th Quantile of x ₁ )

Substitute $x_{1} = 7.8$ into $\widehat{{Q_{R} }}\left( {\tau |x_{2} } \right){\text{ and }}\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right) \,$ to explore the high conditional quantile curves for percent positive test last day equals 7.8 (%). Figure 12 gives a scatter plot of the number of new cases vs the number of hospitalized COVID-19 patients with $\widehat{\mu }_{LS} (x_{2} ), \, \widehat{{Q_{R} }}\left( {\tau |x_{2} } \right){\text{ and }}\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right) \,$ curves for $\tau = 0.95{\text{ and 0}}{.99}$. Table 7 gives the mean and the conditional quantile estimates.

Fig. 12

The 2D plots of the $\widehat{\mu }_{LS} (x_{2} ){\text{ (green)}}, \, \widehat{{Q_{R} }}\left( {\tau |x_{2} } \right){\text{ (blue) and }}\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right){\text{ (red)}}$ quantile curves at a$\tau = 0.95{\text{ and }}$ b $\tau = 0.99$ for the $x_{2}$- number of new cases vs. the y—number of hospitalized COVID-19 patients. Data is in black dots, $n = 103$

Table 7 The number of hospitalized COVID-19 patients (y) relative to the number of new cases ($x_{2}$) when the % positive test on last day $x_{1}$ = 7.8(%)

At first, Table 7 shows that the QR method gives quantile curves crossing errors: when $x_{2}$ = 1250, $\widehat{{Q_{R} }}\left( {\tau = 0.95|x_{2} } \right) \,$ = 1658.91 > $\widehat{{Q_{R} }}\left( {\tau = 0.99|x_{2} } \right) \,$ = 1595.70 (bold numbers), and when $x_{2}$ = 1750, $\widehat{{Q_{R} }}\left( {\tau = 0.95|x_{2} } \right) \,$ = 1785.86 > $\widehat{{Q_{R} }}\left( {\tau = 0.99|x_{2} } \right) \,$ = 1757.36 (bold numbers). Thus, QR estimator gives not reasonable results. QN method never has crossing error result since algorithm in Sect. 3 and $\widehat{F}\left( {y|{\varvec{x}}} \right)$ in (10) has monotonicity which guarantee if $\tau_{1} < \tau_{2} {\text{ then }}$$\widehat{{Q_{N} }}\left( {\tau_{1} |{\varvec{x}}} \right) < \widehat{{Q_{N} }}\left( {\tau_{2} |{\varvec{x}}} \right)$ in (11) at same x.

Based on Fig. 12 and Table 7, for $\tau = 0.95{\text{ and 0}}{.99}$, the $\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right)$ predictions never exceed a value around 2400 hospitalized COVID-19 patients, consistent with the reality that Ontario’s hospital resource are limited. Contrarily, the $\widehat{{Q_{R} }}\left( {\tau |x_{2} } \right)$ predictions increase indefinitely. Thus, the proposed $\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right)$ predictions are more realistic. For example, we also observed that before the $x_{2}$ = 1750 the data y—number of hospitalized COVID-19 patients is not high. Accordingly, when the $x_{2}$ = 1250, $\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right)$ prediction is lower than $\widehat{{Q_{R} }}\left( {\tau |x_{2} } \right)$ predict. Similarly, around $x_{2}$ = 2750 new cases, data has a surge of the y—number of hospitalized COVID-19 patients. This time, the $\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right)$ predictions is higher than $\widehat{{Q_{R} }}\left( {\tau |x_{2} } \right) \,$ predictions. Overall, the proposed $\widehat{{Q_{N} }}\left( {\tau |x_{2} } \right)$ predicts fit the data better than $\widehat{{Q_{R} }}\left( {\tau |x_{2} } \right)$ predicts. At 75% quantile of the number of new cases daily $x_{2}$ = 3442, seems the $\widehat{{Q_{R} }}\left( {\tau |x_{2} } \right)$ is over predicted.

We extend the measure error method [18] to compute the Relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |{\mathbf{x}}} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |{\mathbf{x}}} \right)$. It is measured by

$$ {\text{Relative }}R_{N} \left( \tau \right) = 1 - \frac{{V_{N} \left( \tau \right)}}{{V_{R} \left( \tau \right)}},{ 0} \le R\left( \tau \right) \le 1,\,{\text{where}} $$

(21)

$$ V_{R} \left( \tau \right) = \sum\limits_{{\mathop {y_{i} \ge \varvec{x}_{i}^{T} \widehat{{\varvec{\beta}}}\left( \tau \right)}\limits_{i = 1} }}^{n} {\frac{\tau }{n}} \left| {y_{i} - \varvec{x}_{i}^{T} \widehat{{\varvec{\beta}}}\left( \tau \right)} \right| \, + \sum\limits_{{\mathop {y_{i} \ge \varvec{x}_{i}^{T} \widehat{{\varvec{\beta}}}\left( \tau \right)}\limits_{i = 1} }}^{n} {\frac{1 - \tau }{n}} \left| {y_{i} - \varvec{x}_{i}^{T} \widehat{{\varvec{\beta}}}\left( \tau \right)} \right| $$

(22)

where $\widehat{{\varvec{\beta}}}\left( \tau \right)$ is obtained by Eq. (6) and

$$ V_{N} \left( \tau \right) = \sum\limits_{{\mathop {y_{i} \ge \widehat{{Q_{N} }}\left( {\tau |\varvec{x}_{i} } \right)}\limits_{i = 1} }}^{n} {\frac{\tau }{n}} \left| {y_{i} - \widehat{{Q_{N} }}\left( {\tau |\varvec{x}_{i} } \right)} \right| \, + \sum\limits_{{\mathop {y_{i} < \widehat{{Q_{N} }}\left( {\tau |\varvec{x}_{i} } \right)}\limits_{i = 1} }}^{n} {\frac{1 - \tau }{n}} \left| {y_{i} - \widehat{{Q_{N} }}\left( {\tau |\varvec{x}_{i} } \right)} \right|, $$

(23)

where $\widehat{{Q_{N} }}\left( {\tau |\varvec{x}_{i} } \right)$ is obtained by Eq. (11).

Relative $R_{N} \left( \tau \right)$ given by Eq. (21) computes one minus the ratio of error losses between $V_{N} \left( \tau \right)$ and $V_{R} \left( \tau \right)$. If the value is greater than 0, it means the $\widehat{{Q_{N} }}\left( {\tau |\varvec{x}_{i} } \right)$ model fits the data better than $\widehat{{Q_{R} }}\left( {\tau |\varvec{x}_{i} } \right)$ model. Table 8 provides the relative $R_{N} \left( \tau \right)$ values for quantiles $\tau \in [0.95,0.99]$.

Table 8 Relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |{\mathbf{x}}} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |{\mathbf{x}}} \right)$ for example 1, n = 103

Based on the results in Table 8, all relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |{\mathbf{x}}} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |{\mathbf{x}}} \right)$ values are greater than 0 for various high quantiles $\tau \in \, \left[ {0.95,0.99} \right]$.

Above study shows that the proposed $\widehat{{Q_{N} }}\left( {\tau |{\mathbf{x}}} \right)$ model fits the data better than $\widehat{{Q_{R} }}\left( {\tau |{\mathbf{x}}} \right)$ model. The main conclusions for Example 1 analysis are:

• 1. The $\widehat{{Q_{N} }}\left( {\tau |{\mathbf{x}}} \right)$ predictions of extreme values of the number of hospitalized COVID-19 patients are more accurate and realistic than the $\widehat{{Q_{R} }}\left( {\tau |\varvec{x}_{i} } \right)$ method’s predictions.

• 2. The $\widehat{{Q_{N} }}\left( {\tau |{\mathbf{x}}} \right)$ estimates surfaces fit the data better than the $\widehat{{Q_{R} }}\left( {\tau |{\mathbf{x}}} \right)$ planes for high conditional quantiles $\tau \in \, \left[ {0.95,0.99} \right]$.

This application of quantile regression for the y—number of hospitalized COVID-19 patients can help the government of Ontario allocate scarce medical resources during this pandemic to avoid overwhelming hospitals.

Example 2. Systolic Blood Pressures (January 2017–December 2018)

This section will revisit the NHANES 2017–2018 systolic blood pressures data from Sect. 1. We study the high conditional quantile curves of extreme high systolic blood pressures (SBP), using weight as regressor, as these variables have been closely linked with coronary heart disease. Normal systolic blood pressure is between 90 and 120 mmHg. For this example, SBP higher than 160 mmHg threshold is set to focus on subjects who are in stage 2 hypertension. These subjects have a high risk of having a heart attack, heart disease, stroke, brain problems, and kidney disease (Centers for Disease Control and Prevention, 2021).

In Sect. 1, Example 2, an estimation was made using the least-squares mean regression method. Figure 5 shows the scatter diagram that compares the SBP (mmHg) with weight (kg) for the reduced data set of $n = 249$ subjects (after using a threshold of 160 mmHg with weights less than 125 kg). The least-squares regression line and linear quantile regression line are limited by linearity assumptions. In this Section, we use proposed new nonparametric quantile regression to study the relationship between the extreme value of SBP and weight.

Similar as Example 1, we determine if the reduced data with SBP higher than 160 mmHg is from an extreme value distribution by checking whether it follows a generalized Pareto distribution. We fit the three-parameter GPD as given in Eq. (20) to the $n = 249$ data and use a threshold of 160 mmHg to obtain $\mu = 160$. The maximum likelihood estimates are $\widehat{\gamma }_{MLE} = - 0.2279$ and $\widehat{\sigma }_{MLE} = 19.0375$. The three tests are the Kolmogorov–Smirnov test (K–S), Anderson–Darling (A-D) test, and Cramer-von-Mises test (C-v-M). Table 9 provide the test statistics and each tests’ p-value.

Table 9 Test statistics and p-values of the goodness-of-fit tests using MLE for the y—systolic blood pressures data

Table 9 shows the p-value of the three tests. All three tests showed no evidence to reject hypothesis that the data is from a generalized Pareto distribution at $\alpha =$ 0.01 significance level. The response y data in example 2 likely follows an estimated heavy-tailed GPD distribution. Thus, the high quantile regression is important for analysis this example’s extremes.

The assumption of a linear model is not required for the proposed nonparametric quantile regression method. Following steps given in Sect. 3, we first estimate the conditional c.d.f.$F\left( {y|\varvec{x}} \right)$. A Gaussian kernel and bandwidth of $h_{opt} = \, 8.5263$ is used. For the Nadaraya-Watson estimator, a Gaussian kernel and bandwidth $h = 3.5821$ is used. The proposed nonparametric $\widehat{{Q_{N} }}\left( {\tau |x} \right) \,$ quantile regression curves at $\tau = 0.95{\text{ and }}0.97$ are provided in Fig. 13.

Fig. 13

Plot of the $\widehat{\mu }_{LS} (x)$ (green), $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ (blue) and $\widehat{{Q_{N} }}\left( {\tau |x} \right) \,$ (red) at a $\tau = 0.95{\text{ and }}$ b $0.97$ for the y—SBP (mmHg) versus the x—weight (kg) (< 125 kg) for SBP greater than (160 mmHg). Data is in black dots, $n = 249$

Figure 13 shows the LS lines $\widehat{\mu }_{LS}$(x), QR lines $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ and QN curves $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ at $\tau = 0.95{\text{ and }}0.97$. We observe that the high data pattern is followed closely by the $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ curve. Thus, proposed $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ predictions fit the data better than the $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ predictions. For example, subjects around weight x = 100 kg have a relatively lower SBP than subjects with weight x = 90–20 kg. The $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ curves have a concave around x = 100 kg to represent this fact. Contrarily, the linear $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ lines could not capture this scene and its predictions are higher than $\widehat{{Q_{N} }}\left( {\tau |x} \right)$’s predictions at weight x = 100 kg.

Table 10 provides those high conditional quantiles predictions for SBP (mmHg) given weight x < 125 kg. We can see that $\widehat{{Q_{R} }}\left( {\tau |x} \right) \,$ gives higher SBP predictions than $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ predictions. Is $\widehat{{Q_{R} }}\left( {\tau |x} \right) \,$ over predicted? For subjects’ weight x > 90 kg, the data shows lower SBP values, which leads us to think $\widehat{{Q_{N} }}\left( {\tau |x} \right) \,$ SBP predicts are more reasonable.

Table 10 SBP y (mmHg) relative to weight x (kg) (< 125 kg) estimates $\widehat{\mu }_{LS}$, $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ and $\widehat{{Q_{N} }}\left( {\tau |x} \right)$

Use function (21) to compute the Relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ for compare the nonparametric $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ and regular linear quantile regression $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ methods. (see Table 11).

Table 11 Relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ for the systolic blood pressures data, n = 249

Base on the graphs provided in Fig. 13 and all Relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ in Table 11 values are all greater than 0 for various high quantiles $\tau \in \left[ {0.95,0.99} \right]$. We can conclude that the proposed $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ model fits the Systolic Blood Pressures data with a threshold of 160 (mmHg) when weight x < 125 kg, $n = 249$ data better than the regular $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ linear quantile regression model. Following are the main results for Example 2 analysis are:

• 1. Figure 13 shows that the $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ predictions fit the data better than $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ predictions as all the Relative $R_{N} \left( \tau \right)$ of $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ relative to $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ are positive.

• 2. The proposed $\widehat{{Q_{N} }}\left( {\tau |x} \right)$ predictions result captured the fact that there is a higher chance for people whose weights are between 70 and 90 kg to have high SBPs. On the other hand, the $\widehat{{Q_{R} }}\left( {\tau |x} \right)$ method assumes the relationship between weight and SBP is linear. As a result, its model could not extract the same information.

This application of quantile regression for extreme SBP can be used to identify patients with high risk to have stage 2 hypertension and prevent coronary heart disease.

7 Overall Conclusions and Discussion

7.1 Conclusions

When researchers are interested in extreme events and need to estimate high conditional quantiles, the traditional least-squares estimator used for estimating the conditional mean is not suitable since the extreme events usually follow the heavy-tailed distribution. On the other hand, the quantile regression estimator uses a quantile-weighted $L_{1} {\text{ - loss}}$ function and therefore can estimate the high quantiles.

The regular linear quantile regression method (QR) estimates high quantile curves with a linear model. However, very often, the parametric conditions can not be met in real-world data. In this situation, we should use the nonparametric quantile regression methods to obtain better estimates. In this paper, we proposed a new direct nonparametric quantile regression estimation method (QN). Three studies were performed to compare the proposed method with the regular quantile regression method to check the new method’s capability:

• 1. In Sect. 4, mathematical properties of the proposed direct nonparametric quantile regression method (QN) were examined.

• 2. In Sect. 5, the Monte Carlo simulation was performed to compare the efficiencies of the QN and QR. The QN had better simulation efficiencies than QR.

• 3. In Sect. 6, the QR and QN were used in two applications. The QN had better fits to the data than the QR. The QN method avoided the quantile curve crossing problem of the QR method.

To conclude, the proposed direct nonparametric quantile regression estimator outperforms the regular quantile regression method when estimate high quantile curves of heavy-tailed distributed data. Several recommendations for future research are given take different approach to estimate the c.d.f., use cross validation procedure to find optimal smoothing parameters, and implement the program in other languages with better algorithm and data structures to improve the program’s execution efficiency.

7.2 Discussions: Comparing with Other Quantile Regression Methods

As we mention in Sect. 1. This Section will explore Bayesian quantile regression (B-QR) method. At first, we explore the Laplace likelihood B-QR by using Markov Chain Monte Carlo (MCMC) with Metropolis–Hastings algorithm. [12, 21, 30, 31]. We apply this MCMC method to Example 1 in this paper. We use [31] Yu and Moyeed (2001) R package, the results are in Fig. 14.

Fig. 14

Bayesian Quantile Regression using the MCMC by Metropolis–Hastings algorithm. We draws 55,000 samples, and then burned away the first 5000 samples before getting the estimates: $\widehat{{\beta_{0} }}(\tau = 0.95)$ = 577.531; $\widehat{{\beta_{1} }}(\tau = 0.95)$ = 113.893; $\widehat{{\beta_{2} }}(\tau = 0.95)$ = 0.2190

Next, we do comparison of MCMC B-QR results to the propose direct nonparametric quantile Regression method on Example 1 Hospitalised COVID-19 Hospitalized Patients.

Bayesian Quantile regression by MCMC method in Fig. 14 is given by

$$ \widehat{{Q_{B} }}\left( {0.95|x_{1} ,x_{2} } \right) = \widehat{\beta }_{0} \left( {0.95} \right) + \widehat{\beta }_{1} \left( {0.95} \right)x_{1} + \widehat{\beta }_{2} \left( {0.95} \right)x_{2} = { 577}{\text{.531}} + 113.893x_{1} + 0.2190x_{2} . $$

Figure 15 show comparisons of 2D B-QR with other quantile regression curves in Example 1 Hospitalized COVID-19 Patients in Sect. 6 Figs. 11a and 12a results at $\tau = 0.95$ level, where

$$ \widehat{{Q_{R} }}\left( {0.95|x_{1} } \right)\left| {_{{x_{2} = 3442}} } \right. = 1514.521 + 89.8649x_{1} ,\;{\text{when}}\;x_{2} = 3442 \; \left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{2} } \right) $$

$$ \widehat{{Q_{B} }}\left( {0.95|x_{1} } \right)\left| {_{{x_{2} = 3442}} } \right. = 1331.329 + 113.893x_{1} ,\;{\text{when}}\;x_{2} = 3442 \; \left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{2} } \right) $$

$$ \widehat{{Q_{R} }}\left( {0.95|x_{2} } \right)\left| {_{{x_{1} = 7.8}} } \right. = 1341.5277 + 0.2539x_{2} ,{\text{when}}\;x_{1} = { 7}.{8 } \; \left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{1} } \right) $$

$$ \widehat{{Q_{B} }}\left( {0.95|x_{2} } \right)\left| {_{{x_{1} = 7.8}} } \right. = 1463.8964 + 0.2190x_{2} ,\;{\text{when}}\;x_{1} = { 7}.{8 } \; \left( {{\text{the}}\;0.{75}{{{\text{th}}}} \;{\text{quantile}}\;{\text{of}}\;x_{1} } \right) $$

Fig. 15

MCMC Bayesian quantile regression curves in purple. a $\widehat{{Q_{B} }}\left( {0.95|x_{1} } \right)$. b $\widehat{{Q_{B} }}\left( {0.95|x_{2} } \right)$

Note that $\widehat{{Q_{N} }}\left( {0.95|x_{1} } \right) \,$ and $\widehat{{Q_{N} }}\left( {0.95|x_{2} } \right) \,$ are not linear, in a direct nonparametric form.

We note that in Fig. 15, Bayesian $\widehat{{Q_{B} }}\left( {0.95|x_{1} } \right)$ and $\widehat{{Q_{B} }}\left( {0.95|x_{2} } \right)$ curves (in purple) are close to $\widehat{{Q_{R} }}\left( {0.95|x_{1} } \right)$ and $\widehat{{Q_{R} }}\left( {0.95|x_{2} } \right)$ curves (in blue), respectively. These are reasonable since they are set as linear parametric models. We may conclude that:

• 1. We notice that the Bayesian quantile regression using parametric Laplace likelihood by MCMC Metropolis-Hasting algorithm obtains the estimated quantile regression to be linear which are close to the regular linear quantile regression curves. The MCMC method heavily depends on the Markov chain stationary distribution and M–H algorithm proposal distribution. Further studies may need.

• 2. The proposed direct nonparametric quantile regression represents the data pattern well. In the future, we may further study nonparametric Bayesian quantile regression methods.

• 3. There are other developing quantile regression methods. We will continue to explore and study them to improve current existing quantile regression methods.