1 Introduction

Two-phase flows are present in many industries, and its understanding is necessary to properly design and size storage, pumping, and transport equipment [1]. Gas–liquid two-phase vertical flow is commonly classified in three flow patterns: Bubble, slug, and annular. Nevertheless, other categories can be found, but they correspond to the sub-classification of these patterns.

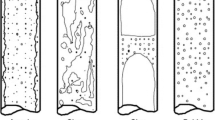
Focusing in annular flow, this can be classified in three different patterns, as shown in Fig. 1: Falling film, Liquid slip, and Wavy annular. At low velocities of liquid and gas, Falling film occurs and is characterized for presenting tiny liquid droplets in the gas core. At higher liquid velocities, the liquid droplets disappear, and more significant portions of liquid are now in the gas core while the liquid film gets thicker, this is called Liquid slip. Finally, at higher velocities of gas and liquid, larger waves in the liquid film appear while there is no presence of liquid in the gas core, this characterizes the Wavy annular pattern [2].

Fig. 1
figure 1

Annular flow classification: a falling film, b wavy annular and c liquid slip

Full size image

1.1 State of the art

Several studies have been conducted for the understanding of two-phase flows. Table 1 summarizes some of the most relevant studies for annular flow patterns on ascending and descending flow on gas–liquid flows. In general, many of the presented studies developed correlations for the prediction of void fraction and pressure drops, while others focused on studying the effects of varying the geometrical configurations of the pipes on the flow patterns.

Table 1 Experimental studies of two-phase flow
Full size table

On the other hand, due to the availability of computational resources, computational fluid dynamics (CFD) tools allow to study multiphase flows at low costs and became an excellent complement to the experimental studies. This allows evaluating the viability of these numerical methods as an alternative tool to understand the behavior of two-phase flows. Table 2 lists some of the most relevant studies carried out in this type of software; many of the CFD studies are focused on horizontal, nearly horizontal and vertical pipes. However, no numerical study on CFD for down- and up-ward flow was found, and moreover, very few articles studied the annular flow pattern.

Table 2 CFD studies of two-phase flow
Full size table

Finally, there are other numerical methods to study multiphase flows beside CFD such as dynamic multiphase flow simulators: Schlumberger’s OLGA. This software is specialized in the analysis of multiphase flows and is widely used in the oil industry. It is capable of modeling transient flows, it allows to size equipment and simulates different operational processes.

Based on this context, the purpose of this study is to develop and present a CFD model capable of simulate air–oil annular flow for down- and up-ward flow. Since many of the studies have not been focused on down- and up-ward flow, the primary purpose of it, is to propose the CFD as a reliable alternative for the prediction of flow patterns and operational parameters such as void fraction in comparison to empirical correlations or other commercial computational codes. For this, it is used to replicate and validate the CFD model against 36 different experimental conditions from Chung [2] and Skopich [23]. Then, a comparison of the obtained results against two other methods like OLGA and 66 empirical correlations for the void fraction prediction will be made.

2 Materials and methods

2.1 Experimental facilities for the oil–gas flow measurements

Two different experimental facilities were used, both located at University of Tulsa (Tulsa, OK, US) and described in detail by Chung [2] and Skopich [23], this section makes a brief description of these facilities.

2.1.1 Down-ward case facility

The general scheme of the facility used by Chung [2] to run the down-ward experiments is presented in Fig. 2. A tank of 2900 gallons is used to store oil, an electrical heater and a pump system are used to recirculate the oil into the container to control the temperature. The mass flow rate and the density of the oil are measured with a flow meter; a dry rotatory screw is used to supply compressed air into the pipe. Finally, control valves are placed before the flow meter to control the gas flow rate.

Fig. 2
figure 2

Scheme of the experimental facility of TUFFP used for the down-ward case, adapted from Chung [2]

Full size image

The test section consists of 22.72 m length pipe and 0.0508 m of ID. A section of 7.61 m is used to obtain the liquid holdup and pressure drop measurements. Quick closing valves were used to measure the liquid holdup in a section of 5.36 m, while differential pressure transducers were used to measure the pressure drop. Figure 2 shows a detailed schematic of the test section. ND-50 mineral oil and compressed air were used in the experiment. Over 150 experimental points were run in this facility using four different oil viscosities.

2.1.2 Up-ward case facility

Skopich [23] tested different inclination angles, including fully vertical, where only 12 points were measured for the up-ward vertical flow. Water with a 0.00084 Pa s viscosity and air were used as liquid and gas phase. The general scheme of the experimental facility is presented in Fig. 3. This facility is divided into four main sections: storage, mixing, study, and drainage. The storage section is composed of a storage tank used to store the liquid phase and is connected to the mixing section by a 21.3 m pipe. On the mixing section, gas is injected to the liquid phase using a compressor and then travel on a 67.1 m length pipe to the study section.

Fig. 3
figure 3

Scheme of the experimental facility of TUFFP used for the up-ward case, adapted from Skopich [23]

Full size image

The study section is divided into two test sections, a 0.0508 and a 0.1016 m ID pipe sections, both of 15.2 m length. Also, each section is divided into three sub-sections: inlet, middle, and outlet. The inlet and outlet subsections are composed by 5.9 m length pipes with quick closing valves used to measure the liquid holdup in both sections, while the middle section is formed by a 3.4 m length pipe where a pressure transducer is used to measure the pressure drop. Finally, the drainage section consists of a storage tank connected at the outlet of the study section.

2.2 CFD model proposed to emulate the annular air–oil flow

The computational simulations were carried on the commercial CFD software STAR-CCM+ v13 (Siemens, Germany). It is essential to note that the main equations solved during a CFD simulation correspond to the continuity equation (Eq. 1) and the momentum equation (Eq. 2).

$$\frac{\delta \rho }{\delta t} + \frac{{\delta \left( {\rho u_{j} } \right)}}{{\delta x_{j} }} = 0$$
(1)
$$\frac{\delta }{\delta t}\left( {\rho u_{i} } \right) + \frac{\delta }{{\delta x_{j} }}\left( {\rho u_{i} u_{j} } \right) = \frac{\delta p}{{\delta x_{i} }} + \frac{\delta }{\delta j}\left[ {\mu_{eff} \left( {\frac{{\delta u_{i} }}{{\delta x_{j} }} + \frac{{\delta u_{j} }}{{\delta x_{i} }} - \frac{2}{3}\delta_{ij} \frac{{\delta u_{i} }}{{\delta x_{i} }} } \right)} \right] + \frac{\delta }{\delta j}\left( { - \rho \overline{{u_{i}^{'} u_{j}^{'} }} } \right)_{i}$$
(2)

where \(u_{i}\) is the velocity of the \(i\) component, \(x_{j}\) the \(j\) spatial coordinate, P the static pressure, \(\mu_{eff}\) is the effective viscosity, \(\left( { - \rho \overline{{u_{i}^{'} u_{j}^{'} }} } \right)_{i}\) the Reynolds stresses and \(\delta_{ij}\) correspond to the Kronecker delta.

2.2.1 Experimental conditions replicated on CFD

Two main groups of simulations were made, 24 for the down-ward flow (0.0508 ID pipe) and 12 for the up-ward flow (0.0508 and 0.1016 ID pipe). Tables 3 and 4 summarizes the experimental conditions modeled in CFD for each case, respectively.

Table 3 Down-ward flow experimental points selected for CFD simulations, from Chung [2]
Full size table
Table 4 Up-ward flow experimental points selected for CFD simulations, from Skopich [23]
Full size table

In addition, it has to be mentioned that for the down-ward case despite having 150 data points to compare, the CFD simulations were restricted to 24 due the limited computational availability, however, as it will be shown in the following sections, for the simulations using the dynamic multiphase flow simulator and the empirical correlations all the 150 data points were taken into account. Nevertheless, for the up-ward case, it was possible to simulate in CFD all the data points.

2.2.2 Geometry and boundary conditions

Regarding the down-ward case, a pipe of 22.72 m length and 0.0508 m of ID was made. To accurately replicate the experimental conditions for the void fraction measurements, the pipe was divided into three sections (Top, study, and bottom). Pineda [36] made a spatial discretization similar to the one used in this study, in which it takes into account the division along the longitudinal and cross-section area of the pipe. The top pipe section of 14.44 m, the study section of 6.09 m, and the bottom of 2.19 m length as mentioned in Sect. 2.1.1. While for the up-ward case, a pipe of 0.0508 m of ID and another one of 0.1016 m ID, both of 15.24 m long, were made. Similarly, to the down-ward case, the pipes were divided into three sections: top (5.89 m), study (3.45 m) and bottom (5.89 m).

A description of the boundary conditions used in both cases is presented in Fig. 4 for the up-ward case. Since the pipes were divided into three different sections, it was necessary to define two interfaces: Top/Study and Study/Bottom. One pipe face was defined as the velocity inlet, in which the condition of superficial velocity was used. Half of the inlet surface was specified as an entry of the gas phase, and the other half corresponds to the liquid phase. Consequently, it was necessary to define the velocity of the phases as double of the one registered by the experiments in order to preserve the volumetric flow rates. The other pipe face was defined as a pressure outlet while the pipe surface was modeled as a non-slip wall condition. Similarly, it was modeled the down-ward case, just changing the gravity direction.

Fig. 4
figure 4

General description of the boundary conditions

Full size image

2.2.3 Physical model to simulate multiphase flow

The multiphase flow physical model used was the volume of fluid (VOF) model, which assumes that the fluids present in the system are immiscible, creating an interface. The principal characteristic of this model is the fact that it only solves a set of equations for mass and momentum transport. For this reason, the model establishes mixing variables and properties by a volumetric weighted average method (i.e., density). Finally, the model also assumes that the phases share the same velocity, pressure, and temperature.

2.2.4 Turbulence model

The turbulence model chosen was the SST k–ω proposed by Menter [37]. This model is a combination between the standard k–ε and the k–ω equations, which allows using the k–ε approach far from the wall (bulk region), while in the nearby area the k–ω model is used. Equations 3 and 4 correspond to the turbulent kinetic energy and specific dissipation rate, respectively.

$$\frac{\delta k}{\delta t} + U_{j} \frac{\delta k}{{\delta x_{j} }} = \tau_{ij} \frac{{U_{i} }}{{x_{j} }} - \beta^{*} k\omega + \frac{\delta }{{\delta x_{j} }} \left[ {\left( {\upsilon + \sigma^{*} \nu_{T} } \right)\frac{\delta k}{{\delta x_{j} }}} \right]$$
(3)
$$\frac{\delta \omega }{\delta t} + U_{j} \frac{\delta \omega }{{x_{j} }} = \alpha \frac{\omega }{k}\tau_{ij} \frac{{\delta U_{i} }}{{\delta x_{j} }} - \beta \omega^{2} + \frac{\delta }{{\delta x_{j} }} \left[ {\left( {\upsilon + \sigma \nu_{T} } \right)\frac{\delta \omega }{{x_{j} }}} \right]$$
(4)

2.2.5 Mesh independency test

An orthogonal mesh was used to carry out the simulations. For each experimental condition (down- and up-ward), a grid independence test was made, modifying two geometric parameters: Cartesian and cylindrical divisions. In both cases, three different meshes were created (fine, normal, and coarse) and tested using the same experimental point. For all cases, it was ensured that the boundary layer was modeled accurately, achieving values for the wall y+ between 1 and 5, enough to provide the correct prediction of the velocity profile, flow pattern, and consequently, the variables of interest such as the void fraction.

2.2.5.1 Down-ward case

In Fig. 5 is presented a transversal view of the three different meshes evaluated for the down-ward case. In Table 5 is summarized the detailed technical information about the three meshes used. For the three meshes, cylindrical divisions were made, and a distance of 0.002 m was set as a start spacing for the divisions. For the transversal divisions, a proportion of 1.3 between the coarse cell size and the fine cell size was maintained, as it is recommended by Celik [38]. Finally, based on a random selection, condition 23 was the experimental point selected for the mesh independency test.

Fig. 5
figure 5

Transversal view of the different meshes used, a coarse, b normal, and c fine mesh

Full size image
Table 5 Geometrical parameters in down-ward case
Full size table
2.2.5.2 Up-ward case

For this case, a mesh independency test was made only for the 0.1016 m ID pipe; regarding the 0.0508 ID pipe, the same mesh settings determined on Sect. 2.2.5.1 was used. Therefore, a different mesh was used for the 0.1016 m ID pipe as it is presented in Table 6. The Cartesian and polar divisions had increases in a 33% and 17% rate between meshes, respectively. Finally, the data point 33 was used to conduct the mesh independence test for the 0.1016 m ID pipe.

Table 6 Geometrical parameters in the up-ward case
Full size table

2.3 OLGA model

OLGA is a commercial software widely used in the oil industry. iI this study OLGA v7.3 was used to predict the flow pattern and the void fraction based on the Point Model, which assumes a steady-state regime and a fully developed flow. Besides, as it was mentioned in Sect. 2.2.1, OLGA was used to simulate all the 150 data points from the down-ward case and all the 12 points from the up-ward case.

2.4 Empirical correlations

For further comparison of the CFD model, 66 empirical correlations [39] were used as an analytical method to predict the void fraction for the different experimental points described in Sect. 2.2.1. The correlations that showed the most accurate void fraction result compared to the experimental results are shown in Table 7. Where \(\varepsilon\) correspond to void fraction; \(U_{SG} , U_{m}\) and \(U_{GM}\) are superficial gas velocity, mixture velocity, and gas drift velocity, respectively; \(C_{o}\) is a distribution parameter.

$$\varepsilon = \frac{{U_{SG} }}{{\left( {C_{o} U_{M} + U_{GM} } \right)}}$$
(5)
Table 7 Summary of the most reliable correlations for the prediction of the void fraction on annular flow on this study
Full size table

3 Results and discussion

This section will present the results on void fraction obtained with the three different studied methods. Firstly, the numerical methods, CFD and OLGA, and lastly the empirical correlations.

3.1 CFD results on void fraction

As it was mentioned before, 36 different simulations were performed on CFD in order to model annular flow and predict the void fraction.

3.1.1 Mesh independency test

To calculate the mean relative error, Eq. 14 was used to determine the deviation of each mesh where the void fraction was the variable compared. Pinilla [39] have used this expression to also examined the mean relative error for a void fraction as well as pressure gradient.

$$error\left( \% \right) = \left[ {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\frac{{\varepsilon_{{num_{i} }} - \varepsilon_{{exp_{i} }} }}{{\varepsilon_{{exp_{i} }} }}} \right)} \right]*100\%$$
(16)

where \(\varepsilon_{num}\) and \(\varepsilon_{exp}\) correspond to the numerical and experimental result of void fraction, respectively. For the down-ward case, the lowest error was achieved by the fine mesh with a 3.65% deviation, while the other two meshes presented up to 10% of deviation. With these results, the fine mesh was used for modelling all the down-ward cases.

Regarding the up-ward case, the lowest error was achieved by the fine mesh with an error of 0.49% and 1.88% for the 0.0508 m and 0.1016 m ID pipe, respectively. Nevertheless, the coarser mesh presented deviations around 0.87% and 2.17%, respectively. Therefore, considering the low difference between the results of two meshes and the considerable savings on computational time, the coarser mesh was used for the modelling of the up-ward case.

3.1.2 Prediction on void fraction

For the down-ward case, the obtained results for the prediction of the void fraction are presented in Fig. 6.

Fig. 6
figure 6

Percent error of the results of the modelling in CFD for the down-ward case

Full size image

According to the results shown in Fig. 6, the relative error is 18.08%. Moreover, most of the experimental points simulated are between the 10% limit errors. These experimental points had the highest superficial liquid velocities (> 0.7 m/s) with the lowest viscosities (0.127 and 0.213 Pa s) indicating the confidence of the developed model flow.

Nevertheless, despite these satisfactory results, it must be mentioned that conform the liquid velocity diminished, the error of the void fraction prediction by the CFD increase, which shows difficulty to model lower velocities. This behavior can be attributed to the mesh used, although it was reliable enough for most of the studied experimental points, it is suggested to make a refinement for the cartesian region to achieve a better prediction of the annular liquid slip flow pattern. However, it is mandatory to ponder the time used for the simulation and the results obtained. Since both cases (down- and up-ward) were modeled with VOF, it is necessary to highlight the assumption of a shared velocity and pressure field inside a control volume, which could lead to some discretization error and could also explain the error percentage obtained in both cases.

Regarding the up-ward case, in Fig. 7 is presented the results obtained for the two studied pipes. The mean relative error is 5.23% and 3.96% for the 0.0508 m and 0.1016 m ID pipes, respectively, which can be considered as a satisfactory result considering that the same numerical model was used for the two pipe configurations.

Fig. 7
figure 7

Percent error of the results of the modeling in CFD for the up-ward case. The error of a combined results. b The ID 0.0508 m results and c the ID 0.1016 m results

Full size image

It was found that the experimental points corresponding to a superficial gas velocity greater or equal to 18.9 m/s presented the lowest error in comparison to the other cases. Therefore, it can be said that there is an inverse relationship between the obtained error and the superficial velocity of the gas. To avoid this behavior, and adjustment or tuning to the VOF model is suggested in terms of the Courant–Friedrichs–Lewy (CFL) upper and lower limits. For the developed simulations, the default values were used, however, to make a more reliable model that can handle a wide range of flow velocities between both phases, a sensibility analysis is suggested for further study to determine which values fit better to obtain more reliable results at lower gas velocities.

3.2 OLGA model

Regarding the down-ward case, Fig. 8 are presented the results of void fraction obtained with OLGA. Additionally, as it was mentioned before, all the experimental points reported by Chung [2] were simulated using this software.

Fig. 8
figure 8

Percent error of the results of the OLGA model for the down-ward case

Full size image

According to Fig. 8, the mean relative error is 18.6%, similar in comparison to the CFD results considering that the data sample used in OLGA is higher in contrast to the CFD study, suggesting more reliability for OLGA in terms of the prediction of void fraction. However, on the prediction of flow patterns, OLGA miss predicted a wide range of points, including many of the aspects analyzed with the CFD model, characterizing them as slug flows instead of annular flows. In this case, the CFD model outperformed OLGA, with the additional benefit of the post-processing capabilities of the commercial CFD codes that give the possibility of further analysis of the hydrodynamics of the two-phase flow.

Regarding the up-ward case, in Fig. 9 are presented the obtained results for a void fraction. A relative error of 1.00% and 1.92% 0.0508 m and 0.1016 m ID pipe respectively were found.

Fig. 9
figure 9

Percent error of the results of the OLGA model for the up-ward case. The error of a the combined results. b The ID 0.0508 m results and c the ID 0.1016 m results

Full size image

Contrary to the down-ward case, the 12 data points were analyzed in the CFD for the up-ward case. In this case, OLGA outperformed the CFD predictions of void fraction. However, it has missed in the prediction of the flow patterns. In this case, OLGA predicted 5 of the 12 points as slug flow. Having this issue, it is suggested the use of the CFD over other numerical codes such as OLGA for the prediction of flow patterns, since it is capable of determining the specific type of annular flow, like those presented in Fig. 1. Regarding this benefit, in Fig. 10, it is shown as an example of the prediction of annular flow for the down-ward flow achieved by the CFD model.

Fig. 10
figure 10

Void fraction profile for a falling film, b wavy annular and c liquid slip annular flow

Full size image

3.3 Empirical correlations

The analytical study was based on 66 empirical correlations, but only the lower error correlations were presented in this section. It has to be clarified that most of the relationships tested were developed not only for vertical flow but also for different flow patterns and pipe configurations, the purpose of this section is also to determine which of these correlations present the best predictions, no matter the range of applications. With this clarification, the results of the best three relationships for the down-ward case are shown in Table 8.

Table 8 Absolute relative errors of empirical correlations for the down-ward case
Full size table

The results presented in Table 8 shows that the empirical correlations, unfortunately, could not give a better prediction for the void fraction compared to the numerical models. Even though Gomez [40] correlation shows the lowest error percentage, it is essential to note that the correlation takes into account inclined pipes (0°–90°) for up-ward flows. Furthermore, these correlations consider different parameters, like the viscosity, liquid density, and the pipe ID, to predict the void fraction. For example, the pipe’s internal diameter used by Chung [2] was within the range of the ID data used by Gomez [40], which comprehends a range between 5.1 and 20.3 cm. Furthermore, the liquid density of the ND-50 mineral oil is similar to those liquid densities used in the correlation.

Also, it must be mentioned that they were developed for bubble or slug flow, clearly different from the annular flow in vertical pipes on which this study focuses. Similarly, Gregory [41] and Hughmark [42] correlations for horizontal pipes and other types of flow patterns. Likewise, Gomez [40], the diameter data range used by Hughmark [42] goes from 2.56 to 9.6 cm, which also comprehends the pipe diameter used by Chung [2]. Moreover, Woldesamayat [1] does an in-depth review of the correlations comparisons made in the past. It must be noted that among them are very few related to a vertical orientation and flow direction (down- and up-ward).

This shows that empirical correlations are not very trustful when a void fraction prediction is needed. Since they have been made under specific circumstances and controlled experiments a “possible” positive prediction would only be possible when the correlation and experimental data have some grade of similarity and not necessarily because of the accuracy capability of the correlation. Moreover, it is impossible to determine a flow pattern if an empirical correlation is used.

Regarding the up-ward case, the results of the best three relationships are shown in Table 9.

Table 9 Absolute relative errors of empirical correlations for the up-ward case
Full size table

In this case, the results were better in comparison to the down-ward case and very similar to the numerical models. However, it was established that there is a discrepancy at the points where the liquid velocity decreases. An explanation of the small error is due to the formulation of the drift-flux model, which is based on taking the two-phase flow as a single-phase flow and, like the VOF model, unify the properties. According to Bhagwat [20], the drift flux models have won some advantage in order to predict the void fraction for several fluid and pipe conditions. Bhagwat [20] refers that many of them could predict the void fraction for inclined and vertical orientations as well for down- and up-ward flow. This could also explain the reason of the significant difference which exists between the best correlation performance for up-ward case compared to the one of the down-ward case since none of the outperforming down-ward correlations correspond to a drift flux model.

Even though the correlations gave acceptable results, they were considered as distrustful as the ones that gave the best predictions were not supposed to present this behavior as the ranges of application considerably differ from the experimental conditions used in this study.

4 Conclusions

For the down-ward case, the results found in CFD are better for specific conditions such as superficial liquid velocity higher than 0.7 m/s and low liquid viscosities (0.127 and 0.213 Pa s). For the up-ward case, the global results for the CFD simulation had a relative error of 4.59%, where the 0.1016 m ID pipe showed the lowest deviation, allowing to conclude that the CFD model provides better predictions for this case rather than the down-ward case. As it was mentioned in the discussion section is suggested to make some adjustments in the CFL of the VOF model in order to handle a broader range of velocities and enhance the prediction capability of the computer tool.

Regarding OLGA, there was not a trend or range in which the prediction of the void fractions for the down-ward case was accurate and reliable, as the mean relative error obtained was 18.08% while for the up-ward case, the relative error was of 1.00% and 1.92% for the 0.0508 m and 0.1016 m ID pipe, respectively. Even though in both cases, OLGA show the same or even a better result than CFD, it fails utterly when a pattern flow identification is mandatory. Consequently, CFD outperformed OLGA because it allowed having a fair void fraction prediction and the possibility to analyze the hydrodynamic of the two-phase flow.

In respect of the empirical correlations, a relative error between 9.82 and 10.04% was found for the down-ward case, and in the up-ward case a lower error, between 2.03 and 2.91% was obtained. The best correlation for down-ward flow corresponds to the general correlation category, while the up-ward case was a drift-flux model correlation. Even though the errors are smaller (down-ward case—CFD and OLGA) or similar (up-ward case—OLGA) than the other tools, they are not reliable since it is developing was made for a specific flow pattern or pipe configuration. Therefore, its prediction is misleading, and it is just an existing coincidence between experimental data and the one used in the correlation. The few ones designed for annular vertical flow were outperformed by correlations intended for the prediction of other flow patterns.

In summary, CFD is a better alternative tool for two-phase flow understanding of the phenomenon itself. Besides, this study shows the capability to predict the void fraction in down- and up-ward flow. Since there are not many studies about CFD in vertical pipes, especially in down-ward flow, this research is a starting point for further studies.