Abstract
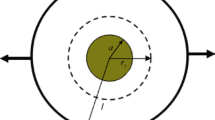
To investigate interfacial diffusion-induced creep and stress relaxation behavior of the particle-reinforced metal matrix composites, analytical solutions are obtained with coupled thermal and mechanical loads. The thermal expansion strains between the matrix and inclusion are considered as eigenstrains. Based on the Eshelby inclusion theory, the driving forces for interface diffusion and slip are obtained, respectively, and the relationship between them is elucidated. The effects of temperature-dependent elastic properties, thermal and mechanical loads on the creep rate and stress relaxation are estimated. Besides, the error caused by the scale effect is amended by fitting the finite element results with nonlinear least square method. The present results provide a straightforward guideline for designing high-quality metal matrix particulate composites.






Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Abu-Abdeen M (2012) The unusual effect of temperature on stress relaxation and mechanical creep of polycarbonate at low strain and stress levels. Mater Des 34:469–473
Alem SAA, Latifi R, Angizi S, Hassanaghaei F, Aghaahmadi M, Ghasali E, Rajabi M (2020) Microwave sintering of ceramic reinforced metal matrix composites and their properties: a review. Mater Manuf Process 35(3):303–327
Aureli M, Doumanidis CC, Gunduz IE, Hussien AGS, Liao YL, Jaffar SM, Rebholz C, Doumanidis CC (2017) Non-equilibrium microscale thermomechanical modeling of bimetallic particulate fractal structures during ball milling fabrication. J Appl Phys 122(2):025118
Bao G, Hutchinson JW, McMeeking RM (1991) Particle reinforcement of ductile matrices against plastic flow and creep. Acta Metall Mater 39(8):1871–1882
Casati R, Vedani M (2014) Metal matrix composites reinforced by nano-particles—a review. Metals 4(1):65–83
Chason E, Sheldon BW, Freund LB, Floro JA, Hearne SJ (2002) Origin of compressive residual stress in polycrystalline thin films. Phys Rev Lett 88(15):156103
Cho S, Lee YH, Ko S, Park H, Lee D, Shin S, Jo I, Kim Y, Lee SB, Lee SK (2020) Enhanced high-temperature compressive strength of TiC reinforced stainless steel matrix composites fabricated by liquid pressing infiltration process. J Alloys Compd 817:152714
Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc R Soc Lond 241(1226):376–396
Fatoba OS, Popoola O, Popoola API (2015) The effects of silicon carbide reinforcement on the properties of Cu/SiCp composites. Silicon 7(4):351–356
Garces G, Onorbe E, Dobes F, Perez P, Antoranz JM, Adeva P (2012) Effect of microstructure on creep behaviour of cast Mg97Y2Zn1 (at.%) alloy. Mater Sci Eng A 539:48–55
Kartal ME, Kiwanuka R, Dunne FPE (2015) Determination of sub-surface stresses at inclusions in single crystal superalloy using HR-EBSD, crystal plasticity and inverse eigenstrain analysis. Int J Solids Struct 67–68:27–39
Khazaali H, Fereshteh-Saniee F (2019) An inclusive experimental investigation on influences of different process parameters in warm incremental forming of AZ31 magnesium sheets. Iran J Sci Technol Trans Mech Eng 43:347–358
Kim KT, McMeeking RM (1995) Power law creep with interface slip and diffusion in a composite material. Mech Mater 20(2):153–164
Ledbetter HM (1982) Temperature behaviour of Young’s moduli of forty engineering alloys. Cryogenics 22(12):653–656
Li YF, Li ZH (2012) Transverse creep and stress relaxation induced by interface diffusion in unidirectional metal matrix composites. Compos Sci Technol 72(13):1608–1612
Li YF, Li S, Li ZH (2014) Interface diffusion-induced creep and stress relaxation in unidirectional metal matrix composites under biaxial loading. Mech Mater 76:20–26
Liu Y, Huang Z, Wang R (1997) On the applicability of Eshelby’s equivalent inclusion method in nonlinear continuum mechanics. Acta Mech Sin 29(4):506–512
Lunt AJG, Korsunsky AM (2020) Eigenstrain boundary layer modelling of the yttria-partially stabilised zirconia–porcelain interface in dental prostheses. Int J Eng Sci 153:103315
Peters PWM, Hemtenmacher J, Schurmann H (2010) The fiber/matrix interface and its influence on mechanical and physical properties of Cu-MMC. Compos Sci Technol 70(9):1321–1329
Phua EJR, Liu M, Cho BK, Liu Q, Amini S, Hu X, Gan CL (2018) Novel high temperature polymeric encapsulation material for extreme environment electronics packaging. Mater Des 141:202–209
Postek E, Sadowski TS (2020) Thermomechanical effects during impact testing of WC/Co composite material. Compos Struct 241:112054
Shabani M, Paydar MH, Moshksar MM (2014) Fabrication and densification enhancement of SiC-particulate-reinforced copper matrix composites prepared via the sinter-forging process. Int J Miner Metall Mater 21(9):934–939
Shishvan SS, Pollock TM, McMeeking RM, Deshpande VS (2017) Interfacial diffusion in high-temperature deformation of composites: a discrete dislocation plasticity investigation. J Mech Phys Solids 98:330–349
Sidhu SS, Kumar S, Batish A (2016) Metal matrix composites for thermal management: a review. Crit Rev Solid State Mater Sci 41(2):132–157
Sofronis P, McMeeking RM (1994) The effect of interface diffusion and slip on the creep resistance of particulate composite materials. Mech Mater 18:55–68
Song WD, Dai LS, Xiao LJ, Wang C, Mao XN, Tang HP (2017) Meso-mechanical constitutive model of particle-reinforced titanium matrix composites at high temperatures. Metals 7:15
Sun Y, Li A, Ren X, Lu Y, Liu M (2017) Interface diffusion-induced creep in metal matrix particulate composites under triaxial loading. Acta Mech 228(7):2471–2481
Sun Y, Li A, Shi L, Liu MB (2021) Interaction between edge dislocation and the inhomogeneity of arbitrary shape and properties under coupled thermo-mechanical strains. J Theor Appl Mech 59:121–133
Sun Y, Li A, Hu YF, Wang XH, Liu MB (2022) Simultaneously enhanced strength-plasticity of graphene/metal nanocomposites via interfacial microstructure regulation. Int J Plast 148:103143
Wang K, Guo HF, Xu AD, Pecht M (2020) Degradation monitoring of insulation systems used in low-voltage electromagnetic coils under thermal loading conditions from a creep point of view. Sensors 20(13):3696
Withers PJ, Stobbs WM, Pederson OB (1989) The application of the Eshelby method of internal stress determination to short fiber metal matrix composites. Acta Metall 37(11):3061–3084
Wynne K, Rice R (1984) Ceramics via polymer pyrolysis. Annu Rev Mater Sci 14:297–334
Xu BB, Guo FL (2019) A micromechanics method for transverse creep behavior induced by interface diffusion in unidirectional fiber-reinforced metal matrix composites. Int J Solids Struct 159:126–134
Xu BB, Guo FL (2021) Upper and lower bounds on the creep strain and stress relaxation induced by interface diffusion in metal-matrix particulate composites. Int J Solids Struct 216:222–230
Xu BB, Xu WX, Guo FL (2020) Creep behavior due to interface diffusion in unidirectional fiber-reinforced metal matrix composites under general loading conditions: a micromechanics analysis. Acta Mech 231(4):1321–1335
Acknowledgements
The authors would like to acknowledge the financial support by the Key Research and Development Plan of Shaanxi (Grant No. 2018ZDCXL-GY-03-01), the Natural Science Foundation of Shaanxi Province (Grant No. 2021JQ-466), and the Scientific Research Project of Shaanxi Education Department (Grant No. 20JK0799) and the Opening Fund of State Key Laboratory for Strength and Vibration of Mechanical Structures (Grant No. SV2021-KF-11).
Author information
Authors and Affiliations
Corresponding authors
Appendix
Appendix
1.1 Appendix A. Explicit Formulations of Parameters in Eqs. (13) and (18)
The parameters in Eqs. (13) are listed as
where \(\alpha = {{E_{i} } \mathord{\left/ {\vphantom {{E_{i} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}\); Ei and Em are the modulus of inclusion and matrix, respectively; ν is the Poisson’s ratio of matrix; ΔCTE is the difference of the thermal expansion coefficient between inclusion and matrix.
The parameters in Eq. (18) are listed as follows:
Rights and permissions
About this article
Cite this article
Sun, Y., Li, A., Wang, X. et al. Creep and Stress Relaxation Behavior of Metal Matrix Particulate Composites Induced by Interface Diffusion with Coupled Thermomechanical Strains. Iran J Sci Technol Trans Mech Eng 46, 1121–1128 (2022). https://doi.org/10.1007/s40997-021-00483-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40997-021-00483-9