Abstract
This note constructs sharp obstructions for stabilized symplectic embeddings of an ellipsoid into a ball, in the case when the initial four-dimensional ellipsoid has ‘eccentricity’ of the form \(3\ell -1\) for some integer \(\ell \).


Similar content being viewed by others
Notes
The capacity, being an area, is a much more natural measure in symplectic geometry than the radius.
See [3] for further discussion of the significance of this function.
The symplectic gradient vector field \(X_H\) is given by the identity
 , and is tangent to the kernel of \(\omega |_{H=\mathrm{const}}.\)
, and is tangent to the kernel of \(\omega |_{H=\mathrm{const}}.\)
Strictly speaking, by “curve” we mean an equivalence class of maps
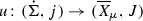 , where we quotient out by the finite dimensional group of biholomorphisms of the domain. In the situations considered here, this group is trivial whenever the total number of punctures or marked points on the domain is at least three.
, where we quotient out by the finite dimensional group of biholomorphisms of the domain. In the situations considered here, this group is trivial whenever the total number of punctures or marked points on the domain is at least three.See [3, Section2] for more details of these calculations. Further, the degree of C is the number of times it intersects the line at infinity.
A negative end is modelled on
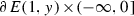 , while a positive end is modelled on
, while a positive end is modelled on 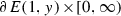 . Thus negative ends are concave (contracting as one moves towards \(-\infty \)), while positive ends are convex (expanding towards \(+\infty \)).
. Thus negative ends are concave (contracting as one moves towards \(-\infty \)), while positive ends are convex (expanding towards \(+\infty \)).By definition, a trivial cylinder in a symplectization
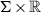 is an unbranched multiple cover of the cylinder
is an unbranched multiple cover of the cylinder 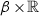 over an asymptotic Reeb orbit \(\beta \) in \({\mathrm{\Sigma }}\). One might be able to weaken this requirement, but to do this would require detailed analysis of the gluing argument. The point is that in this case the argument is not local to the top end of u, but because of its invariance under the \({\mathbb R}\)-action, involves a neighborhood of the whole curve.
over an asymptotic Reeb orbit \(\beta \) in \({\mathrm{\Sigma }}\). One might be able to weaken this requirement, but to do this would require detailed analysis of the gluing argument. The point is that in this case the argument is not local to the top end of u, but because of its invariance under the \({\mathbb R}\)-action, involves a neighborhood of the whole curve.The precise value of \(\lambda \) is irrelevant, since all the curves we construct here persist under deformations.
This somewhat surprising interpretation of the ECH index holds because the latter is a sum of Conley–Zehnder Fredholm-type indices that as above have the form
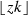 and hence are related to numbers of integer points: see [11].
and hence are related to numbers of integer points: see [11].Despite appearances, this example is not completely random. Indeed, \( {76}/{11} = 7- 1/{11}\) bears the same relation to 11 as the Fibonacci quotient 55 / 8 does to 8: i.e. in the notation of [15, Lemma 4.1.2] we have \({76}/{11}= v_1(10)\) while \({55}/{8}= v_1(7)\). Thus 76 / 11 is the first in the next set of generalized ghost stairs.
Note that we cannot assert the existence of such a building by means of a cobordism argument in cylindrical contact homology because the top end is not cylindrical. Indeed, when one removes a line from
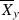 and completes the resulting manifold at its positive end, the curve C becomes asymptotic to a curve \(C'\) with three ends each of multiplicity 1, rather than one end of multiplicity 3.
and completes the resulting manifold at its positive end, the curve C becomes asymptotic to a curve \(C'\) with three ends each of multiplicity 1, rather than one end of multiplicity 3.
References
Bourgeois, F., Eliashberg, Ya., Hofer, H., Wysocki, K., Zehnder, E.: Compactness results in symplectic field theory. Geom. Topol. 7(2), 799–888 (2003)
Cristofaro-Gardiner, D., Hind, R.: Symplectic embeddings of products (2015). arXiv:1702.03607 (submitted to Comment. Math. Helv.)
Cristofaro-Gardiner, D., Hind, R., McDuff, D.: The ghost stairs stabilize to sharp symplectic embedding obstructions (2017). arXiv:1702.03607
Ekholm, T., Oancea, A.: Symplectic and contact differential graded algebras. Geom. Topol. 2(4), 2161–2230 (2017). arXiv:1506.01078
Gutt, J.: The positive equivariant symplectic homology as an invariant for some contact manifolds (2015). arXiv:1503.01443
Hind, R.: Some optimal embeddings of symplectic ellipsoids. J. Topol. 8(3), 871–883 (2015)
Hind, R., Kerman, E.: New obstructions to symplectic embeddings. Invent. Math. 196(2), 383–452 (2014)
Hind, R., Kerman, E.: Corrigendum to “New obstructions to symplectic embeddings”. https://faculty.math.illinois.edu/~ekerman/corrigendum.pdf
Hind, R., Kerman, E.: J-holomorphic cylinders between ellipsoids in dimension 4. arXiv:1707.08635
Hofer, H.: Pseudoholomorphic curves in symplectizations with application to the Weinstein conjecture in dimension three. Invent. Math. 114(3), 515–563 (1993)
Hutchings, M.: Lecture notes on embedded contact homology. In: Bourgeois, F., Colin, V., Stipsicz, A. (eds.) Contact and Symplectic Topology. Bolyai Society Mathematical Studies, vol. 26, pp. 389–484. János Bolyai Mathematical Society, Budapest (2014)
Hutchings, M., Nelson, J.: Cylindrical contact homology for dynamically convex contact forms in three dimensions. J. Symplectic Geom. 14(4), 983–1012 (2016). arXiv:1407.2898
Hutchings, M., Taubes, C.: Gluing pseudoholomorphic curves along branched covered cylinders, I. J. Symplectic Geom. 5(1), 43–137 (2007)
McDuff, D.: Symplectic embeddings of \(4\)-dimensional ellipsoids. J. Topol. 2(1), 1–22 (2009). Corrigendum: J. Topol. 8(4), 1119–1122 (2015)
McDuff, D., Schlenk, F.: The embedding capacity of \(4\)-dimensional symplectic ellipsoids. Ann. Math. 175(3), 1191–1282 (2012)
Pardon, J.: Contact homology and virtual fundamental cycles (2015). arXiv:1508.03873
Schlenk, F.: Symplectic embedding problems, old and new. Bull. Amer. Math. Soc. (2017). doi:10.1090/bull/1587
Wendl, C.: Automatic transversality and orbifolds of punctured holomorphic curves in dimension four. Comment. Math. Helv. 85(2), 347–407 (2010)
Acknowledgements
This paper is an offshoot of my joint project with Dan Cristofaro-Gardiner and Richard Hind to calculate \(c_k(x)\) for all \(x>\tau ^4\). I wish to thank them for being such wonderful mathematicians to work with, Michael Hutchings for help with understanding obstruction bundle gluing, and finally the referee whose careful comments helped clarify the exposition. Also I wish to recognize Dr. Edge who taught me when I was an undergraduate at Edinburgh University in 1962–1967. He gave an inspiring course on projective geometry: I still remember him telling us that the secret of the 27 lines on the cubic surface lay in four dimensions—very mysterious to me at the time!
Author information
Authors and Affiliations
Corresponding author
Additional information
Partially supported by NSF Grant DMS1308669.
Rights and permissions
About this article
Cite this article
McDuff, D. A remark on the stabilized symplectic embedding problem for ellipsoids. European Journal of Mathematics 4, 356–371 (2018). https://doi.org/10.1007/s40879-017-0184-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0184-y





 , and is tangent to the kernel of
, and is tangent to the kernel of 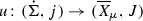 , where we quotient out by the finite dimensional group of biholomorphisms of the domain. In the situations considered here, this group is trivial whenever the total number of punctures or marked points on the domain is at least three.
, where we quotient out by the finite dimensional group of biholomorphisms of the domain. In the situations considered here, this group is trivial whenever the total number of punctures or marked points on the domain is at least three.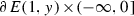 , while a positive end is modelled on
, while a positive end is modelled on 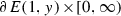 . Thus negative ends are concave (contracting as one moves towards
. Thus negative ends are concave (contracting as one moves towards  in [
in [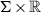 is an unbranched multiple cover of the cylinder
is an unbranched multiple cover of the cylinder 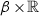 over an asymptotic Reeb orbit
over an asymptotic Reeb orbit 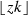 and hence are related to numbers of integer points: see [
and hence are related to numbers of integer points: see [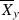 and completes the resulting manifold at its positive end, the curve C becomes asymptotic to a curve
and completes the resulting manifold at its positive end, the curve C becomes asymptotic to a curve