Skip to main content
SpringerLink
Log in

Dynamic Modeling of Antibody Level Changes with Individual Age: The Case of COVID-19 Spread in China

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

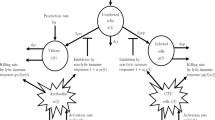
COVID-19 is a ribonucleic acid virus with a high mutation frequency and will continue to mutate as time goes on. At the same time, the number of antibodies in the human body will gradually decrease with time. This paper analyzed the dissemination mechanism of COVID-19 in China after implementing the liberalization policy, established a waning immunity model with age heterogeneity, and explored the threshold dynamics of the system and the dynamic behavior of equilibrium. According to the latest release of COVID-19 data from China, the model parameters were fitted and analyzed using the least squares method to verify the model. We also predicted that the peak of the next epidemic in China would come around June 27. Furthermore, we used numerical simulations to research the impact of different infection rates on disease and compare them with the absence of waning immunity. Finally, using the cost-effectiveness analysis method, we determined the best strategy based on the number of deaths and medical resources. The results show that when \({{\beta }_{11}}>0.27\), controlling the transmission rate between people under 65 is the optimal solution; however, when \({{\beta }_{11}}<0.27\), we should pay more attention to the infected people aged 65 and above.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  1. World Health Organization (2023) Who coronavirus (covid-19) dashboard. https://covid19.who.int/WHO-COVID-19-global-data.csv

  2. Zhou, B., Thao, T.T.N., Hoffmann, D., Taddeo, A., Ebert, N., Labroussaa, F., Pohlmann, A., King, J., Steiner, S., Kelly, J.N., et al.: Sars-cov-2 spike d614g change enhances replication and transmission. Nature 592(7852), 122–127 (2021)

    Article  Google Scholar 

  3. World Health Organization: Covid-19 clinical management: living guidance, 25 Jan 2021. https://apps.who.int/iris/handle/10665/338882 (2021)

  4. Choe, P.G., Kang, C.K., Suh, H.J., Jung, J., Song, K.H., Bang, J.H., Kim, E.S., Kim, H.B., Park, S.W., Kim, N.J., et al.: Waning antibody responses in asymptomatic and symptomatic sars-cov-2 infection. Emerg. Infect. Dis. 27(1), 327 (2021)

    Article  Google Scholar 

  5. Chia, W.N., Zhu, F., Ong, S.W.X., Young, B.E., Fong, S.W., Le Bert, N., Tan, C.W., Tiu, C., Zhang, J., Tan, S.Y., et al.: Dynamics of sars-cov-2 neutralising antibody responses and duration of immunity: a longitudinal study. Lancet Microbe 2(6), e240–e249 (2021)

    Article  Google Scholar 

  6. Musa, S., Gao, D., Zhao, S., Yang, L., Lou, Y., He, D.: Mechanistic modeling of the coronavirus disease 2019 (covid-19) outbreak in the early phase in Wuhan, China, with different quarantine measures. Acta Math. Appl. Sin. 43(2), 350–364 (2020)

    MathSciNet  MATH  Google Scholar 

  7. Lai, S., Ruktanonchai, N.W., Zhou, L., Prosper, O., Luo, W., Floyd, J.R., Wesolowski, A., Santillana, M., Zhang, C., Du, X., et al.: Effect of non-pharmaceutical interventions to contain covid-19 in china. nature 585(7825), 410–413 (2020)

  8. Gozzi, N., Chinazzi, M., Davis, J.T., Mu, K., Piontti, A.P.Y., Vespignani, A., Perra, N.: Preliminary modeling estimates of the relative transmissibility and immune escape of the omicron sars-cov-2 variant of concern in south africa. medRxiv pp. 2022-01 (2022)

  9. Centers for Disease Control and Prevention: Covid data tracker. https://covid.cdc.gov/covid-data-tracker/#variant-proportions (2023)

  10. Torjesen, I.: Covid-19: Researchers question policy of closing schools after finding under 20s have low susceptibility to virus (2020)

  11. Collier, A.R.Y., Yu, J., McMahan, K., Liu, J., Chandrashekar, A., Maron, J.S., Atyeo, C., Martinez, D.R., Ansel, J.L., Aguayo, R., et al.: Differential kinetics of immune responses elicited by covid-19 vaccines. N. Engl. J. Med. 385(21), 2010–2012 (2021)

  12. Wang, X., Wu, H., Tang, S.: Assessing age-specific vaccination strategies and post-vaccination reopening policies for covid-19 control using seir modeling approach. Bull. Math. Biol. 84(10), 108 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  13. Duan, M., Jin, Z.: The heterogeneous mixing model of covid-19 with interventions. J. Theor. Biol. 553, 111258 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  14. Iyaniwura, S.A., Falcão, R.C., Ringa, N., Adu, P.A., Spencer, M., Taylor, M., Colijn, C., Coombs, D., Janjua, N.Z., Irvine, M.A., et al.: Mathematical modeling of covid-19 in British Columbia: an age-structured model with time-dependent contact rates. Epidemics 39, 100559 (2022)

    Article  Google Scholar 

  15. National Health Commission of the People’s Republic of China: notice on the issuance of the general plan for the implementation of "category b" management of novel coronavirus infection. http://www.nhc.gov.cn/xcs/zhengcwj/202212/e97e4c449d7a475794624b8ea12123c6.shtml (2023)

  16. Chinese Center for Disease Control and Prevention: National outbreak of novel coronavirus infection. https://www.chinacdc.cn/jkzt/crb/zl/szkb_11803/jszl_13141/202303/t20230325_264584.html (2023)

  17. National Health Commission of the People’s Republic of China: State department joint prevention and control mechanism January 14, 2023 press conference transcript. http://www.nhc.gov.cn/xcs/s3574/202301/a68301ee500b436b989ec5be2a35cad2.shtml (2023)

  18. Xinjing News: As of november 11 of this year, china’s new crown vaccine covers 1.34 billion people. http://news.hexun.com/2022-11-12/207090030.html (2022)

  19. Van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  20. Thieme, H.R.: Convergence results and a Poincaré–Bendixson trichotomy for asymptotically autonomous differential equations. J. Math. Biol. 30(7), 755–763 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  21. Smith, H.L., Waltman, P.: The Theory of the Chemostat: Dynamics of Microbial Competition, vol. 13. Cambridge University Press (1995)

  22. Wang, W., Zhao, X.Q.: An epidemic model in a patchy environment. Math. Biosci. 190(1), 97–112 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  23. Thieme, H.R.: Persistence under relaxed point-dissipativity (with application to an endemic model). SIAM J. Math. Anal. 24(2), 407–435 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  24. Michlmayr, D., Hansen, C.H., Gubbels, S.M., Valentiner-Branth, P., Bager, P., Obel, N., Drewes, B., Møller, C.H., Møller, F.T., Legarth, R., et al.: Observed protection against sars-cov-2 reinfection following a primary infection: a Danish cohort study among unvaccinated using two years of nationwide PCR-test data. Lancet Regional Health-Europe 20, 100452 (2022)

    Article  Google Scholar 

  25. National Bureau of Statistics: China statistical yearbook. http://www.stats.gov.cn/sj/ndsj/2022/indexch.htm (2022)

Download references

Funding

This research is partially supported by National Natural Science Foundation of China under Grant 12271314 and Graduate Innovation Project of Shanxi Province 2022Y587.

Author information

Authors and Affiliations

  1. School of Computer and Information Technology, Shanxi University, Taiyuan, 030006, Shanxi, China

    Li Li & Yangqing Wang

  2. Data Science and Technology, North University of China, Taiyuan, 030051, China

    Wei Zhang

Authors
  1. Li Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yangqing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li Li.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Wang, Y. & Zhang, W. Dynamic Modeling of Antibody Level Changes with Individual Age: The Case of COVID-19 Spread in China. Int. J. Appl. Comput. Math 9, 83 (2023). https://doi.org/10.1007/s40819-023-01592-6

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-023-01592-6

Keywords

Search

Navigation