Introduction

Wettability is an important petro-physical property of subsurface hydrocarbon reservoirs, which affects the multiphase flow and controls residual oil saturation (Clinch et al. 1995). Published work (Dang et al. 2016; Morrow and Buckley 2011a; Pouryousefy et al. 2016; RezaeiDoust et al. 2011; Tang and Morrow 1999; Thyne and Siyambalagoda Gamage 2011) showed that manipulating injected water chemistry, e.g., add CO2 or tune salts concentration and ion type, would promote the hydrophilicity of oil-brine-rock system, thereby improving oil relative permeability and lowering residual oil saturation.

However, research to date have not fully explained why engineered waterflooding at secondary mode usually exhibits a greater oil recovery than tertiary mode, presenting a substantial impediment in terms of a timing of the engineered waterflooding. For example, core flooding experiments showed that LSW at secondary mode yielded 64% oil recovery, whereas 50% of OOIP was recovered by tertiary LSW (Piñerez Torrijos et al. 2016). Similarly, micromodel experiments showed that secondary LSW gave 4% of incremental oil recovery, but only 1.7% of OOIP was recovered at tertiary mode (Wei et al. 2017). At field scale, secondary LSW recovered 10–15% of STOIIP in Omar Field in Syria, while negligible low salinity effect was observed during tertiary LSW (Mahani et al. 2011).

To explain why LSW at secondary mode is more favourable than at tertiary mode, two mechanisms have been proposed: (1) viscoelasticity increase (Ayirala et al. 2018; Garcia-Olvera and Alvarado 2017); (2) wettability alteration (Al Maskari et al. 2019; Amiri and Gandomkar 2018; Aziz et al. 2019; Brady et al. 2015; Buckley and Lord 2003; Mahani et al. 2015; Xie et al. 2017). The emulsion generation in LSW increases the viscoelasticity between oil and brine and reduces snap-off. Microscopy images showed that emulsion concentration increased between oil-brine interface when salinity decreases from 4.2 to 0.021% (Wei et al. 2017). NMR results further confirmed that LSW likely generated oil-brine emulsion in particular for oils rich in high acid component (Garcia-Olvera et al. 2016). Micro CT identified the oil-brine emulsion generation after LSW (Bartels et al. 2017b), which revealed that emulsion generation could increase the viscoelasticity and suppress snap-off of oil ganglion (Bartels et al. 2019). To further confirm this mechanism, interfacial rheology of brine-oil interface was measured in low salinity water, which showed that seawater gave elastic interfacial modulus of 5 mN/m, whereas 10 times diluted seawater increased the elastic interfacial modulus five times to 25 mN/m (Garcia-Olvera and Alvarado 2017). Taken together, the increased viscoelasticity of oil-brine interfaces likely reduces oil ganglion trapping and promotes oil banking and coalescence after LSW, which explains in part why LSW yields a greater additional oil recovery than tertiary mode.

Wettability alteration is recognized to be an important physicochemical process for low salinity effect (Chen et al. 2018b; Morrow and Buckley 2011b; Nasralla et al. 2013; Strand et al. 2006). Contact angle tests showed that the oil-brine-rock turns to be more water-wet in low salinity brine. For example, Haagh et al. (2018) studied the wettability alteration on silicate surface in artificial seawater and 30 times diluted artificial seawater. The contact angles decreased around 30° in diluted artificial seawater. Chen et al. (2018a) investigated the wettability in different salinity brines on calcite surface and found that the contact angle decreased from 120° in 1 mol/L NaCl to 55° in 0.01 mol/L NaCl. The contact angle can also drop from 73° to 43° in 1 mol/L CaCl2 brine and 0.01 CaCl2 mol/L brine. Furthermore, the in-situ contact angle was measured from micromodel and Micro CT scanning. That confirms that LSW shifts wettability towards water-wet. Microfluidic experiments showed that the contact angle decreased to 88° after LSW (Amirian et al. 2019). Khishvand et al. (2017) imaged the in-situ wettability in sandstone after LSW. The in-situ contact angle decreased from 115° to 89° after LSW. Our latest work also revealed water film propagation during LSW at pore surfaces (sandstone) from Micro CT scanning (Chen et al. 2020, 2021), which is associated with geochemical controls on wettability alteration at pore scale. Taken together, published work confirm that wettability alteration process plays a vital role in oil recovery during LSW.

Therefore, to understand the controlling factor(s) behind the oil recovery difference between secondary and tertiary mode, we aimed to reveal the pore scale fluid dynamics as a function of wettability. We hypothesize that HSW would trigger a preferential flow path at pore space (in an oil-wet or intermediate-wet system), which mitigates the displacement area of subsequent low salinity waterflooding (in a water-wet system). To test this hypothesis, we assumed that high salinity brine results in an oil-wet system and low salinity brine yields a water-wet system. We performed a pore scale modelling with different wetting surface in light of volume of fluid method (VOF) using OpenFOAM. The pore scale fluid dynamics is computed to analyse fluid occupancy and between secondary and tertiary injection modes to test the hypothesis.

Pore-scale dynamic fluid computation

Governing equations

To model the LSW at pore scale, we used OpenFOAM simulator, where Navier–Stokes equations were employed to model the flow process. Given that the compressibility of oil and brine plays a negligible role in pore-scale fluids flow due to limited pressure gradient cross the pore, the fluids were assumed to be incompressible and immiscible in an isothermal system. Therefore, the pore-scale flow process can be described by the following continuity equation and momentum equation.

Continuity Equation: For constant-density flow, i.e., incompressible flow, Eq. 1 is used to describe the incompressible flow.

$$\frac{\partial u}{{\partial x}} = 0$$
(1)

Momentum equation is given as Eq. 2.

$$\frac{\partial (\rho u)}{{\partial t}} + \frac{\partial }{\partial x}(\rho u) = - \frac{\partial p}{{\partial x}} + \frac{\partial \tau }{{\partial x}} + \rho g + f$$
(2)

where \(u\) (m/s) represents fluids velocity. It is worth noting that since we deal with fluids flow at pore-scale, the gravitational effect is neglected (i.e.,\(g = 0\)).\(p\) (Pa) is the fluid pressure. \(\tau\)\((Pa \cdot s)\) is the viscosity, \(f\) (N/m) is the interfacial tension (IFT).

The density of the fluid is defined as:

$$\rho = \alpha \rho_{1} + (1 - \alpha )\rho_{2}$$
(3)

\(\alpha\) is water volume fraction of phase 1, where \(\alpha = 1\) means that the pore is fully saturated with phase 1; \(\alpha = 0\) means that the water saturation of phase 1 is 0. It is modelled as continuum surface force (CSF) as the following. Furthermore, the in Eq. (2) is calculated as in Eq. (4):

$$f = \sigma \kappa \frac{\partial \alpha }{{\partial x}}$$
(4)

where \(\kappa\) is curvature, which can be calculated as the following:

$$\kappa = - \frac{{\partial n_{i} }}{{\partial x_{i} }} = - \frac{\partial }{{\partial x_{i} }}\left( {\frac{{{{\partial \alpha } \mathord{\left/ {\vphantom {{\partial \alpha } {\partial x_{i} }}} \right. \kern-\nulldelimiterspace} {\partial x_{i} }}}}{{\left| {{{\partial \alpha } \mathord{\left/ {\vphantom {{\partial \alpha } {\partial x_{i} }}} \right. \kern-\nulldelimiterspace} {\partial x_{i} }}} \right|}}} \right)$$
(5)

Interphase equation is given in the Eq. 6.

$$\frac{\partial \alpha }{{\partial t}} + \frac{{\partial \left( {\alpha u_{j} } \right)}}{{\partial x_{j} }} = 0$$
(6)

In the pore-scale flow computation, the inlet is set to be constant injection velocity and outlet is set at constant pressure, similar to routine core flooding experiments.

Modelling procedure

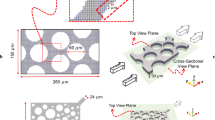
The pore scale fluid dynamics was performed on OpenFOAM-dev platform. Equation (1)–(6) were solved to characterize the two incompressible and immiscible phases flow. The flow domain is shown in Fig. 1. To mesh the flow domain, we used ICEM-CFD (version 18.2, academic license) to generate an unstructured triangle mesh. The maximum mesh size is 1 µm, minimum mesh size is 0.5 µm. All the visualizations were implemented in ParaView version 5.60.

Fig. 1
figure 1

Pore geometry and meshing information

Full size image

To be consistent with the core flooding experiments, a constant velocity of 0.001 m/s (Karadimitriou et al. 2016) was set in the inlet end as the pore velocity. The outlet velocity was set to be a constant pressure boundary with pressure equal to atmosphere pressure. Given the published micro-model and core flooding experimental results, we believe that the absolute value of the velocity at pore level plays a minor role in the effect of wettability alteration on fluids flow at pore space.

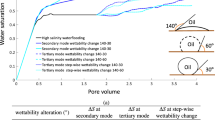
To model the pore scale wettability alteration process, we did not explicitly model the geochemical reactions at pore surface (Maes and Geiger 2018). Rather, we used contact angle at oil-brine-rock interface to represent the wettability alteration. Given that Mahani et al. (2014) observed that kinetic contact angles drop from 110°–120° to 30°–55°, we used contact angle of 135° to represent an oil-wet system in high salinity brine; To model flow in low salinity waterflooding, we used contact angle 45° for water-wet system. Considering that salinity plays a negligible role in interfacial tension (Khaksar Manshad et al. 2016; Lashkarbolooki et al. 2016), in our modelling, the IFT between oil and water is set to be 25 mN/m for both low salinity and high salinity brines. We noticed that the contact angle reduction at pore scale from Micro CT core flooding experiments [for example dropping from 115° to 89° (Khishvand et al. 2017)] appears to be lower than that in the contact angle measurements using flat surfaces. However, we assumed a greater contact angle decrease during low salinity waterflooding to explicitly visualize how wettability alteration process governs the fluid dynamics at pore scale through computational fluid dynamics and show the cause of the discrepant oil recovery between secondary and tertiary modes (Table 1).

Table 1 Simulation Schemes for different low salinity water injection modes
Full size table

Mesh independency study

To balance computation accuracy and efficiency, 1.0 µm maximum mesh size was chosen as the computation mesh. Prior to the modelling, we examined the effect of mesh size (0.7 µm, 1.0 µm, 5.0 µm and 10.0 µm) on calculation results by performing mesh independency study with single phase flow (using the pure water in the domain with same injection velocity at 0.001 m/s). Figure 2a shows the monitor position (line between A and B) and Fig. 2b shows that the velocity distribution. The calculated velocity follows the same pattern that velocity is symmetric distributed with pore center. However, the accuracy varies at different mesh sizes. For example, the velocity distribution curve is not smooth for the 10 µm mesh, which means that the mesh grid is not even distributed and thus calculation fluctuates. With increasing mesh size, the velocity distribution gradually reaches stable, which can be seen from the inlet and outlet velocity distribution (Fig. 2b). The inlet and outlet velocity increases with the mesh size and reaches stable at mesh size of 1.0 µm. Figure 2b shows that velocity does not change when maximum mesh size increases from 1.0 to 0.7 µm, indicating that the calculation is stable with maximum mesh size at 1.0 µm. However, considering the long calculation time with 0.7 µm mesh, we select mess size with 1.0 µm maximum to balance the computation accuracy and efficiency. Note: we did not seek an optimal mesh size here instead finding an acceptable calculation rate is the purpose of the mesh indecency study.

Fig. 2
figure 2

a Position of monitor line, b velocity profile comparison for different meshes (MMS refers to maximum mesh size in the unstructured mesh. Scalar velocity is the square root of sum of vector velocity square in x, y, z direction)

Full size image

Results and discussion

Fluid distribution in water wet pore during engineered waterflooding

Pore surface wettability governs pore scale fluid distribution. A higher water occupancy can be identified in hydrophilic pores (Fig. 4). During secondary HSW, water is injected into the oil-wet (contact angle = 135°) pore from the beginning to 3.0 s, then the pore surface is alternated to water-wet (contact angle = 45°) at 3.0 s, and water injection continues until 10.0 s. After secondary HSW, the water area increased to 54% and kept at 54% until end of secondary HSW (as shown in Fig. 3). Subsequent tertiary LSW increases the water area to 68.1% at 6 s and 89.6% at 8 s. This result can be supported by literature recordings. Secondary HSW yielded 50% to 65% oil recovery, which is in line with Morrow et al. (Morrow and Buckley 2011a). Bartels et al. (2017a) performed HSW in a glass micromodel, which estimated a higher than 50% water area after secondary HSW. Taken together, the pore scale fluid occupancy confirmed that the wettability of the pore surface can govern the pore scale fluid distribution.

Fig. 3
figure 3

Change of water phase area with time during tertiary low salinity waterflooding mode

Full size image

Tertiary LSW afterwards further recovered 15% additional oil. However, given enough flooding time in a water-wet pore, the water occupancy would reach 100% in the single pore model, which may not take place in an actual porous media under tertiary LSW. This can be attributed to the fact that the simulated mode is composed of a single pore instead of a pore network. In the actual pore network, pores with multiple throats connecting with neighbour pores, the oil in pore space would be trapped after water breakthrough. The trapped water will not be able to mobilize with further flooding due to that the capillary trapping can only be eased with dramatically decreasing interfacial tension (Chalbaud et al. 2006; Khaksar Manshad et al. 2016; Nowrouzi et al. 2018) (Fig. 4).

Fig. 4
figure 4

Computed phase’s distribution with a strong water wet pore surface during low salinity waterflooding (note: the blue phase is water, the red phase is oil)

Full size image

Mapping streamline in secondary and tertiary engineered waterflooding

The streamline was analysed to show the fluid velocity distribution in secondary and tertiary flooding mode. The streamline distribution indicates that a pre-existing flow path leads to the low water occupancy during tertiary flooding mode. In the tertiary flooding mode, it can be noticed that the streamline distributes in the center of the pore after tertiary LSW, while the streamline spreads in the pore during secondary LSW (secondary LS and tertiary LS in Fig. 5). This streamline created by secondary HSW concentrates in the pore center, which directs the injected low salinity water straight to the outlet without sweeping the sides area. This flow path acts as a preferential flow pathway for tertiary injected fluid. This streamline distribution shows that the injected water prefers to flowing along the flow path created by secondary flooding in oil-wet pore (tertiary LS in Fig. 5) and the sweeping efficiency is suppressed due to short detaining time. However, during secondary flooding mode, water is injected into water wet pore at the very beginning and no pre-existing flow path exists. The injected water moves to and sweeps oil in the side area, which could be bypassed during tertiary LSW. The pre-existing flow path controlled fluid distributions were observed in literature. Aziz et al. (Aziz et al. 2019) observed scatter distributed water phase after secondary HSW [Fig. 2b of Aziz et al. (2019)]. The subsequent tertiary LSW flowed the existing preferential flow path and distributed in scatter. However, a continuous regular water configuration can be observed after secondary LSW [Fig. 9b of Farzaheh et al. (2017)]. This water phase distributions can be explained by wettability controlled pre-existing flow path and streamline distribution. Water front moves forward like a piston in water wet pore space during secondary mode, while water front prefers flowing along the pore centre leaving side oil trapped.

Fig. 5
figure 5

Streamline of low salinity waterflooding with strong water wet low salinity water (note: The low salinity waterflooding starts at 1.5 s. Thus, the streamline at 1.5 s refers to final streamline of high salinity waterflooding. The colour of line stands for flow velocity)

Full size image

Compared with tertiary flooding mode, the flow rate is slower at secondary injection model, which can be visually demonstrated by streamline colour in Fig. 5 (the lighter colour indicates slower flow rate). The slower fluid rate during secondary flooding indicates that injected fluid can retain and sweep larger area in the pore. In the contrast, a higher flow rate was during the tertiary LSW, which suggested that the injected low salinity water flowed directly to the outlet instead of retaining and sweeping the pore. This character can be supported by experiments with different wetting pores. Torrijos et al. (2016) found that 59% oil recovery can achieved after secondary LSW with 2 PVs low salinity water injection, which is 10% higher than total tertiary low salinity water injection (14 PVs). In conclusion, the pre-existing flow path provides a low resistant flow channel for the tertiary injected low salinity brine and suppresses the wettability alteration process.

Role of pre-existing flow path in carbonated waterflooding

Similar to LSW, carbonated waterflooding improves oil recovery by alternating wettability (Chen et al. 2018a, 2019a; b; Seyyedi et al. 2015, 2017). Secondary carbonated waterflooding was reported to recover more oil than tertiary carbonated waterflooding in the literature. However, source of additional oil under secondary recovery model is unclear. To explain the source of additional oil recovery under secondary carbonated waterflooding, Mosavat et al. (Mosavat and Torabi 2016) flooded a micromodel with carbonated water. Their results showed a piston like water front under the secondary injection mode [Fig. 7 of Mosavat and Torabi (2016)]. However, the tertiary carbonated water flowed along the existing pathways created by the secondary conventional waterflooding, which reduced the contact area and residential time and thus lowered the sweep efficiency of tertiary carbonated waterflooding [as shown in Fig. 10 of Mosavat et al.]. Moreover, the water was dyed to illustrate the concentration in the pore. The water colour is lighter under tertiary mode, which indicates that the water flowed directly to the outlet and mass diffusion between inject fluid and connate fluid was weak. This slow mass transfer can further be explained by the shorter retention time under tertiary mode. Collectively, as a result of the pre-existing flow path, the carbonated water reduced the retaining time in the pore network and less pore area is swept in tertiary flooding mode, which agrees with the calculated fluids distribution in Figs. 4 and 5.

The modelling results can explain the different breakthrough time between secondary and tertiary carbonated waterflooding. 4.8% additional oil was recovered at secondary injection mode at breakthrough time [Fig. 8 in Mahdavi and James (2019)]. The secondary carbonated waterflooding can breakthrough 0.2 PV later than tertiary carbonated waterflooding. This long fluid retaining time during secondary flooding mode is consistent with the streamline analysis (Fig. 5), which suggested the pre-existing flow path lowers the fluid retention time in the pore. Taken together, both the simulation and carbonated waterflooding support that the streamline distribution can affect the flow rates, regulate the retaining time, and thus govern the final oil recovery.

Conclusions and implications

Engineered waterflooding has been recognized as a cost-effective and environmentally friendly recovery method. Literature showed that secondary engineered waterflooding can achieves 5–10% higher oil recovery than tertiary model (Chávez-Miyauch et al. 2019; Chen et al. 2020; Jackson et al. 2016; Mahani et al. 2011; Xie et al. 2014; Yousef et al. 2012; Zahid et al. 2012). Wettability alteration process appears to be one of leading factors to account for the additional oil recovery. However, far too little attention has been paid to evaluate how wettability alteration attributes to the difference of incremental oil recovery between secondary and tertiary modes. Compared with previous work (Akai et al. 2020; Maes and Geiger 2018), this work unveils the critical role of preferential flow in low salinity effects at pore scale.

We therefore examined the effect of wettability alteration on the flow schemes at pore scale using computational fluid dynamics. We compared the pore scale flow under various injection modes with different wettability conditions. We revealed that pore scale wettability alteration accounts for a greater secondary incremental oil recovery compared with tertiary mode. To be more specific, the pre-existing flow channel created by high salinity brine fails to retain the following low salinity water injection. The injected low salinity water would bypass from the pre-existing flow path, reduce the spread of low salinity water, and shorten contact time between injected fluid and connate fluid. Therefore, the pre-existing flow channel established during secondary reduces the sweep efficiency of the subsequent tertiary LSW. This explains at least in part why low salinity waterflooding secondary mode usually yields a higher incremental oil recovery compared with tertiary mode.

The preferential flow path induced sweep area difference has been identified as the underlying reason of recovery difference between secondary and tertiary engineered waterflooding. The pore scale streamline distribution suggests that early engineered waterflooding would favour the final oil recovery as a result of pore-scale wettability alteration. The same methodology can be also applied to understand other EOR techniques which are associated with wettability alteration process [e.g., surfactant flooding, polymer flooding (Yang et al. 2020; Yang 2019)].