Current achievements and future perspectives for projection-based particle methods with applications in ocean engineering

Abstract

The paper aims at providing a comprehensive and up-to-date review on the latest achievements made in the context of particle methods, in particular the projection-based ones, with applications in ocean engineering. The latest achievements corresponding to stability, accuracy, energy conservation and boundary condition enhancements as well as advancements related to improved simulations of multiphase flows, surface tension and fluid–structure interactions are reviewed. The future perspectives for enhancement of applicability and reliability of these methods for ocean engineering applications are also highlighted.

1 Introduction

Due to their mesh-free, Lagrangian nature, particle methods have been proven to provide a substantial potential for simulation of free-surface fluid flows and their interactions with the environment that are often encountered in ocean engineering. During the past two decades a vast number of researches have been conducted on development and application of particle methods, including both SPH (smoothed particle hydrodynamics; Gingold and Monaghan 1977) and MPS (moving particle semi-implicit; Koshizuka and Oka 1996) methods, for different fields of engineering, including ocean engineering. These researches were mainly focused on enhancements of stability/accuracy as well as extension of applications, including ocean engineering related ones.

The existing applications of particle methods in ocean engineering include wave breaking (e.g. Gotoh and Sakai 1999; Khayyer and Gotoh 2008; Farahani and Dalrymple 2014), wave overtopping (e.g. Gotoh et al. 2005; Shao et al. 2006), wave run-up (e.g. Shadloo et al. 2015), wave impact (e.g. Khayyer and Gotoh 2009a; Lee et al. 2011; Altomare et al. 2015), wave-induced nearshore circulation system (Farahani et al. 2014), violent sloshing (e.g. Delorme et al. 2009; Gotoh et al. 2014), oil spilling (e.g. Violeau et al. 2007), green water on ships (e.g. Shibata and Koshizuka 2007; Le Touzé et al. 2010), sediment transport (e.g. Gotoh and Sakai 2006), landslide-generated waves (e.g. Panizzo and Dalrymple 2004; Fu and Jin 2015) and fluid–structure interactions (e.g. Rafiee and Thiagarajan 2009; Shibata et al. 2012; Hwang et al. 2014; Colagrossi et al. 2015; Wei et al. 2015).

In general, particle methods applied for free-surface fluid flows can be categorized into two groups of weakly compressible and incompressible ones. The weakly compressible particle methods such as Weakly Compressible SPH (WCSPH; e.g. Colagrossi and Landrini (2003); Dalrymple and Rogers 2006) or Weakly Compressible MPS (WCMPS; e.g. Shakibaeinia and Jin 2012; Tayebi and Jin 2015) methods solve an appropriate equation of state in a fully explicit form. The incompressible particle methods such as MPS or incompressible SPH (ISPH; e.g. Shao and Lo 2003) methods solve a Poisson pressure equation (PPE) through a Helmholtz-Hodge decomposition and application of Chorin’s projection method (Chorin 1968). Hence, they can be referred to as projection-based particle methods. The concept of Chorin’s projection is illustrated for both ISPH and MPS methods by Khayyer and Gotoh (2009b) and Khayyer and Gotoh (2011).

Several studies have compared the performance of ISPH with respect to WCSPH (e.g. Lee et al. 2008; Hughes and Graham 2010; Khayyer and Gotoh 2010a; Shadloo et al. 2012; Zheng et al. 2014a). In general, projection-based particle methods are expected to provide higher accuracy in terms of pressure calculation and volume conservation (Gotoh et al. 2013). However, from computational point of view, solving a PPE may bring about distinct challenges, especially for parallelized and/or GPU-based computations (e.g. Hori et al. 2011).

This paper aims at reviewing the latest achievements made in the field of particle methods, especially the projection-based ones with applications in ocean engineering. The ongoing researches and future perspectives will be also discussed. The latest achievements correspond to enhancements of stability, accuracy, energy conservation, boundary conditions and improved simulations of multiphase flows, surface tension, fluid–structure interactions, etc. Despite the advancements made, several key aspects still remain to be not comprehensively resolved. Examples of such remaining unresolved issues include stability, convergence, adaptivity, boundary conditions and consistency/conservation. The first four issues are considered as SPH grand challenges by the SPHERIC (SPH European Research Interest Community).

2 Latest achievements

In general, both weakly compressible and incompressible particle methods for free-surface fluid flows provide solutions, on the basis of particle-based discretizations, to the continuity and Navier–Stokes equations that are expressed as follows, in a continuous framework:

$$\begin{aligned}&\frac{1}{\rho }\frac{\mathrm{D}\rho }{\mathrm{D}t}+\nabla \cdot \varvec{u}=0\end{aligned}$$

(1)

$$\begin{aligned}&\frac{{\mathrm{{D}}\varvec{u}}}{{\mathrm{{D}}t}}=-\frac{1}{\rho }\nabla p+\varvec{g}+\nu \nabla ^{2}\varvec{u}, \end{aligned}$$

(2)

where ${\varvec{u}}$ denotes particle velocity vector; t stands for time; $\rho$ represents fluid density;p symbolizes particle pressure; ${\varvec{g}}$ signifies gravitational acceleration vector and $\upsilon$ represents laminar kinematic viscosity. It should be noted that Eq. 1 is written in the form of a compressible flow. In projection-based particle methods, incompressibility is enforced by setting D$\rho$/Dt equal to zero at each particle at each calculation time step through application of Helmholtz-Hodge decomposition and a prediction-correction process. The latest advancements corresponding to particle methods, and in particular projection-based ones, in solving the abovementioned governing equations (together with other related governing equations) are discussed in this section.

2.1 Stability enhancement

The stability issue is of crucial importance for proper and reliable application of particle methods to engineering problems including those encountered in ocean engineering. In general, the numerical instabilities associated with particle methods can be categorized into two major categories of rank deficiency and stress state instabilities. The rank deficiency instability is related to spurious singular or zero-energy modes occurring when the field variables and their derivatives are calculated at the same calculation points (Beissel and Belytschko 1996). This particular instability is not limited to particle methods and it can be found in grid-based methods including finite element and finite difference methods (Vignjevic 2004). As the name indicates, stress state instabilities, including so-called compressive and tensile instabilities, depend on the state of stress and growth of perturbations with kernel-based approximations of inter-particle interactions. The compressive instability occurs in the presence of repulsive inter-particle forces when inter-particle interaction strength decreases as the particles approach (Swegle et al. 1994; Johnson et al. 1996). On the other hand, tensile instability occurs in the presence of attractive inter-particle forces when inter-particle interaction strength increases as the particles approach (Swegle et al. 1994; Swegle 2000; Khayyer and Gotoh 2011).

By performing a one-dimensional von Neumann stability analysis for the SPH method, Swegle et al. (1995) found a criterion for an unstable growth of perturbations based on the sign of the stress and kernel’s second derivative. A similar criterion was identified for stability of MPS by Khayyer and Gotoh (2011). Several studies (e.g. Balsara 1995; Morris 1996; Robinson 2009; Dehnen and Aly 2012) highlighted the significance of the Fourier transform of the kernel function in stability properties of SPH. However, none of the above mentioned papers provided an explicit criterion for the maximum allowable time step.

Morris et al. (1997) proposed a criterion for maximum allowable time step in WCSPH context. Through performing a rigorous theoretical stability analysis for unbounded flows, Violeau and Leroy (2014) derived an analytical formula for the stability condition and thus the maximum allowable time step for WCSPH. They later extended their rigorous work to ISPH (Violeau and Leroy 2015). The maximum CFL number for ISPH at large Reynolds numbers was found to be twice smaller than that of WCSPH and thus, resulting in an optimal time step size of only five times larger for ISPH.

There have been a wide range of efforts to minimize the possibility of occurrence of instabilities in particle methods, including those targeting tensile instability. However, as highlighted by Belytschko and Xiao (2002), perfect elimination of tensile instability appears to be unachievable as long as an Eulerian kernel is used with a purely Lagrangian description of motion. Thus, such instability tends to arise in both weakly compressible particle methods as well as projection-based ones. Belytschko and Xiao (2002) showed that tensile instability can be eliminated when the kernel is a function of material coordinates (i.e. a Lagrangian kernel). The problem related to the Lagrangian kernels is that they may not tolerate large deformations as in case of fluid flows (Belytschko and Xiao 2002; Rabczuk et al. 2004), particularly the violent ones. The efforts corresponding to minimization of probability of tensile instability occurrence can be categorized into the following distinct groups:

• (i) Artificial repulsive forces To resolve the problem of tensile instability in SPH, Monaghan (2000) and Gray et al. (2001) proposed artificial repulsive forces proportional to the fluid pressure and the stress tensor, respectively. In particular, in fluid–structure interaction (FSI) simulations, such kind of treatment has been repeatedly used to ensure the stability of calculations (e.g. Antoci et al. 2007; Rafiee and Thiagarajan 2009; Kondo et al. 2010). As shown by Tsuruta et al. (2013), application of artificial repulsive forces may adversely affect the reproduced physics of simulations, in particular due to possible generation of excessive repulsive forces that are more adequate for numerical stabilization. Tsuruta et al. (2013) presented a so-called dynamic stabilization (DS) scheme which is aimed to produce exactly adequate repulsive forces to ensure the numerical stability. The applicability and effectiveness of this scheme has to be further examined for a wider range of free-surface, internal and multi-phase flows.

• (ii) Corrective functions for enhancements of kernel estimates Dilts (1999) showed that accurate estimation of derivatives is a key point in removal of tensile instability. This is mainly due to the fact that tensile instability is triggered when unphysical perturbations in particle motions exist. Khayyer and Gotoh (2011) proposed a gradient correction (GC) for MPS method to minimize the unphysical perturbations in particle motions and achieved improved stability performance. Similar approaches have been introduced in the context of SPH method. For instance, Chen et al. (1999) proposed a corrective SPH (CSPH) to improve the stability of SPH. In projection-based particle methods, corrective or error minimizing schemes can be introduced in the source term of Poisson pressure equation (PPE) to minimize the projection-related errors to achieve enhanced pressure field and uniform particle distributions throughout the simulation that minimizes the perturbations in particle motions. For instance, Khayyer and Gotoh (2011) introduced so-called error compensating source (ECS) terms of PPE with dynamic coefficients as functions of instantaneous flow features. The ECS scheme could be considered as an enhanced and updated version of the scheme proposed by Kondo and Koshizuka (2011).

• (iii) Conservative smoothing Based on the von Neumann–Richtmyer discrete representation of conservation of volume, Guenther et al. (1994) presented a conservative smoothing formalism for SPH. They showed that a proper conservative smoothing produces significantly more stable and accurate solutions compared to commonly used artificial viscosity. The effectiveness of conservative smoothing in minimization of occurrence probability of tensile instability is proved in the studies by Hicks and Liebrock (2004) and Xu et al. (2008). To the best knowledge of authors, the conservative smoothing technique has not been applied yet within the framework of projection-based particle methods. However, its applicability can be tested for applications that are prone to numerical instability, for instance, multiphase flows with high density ratios.

• (iv) Stress-points Dyka et al. (1997) proposed an alternative approach to tackle the problem of tensile instability in particle methods. This approach was founded on introduction of a set of additional particles in between the original particles to serve as additional quadrature points. Randles and Libersky (2000) later extended this method to higher dimensions. Belytschko et al. (2000) showed that the stress point technique stabilizes SPH by removing the instability that arises due to rank deficiency, while the stress state related tensile instability can be avoided only by using a Lagrangian kernel.

• (v) Lagrangian kernels As previously stated, although a careful implementation of stress points removes the zero-energy modes, it does not eliminate the tensile instability (Belytschko et al. 2000). Belytschko and Xiao (2002) highlighted the fact that tensile instability occurs when an Eulerian kernel is used with a Lagrangian description of motion. They showed that this instability is eliminated when the kernel is a function of material coordinates (i.e. a Lagrangian kernel). It was also found that the best approach to stabilize particle-based methods is to use Lagrangian kernels with stress points. However, apart from the increased complexity of mathematical formulations, in case of application of stress points, the stability and convergence would depend on the distribution of particles in the domain, where a poor convergence rate would be obtained for irregular particle distributions (Fries and Belytschko 2008). Furthermore, Lagrangian kernels do not appear to be proper for problems involving large deformations, as in case of free-surface fluid flows.

• (vi) Total Lagrangian formalism Vignjevic et al. (2006) showed that the tensile instability can be resolved through a total Lagrangian description of continuum. They also introduced consistency corrections into the total Lagrangian SPH formalism to enhance the accuracy of their SPH solid mechanics simulations.

It should be noted here that to the best knowledge of authors, stress points, Lagrangian kernels and total Lagrangian formalism have not been tested yet in the context of projection-based particle methods. However, all of the mentioned techniques appear to be applicable within this context as well, for instance, in FSI simulations by a coupled fully Lagrangian solver comprising of a projection-based fluid model and an elastic structure model. These techniques tend to stabilize the structure model, and thus the overall FSI solver, by removing the spurious zero-energy modes and/or minimizing incidence of tensile instability.

In addition to the abovementioned approaches, a distinct category of schemes, proven to be effective for both stability and accuracy enhancement of particle methods, corresponds to the particle regularization schemes. A concise review of this class of schemes is presented in Sect. 2.2.2.

2.2 Accuracy enhancement

One of the main shortcomings of particle methods, including projection-based ones, corresponds to presence of unphysical pressure oscillations (e.g. Gotoh et al. 2005, 2013; Khayyer and Gotoh 2009a, b). This shortcoming could have limited the application of particle methods to ocean engineering. However, there have been substantial efforts and progresses corresponding to this distinct shortcoming (e.g. Ataie-Ashtiani et al. 2008; Khayyer et al. 2009; Koshizuka 2011; Gotoh et al. 2014). These efforts could result in reliable particle methods that provide acceptable solutions to the considered governing equations.

In the context of weakly compressible SPH, the so-called delta-SPH (Antuono et al. 2012) as well as Riemann SPH (Inutsuka 1994, 2002; Monaghan 1997; Gao et al. 2012; Rafiee et al. 2012) schemes have been proposed to enhance the accuracy, especially in terms of reproduced pressure field. Several rigorous studies also investigate the accuracy of SPH and highlight the importance of higher order interpolation schemes to improve the method’s performance (e.g. Le Touzé et al. 2013). Corrected SPH methods with corrective terms to restore the completeness or consistency (Colagrossi et al. 2011) of formulations (e.g. Randles and Libersky 1996; Chen et al. 1999; Oger et al. 2007; Schwaiger 2008; Fatehi and Manzari 2011a; Jiang et al. 2012) as well as momentum conservation (e.g. Bonet and Lok 1999; Hopkins 2015) have also been developed and applied to ocean engineering problems (e.g. Sun et al. 2010; Xie et al. 2012).

As for projection-based particle methods, refined differential operator models have been proposed for discretization of source term and Laplacian of PPE as well as corrective terms to restore consistency of approximations (e.g. Khayyer and Gotoh 2011; Ikari et al. 2015a) and momentum conservation (e.g. Khayyer et al. 2008; Khayyer and Gotoh 2008). Khayyer and Gotoh (2009a) proposed a Higher-order Source term of PPE abbreviated as HS scheme. Later in 2010, a Higher-order Laplacian (HL) model was proposed (Khayyer and Gotoh 2010b) to further enhance the pressure field calculations. The HL scheme was extended to three dimensions (Khayyer and Gotoh 2012) and its enhancing performance with respect to the standard MPS Laplacian was demonstrated by a number of benchmark tests including ocean engineering related ones. To enhance volume conservation and projection-related errors, the ECS (error compensating source of PPE) was proposed for both MPS (Khayyer and Gotoh 2011) and ISPH (Gotoh et al. 2014) methods. The ISPH version of HL was also shown to provide improved results with respect to the commonly applied hybrid SPH-finite difference Laplacian model of SPH (Shao and Lo 2003) in simulation of violent sloshing flows (Gotoh et al. 2014).

Recently, Zheng et al. (2014b) proposed a new ISPH based on Rankine source solution that transforms the PPE into a form that does not require any direct approximations for function derivatives. The advantage of the so-called ISPH-R (ISPH with Rankine source solution) mainly corresponds to absence of the need to approximate second-order derivatives in the PPE. The enhanced performance of ISPH-R with respect to standard ISPH was shown through a number of benchmark tests including those related to water waves and violent sloshing flows. Ngo-Cong et al. (2015) proposed an improved ISPH method through solving the PPE on a set of so-called moving integrated radial basis function networks.

Among other impressive works corresponding to accuracy enhancement in the context of projection-based particle methods, we can mention the multiphase projection formulation of Hu and Adams (2007), in which both the zero-density-variation and velocity-divergence-free constraints of the incompressibility condition were enforced through the resolution of two PPEs and via application of a fractional time-step integration algorithm.

Two different classes of schemes corresponding to accuracy and stability enhancements of projection-based particle methods, namely refined schemes and particle regularization schemes are briefly reviewed in Sects. 2.2.1 and 2.2.2, respectively.

2.2.1 Refined schemes for accuracy and stability enhancements

2.2.1.1 HS and HL schemes

In general, in projection-based particle methods the PPE is formulated as follows (Gotoh 2009; Khayyer and Gotoh 2011):

$$\begin{aligned}&\left\langle {\nabla ^{2}p_{k+1}} \right\rangle _{i} =\frac{1}{\Delta t}\left( {\frac{\mathrm{D}\rho }{\mathrm{D}t}}\right) _{i}^*;\nonumber \\&\rho =m\sum \limits _{i\ne j} {w(\left| {\varvec{r}_{ij} }\right| )} =m\sum \limits _{i\ne j} {w_{ij} }\, ;\quad \varvec{r}_{ij} =\varvec{r}_j -\varvec{r}_i, \end{aligned}$$

(3)

where m denotes particle mass, $\varvec{r}$ presents the particle position vector, w presents kernel function, k signifies the calculation step number and $\Delta t$ symbolizes the calculation time step. In Eq. 3, i and j represent a target particle i and a typical neighboring particle j. The superscript $^{*}$ denotes the pseudo-time step k + 1/2, corresponding to the end of prediction step. Considering the concept of particle number density, n, in MPS, the PPE is written as

$$\begin{aligned} \left\langle {\nabla ^{2}p_{k+1}}\right\rangle _{i} =\frac{\rho }{n_{0} \Delta t}\left( {\frac{\mathrm{D}n}{\mathrm{D}t}}\right) _{i}^{*} ;\quad n=\sum \limits _{i\ne j} {w\left( \left| {\varvec{r}_{ij}}\right| \right) } =\sum \limits _{i\ne j} {w_{ij}}, \end{aligned}$$

(4)

where $n_{0}$ represents the reference particle number density, n. Discretization of the source term of PPE (right-hand side of Eq. 4) and the Laplacian of pressure (left-hand side of Eq. 4) by HS (higher order source; Khayyer and Gotoh 2009a) and HL (higher order Laplacian; Khayyer and Gotoh 2010b, 2012) schemes are conducted as follows:

$$\begin{aligned} \left( {\frac{\mathrm{D}n}{\mathrm{D}t}}\right) _{i}^{*} =\sum \limits _{j\ne i} {\left( {\frac{\partial w_{ij}}{\partial r_{ij}}}\right) \frac{\varvec{r}_{ij} \cdot \varvec{u}_{ij}^*}{\left| {\varvec{r}_{ij} } \right| }} \end{aligned}$$

(5)

$$\begin{aligned}&\left\langle {\nabla ^{2}p_{k+1}} \right\rangle _{i}\nonumber \\&\quad =\frac{1}{n_0 }\sum \limits _{j\ne i} {\left\{ {\frac{\partial p_{ij} }{\partial r_{ij} }\frac{\partial w_{ij} }{\partial r_{ij} }+p_{ij} \left( {\frac{\partial ^{2}w_{ij} }{\partial r_{ij}^{2} }+\frac{D_s -1}{r_{ij} }\frac{\partial w_{ij} }{\partial r_{ij} }}\right) } \right\} },\nonumber \\ \end{aligned}$$

(6)

where u and v denote horizontal and vertical components of velocity vector $\varvec{u},p_{ij} =p_j -p_{i;} r_{ij} =r_j -r_i ;\,r=\left| \varvec{r} \right| \,;u_{ij} =u_j -u_i\,\,\mathrm{and}\,\,v_{ij} =v_j -v_i .$ The variable $D_{s}$ in Eq. 6 corresponds to the number of space dimensions. Recently, Ikari et al. (2015b) presented a corrected HL (CHL) scheme by carefully taking the divergence of a corrected gradient model. The enhanced performance of CHL with respect to HL could be verified, especially for calculation cases with irregular initial arrangements.

2.2.1.2 ECS scheme

As previously stated and as it has been explained in details by Khayyer and Gotoh (2011), discretization of the source term of PPE even by accurate differential operator models does not guarantee a divergence-free velocity field corresponding to an incompressible fluid flow. The ECS (error compensating source) scheme proposed by Khayyer and Gotoh (2011) is written in the following form:

$$\begin{aligned} \left\langle {\nabla ^2p_{k+1} } \right\rangle _i =\frac{\rho }{n_0 \Delta t}\left( {\frac{Dn}{Dt}}\right) _i^*+\varLambda _\mathrm{{ECS}} \end{aligned}$$

(7)

$$\begin{aligned} \varLambda _\mathrm{{ECS}}= & {} \frac{\rho }{\Delta t}\left\{ {\frac{\alpha }{n_{0}}\left( {\frac{Dn}{Dt}}\right) _{i}^{k} +\frac{\beta }{\Delta t}\frac{n_{i}^{k}-n_{0}}{n_{0} }} \right\} ;\nonumber \\ \alpha= & {} \left| {\frac{n_{i}^{k}-n_{0}}{n_{0}}} \right| ; \beta =\left| {\frac{\Delta t}{n_{0}}\left( {\frac{Dn}{Dt}}\right) _{i}^{k}} \right| \end{aligned}$$

Accordingly, the source term of PPE will be comprised of a high-order main term (HS scheme) and two error mitigating terms multiplied by dynamic coefficients ($\alpha$, $\beta )$ as functions of instantaneous flow field. In Eq. 7, the first error mitigating term (which is multiplied by coefficient $\alpha )$ corresponds to the instantaneous time variation of particle density at time step k. The second term (which is multiplied by coefficient $\beta )$ reflects the deviation of particle density at time step k from the theoretical constant one ($\rho _{0})$. In other words, the first- and second-error mitigating terms correspond to the instantaneous and accumulative density deviations, respectively. The dynamic coefficients adjust the intensities of these two error mitigating terms depending on the instantaneous state of flow field. Similar ECS scheme has been formulated and validated for the ISPH (Gotoh et al. 2014).

Fig. 1

a A graphical representation of the concept of DS (dynamic stabilization) scheme, b effectiveness of DS scheme in proper modeling of settlement of heavy particles in water (Tsuruta et al. 2013)

2.2.1.3 GC and DS schemes

A proper Taylor-series consistent pressure gradient model with gradient correction (GC; Khayyer and Gotoh 2011) and dynamic stabilization (DS; Tsuruta et al. 2013) schemes is expressed as follows:

$$\begin{aligned} \left\langle {\frac{\nabla p}{\rho }} \right\rangle _{i} =\frac{D_{s}}{\rho n_{0}}\sum \limits _{j\ne i} {\frac{p_{j}-p_{i} }{\left| {\varvec{r}_{ij}} \right| ^{2}}\varvec{C}_{i} \varvec{r}_{ij} w_{ij}} +\varLambda _\mathrm{{DS}}, \end{aligned}$$

(8)

where the gradient correction (GC) matrix, $\varvec{C}_{i}$, is expressed as follows:

$$\begin{aligned} \varvec{C}_{i} =\frac{1}{D_{s}}\left( {V_{i}\sum \limits _{j\ne i} {\frac{\varvec{r}_{ij} \otimes \varvec{r}_{ij} }{\left| {\varvec{r}_{ij} } \right| ^2}w_{ij} } }\right) ^{-1} \text{; } \quad V_{i} =\frac{1}{\sum \limits _{j\ne i} {w_{ij} } } \end{aligned}$$

(9)

In Eq. 8, the DS scheme (Tsuruta et al. 2013) is formulated as follows:

$$\begin{aligned}&\varLambda _\mathrm{{DS}} =V_i \sum \limits _{j\ne i} {\varvec{F}_{ij}^\mathrm{{DS}}} w_{ij} \quad ;\nonumber \\&\varvec{F}_{ij}^\mathrm{{DS}} =\left\{ \begin{array}{ll} 0&{}\qquad \left| {\varvec{r}_{ij} ^*} \right| \ge d_{ij} \nonumber \\ -\rho _{i} \Pi _{ij} \frac{\varvec{r}_{ij} }{\left| {\varvec{r}_{ij} } \right| }&{}\quad \quad \left| {\varvec{r}_{ij} ^*} \right| <d_{ij} \\ \end{array}\right. \end{aligned}$$

$$\begin{aligned} d_{ij} =\alpha _\mathrm{{DS}} \frac{d_i +d_j }{2};\quad \alpha _\mathrm{{DS}} =1-\alpha _{dt} \end{aligned}$$

(10)

$$\begin{aligned} \Pi _{ij} =\frac{\rho _j }{( {\Delta t})^2( {\rho _i +\rho _j })}\left( {\sqrt{d_{ij} ^2-\left| {\varvec{r}_{ij\bot }^*} \right| ^{2}} -\left| {\varvec{r}_{ij\parallel }^*} \right| }\right) , \end{aligned}$$

where $\varvec{F}_{ij}^\mathrm{{DS}}$ is the stabilizing force for target particle i from its neighboring particle j; $\Pi _{ij }$is the parameter to adjust the magnitude of ${\varvec{F}}_{ij}^\mathrm{{DS}}$;$\alpha _\mathrm{{DS}}$ is a constant for adjusting active range of ${\varvec{F}}_{ij}^\mathrm{{DS}}$; $\alpha _{dt}$ is the ratio of the time step to Courant number; d represents the particle diameter; ${{\varvec{r}}_{{ij}{\parallel }}^{*}}$ is the parallel vector of ${\varvec{r}}_{ij}^{*}$ and ${\varvec{r}}_{{ij}{\bot }}^{*}$is the normal vector of ${\varvec{r}}_{ij}^{*}$ with ${\varvec{r}}_{ij}^{*}$= ${{\varvec{r}}_{{ij}{\parallel }}^{*}}$ + ${\varvec{r}}_{{ij}{\bot }}^{*}$. Figure 1 shows a graphical representation of the concept of DS scheme as well as its effectiveness in providing proper settlement of heavy particles in water. The so-called CMPS-HS (Khayyer and Gotoh 2009a) has not been able to reproduce this settlement due to excessive repulsive forces corresponding to a repulsive pressure gradient model. Details of this numerical test are provided in the paper by Tsuruta et al. (2013). The corresponding simulations were conducted by a total number of 7000 particles with diameter of 2.5 mm. Densities of the light and heavy particles were set as 1000 and 2650 kg/m$^{3}$, respectively.

Without application of DS scheme, the stability of simulations performed by a Taylor-series consistent pressure gradient model is generally not guaranteed. Thus, purely repulsive (and conditionally Taylor-series consistent; Khayyer and Gotoh 2013) pressure gradient models were suggested to be used. For instance, a commonly applied MPS gradient model that results in purely repulsive pressure interacting forces is (Koshizuka et al. 1998)

$$\begin{aligned} \left\langle {\frac{\nabla p}{\rho }} \right\rangle _{i} =\frac{D_{s} }{\rho n_{0} }\sum \limits _{j\ne i} {\frac{p_{j} -\hat{p}_{i}}{\left| {\varvec{r}_{ij} } \right| ^{2}}\varvec{r}_{ij} w_{ij} } \end{aligned}$$

(11)

$$\begin{aligned} \hat{p}_i =\mathop {\min }\limits _{j\in J} ( {\,p_i ,p_j });\quad J=\left\{ {\,j:w_{ij} \ne 0} \right\} \end{aligned}$$

In the context of ISPH, the specific formulations of HS, HL and ECS are given by Gotoh et al. (2014). Here, a considered corrected Taylor-series consistent pressure gradient model with DS scheme is formulated.

$$\begin{aligned} \left\langle {\frac{\nabla p}{\rho }} \right\rangle _{i} =\sum \limits _{j\ne i} {\frac{m_{j}}{\rho _{i}\rho _{j}}} ( {\,p_{j}-p_{i} })\,\,\varvec{C}_{i} \nabla _{i} w_{ij} +\varLambda _\mathrm{{DS}}, \end{aligned}$$

(12)

where $\nabla _{i}w_{ij}$ denotes the gradient of weight function $w_{ij}$ calculated at the target particle i. In Eq. 12, the gradient correction matrix is written as follows:

$$\begin{aligned} \varvec{C}_{i} =\left( {V_i \sum \limits _{j\ne i} {\nabla w_{ij} \otimes \varvec{r}_{ij} } }\right) ^{-1} \end{aligned}$$

(13)

A symmetric repulsive pressure gradient model frequently applied in ISPH simulations because of its superior stability features (e.g. Shao and Lo 2003; Khayyer et al. 2008; Lee et al. 2008) is expressed as follows:

$$\begin{aligned} \left\langle {\frac{\nabla p}{\rho }} \right\rangle _i =\sum \limits _{j\ne i} {m_j \left( {\frac{p_j }{\rho _j^2 }+\frac{p_i }{\rho _i^2 }}\right) \nabla } w_{ij} \end{aligned}$$

(14)

As will be discussed in Sect. 2.3, repulsive pressure gradient models including Eqs. 11 and 14 result in a remarkably inferior energy conservation. Hence, they appear not to be thoroughly reliable, especially for applications where energy conservation properties become important.

2.2.2 Particle regularization schemes

A distinct category of methods developed for enhancement of both accuracy and stability for both explicit and semi-implicit projection-based particle methods correspond to particle regularization schemes that tend to regularize the anisotropic distributions of particles prone to be formed due to Lagrangian characteristics of particle methods. The most well-known and the simplest approach is the so-called XSPH scheme (Monaghan 1992) which helps the particles to move with a velocity close to that of their neighboring particles. Thus, the XSPH scheme improves the smoothness of velocity field. However, it is based on an arbitrarily tuned velocity smoothing, may lead to numerical dispersions (Fatehi and Manzari 2011b) and inaccurate results in case of sharp velocity gradients (Shahriari et al. 2013). Monaghan (2005) highlighted the fact that the XSPH scheme does not conserve energy and proposed an implicit XSPH to resolve this issue.

A relatively new particle regularization technique is the particle shifting scheme of Xu et al. (2009) which slightly shifts the particles to prevent anisotropic particle structures. A generalized version of this scheme has been proposed by Lind et al. (2012), allowing extended applications to free-surface flows. The particle shifting scheme is founded on Fick’s diffusion law and relies on a Taylor expansion for evaluation of particle quantities in new positions. Despite its simplicity and effectiveness, the particle shifting scheme may violate the overall conservation properties (Lind et al. 2012) including conservations of momentum and energy. On the contrary, the DS scheme, which can also be considered as a particle regularization scheme, provides radial and anti-symmetric inter-particle forces and thus, at least, this scheme preserves both linear and angular momentum exactly. A detailed comparative study in between DS and particle shifting is currently being conducted by the authors.

Fig. 2

Sinusoidal wave propagation on a long flat bottom–a schematic sketch of calculation domain, b typical snapshot of fluid particles together with pressure field, c time history of water elevation at x = 5.0 m, and d x = 15.0 m

In the context of weakly compressible SPH, Adami et al. (2013) proposed a particle velocity correction together with a consistent additional term in the momentum equation to take into account the required modification of the advection velocity. The scheme was proven to be effective in enhancing the accuracy and stability of internal flows. However, extensions to free-surface flows does not appear to be straightforward. Recently, Oger et al. (2015) proposed a specific transport velocity within an ALE formalism where the method is shown to be robust and accurate for both internal and free-surface flows. This scheme appears to be applicable within the context of projection-based particle methods to resolve the issue with anisotropic particle distributions prone to be formed due to purely Lagrangian descriptions.

2.3 Energy conservation improvement

In the context of weakly compressible SPH, Fang et al. (2009) presented a SPH variant by deriving a set of general discrete hydrodynamic equations within an energy-based framework. They highlighted that their formulations are also consistent with those derived from a variational approach by Bonet and Lok (1999). The connection in between variational principle and energy conservation in SPH has been well illustrated (e.g. Monaghan and Price 2001; Violeau 2012). Violeau (2012) highlighted the compatibility, and more precisely, the skew-adjointness of gradient and divergence operators for energy conservation. In the context of projection-based particle methods, this important property is required for an exact projection (Cummins and Rudman 1999) which is a necessity for an exact energy conservation.

Recently, Khayyer et al. (2015a) performed a study on energy conservation properties of projection-based particle methods, i.e. MPS and ISPH. Their study highlighted the significance of Taylor-series consistent pressure gradient models (e.g. Eqs. 8, 12) and enhancing effect of the consistency-related Gradient Correction (GC) scheme in providing enhanced energy conservation.

By applying Eq. 8 together with the refined schemes of HS, HL and ECS, enhanced energy conservations and acceptable predictions of physical dissipations could be achieved in the study by Khayyer et al. (2015a).

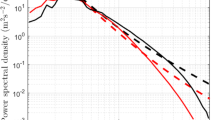
Figure 2 illustrates the appropriateness of Eq. 8 with respect to Eq. 11 in providing minimized numerical dissipation in a long-term wave propagation simulation. The considered wave is a sinusoidal one with wave period of 1.2 s, wave height of 0.11 m and wave length of 2.1 m. A total number of 383,815 particles were employed in the domain. The particle diameter, $d_{0}$, was considered to be 0.01 m. Figure 2a shows a schematic sketch of calculation domain. Figure 2b presents a typical snapshot of fluid particles together with calculated pressure field by the enhanced MPS incorporating Eq. 8 (MPS-GC-DS) together with HS, HL and ECS schemes so that the method is referred to as MPS-HS-HL-ECS-GC-DS. Quantitative comparisons of water elevations at horizontal positions of x = 5 and 15 m are presented in Fig. 2c, d, respectively.

Fig. 3

Simulations of a standing wave by ISPH-based methods with symmetric repulsive pressure gradient model (a) and Taylor-series consistent one (b)–quantitative comparison in terms of water level elevation at the center of the tank (c)

Figure 3 shows results of simulations of a standing wave by ISPH-based methods, where exactly similar tendency as MPS-based simulations could be observed. In other words, a Taylor-series consistent SPH pressure gradient model with a consistency-related correction has provided far better results compared with the symmetric repulsive pressure gradient model (Eq. 14). Conditions of the performed simulations shown in Fig. 3 correspond to those in Suzuki et al. (2007). In other words, the water depth h is 1 m and the bottom width is 2 m. Initial profile of water surface is given as follows:

$$\begin{aligned} \eta _0 (x)=A\cos [k(x+\lambda )/2], \end{aligned}$$

(15)

where $\eta _{0}$ is the initial surface elevation (above the mean water level at y = 1.0 m), A = 0.1h is the wave amplitude, k = 2$\pi /\lambda$ is the wave number and $\lambda$(=2 m) is the wave length. Initial velocity is set as zero for all the particles. The calculation time step is obtained based on the Courant stability condition and a maximum allowable time step of $\Delta t$ = 2.5E$-$4 s. The diameter of particles is set as $d_{0}$ = 0.01 m.

Fig. 4

The normal impact of two rectangular fluid patches a–d snapshots of particles together with pressure field, e time history of the evolution of mechanical energy

Figure 4 illustrates the improved MPS results of the normal impact of two rectangular fluid patches (Marrone et al. 2015). The rectangular patches have a length L, width 2H and the impact occurs at t = 0. The fluid is considered to be inviscid and incompressible, and thus the impact will be associated with a theoretically sudden loss of a fraction of the initial energy (Szymczak et al. 1994). For the performed simulations L = 1.0 m, H = 0.33 m and U = 3.4 m/s. The maximum allowable time step is set as $\Delta t$= 5.0E$-$5 s and the particles are set to be of 0.01 m in diameter, i.e. $d_{0}$ = 0.01 m. A set of typical snapshots illustrating this phenomenon is presented in Fig. 4a–d. From Fig. 4e, the enhanced MPS method which benefits from five refined schemes, namely HS-HL-ECS-GC-DS has been able to properly reproduce this loss of energy. The MPS with a repulsive-based pressure gradient model (Eq. 11) has been inaccurate even by employment of HS and HL schemes. The figure also portrays the enhancing effect of ECS scheme.

2.4 Improvement of boundary conditions

There are several important aspects to be considered for a proper enforcement of boundary conditions including solid, free-surface, inlet/outlet boundaries, etc. These issues as discussed by the SPHERIC boundary conditions’ working group correspond to preservation of conservation and consistency properties of particle methods. In this section, we review the latest advancements made for treatment of solid (wall), free-surfaces as well as inlet/outlet boundaries.

2.4.1 Solid or wall boundaries

Non-conservative, inconsistent wall boundary conditions result in non-conservation of volume and momentum, and accordingly may either result in unphysical wall penetrations or gaps in between wall particles and fluid ones.

Treatment of solid wall boundaries in particle methods, and in particular in SPH, has been carried out mainly by the use of so-called ghost (Colagrossi and Landrini 2003) or mirror (Basa et al. 2009) particles as fictitious neighboring particles that are positioned to complete the truncated kernel supports at boundaries. By applying a pressure boundary condition founded on local force balance in between wall and fluid particles, Adami et al. (2012) proposed a generalized wall boundary condition for SPH which correctly imposes no-slip conditions even for complex geometries. Despite being relatively simple for implementation, application of mirror particles may lead to inaccuracies in the convergence of differential operator models (Macià et al. 2011). A more favored and recent approach is related to development of so-called semi-analytical wall boundary conditions.

Di Monaco et al. (2011) developed a semi-analytic approach for treatment of wall boundaries that can be considered as an integral version of the mirror particles of Adami et al. (2012) for fixed boundaries. Similar approaches have been proposed by Ferrand et al. (2013) and Mayrhofer et al. (2013) that provide accurate and direct modeling of boundary integrals at the frontiers of the fluid domain resulting in precise pressure forces, wall friction and turbulent conditions. The importance of proper modeling of boundary conditions by careful implementation of boundary integrals for accuracy, consistency and convergence of both weakly compressible SPH and ISPH was shown in a study by Macià et al. (2012).

Another class of wall boundary conditions commonly applied in SPH corresponds to the repulsive boundary forces (Monaghan 2005) that may not properly model the actual physics in the vicinity of the boundary due to possible generation of excessive repulsive forces.

Fig. 5

A graphical representation of the SPP (space potential particles) scheme (a), effectiveness of SPP in elimination of unphysical voids in a Karman vortex simulation (b) (Tsuruta et al. 2015)

As for projection-based particle methods, uniformly spaced, fixed dummy particles are commonly applied to treat the wall boundaries (e.g. Gotoh and Sakai 1999; Shao and Lo 2003; Gotoh et al. 2005; Lee et al. 2008). In general, a few layers of dummy particles are added to provide a complete compact support for particles in the vicinity of wall boundaries, while only one or two layers of dummy particles are considered in the pressure solution process. For enhanced particle methods (e.g. Gotoh et al. 2014; Khayyer and Gotoh 2013) that provide acceptable pressure field and volume conservation, at least the pressure forces at the wall boundaries are calculated physically and precisely. Hence, the problem of unphysical wall penetration would become unlikely. On the other hand, for proper modeling of wall friction and turbulent conditions appropriate sub-models and careful considerations need to be taken into account.

It should be stated here that the concept of mirror particles has also been incorporated with projection-based particle methods such as the ISPH. For instance, Liu et al. (2013) proposed an improved mirror particle treatment in their ISPH-based simulations of wave–structure interactions. An advantage of mirror particle technique with respect to the popular dummy particle approach (that assigns a zero velocity to all boundary particles) is that mirror particles theoretically impose the no-slip boundary condition more accurately as they are intrinsically founded on a linear extrapolation concept (Violeau 2012).

Recently, Leroy et al. (2014) extended the unified semi-analytical wall boundary condition of Ferrand et al. (2013) for the projection-based particle methods, and more precisely, the ISPH method. The main feature of their work was the exact enforcement of a non-homogeneous Neumann boundary condition on the pressure field that resulted in a distinct form of PPE. The ISPH model of Leroy et al. (2014) was further extended to buoyancy modeling for both laminar and turbulent flows (Leroy et al. 2015a) where buoyancy effects were modeled through the coupling of Boussinesq approximation and a heat equation.

2.4.2 Free-surface boundary condition

In projection-based particle methods, a challenging issue is to detect free-surface particles accurately to impose the dynamic free-surface boundary condition, i.e. p equal to zero, on them. This would also be an important condition in the solution process of the PPE. There have been several free-surface detection techniques including the simplest scheme founded on the fact that particle number density sharply drops at the free-surface (e.g. Koshizuka and Oka 1996; Shao and Lo 2003; Gotoh and Sakai 2006). Lee et al. (2008) used a property corresponding to divergence of particle positions to detect the free-surface particles. Khayyer et al. (2009) proposed an auxiliary condition based on the non-symmetric distribution of free-surface particles to be used together with the original simple criterion. Ma and Zhou (2009) proposed a mixed particle number density and auxiliary function method (MPAM) for identifying the free surface particles in their Meshless local Petrov–Galerin method based on Rankine source solution (MLPG-R) method. Park et al. (2014) used a so-called Arc Method for an accurate assessment of free-surface particles.

Skillen et al. (2013) proposed a new idea of gradually introducing the effect of discontinuous free-surface with the aim of minimizing the temporal pressure noise. Nair and Tomar (2014) presented a semi-analytical approach to impose Dirichlet boundary conditions on the free surface and, therefore, the need for free-surface particle assessment was eliminated in their study. This necessity was also eliminated by proposal of a new free-surface boundary condition referred to as Space Potential Particles (SPP; Tsuruta et al. 2015) and through introduction of a potential in void space to reproduce physical motions of particle around free-surface through a particle–void interaction. Figure 5 shows a graphical representation of the SPP scheme as well as its effectiveness in elimination of unphysical voids in a Karman vortex simulation corresponding to a Reynolds number of 1200. Details of this simulation are given by Tsuruta et al. (2015). For this Karman vortex simulation the calculation domain is set as a channel with 0.45 m length and 0.24 m width. A cylinder with a diameter of 0.3 m was set at a position of (x, y) being (0.09 m, 0.12 m). The water particles were considered to be 3 mm in diameter.

2.4.3 Inlet/outlet boundary conditions

The most crucial and challenging issue in implementation of inlet/outlet boundary conditions corresponds to accurate enforcement of mass (or volume) conservation. There have been a number of researches specifically targeting inlet/outlet boundary conditions in both weakly compressible (e.g. Lastiwka et al. 2009) and incompressible (e.g. Khorasanizade and Sousa 2016) frameworks.

In order to enhance the ISPH solution for both pressure and velocity near the boundaries including inlet/outlet ones, Hosseini and Feng (2011) presented an approach which utilizes a rotational pressure-correction scheme with a consistent pressure boundary condition. Shibata et al. (2011) presented a so-called transparent boundary condition for an accurate absorption of Stokes wave at absorbing boundaries. Liu et al. (2015) presented a non-reflection internal wave maker for the ISPH method. A novel formulation for inflow–outflow boundary conditions in an ISPH framework is recently proposed by Leroy et al. (2015b). This formulation is founded on the unified semi-analytical technique proposed for treatment of wall boundary conditions (Ferrand et al. 2013) and extended to open boundaries (Kassiotis et al. 2013) in WCSPH framework.

2.5 Multi-phase flows

A key challenge in particle-based simulations of multiphase flows, especially those characterized by large density ratios corresponds to the sharp and abrupt density drop at the phase interface that would lead to a mathematical discontinuity of density and accordingly a discontinuous pressure gradient field. Thus, even slight inaccuracies in pressure gradient calculation would bring about numerical instabilities that may end up in a complete blow-up of simulation.

In the context of particle methods, there have been several attempts to propose stable and accurate multiphase methods that can deal with the mathematical discontinuity of density at the phase interfaces. The so-far conducted researches conducted in the framework of weakly compressible (or fully explicit) particle methods can be categorized into the following three distinct groups:

• (i) Density evaluation through a spatial averaging: The most common approach is to calculate the densities at target particles by performing a proper spatial weighted averaging through the implementation of a corrected kernel (e.g. Colagrossi and Landrini 2003; Grenier et al. 2009). In addition to applying a spatially averaged density, the SPH-based multiphase simulations of Colagrossi and Landrini (2003) and Grenier et al. (2009) were carried out by use of some sort of numerical stabilizers, e.g. an unphysical surface tension term (as in Colagrossi and Landrini 2003) or an unphysical repulsive pressure force between particles of different fluids (as in Grenier et al. 2009). Despite improving the stability and minimizing the numerical dispersions at the phase interfaces, such unphysical forces will result in an unphysical gap in between the fluids of different phases. Shakibaeinia and Jin (2012) applied a modified version of a so-called weakly compressible MPS to simulation of multiphase flows with low-density ratios. The modifications comprised of density and viscosity smoothening schemes, and more precisely, application of the simplest possible spatial averaging of density (corresponding to a zeroth-order accurate SPH scheme) and a harmonic mean for viscosity. Despite being helpful in dealing with the mathematical discontinuity of density at a phase interface, the considered scheme by Shakibaeinia and Jin (2012) simply results in an unphysical diffusion and accordingly an unphysical smoothening of density as well as unphysical dispersions of fluid particles at the phase interfaces.

• (ii) Lagrangian equations: Monaghan and Rafiee (213) proposed a robust SPH algorithm based on the Lagrangian equations and successfully simulated several multiphase flows with high-density ratios without a density smoothening scheme. Nevertheless, their simulations were performed using a repulsive pressure force between particles of different fluids as well as an artificial viscosity term. Further, in some cases, simulation results of Monaghan and Rafiee (213) showed unphysical perturbations at the phase interfaces.

• (iii) Energy density-based smoothing: Saitoh and Makino (2013) developed an alternative SPH model which incorporates energy density, rather than mass density, as the basis for smoothing. By utilizing this approach, density differentiability is no longer a prerequisite and hence contact discontinuities can be handled efficiently. Nevertheless, the simulation results of Saitoh and Makino (2013) are still characterized by notable numerical diffusion of density resulting in an unphysical smoothening of the interface sharpness.

Fig. 6

Typical snapshots corresponding to a multiphase violent flow sloshing characterized by air entrainment/entrapment illustrating the effectiveness of FDS scheme–snapshots of air/water particles (a, b) and snapshots of particle together with density field (c, d) (Khayyer and Gotoh 2013)

As for projection-based particle methods, the so-far developed methods either consider a special treatment at the phase interface or tend to use a combined grid-based and gridless approach.

• (i) Consideration of an interactive force at the phase interface: Ikari et al. (2004) were the first to propose a gas–liquid two-phase MPS method by treating the gas and liquid phases as discrete particles and considering an interaction force in between them. To assure the stability of their calculations, they defined a specific procedure to maintain the gas particles in adequate distances from the liquid particles by introducing interacting repulsive forces. The multiphase MPS methods of Ikari et al. (2004) was verified mainly qualitatively and solely by coastal engineering related applications. Shao (2012) proposed a decoupled ISPH method through a special treatment of interface particles and consideration of particular interface boundary conditions to tackle the discontinuity of density at the phase interface in their multi-fluid simulations.

• (ii) Hybrid particle-mesh methods: In order to deal with the mathematical discontinuity of density, Liu et al. (2005) proposed a hybrid MPS-FVM particle-mesh method where the heavier phase was represented by particles and the lighter one was defined on a mesh. The discontinuities were resolved by extrapolating the density and viscosity of interfacial particles onto the mesh.

• (iii) Application of particle shifting technique: In order to deal with particle non-uniformity issues at the phase interface, Lind et al. (2015) applied the particle shifting technique (Lind et al. 2012) in their incompressible–compressible SPH simulations of water–air wave slamming through a proper coupling of a weakly compressible SPH for the gas phase and an incompressible SPH for the liquid one. The effectiveness of the particle shifting technique was further illustrated in the recent paper by Lind et al. (2016) where a thoroughly validated compressible–incompressible SPH was presented. The proposed multiphase SPH method of Lind et al. (2016) was shown to maintain a true material discontinuity at the phase interface together with physically correct and continuous pressure/velocity fields.

• (iv) Density evaluation through a spatial averaging: To deal with the discontinuity of density, Hu and Adams (2006) reformulated their incompressible SPH schemes by considering the so-called “particle number density”, consistent with MPS descriptions, that resulted in a continuous form of pressure gradient formulation.

Khayyer and Gotoh (2013) presented an improved MPS method for multiphase flows characterized by large density ratios. The stability of their calculations was guaranteed through the application of a first-order-accurate Taylor-series-based Density Smoothing (FDS) scheme, and accuracy enhancement was achieved through the application of a PPE’s error mitigating term (ECS) and refined discretizations of source term (HS) and Laplacian of pressure (HL). The FDS scheme was shown to provide significantly improved results with respect to the ZDS (Zeroth-order accurate Density Smoothing) one. Figure 6 presents two typical snapshots corresponding to a violent sloshing flow with reproduced distributions of gas–liquid particles (a, b) as well as density field (c, d) by an enhanced multiphase MPS incorporating the FDS scheme. Conditions of the performed sloshing simulation corresponded to the experiment by Rognebakke et al. (2006). Sinusoidal excitations with maximum amplitude of 150 mm and frequency of 1.2 Hz were considered. The particles were 5.0 mm in diameter and the calculation time step was set according to the Courant stability condition and a maximum allowable time increment of 4.0E$-$5s.

Fig. 7

Typical snapshots illustrating a water slamming corresponding to the experiment by Lin and Shieh (1997) by an enhanced multiphase MPS (a) and an enhanced single-phase MPS (b)–time history of pressure at the center of the plate (c)–quantitative comparison of slamming induced pressure at the center of a plate corresponding to the experiment by Verhagen (1967), results by enhanced multiphase MPS, multiphase SPH (Lind et al. 2015) and multiphase FVM (Ma et al. 2014) (d) (Khayyer and Gotoh 2016)

Recently, Khayyer and Gotoh (2016) extended their ECS scheme to minimize the projection-related errors in an air–water compressible–incompressible multiphase calculation of wave slamming. The extended ECS was referred to as CIECS (compressible incompressible ECS). For their calculations, Khayyer and Gotoh (2016) considered an integrated set of equations for the gas and liquid phases with compressible forms of continuity equations and by implementations of actual speeds of sounds in air and water. Figure 7 shows a set of results corresponding to this study. Figure 7a–c depicts the water slamming simulation results related to the experiment by Lin and Shieh (1997) by multiphase and single-phase MPS methods. The figure highlights the importance of consideration of air and its cushioning effect for prediction of slamming-induced pressures. Figure 7d portrays a comparison in between the multiphase MPS with CIECS scheme with results by Lind et al. (2015) and Ma et al. (2014) with respect to the experiment by Verhagen (1967). A common experiment-simulation inconsistency seen in this figure corresponds to inaccurate prediction of post-impact negative pressure. In the performed water slamming simulations, the diameter of particles was set as 3 mm. Considered viscosities for the water and air phases corresponded to their physics ones, i.e. $\nu _{w}$ = 1.0E$-$6 m$^{2}$/s and $\nu _\mathrm{a}$ = 1.5E$-$5 m$^{2}$/s. The calculation time step was set based on the Courant stability condition and $\Delta t_\mathrm{{max}}$ = 1.0E$-$4 s.

Indeed, the multiphase simulations by particle methods are not limited to only liquid–gas simulations, but also solid–liquid simulations (e.g. Gotoh and Sakai 2006). The pioneering work related to multiphase flow simulations by projection-based particle methods corresponds to that by Gotoh and Fredsøe (2000) who developed a solid–liquid two-phase MPS method. A number of interesting ocean or coastal engineering applications have been studied by solid–liquid MPS methods as illustrated by Gotoh and Sakai (2006).

2.6 Surface tension

Consideration of surface tension becomes important when deformations of fluid surfaces are involved. For example, surface tension plays a key role in splash generation due to finger-jet break-up at the tip of the wave-breaking jet. The splash generation drastically increases the surface area of water drops which enhances gas exchange between atmosphere and seawater. Another example corresponds to the later phases of the spreading of oil in water which is driven by surface tension forces. Thus, surface tension modeling is of significant importance in ocean/offshore engineering.

The approaches applied for modeling surface tension in macroscopic particle-based methods can be divided into two main categories, namely, the so-called potential approach and the so-called continuum approach.

2.6.1 Potential approach

In this approach the surface tension is modeled by assuming that microscopic cohesive intermolecular forces can be mimicked by macroscopic inter-particle forces. The main advantage of this approach corresponds to its computational simplicity in that surface tension is modeled via particle–particle interactions explicitly without the necessity of calculating surface normals and curvatures as required in the continuum approach. The major disadvantage of potential approach is related to the fact that the surface tension forces depend on the intensity of particle–particle interactions. These interactions have to be adjusted numerically by varying the macroscopic input parameters depending on the simulation case to reproduce desired surface tension forces. Thus, this approach is not preferable from the practical engineering viewpoint unless the considered particle method is extended to micro/nano scales. It is also worth mentioning that with given parameters, the potential-based surface tension modeling approach is resolution dependent and the modeled surface tension does not converge to a fixed value with refinement of resolution (Adami et al. 2010).

A number of potential-based surface tension modeling exist in the field of particle method research. Nugent and Posch (2000) applied cohesive van der Waals type potentials between two fluids in their multi-phase calculation of 2D liquid drop condensations. They highlighted the fact that for stable simulations the interaction range of particle interactions should be about twice of that of SPH smoothing length, which results in a less computationally efficient calculation. Tartakovsky and Meakin (2005) utilized a similar approach but instead of van der Waals type interactions, a combination of attractive and repulsive forces was considered within the range of standard SPH kernels. Due to its simplicity, several multiphase SPH calculations including those related to flows in porous media (e.g. Alvarado-Rodriguez et al. 2015) have been founded on this approach. Recently, Tartakovsky and Panchenko (2016) proposed an updated molecular-like Pairwise Force-SPH model for incorporation of surface tension and contact line dynamics. Their model is characterized by new approximate relationships between the molecular-like forces and macroscopic properties of a multiphase flow.

In the field of MPS research, Shirakawa et al. (1999) presented the first potential-based surface tension modeling similar to molecular dynamics approach. In general the considered potential functions have been proposed by either discontinuous (e.g. Shirakawa et al. 1999) or continuous (e.g. Kondo et al. 2007) functions. Several studies have been devoted to proposal of an appropriate potential function for a more reliable simulation of surface tension (e.g. Ishii and Kohira 2009; Ishii and Sugii 2011; Natsui et al. 2012).

Another computational issue corresponding to potential approach is related to probable occurrence of numerical instability, especially when the particles are not regularly distributed (Zhang et al. 2008). Different smoothing procedures have been proposed to tackle this problematic issue (e.g. Zhang et al. 2008; Ishii and Sugii 2011).

2.6.2 Continuum approach

The most common approach for incorporation of surface tension in macroscopic particle-based simulations is based on the continuum surface force (CSF) model introduced by Brackbill et al. (1992). In this approach, the surface tension is treated as a continuous, three-dimensional effect across the interface, derived directly from the Young–Laplace equation:

$$\begin{aligned} \Delta p=-\sigma \,\mathrm{div}(\varvec{n}), \end{aligned}$$

(16)

where $\Delta p$ is the pressure jump across the interface, $\sigma$ is the surface tension coefficient and $\varvec{n}$ is the interface normal pointing out towards the gas phase. This pressure jump is applied via a volume force normal to the interface:

$$\begin{aligned} \varvec{F}=-\,\sigma \,\kappa \,\varvec{n}\,\delta _s, \end{aligned}$$

(17)

where $\kappa$ is the average curvature which is obtained by taking the divergence of the normal vector ($\kappa =-\,\nabla \cdot \,\varvec{n})$ and $\delta _{s}$ stands for the surface-delta function. In order to approximate the characteristics of the interface, i.e. normal direction and curvature, a volume fraction function, usually referred to as color function C, is defined. The normal vector $\varvec{n}$ is determined as the normalized gradient of this color function, i.e. $\varvec{n}={\nabla C}/{\left| {\nabla C} \right| }$.

Morris (2000) showed several possible implementations of CSF model in SPH, both with and without exact conservation of momentum, and highlighted the challenges in accurate calculations of interface curvature. These challenges are not only limited to difficulties in accurate particle-based calculation of Laplacian of color function for approximation of interface curvature, but also to the fact that a smoothed color function is usually used. The use of a smoothed color function may become problematic for approximation of interface normals near the boundaries and sharp-angled areas. Recently, Duan et al. (2015) proposed a so-called CCSF (contoured continuum surface force) model characterized by a cumbersome analytical calculation of interface curvature based on a locally constructed smoothed color function within the MPS framework. The authors applied a well-known formulation applied in Eulerian Level Set methods by considering contours of a smoothed color function to obtain an estimation of interface curvature. In addition to the presence of complexity, the accuracy of their proposed method appeared to be dependent upon the choice of smoothing radius, while this is not the case in well-known established SPH surface tension models.

In order to resolve these two challenging issues, Hu and Adams (2006) presented a continuous surface stress model (CSS) using a discontinuous, sharp color function to directly calculate the pressure jump from the interface stress tensor and modeled the surface tension in a more accurate and momentum conservative manner. In their model, calculation of surface curvature was avoided due to consideration of a surface stress tensor. Further, since the magnitude of this tensor is proportional to that of the color gradient, the contribution of a small color gradient at the edge of transition bands does not bring about numerical difficulties (Adami et al. 2010).

A set of efforts has been focused on enhancing the particle-based CSF model by providing more accurate schemes for approximation of interface normal and curvature. For instance, Adami et al. (2010) proposed a new formulation for the surface curvature by applying a reproducing divergence approximation. Qiang et al. (2011) applied a Taylor-series based correction leading to more accurate interface normals and thus curvatures.

In the field of MPS research, the CSF-based simulations can be categorized into two distinct groups, depending on the computational procedure for calculation of the curvature and the normal vector. These two categories are: arc fitting at interface (Nomura et al. 2001) and differential approach (e.g. Ichikawa and Labrosse 2010).

2.6.2.1 Arc fitting at interface

As the name indicates the arc fitting approach is aimed at approximating the normal vector and curvature by constructing local arcs at the surface particles. To achieve this approximation, a layer of fluid particles at the interface, with a thickness of $d_\mathrm{st}$, is considered as free-surface for which surface tension forces are to be calculated. Specific particle number densities including an initial one and a revised one are calculated to approximate the curvature and the unit normal. Despite its simple and comprehensible algorithm, the accuracy of this approach is highly dependent upon the instantaneous smoothness of the free-surface. This fact is highlighted by Gotoh et al. (2004, 2005) and Ikari et al. (2004). Furthermore, even in the presence of a smooth free-surface, accomplishment of a continuous curvature calculation would be difficult, in both time and spatial domain. This is due to the calculation of curvature and normal vectors by discrete values of particle number densities as well as simple finite difference schemes for evaluation of normal vectors. It should be noted that despite these deficiencies, improved models for approximation of the unit normal can be obtained by applying higher order finite difference approximations. For instance, Rong and Chen (2010) applied a fourth-order central differencing scheme to approximate the derivatives used for the unit normal vector.

2.6.2.2 Differential approach

The favored approach for modeling surface tension by particle methods, including projection-based ones, is to calculate the continuum surface forces by applying consistent and accurate differential operator models for both gradient and Laplacian so that accurate approximations of the unit normal vector and the curvature can be obtained. Shirakawa et al. (1999) were among the first who illustrated possible development of a differential CSF-based surface tension model for MPS. However, they pointed out that this approach is not preferable due to the difficulty of curvature evaluation at a free-surface cusp. Liu et al. (2005) and Zhang et al. (2007) applied differential CSF-based surface tension modeling in their hybrid particle methods. Alam et al. (2007) applied this approach for surface tension modeling in their MPS simulations of water splash phenomena.

Fig. 8

Enhanced modeling of surface tension forces by a Laplacian-based model–typical snapshots corresponding to a non-equilibrium rod (a, b), and a water drop impact corresponding to the experiment by Liow (2001) (c–e)

In most cases, the evaluation of normal vector was conduced by use of original MPS gradient model, while the curvature was obtained by applying the original MPS divergence model to the approximated unit normal vector, illustrating that the curvature calculation is obtained by a simplified approximation based on approximated values. This would highlight the need to enhance the accuracy of unit normal vector calculation beforehand if the curvature model would be directly dependent upon the approximated unit normal vector. In an attempt to improve the accuracy of differential CSF-based surface tension modeling in MPS, Ichikawa and Labrosse (2010) applied a SPH-based scheme to evaluate the unit normal vector, yet the curvature was found by the original MPS divergence model.

By conducting a simple comparison, Park and Jeun (2011a) showed that approximation of normal vector by a differential operator model is more accurate than that by a so-called four-point technique as used in arc fitting approach. A differential CSF-based model was also used by these authors in their isothermal multiphase MPS calculations (Park and Jeun 2011b). Khayyer et al. (2014) proposed a new differential CSF-based model in the context of MPS. Their model benefits from a novel formulation for curvature estimation using direct second-order derivatives of color function via a meticulous and comprehensive discretization. By applying a high-order Laplacian scheme including the approximation of boundary integrals, relatively accurate approximation of interface curvature and thus surface tension could be achieved. In the work by Khayyer et al. (2014), the Laplacian of color function, C, at an interface target particle i is calculated as

$$\begin{aligned} ( {\nabla ^2C})_{\,i}= & {} \frac{1}{n_0 }\sum \limits _{i\ne j} {\left\{ {\frac{\partial C_{ij} }{\partial r_{ij} }\frac{\partial w_{ij} }{\partial r_{ij} }+C_{ij} \left( {\frac{\partial ^2w_{ij} }{\partial r_{ij}^2 }+\frac{D_s -1}{r_{ij} }\frac{\partial w_{ij} }{\partial r_{ij} }}\right) } \right\} }\nonumber \\&+\mathrm{BI}, \end{aligned}$$

(18)

where $C_{ij}=C_{j}-C_{i}$ and BI denotes the boundary integrals (Souto-Iglesias et al. 2013) formulated as

$$\begin{aligned} \mathrm{BI}=\int _{\partial \Omega } {\,\nabla C} \,\,\cdot \varvec{n}\,w( {\left| {\varvec{r}_{ij} } \right| })\,\,\mathrm{d}S\approx \frac{1}{n_0 }\sum \limits _{j\in \partial \Omega } {\,\frac{C_{ij} \,\varvec{r}_{ij} \cdot \varvec{n}_{j}}{\left| {\varvec{r}_{ij} } \right| ^{2}}} \,w( {\left| {\varvec{r}_{ij} }\right| })\,S_j, \end{aligned}$$

(19)

where for 2D simulations, $S_{j}$ signifies the length (diameter) of boundary particle j. Therefore, the surface tension force is evaluated via achieving a direct Laplacian-based approximation of curvature.

The enhanced performance of the abovementioned Laplacian-based surface tension model with respect to the arc fitting one (Nomura et al. 2001) is illustrated in Fig. 8, corresponding to simulations of a non-equilibrium rod (a, b) and water drop impact (c–e). The non-equilibrium rod corresponds to oscillation of an initially square drop under the action of surface tension forces. The initial square is an inviscid liquid with a diameter of D = 4 mm, density of $\rho$ = 1000 kg/m$^{3}$ and surface tension coefficient of $\sigma$ = 0.10 N/m. The particle size is considered to be 0.1 mm. Due to the initial square shape of drop with theoretically infinite surface tension forces at the corners, the drop is set into oscillations towards an equilibrium circular shape. The Laplacian-based surface tension model has been able to reproduce an almost circular drop characterized by a smooth free-surface.

The snapshots shown in Fig. 8c–e correspond to the water drop impact experiments by Liow (2001), for Froude and Weber numbers of 639 and 395, respectively. The figure portrays the properness of Laplacian-based surface tension model in better reproduction of crown development and splash drops.

In another recent work, a differential CSF-based model was incorporated by Tiwari et al. (2016) for computation of surface tension in two-phase flows driven by wetting effects. The MLS (moving least square) method was used in that study for approximation of differential operators at each target particle based on the information at neighboring particles.

2.7 Fluid–structure interactions

Many problems in ocean engineering involve fluid–structure interaction (FSI) processes where the flow field is altered by the encountered structures and their simultaneous responses to the hydrodynamic loads. Examples include tsunami impact on coastal/offshore structures, sloshing in LNG tanks with elastic baffles and wave interactions with floating bodies. Hence, accurate simulation of FSI problems including proper resolutions of instantaneous flow field and structural response should be of significant importance in ocean engineering.

Despite their significant importance, FSI problems encountered in ocean engineering are challenging to analyze due to the presence of violent free-surface flows inducing large/abrupt hydrodynamic loads and thus considerable structural responses, possibly leading to large structural deformations and/or structural failures. From mathematical-numerical viewpoint, existence of multi-domain characteristics and interface coupling conditions will further add to the existing complexities.

In the context of FSI simulations, particle methods including projection-based ones appear to be suitable computational tools. These methods have been applied to simulate interactions in between fluid flows with either rigid (e.g. Liu et al. 2013) or flexible (e.g. Rafiee and Thiagarajan 2009) structures. In the latter case, a proper structural model should be carefully coupled with the fluid solver.

In the field of particle methods, Libersky et al. (1993) and Gray et al. (2001) applied the SPH method to dynamic problems of elastic body. Antoci et al. (2007) and Oger et al. (2010) applied the SPH method for fully Lagrangian simulations of FSI problems involving weakly compressible flows interacting with deformable elastic structures. Yang et al. (2012) proposed a coupled weakly compressible SPH-FEM (finite element method) solver for FSI problems related to elastic structures.

In the framework of projection-based particle methods, Lee et al. (2007) developed a MPS–FEM coupled method to study incompressible fluid flow interactions with elastic structures. Rafiee and Thiagarajan (2009) proposed a fully Lagrangian SPH-based solver for simulation of incompressible fluid–hypoelastic structure interactions. In their study, the PPE was solved simply using an approximate explicit scheme. Hwang et al. (2014) developed a fully Lagrangian MPS-based FSI analysis method for incompressible fluid–linear elastic structure interactions. The key feature of the numerical method of Hwang et al. (2014) corresponded to its being free of any numerical stabilizing terms with calibration constants commonly applied in other particle-based FSI solvers. Such artificial stabilizing terms have been used in forms of artificial viscosity, artificial stress term or collision models to mainly deal with the tensile instability for both fluid and structure simulations in both SPH (e.g. Monaghan 1994; Antoci et al. 2007; Amanifard et al. 2011) and MPS (e.g. Lee et al. 213; Kondo et al. 2010; Shao et al. 2013) frameworks. This key feature of the study by Hwang et al. (2014) was achieved through application of a proper coupling algorithm and by taking the advantage of prediction-correction solution process of MPS as a projection-based method.

Fig. 9

Simulation results corresponding to an entry of a deformable beam into an undisturbed water (Oger et al. 2010)–schematic sketch of problem (a), snapshots of pressure and stress fields (b, c), time history of deflection at measuring point C (d) and pressure at measuring point D (e)–improved results by an enhanced coupled MPS-based FSI solver

Khayyer et al. (2015b) presented a further enhanced version of Hwang et al.’s method, by incorporating the ECS and DS schemes for the fluid phase as well as applying a Wendland kernel (Wendland 1995; Dehnen and Aly 2012) for calculation of fluid forces on structure. The achieved enhancements as well as applicability of developed MPS-based FSI solver are illustrated in Figs. 9 and 10, corresponding to simulations of an entry of a deformable beam into an undisturbed water and a dam break flow impacting on an elastic plate.

Figure 9a illustrates an schematic sketch of the deformable beam entry test, where an aluminum beam enters an undisturbed water with a constant velocity of 30 m/s. A qualitative comparison in between the coupled MPS-based FSI solver and its enhanced version is presented in Fig. 9b, c. The snapshots depict the pressure and stress fields in fluid and beam, respectively. The snapshots by enhanced method tend to be characterized by improved and almost symmetric pressure fields. A quantitative comparison in terms of time histories of deflection at point C and time histories of pressure at point D is provided in Fig. 9d, e. From Fig. 9d, the enhanced FSI solver is found to provide a more accurate time history of deflection at point C, quite consistent with the analytical solution (Scolan 2004) as well as a refined coupled SPH solver (Oger et al. 2010). Focusing on Fig. 9e, the enhanced coupled MPS solver has resulted in a more acceptable pressure time history compared with the coupled MPS as well as coupled SPH solvers. For this aluminum beam entry test, the analytical solutions were derived by Scolan (2004), on the basis of the hydrodynamic Wagner’s model and linear Wan’s theory. The material properties of the aluminum beam, namely its Young’s modulus, Poisson ratio and density were considered as 67.5 GPa, 0.34 and 2700 kg/m$^{3}$, respectively. Both structural and fluid particles were 0.01 m in size.

Fig. 10

Simulation results illustrating a dam break with an elastic plate corresponding to the experiment by Liao et al. (2014, 2015)–a schematic sketch of calculation domain (a), results by MPS FSI solver (b, d) and its enhanced version (c, e)

Figure 10 corresponds to a dam break simulation with an elastic plate related to the experimental study of Liao et al. (2014, 2015). A schematic sketch of calculation domain as well as simulation conditions is presented in Fig. 10a. Both structural and fluid particles are considered to be 0.001 m in size. Figure 10b–e portrays a set of typical snapshots by coupled MPS (b,d) and enhanced coupled MPS (c,e) solvers together with their corresponding experimental photos as well as results by a FDM-FEM solver (Liao et al. 2014). The superior performance of enhanced MPS is clearly illustrated in this figure as this method provides more consistent deflections of the elastic plate both at t = 0.35 s and t = 0.39 s. In particular, at t = 0.35 s, there appears to be a non-physical separation of plate from the main incoming flow. At t = 0.39 s, the enhanced coupled MPS has been able to better reproduce the overall shape of the plate with a clear inflection point.

2.8 Enhancement of computational efficiency

A challenging issue corresponding to particle methods is related to their relatively high computational cost. Until recently, the high computational cost of particle methods was hindering their application to real-life problems, including large-scale scientific and engineering ones. The implementation of particle method codes on massively parallel computers, especially on GPUs (graphics processing unit), is definitely among the recent breakthroughs that widens the applicability of these methods. In this context, Hérault et al. (2010) and Crespo et al. (2011) were among the pioneers of implementing SPH on GPUs. They showed that remarkable speedups of up to two orders of magnitude could be achieved by using a single GPU-card in place of a single-core CPU for simulations dealing with more than one million particles. Oger et al. (2016) highlighted various key points corresponding to massive parallelization of explicit particle methods on distributed memory. Mokos et al. (2015) presented a GPU-based implementation of an explicit multiphase SPH code.

In the context of projection-based particle methods, Hori et al. (2011) presented a GPU-based implementation of MPS method. In this case, the speedup was limited to only one order of magnitude, mainly due to iterative solution process of Poisson pressure equation (PPE). The same order of speedup is achieved in other GPU-based implementations of projection-based particle methods, including MPS (e.g. Kakuda et al. 2013) and ISPH (Qiu 2014).

2.9 Other applications

An interesting application of particle methods is related to simulation of flow-induced scouring by coupling the fluid solver with an appropriate soil model. By considering the following momentum equations for fluid (Eq. 20) and soil (Eq. 21) as well as a proper stress–strain relationship (Eq. 22; Bui et al. 2008) together with advection-diffusion equation for the suspended sediment (Eq. 23), Ikari et al. (2015a) conduced a study on scouring due to a submerged vertical jet with a sub-particle-scale suspended sediment load model.

$$\begin{aligned} \gamma \rho _l \frac{\mathrm{D}\varvec{u}_{l} }{\mathrm{D}t}=-\gamma \nabla p_{l} +(\mu +\rho _{l} \nu _{t})\nabla ^{2}\varvec{u}_{l} +\gamma \rho _{l} \varvec{g}+\frac{\gamma ^{2}\rho _{l} g}{k_c }(\varvec{u}_{s} -\varvec{u}_{l}) \end{aligned}$$

(20)

$$\begin{aligned} (1-\gamma )\rho _{s} \frac{\mathrm{D}\varvec{u}_{s}}{\mathrm{D}t}= & {} -\nabla \cdot \varvec{\sigma } -(1-\gamma )\nabla p_{l} +(1-\gamma )\rho _{s} \varvec{g}\nonumber \\&+\frac{\gamma ^{2}\rho _{l} g}{k_{c}}(\varvec{u}_{l}-\varvec{u}_{s} ) \end{aligned}$$

(21)

$$\begin{aligned} {\dot{\varvec{{\sigma }}}}={\dot{\varvec{{\omega }}}}{\varvec{\sigma }} -\varvec{\sigma } {\dot{\varvec{{\omega }}}}+\lambda _{e} \mathrm{tr}({\dot{\varvec{\varepsilon }}})\varvec{I}+2\mu _{e} {\dot{\varvec{\varepsilon }}}-{\dot{\varvec{\sigma }}}_{p} \end{aligned}$$

(22)

$$\begin{aligned} \frac{\mathrm{D}C}{\mathrm{D}t}+\varvec{w}_{s} \cdot \nabla C=\frac{\nu _{t}}{\sigma _{c}}\nabla ^{2}C+Q, \end{aligned}$$

(23)

where $\gamma$ is the porosity, $\rho$ is the density, $\varvec{u}$ is the velocity, p is the pressure, $\mu$ is the dynamic viscosity coefficient, $\upsilon _{t}$ is the kinematic eddy viscosity coefficient, g, $\varvec{g}$ are the gravitational acceleration in absolute and vector forms, $k_{c}$ is the permeability, $\varvec{\sigma }$ is the stress, ${\dot{\varvec{\sigma }}}$ is the stress rate, ${\dot{\varvec{\omega }}}$ is the spin tensor, $\lambda _{e} ,\, \mu _{e}$ are the Lamé parameters, $\varvec{I}$ is the unit tensor, ${\dot{\varvec{\varepsilon }}}$ is the strain rate, ${\dot{\varvec{\sigma }}_{p}}$ is the stress rate due to plastic strain, C is the concentration, $\varvec{w}_{s}$ is the settling velocity, $\sigma _{c}$ is the Schmidt number and Q is the balance of suspended sediment from sand bed.

Fig. 11

Simulation results of scouring due to a submerged vertical jet with a sub-particle-scale suspended sediment load model–a snapshots of fluid and soil particles together with suspended sediment concentration, b quantitative comparison of bed profile with corresponding experiment (Akashi and Saito 1980)

Figure 11a shows a set of snapshots corresponding to the conducted simulation, illustrating the jet-induced scouring as well as time evolution of distribution of sub-particle-scale suspended sediment. Figure 11b presents a quantitative comparison of scouring pattern with the corresponding experiment (Akashi and Saito (1980)), illustrating an almost acceptable agreement, especially in terms of the maximum scour depth. For the scouring simulation presented in Fig. 11, the depth of soil region is 0.1 m and the water depth above the initial soil–water interface is 0.2 m. The inflow boundary corresponding to the vertical submerged jet has a width of 0.02 m, placed 0.1 m above the initial soil–water interface. The vertical downward jet has a constant speed of 0.74 m/s. The mass median diameter (D50) of soil is considered to be 8.4E$-$4, the same as that in the corresponding experiment (Akashi and Saito 1980). Both fluid and soil particles, i.e. computational spatial resolutions, are considered to be 5 mm in diameter.

There are also other studies that simply couple the incompressible SPH with simple soil erosion models to estimate the erosion rate and its associated scouring (e.g. Manenti et al. 2012; Ran et al. 2015). A SPH-based two-phase flow model was also presented by Zanganeh et al. (2012) to predict scouring below marine pipelines. In their study, the soft contact approach of Cundall and Strack (1979) was considered for calculation of inter-particle forces for the granular sediment particles.

In the context of weakly compressible SPH, Ulrich et al. (2013) presented a set of interesting multi-physics marine-engineering-related SPH simulations including full-scale applications involving floating-body/water/soil interactions (e.g. installation process of a gravity foundation for offshore wind turbines).

In addition to scouring and suspended-sediment-transport applications, other interesting applications of particle methods in ocean engineering correspond to waves interacting with and flowing through porous structures (e.g. Shao 2010; Akbari and Montazeri Namin 2013), rigid bodies driven by flows (e.g. Tofighi et al. 2015), floating body dynamics (e.g. Shao and Gotoh 2004; Sueyoshi et al. 2008) and non-Newtonian free-surface flows (e.g. Xenakis et al. (2015)).

In general, particle methods, including projection-based ones, are well-suited for multi-scale, multi-physics applications, as highlighted by Violeau and Rogers (2016) as well as Liu and Liu (2016). In this regard, coupling of Lagrangian particle methods with either classical Eulerian solvers (e.g. finite volume method or finite element method) or other Lagrangian methods (e.g. Discrete Element Method) has gained interest for efficient and reliable simulations by considering the intrinsic characteristics of each method. Examples include hybrid SPH-FVM (e.g. Marrone et al. 2016) or MPS-FVM (e.g. Liu et al. 2005), as well as SPH-FEM (e.g. Chuzel-Marmot et al. 2011), ISPH-FEM (e.g. Asai et al. 2011) or MPS-FEM (e.g. Hashimoto and Le Touzé 2014; Mitsume et al. 2014a, b).

Particle methods have also been coupled with other Lagrangian methods such as DEM for multi-scale simulations of physical phenomena. Examples include hybrid MPS-DEM solvers for simulations of solid–liquid flows (e.g. debris avalanche analysis by Toyoshi et al. 2011) or fluid flow–rigid solid interactions (e.g. wave–armor block interactions in front of a caisson breakwater by Gotoh et al. 2009). In a recent interesting work, Canelas et al. (2016) integrated the advanced contact mechanics theories with SPH and presented a so-called SPH-DCDEM (Distributed Contact Discrete Element Method) for resolved, accurate simulations of fluid–solid phases.

3 Future perspectives

Despite the significant advancements achieved, rigorous and careful researches should be conducted to further enhance the reliability and accuracy of particle methods for practical engineering purposes including those corresponding to ocean engineering.

During the past decade, the stability and accuracy of particle methods, including projection-based ones, have been substantially enhanced. However, as for stability, the currently developed particle methods apply some sort of stabilization schemes such as the particle shifting (Lind et al. 2012) or dynamic stabilization (Tsuruta et al. 2013) ones, in order to guarantee the methods’ stability for a wide range of calculations. The probable adverse effects of such schemes in terms of conservation and convergence must be rigorously studied. The stability of particle methods is also preferred to be enhanced by refinement of differential operator models, such as gradient and Laplacian operators, corresponding to the terms that directly appear in the considered governing equations, or through applications of higher-order accurate numerical solution processes (e.g. higher-order projection methods, for instance).

As for accuracy, in spite of significant improvements, the problem of unphysical pressure fluctuations remain to be not fully resolved. Further enhancements of accuracy are expected to be achieved thanks to the profound and meticulous studies that are being conducted in this field.

As for boundary conditions and as it was stated in this paper, several important developments have been made during the past couple of years. The ongoing and future researches will further target this important aspect with rigorous studies on consistency, conservation and convergence of implemented boundary conditions. In particular, development of more accurate, consistent free-surface and inflow–outflow boundary conditions will further enhance the reliability of particle methods for ocean engineering applications.

As for enhancement of energy conservation properties of projection-based particle methods, special focus should be given to revisit/derive the formulations with respect to an energy-based framework. In this regard, compatibility of differential operator models is a key issue, as highlighted in Sect. 2.3.

As for multiphase flow simulations, especially those characterized by large density ratios, the currently developed particle methods consider some numerical treatments, such as stabilizers or smoothing schemes. Further reliable multiphase particle methods are expected to be proposed as the stability and accuracy of these methods progress.

As for fluid–structure interactions corresponding to deformable structures, further advancements are expected by improvements in both flow field as well as incorporated mathematical/numerical models for the structure.

An important research category for further enhancement of the reliability of particle methods for ocean engineering applications corresponds to turbulence modeling. Up to now, several studies have incorporated different types of turbulence models in the context of both explicit particle methods (e.g. Issa et al. 2010; De Padova et al. 2013; Mayrhofer 2014) and the semi-implicit projection-based ones (e.g. Shao and Lo 2003; Gotoh and Sakai 2006; Leroy et al. 2015a). Researches on proper modeling of turbulence by either time-averaged (e.g. Violeau and Issa 2007) or spatially averaged (e.g. sub-particle-scale; Gotoh et al. 2001) turbulence models are continuously advancing (e.g. Mayrhofer et al. 2015).

As for future applications, couplings of proper soil (e.g. Ikari and Gotoh 2016) and structure models with projection-based ISPH or MPS methods potentially result in enhanced multi-scale, multi-physics simulations including those related to ocean engineering (e.g. submarine debris flow impact on pipelines). Further advanced multi-scale and multi-physics applications of particle methods are expected to be achieved with forthcoming theoretical and computational enhancements. In particular, enhancements of stability, accuracy and conservation properties of particle methods along with advancements made in high-performance computing as well as developments of accurate variable resolution schemes (e.g. Vacondio et al. 2016) will enable particle methods to serve as advanced, reliable and efficient computational methods.

In all cases, it is important to keep the developed numerical methods free of any numerical term with constants that require calibration. This important issue is also highlighted in an excellent review paper by Violeau and Rogers (2016). Indeed, prior to any practical application, rigorous and meticulous verification of particle-based codes must be conducted by consideration of appropriate benchmark tests with analytical solutions in terms of reproduced velocity, pressure together with comprehensive investigations on conservation and convergence properties.

4 Concluding remarks

Current achievements corresponding to development of particle methods with applications in ocean engineering are discussed, with special focus on a distinct category of these methods, namely, projection-based particle methods, including both MPS and ISPH methods. Latest advancements corresponding to enhancements of stability, accuracy, energy conservation, boundary conditions and improved simulations of multiphase flows and fluid–structure interactions are reviewed. The future perspectives for further development of these methods for more reliable applications in engineering fields, including ocean engineering, are also highlighted.