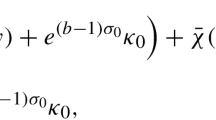Poisson and Szegö kernel scaling asymptotics on Grauert tube boundaries (after Zelditch, Chang and Rabinowitz)

Abstract

We review and elaborate on recent work of Chang and Rabinowitz on scaling asymptotics of Poisson and Szegö kernels on Grauert tubes, providing additional results that may be useful in applications. In particular, focusing on the near-diagonal case, we give an explicit description of the leading order coefficients, and an estimate on the growth of the degree of certain polynomials describing the rescaled asymptotics. Furthermore, we allow rescaled asymptotics in a range $O\left( \lambda ^{\delta -1/2}\right)$ in all the variables involved, where $\lambda \rightarrow +\infty$ is the asymptotic parameter, rather than rescale according to Heisenberg type.

1 Introduction

It was shown by Bruhat and Whitney [6] that a real-analytic compact and connected manifold M has an essentially unique complexification $({\tilde{M}},J)$, that is, a complex manifold in which M sits as a totally real submanifold. If furthermore $\kappa$ is a real-analytic Riemannian metric on M, it was proved independently by Guillemin and Stenzel [17, 18] and by Lempert and Szöke [22, 23, 39] that ${\tilde{M}}$ can be endowed with a canonically determined Kähler structure $({\tilde{M}},J,\Omega )$, with the following two properties. First, the symplectic manifold $({\tilde{M}},\Omega )$ is symplectomorphic to a tubular neighbourhood of the zero section in the cotangent bundle $T^\vee M$ of M, endowed with its canonical symplectic structure (and the symplectomorphism, of course, is the identity on M). Second, the square norm of $\kappa$ pulls back on ${\tilde{M}}$ to a Kähler potential for $\Omega$, while the norm pulls back on ${\tilde{M}}{\setminus } M$ to a solution of the complex homogeneous Monge–Ampère equation. Viewed the other way, this construction endows the cotangent bundle of M, near the zero section, with a canonical compatible complex structure, with the property that the Riemannian and Monge–Ampère foliations coincide. This intrinsic complex structure was called adapted by Lempert and Szöke. The sphere bundles of sufficiently small radii $\tau >0$ in $T^\vee M$ correspond to boundaries $X^\tau$ of strictly pseudoconvex domains in $M^\tau \subseteq {\tilde{M}}$, so-called Grauert tubes, corresponding to disc bundles in $T^\vee M$; furthermore, the homogeneous geodesic flow on the sphere bundles is closely related to the flow of the Reeb vector field on $X^\tau$.

The analysis and geometry of the Grauert tubes and their boundaries have been studied extensively in recent years, giving rise to a vast literature. Obviously with no pretense of completeness, let us mention a few foundational references most relevant to the present discussion: [2, 3, 7, 8, 10, 11, 16,17,18, 21,22,23, 31, 32, 37,38,39, 43,44,48].

A basic problem in this context, partly motivated by certain analogies with the setting of positive line bundles on complex projective manifolds, is to study the asymptotic concentration behaviour of the eigenfunctions of the generator of the homogeneous geodesic flow (transported to $X^\tau$). This involves the local study of certain smoothed spectral projectors, which are the Toeplitz counterpart of commonly studied objects in spectral theory (see e.g. [12, 15]). However, in sharp contrast to the line bundle setting, the latter flow is generally not CR-holomorphic. This is a source of difficulty in the adaptation to the Grauert tube setting of the Szegö kernel techniques that have proved successful in the line bundles setting [1, 35, 42].

A related issue, which is instead genuinely intrinsic to the Grauert tube setting, concerns analytic continuation of the eigenfunctions of the non-negative Laplacian $\Delta$ of $(M,\kappa )$. Let $(\varphi _j)_{j=1}^\infty$ be a complete orthonormal system of $L^2(M)$ composed of eigenfunctions of $\Delta$. Being real-analytic, each $\varphi _j$ extends to a holomorphic function ${\tilde{\varphi }}_j$ to some sufficiently small Grauert tube $M^\tau \subseteq {\tilde{M}}$; here in principle $\tau$ depends on j. It was a deep discovery of Boutet de Monvel [2, 3] that for sufficiently small $\tau >0$ every $\varphi _j$ extends to $M^\tau$ (see also [18, 20, 37, 38, 44, 47] for discussions and different proofs). As explained in [43, 44, 48], the relation between the eigenfunctions $\varphi _j$ and their analytic continuations ${\tilde{\varphi }}_j$ is governed by the so-called Poisson-wave operator, obtained by analytically continuing the Schwartz kernel of the wave operator on M (in both time and space). The study of the asymptotic distribution of the analytic continued eigenfunctions, pioneered by Zeldtich, involves certain ‘complexified spectral projectors’, bearing resemblance to the smoothed spectral projectors above.

In two striking recent papers [10, 11], Chang and Rabinowitz have made significant progress in pushing forward the analogy between the line bundle and the Grauert tube settings. Their analysis rests on two pillars. One is the description, due to Zelditch, of certain unitary groups of Toeplitz operators as ‘dynamical Toeplitz operators’[41, 44, 48]; another is a clever use of the Heisenberg (or normal) local coordinates adapted to a hypersurface in a complex manifold introduced by Folland and Stein in [13] and [14].

The goal of the present paper is partly to present a gentle introduction to the promising and efficient approach of Chang and Rabinowitz, and partly to provide some complementary results that may be useful in future applications. We shall restrict the present discussion to the near-diagonal situation. In particular, we shall give near-diagonal scaling asymptotics for the smoothing kernels hinted at above, in a range $O\left( \lambda ^{\delta -1/2}\right)$ in all variables involved, rather than according to Heisenberg type. More precisely, in an appropriate set of local coordinates centered at $x\in X^\tau$, we shall consider rescaled displacements of the form $x+(\theta /\sqrt{\lambda },{\textbf{v}}/\sqrt{\lambda })$ with $\Vert (\theta ,{\textbf{v}})\Vert \le C\,\lambda ^{\delta }$ (here $\delta \in (0,1/6)$, say). Furthermore, we shall provide an explicit numerical determination of the leading order factor in the asymptotic expansion. Also, we shall give a bound in the degree of the polynomials in the rescaled variables $(\theta ,{\textbf{v}})$ that appear in the lower order terms of the expansion; this is useful in ensuring that, when $(\theta ,{\textbf{v}})$ are allowed to expand at a controlled pace as above, one actually obtains an asymptotic expansion.

In order to give a more precise description of the content of this paper, it is in order to premise a more detailed account of the geometric setting involved.

Let M be a d-dimensional compact connected real-analytic (in the following, ${\mathcal {C}}^\varpi$) manifold. As mentioned, there is a complex manifold $({\tilde{M}},J)$, the Bruhat–Whitney complexification of M [6], in which M embeds as a totally real submanifold. If $\jmath :M\hookrightarrow {\tilde{M}}$ is the inclusion, then ${\tilde{M}}$ is uniquely determined locally along $\jmath (M)$, up to unique biholomorphism. Therefore, since $({\tilde{M}},J)$ and $({\tilde{M}},-J)$ are both complexifications of M, there is an anti-holomorphic involution $\sigma :{\tilde{M}}\rightarrow {\tilde{M}}$ with fixed locus $\jmath (M)$ [6, 17, 21]. We shall identify M with $\jmath (M)$ in the following.

Furthermore, the choice of a ${\mathcal {C}}^\varpi$ Riemannian metric $\kappa$ on M determines a canonical Kähler structure on $({\tilde{M}},J)$, with a canonical Kähler potential [17, 23, 32]. More precisely, perhaps after replacing ${\tilde{M}}$ with some smaller tubular neighborhood of M, there exists a unique ${\mathcal {C}}^\varpi$ function $\rho :{\tilde{M}}\rightarrow [0,+\infty )$ with the following properties:

• 1. $\rho ^{-1}(0)=M$ and $\rho \circ \sigma =\rho$;

• 2. $\rho$ is strictly plurisubharmonic, that is, $\Omega :=\imath \,\partial \,{\overline{\partial }}\rho$ is a Kähler form on $({\tilde{M}},J)$, whose associated associated Riemannian metric on ${\tilde{M}}$ will be denoted by ${\hat{\kappa }}=\Omega \big (\cdot ,J(\cdot )\big )$;

• 3. ${\hat{\kappa }}$ restricts to $\kappa$ along M, i.e. $\kappa =\jmath ^*\left( {\hat{\kappa }} \right)$;

• 4. $\sqrt{\rho }$ satisfies the homogeneous–Ampère equation on ${\tilde{M}}{\setminus } M$: in local holomorphic coordinates $(z_j)$,

  $$\begin{aligned} \det \left( \frac{\partial ^2}{\partial z_i\,\partial {\overline{z}}_j}\sqrt{\rho }\right) =0. \end{aligned}$$

Remark 1

The proof of the existence of $\rho$ given in [17] uses an appealing conceptual description, which we shall only briefly touch upon below (see also the discussions in [46], §14.1 of [47] or [10]).

Namely, let $\overline{{\tilde{M}}}$ denote the conjugate manifold to ${\tilde{M}}$ (that is, ${\tilde{M}}$ with the opposite complex struture $-J$). Thus the diagonal $\Delta$ of ${\tilde{M}}$ is a complex submanifold of ${\tilde{M}}\times {\tilde{M}}$, but it is a totally real submanifold of ${\tilde{M}}\times \overline{{\tilde{M}}}$. Hence ${\tilde{M}}\times \overline{{\tilde{M}}}$ has two natural totally real submanifolds: $M\times M$ and $\Delta$.

Let $r:M\times M\rightarrow {\mathbb {R}}$ be the Riemannian distance function for $\kappa$. Then $r^2$ is real-analytic on some neighourhood U of the real diagonal $\Delta _M$ in $M\times M$. Therefore, $r^2$ admits a holomorphic extension $r^2_{\mathbb {C}}:{\tilde{U}}\rightarrow {\mathbb {C}}$ to some open neighbourhood ${\tilde{U}}$ of U in ${\tilde{M}}\times \overline{{\tilde{M}}}$. The intersection ${\tilde{U}}\cap \Delta$ is an open neighbourhood of $\Delta _M$ in $\Delta$; hence, upon identifying $\Delta$ with ${\tilde{M}}$ and $\Delta _M$ with M in the natural manner, we may view the restriction of $r^2_{\mathbb {C}}$ to ${\tilde{U}}\cap \Delta$ as being defined on a neighbourhood of M in ${\tilde{M}}$. In local holomorphic coordinates $\zeta$ on ${\tilde{M}}$, we shall denote this restriction by $r^2_{\mathbb {C}}(\zeta ,{\overline{\zeta }})$. Then one has $\rho (\zeta )=-r^2_{\mathbb {C}}(\zeta ,{\overline{\zeta }})/4$.

Since $\rho$ is strictly plurisubharmonic, for some maximal $\tau _{max}\in (0,+\infty ]$ and for every $\tau \in (0,\tau _{max})$,

$$\begin{aligned} {\tilde{M}}^\tau :=\rho ^{-1}\left( [0,\tau ^2)\right) \end{aligned}$$

is a strictly pseudoconvex domain in ${\tilde{M}}$; its boundary is the compact smooth hypersurface

$$\begin{aligned} X^\tau :=\rho ^{-1}(\tau ^2)\subset {\tilde{M}}{\setminus } M. \end{aligned}$$

One calls ${\tilde{M}}^\tau$ the open Grauert tube of radius $\tau$, and $\sqrt{\rho }$ the tube function of $(M,\kappa )$. We shall generally also write J (rather than $J^\tau$) for the the CR structure on $X^\tau$. We shall denote by $H(X^\tau )\subset L^2(X^\tau )$ the Hardy space of $X^\tau$, and by

$$\begin{aligned} \Pi ^\tau :L^2(X^\tau )\rightarrow H(X^\tau ) \end{aligned}$$

(1)

the orthogonal projector, that is, the Szegö projector of the CR manifold $X^\tau$.¹

The relation between the value of $\tau _{max}$ and the geometry of $(M,\kappa )$ has been elucidated by Lempert and Szöke (see §1 and §2 of [23]). Namely, $\tau _{max}=+\infty$ only if $(M,\kappa )$ is non-negatively curved. On the other hand, if $(M,\kappa )$ has a negative sectional curvature of value $-a$, then $\pi /(2\,\sqrt{a})\ge \tau _{max}$.

One also has the following alternative perspective. Rather than starting from the complexification $({\tilde{M}},J)$, and then considering a Kähler structure $\Omega$ on $({\tilde{M}},J)$ canonically induced by $\kappa$, one can start instead from the canonical symplectic structure $\Omega _{can}$ on the cotangent bundle $T^\vee M$, locally given by $\textrm{d}{\textbf{q}}\wedge \textrm{d}{\textbf{p}}$, where ${\textbf{q}}$ denotes local coordinates on M and ${\textbf{p}}$ the induced fiberwise linear coordinates on the cotangent spaces; then one introduces a compatible complex structure $J_{ad}$ on a suitable neighborhood of the zero section in $(T^\vee M,\Omega _{can})$, again canonically induced by $\kappa$. In fact, $J_{ad}$ is uniquely determined by the condition that the maps ${\mathbb {C}}\rightarrow TM$ parametrizing the leaves of the Riemann foliation are holomorphic, when suitably restricted. Lempert and Szöke call $J_{ad}$ adapted [17, 22, 23, 39].

More explicitly, if $(m,v)\in TM$ and $v\ne 0$, let $\gamma :{\mathbb {R}}\rightarrow M$ denote the unique geodesic with initial condition (m, v), and ${\dot{\gamma }}:{\mathbb {R}}\rightarrow TM$ its velocity vector. For every $b>0$, let $N_b:TM\rightarrow TM$ denote dilation by b. Consider the smooth map

$$\begin{aligned} \psi _\gamma :a+\imath \,b\in {\mathbb {C}}\mapsto N_b\left( {\dot{\gamma }}(a)\right) \in TM. \end{aligned}$$

(2)

The submanifolds $\psi _\gamma ({\mathbb {C}}{\setminus } {\mathbb {R}})$ are the leaves of the Riemann foliation of $TM{\setminus } M_0$ (here $M_0\cong M$ is the image of the zero section); furthermore, the complex structure induced on $\psi _\gamma ({\mathbb {C}}{\setminus } {\mathbb {R}})$ by declaring $\psi _\gamma : {\mathbb {C}}{\setminus } {\mathbb {R}}\rightarrow \psi _\gamma ({\mathbb {C}}{\setminus } {\mathbb {R}})$ to be holomorphic is invariant under reparametrization of $\gamma$.

If

$$\begin{aligned} T^\tau M:= \left\{ (m,v):m\in M,\,v\in T_m M,\,\Vert v\Vert _m<\tau \right\} , \end{aligned}$$

then $J_{ad}$ is characterized by the property that the maps $\psi _\gamma$ are holomorphic from a suitable strip $S_\gamma ^\tau \subseteq {\mathbb {C}}$ to $T^\tau M$ (see [32] and §3–4, [39]). More precisely, for $\tau \in (0,\tau _{max}]$ let us set

$$\begin{aligned} S_\gamma ^\tau :=\left\{ a+\imath \,b\,\in {\mathbb {C}}:\,a\in {\mathbb {R}},\, 0<b<\tau /\Vert {\dot{\gamma }}\Vert \right\} . \end{aligned}$$

Then $\psi _\gamma (S_\gamma ^\tau )\subseteq T^\tau M$, and the restriction $\psi _\gamma :S_\gamma ^\tau \rightarrow T^\tau M$ is a $J_{ad}$-holomorphic curve.

After [23] and [21], the two approaches are related by the imaginary time exponential map of $\kappa$ (see also the discussions in [43, 44, 48] ). Let us identify TM and $T^\vee M$ by $\kappa$, and view $\Omega _{can}$ as a symplectic structure on TM. Given $m\in M$, let $\exp _m:U_m\rightarrow M$ be the exponential map at m for $\kappa$; here $U_m\subseteq T_mM$ is some neighborhood of the origin. Let $T_m^{\mathbb {C}}M:=T_mM\otimes _{\mathbb {R}}{\mathbb {C}}$ be the complexified tangent space at m; being ${\mathcal {C}}^\varpi$, $\exp _m$ extends to a holomorphic map $E_m:{\tilde{U}}_m\rightarrow {\tilde{M}}$, where ${\tilde{U}}_m\subseteq T_m^{\mathbb {C}}M$ is some open neighborhood of $U_m$. As M is compact, we may assume that for $\tau >0$ sufficiently small one has

$$\begin{aligned} {\tilde{U}}_m\supseteq \left\{ (m,\imath \,v):\,v\in T_m M,\,\Vert v\Vert _m<\tau \right\} \quad \forall m\in M. \end{aligned}$$

Therefore, for all such $\tau$ one obtains a ${\mathcal {C}}^\varpi$ map

$$\begin{aligned} E^\tau :\,(m,v)\in T^\tau M\mapsto E_m(\imath \,v)\in {\tilde{M}}, \end{aligned}$$

(3)

such that $E^\tau (m,0)=m,\,\forall \,m\in M$; $E^\tau$ has the following properties:

• 1. $E^\tau$ intertwines the square norm function $\Vert \cdot \Vert ^2:TM\rightarrow {\mathbb {R}}$ and $\rho$:

  $$\begin{aligned} {E^\tau }^*(\rho )=\Vert \cdot \Vert ^2, \end{aligned}$$

  (4)

  hence it maps $T^{\tau '} M$ to ${\tilde{M}}^{\tau '}$, for all $\tau '\in (0,\tau )$;

• 2. for sufficiently small $\tau >0$, $E^\tau$ is a ${\mathcal {C}}^\varpi$ symplectomorphism between $(T^\tau M,\Omega _{can})$ and $({\tilde{M}}^\tau ,\Omega )$, that is,

  $$\begin{aligned} {E^\tau }^*(\Omega )=\Omega _{can}, \end{aligned}$$

  (5)

  and similarly replacing $\tau$ with any $\tau '\in (0,\tau )$;

• 3. consequently, $E^\tau$ intertwines the Hamiltonian flow of $\Vert \cdot \Vert$ on $(T^\tau M{\setminus } M_0,\Omega _{can})$, which is the homogeneous geodesic flow, with the Hamiltonian flow of $\sqrt{\rho }$ on $({\tilde{M}}{\setminus } M,\Omega )$;

• 4. the relation ${E^\tau }^*(\Omega )=\Omega _{can}$ also implies that ${E^\tau }^*(J)$ is a compatible complex structure on $(T^\tau M,\Omega _{can})$, and in fact $J_{ad}={E^\tau }^*(J)$;

• 5. $E^\tau$ intertwines the Riemann foliation of $(M,\kappa )$ with the Monge–Ampère foliation of $\sqrt{\rho }$ [21, 23].

In short, $E^\tau$ yields an isomorphism of Kähler manifolds

$$\begin{aligned} (T^\tau M,\,\Omega _{can},\,J_{ad})\rightarrow ({\tilde{M}}^\tau ,\Omega ,J), \end{aligned}$$

and if $\tau '\in (0,\tau )$ then the Grauert tube boundary $X^{\tau '}\subseteq {\tilde{M}}^\tau$ is identified with the (co)sphere bundle of radius $\tau '$ in $T^\vee M\cong TM$.

There are natural choices for primitives of both $\Omega _{can}$ and $\Omega$, and these also get intertwined by $E^\tau$. More precisely, let $\lambda _{can}\in \Omega ^1(T^\vee M)$ be the canonical 1-form, locally expressed as ${\textbf{p}}\,\textrm{d}{\textbf{q}}$; thus $\Omega _{can}=-\textrm{d}\lambda _{can}$. Furthermore, let

$$\begin{aligned} \lambda :=\Im ({\overline{\partial }}\rho )\in \Omega ^1\big ({\tilde{M}}^\tau \big ); \end{aligned}$$

(6)

thus $\Omega =-\textrm{d}\lambda$. Then on $T^\tau M$

$$\begin{aligned} \lambda _{can}={E^\tau }^*(\lambda ). \end{aligned}$$

(7)

Let us set

$$\begin{aligned} \alpha :=-\lambda =\Im (\partial \rho ) =\frac{1}{2\,\imath }\,\left( \partial \rho -{\overline{\partial }}\rho \right) \qquad \text {and} \qquad \omega :=\frac{1}{2}\,\Omega , \end{aligned}$$

(8)

so that

$$\begin{aligned} \Omega =-\textrm{d}\lambda =\textrm{d}\alpha =2\,\omega =\imath \,\partial \,{\overline{\partial }}\rho . \end{aligned}$$

(9)

If $M'\subseteq {\tilde{M}}$ is open and $f\in {\mathcal {C}}^\infty (M')$, $\upsilon _f\in {\mathfrak {X}}(M')$ will denote the Hamiltonian vector field of f with respect to $\Omega$. By the above, the homogeneous geodesic flow on $T^\vee M{\setminus } M_0$ is intertwined by $E^\tau$ with the flow of $\upsilon _{\sqrt{\rho }}$ on ${\tilde{M}}{\setminus } M$. The following holds (see Sect. 3).

• 1. $\alpha$ is invariant under the flow of $\upsilon _{\sqrt{\rho }}$; equivalently, $\lambda _{can}$ is preserved by the homogeneous geodesic flow;

• 2. if $\jmath ^\tau :X^\tau \hookrightarrow {\tilde{M}}$ is the inclusion, then $\alpha ^\tau :={\jmath ^\tau }^*(\alpha )$ is a contact form;

• 3. the cone (closed in the complement of the zero section)

  $$\begin{aligned} \Sigma ^\tau :=\left\{ (x,\,r\,\alpha _x^\tau ):\, x\in X^\tau ,\,r>0\right\} \subseteq T^\vee X^\tau {\setminus } X_0 \end{aligned}$$

  (10)

  is symplectic (for the standard symplectic structure of $T^\vee X^\tau$);

• 4. being tangent to $X^\tau$, $\upsilon _{\sqrt{\rho }}$ induces by restriction a smooth vector field $\upsilon _{\sqrt{\rho }}^\tau \in {\mathfrak {X}}(X^\tau )$, and by the above the flow of $\upsilon _{\sqrt{\rho }}^\tau$ preserves the volume form on $X^\tau$;

• 5. consequently, the differential operator

  $$\begin{aligned} D_{\sqrt{\rho }}^\tau :=\imath \,\upsilon _{\sqrt{\rho }}^\tau \end{aligned}$$

  (11)

  is formally self-adjoint on $L^2(X^\tau )$;

• 6. the principal symbol $\sigma (D_{\sqrt{\rho }}^\tau )$ of $D_{\sqrt{\rho }}^\tau$ is positive along $\Sigma ^\tau$.

These facts have the following consequence. Consider the composition

$$\begin{aligned} {\mathfrak {D}}_{\sqrt{\rho }}^\tau :=\Pi ^\tau \circ D_{\sqrt{\rho }}^\tau \circ \Pi ^\tau ; \end{aligned}$$

(12)

in the terminology of [16] and [4], ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$ is a self-adjoint first-order Toeplitz operator on $X^\tau$. Its principal symbol (as a Toeplitz operator) is, by definition, the restriction of $\sigma (D_{\sqrt{\rho }}^\tau )$ to $\Sigma ^\tau$, and is therefore strictly positive. Hence ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$ is an elliptic Toeplitz operator. By the theory in §2 of [4] (especially Proposition 2.4), the spectrum of ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$ is discrete, bounded from below and has only $+\infty$ as accumulation point (see Sect. 3.5 below).

Let then

$$\begin{aligned} \lambda _1^\tau< \lambda _2^\tau <\cdots \uparrow +\infty \end{aligned}$$

be the distinct eigenvalues of ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$; for $j=1,2,\ldots$ let $1\le \ell _j^\tau <+\infty$ denote the multiplicity of $\lambda _j$, and let $H_j(X^\tau )\subseteq H(X^\tau )$ be the ($\ell _j^\tau$-dimensional) eigenspace of $\lambda _j^\tau$. If we choose orthonormal basis $(\rho _{j,k}^\tau )_{k=1}^{\ell _j^\tau }$ of every $H_j(X^\tau )$, then $(\rho _{j,k}^\tau )_{j,k}$ is a complete orthonormal system of $H(X^\tau )$. We shall henceforth leave dependence on $\tau$ of these spectral data for ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$ implicit, and drop the suffix $\tau$.

In order to obtain spectral or eigenfunction asymptotics, it is common to consider smoothed versions of the spectral kernels associated to each eigenvalue (see e.g. [12] and [15]). In the present setting, the ${\mathcal {C}}^\infty$ function

$$\begin{aligned} \Pi ^\tau _j(x,y):=\sum _{k=1}^{\ell _j}\,\rho _{j,k}(x) \cdot \overline{\rho _{j,k}(y)} \end{aligned}$$

(13)

on $X^\tau \times X^\tau$ is the Schwartz kernel of the orthogonal projector $\Pi ^\tau _j:L^2(X^\tau )\rightarrow H_j(X^\tau )$.² Suppose $\chi \in {\mathcal {C}}^\infty _c\big ((-\epsilon ,\epsilon )\big )$ with $\epsilon >0$ suitably small; as in [10, 11, 48], let us consider the ‘smoothed spectral projector’

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }:= \sum _{j=1 }^{+\infty }\,{\hat{\chi }}(\lambda -\lambda _j)\,\Pi ^\tau _j, \end{aligned}$$

(14)

whose distributional kernel is the ${\mathcal {C}}^\infty$ function of $(\lambda ,x,y)\in {\mathbb {R}}\times X\times X$

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x,y):= \sum _{j=1 }^{+\infty }\,{\hat{\chi }}(\lambda -\lambda _j)\,\sum _{k=1}^{\ell _j}\,\rho _{j,k}(x) \cdot \overline{\rho _{j,k}(y)}; \end{aligned}$$

(15)

heuristically, (15) is a slight smoothing of a spectral projector kernel relative to a spectral band travelling to the right as $\lambda \rightarrow +\infty$. The near-diagonal asymptotics of (15) encode information about the local concentration behaviour of the $\rho _{j,k}$’s, and globally on the global asymptotic distribution of the $\lambda _j$’s. For a discussion in the specific context of Grauert tubes, see [44] and [47]; for applications to the Toeplitz quantization of Kähler manifolds, with an emphasis on scaling asymptotics, see [25,26,27,28,29,30, 49,50,51]). For recent work on general CR manifolds, see [19].

In [10] an [11], the authors provide near-diagonal and near-graph scaling asymptotics for (15), strikingly similar to the Szegö kernel asymptotics holding in the line bundle setting [1, 35, 42] and to those holding for Toeplitz spectral projectors in [26].

As emphasized in [10], the asymptotic analysis of (15) is a complex analogue of the analysis of the real spectral projection kernel of $\sqrt{\Delta }$. Replacing $D_{\sqrt{\rho }}^\tau$ with the Toeplitz operator ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$ in (12) is forced by the lack of holomorphy of the homogeneous geodesic flow. Remarkably, the Heisenberg-type scaling asymptotics of $\Pi ^\tau _{\chi ,\lambda }$ are the complex counterpart of the Bessel-type scaling asymptotics in [9].

In the present work, we shall survey the approach of [10], focusing on the near-diagonal case, and provide some complements to their results.

Prior to precise statements, some additional notation is in order. To begin with, we introduce an invariant, denoted $\psi _2$, which is related to a Hermitian vector space and ubiquitously appears in various guises as the exponent controlling equivariant Szegö kernel scaling asymptotics [1, 35].

Definition 2

Let V be a finite-dimensional compòex vector space, and let $h:V\times V\rightarrow {\mathbb {C}}$ be a Hermitian product. Then $g:=\Re (h)$ and $\omega :=-\Im (h)$ are, respectively, an Euclidean scalar product and a symplectic form on V (viewed as a real vector space), compatible with the complex structure. If $\Vert \cdot \Vert _h$ is the norm function on V associated to h (or g), let us define

$$\begin{aligned} \psi _2^h:(u,v)\in V\times V\rightarrow -\frac{1}{2}\Vert u-v\Vert ^2_h-\imath \,\omega (u,v)\in {\mathbb {C}}. \end{aligned}$$

Clearly, $\psi _2^h(u,v)$ is positively homogeneous of degree 2 in the pair (u, v), and of degree 1 in h (or $\omega$).

For instance, if $V={\mathbb {C}}^k$ and $h_{st}:{\mathbb {C}}^k\times {\mathbb {C}}^k\rightarrow {\mathbb {C}}$ is the standard Hermitian product, then $h_{st}=g_{st}-\imath \,\omega _{st}$, where $g_{st}$ and $\omega _{st}$ denote, respectively, the standard Euclidean product and the standard symplectic structure on ${\mathbb {R}}^{2k}\cong {\mathbb {C}}^k$. Then $\psi _2:=\psi _2^{h_{st}}:{\mathbb {C}}^k\times {\mathbb {C}}^k\rightarrow {\mathbb {C}}$ is given by

$$\begin{aligned} \psi _2({\textbf{u}},{\textbf{v}}):= -\frac{1}{2}\,\Vert {\textbf{u}}-{\textbf{v}}\Vert ^2-\imath \, \omega _{st}({\textbf{u}},{\textbf{v}})= -\frac{1}{2}\,\Vert {\textbf{u}}\Vert ^2-\frac{1}{2}\,\Vert {\textbf{v}}\Vert ^2 +{\textbf{u}}\cdot \overline{{\textbf{v}}}. \end{aligned}$$

If $k=\dim _{\mathbb {C}}(V)$, and ${\mathcal {B}}$ is an orthonormal basis of (V, h), let $M_{\mathcal {B}}:V\rightarrow {\mathbb {C}}^k$ be the associated unitary isomorphism. Then $\psi ^h_2=\psi _2\circ (M_{\mathcal {B}}\times M_{\mathcal {B}})$. With this in mind, when no confusion seems likely, we shall occasionally leave dependence on h implicit and write $\psi _2$ for $\psi _2^h$.

Recall that $\omega :=\frac{1}{2}\,\Omega$; thus $({\tilde{M}},\omega ,J)$ is a Kähler manifold, with associated Riemannian metric ${\tilde{\kappa }}:=\frac{1}{2}\,{\hat{\kappa }}$. If $x\in {\tilde{M}}$, with tangent space $T_x{\tilde{M}}$, we correspondingly have a function

$$\begin{aligned} \psi _2^{\omega _x}: T_x{\tilde{M}}\times T_x{\tilde{M}} \rightarrow {\mathbb {C}}. \end{aligned}$$

(16)

As mentioned, the near-diagonal asymptotic expansion for $\Pi ^\tau _{\chi ,\lambda }$ at $x\in X^\tau$ in [10] rests on the choice of so-called Heisenberg local coordinates (called normal in [13, 14]). The concept of Heisenberg local coordinates is twofold: one first introduces Heisenberg local coordinates on ${\tilde{M}}$ centered at x, and adapted to $X^\tau$; then Heisenberg local coordinates on $X^\tau$ centered at x. The latter will be induced by the former by restriction and projection. More precisely, Heisenberg local coordinates on ${\tilde{M}}$ will be a system of holomorphic local coordinates centered at x, in which the defining equation $\phi ^\tau :=\rho -\tau ^2$ for $X^\tau$ takes a certain canonical form (Definition 30). Let $U\subset {\tilde{M}}$ be an open neighbourhood of $x\in X^\tau$ on which Heisenberg local coordinates $(z_0,z_1,\ldots ,z_{d-1}): U\rightarrow {\mathbb {C}}^d$ (centered at x and adapted to $X^\tau$) have been chosen. Set $\theta :=\Re (z_0):U\rightarrow {\mathbb {R}}$ and $U^\tau :=X^\tau \cap U$; then

$$\begin{aligned} \varphi ^\tau : \left. (\theta ,z_1,\ldots ,z_{d-1})\right| _{U^\tau }: {U^\tau }\rightarrow {\mathbb {R}}\times {\mathbb {C}}^{d-1} \end{aligned}$$

will be a system of Heisenberg local coordinates on $X^\tau$ centered at x. We shall generally redefine the $z_i$’s and omit symbols of restriction, and write $z'=(z_1,\ldots ,z_{d-1})$. Alternatively, we shall use real notation and write

$$\begin{aligned} \varphi ^\tau =(\theta ,{\textbf{u}}):U^\tau \rightarrow {\mathbb {R}}\times {\mathbb {R}}^{2d-2}. \end{aligned}$$

Furthermore, we shall often adopt the additive short-hand

$$\begin{aligned} x+(\theta ,{\textbf{u}}):=(\varphi ^\tau )^{-1}(\theta ,{\textbf{u}}). \end{aligned}$$

Actually, it will be convenient to work with a slightly more restrictive class of local coordinates, that will be called normal Heisenberg local coordinates adapted to $X^\tau$ at x (see Sect. 3.3.3).

In the line bundle setting, $X^\tau$ is a fixed-radius circle bundle in the dual of the polarizing line bundle. Translation in $\theta$ may be then be assumed to correspond to fiberwise rotation, hence to the flow of the Reeb vector field, which is CR-holomorphic.

In the Grauert tube setting, instead, neither is the Reeb flow generally CR-holomorphic nor may it be assumed to correspond to translation in $\theta$. Namely, let ${\mathcal {R}}^\tau \in {\mathfrak {X}}(X^\tau )$ be the Reeb vector field of $(X^\tau ,\alpha ^\tau )$. While we do have ${\mathcal {R}}^\tau (x)=\partial /\partial \theta |_x$ (see (60) below), there is no reason to expect that ${\mathcal {R}}^\tau =\partial /\partial \theta$ on $U^\tau$ (see e.g. Theorem 18.5 in [13]). Hence the curves $\theta \mapsto x+(\theta ,{\textbf{0}})$ deflect from the trajectories of ${\mathcal {R}}^\tau$, which are a rescaling of the geodesic flow. This is a sharp difference with the line bundle situation, and contributes to making the derivation of the asymptotics technically more involved.

We need one last piece of notation before formulating the near-diagonal scaling asymptotics of the smoothed spectral projectors $\Pi ^\tau _{\chi ,\lambda }$. Let $\Gamma ^\tau _t:X^\tau \rightarrow X^\tau$ be, with abuse of language warranted by the previous identifications, the homogeneous geodesic flow at time t (to be precise, this is the flow of $\upsilon _{\sqrt{\rho }}$).

Definition 3

If $\chi \in {\mathcal {C}}^\infty _c({\mathbb {R}})$ and $x\in X^\tau$, let us set

$$\begin{aligned} x^\chi :=\left\{ \Gamma ^\tau _t(x):\,t\in \textrm{supp}(\chi )\right\} . \end{aligned}$$

Theorem 4

Suppose $\tau \in (0,\tau _{max})$, $x\in X^\tau$, and $\chi \in {\mathcal {C}}^\infty _c\big ((-\epsilon ,\epsilon )\big )$ for some suitably small $\epsilon >0$. Then the following holds.

• 1. Suppose $C,\,\delta >0$ are constants. Then (with the notation of Definition 3)

  $$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)=O\left( \lambda ^{-\infty } \right) \end{aligned}$$

  uniformly for $\textrm{dist}_{X^\tau }\left( x_1,x_2^\chi \right) \ge C\,\lambda ^{\delta -1/2}$.

• 2. Suppose $x\in X^\tau$, and let us choose a system of normal Heisenberg local coordinates on $X^\tau$ centered at x. If $C>0$ and $\delta \in (0,1/6)$, uniformly for $\Vert (\theta _j/\tau ,{\textbf{v}}_j)\Vert \le C\,\lambda ^{\delta }$ there is an asymptotic expansion

  $$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }\left( x+\left( \frac{\theta _1}{\sqrt{\lambda }},\frac{{\textbf{v}}_1}{\sqrt{\lambda }} \right) , x+\left( \frac{\theta _2}{\sqrt{\lambda }}, \frac{{\textbf{v}}_2}{\sqrt{\lambda }} \right) \right) \\{} & {} \quad \sim \frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\,e^{\imath \, \sqrt{\lambda }\,\frac{\theta _1-\theta _2}{\tau }}\cdot \chi (0)\cdot e^{\frac{1}{\tau }\,\psi _2({\textbf{v}}_1,{\textbf{v}}_2)}\\{} & {} \qquad \cdot \left[ 1+\sum _{j\ge 1}\lambda ^{-j/2}\,A_j^\tau (x;\theta _1,{\textbf{v}}_1, \theta _2,{\textbf{v}}_2)\right] , \end{aligned}$$

  where, as a function of $(\theta _1,{\textbf{v}}_1, \theta _2,{\textbf{v}}_2)$, $A_j^\tau$ is a polynomial of degree $\le 3\,j$ and parity j.

Corollary 5

Under the same assumptions as in Theorem 4,

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }\left( x, x \right) \sim \frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\cdot \chi (0)\cdot \left[ 1+\sum _{j\ge 1}\lambda ^{-j}\,B_j^\tau (x)\right] , \end{aligned}$$

for certain smooth functions $B_j\in {\mathcal {C}}^\infty (X^\tau )$.

We recover the near-diagonal asymptotic expansion of Chang and Rabinowitz (Theorem 1.1 of [10]) rescaling according to Heisenberg type, holding $\theta _j$ and ${\textbf{v}}_j$ fixed.

Corollary 6

If $\theta _1,\theta _2\in {\mathbb {R}}$ and ${\textbf{v}}_1, \,{\textbf{v}}_2\in {\mathbb {R}}^{2n-2}$, then

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }\left( x+\left( \frac{\theta _1}{\lambda },\frac{{\textbf{v}}_1}{\sqrt{\lambda }} \right) , x+\left( \frac{\theta _2}{\lambda }, \frac{{\textbf{v}}_2}{\sqrt{\lambda }} \right) \right) \\{} & {} \quad \sim \frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\cdot e^{\imath \,\frac{\theta _1-\theta _2}{\tau }}\cdot \chi (0)\cdot e^{\frac{1}{\tau }\,\psi _2({\textbf{v}}_1,{\textbf{v}}_2)}\\{} & {} \qquad \cdot \left[ 1+\sum _{j\ge 1}\lambda ^{-j/2}\,R_j^\tau (x;\theta _1,{\textbf{v}}_1, \theta _2,{\textbf{v}}_2)\right] , \end{aligned}$$

where, as a function of $(\theta _1,{\textbf{v}}_1, \theta _2,{\textbf{v}}_2)$, $R_j^\tau$ is a polynomial (again, of degree $\le 3\,j$ and parity j).

Similar considerations apply to the complexified spectral projectors associated to the Poisson wave operator. This issue relates to a fundamental extension property of the Laplacian eigenfunctions on a compact real-analytic Riemannian manifold, and is specific to Grauert tubes [2, 3, 18, 20, 21, 37, 38, 44].

Let $0=\mu _1^2< \mu _2^2< \cdots$ be the distinct eigenvalues of the positive Laplacian $\Delta$ of $(M,\kappa )$, with respective multiplicities $\ell '_j$. Let $V_j\subset {\mathcal {C}}^\infty (M)$ denote the corresponding eigenspaces, of dimension $\dim (V_j)=\ell '_j$. For $j=1,2,\ldots$, let $(\varphi _{j,k})_{k=1}^{\ell '_j}$ be an orthonormal basis of $V_j$, so that $(\varphi _{j,k})_{j,k}$ is a complete orthonormal system in $L^2(M)$ for the $L^2$-norm defined by the Riemannian density.

Being of class ${\mathcal {C}}^\varpi$, each $\varphi _{j,k}$ admits a holomorphic extension ${\tilde{\varphi }}_{j,k}$ to some open neighborhood of M in ${\tilde{M}}$, which a priori depends on (j, k). Boutet de Monvel discovered that a much stronger result is true: there exists $\tau _0>0$ such that every $\varphi _{j,k}$ extends holomorphically to $\overline{{\tilde{M}}^{\tau _0}}$. Therefore, for $\tau \in (0,\tau _0]$ the restriction ${\tilde{\varphi }}_{j,k}^\tau := \left. {\tilde{\varphi }}_{j,k}\right| _{X^\tau }$ is a CR function.

This collective extension property is closely related to the analytic extension of the Schwartz kernel of the Poisson operator

$$\begin{aligned} U(\imath \,\tau )=e^{-\tau \,\sqrt{\Delta }}:L^2(M)\rightarrow L^2(M) \end{aligned}$$

for $\tau >0$ (see [2, 10, 11, 18, 21, 44, 48] for discussion and motivation). Assuming that the $\varphi _{j,k}$’s are real, the distributional kernel of $U(\imath \,\tau )$ admits the spectral representation

$$\begin{aligned} U(\imath \,\tau ,m,n):=\sum _{j=1}^{+\infty }\,e^{-\tau \,\mu _j}\,\sum _{k=1}^{\ell '_j} \varphi _{j,k}(m)\,\varphi _{j,k}(n) \qquad (\tau \in {\mathbb {R}}_+,\, m,n\in M), \end{aligned}$$

(17)

which is globally real-analytic on $M\times M$ for any $\tau >0$ [44]. If $\tau >0$ is sufficiently small, analytic extension in m, followed by restriction to $X^\tau$, yields the kernel

$$\begin{aligned} P^\tau (x,n):=\sum _{j=1}^{+\infty }\,e^{-\tau \,\mu _j}\,\sum _{k=1}^{\ell '_j} {\tilde{\varphi }}_{j,k}(x)\,\varphi _{j,k}(n) \qquad (x\in X^\tau ,\,n\in M). \end{aligned}$$

(18)

As an operator, $P^\tau$ is a Fourier integral operator with complex phase of positive type and order $-(d-1)/4$. It is in fact a Fourier–Hermite operator in the sense of [4], adapted to a homogeneous symplectic equivalence $\chi _{\tau }:T^\vee M{\setminus } M_0\rightarrow \Sigma ^\tau$ (see (10)). Hence $P^\tau$ is continuous $L^2(M)\rightarrow W^{\frac{d-1}{4}}(X^\tau )$, where $W^s(X^\tau )$ denotes the s-th Sobolev spaces of $X^\tau$. More precisely, $P^\tau$ is a continuous isomorphism $P^\tau :L^2(M)\rightarrow {\mathcal {O}}^{\frac{d-1}{4}}(X^\tau )$, where ${\mathcal {O}}^{s}(X^\tau )$ is the space of boundary values of holomorphic functions on $X^\tau$ that are in $W^s(X^\tau )$; thus $H(X^\tau )={\mathcal {O}}^2(X^\tau )$ (see [37, 44], §3 of [46]).

The complexified Poisson kernel $P^\tau$ governs the analytic continuation of eigenfunctions: for any j,

$$\begin{aligned} {\tilde{\varphi }}_{j,k}^\tau =e^{\tau \,\mu _{j}}\, P^\tau (\varphi _{j,k}). \end{aligned}$$

(19)

The composition

$$\begin{aligned} U_{\mathbb {C}}(2\,\imath \,\tau ):=P^\tau \circ {P^\tau }^*:H(X^\tau )\rightarrow H(X^\tau ) \end{aligned}$$

(20)

is a Fourier integral operator with complex phase of positive type and of degree $-(d-1)/2$ on $X^\tau$; it is in fact a Fourier–Hermite operator adapted to the identity of $\Sigma ^\tau$, hence with the same complex canonical relation as $\Pi ^\tau$ (the relation between $U_{\mathbb {C}}(2\,\imath \,\tau )$ and $\Pi ^\tau$ is discussed in §3.1 of [46]). The definition of (20) depends on the choice of a Riemannian density on $X^\tau$; given this, we may identify its distributional kernel with the generalized function

$$\begin{aligned} U_{\mathbb {C}}(2\,\imath \,\tau ,x,y)= & {} \sum _{j} e^{-2\,\tau \,\mu _{j}}\,\sum _k {\tilde{\varphi }}_{j,k}^\tau (x)\,\overline{{\tilde{\varphi }}_{j,k}^\tau (y)}= \sum _{j=1}^{+\infty } U^\tau _j(x,y), \end{aligned}$$

(21)

where $U^\tau _j\in {\mathcal {C}}^\infty (X^\tau \times X^\tau )$ is given by

$$\begin{aligned} U^\tau _j(x,y):= \sum _{k=1}^{\ell '_j}\, P^\tau (\varphi _{j,k})(x)\,\overline{P^\tau (\varphi _{j,k})(y) }. \end{aligned}$$

As $\left( P^\tau (\varphi _{j,k})\right) _{j,k}$ is not an orthonormal system, neither $U_{\mathbb {C}}(2\,\imath \,\tau )$ nor $U^\tau _j$ are orthogonal projectors. Nonetheless, $U_{\mathbb {C}}(2\,\imath \,\tau )$ plays a role in the asymptotic study of analytic extensions reminiscent of $\Pi ^\tau$ (§6 of [48]).

Suppose as above that $\chi \in {\mathcal {C}}^\infty _0\big ((-\epsilon ,\epsilon )\big )$, for a suitably small $\epsilon >0$. The asymptotic concentration of the complexified eigenfunctions pertaining to a spectral band drifting to infinity is probed by the following smoothed version of (21):

$$\begin{aligned} P_{\chi ,\lambda }^\tau (x,y):= & {} \sum _{j} {\hat{\chi }}(\lambda -\mu _j)\,e^{-2\,\tau \,\mu _j}\,\sum _{k=1}^{\ell _j'} {\tilde{\varphi }}_{j,k}(x)\cdot \overline{{\tilde{\varphi }}_{j,k}(y)}\nonumber \\= & {} \sum _{j} {\hat{\chi }}(\lambda -\mu _j)\,U^\tau _j(x,y)\quad (x, y\in X^\tau ). \end{aligned}$$

(22)

Heuristically, $P_{\chi ,\lambda }^\tau \in {\mathcal {C}}^\infty (X^\tau \times X^\tau )$ is a complex (tempered) analogue of the smoothed spectral projector kernel (15). The diagonal restriction of $P_{\chi ,\lambda }^\tau$ is the non-negative function

$$\begin{aligned} P_{\chi ,\lambda }^\tau (x,x):=\sum _{j,k} {\hat{\chi }}(\lambda -\mu _j)\,e^{-2\,\tau \,\mu _j}\, \left| {\tilde{\varphi }}_{j,k}(x)\right| ^2\quad (x\in X^\tau ). \end{aligned}$$

(23)

The complexified Poisson operator is a special instance of the complexified Poisson wave operator (see (158) below), which was proved by Zelditch to be describable in terms of dynamical Toeplitz operators (see e.g. [44], especially §8–9). Building on this, and on their use of the normal local coordinates of Folland and Stein, Chang and Rabinowitz proved in [10] a near-diagonal asymptotic expansion for $P_{\chi ,\lambda }^\tau$ very similar to the one holding for $\Pi ^\tau _{\chi ,\lambda }$. The corresponding version that we shall provide here runs parallel to Theorem 4.

Theorem 7

Suppose $\tau \in (0,\tau _{max})$, $x\in X^\tau$, and $\chi \in {\mathcal {C}}^\infty _c\big ((-\epsilon ,\epsilon )\big )$ for some suitably small $\epsilon >0$. Then the following holds.

• 1. Suppose $C,\,\delta >0$ are constants. Then (with the notation of Definition 3)

  $$\begin{aligned} P^\tau _{\chi ,\lambda }(x_1,x_2)=O\left( \lambda ^{-\infty } \right) \end{aligned}$$

  uniformly for $\textrm{dist}_{X^\tau }\left( x_1,x_2^\chi \right) \ge C\,\lambda ^{\delta -1/2}$.

• 2. Suppose $x\in X^\tau$, and let us choose a system of normal Heisenberg local coordinates on $X^\tau$ centered at x. If $C>0$ and $\delta \in (0,1/6)$, uniformly for $\Vert (\theta _j/\tau ,{\textbf{v}}_j)\Vert \le C\,\lambda ^{\delta }$ there is an asymptotic expansion

  $$\begin{aligned}{} & {} P^\tau _{\chi ,\lambda }\left( x+\left( \frac{\theta _1}{\sqrt{\lambda }},\frac{{\textbf{v}}_1}{\sqrt{\lambda }} \right) , x+\left( \frac{\theta _2}{\sqrt{\lambda }}, \frac{{\textbf{v}}_2}{\sqrt{\lambda }} \right) \right) \\{} & {} \quad \sim \frac{\gamma _{0,0}^\tau (x)}{\sqrt{2\,\pi }}\cdot \left( \frac{1}{2\,\pi \tau }\right) ^{d-1}\cdot \lambda ^{\frac{d-1}{2}}\cdot e^{\imath \,\sqrt{\lambda }\,\frac{\theta _1-\theta _2}{\tau }}\cdot \chi (0)\cdot e^{\frac{1}{\tau }\,\psi _2({\textbf{v}}_1,{\textbf{v}}_2)}\\{} & {} \qquad \cdot \left[ 1+\sum _{j\ge 1}\lambda ^{-j/2}\,F_j^\tau (x;\theta _1,{\textbf{v}}_1, \theta _2,{\textbf{v}}_2)\right] , \end{aligned}$$

  for a certain constant $\gamma _{0,0}^\tau (x)$ (to specified below) and where, as a function of $(\theta _1,{\textbf{v}}_1, \theta _2,{\textbf{v}}_2)$, $F_j^\tau$ is a polynomial of degree $\le 3\,j$ and parity j.

Remark 8

We shall verify a posteriori that $\gamma _{0,0}^\tau (x)=\tau ^{(d-1)/2}$ (see below).

Corollary 9

Under the assumptions of Theorem 7,

$$\begin{aligned} P^\tau _{\chi ,\lambda }\left( x, x \right) \sim \frac{\gamma _{0,0}^\tau (x)}{\sqrt{2\,\pi }}\cdot \left( \frac{1}{2\,\pi \tau }\right) ^{d-1}\cdot \lambda ^{\frac{d-1}{2}}\cdot \chi (0)\cdot \left[ 1+\sum _{j\ge 1}\lambda ^{-j}\,Q_j^\tau (x)\right] , \end{aligned}$$

for certain smooth functions $Q_j^\tau \in {\mathcal {C}}^\infty (X^\tau )$.

We shall leave it to the reader to formulate the corresponding analogue of Corollary 6. As an application of the on-diagonal asymptotic expansions for $\Pi ^\tau _{\chi ,\lambda }$ and $P^\tau _{\chi ,\lambda }$, we provide local Weyl laws by a standard argument, similar to the one in [25] for the line bundle setting (inspired by the discussion in [15]). The stated equality $\gamma _{0,0}^\tau (x)=\tau ^{(d-1)/2}$ will follow by comparison with the local Weyl law in Proposition 3.8 of [46]. For $x\in X^\tau$, let us note the identities

$$\begin{aligned} \Pi _j^\tau (x,x)= \sum _{k=1}^{\ell _j}\, \left| \rho _{j,k}(x) \right| ^2,\quad U^\tau _j(x,x)=e^{-2\,\tau \,\mu _{j}}\, \sum _{k=1}^{\ell '_j} \left| {\tilde{\varphi }}_{j,k}^\tau (x) \right| ^2, \end{aligned}$$

where notation is as in (13) and (21). Let us further define, for $x\in X^\tau$ and $\lambda \in {\mathbb {R}}$,

$$\begin{aligned} {\mathcal {W}}_x^\tau (\lambda ):=\sum _{j:\lambda _j\le \lambda }\, \Pi _j^\tau (x,x)=\sum _j\,H(\lambda -\lambda _j)\, \Pi _j^\tau (x,x), \end{aligned}$$

(24)

$$\begin{aligned} {\mathcal {P}}_x^\tau (\lambda ):=\sum _{j:\lambda _j\le \lambda }\, U_j^\tau (x,x)=\sum _j\,H(\lambda -\lambda _j)\, U_j^\tau (x,x), \end{aligned}$$

(25)

where H is the Heaviside function.

Proposition 10

Uniformly in $x\in X^\tau$, we have for $\lambda \rightarrow +\infty$

$$\begin{aligned} {\mathcal {W}}_x(\lambda )=\frac{\tau }{d}\cdot \left( \frac{\lambda }{2\,\pi \,\tau }\right) ^d +O\left( \lambda ^{d-1}\right) \end{aligned}$$

(26)

and

$$\begin{aligned} {\mathcal {P}}_x^\tau (\lambda )= \frac{1}{(2\,\pi )^d}\,\left( \frac{\lambda }{\tau }\right) ^{\frac{d-1}{2}}\cdot \frac{\gamma _{0,0}^\tau (x)}{\tau ^{\frac{d-1}{2}}}\,\left[ \frac{\lambda }{\frac{d-1}{2}+1}+O(1)\right] . \end{aligned}$$

(27)

Comparing with Proposition 3.8 of [46] we finally conclude

Corollary 11

$\gamma _{0,0}^\tau (x)=\tau ^{\frac{d-1}{2}}$.

2 An example

The geometric setting is clarified by the following example (see [17, 32], and §2.1 of [43] for this and other model examples).

Consider the compact torus $M:={\mathbb {R}}^d/{\mathbb {Z}}^d$; its complexification is ${\tilde{M}}:={\mathbb {C}}^d/{\mathbb {Z}}^d$. If ${\textbf{u}}\in M$, the (real) exponential map at ${\textbf{u}}$ is $\exp _{{\textbf{u}}}({\textbf{v}})={\textbf{u}}+{\textbf{v}}$ (${\textbf{v}}\in T_{{\textbf{u}}}M\cong {\mathbb {R}}^d$); here, by abuse of notation, elements of ${\mathbb {R}}^d$ are identified with their classes in M, and the sum is meant in M. The complexified exponential map $E_{{\textbf{u}}}:T_{{\textbf{u}}}^{\mathbb {C}}M\rightarrow {\tilde{M}}$ at ${\textbf{u}}$ is thus $E_{{\textbf{u}}}({\textbf{v}}_1+\imath \,{\textbf{v}}_2):= ({\textbf{u}} +{\textbf{v}}_1)+\imath \,{\textbf{v}}_2$. Hence the imaginary time exponential $E:TM\cong M\times {\mathbb {R}}^d\rightarrow {\tilde{M}}$ is

$$\begin{aligned} E({\textbf{u}},{\textbf{v}}):= {\textbf{u}} +\imath \, {\textbf{v}} \qquad ({\textbf{u}}\in M,\,{\textbf{v}}\in {\mathbb {R}}^d). \end{aligned}$$

In particular, writing ${\textbf{z}}={\textbf{u}}+\imath \,{\textbf{v}}$, we see that the standard symplectic structure $\Omega :=(\imath /2)\,\textrm{d}{\textbf{z}}\wedge \textrm{d}\overline{{\textbf{z}}}$ pulls back to

$$\begin{aligned} \textrm{d}{\textbf{u}}\wedge \textrm{d}{\textbf{v}}= -\textrm{d}({\textbf{v}}\,\textrm{d}{\textbf{u}}) =-\textrm{d}\lambda _{can}=\Omega _{can}. \end{aligned}$$

Hence, the pull-back of the standard complex structure on ${\tilde{M}}$ by E is indeed compatible with $\Omega _{can}$.

The geodesic $\gamma =\gamma _{{\textbf{u}},{\textbf{v}}}$ with initial conditions $({\textbf{u}},{\textbf{v}})$ is $\gamma (\sigma )={\textbf{u}}+\sigma \,{\textbf{v}}$, with tangent lift ${\dot{\gamma }}(\sigma ):=({\textbf{u}}+\sigma \,{\textbf{v}},{\textbf{v}})$. The composition $E\circ \psi _\gamma$, with $\psi _\gamma :{\mathbb {C}}\rightarrow TM$ as in (2), is then

$$\begin{aligned} E\circ \psi _\gamma (\sigma +\imath \,\tau )= E({\textbf{u}}+\sigma \,{\textbf{v}},\tau \,{\textbf{v}})={\textbf{u}} +(\sigma +\imath \,\tau )\,{\textbf{v}}, \end{aligned}$$

(28)

which is holomorphic. Hence $J_{ad}={E}^*(J)$ is the adapted complex structure of TM, in the terminology of [23].

Let us henceforth identify TM with ${\tilde{M}}$ by E, and consider the functions

$$\begin{aligned} \rho ({\textbf{u}}+\imath \,{\textbf{v}}):=\Vert {\textbf{v}}\Vert ^2,\quad \sqrt{\rho }({\textbf{u}}+\imath \,{\textbf{v}})=\Vert {\textbf{v}}\Vert . \end{aligned}$$

We have, with $z_j:=u_j+\imath \,v_j$,

$$\begin{aligned} \partial \rho =\frac{1}{\imath }\sum _j\,v_j\,\textrm{d}z_j,\quad \alpha :=\Im (\partial \rho )=-\sum _j\,v_j\,\textrm{d}u_j=-\lambda _{can} =-\Im \left( {\overline{\partial }}\rho \right) . \end{aligned}$$

Furthermore,

$$\begin{aligned} \imath \,\partial \,{\overline{\partial }}\rho =\frac{\imath }{2}\, \sum _j\,\textrm{d}z_j\wedge \textrm{d}{\overline{z}}_j =-\textrm{d}\lambda _{can}=\Omega _{can}. \end{aligned}$$

Thus $\rho$ is a Kähler potential for $\Omega _{can}$.

A direct computation shows that the differential form $\imath \,\partial \,{\overline{\partial }}\,\sqrt{\rho }$, which is defined where ${\textbf{v}}\ne {\textbf{0}}$, is given by

$$\begin{aligned} \imath \,\partial \,{\overline{\partial }}\,\sqrt{\rho }= & {} \frac{\imath }{2\,\rho ^{3/2}}\,\left[ \Vert {\textbf{v}}\Vert ^2\,\sum _j\textrm{d}z_j\wedge \textrm{d}{\overline{z}}_j-\sum _{j,k}v_j\,v_k\, \textrm{d}z_j\wedge \textrm{d}{\overline{z}}_k\right] , \end{aligned}$$

with constant rank $2d-2$. Furthermore, its 2-dimensional kernel at ${\textbf{u}}+\imath \,{\textbf{v}}$ is generated by the tangent vectors $({\textbf{v}},{\textbf{0}})$ and $({\textbf{0}},{\textbf{v}})$; by (28), this is the tangent space of the Riemann foliation, which therefore coincides with the Monge–Ampère foliation.

Since $\textrm{d}\rho =2\,\sum _jv_j\,\textrm{d}v_j$ and $\Omega _{can}=\sum _j\textrm{d}u_j\wedge \textrm{d}v_j$, letting $\upsilon _\rho$ denote the Hamiltonian vector field of $\rho$ with respect to $\Omega$ we have

$$\begin{aligned} \upsilon _\rho =2\,\sum _j\,v_j\,\frac{\partial }{\partial u_j},\qquad \iota (\upsilon _\rho )\,\alpha =-2\,\Vert {\textbf{v}}\Vert ^2=-2\,\rho , \qquad \upsilon _{\sqrt{\rho }}=\frac{1}{\Vert {\textbf{v}}\Vert }\, \sum _j v_j\,\frac{\partial }{\partial u_j}. \end{aligned}$$

Let us set

$$\begin{aligned} {\mathcal {R}}:=-\frac{1}{2\,\rho }\,\upsilon _\rho =-\frac{1}{2}\,\upsilon _{\ln (\rho )}= -\frac{1}{\sqrt{\rho }}\,\upsilon _{\sqrt{\rho }}. \end{aligned}$$

(29)

Then $\alpha ({\mathcal {R}})\equiv 1$, and ${\mathcal {R}}$ is itself a Hamiltonian vector field

$$\begin{aligned} \iota ({\mathcal {R}})\,\textrm{d}\alpha =\iota ({\mathcal {R}})\,\Omega = \textrm{d}\ln \left( \rho ^{-1/2}\right) . \end{aligned}$$

For $\tau >0$, set $X^\tau :=\left\{ {\textbf{u}}+\imath \,{\textbf{v}}\,:\, \Vert {\textbf{v}}\Vert =\tau \right\}$, so that $X^\tau$ is the boundary of a strictly pseudoconvex domain in ${\tilde{M}}$. Let $\jmath ^\tau :X^\tau \hookrightarrow {\tilde{M}}$ be the inclusion, and set $\alpha ^\tau :={\jmath ^\tau }^*(\alpha )$. Then ${\mathcal {R}}$ is tangent to $X^\tau$ and restricts to a vector field ${\mathcal {R}}^\tau$ on $X^\tau$, which satisfies

$$\begin{aligned} \iota ({\mathcal {R}}^\tau )\,\alpha ^\tau = 1,\qquad \iota ({\mathcal {R}}^\tau )\, \textrm{d}\alpha ^\tau =0. \end{aligned}$$

In other words, ${\mathcal {R}}^\tau$ is the Reeb vector field of the contact manifold $(X^\tau ,\alpha ^\tau )$.

Similarly, $\upsilon _{\sqrt{\rho }}$ is also tangent to $X^\tau$, and in view of (29) it restricts along $X^\tau$ to a vector field $\upsilon _{\sqrt{\rho }}^\tau$ satisfying $\upsilon _{\sqrt{\rho }}^\tau =-\tau \,{\mathcal {R}}^\tau$.

We have $\Vert \upsilon _{\sqrt{\rho }}\Vert =1$, hence $\sqrt{\rho }$ is a distance function on the Riemannian manifold $({\tilde{M}}{\setminus } M,\kappa )$ (here ‘distance function’ is meant in the sense of, say, §3.2.2 of [33]; see also the discussion at the end of Sect. 3.2.2 below). The (Hamiltonian) flow of $\upsilon _{\sqrt{\rho }}$ is

$$\begin{aligned} \Gamma _t({\textbf{u}}+\imath \,{\textbf{v}})= \left( {\textbf{u}}+t\,\frac{{\textbf{v}}}{\Vert {\textbf{v}}\Vert }\right) + \imath \,{\textbf{v}}, \end{aligned}$$

which (with the identification provided by E) corresponds to the homogeneous geodesic flow.

Finally, let us consider the cones

$$\begin{aligned} \Sigma ^\tau =\left\{ ({\textbf{u}}+\imath \,{\textbf{v}}, r\,\alpha ^\tau _{{\textbf{u}}+\imath \,{\textbf{v}}}):\, \Vert {\textbf{v}}\Vert =\tau ,\,r>0\right\} \subseteq T^\vee X^\tau , \end{aligned}$$

where as above $\alpha ^\tau =- \sum _j v_j\,\textrm{d}u_j$. The symbol of the differential operator $D_{\sqrt{\rho }}^\tau :=\imath \,\upsilon _{\sqrt{\rho }}^\tau$ along $\Sigma ^\tau$ is then

$$\begin{aligned} \sigma (D_{\sqrt{\rho }}^\tau )\left( r\,\alpha ^\tau _{{\textbf{u}}+\imath \,{\textbf{v}}} \right)= & {} e^{\imath \,r\,\sum _kv_k\,u_k}\,\imath \,\upsilon _{\sqrt{\rho }}^\tau \left( e^{-\imath \,r\,\sum _kv_k\,u_k} \right) \\= & {} \frac{\imath }{\Vert {\textbf{v}}\Vert }\, \sum _j v_j\,\frac{\partial }{\partial u_j} \left( -\imath \,r\,\sum _kv_k\,u_k \right) =r\,\Vert {\textbf{v}}\Vert =r\,\tau >0. \end{aligned}$$

3 Preliminaries

3.1 Notation

For the reader’s convenience, we collect here some of the notation and conventions adopted in the paper.

Fourier transform. Given $f\in {\mathcal {S}}^d({\mathbb {R}}^k)$ (smooth functions of rapid decay on ${\mathbb {R}}^k$) its Fourier transform ${\hat{f}}\in {\mathcal {S}}^d({\mathbb {R}}^k)$ is given by

$$\begin{aligned} {\hat{f}}(\xi ):=\frac{1}{(2\,\pi )^{k/2}}\, \int _{{\mathbb {R}}^k}e^{-\imath \,\langle \xi ,x\rangle }\,f(x)\, \textrm{d}x\quad (\xi \in {\mathbb {R}}^k), \end{aligned}$$

(30)

so that the Fourier inversion formula has the form

$$\begin{aligned} f(x)=\frac{1}{(2\,\pi )^{k/2}}\, \int _{{\mathbb {R}}^k}e^{\imath \,\langle \xi ,x\rangle }\,{\hat{f}}(\xi )\, \textrm{d}\xi \quad (x\in {\mathbb {R}}^k). \end{aligned}$$

Densities and functions. Our manifolds will be endowed with naturally given volume forms, and we shall identify densities, half-densities and functions.

Schwartz kernels. Given a manifold N, we shall use the same letter for a continuous linear operator $F:{\mathcal {C}}^\infty _0(N)\rightarrow {\mathcal {D}}'(N)$ and its distributional kernel $F(\cdot ,\cdot )\in {\mathcal {D}}'(N\times N)$.

Induced vector fields. Given a smooth action of a Lie group G on a manifold R, for any $\xi \in {\mathfrak {g}}$ (the Lie algebra of G) we shall denote by $\xi _R\in {\mathfrak {X}}(R)$ (the Lie algebra of smooth vector fields on R) the vector field induced by $\xi$.

Riemannian and Kähler structures, I. $(M,\kappa )$ is the reference real-analytic Riemannian manifold, $\rho$ the associated strictly pseudoconvex function defined on a neighbourhood on M in ${\tilde{M}}$, $\Omega =\imath \,\partial \,{\overline{\partial }}\,\rho$ the corresponding Kähler form, ${\hat{\kappa }}:=\Omega (\cdot ,J\cdot )$ the induced Riemannian structure on ${\tilde{M}}^\epsilon$; thus $(M,\kappa )$ is a Riemannian submanifold of $({\tilde{M}}^\epsilon ,{\hat{\kappa }})$.

Hamiltonian vector fields. Given $f\in {\mathcal {C}}^\infty ({\tilde{M}}^\epsilon )$, $\upsilon _f\in {\mathfrak {X}}({\tilde{M}}^\epsilon )$ will denote its Hamiltonian vector field w.r.t. $\Omega$: $\textrm{d}f=\Omega (\upsilon _f,\cdot )$.

Riemannian and Kähler structures, II. We shall also use $\omega :=\frac{1}{2}\,\Omega$, and the corresponding Riemannian metric ${\tilde{\kappa }}:=\frac{1}{2}\,{\hat{\kappa }}$.

Riemannian distance function ${\hat{\kappa }}^\tau$ is the Riemannian metric on $X^\tau$ given by the restriction of ${\hat{\kappa }}$, and $\textrm{dist}_{X^\tau }:X^\tau \times X^\tau \rightarrow {\mathbb {R}}$ denotes the corresponding distance function.

Reeb vector fields. ${\mathcal {R}}$ is the Reeb vector field of $(M,\kappa )$ (Definition 16); it is tangent to every $X^\tau$, and restricts along $X^\tau$ to the Reeb vector field ${\mathcal {R}}^\tau$ of $(X^\tau ,\alpha ^\tau )$.

Volume form. $\textrm{vol}^R_{X^\tau }$ is the Riemannian volume form on $X^\tau$, in terms of which the Hilbert structure on $L^2(X^\tau )$ is defined.

Geodesic flow. $\Gamma ^\tau _t:X^\tau \rightarrow X^\tau$ denotes the homogeneous geodesic flow along $X^\tau$ at time t.

Zero section. For a manifold R, $R_0\subseteq T^\vee R$ is the image of the zero section in the cotangent bundle.

CR structures. With slight abuse, we shall denote by J both the complex structure on ${\tilde{M}}$ and (rather than by $J^\tau$) the induced CR structure on $X^\tau$; similarly, $J_t$ is the CR structure intertwined with J by the homogeneous geodesic flow at time t (see Sect. 3.6 for precise definitions).

3.2 The geometric setting

3.2.1 The homogeneous geodesic flow

As remarked, for $\tau >0$ sufficiently small $E^\tau$ intertwines the homogenous geodesic flow on $T^\tau M{\setminus } M_0$ (that is, the Hamiltonian flow with respect to $\Omega _{can}$ of the norm function induced by $\kappa$) with the Hamiltonian flow of $\sqrt{\rho }$ on ${\tilde{M}}^\tau {\setminus } M$ with respect to $\Omega$. Neither flow is generally holomorphic (of course, the former is if and only if so is the latter).

Recall that we identify TM and $T^\vee M$ by means of $\kappa$.

Lemma 12

The canonical 1-form $\lambda _{can}$ on $T^\vee M$ is invariant under the homogenous geodesic flow. Similarly, $\alpha$ in (8) is invariant under the flow of $\upsilon _{\sqrt{\rho }}$.

Proof

The two statements are equivalent by (7). To verify the former, we may work in a local coordinate chart (q, p) for the cotangent bundle associated to a system of local coordinates q for M. Let $K=(\kappa ^{ij})$, where $\kappa ^{ij}=\kappa ^{ij}(q)$, denote the inverse metric tensor, and set $\varrho :=\Vert \cdot \Vert ^2$; then

$$\begin{aligned} \sqrt{\varrho } =\sqrt{\kappa ^{ij}p_i\,p_j}=\sqrt{p^t\,K\,p}. \end{aligned}$$

Since locally $\Omega _{can}=\textrm{d}q\wedge \textrm{d}p$, the Hamiltonian vector field of $\sqrt{\rho }$ is

$$\begin{aligned} V_{\sqrt{\varrho }}= & {} \left( \frac{\partial \sqrt{\varrho }}{\partial p}\right) ^t\,\frac{\partial }{\partial q}-\left( \frac{\partial \sqrt{\varrho }}{\partial q}\right) ^t\,\frac{\partial }{\partial p}\nonumber \\= & {} \frac{1}{\sqrt{\varrho }}\,(p^t\,K)\,\,\frac{\partial }{\partial q}- \left( \frac{\partial \sqrt{\varrho }}{\partial q}\right) ^t\,\frac{\partial }{\partial p}. \end{aligned}$$

Since locally $\lambda _{can}=p\,\textrm{d}q$,

$$\begin{aligned} \iota (V_{\sqrt{\varrho }})\,\lambda _{can}= \frac{1}{\sqrt{\varrho }}\,(p^t\,K\,p)=\sqrt{\varrho }. \end{aligned}$$

Hence the Lie derivative of $\lambda _{can}$ along $V_{\sqrt{\varrho }}$ is

$$\begin{aligned} L_{V_{\sqrt{\varrho }}}(\lambda _{can})=\textrm{d}\big (\iota (V_{\sqrt{\varrho }})\,\lambda _{can}\big )-\iota (V_{\sqrt{\varrho }})\,\Omega =\textrm{d}\sqrt{\varrho }-\textrm{d}\sqrt{\varrho }=0. \end{aligned}$$

$\square$

For a more general statement, see Lemma 22.

3.2.2 The Reeb vector field of (M, k)

As shown in [17], the condition that $\sqrt{\rho }$ satisfies the complex Monge–Ampère equation may be reformulated in terms of the norm of the gradient $\textrm{grad}_\rho$ of $\rho$. Let us briefly recall the argument in [17]. Let $\Xi \in {\mathfrak {X}}({\tilde{M}})$ be defined by the identity

$$\begin{aligned} \iota (\Xi )\,\Omega =\alpha . \end{aligned}$$

(31)

Then $\Xi$ is the gradient vector field with respect to ${\hat{\kappa }}$ of $\rho /2$, that is,

$$\begin{aligned} \Xi =\frac{1}{2}\, J(\upsilon _\rho )=\frac{1}{2}\, \textrm{grad}_{\rho }. \end{aligned}$$

Lemma 13

(Guillemin and Stenzel) The following conditions are equivalent:

• 1. $\sqrt{\rho }$ satisfies the homogeneous complex Monge–Ampère equation on ${\tilde{M}}{\setminus } M$;

• 2. $\Xi (\rho )=2\,\rho$.

Proof

(See [17]) Given $f\in {\mathcal {C}}^\infty ({\mathbb {R}}_+)$, let us consider the composition $f(\rho ):{\tilde{M}}{\setminus } M\rightarrow {\mathbb {R}}$. We have

$$\begin{aligned} \partial \,{\overline{\partial }}f(\rho )= & {} \partial \left[ f'(\rho )\,{\overline{\partial }}\rho \right] \nonumber \\= & {} f''(\rho )\,\partial \rho \wedge \,{\overline{\partial }}\rho +f'(\rho )\, \partial \,{\overline{\partial }}\rho \nonumber \\= & {} f''(\rho )\,\partial \rho \wedge \,{\overline{\partial }}\rho -\imath \,f'(\rho )\, \Omega . \end{aligned}$$

(32)

Furthermore,

$$\begin{aligned} \textrm{d}\rho \wedge \alpha= & {} \frac{1}{2\,\imath }\,\left( \partial \rho +{\overline{\partial }}\rho \right) \wedge \left( \partial \rho -{\overline{\partial }}\rho \right) \nonumber \\= & {} \frac{1}{2\,\imath }\, \left( -2\,\partial \rho \wedge {\overline{\partial }}\rho \right) \nonumber \\= & {} -\frac{1}{\imath }\,\partial \rho \wedge {\overline{\partial }}\rho \nonumber \\= & {} \imath \,\partial \rho \wedge {\overline{\partial }}\rho . \end{aligned}$$

(33)

Hence

$$\begin{aligned} \left[ \partial \,{\overline{\partial }}f(\rho )\right] ^d= & {} (-\imath )^d\,f'(\rho )^d\, \Omega ^d+d\,(-\imath )^{d-1}\,f''(\rho )\,f'(\rho )^{d-1} \,\partial \rho \wedge \,{\overline{\partial }}\rho \wedge \Omega ^{d-1}\nonumber \\= & {} (-\imath )^d\,f'(\rho )^d\, \Omega ^d+d\,(-\imath )^{d}\,f''(\rho )\,f'(\rho )^{d-1} \,\textrm{d}\rho \wedge \alpha \wedge \Omega ^{d-1}\nonumber \\= & {} (-\imath )^d\,f'(\rho )^d\,\left[ \Omega ^d+d\,\frac{f''(\rho )}{f'(\rho )}\, \textrm{d}\rho \wedge \alpha \wedge \Omega ^{d-1}. \right] \end{aligned}$$

(34)

On the other hand,

$$\begin{aligned} \iota (\Xi )\,\Omega ^d=d\cdot \iota (\Xi )\Omega \wedge \Omega ^{d-1}= d\cdot \alpha \wedge \Omega ^{d-1}. \end{aligned}$$

Therefore

$$\begin{aligned} \left[ \partial \,{\overline{\partial }}f(\rho )\right] ^d= & {} (-\imath )^d\,f'(\rho )^d\,\left[ \Omega ^d+\frac{f''(\rho )}{f'(\rho )}\, \textrm{d}\rho \wedge \iota (\Xi )\,\Omega ^d \right] . \end{aligned}$$

(35)

Furthermore, since $\textrm{d}\rho \wedge \Omega ^d=0$

$$\begin{aligned} 0=\iota (\Xi )\,\left( \textrm{d}\rho \wedge \Omega ^d\right) = \textrm{d}\rho (\Xi )\,\Omega ^d-\textrm{d}\rho \wedge \iota (\Xi )\,\Omega ^d. \end{aligned}$$

(36)

We conclude

$$\begin{aligned} \left[ \partial \,{\overline{\partial }}f(\rho )\right] ^d= & {} (-\imath )^d\,f'(\rho )^d\,\left[ \Omega ^d+\frac{f''(\rho )}{f'(\rho )}\, \textrm{d}\rho (\Xi )\,\Omega ^d \right] \nonumber \\= & {} (-\imath )^d\,f'(\rho )^d\,\left[ 1+\frac{f''(\rho )}{f'(\rho )}\, \textrm{d}\rho (\Xi ) \right] \,\Omega ^d. \end{aligned}$$

(37)

If $f=\sqrt{\cdot }$, then

$$\begin{aligned} f'(x)=\frac{1}{2}\,x^{-1/2},\quad f''(x)=-\frac{1}{4}\,x^{-3/2}\quad \Rightarrow \quad \frac{f''(x)}{f'(x)}=-\frac{1}{4}\,x^{-3/2}\,2\,x^{1/2}= -\frac{1}{2\,x}. \end{aligned}$$

Summing up,

$$\begin{aligned} \left[ \partial \,{\overline{\partial }}f(\rho )\right] ^d= & {} (-\imath )^d\,f'(\rho )^d\,\left[ \Omega ^d+\frac{f''(\rho )}{f'(\rho )}\, \textrm{d}\rho (\Xi )\,\Omega ^d \right] \nonumber \\= & {} (-\imath )^d\,f'(\rho )^d\,\left[ 1-\frac{1}{2\,\rho }\, \textrm{d}\rho (\Xi ) \right] \,\Omega ^d, \end{aligned}$$

(38)

which vanishes if and only if $\textrm{d}\rho (\Xi )=2\,\rho$.

$\square$

Corollary 14

With $\Xi$ as in (31), the square norm of $\Xi$ with respect to ${\hat{\kappa }}$ is $\Vert \Xi \Vert _{{\hat{\kappa }}}^2=\rho$.

Corollary 15

$\alpha (\upsilon _\rho )=-2\,\rho$.

Proof

Since $\textrm{grad}_\rho =J(\upsilon _\rho )$,

$$\begin{aligned} 4\,\rho =\Vert \textrm{grad}_\rho \Vert _{{\hat{\kappa }}}^2= & {} \textrm{d}\rho (\textrm{grad}_\rho )=\left( \partial \rho +{\overline{\partial }}\rho \right) (J\,\upsilon _\rho )\nonumber \\= & {} \imath \,\left( \partial \rho (\upsilon _\rho )- {\overline{\partial }}\rho (\upsilon _\rho )\right) = -2\,\alpha (\upsilon _\rho ). \end{aligned}$$

(39)

$\square$

Definition 16

Let us set

$$\begin{aligned} {\mathcal {R}}:=-\frac{\upsilon _{\rho /2}}{\rho }= -\frac{\upsilon _{\rho }}{2\,\rho }=\frac{1}{\rho }\, J(\Xi ) \in {\mathfrak {X}}({\tilde{M}}{\setminus } M). \end{aligned}$$

(40)

We shall call ${\mathcal {R}}$ in (40) the Reeb vector field of $(M,\kappa )$.

Corollary 17

${\mathcal {R}}$ is uniquely determined in ${\mathfrak {X}}({\tilde{M}}{\setminus } M)$ by the conditions

• 1. $\alpha ({\mathcal {R}})=1$;

• 2. ${\mathcal {R}}\in {\mathcal {C}}^\infty ({\tilde{M}}{\setminus } M)\,\upsilon _\rho$.

The motivation for this definition is the following. Suppose $\tau \in (0,\epsilon )$. Since ${\mathcal {R}}$ is tangent to $X^\tau$, it restricts to a vector field ${\mathcal {R}}^\tau \in {\mathfrak {X}}(X^\tau )$. Furthermore, the Lie derivative

$$\begin{aligned} L_{\mathcal {R}}(\alpha )=\iota ({\mathcal {R}})\,\Omega +\textrm{d}(1)=-\frac{1}{2\,\rho } \,\textrm{d}\rho \end{aligned}$$

(41)

has vanishing pull-back to $X^\tau$; therefore $L_{{\mathcal {R}}^\tau }(\alpha ^\tau )=0$. In other words, ${\mathcal {R}}^\tau \in {\mathfrak {X}}(X^\tau )$ is the (genuine) Reeb vector field of $(X^\tau ,\alpha ^\tau )$. We also have

$$\begin{aligned} {\mathcal {R}}=-\frac{1}{\sqrt{\rho }}\,\upsilon _{\sqrt{\rho }}. \end{aligned}$$

(42)

Corollary 14 implies:

$$\begin{aligned} \Vert \upsilon _{\sqrt{\rho }}\Vert _{{\hat{\kappa }}}^2=1,\quad \Vert {\mathcal {R}}\Vert _{{\hat{\kappa }}}^2=\frac{1}{\rho }, \end{aligned}$$

(43)

hence $\sqrt{\rho }$ is a ‘distance function’  on ${\tilde{M}}{\setminus } M$ for ${\hat{\kappa }}$ (in the terminology of §3.2.2 of [33]). In fact, while the flow of $\upsilon _{\sqrt{\rho }}$ is intertwined by $E^\tau$ with the homogeneous geodesic flow, the trajectories of the gradient vector field $\textrm{grad}_{\sqrt{\rho }}=J(\upsilon _{\sqrt{\rho }} )$ are unit speed geodesics for ${\hat{\kappa }}$, perpendicular to the hypersurfaces $X^\tau$ and minimizing the distance between them (see §3 of [23]). By (42), the flows of ${\mathcal {R}}^\tau$ and $\upsilon _{\sqrt{\rho }}^\tau$ on $X^\tau$ are related by a rescaling by the factor $-1/\tau$ in the time variable.

3.2.3 The volume form on $X^\tau$

Suppose $\tau '>0$ is sufficiently small. Then the Riemannian volume form on the Kähler manifold $({\tilde{M}}^{\tau '},\Omega ,J)$ is

$$\begin{aligned} \textrm{vol}_{{\tilde{M}}^{\tau '}}:=\frac{1}{d!}\,\Omega ^{\wedge d}; \end{aligned}$$

it pulls back under $E^{\tau '}$ to the symplectic volume form $\textrm{vol}_{can}:=\frac{1}{d!}\,\Omega _{can}^{\wedge d}$ (here we omit restriction symbols to open sets for notational simplicity).

Suppose $\tau \in (0,\tau ')$. There are various natural alternatives in the literature for a volume form on $X^\tau$; different choices yield the same topology, but alter the construction of certain adjoint operators. Let us dwell to specify the choice in this paper.

Given that that $\textrm{grad}_{\sqrt{\rho }}$ is a unit normal vector field to $X^\tau$ by (43), the Riemannian volume form is

$$\begin{aligned} \textrm{vol}^R_{X^\tau }:= & {} {\jmath ^\tau }^*\left( \iota (\textrm{grad}_{\sqrt{\rho }})\,\textrm{vol}_{{\tilde{M}}^{\tau '}}\right) \nonumber \\= & {} {\jmath ^\tau }^*\left( \iota (\textrm{grad}_{\sqrt{\rho }})\,\Omega \wedge \frac{1}{(d-1)!}\,\Omega ^{\wedge (d-1)}\right) . \end{aligned}$$

(44)

An alternative choice is the contact volume form

$$\begin{aligned} \textrm{vol}^C_{X^\tau }:={\jmath ^\tau }^*\left( \alpha \wedge \frac{1}{(d-1)!}\,\Omega ^{\wedge (d-1)} \right) . \end{aligned}$$

(45)

Let us clarify the relation between $\textrm{vol}^R_{X^\tau }$ and $\textrm{vol}^C_{X^\tau }$.

Lemma 18

$\alpha =\sqrt{\rho }\,\iota (\textrm{grad}_{\sqrt{\rho }})\,\Omega =\frac{1}{2}\,\iota (\textrm{grad}_\rho )\,\Omega$.

Proof

The two equalities are clearly equivalent. As to the latter,

$$\begin{aligned} \iota (\textrm{grad}_\rho )\,\Omega= & {} \Omega (\textrm{grad}_\rho ,\cdot ) =\Omega (J\upsilon _\rho ,\cdot )=-\Omega (\upsilon _\rho ,J\cdot ) =-\textrm{d}\rho \circ J\\= & {} -\imath \,\left( \partial \rho -{\overline{\partial }}\rho \right) =2\,\alpha . \end{aligned}$$

$\square$

Corollary 19

$\textrm{vol}^C_{X^\tau }=\tau \cdot \textrm{vol}^R_{X^\tau }$.

Our choice for a volume form on $X^\tau$ will be $\textrm{vol}^R_{X^\tau }$. Let us consider its homogeneity properties. For $\lambda >0$ let $\delta _\lambda :T^\vee M\rightarrow T^\vee M$ denote fibrewise dilation by $\lambda$. Then $\delta _\lambda$ is intertwined with a diffeomorphism $\delta '_\lambda : M^{\epsilon /\lambda }\rightarrow M^\epsilon$.

Let $\Xi _{can}\in {\mathfrak {X}}(T^\vee M)$ be the vector field correlated with $\Xi$ by $E^\tau$. Since locally $\Omega =\textrm{d}q\wedge \textrm{d}p$ and $\alpha =-p\,\textrm{d}q$, we have

$$\begin{aligned} \iota (\Xi _{can})\,\Omega _{can}=\alpha _{can}\,\Rightarrow \Xi _{can}=p\,\frac{\partial }{\partial p}, \end{aligned}$$

which is homogeneous of degree zero with respect to $\delta _\lambda$. Therefore the same holds of $\Xi$ with respect to $\delta '_\lambda$. Since $\sqrt{\rho }$ is homogenous of degree 1,

$$\begin{aligned} \textrm{grad}_{\sqrt{\rho }}=\frac{1}{\sqrt{\rho }}\,\Xi \end{aligned}$$

is homogenous of degree $-1$. Hence by (44) $\textrm{vol}^R_{X^\tau }$ is homogeneous of degree $d-1$ in $\tau$. We conclude

Lemma 20

For a constant $D>0$, $\textrm{Vol}^R(X^\tau ):=\int _{X^\tau }\textrm{vol}^R_{X^\tau }=D\,\tau ^{d-1}$.

3.2.4 Induced vector fields and Hamiltonians

For any sufficiently small $\tau >0$, the Kähler structure makes $T{\tilde{M}}^\tau$ into a complex Hermitian vector bundle. Being everywhere non-vanishing, $\upsilon _{\sqrt{\rho }}$ spans on ${\tilde{M}}^\tau {\setminus } M$ a 1-dimensional complex subbundle ${\mathcal {V}}$ of $(T{\tilde{M}}^\tau ,J)$:

$$\begin{aligned} {\mathcal {V}}_x:= \textrm{span}_{\mathbb {C}}\big (\upsilon _{\sqrt{\rho }}(x) \big ) =\textrm{span}_{{\mathbb {R}}}\big (\upsilon _{\sqrt{\rho }}(x),\, \textrm{grad}_{\sqrt{\rho }}(x) \big ) \qquad (x\in {\tilde{M}}^\tau {\setminus } M). \end{aligned}$$

Hence there is on ${\tilde{M}}^\tau {\setminus } M$ a decomposition of $(T{\tilde{M}},J)$ as the orthogonal direct sum of complex vector sub-bundles

$$\begin{aligned} T{\tilde{M}}={\mathcal {V}}\oplus {\mathcal {H}},\quad \text {where}\quad {\mathcal {H}}:= {\mathcal {V}}^{\perp }. \end{aligned}$$

(46)

Let ${\mathcal {T}}\subset {\mathcal {V}}$ be the real vector subbundle generated on ${\tilde{M}}^\tau {\setminus } M$ by $\upsilon _{\sqrt{\rho }}$; thus

$$\begin{aligned} {\mathcal {T}}\oplus {\mathcal {H}}=\ker (\textrm{d}\rho ) \subset T{\tilde{M}}^\tau . \end{aligned}$$

(47)

The ${\mathcal {C}}^\infty$ sections of ${\mathcal {T}}\oplus {\mathcal {H}}$ are the smooth vector fields that are tangent to $X^\tau$, for every $\tau \in (0,\tau _{max})$. The decomposition (47) restricts to a corresponding orthogonal direct sum decomposition for the tangent bundle $TX^\tau$:

$$\begin{aligned} T X^\tau = {\mathcal {T}}^\tau \oplus {\mathcal {H}}^\tau , \end{aligned}$$

(48)

where ${\mathcal {T}}^\tau :={\jmath ^\tau }^*({\mathcal {T}})$ and ${\mathcal {H}}^\tau :={\jmath ^\tau }^*({\mathcal {H}})$. If $x\in X^\tau$, ${\mathcal {T}}^\tau (x)=\textrm{span}_{\mathbb {R}}\big ({\mathcal {R}}^\tau (x)\big )$, and ${\mathcal {H}}^\tau (x)$ is the maximal complex subspace of $T_xX^\tau$.

Lemma 21

We have

$$\begin{aligned} J({\mathcal {T}})\oplus {\mathcal {H}}=\ker (\alpha ),\quad {\mathcal {H}}^\tau =\ker (\alpha ^\tau ). \end{aligned}$$

Proof

Suppose $x\in {\tilde{M}}^\epsilon {\setminus } M$ and decompose ${\mathcal {R}}_x$ according to the complex structure: ${\mathcal {R}}_x={\mathcal {R}}_x^{1,0}+{\mathcal {R}}_x^{0,1}$. Since $\textrm{d}\rho ({\mathcal {R}})=0$,

$$\begin{aligned} 2\,\imath \,\alpha _x\big (J_x({\mathcal {R}}_x)\big )= & {} \imath \,\left( \partial _x\rho -{\overline{\partial }}_x\rho \right) \left( {\mathcal {R}}_x^{1,0}-{\mathcal {R}}_x^{0,1}\right) \nonumber \\= & {} \imath \,\left[ \partial _x\rho \left( {\mathcal {R}}_x^{1,0}\right) + {\overline{\partial }}_x\rho \left( {\mathcal {R}}_x^{0,1}\right) \right] =\imath \,\textrm{d}_x\rho ({\mathcal {R}}_x)=0. \end{aligned}$$

(49)

Hence $J_x({\mathcal {T}}_x)\subseteq \ker (\alpha _x)$. One argues similarly for ${\mathcal {H}}$. $\square$

For a vector bundle ${\mathcal {E}}$ on ${\tilde{M}}^\epsilon {\setminus } M$, let $\Gamma ({\mathcal {E}})$ be the space of its smooth sections. Any $V\in \Gamma ({\mathcal {T}}\oplus {\mathcal {H}})=\Gamma ({\mathcal {T}})\oplus \Gamma ({\mathcal {H}})\subseteq {\mathfrak {X}}({\tilde{M}}^\epsilon {\setminus } M)$ may be uniquely decomposed as

$$\begin{aligned} V=V^\sharp -\varphi \,{\mathcal {R}}, \end{aligned}$$

(50)

where, since $\alpha ({\mathcal {R}})=1$,

$$\begin{aligned} \varphi :=-\alpha (V)\in {\mathcal {C}}^\infty ({\tilde{M}}{\setminus } M),\quad V^\sharp \in \Gamma ({\mathcal {H}}). \end{aligned}$$

Then

$$\begin{aligned} L_V(\alpha )=\iota (V)\,\Omega -\textrm{d}\varphi . \end{aligned}$$

This implies the following.

Lemma 22

Let $V\in \Gamma ({\mathcal {T}}\oplus {\mathcal {H}})$ be as in (50). Then the following conditions are equivalent:

• 1. $L_V\alpha =0$;

• 2. V is the Hamiltonian vector field of $\varphi =-\alpha (V)$ with respect to $\Omega$.

Since $\upsilon _{\sqrt{\rho }}=-\sqrt{\rho }\,{\mathcal {R}}$ by (42), Lemma 22 generalizes Lemma 12.

3.3 Heisenberg local coordinates

As emphasized in the Sect. 1, Chang and Rabinowitz in [10] and [11] considerably simplified the application of the ideas and techniques from the line bundle setting in [1, 35, 42] to the Grauert tube context, and their approach is partly based on Folland and Stein’s construction of Heisenberg local coordinates for a strictly pseudoconvex hypersurface in a complex manifold [13, 14].

3.3.1 Heisenberg-type order

The notion of Heisenberg local coordinates on a complex manifold adapted to a strictly pseudoconvex hypersurface rests on the concept of Heisenberg-type order of vanishing of a smooth function at a given point with respect to a local holomorphic chart [13, §14 and §18].

Suppose $x\in {\tilde{M}}$ and let $(U,\varphi ,A)$ be a local holomorphic chart for ${\tilde{M}}$ centered at x; thus U is an open neighborhood of x in ${\tilde{M}}$, and $A\subseteq {\mathbb {C}}^d$ is open. Let us write $\varphi =(z_0,z_1,\ldots ,z_{d-1})$, where $z_j:U\rightarrow {\mathbb {C}}$.

Definition 23

Let ${\mathfrak {J}}_x({\tilde{M}})$ be the ring of germs of (non necessarily smooth, real or complex) functions on ${\tilde{M}}$ at x, and let ${\mathfrak {m}}_x({\tilde{M}})\unlhd {\mathfrak {J}}_x({\tilde{M}})$ be the ideal of those germs that vanish at x. Let ${\mathcal {C}}^\infty ({\tilde{M}})_x\subseteq {\mathfrak {J}}_x({\tilde{M}})$ be the subring of germs of smooth functions. Suppose $f\in {\mathfrak {m}}_x({\tilde{M}})$. Then

• 1. f is said to be $O_\varphi ^1$ if, for ${\tilde{M}}\ni y\sim x$,

  $$\begin{aligned} f(y)=O\left( \sum _{j=1}^{d-1}|z_j(y)|+|z_0(y)|^{1/2}\right) ; \end{aligned}$$

• 2. ${\mathfrak {O}}_\varphi ^1({\tilde{M}}):=\left\{ f\in {\mathfrak {m}}_x({\tilde{M}})\,:\, f \text {is} O_\varphi ^1 \right\}$;

• 3. inductively, for $k\ge 2$ we define ${\mathfrak {O}}_\varphi ^k({\tilde{M}}):={\mathfrak {O}}_\varphi ^{k-1}({\tilde{M}})\cdot {\mathfrak {O}}_\varphi ^1({\tilde{M}})$;

• 4. for any integer $k\ge 2$, f is said to be $O_\varphi ^k$ if $f\in {\mathfrak {O}}_\varphi ^k({\tilde{M}})$;

• 5. finally, ${\mathfrak {C}}_\varphi ^k({\tilde{M}}):={\mathcal {C}}^\infty ({\tilde{M}})_x \cap {\mathfrak {O}}_\varphi ^k({\tilde{M}})$.

For example, if $x_j:=\Re (z_j)$ and $y_j:=\Im (z_j)$ then $\sqrt{|x_0|},\,\sqrt{|y_0|}\in {\mathfrak {O}}_\varphi ^1({\tilde{M}})$; therefore, $x_0=\textrm{sgn}(x_0)\,\sqrt{|x_0|}\cdot \sqrt{|x_0|}\in {\mathfrak {C}}_\varphi ^2(M)$, and similarly for $y_0$ and $z_0$. For every $k\ge 1$, we have $|x_0|^{\frac{k+1}{2}}=|x_0|^{\frac{k}{2}}\cdot |x_0|^{\frac{1}{2}}$, and it follows inductively that $|x_0|^{\frac{l}{2}}\in {\mathfrak {O}}_\varphi ^l({\tilde{M}})$ for every $l\ge 1$. On the other hand, $x_j,\,y_j\in {\mathfrak {C}}_\varphi ^1({\tilde{M}})$ for every $j\ge 1$, and one obtains inductively that $x_j^l\in {\mathfrak {C}}_\varphi ^l({\tilde{M}})$ for every $l\ge 1$.

We shall occasionally abridge the notation ${\mathfrak {O}}_\varphi ^k({\tilde{M}})$ to ${\mathfrak {O}}_\varphi ^k$. By the inductive definition,

$$\begin{aligned} {\mathfrak {O}}_\varphi ^k= \underbrace{{\mathfrak {O}}_\varphi ^1\cdot {\mathfrak {O}}_\varphi ^1\cdots {\mathfrak {O}}_\varphi ^1}_{k \,\text {times}}, \end{aligned}$$

(51)

i.e. any $f\in {\mathfrak {O}}_\varphi ^k$ is a (finite) linear combination of products $f_1\cdots f_k$ with $f_j\in {\mathfrak {O}}_\varphi ^1$.

Corollary 24

${\mathfrak {O}}_\varphi ^k\cdot {\mathfrak {O}}_\varphi ^l ={\mathfrak {O}}_\varphi ^{k+l}$ for any $k,l\ge 1$.

Let us set $z':=(z_1,\ldots ,z_{d-1}):U\rightarrow {\mathbb {C}}^{d-1}$; thus $\varphi =(z_0,\,z')$.

Lemma 25

Suppose $f\in {\mathfrak {m}}_x({\tilde{M}})$ Then the following conditions are equivalent:

• 1. $f\in {\mathfrak {O}}_\varphi ^k$;

• 2. $f(y)=O\left( |z'(y)|^k+|z_0(y)|^{k/2}\right)$ for ${\tilde{M}}\ni y\sim x$.

Proof

Let $0<d_k<D_k$ be constants, depending only on $k\ge 1$, such that for any pair $a,b\ge 0$ one has

$$\begin{aligned} d_k\,(a^k+b^k)\le (a+b)^k\le D_k\,(a^k+b^k). \end{aligned}$$

Suppose $f\in {\mathfrak {O}}_\varphi ^k$. Then f is a sum of products of the form $f_1\cdots f_k$ with each $f_j\in {\mathfrak {O}}_\varphi ^1$. We may thus assume that f itself is of this form. Hence there is a constant $C>0$ (depending on f) such that

$$\begin{aligned} |f_j(y)|\le C\,\left( |z'(y)|+|z_0(y)|^{1/2}\right) \qquad (j=1,\ldots ,k); \end{aligned}$$

therefore

$$\begin{aligned} |f(y)|\le & {} C^k\,\left( |z'(y)|+|z_0(y)|^{1/2}\right) ^k\\\le & {} C^k\,D_k\,\left( |z'(y)|^k+|z_0(y)|^{k/2}\right) . \end{aligned}$$

Hence 2. holds.

Conversely, assume that 2. holds. Then $f\in {\mathfrak {O}}_\varphi ^1$ by definition for $k=1$. Suppose that $k\ge 2$. Then

$$\begin{aligned} f(y)=O\left( |z'(y)|^k+|z_0(y)|^{k/2}\right) =O\left( (|z'(y)|+|z_0(y)|^{1/2})^k\right) . \end{aligned}$$

In some neighbourhood U of x in ${\tilde{M}}$, let us define $g:U\rightarrow {\mathbb {C}}$ by

$$\begin{aligned} g(y):=\frac{f(y)}{\left( |z'(y)|+|z_0(y)|^{1/2}\right) ^{k-1}}\quad \text {if } y\ne x;\quad g(x)=0. \end{aligned}$$

When $y\ne x$,

$$\begin{aligned} |g(y)|\le \frac{C\,\left( |z'(y)|+|z_0(y)|^{1/2}\right) ^k}{\left( |z'(y)|+|z_0(y)|^{1/2}\right) ^{k-1}}= C\,\left( |z'(y)|+|z_0(y)|^{1/2}\right) . \end{aligned}$$

Hence $g\in {\mathfrak {O}}_\varphi ^1$, and

$$\begin{aligned} f(y)=g(y)\cdot \left( |z'(y)|+|z_0(y)|^{1/2}\right) ^{k-1}. \end{aligned}$$

Thus $f\in {\mathfrak {O}}_\varphi ^1\cdot {\mathfrak {O}}_\varphi ^{k-1}= {\mathfrak {O}}_\varphi ^{k}$.

$\square$

Let us focus on ${\mathfrak {C}}_\varphi ^{k}$.

Definition 26

For ${\textbf{a}},\,{\textbf{b}}\in {\mathbb {Z}}_{\ge 0}^d$, consider the monomial function of $z:=\begin{pmatrix} z_0&\cdots&z_{d-1} \end{pmatrix}\in {\mathbb {C}}^d$ given by

$$\begin{aligned} P_{{\textbf{a}},{\textbf{b}}}(z):= z_0^{a_0}\,{\overline{z}}_0^{b_0}\,\prod _{j=1}^{d-1} z_j^{a_j}\,{\overline{z}}_j^{b_j}. \end{aligned}$$

(52)

The weighted degree of $P_{{\textbf{a}},{\textbf{b}}}$ is

$$\begin{aligned} \textrm{wdg}(P_{{\textbf{a}},{\textbf{b}}}):= 2\,(a_0+b_0)+\sum _{j=1}^{d-1}(a_j+b_j). \end{aligned}$$

Proposition 27

Suppose $f\in {\mathcal {C}}^\infty (M)_x$. Then the following conditions are equivalent.

• 1. $f\in {\mathfrak {C}}^k_\varphi$;

• 2. every monomial contributing to the Taylor expansion of $f\circ \varphi ^{-1}$ at ${\textbf{0}}$ has weighted degree $\ge k$.

If $M={\mathbb {C}}^d$, $U=A\subseteq {\mathbb {C}}^d$ is open and $\varphi =\textrm{id}_A$, we shall write ${\mathfrak {C}}^k$ for ${\mathfrak {C}}_\varphi ^{k}$. Since in the general setting $f\in {\mathfrak {C}}_\varphi ^{k}$ if and only if $f\circ \varphi ^{-1}\in {\mathfrak {C}}^k$, we may identify U with A and work directly on $A\subseteq {\mathbb {C}}^d$ (and prove the statement for ${\mathfrak {C}}^k$).

Proof

We may assume without loss that $A=D({\textbf{0}},{\textbf{r}})$ is a polydisc centered at the origin, of multiradius ${\textbf{r}}=(r_0,\ldots ,r_{d-1})$, with $r_0\in (0,1]$. Let us denote the linear complex coordinates on A by $(w_0,w_1,\ldots ,w_{d-1})=(w_0,w')$.

Let $h:A\rightarrow A$ be given by

$$\begin{aligned} h(w_0,w_1,\ldots ,w_{d-1}):= \left( w_0^2,w_1,\ldots ,w_{d-1} \right) =(w_0^2,w'). \end{aligned}$$

A monomial $P_{{\textbf{a}},{\textbf{b}}}(z)$ pulls back to

$$\begin{aligned} h^*( P_{{\textbf{a}},{\textbf{b}}})(w)= w_0^{2\,a_0}\,{\overline{w}}_0^{2\,b_0}\,\prod _{j=1}^{d-1} w_j^{a_j}\,{\overline{w}}_j^{b_j}; \end{aligned}$$

(53)

hence

$$\begin{aligned} \textrm{deg}\left( h^*( P_{{\textbf{a}},{\textbf{b}}})\right) = 2\,(a_0+b_0)+\sum _{j=1}^{d-1}(a_j+b_j)=\textrm{wdg}(P_{{\textbf{a}},{\textbf{b}}}). \end{aligned}$$

On the other hand, if f is a germ of smooth function at the origin on ${\mathbb {C}}^d$, then the Taylor expansion of $f\circ h$ a the origin is the pull-back by h of the one of f. Hence 2. holds if and only if the Taylor expansion of $f\circ h$ only contains monomials of degree $\ge k$, i.e. if $f\circ h$ vanishes to k-th order at the origin.

Assume $f\in {\mathfrak {C}}^{k}$. Then $f\circ h$ is smooth and by Lemma 25

$$\begin{aligned} f\circ h(w)=O\left( |w'|^k+|w_0|^k\right) \end{aligned}$$

for $w\sim 0$; hence the Taylor expansion of $f\circ h$ at ${\textbf{0}}$ only contains terms of degree $\ge k$, i.e. 2. holds.

Suppose, conversely, that 2. holds; equivalently, the Taylor expansion of $f\circ h$ at the origin only contains monomials of degree $\ge k$. Hence on a neighbourhood of the origin

$$\begin{aligned} |f\circ h(w)| \le C\,\left( |w'|^k+|w_0|^k\right) \end{aligned}$$

for some constant $C>0$. If $z=h(w)$, this means

$$\begin{aligned} |f(z)|\le C\,\left( |z'|^k+|z_0|^{k/2}\right) , \end{aligned}$$

so that $f\in {\mathfrak {C}}^k$.

$\square$

3.3.2 Heisenberg type order and holomorphic extensions

A notational clarification is in order. Consider a d-dimensional complex manifold Z, with complex structure J. We shall denote by ${\overline{Z}}$ the conjugate complex manifold (that is, ${\overline{Z}}=Z$ as differentiable manifolds, but with complex structure $-J$). In particular, let $J_0$ be the standard complex structure on ${\mathbb {C}}^d$; an open subset $A\subseteq {\mathbb {C}}^d$ is a complex manifold with the induced complex structure, which shall also be denoted $J_0$. Then ${\overline{A}}$ is the same open subset, endowed with the complex structure $-J_0$.

On the other hand, let $c:{\mathbb {C}}^d\rightarrow {\mathbb {C}}^d$ denote complex conjugation. We shall set $A^c:=c(A)$, with the complex structure $J_0$. Then c yields by restriction an anti-holomorphic diffeomorphism $c:A\rightarrow A^c$, or equivalently a biholomorphism $c:{\overline{A}}\rightarrow A^c$.

Consider a holomorphic local chart $(U,\varphi ,A)$ of Z; thus $U\subseteq Z$ is an open subset with the complex structure J and $\varphi :U\rightarrow A$ is a biholomorphism for J and $J_0$. We obtain two ‘holomorphic charts’  for ${\overline{Z}}$, both defined on U: $({\overline{U}},\varphi ,{\overline{A}})$, and $({\overline{U}},c\circ \varphi , A^c)$ (to be precise, both are biholomorphisms, but only the latter is a genuine holomorphic chart).

Suppose $f\in {\mathcal {O}}({\overline{U}})$, that is, $f:U\rightarrow {\mathbb {C}}$ is $(-J)$-holomorphic. Then $f\circ \varphi ^{-1}: {\overline{A}}\rightarrow {\mathbb {C}}$ is holomorphic on ${\overline{A}}$; hence it locally admits a power series expansion in the conjugate variables ${\overline{z}}_j$’s. Instead, $f\circ ( c\circ \varphi )^{-1}=(f\circ \varphi ^{-1})\circ c$ is holomorphic on $A^c$; hence it locally admits a power series expansion in the standard variables $z_j$’s.

The diagonal $\Delta \subset {\tilde{M}}\times \overline{{\tilde{M}}}$ is a totally real submanifold, real-analytically diffeomorphic to ${\tilde{M}}$. Let $(U,\varphi ,A)$ be holomorphic local chart for M centered at x. Then $(U\times {\overline{U}},\varphi \times \varphi ,A\times {\overline{A}})$ is a ‘holomorphic local chart’  for ${\tilde{M}}\times \overline{{\tilde{M}}}$ centered at (x, x). Let $z_j$ and $u_j$ denote, respectively, the standard complex linear coordinates on the two factors of ${\mathbb {C}}^d\times {\mathbb {C}}^d$, respectively. If $F:{\tilde{M}}\times \overline{{\tilde{M}}}\rightarrow {\mathbb {C}}$ is holomorphic, then $F\circ (\varphi \times \varphi )^{-1}$ can be expanded in a power series in the $z_j$’s and the ${\overline{u}}_j$’s.

Any real-analytic function f on ${\tilde{M}}$ may be viewed as a real-analytic function on $\Delta$; as such, it has a holomorphic extension ${\tilde{f}}$ to an open neighborhood of $\Delta$ in ${\tilde{M}}\times \overline{{\tilde{M}}}$. Suppose that $f\in {\mathfrak {C}}^k_\varphi$ for some $k\ge 1$. By Proposition 27, the only contributions to the power series expansion of $f\circ \varphi ^{-1}\in {\mathfrak {C}}^k$ come from monomials (52) such that $2\,(a_0+b_0)+\sum _{j=1}^{d-1}(a_j+b_j)\ge k$. On the other hand, the holomorphic extension of (52) to ${\mathbb {C}}^d\times \overline{{\mathbb {C}}^d}$ has the form

$$\begin{aligned} z_0^{a_0}\,{\overline{u}}_0^{b_0}\,\prod _{j=1}^{d-1} z_j^{a_j}\,{\overline{u}}_j^{b_j}. \end{aligned}$$

(54)

When we match Heisenberg type ordering with holomorphic extension of real analytic functions, we are thus led to introduce the following two rings.

Definition 28

Let $k\ge 1$ be an integer.

• 1. ${\mathcal {O}}^k$ will denote the ring of germs of holomorphic functions F on ${\mathbb {C}}^d\times \overline{{\mathbb {C}}^d}$ at $({\textbf{0}},{\textbf{0}})$ with the following property: if a monomial (54) gives a non-trivial contribution to the power series expansion of F, then $2\,(a_0+b_0)+\sum _{j=1}^{d-1}(a_j+b_j)\ge k$;

• 2. ${\mathcal {O}}^k_{\varphi \times \varphi }$ will denote the ring of germs of holomorphic functions F on ${\tilde{M}}\times \overline{{\tilde{M}}}$ at (x, x) such that $F\circ (\varphi \times \varphi )^{-1}\in {\mathcal {O}}^k$.

Corollary 29

Let $(U,\varphi ,A)$ be a holomorphic local chart for M centered at x. Then the following holds.

• 1. ${\mathcal {O}}^k_{\varphi \times \varphi }$ consists of the holomorphic extensions (for $(J,-J)$) of the real-analytic germs in ${\mathfrak {C}}^k_\varphi$;

• 2. if F is a germ of holomorphic function on ${\tilde{M}}\times \overline{{\tilde{M}}}$ at (x, x), then $F\in {\mathcal {O}}^k_{\varphi \times \varphi }$ if and only if

  $$\begin{aligned} \left| F\circ (\varphi \times \varphi )^{-1}(z,u)\right| =O\left( \Vert z'\Vert ^k+\Vert u'\Vert ^k+|z_0|^{\frac{k}{2}}+ |u_0|^{\frac{k}{2}}\right) \end{aligned}$$

  for $(z,w)\sim ({\textbf{0}},{\textbf{0}})$.

We shall occasionally simplify notation and identify F(z, u) with $F\circ (\varphi \times \varphi )^{-1}(z,u)$ in Corollary 29.

3.3.3 Heisenberg local coordinates adapted to a hypersurface

In §18 of [13], a special system of local holomorphic coordinates is constructed on a complex manifold near a point lying on a strictly pseudoconvex hypersurface; this construction was profitably put to use in [10] and [11] to study the asymtptotics of Szegö and Poisson kernels on Grauert tubes. In such a system of coordinates, the local geometry of the hypersurface is well approximated by the local geometry of the Heisenberg group; for this reason, these systems of coordinates are naturally referred to as Heisenberg local coordinates (see e.g. [10, 11, 35]), although they were originally called normal coordinates in [13]. In our setting, up to a simple rescaling this amounts to the existence of coordinates as in following definition.

Definition 30

If $\tau \in (0,\epsilon )$ and $x\in X^\tau \subseteq {\tilde{M}}^\epsilon$, a system of Heisenberg local coordinates on ${\tilde{M}}$ adapted to $X^\tau$ at x is a holomorphic local chart $(U,\varphi ,A)$ for ${\tilde{M}}$ centered at x, with the following properties:

• 1. $\left. \frac{\partial }{\partial z_0}\right| _x \in \textrm{span}_{{\mathbb {C}}}\left( {\mathcal {R}}(x) \right)$;

• 2. $\left. \frac{\partial }{\partial z_j}\right| _x \in {\mathcal {H}}^{(1,0)}(x):= \big ({\mathcal {H}}(x)\otimes {\mathbb {C}}\big )\cap T^{(1,0)}{\tilde{M}}^\tau$, for $j=1,\ldots ,d-1$;

• 3. the defining function $\phi ^\tau :=\rho -\tau ^2$ for $X^\tau$ takes the form

  $$\begin{aligned} \phi ^\tau \circ \varphi ^{-1}(z)=-2\,\Im (z_0)+\Vert z'\Vert ^2+f(z), \end{aligned}$$

  (55)

  where $f\in {\mathfrak {C}}^3$ (clearly f is real valued and real-analytic).

Caveat 31

The norm $\Vert \cdot \Vert$ in (55) is for now simply the Euclidean norm in the given coordinate system, but it will be shown below to have an metric intrinsic meaning (see (63)).

As mentioned in the Introduction, it will be convenient to make a slightly more specific choice of coordinates (without altering the previous properties). Since $f\in {\mathfrak {C}}^3$ and is real-analytic, for suitable coefficients $c\in {\mathbb {R}}$ and $a_l,b_j\in {\mathbb {C}}$ we have

$$\begin{aligned} f(z)=c\,\,|z_0|^2+\Im \left( 2\,z_0\sum _{j=0}^{d-1}a_j\,z_j+ z_0\sum _{j=1}^{d-1}b_j\,{\overline{z}}_j\right) +R_3(z,{\overline{z}}), \end{aligned}$$

(56)

where $R_3$ is the third order remainder, i.e. a convergent power series near ${\textbf{0}}$ in $(z,{\overline{z}})$ involving only monomials of total ordinary degree $\ge 3$. If we make the change of variables

$$\begin{aligned} w_0:=z_0-z_0\sum _{j=0}^{d-1}a_j\,z_j,\quad w_j':=z_j\quad \text {for } j=1,\ldots ,d-1, \end{aligned}$$

and replace z by w in (55), we reduce to the case where all $a_j=0$ (possibly with a new $R_3$). With this adjustment, we shall refer to $(U,\varphi ,A)$ as a system of normal Heisenberg local coordinates adapted to $X^\tau$ at x.

With abuse of notation, if $\gamma$ is a locally defined differential form on ${\tilde{M}}$, we shall occasionally also denote by $\gamma$ its local coordinate representation ${\varphi ^{-1}}^*(\gamma )$.

Lemma 32

Referring to (56), we have $c>0$ and $b_j=0$ for every $j=1,\ldots ,d-1$.

Proof

Since $\Omega =\imath \,\partial \,{\overline{\partial }}\rho =\imath \,\partial \,{\overline{\partial }}\phi ^\tau$, one concludes from (55) and (56) that

$$\begin{aligned} \Omega= & {} \imath \,\left( c\,\textrm{d}z_0\wedge \textrm{d}{\overline{z}}_0+ \textrm{d}z'\wedge \textrm{d}{\overline{z}}'\right) +\Re \left( \sum _{j=1}^{d-1} b_j\,\textrm{d}z_0\wedge \textrm{d}{\overline{z}}_j\right) +R_1(z,{\overline{z}}). \end{aligned}$$

(57)

Let us write $b_j=b_j'+\imath \, b_j''$, where $b_j',\,b_j''\in {\mathbb {R}}$, and let

$$\begin{aligned} \theta _k:=\Re (z_k),\,\eta _k:=\Im (z_k), \quad \forall \,k=0,\ldots ,d-1. \end{aligned}$$

Then

$$\begin{aligned}{} & {} \Re \left( \sum _{j=1}^{d-1} b_j\,\textrm{d}z_0\wedge \textrm{d}{\overline{z}}_j\right) \\{} & {} \quad =\sum _{j=1}^{d-1}\left[ b'_j\,\big (\textrm{d}\theta _0 \wedge \textrm{d}\theta _j+\textrm{d}\eta _0 \wedge \textrm{d}\eta _j\big )-b_j''\,\big ( \textrm{d}\eta _0\wedge \textrm{d}\theta _j-\textrm{d}\theta _0\wedge \textrm{d}\eta _j\big )\right] . \end{aligned}$$

On the other hand, given the Hermitian orthogonality of $\partial /\partial z_0$ and $\partial /\partial z_j$ for $j\ge 1$ at x, $\partial /\partial \theta _0$ and $\partial /\partial \eta _0$ are symplectically orthogonal to $\partial /\partial \theta _j$ and $\partial /\partial \eta _j$ at x for $j\ge 1$. Hence $b_j'=b_j''=0$. $\square$

Therefore,

$$\begin{aligned} \Omega _x= \imath \,\left( c\,\textrm{d}_x z_0\wedge \textrm{d}_x{\overline{z}}_0+ \textrm{d}_xz'\wedge \textrm{d}_x{\overline{z}}'\right) =2\,\left( c\,\textrm{d}_x \theta _0\wedge \textrm{d}_x\eta _0+ \sum _{j=1}^{d-1}\textrm{d}_x\theta _j\wedge \textrm{d}_x\eta _j\right) . \end{aligned}$$

Hence ${\hat{\kappa }}_x(\cdot ,\cdot )=\Omega _x\big (\cdot ,J_x(\cdot )\big )$ is given by

$$\begin{aligned} {\hat{\kappa }}_x= & {} 2\,c\,\left( \textrm{d}_x \theta _0\otimes \textrm{d}_x \theta _0+\textrm{d}_x \eta _0\otimes \textrm{d}_x \eta _0\right) \nonumber \\{} & {} +2\,\sum _{j=1}^{d-1} \left( \textrm{d}_x \theta _j\otimes \textrm{d}_x \theta _j+\textrm{d}_x \eta _j\otimes \textrm{d}_x \eta _j\right) . \end{aligned}$$

(58)

In particular,

$$\begin{aligned} \left. \frac{\partial }{\partial \eta _0}\right| _x =2\,c\,\textrm{grad}^{{\hat{\kappa }}}_x(\eta _0). \end{aligned}$$

We conclude that

• 1. x is a critical point for the restriction of $\eta _0$ to $X^\tau$ (recall (55));

• 2. therefore, $\partial /\partial \eta _0|_x$ is orthogonal to $T_xX^\tau$ with respect to ${\hat{\kappa }}$, whence a non-zero multiple of $\Theta (x)$;

• 3. hence, $\partial /\partial \theta _0$ and $\partial /\partial \theta _j$, $\partial /\partial \eta _j$ for $j=1,\ldots ,d-1$ are all tangent to $X^\tau$ at x;

• 4. $(\theta _0,\theta _1,\eta _1,\ldots ,\theta _{d-1},\eta _{d-1})$ restrict to a system of local coordinates on $X^\tau$ centered at x;

• 5. $\left. \partial /\partial \theta _0\right| _x$ is a non-zero multiple of ${\mathcal {R}}(x)$.

Given (8) and (55), the local coordinate expression for $\alpha$ is then

$$\begin{aligned} \alpha= & {} \Im \partial \rho =\Im \partial \phi ^\tau \nonumber \\= & {} \textrm{d}\theta _0+\frac{c}{2\,\imath }\,\left( {\overline{z}}_0\,\textrm{d}z_0- z_0\,\textrm{d}{\overline{z}}_0\right) +\frac{1}{2\,\imath }\,\left( {\overline{z}}'\cdot \textrm{d}z' -z'\,\textrm{d}{\overline{z}}' \right) +R_2(z,{\overline{z}}), \end{aligned}$$

(59)

where $R_2(z,{\overline{z}})$ denotes a differential 1-form whose coefficients vanish to second order at x.

In particular, $\alpha _x=\textrm{d}_x\theta _0$. On the other hand ${\mathcal {R}}(x)$ is a multiple of $\partial /\partial \theta _0|x$ and $\alpha ({\mathcal {R}})\equiv 1$. Hence

$$\begin{aligned} {\mathcal {R}}(x)=\left. \frac{\partial }{\partial \theta _0}\right| _x. \end{aligned}$$

(60)

Lemma 33

$c=\dfrac{1}{2\,\tau ^2}$.

Proof

By (43) and (58)

$$\begin{aligned} \frac{1}{\tau ^2}= & {} \Vert {\mathcal {R}}(x)\Vert _{{\hat{\kappa }}_x}^2= \left\| \left. \frac{\partial }{\partial \theta _0}\right| _x\right\| ^2_{{\hat{\kappa }}_x}= 2\,c. \end{aligned}$$

(61)

$\square$

We reach the following conclusion.

Proposition 34

Let $(U,\varphi ,A)$ be a normal Heisenberg local chart for ${\tilde{M}}$, centered at $x\in X^\tau$ and adapted to $X^\tau$. Then the local coordinate expressions of $\phi ^\tau$, $\alpha$ and $\Omega$ are as follows:

$$\begin{aligned} \phi ^\tau \circ \varphi ^{-1}(z)= & {} -2\,\Im (z_0)+ \frac{1}{2\,\tau ^2}\,\,|z_0|^2+\Vert z'\Vert ^2 +R_3(z,{\overline{z}}),\\ \alpha= & {} \textrm{d}\theta _0-\frac{\imath }{4\,\tau ^2}\,\left( {\overline{z}}_0\,\textrm{d}z_0- z_0\,\textrm{d}{\overline{z}}_0\right) +\frac{1}{2\,\imath }\,\left( {\overline{z}}'\cdot \textrm{d}z' -z'\,\textrm{d}{\overline{z}}' \right) +R_2(z,{\overline{z}}),\\ \Omega= & {} \imath \,\left( \frac{1}{2\,\tau ^2}\,\textrm{d}z_0\wedge \textrm{d}{\overline{z}}_0+ \textrm{d}z'\wedge \textrm{d}{\overline{z}}'\right) +R_1(z,{\overline{z}}),\\ {\hat{\kappa }}= & {} \frac{1}{\tau ^2}\,\left( \textrm{d}\theta _0\otimes \textrm{d} \theta _0+\textrm{d} \eta _0\otimes \textrm{d} \eta _0\right) \\{} & {} +2\,\sum _{j=1}^{d-1} \left( \textrm{d} \theta _j\otimes \textrm{d} \theta _j+\textrm{d} \eta _j\otimes \textrm{d} \eta _j\right) +R_1\left( z,{\overline{z}}\right) , \end{aligned}$$

where $R_j$ denotes an expression of the appropriate type (function, differential 1- or 2-form, metric tensor respectively) vanishing to j-th order at the origin.

In Heisenberg local coordinates for ${\tilde{M}}$ at $x\in X^\tau$, $(w,{\textbf{u}})\in {\mathbb {C}}\times {\mathbb {C}}^{d-1}$ corresponds to the real tangent vector

$$\begin{aligned} V:=w\,\left. \frac{\partial }{\partial z_0}\right| _x+{\overline{w}}\, \left. \frac{\partial }{\partial {\overline{z}}_0}\right| _x +{\textbf{u}}\cdot \left. \frac{\partial }{\partial z'}\right| _x +\overline{{\textbf{u}}}\cdot \left. \frac{\partial }{\partial {\overline{z}}'} \right| _x\in T_x{\tilde{M}}. \end{aligned}$$

(62)

Corollary 35

With V as in (62), the square norm of V with respect to ${\hat{\kappa }}$ is

$$\begin{aligned} \Vert V\Vert _{{\hat{\kappa }}_x}^2 =\frac{1}{\tau ^2}\,|w|^2+2\,\Vert {\textbf{u}}\Vert ^2. \end{aligned}$$

As in the Introduction, let us set $\omega :=\frac{1}{2}\,\Omega$; thus the Riemannian metric on the Kähler manifold $({\tilde{M}}^\epsilon ,\omega ,J)$ is ${\tilde{\kappa }}:=\frac{1}{2}\,{\hat{\kappa }}$. With V as in (62) then

$$\begin{aligned} \Vert V\Vert _{{\tilde{\kappa }}_x}^2= \omega _x\big (V,J_x(V)\big )= \frac{1}{2\,\tau ^2}\,|w_0|^2+\Vert {\textbf{u}}\Vert ^2. \end{aligned}$$

(63)

3.3.4 Heisenberg local coordinates on $X^\tau$

The local expression for $\phi ^\tau$ in Proposition 34 yields an estimate on $\Im (z_0)$ on $X^\tau$.

Corollary 36

Assume $x\in X^\tau$, and let $(U,\varphi ,A)$ be a normal Heisenberg local chart on ${\tilde{M}}$ adapted to $X^\tau$ at x. If $y\in U\cap X^\tau$ and $\varphi (y)=(z_0,z')$ with $z_0=\Re (z_0)+\imath \,\Im (z_0)$, then

$$\begin{aligned} \Im (z_0)=\frac{1}{4\,\tau ^2}\,\,\Re (z_0)^2+\frac{1}{2}\,\Vert z'\Vert ^2 +R_3\left( \Re (z_0),z',{\overline{z}}'\right) . \end{aligned}$$

Under the same assumptions, $|z_0|^2=\Re (z_0)^2+R_4(\Re (z_0),z')$.

Corollary 37

There exists a constant $C_\tau >0$, such that if $y\in U\cap X^\tau$ and $\varphi (y)=(z_0,z')$, then

$$\begin{aligned} |\Im (z_0)|\le C_\tau \,\left( \theta _0^2+\Vert z'\Vert ^2\right) . \end{aligned}$$

In the following, $\theta :=\left. \theta _0\right| _{X^\tau }$ (with $\theta _0=\Re (z_0)$). Let us set $U^\tau :=U\cap X^\tau$ and define $\varphi ^\tau :U^\tau \rightarrow {\mathbb {R}}\times {\mathbb {C}}^{d-1}$ by

$$\begin{aligned} \varphi ^\tau (x'):=\begin{pmatrix} \theta (x')&z'(x') \end{pmatrix}. \end{aligned}$$

(64)

Set $A^\tau :=\varphi ^\tau (U^\tau )$. Perhaps after restricting U, $A^\tau$ is an open subset of ${\mathbb {R}}\times {\mathbb {C}}^{d-1}$ and $(U^\tau ,\varphi ^\tau ,A^\tau )$ is local coordinate chart for $X^\tau$ centered at x.

Definition 38

We shall call $(U^\tau ,\varphi ^\tau ,A^\tau )$ the Heisenberg local chart for $X^\tau$ at x induced by $(U,\varphi ,A)$, and say that $(U^\tau ,\varphi ^\tau ,A^\tau )$ is a normal Heisenberg local chart for $X^\tau$ if so is $(U,\varphi ,A)$ for ${\tilde{M}}$. We shall often use additive notation for $\varphi ^\tau$, in the following ways. First, if $x'\in U^\tau$ and $\varphi ^\tau (x')$ is as in (64), we shall write $x'=x+\big (\theta (x'),\,z'(x')\big )$. When viewing $z'\in {\mathbb {C}}^{d-1}$ as an element of ${\mathbb {R}}^{2d-2}$, we shall use bold notation and write $x'=x+\big (\theta (x'),\,{\textbf{v}}(x')\big )$.

Furthermore, let us identify $T_xX^\tau$ with ${\mathbb {R}}\times {\mathbb {C}}^{d-1}$, by letting $(a,u)\in {\mathbb {R}}\times {\mathbb {C}}^{d-1}$ correspond to the tangent vector

$$\begin{aligned} W:=a\,\left. \frac{\partial }{\partial \theta }\right| _x +u\cdot \left. \frac{\partial }{\partial z'}\right| _x +{\overline{u}}\cdot \left. \frac{\partial }{\partial {\overline{z}}'}\right| _x. \end{aligned}$$

(65)

We shall then also write $x+W:=(\varphi ^\tau )^{-1}(a,u)=x+(a,u)$.

Remark 39

By (60), if the tangent vectors on the right hand side of (65) are meant in terms of the coordinates on ${\tilde{M}}$, they are actually all tangent to $X^\tau$ at x. Hence (65) may as well be interpreted in terms of the (restricted) local coordinates on $X^\tau$. Thus the additive short-hand $x+W$ has different meanings according to whether we think of W as tangent to $X^\tau$ and refer to $\varphi ^\tau$, or to ${\tilde{M}}$ and refer to $\varphi$. The context should clarify the potential ambiguity.

We can extend the notion of Heisenberg-type order of vanishing to functions on $X^\tau$ with respect to $(U^\tau ,\varphi ^\tau ,A^\tau )$, by the following variant of Definition 23 (see §18 of [13]).

Definition 40

Let $(U^\tau ,\varphi ^\tau ,A^\tau )$, $\varphi ^\tau =(\theta ,z')$, be a system of Heisenberg local coordinates on $X^\tau$ centered at x. Let ${\mathfrak {J}}_x(X^\tau )$ be the ring of germs of (non necessarily smooth, real or complex) functions on $X^\tau$ at x; let ${\mathfrak {m}}_x(X^\tau )\unlhd {\mathfrak {J}}_x(X^\tau )$ be the ideal of those germs that vanish at x. Let ${\mathcal {C}}^\infty (X^\tau )_x\subseteq {\mathfrak {J}}_x(X^\tau )$ be the subring of germs of smooth functions. Suppose $f\in {\mathfrak {m}}_x(X^\tau )$. Then

• 1. f is said to be $O_{\varphi ^\tau }^1$ if, for $X^\tau \ni y\sim x$,

  $$\begin{aligned} f(y)=O\left( \sum _{j=1}^{d-1}|z_j(y)|+|\theta (y)|^{1/2}\right) ; \end{aligned}$$

• 2. ${\mathfrak {O}}_{\varphi ^\tau }^1(X^\tau ):=\left\{ f\in {\mathfrak {m}}_x(X^\tau )\,:\, f \text {is} O_{\varphi ^\tau }^1 \right\}$;

• 3. inductively, for $k\ge 2$ we define ${\mathfrak {O}}_{\varphi ^\tau }^k(X^\tau ):= {\mathfrak {O}}_{\varphi ^\tau }^{k-1}(X^\tau )\cdot {\mathfrak {O}}_{\varphi ^\tau }^1(X^\tau )$;

• 4. for any integer $k\ge 2$, f is said to be $O_{\varphi ^\tau }^k$ if $f\in {\mathfrak {O}}_{\varphi ^\tau }^k(X^\tau )$;

• 5. finally, ${\mathfrak {C}}_{\varphi ^\tau }^k(X^\tau ):={\mathcal {C}}^\infty (X^\tau )_x \cap {\mathfrak {O}}_{\varphi ^\tau }^k(X^\tau )$.

Let $(U^\tau ,\varphi ^\tau ,A^\tau )$ be induced by the system of Heisenberg local coordinates $(U,\varphi ,A)$ adapted to $X^\tau$ at x. The definition of $O_{\varphi ^\tau }^k$ entails the following.

Lemma 41

Let $\jmath ^\tau :X^\tau \hookrightarrow {\tilde{M}}$ be the inclusion. Then

$$\begin{aligned} {\mathfrak {O}}_{\varphi ^\tau }^k(X^\tau )= {\jmath ^\tau }^*\left( {\mathfrak {O}}_{\varphi }^k({\tilde{M}})\right) . \end{aligned}$$

Proof

The statement follows readily from the definition in case $k=1$. For general k, ${\mathfrak {O}}_{\varphi ^\tau }^k(X^\tau )= {\mathfrak {O}}_{\varphi ^\tau }^1(X^\tau )\cdots {\mathfrak {O}}_{\varphi ^\tau }^1(X^\tau )$ (k times). The claim follows from this and (51) since ${\jmath ^\tau }^*$ is multiplicative morphism. $\square$

Let us express $\textrm{vol}^R_{X^\tau }(x)$ in terms of $\varphi ^\tau$ (recall (45) and Corollary 19). By Corollary 36, ${\jmath ^\tau }^*(\textrm{d}_x z_0)= \textrm{d}_x\theta _0$. In view of Proposition 34

$$\begin{aligned} \textrm{vol}^R_{X^\tau }(x)= & {} \frac{1}{\tau }\, \textrm{vol}^C_{X^\tau }(x)\nonumber \\= & {} \frac{1}{\tau }\,\left. {\jmath ^\tau }^*\left( \alpha \wedge \frac{1}{(d-1)!}\,\Omega ^{\wedge (d-1)} \right) \right| _x\nonumber \\= & {} \frac{\imath ^{d-1}}{\tau \,(d-1)!}\, \textrm{d}_x\theta \wedge {\jmath ^\tau }^* \left( \frac{1}{2\,\tau ^2}\,\textrm{d}_xz_0\wedge \textrm{d}_x{\overline{z}}_0+ \textrm{d}_x z'\wedge \textrm{d}_x{\overline{z}}'\right) ^{\wedge (d-1)}. \end{aligned}$$

(66)

By Corollary 36, ${\jmath ^\tau }^*(\textrm{d}_x z_0)= \textrm{d}_x\theta _0$. Hence

$$\begin{aligned} \textrm{vol}^R_{X^\tau }(x)= & {} \frac{\imath ^{d-1}}{\tau \,(d-1)!}\, \textrm{d}_x\theta \wedge \left( \textrm{d}_x z'\wedge \textrm{d}_x{\overline{z}}'\right) ^{\wedge (d-1)}\nonumber \\= & {} \frac{2^{d-1}}{\tau }\,\textrm{d}_x\theta \wedge \frac{1}{(d-1)!}\,\left( \frac{\imath }{2}\, \textrm{d}z'\wedge \textrm{d}{\overline{z}}'\right) ^{\wedge (d-1)}. \end{aligned}$$

(67)

The latter factor is the standard volume form on ${\mathbb {C}}^{d-1}\cong {\mathbb {R}}^{2d-2}$ in the linear coordinates $z'$.

3.3.5 Comparison of Heisenberg local coordinates

Suppose $x\in X^\tau$ and let $\varphi =(z_0,z')$ and $\Phi =(w_0,w')$ are normal Heisenberg local charts adapted to $X^\tau$ at x. By (60) and (63)

$$\begin{aligned} w_0=z_0+f(z_0,z'),\quad w'=A\,z'+{\textbf{f}}(z_0,z'), \end{aligned}$$

(68)

where $A\in U(d-1)$ and $f,\,{\textbf{f}}$ are holomorphic and vanish to second order at x. Consider $y\sim x$ and suppose $(z_0,z')=\varphi (y)$, $(w_0,w')=\Phi (y)$. Let as usual $R_j$ denote a generic smooth function vanishing to j-th order at x; by Proposition 34 and (68),

$$\begin{aligned} \phi ^\tau (y)= & {} -2\,\Im (w_0)+ \frac{1}{2\,\tau ^2}\,|w_0|^2+\Vert w'\Vert ^2+R_3(w_0,w')\\= & {} -2\,\Im (z_0)-2\,\Im \big (f(z_0,z') \big ) +\frac{1}{2\,\tau ^2}\,|z_0|^2+\Vert z'\Vert ^2+R_3(z_0,z'). \end{aligned}$$

Given that $\varphi$ is also a normal Heisenberg chart, in view of the same Proposition we also have

$$\begin{aligned} \phi ^\tau (y)= & {} -2\,\Im (z_0) +\frac{1}{2\,\tau ^2}\,|z_0|^2+\Vert z'\Vert ^2+R_3(z_0,z'). \end{aligned}$$

Thus $\Im \big (f(z_0,z') \big )$ vanishes to third order at x (that is, at the origin). Since f is holomorphic, f itself vanishes to third order at x. We conclude the following.

Lemma 42

Let $\varphi =(z_0,z'),\,\Phi =(w_0,w'):U\rightarrow {\mathbb {C}}^d$ be two normal Heisenberg local charts on ${\tilde{M}}$ adapted to $X^\tau$ at x. Then $w_0-z_0$ vanishes to third order at x.

3.3.6 The geodesic flow in Heisenberg coordinates

Since the vector field ${\mathcal {R}}$ of Definition 16 is tangent to the compact hypersurfaces $X^\tau$, it is complete on ${\tilde{M}}{\setminus } M$. Given $x\in X^\tau$, let us choose a system of Heisenberg normal coordinates $(U,\varphi ,A)$ adapted to $X^\tau$ at x. Let $\Lambda _x:{\mathbb {R}}\rightarrow X^\tau$ be the integral curve of ${\mathcal {R}}$ passing through x at $t=0$. For t sufficiently small,

$$\begin{aligned} \Lambda _x(t)=x+\big (z_0(t),z'(t)\big ), \quad \text {where}\quad z_0(0)=0\in {\mathbb {C}},\,z'(0)={\textbf{0}} \in {\mathbb {C}}^{d-1}. \end{aligned}$$

Let us write $z_0(t)=\theta (t)+\imath \,\eta (t)$, where $\theta (t)=\Re \big (z_0(t)\big )$ and $\eta (t)=\Im \big (z_0(t)\big )$; in view of (60), we have

$$\begin{aligned} \theta (0)=0,\,{\dot{\theta }}(0)=1,\quad \eta (0)= {\dot{\eta }}(0)=0,\quad z'(0)={\dot{z}}'(0)={\textbf{0}}. \end{aligned}$$

Hence $\theta (t)-t$, $\eta (t)$, and $z'(t)$ vanish to second order at the origin. Thus

$$\begin{aligned} z_0(t)=t+f(t), \quad z'(t)={\textbf{F}}(t), \end{aligned}$$

(69)

where f and ${\textbf{F}}$ are smooth and vanish to second order at $0\in {\mathbb {R}}$.

Since $\Lambda _x$ is an integral curve of ${\mathcal {R}}$,

$$\begin{aligned} \langle \alpha _{\gamma _x (t)},{\dot{\gamma }}_x(t)\rangle =\langle \alpha ,{\mathcal {R}}\rangle \circ \Lambda _x(t) \equiv 1. \end{aligned}$$

Expressing this condition by means of Proposition 34 yields

$$\begin{aligned} 1= & {} {\dot{\theta }}(t)-\frac{\imath }{4\,\tau ^2}\,\left[ \big ( t+{\overline{f}}(t)\big )\cdot \big ( 1+{\dot{f}}(t) \big )- \big ( t+f(t) \big )\cdot \left( 1+\dot{{\overline{f}}}(t) \right) \right] \nonumber \\{} & {} +\frac{1}{2\,\imath }\,\left( \overline{{\textbf{F}}}(t)\cdot \dot{{\textbf{F}}}(t) -{\textbf{F}}(t)\,\dot{\overline{{\textbf{F}}}}(t) \right) +R_2(t)={\dot{\theta }}(t)+R_2(t). \end{aligned}$$

(70)

Thus $\theta (t)=t+R_3(t)$. We conclude:

Lemma 43

If $\Lambda _x:{\mathbb {R}}\rightarrow X^\tau$ is the integral curve of ${\mathcal {R}}$ through x, then in normal Heisenberg local coordinates for $X^\tau$ at x we have

$$\begin{aligned} \varphi ^\tau \circ \Lambda _x(t)=\big (t+R_3(t),{\textbf{R}}_2(t) \big ). \end{aligned}$$

In additive notation as in Definition 38, $\Lambda _x(t)=x+\big (t+R_3(t),{\textbf{R}}_2(t) \big )$.

Since any smooth function vanishing to first order at x is in ${\mathfrak {C}}_{\varphi ^\tau }^1(X^\tau )$, we reach the following conclusion (a slight refinement of Lemma 3.6 of [10]).

Corollary 44

Suppose $y=x+(\theta ,{\textbf{u}})\in U^\tau$ and let $\Lambda _y:{\mathbb {R}}\rightarrow X^\tau$ be the integral curve of ${\mathcal {R}}$ with initial condition y. Then for t small we have

$$\begin{aligned} \Lambda _y(t)=x+\big (\theta +t+R_3(t)+ t\cdot f(t,\theta ,{\textbf{u}}),{\textbf{u}}+ {\textbf{R}}_2(t)+ t\cdot {\textbf{f}}(t,\theta ,{\textbf{u}})\big ), \end{aligned}$$

where $f(t,\cdot ,\cdot )$ and (every component of) ${\textbf{f}}(t,\cdot ,\cdot )$ are in ${\mathfrak {C}}_{\varphi ^\tau }^1(X^\tau )$ (that is, they are $O_{\varphi ^\tau }^1$).

The previous statement may be converted into one concerning the homogeneous geodesic flow. The latter is intertwined by $E^\tau$ with the flow of $\upsilon _{\sqrt{\rho }}$; on the other hand by (42) we have $\upsilon _{\sqrt{\rho }}^\tau =-\tau \,{\mathcal {R}}^\tau$ on $X^\tau$. Thus $\gamma (\cdot )$ is an integral curve of ${\mathcal {R}}^\tau$ if and only if $\gamma (-\tau \cdot )$ is an integral curve of $\upsilon _{\sqrt{\rho }}^\tau$. Let us denote by $\Gamma ^\tau _t:X^\tau \rightarrow X^\tau$ the restricted geodesic flow at time t.

Corollary 45

Suppose $y=x+(\vartheta ,{\textbf{u}})\in U^\tau$. Then for t small we have

$$\begin{aligned} \Gamma ^\tau _t(y)=x+\big (\vartheta -\tau \,t+R_3(\tau \,t)+ \tau \,t\cdot f(\tau \,t,\vartheta ,{\textbf{u}}),{\textbf{u}} + {\textbf{R}}_2(\tau \,t)+ \tau \,t\cdot {\textbf{f}}(\tau \,t,\vartheta ,{\textbf{u}})\big ), \end{aligned}$$

where $f(t,\cdot ,\cdot )$, ${\textbf{f}}(t,\cdot ,\cdot )$ are as in the statement of Corollary 44.

Corollary 46

$\left. \upsilon _{\sqrt{\rho }}^\tau (\theta )\right| _y= -\tau +\tau \,f(0,\vartheta ,{\textbf{u}})$.

3.3.7 Horizontal curves in Heisenberg coordinates

Let $I\subseteq {\mathbb {R}}$ be an interval; a smooth curve $\gamma :I\rightarrow X^\tau$ will be called horizontal if $\langle \alpha _{\gamma (t)},{\dot{\gamma }}(t)\rangle =0$ $\forall \, t\in I$. Lemma 47 below concerns the local description, in normal Heisenberg coordinates, of a horizontal curve. Although it won’t be used elsewhere in this paper, it is a natural complement to the results in Sect. 3.3.6 (and potentially useful in future applications).

Suppose $I=(-\epsilon ',\epsilon ')$ for some $\epsilon '>0$, and let $\gamma$ be smooth, horizontal, and such that $\gamma (0)=x$.

For $t\sim 0$, in normal Heisenberg coordinates $\gamma (t)=x+\big (\theta (t),z'(t)\big )$; recall that $\theta =\left. \theta _0\right| _{U^\tau }$. By assumption ${\dot{\theta }}(0)=0$, so that $\theta (t)=R_2(t)$. Furthermore, $z'(t)={\textbf{R}}_1(t)$, hence $z'(t)=t\,{\textbf{u}}+{\textbf{R}}_2(t)$ where ${\textbf{u}}\in {\mathbb {C}}^{d-1}$ and ${\textbf{R}}_2$ is smooth and vanishes to second order at the origin. By Corollary 37, $\eta \big (\gamma (t)\big ) =R_2(t)$. Thus $z_0\big (\gamma (t)\big )=R_2(t)$.

Hence by Proposition 34

$$\begin{aligned} 0=\alpha _{\gamma (t)}\left( {\dot{\gamma }}(t) \right) = {\dot{\theta }}_0(t)+R_2(t)\quad \Rightarrow \quad \theta (t)=R_3(t). \end{aligned}$$

(71)

We conclude the following.

Lemma 47

If $\gamma :(-\epsilon ,\epsilon )\rightarrow X^\tau$ is horizontal and $\gamma (0)=x$, then in normal Heisenberg local coordinates for $X^\tau$ at x we have

$$\begin{aligned} \gamma (t)=x+\big (R_3(t),{\textbf{R}}_1(t)\big ). \end{aligned}$$

3.4 The Szegö kernel and its phase

Recall that $L^2(X^\tau )$ denotes the Hilbert space of square summable functions on $X^\tau$ with respect to $\textrm{vol}^R_{X^\tau }$ in Sect. 3.2.3, $H(X^\tau )\subseteq L^2(X^\tau )$ is the corresponding Hardy space, and $\Pi ^\tau :L^2(X^\tau )\rightarrow H(X^\tau )$, the Szegö projector, is the orthogonal projector. By [5], $\Pi ^\tau$ is a Fourier integral operator with complex phase; its wave front $\textrm{WF}(\Pi ^\tau )= {\Sigma ^\tau }^\sharp$ is the anti-diagonal of $\Sigma ^\tau$ in (10):

$$\begin{aligned} {\Sigma ^\tau }^\sharp= & {} \left\{ \left( x,r\alpha ^\tau _x,x,-r\,\alpha ^\tau _x\right) :\, x\in X^\tau ,\,r>0\right\} \nonumber \\\subseteq & {} \left( T^\vee X^\tau {\setminus } X_0\right) \times \left( T^\vee X^\tau {\setminus } X_0\right) . \end{aligned}$$

(72)

More precisely, up to a smoothing term the distributional kernel of $\Pi ^\tau$ (a.k.a. the Szegö kernel of $X^\tau$) is microlocally of the form

$$\begin{aligned} \Pi ^\tau (x',x'')\simeq \int _0^{+\infty }e^{\imath \,u\,\psi ^\tau (x',x'')} \,s^\tau (x',x'',u)\,\textrm{d}u, \end{aligned}$$

(73)

where the amplitude $s^\tau$ and the phase $\psi ^\tau$ are as follows (see [5]).

• 1. $s^\tau$ is a semiclassical symbol admitting an asymptotic expansion

  $$\begin{aligned} s^\tau (x',x'',u)\sim \sum _{j\ge 0}\,u^{d-1-j}\,s^\tau _j(x',x''). \end{aligned}$$

  (74)

• 2. $\psi ^\tau$ satisfies $\Im (\psi ^\tau )\ge 0$ and is essentially determined along the diagonal of $X^\tau$ by the Taylor expansion of the defining function $\phi ^\tau$; in the present real-analytic setting we may assume that

  $$\begin{aligned} \psi ^\tau :=\left. \frac{1}{\imath }\, {\tilde{\phi }}^\tau \right| _{X^\tau \times X^\tau }, \end{aligned}$$

  (75)

  where ${\tilde{\phi }}^\tau$ denotes the holomorphic extension of $\phi ^\tau$ to ${\tilde{M}}\times \overline{{\tilde{M}}}$ (see the discussion preceding Definition 28).

Let us express $\psi ^\tau$ in the neighbourhood of (x, x) in $X^\tau \times X^\tau$ using normal Heisenberg local coordinates $\varphi ^\tau =(\theta ,z')$ on $X^\tau$ centered at x, defined on an open subset $U^\tau \subseteq X^\tau$. Let $\psi _2^{\omega _x}$ be as in (16).

Proposition 48

Suppose that

$$\begin{aligned} x',\,x''\in U^\tau ,\quad (\theta ,z')=\varphi ^\tau (x'),\quad (\eta ,u')=\varphi ^\tau (x''). \end{aligned}$$

Then

$$\begin{aligned} \imath \,\psi ^\tau (x',x'')= \imath \,(\theta -\eta )-\frac{1}{4\,\tau ^2}\, \left( \theta -\eta \right) ^2 +\psi _2^{\omega _x}\left( z',u'\right) +R_3(\theta ,\eta ,z',{\overline{z}}',u',{\overline{u}}'), \end{aligned}$$

where the latter term denotes a power series in the indicated variables, involving only terms of total degree $\ge 3$.

Proof

Let $\varphi$ be the normal Heisenberg local chart on ${\tilde{M}}$ centered at x inducing $\varphi ^\tau$. Let $(z_0,z'):=\varphi (x')$ and $(u_0,u'):=\varphi (x'')$, so that $\theta =\Re (z_0)$, $\eta =\Re (w_0)$. By Proposition 34 and (75),

$$\begin{aligned} \imath \,\psi ^\tau (x',x'')= & {} \imath \,(z_0-{\overline{u}}_0) +\frac{1}{2\,\tau ^2}\,\,z_0\,{\overline{u}}_0+z'\cdot {\overline{u}}' +R_3(z,{\overline{u}}) \nonumber \\= & {} \imath \,(\theta -\eta )-\big (\Im (z_0)+\Im (u_0)\big ) +\frac{1}{2\,\tau ^2}\,\,z_0\,{\overline{u}}_0 +z'\cdot {\overline{u}}'+R_3(z,{\overline{u}}). \end{aligned}$$

(76)

Let us abridge the third order term to $R_3$. Applying Corollary 36 and (63), we obtain

$$\begin{aligned} \imath \,\psi ^\tau (x',x'')= & {} \imath \,(\theta -\eta )-\frac{1}{4\,\tau ^2}\,\left( \theta ^2+\eta ^2 -2\,\theta \,\eta \right) -\frac{1}{2}\,\left( \Vert z'\Vert ^2+\Vert u'\Vert ^2-2\,z'\cdot {\overline{u}}'\right) +R_3 \nonumber \\= & {} \imath \,(\theta -\eta )-\frac{1}{4\,\tau ^2}\,\left( \theta -\eta \right) ^2 +\psi _2^{\omega _x}\left( z',u'\right) +R_3. \end{aligned}$$

(77)

$\square$

The following property follows from the general construction of the phase of the Szegö kernel in [5]; here it can be read immediately from Propositions 34 and 48.

Corollary 49

For any $x\in X^\tau$, $\textrm{d}_{(x,x)}\psi ^\tau =(\alpha _x,-\alpha _x)$.

Proof

Let notation be as in Proposition 48. Then $\textrm{d}_{(x,x)}\psi ^\tau = (\textrm{d}_x\theta ,-\textrm{d}_x\eta )$. The statement then follows from Proposition 34. $\square$

Again, the following statement follows from the general theory of [5], but it can also be verified by direct inspection of (77). Let $\textrm{dist}_{X^\tau }:X^\tau \times X^\tau \rightarrow {\mathbb {R}}$ be the Riemannian distance function.

Corollary 50

There are a neighborhood $X'\subseteq X^\tau \times X^\tau$ of the diagonal and a constant $C^\tau >0$ such that

$$\begin{aligned} \Im \psi ^\tau (x',x'')\ge C^\tau \,\textrm{dist}_{X^\tau }(x',x'')^2 \end{aligned}$$

for all $(x',x'')\in X'$.

3.4.1 The leading order term of the amplitude

We aim to determine the evaluation $s^\tau _0(x,x)$ of the leading order term in (74); we shall follow the argument in §4 of [5], and apply Proposition 48.

Theorem 51

In a system of normal Heisenberg local coordinates on $X^\tau$ centered at x, $s^\tau _0(x,x)=\tau /(2\,\pi )^d$.

Remark 52

Recall that $\Pi ^\tau$ is the Szegö kernel for the Hermitian structure on $L^2(X^\tau )$ associated to $\textrm{vol}_{X^\tau }^R$. Integration with respect to $\textrm{vol}_{X^\tau }^R$ in a variable y will be denoted by the short-hand $\textrm{d}V_{X^\tau }(y)$. A different choice of volume form would clearly lead to a different result.

Proof

By the idempotency of $\Pi ^\tau$, for all $(x',x'')\in X^\tau \times X^\tau$ we have

$$\begin{aligned} \Pi ^\tau (x',x'')=\left( \Pi ^\tau \circ \Pi ^\tau \right) (x',x'') = \int _{X^\tau }\,\Pi ^\tau (x',y)\,\Pi ^\tau (y,x'')\, \textrm{d}V_{X^\tau }(y). \end{aligned}$$

(78)

Since the singular support of $\Pi ^\tau$ is the diagonal in $X^\tau \times X^\tau$, at the cost of a smoothing term we can localize (78) to some small $\delta$-neighbourhood where $x',x'',y\sim x$. Leaving the cut-off in y implicit, in view of (73) up to a smoothing contribution we have

$$\begin{aligned} \left( \Pi ^\tau \circ \Pi ^\tau \right) (x',x'')\simeq & {} \int _0^{+\infty }\textrm{d}u\,\int _0^{+\infty }\textrm{d}v\,\int _{X^\tau } \textrm{d}V_{X^\tau }(y)\nonumber \\{} & {} \left[ e^{\imath \,[u\,\psi ^\tau (x',y)+v\,\psi ^\tau (y,x'')]}\, s^\tau (x',y,u)\, s^\tau (y,x'',v) \right] \nonumber \\= & {} \int _0^{+\infty }\,I(u,x',x'')\,\textrm{d}u, \end{aligned}$$

(79)

where, setting $v=u\,\sigma$,

$$\begin{aligned} I(u,x',x'')\nonumber \\:= & {} \int _0^{+\infty }\textrm{d}\sigma \,\int _{X^\tau } \textrm{d}V_{X^\tau }(y) \left[ e^{\imath \,u\,\Upsilon ^\tau (x',x'';y,\sigma )}\,u\, s^\tau (x',y,u)\, s^\tau (y,x'',u\,\sigma ) \right] \nonumber \\ \end{aligned}$$

(80)

with

$$\begin{aligned} \Upsilon ^\tau (x',x'';y,\sigma ):= \psi ^\tau (x',y)+\sigma \,\psi ^\tau (y,x''). \end{aligned}$$

(81)

Since $x',x'',y$ all belong to a $\delta$-neighborhood of x,

$$\begin{aligned} \textrm{d}_y\Upsilon ^\tau (x',x'';y,\sigma )= -\alpha _y+\sigma \,\alpha _y+O(\delta ); \end{aligned}$$

therefore, iterated ‘integration by parts’  in y shows that only a negligible contribution in $u\rightarrow +\infty$ is lost, if integration in $\sigma$ is restricted to a suitable neighborhood of 1. Hence the asymptotics in $u\rightarrow +\infty$ are unaltered, if the integrand is multiplied by $\gamma (\sigma )$, with $\gamma \in {\mathcal {C}}^\infty _0({\mathbb {R}}_+)$ identically equal to 1 on $(\epsilon ',1/\epsilon ')$, for some $\epsilon '>0$. Thus integration in $\sigma$ may also be assumed to be compactly supported. Again, the latter cut-off will be left implicit.

As in [5], in order to evaluate (80) asymptotically we first look for stationary points of $\Upsilon ^\tau$ when $x'=x''=x$. To this end, let us fix normal Heisenberg local coordinates on $X^\tau$ at x, and set $y=x+(\theta ,{\textbf{v}})$. By Proposition 48,

$$\begin{aligned} F_x(\sigma ,\theta ,{\textbf{v}}):= & {} \Upsilon ^\tau (x,x;x+(\theta ,{\textbf{v}}),\sigma )\nonumber \\= & {} -\theta +\imath \,\frac{1}{4\,\tau ^2}\,\theta ^2 +\frac{\imath }{2}\,\Vert {\textbf{v}}\Vert ^2+\sigma \,\theta +\imath \,\frac{\sigma }{4\,\tau ^2}\,\theta ^2 +\imath \,\frac{\sigma }{2}\,\Vert {\textbf{v}}\Vert ^2 +R_3(\theta ,{\textbf{v}}) \nonumber \\= & {} \theta \,(\sigma -1) +\imath \,\left[ \frac{\sigma +1}{4\,\tau ^2}\,\theta ^2 +\frac{\sigma +1}{2}\,\Vert {\textbf{v}}\Vert ^2\right] +R_3(\theta ,{\textbf{v}})+ \sigma \,R_3(\theta ,{\textbf{v}}).\nonumber \\ \end{aligned}$$

(82)

Here $(\theta ,{\textbf{v}})\sim {\textbf{0}}$, and the only real critical point near the origin is $(1,0,{\textbf{0}})$. The Hessian matrix at the critical point is

$$\begin{aligned} H(F_x)(1,0,{\textbf{0}})= \begin{pmatrix} 0&{}\quad 1 &{}\quad {\textbf{0}}^t \\ 1&{}\quad \imath /\tau ^2&{}\quad {\textbf{0}}^t \\ {\textbf{0}}&{}\quad {\textbf{0}}&{}\quad 2\,\imath \,I_{2d-2} \end{pmatrix}, \end{aligned}$$

(83)

with $\det \big (-\imath \, H(F_x)(1,0,{\textbf{0}})\big ) =(-1)^d\,2^{2d-2}\cdot (-1)^{d}=2^{2d-2}\ne 0$. In addition,

$$\begin{aligned}{} & {} \det \big (s\,I_{2\,d}-\imath \,(1-s)\, H(F_x)(1,0,{\textbf{0}})\big )\nonumber \\{} & {} \quad =\begin{vmatrix} s&-\imath (1-s)&{\textbf{0}}^t \\ -\imath (1-s)&s+(1-s)/\tau ^2&{\textbf{0}}^t \\ {\textbf{0}}&{\textbf{0}}&(2-s)\,I_{2d-2} \end{vmatrix}\nonumber \\{} & {} \quad =\left[ s^2+\frac{s\,(1-s)}{\tau ^2} +(1-s)^2\right] \cdot (2-s)^{2d-2}>0,\qquad \forall s\in [0,1]. \end{aligned}$$

(84)

Hence by Theorem 2.3 of [24] we may apply the complex version of the stationary phase Lemma, with

$$\begin{aligned} \sqrt{\det \big (-\imath \, H(F_x)(1,0,{\textbf{0}})\big )}= 2^{d-1}. \end{aligned}$$

Recalling (67), to leading order in u we obtain for (80)

$$\begin{aligned}{} & {} I(u,x',x'')\nonumber \\{} & {} \quad \sim e^{\imath \,u\,\psi _1(x',x'')}(2\,\pi )^d\,\frac{1}{2^{d-1}}\, u^{-d}\,u\, s_0^\tau \big (x',y_c(x',x'')\big )\cdot s_0^\tau \big (y_c(x',x''),x''\big )\,u^{2d-2}\, \frac{2^{d-1}}{\tau }\nonumber \\{} & {} \quad = e^{\imath \,u\,\psi _1(x',x'')}(2\,\pi )^d\, s_0^\tau \big (x',y_c(x',x'')\big )\cdot s_0^\tau \big (y_c(x',x''),x''\big )\,u^{d-1}\, \frac{1}{\tau } \end{aligned}$$

(85)

where $\psi _1(x',x'')$ is the critical value of a holomorphic extension of $\Upsilon ^\tau$. More precisely, let ${\tilde{X}}^\tau$ denote a complexification of the real-analytic manifold $X^\tau$. The real-analytic function $\Upsilon ^\tau (x',x'';\cdot ,\cdot ):X^\tau \times {\mathbb {R}}\rightarrow {\mathbb {C}}$, depending on the parameter $(x',x'')\in X^\tau \times X^\tau$, extends uniquely to a holomorphic function ${\tilde{\Upsilon }}^\tau (x',x'';\cdot ,\cdot )$ to an open neighbourhood of $X^\tau \times {\mathbb {R}}$ in ${\tilde{X}}^\tau \times {\mathbb {C}}$. We have seen that $\Upsilon ^\tau (x,x;\cdot ,\cdot )$ admits a unique and non-degenerate critical point near (x, 1), namely (x, 1). By the theory in [24], ${\tilde{\Upsilon }}^\tau (x',x'';\cdot ,\cdot )$ has a unique critical point $\big (y_{cr}(x',x''),\sigma _{cr}(x',x'')\big )\in {\tilde{X}}^\tau \times {\mathbb {C}}$ for $x',\,x''\sim x$ which tends to (x, 1) when $x',x''\rightarrow x$. Then

$$\begin{aligned} \psi _1(x',x''):= \Upsilon ^\tau \big (x',x'',y_{cr}(x',x''),\sigma _{cr}(x',x'')\big ). \end{aligned}$$

(86)

Proposition 53

$\psi _1(x',x'')=\psi (x',x'')$ for all $x',x''\sim x$ in $X^\tau$.

This is (a special case of) Proposition 4.8 of [5]. Nonetheless, we provide the proof below for the reader’s convenience and because the argument appears somewhat more concrete in the current real-analytic setting.

Let us premise a few remarks. Let us fix normal Heisenberg coordinates on ${\tilde{M}}$ adapted to $X^\tau$ at x, and with abuse of notation identify functions on M with their coordinate representations. As above, let us identify ${\tilde{M}}$ (as a differentiable manifold) with the totally real submanifold $\Delta _{{\tilde{M}}}:=\textrm{diag}({\tilde{M}})\subset {\tilde{M}}\times \overline{{\tilde{M}}}$. In local coordinates, we shall write Z for $x+Z$, where $Z=(z_0,z')$. Thus Z is mapped to $(Z,Z)\in \Delta _{{\tilde{M}}}$. In addition, $\phi ^\tau$ may be written (locally near x) as a convergent power series $\phi ^\tau (Z,{\overline{Z}})$; its holomorphic extension to ${\tilde{M}}\times \overline{{\tilde{M}}}$ is then locally given by ${\tilde{\phi }}^\tau \left( Z,{\overline{W}}\right)$. By (75),

$$\begin{aligned} \psi (x+Z,x+W)=\frac{1}{\imath }\,{\tilde{\phi }}^\tau \left( Z,{\overline{W}}\right) . \end{aligned}$$

(87)

By the embedding $X^\tau \hookrightarrow {\tilde{M}}\cong \Delta _{{\tilde{M}}}\subset {\tilde{M}}\times \overline{{\tilde{M}}}$, we can locally realize the real-analytic hypersurface $X^\tau$ as the manifold of ${\mathbb {C}}^d\times \overline{{\mathbb {C}}^d}$

$$\begin{aligned} {X^\tau }':=\left\{ (Z,Z):\,{\tilde{\phi }}^\tau \left( Z,{\overline{Z}}\right) =0\right\} . \end{aligned}$$

The complexification $\widetilde{X^\tau }$ is then locally describable as the holomorphic hypersurface of ${\mathbb {C}}^d\times \overline{{\mathbb {C}}^d}$

$$\begin{aligned} {\widetilde{X^\tau }}':= \left\{ (Z,W):\,{\tilde{\phi }}^\tau \left( Z,{\overline{W}}\right) =0\right\} \end{aligned}$$

(to be precise, here (Z, W) belongs to a neighbourhood of the diagonal).

If $(Z,W)\in {\widetilde{X^\tau }}'$, the holomorphic tangent space to ${\widetilde{X^\tau }}'$ is

$$\begin{aligned} T^{(1,0)}_{(Z,W)}{\widetilde{X^\tau }}' =\left\{ (\delta Z, \delta W):\,\langle \partial _Z{\tilde{\phi }}^\tau , \delta Z\rangle +\langle {\overline{\partial }}_W{\tilde{\phi }}^\tau , \overline{\delta \, W}\rangle =0\right\} , \end{aligned}$$

with complex multiplication given by $\lambda \cdot (\delta Z,\delta W):= (\lambda \,\delta \,Z,{\overline{\lambda }}\,\delta \,W)$.

Let us consider the complex vector sub-bundles $H',\,H'' \subseteq T^{(1,0)}{\widetilde{X^\tau }}'$ given by

$$\begin{aligned} H'_{(Z,W)}:= & {} \left\{ (\delta Z, 0):\,\left\langle \left. \partial _Z{\tilde{\phi }}^\tau \right| _{(Z,W)}, \delta Z\right\rangle =0\right\} ,\nonumber \\ H''_{(Z,W)}:= & {} \left\{ (0, \delta W):\,\left\langle \left. {\overline{\partial }}_W{\tilde{\phi }}^\tau \right| _{(Z,W)}, \overline{\delta \, W}\right\rangle =0 \right\} ; \end{aligned}$$

(88)

we have emphasized that $\partial {\tilde{\phi }}^\tau$ only involves Z-derivatives, while ${\overline{\partial }}{\tilde{\phi }}^\tau$ only involves W-derivatives, since ${\tilde{\phi }}^\tau$ is $(J,-J)$-holomorphic.

Restricted to $X^\tau$, $H'$ (respectively, $H''$) is the vector bundle of tangent vectors tangent to $X^\tau$ and of type (1, 0) (respectively, (0, 1)). Furthermore, if $(Z,Z)\in X^\tau$ then $H'_{(Z,Z)}=\overline{H''_{(Z,Z)}}$, and $H'_{(Z,Z)}$ and $H''_{(Z,Z)}$ are non-singularly paired under the Levi form along $X^\tau$. Sufficiently close to $X^\tau$ in ${\tilde{X}}^\tau$, therefore, by continuity $H'_{(Z,W)}$ and $H''_{(Z,W)}$ are still non-singularly paired under the Levi form (locally represented by the matrix $\left[ \partial ^2{\tilde{\phi }}^\tau / \partial Z_i\,\partial {\overline{W}}_j\right] )$.

Proof of Proposition 53

The real-analytic phase $\Upsilon ^\tau (x',x'';\cdot ,\cdot ):X^\tau \times {\mathbb {R}}_+ \rightarrow {\mathbb {C}}$ in (81) may be locally expressed as follows. Let us write $x'=x+Z',\,x''=x+Z'', y=x+U\in X^\tau$, corresponding to pairs $(Z',Z'),\,(Z'',Z''), (U,U)$ satisfying ${\tilde{\phi }}^\tau (Z',{\overline{Z}}') ={\tilde{\phi }}^\tau (Z'',{\overline{Z}}'') ={\tilde{\phi }}^\tau (U,{\overline{U}})=0$. Then by (81) and (87) we have

$$\begin{aligned} \Upsilon ^\tau (x',x'';y,\sigma )= \frac{1}{\imath }\,\left[ {\tilde{\phi }}^\tau (Z',{\overline{U}}) +\sigma \,{\tilde{\phi }}^\tau (U,{\overline{Z}}'') \right] . \end{aligned}$$

(89)

Consider the holomorphic extension ${\tilde{\Upsilon }}^\tau (x',x'';\cdot ,\cdot ):{\tilde{X}}^\tau \times {\mathbb {C}} \rightarrow {\mathbb {C}}$. Let us write the general point ${\tilde{y}}\in {\tilde{X}}^\tau$ near x, by the previous identifications, as $(x+U,x+W)$, corresponding to a pair (U, W) with ${\tilde{\phi }}^\tau \left( U,{\overline{W}}\right) =0$. Then

$$\begin{aligned} {\tilde{\Upsilon }}^\tau (x',x'';{\tilde{y}},{\tilde{\sigma }})= \frac{1}{\imath }\,\left[ {\tilde{\phi }}^\tau (Z',{\overline{W}}) +{\tilde{\sigma }}\,{\tilde{\phi }}^\tau (U,{\overline{Z}}'') \right] . \end{aligned}$$

(90)

We have seen that $\Upsilon ^\tau (x,x;\cdot ,\cdot )$ admits a unique (real) non-degenerate critical point near (x, 1), namely (x, 1) itself. For all $x',x''\sim x$, therefore, ${\tilde{\Upsilon }}^\tau (x',x'';\cdot ,\cdot )$ admits a unique critical point in the complex domain near (x, 1), which will be a real-analytic function of $(x',x'')$.

At such critical point, $0=\partial _{{\tilde{\sigma }}}{\tilde{\Upsilon }}^\tau (x',x'';{\tilde{y}},{\tilde{\sigma }})=-\imath \,{\tilde{\phi }}^\tau (U,{\overline{Z}}'')$. Hence, $(U,Z'')\in {\widetilde{X^\tau }}'$.

Let us consider the subspace $H'_{(U,W)}\subset T^{1,0}_{(U,W)}{\widetilde{X^\tau }}'$. By its definition in (88),

$$\begin{aligned} \partial _U \left. {\tilde{\phi }}^\tau \right| _{(U,W)} =0\quad \text {on}\quad H'_{(U,W)}. \end{aligned}$$

(91)

On the other hand, since $({\tilde{y}},{\tilde{\sigma }})$ is a critical point of (90), and ${\tilde{y}}$ corresponds to (U, W) in local coordinates, by (90) we also have

$$\begin{aligned} \partial _U \left. {\tilde{\phi }}^\tau \right| _{(U,Z'')} =0\quad \text {on}\quad H'_{(U,W)}. \end{aligned}$$

(92)

Since $(U,W),\, (U,Z'')\in {\widetilde{X^\tau }}'$, to first order in $Z''-W$, and with some abuse of notation, we may regard $(0,Z''-W)$ as an element of $T^{1,0}_{(U,W)}{\widetilde{X^\tau }}'$. We have

$$\begin{aligned} \partial _U \left. {\tilde{\phi }}^\tau \right| _{(U,Z'')}= \partial _U \left. {\tilde{\phi }}^\tau \right| _{(U,W)} +\left[ \frac{\partial ^2{\tilde{\phi }}^\tau }{\partial U_i\,\partial {\overline{W}}_j}\right] \,({\overline{Z}}''-{\overline{W}})+R_2(Z''-W), \end{aligned}$$

where $R_2$ vanishes to second order at the origin. By (91) and (92), the tangent vector $Z''-W$ is in the kernel of the Levi form at (U, W). Since the latter is non-degenerate, we conclude that $W=Z''$.

Since ${\tilde{\phi }}^\tau (U,{\overline{W}})=0$ and ${\tilde{\phi }}^\tau (Z',{\overline{Z}}'')=\imath \,\psi (x',x'')$, in view of (86) the claim follows by replacing W with $Z''$ in (90).

$\square$

We can now conclude the proof of Theorem 51. By (79), Proposition 53), and idempotency, $\Pi ^\tau$ is a Fourier integral operator with phase $\psi ^\tau$ and a symbol of order $d-1$ whose leading order term must coincide with the one in (73). Since $y_c(x,x)=x$, equating the leading order coefficients in (74) and (79), we obtain

$$\begin{aligned} s^\tau _0(x,x)= (2\,\pi )^d\, s_0^\tau \big (x,x\big )^2\, \frac{1}{\tau }. \end{aligned}$$

The claim follows. $\square$

3.5 Symbols and Toeplitz operators

Suppose $\tau \in (0,\epsilon )$ and $W\in {\mathfrak {X}}(X^\tau )$. Let us decompose W in terms of the direct sum (48):

$$\begin{aligned} W=W^\sharp -\lambda \,{\mathcal {R}}^\tau . \end{aligned}$$

(93)

Here $W^\sharp$ is a smooth section of ${\mathcal {H}}^\tau$, and $\lambda =-\alpha ^\tau (W)\in {\mathcal {C}}^\infty (X^\tau )$.

Assume that $L_W(\alpha ^\tau )=0$. Then the flow of W preserves $\textrm{vol}^C_{X^\tau }$ by (45); hence it also preserves $\textrm{vol}^R_{X^\tau }$ by Corollary 19. Therefore the flow of W induces in a standard manner a one-parameter group of unitary automorphisms of $L^2(X^\tau )$. It follows that, as a differential operator on $X^\tau$, W is skew-symmetric; thus the Toeplitz operator

$$\begin{aligned} {\mathfrak {W}}:=\imath \,\Pi ^\tau \circ W\circ \Pi ^\tau \end{aligned}$$

is formally self-adjoint.

By [4], Toeplitz operators on $X^\tau$ have well-defined principal symbols, which are smooth functions on the closed symplectic cone

$$\begin{aligned} \Sigma ^\tau :=\left\{ \left( x,\,r\,\alpha ^\tau _x\right) :\, x\in X^\tau ,\,r>0 \right\} \subseteq T^\vee X^\tau {\setminus } X_0. \end{aligned}$$

(94)

Let us compute the principal symbol $\sigma ({\mathfrak {W}})$ of ${\mathfrak {W}}$ at $\left( x,\,r\,\alpha ^\tau _x\right)$. We consider a system of normal Heisenberg local coordinates on ${\tilde{M}}$ adapted to $X^\tau$ at x (Definition 30), and the corresponding Heisenberg local chart for $X^\tau$ at x (Definition 38); we denote the latter by $\varphi ^\tau =(\theta ,z')$. By Proposition 34, $\alpha ^\tau _x=\textrm{d}_x\theta$. On the other hand, by (60) and (93),

$$\begin{aligned} W(x)=W^\sharp (x)-\lambda (x)\, \left. \frac{\partial }{\partial \theta }\right| _x. \end{aligned}$$

Thus,

$$\begin{aligned} \sigma ({\mathfrak {W}})(x,r\,\alpha ^\tau _x)= \imath \,e^{-\imath \,r\,\theta }\,W(x) \left( e^{\imath \,r\,\theta } \right) = \imath \,\big (-\lambda (x)\,\imath \,r\big )=r\,\lambda (x). \end{aligned}$$

(95)

If $\lambda >0$, therefore, ${\mathfrak {W}}$ is a positive self-adjoint Toeplitz operator, so that its spectrum is discrete, bounded from below and accumulates at $+\infty$ (see [4]). This applies in particular if $W=\upsilon _{\sqrt{\rho }}$ by (42), with $\lambda =\sqrt{\rho }$. Then ${\mathfrak {W}}={\mathfrak {D}}_{\sqrt{\rho }}^\tau$ (see (12)).

3.6 Dynamical Toeplitz operators

As mentioned in the Introduction, the homogenous geodesic flow is generally not holomorphic for $J_{ad}$. Equivalently, the (1, 0)-component of $\upsilon _{\sqrt{\rho }}$ needn’t be holomorphic on ${\tilde{M}}{\setminus } M$. Therefore, when viewed a differential operator, $\upsilon _{\sqrt{\rho }}^\tau$ does generally not preserve the Hardy space $H(X^\tau )$. A natural replacement is the self-adjoint, first order Toeplitz operator ${\mathfrak {D}}_{\sqrt{\rho }}^\tau :=\Pi ^\tau \circ D_{\sqrt{\rho }}\circ \Pi ^\tau$ (Sect. 3.5). The latter generates the 1-parameter group of unitary Toeplitz operators

$$\begin{aligned} U_{\sqrt{\rho }}^\tau (t):=e^{\imath \,t\,{\mathfrak {D}}_{\sqrt{\rho }}^\tau }:H(X^\tau )\rightarrow H(X^\tau ). \end{aligned}$$

(96)

In view of (11),

$$\begin{aligned} \imath \,t\,{\mathfrak {D}}_{\sqrt{\rho }}^\tau = \imath \,t\,\Pi ^\tau \circ D_{\sqrt{\rho }}\circ \Pi ^\tau =-t\,\Pi ^\tau \circ \upsilon _{\sqrt{\rho }}^\tau \circ \Pi ^\tau . \end{aligned}$$

Hence, heuristically $U_{\sqrt{\rho }}^\tau (t)$ is a Toeplitz quantization of the geodesic flow at time $-t$. In the notation of the Introduction, the distributional kernel $U_{\sqrt{\rho }}^\tau (t;\cdot ,\cdot )\in {\mathcal {D}}'(X^\tau \times X^\tau )$ of (96) admits the spectral description

$$\begin{aligned} U_{\sqrt{\rho }}^\tau (t;x,y) =\sum _{j=1}^{+\infty }e^{\imath \,t\,\lambda _j} \cdot \sum _{k=1}^{\ell _j}\,\rho _{j,k}(x) \cdot \overline{\rho _{j,k}(y)}, \end{aligned}$$

(97)

where $(\rho _{j,k})_{k=1}^{\ell _j}$ is an orthonormal basis of the $\ell _j$-dimensional eigenspace of ${\mathfrak {D}}_{\sqrt{\rho }}^\tau$ corresponding to the eigenvalue $\lambda _j$.

Arguing, say, as in §12 of [15], and using (15) and (30), one obtains

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x,y)= & {} \sum _{j=1 }^{+\infty }\,{\hat{\chi }}(\lambda -\lambda _j)\,\sum _{k=1}^{\ell _j}\,\rho _{j,k}(x) \cdot \overline{\rho _{j,k}(y)}\nonumber \\= & {} \frac{1}{\sqrt{2\,\pi }}\, \int _{-\infty }^{+\infty }e^{-\imath \,\lambda \,t}\, \chi (t)\,U_{\sqrt{\rho }}^\tau (t;x,y)\,\textrm{d}t. \end{aligned}$$

(98)

It was shown by Zelditch that, up to smoothing Toeplitz operators, $U_{\sqrt{\rho }}^\tau (t)$ is a ‘dynamical Toeplitz operator’  associated to the geodesic flow at time $-t$, composed with a suitable pseudodifferential operator (see e.g. §5.3 of [48]). To express this precisely, recall that $\Gamma ^\tau _t:X^\tau \rightarrow X^\tau$ denotes the geodesic flow along $X^\tau$ (Corollary 45); for $t\in {\mathbb {R}}$ let us set $\Pi _t^{\tau }:={\Gamma ^\tau _t}^*\circ \Pi ^\tau$. Thus $\Pi _t^{\tau }$ has Schwartz kernel

$$\begin{aligned} \Pi _t^{\tau }(x,y):=\Pi ^\tau \left( {\Gamma ^\tau _t}(x),y\right) = \left( \Pi ^\tau _t\times \textrm{id}_{X^\tau }\right) ^*(\Pi ^\tau ) (x,y). \end{aligned}$$

Remark 54

When defining the pull-back under a diffeomorphism, one ought to distinguish whether $\Pi ^\tau$ is referred to as a (generalized) function, density, or half-density. There is no ambiguity in the present case, since these are being identified by means of $\textrm{vol}^R_{X^\tau }$, which is invariant under $\Gamma _t^{\tau }$.

Before stating the following result of Zelditch, we need a further piece of notation. For any $t\in {\mathbb {R}}$, let us set

$$\begin{aligned} \Pi ^{\tau }_{(t)}:=\left( \Gamma ^\tau _{-t}\right) ^* \circ \Pi ^\tau \circ \left( \Gamma ^\tau _t\right) ^*:L^2(X^\tau )\rightarrow L^2(X^\tau ), \end{aligned}$$

where the brackets in the suffix (t) are intended to avoid confusion with the operator $\Pi ^\tau _t$ just defined. Just as $\Pi ^\tau$, $\Pi ^{\tau }_{(t)}$ is an orthogonal projector onto its image $H(X^\tau )_{t}:=\left( \Gamma ^\tau _{-t}\right) ^*\left( H(X^\tau )\right)$. In particular, its Schwartz kernel is

$$\begin{aligned} \Pi ^{\tau }_{(t)}(x,y)=\Pi ^\tau \left( \Gamma ^\tau _{-t}(x), \Gamma ^\tau _{-t}(y) \right) =\left( \Gamma ^\tau _{-t}\times \Gamma ^\tau _{-t} \right) ^*(\Pi ^\tau ) (x,y). \end{aligned}$$

Thus, $\Pi ^{\tau }_{(t)}$ is the Szegö projector onto the Hardy space associated to the new CR structure

$$\begin{aligned} J_t:= \textrm{d}\Gamma ^\tau _t \circ J\circ \textrm{d}\Gamma ^\tau _{-t}: {\mathcal {H}}^\tau \rightarrow {\mathcal {H}}^\tau , \end{aligned}$$

where ${\mathcal {H}}^\tau$ is as in (48).

As discussed in, say, [41], given a finite dimensional symplectic vector space $(E,\sigma )$ and two compactible (linear) complex structures $J_1,\,J_2\in {\mathcal {J}}(E,\sigma )$, there exists a well-defined invariant $\langle J_1,J_2\rangle$, given by the overlap of two normalized Gaussians associated to $J_1$ and $J_2$; in particular, $\langle J_1,J_2\rangle$ is non-vanishing, and equals 1 for $J_1=J_2$.

Theorem 55

(Zelditch) There exist a zeroth order polyhomogeneous complete classical symbol of the form

$$\begin{aligned} \sigma ^\tau _t(x,r)\sim \sum _{j=0}^{+\infty } \sigma ^\tau _{t,j}(x)\,r^{-j}\quad (x\in X^\tau ,\,r>0), \end{aligned}$$

(99)

and a zeroth order pseudodifferential operator ${\mathfrak {P}}^\tau _t \sim \sigma ^\tau _t(x,D_{\sqrt{\rho }}^\tau )$ such that

$$\begin{aligned} U_{\sqrt{\rho }}^\tau (t)\simeq \Pi ^\tau \circ {\mathfrak {P}}^\tau _t \circ \Pi _{-t}^{\tau }, \end{aligned}$$

(100)

where $\simeq$ means ‘equal modulo smoothing Toeplitz operators’. Furthermore, up to a multiplicative factor of modulus 1, the principal symbol $\sigma ^\tau _{t,0}(x)$ is given by $\langle J_x,{J_t}_x\rangle ^{-1}$; in particular, $\sigma ^\tau _{0,0}(x)=1$.

Up to smoothing terms, the Schwartz kernel of $\Pi _{-t}^{\tau }$ has the form

$$\begin{aligned} \Pi _{-t}^{\tau }(x_1,x_2)\sim \int _0^{+\infty } e^{\imath \,u\,\psi ^\tau \left( \Gamma ^\tau _{-t}(x_1),x_2 \right) }\, s^\tau \left( \Gamma ^\tau _{-t}(x_1),x_2,u\right) \,\textrm{d}u, \end{aligned}$$

(101)

where $\psi ^\tau$ and $s^\tau$ are as in (73). Using classical results on the composition of pseudodifferential and Fourier integral operators [36, 40], we reach the following conclusion.

Lemma 56

Up to smoothing terms, the Schwartz kernel of the composition ${\mathcal {R}}^\tau _t:= {\mathfrak {P}}^\tau _t\circ \Pi _{-t}^{\tau }$ has the form

$$\begin{aligned} {\mathcal {R}}^\tau _t(x_1,x_2)\sim \int _0^{+\infty } e^{\imath \,u\,\psi ^\tau \left( \Gamma ^\tau _{-t}(x_1),x_2 \right) }\, r^\tau _t\left( x_1,x_2,u\right) \,\textrm{d}u, \end{aligned}$$

(102)

where

$$\begin{aligned} r^\tau _t\left( x_1,x_2,u\right) \sim \sum _{j\ge 0}\,u^{d-1-j}\,r^\tau _{t\,j}(x_1,x_2),\quad r^\tau _{t\,0}(x_1,x_2)= \sigma ^\tau _{t,0}\left( x_1\right) \cdot s^\tau _0\left( \Gamma ^\tau _{-t}(x_1),x_2\right) . \end{aligned}$$

By (100), we have

$$\begin{aligned} U_{\sqrt{\rho }}^\tau (t)\simeq \Pi ^\tau \circ {\mathcal {R}}^\tau _t. \end{aligned}$$

(103)

4 Near-diagonal asymptotics for $\Pi ^\tau _{\chi ,\lambda }$

Before delving into the proof of Theorem 4, let us premise some notation.

The choice of a normal Heisenberg local chart $\varphi ^\tau$ for $X^\tau$ at x determines an isomorphism $T_xX^\tau \cong {\mathbb {R}}\times {\mathbb {R}}^{2d-2}$; a general $\upsilon \in T_xX^\tau$ will be written accordingly as a pair $\upsilon =(\theta ,{\textbf{u}})$. The subspaces ${\mathbb {R}}\times \{{\textbf{0}}\}$ and $\{0\}\times {\mathbb {R}}^{2d-2}$ correspond, respectively, to ${\mathcal {T}}^\tau (x)$ and ${\mathcal {H}}^\tau (x)$ (see (48)). By (63), the isomorphism ${\mathbb {C}}^{d-1}\cong \{0\}\times {\mathbb {R}}^{2d-2} \rightarrow {\mathcal {H}}^\tau (x)$ is unitary, when ${\mathcal {H}}^\tau (x)$ is endowed with the Hermitian structure associated to $\omega _x=\frac{1}{2}\,\Omega _x$.

With the notation of Corollary 46, let $(a_x,{\textbf{A}}_x)\in {\mathbb {R}}\times {\mathbb {R}}^{2d-2}$ be defined by

$$\begin{aligned} \tau \,f(0,\vartheta ,{\textbf{u}})=\frac{1}{2\,\tau ^2}\, a_x\,\vartheta +\langle {\textbf{A}}_x,{\textbf{u}}\rangle +F_2^\tau (\vartheta ,{\textbf{u}}), \end{aligned}$$

(104)

where $F_2^\tau$ vanishes to second order at the origin. We may then reformulate the conclusion of Corollary 45 writing

$$\begin{aligned} \Gamma ^\tau _t(y)= & {} x+\left( \vartheta -\tau \,t+ t\,\left( \frac{1}{2\,\tau ^2}\, a_x\,\vartheta +\langle {\textbf{A}}_x,{\textbf{u}}\rangle \right) + R_3(\tau \,t,\vartheta ,{\textbf{u}}),\right. \nonumber \\{} & {} {\textbf{u}} + {\textbf{R}}_2(\tau \,t,\vartheta ,{\textbf{u}})\Big ). \end{aligned}$$

(105)

We shall verify a posteriori that $(a_x,{\textbf{A}}_x)=(0,{\textbf{0}})$.

Definition 57

With $(a_x,{\textbf{A}}_x)$ as in (104), let us set

$$\begin{aligned} {\textbf{a}}_x(\theta _1,\theta _2):=\frac{\theta _1-\theta _2}{\tau }\,{\textbf{A}}_x. \end{aligned}$$

We further define

$$\begin{aligned} \Psi _2:T_xX^\tau \times T_xX^\tau \rightarrow {\mathbb {C}} \end{aligned}$$

by setting, given $\upsilon _j=(\theta _j,{\textbf{v}}_j)$,

$$\begin{aligned} \Psi _2(\upsilon _1,\upsilon _2):= & {} -\imath \,\omega _x\left( {\textbf{v}}_1,{\textbf{v}}_2\right) -\frac{\imath }{2}\,\omega _x\left( J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{v}}_1+{\textbf{v}}_2\right) \nonumber \\{} & {} -\frac{1}{4}\,\Vert {\textbf{v}}_1-{\textbf{v}}_2\Vert ^2 -\frac{1}{4}\,\left\| {\textbf{v}}_1-{\textbf{v}}_2 +J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big )\right\| ^2. \end{aligned}$$

(106)

Proof of Theorem 4

By (98) and (100), we can rewrite (15) in the following form:

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)\sim & {} \frac{1}{\sqrt{2\,\pi }}\,\int _{X^\tau } \int _{-\epsilon }^{+\epsilon }\left[ e^{-\imath \,\lambda \,t}\, \chi (t)\,\Pi ^\tau (x_1,y)\, \left[ P^\tau _t\circ \Pi _{-t}^{\tau }\right] (y,x_2)\right] \nonumber \\{} & {} \quad \,\textrm{d}t\,\textrm{d}V_{X^\tau }(y), \end{aligned}$$

(107)

where $\sim$ stands for ‘has the same asymptotics for $\lambda \rightarrow +\infty$ as’.

The wave front set of $\Pi ^\tau$ is given by (72). Therefore, given that the geodesic flow preserves $\alpha$ (Lemma 12), the wave front of $P^\tau _t\circ \Pi _{-t}^{\tau }$ is

$$\begin{aligned} \textrm{WF}\left( P^\tau _t\circ \Pi _{-t}^{\tau } \right)= & {} \textrm{WF}\left( \Pi _{-t}^{\tau } \right) =\left( \Gamma _{-t}^{\tau }\times \textrm{id}_{X^\tau }\right) ^* \big (\textrm{WF}(\Pi ^\tau ) \big )\\= & {} \left\{ \left( \Gamma ^\tau _{t}(x), r\alpha ^\tau _{\Gamma ^\tau _{t}(x)}, x,-r\,\alpha ^\tau _x\right) :\, x\in X^\tau ,\,r>0\right\} . \end{aligned}$$

Hence the singular supports of $\Pi ^\tau$ and $P^\tau _t\circ \Pi _{-t}^{\tau }$ are, respectively, the diagonal and the graph of $\Gamma ^\tau _{-t}$ in $X^\tau \times X^\tau$.

Lemma 58

Let $c>0$ be such that

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(x),x\right) \le c\,|t|,\quad \forall \, x\in X^\tau ,\,t\in {\mathbb {R}}. \end{aligned}$$

(108)

Then, provided $\epsilon >0$ is sufficiently small, if $\textrm{dist}_{X^\tau }(x_1,x_2)\ge 3\,c\,\epsilon$ we have

$$\begin{aligned} \max \left\{ \textrm{dist}_{X^\tau }\left( x_1,y\right) , \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_2\right) \right\} \ge c\,\epsilon , \quad \forall \,y\in X^\tau ,\, t\in \textrm{supp}(\chi ). \end{aligned}$$

Proof

For any $y\in X^\tau$ and $t\in (-\epsilon ,\epsilon )$

$$\begin{aligned} 3\,c\,\delta\le & {} \textrm{dist}_{X^\tau }\left( x_1,x_2\right) \nonumber \\\le & {} \textrm{dist}_{X^\tau }\left( x_1,y\right) +\textrm{dist}_{X^\tau }\left( y,\Gamma ^\tau _{-t}(y)\right) + \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_2\right) \nonumber \\\le & {} \textrm{dist}_{X^\tau }\left( x_1,y\right) +c\,\epsilon + \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_2\right) . \end{aligned}$$

(109)

Hence,

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( x_1,y\right) + \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_2\right) \ge 2\,c\,\epsilon \quad \forall \,t\in \textrm{supp}(\chi ). \end{aligned}$$

$\square$

Lemma 59

For any $\epsilon \sim 0^+$, if $\textrm{supp}(\chi )\subset [-\epsilon ,\epsilon ]$ and $\textrm{dist}_{X^\tau }(x_1,x_2)\ge 3\,c\,\epsilon$, then $\Pi ^\tau _{\chi ,\lambda }(x_1,x_2)=O\left( \lambda ^{-\infty }\right)$.

Proof

Let us define

$$\begin{aligned} U_1:= & {} \left\{ y\in X^\tau :\, \textrm{dist}_{X^\tau }\left( x_1,y\right)>\frac{c\,\epsilon }{2}\right\} ,\\ U_2:= & {} \left\{ y\in X^\tau :\, \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_2\right) >\frac{c\,\epsilon }{2},\,\forall \,t\in \textrm{supp}(\chi )\right\} . \end{aligned}$$

By Lemma 58, ${\mathcal {U}}:=\{U_1,\,U_2\}$ is an open cover of $X^\tau$. Let $\gamma _1+\gamma _2=1$ be a partition of unity of $X^\tau$ subordinate to ${\mathcal {U}}$. Then

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)\sim \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)_1+ \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)_2, \end{aligned}$$

where

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)_j\nonumber \\{} & {} \quad := \frac{1}{\sqrt{2\,\pi }}\, \int _{-\infty }^{+\infty }e^{-\imath \,\lambda \,t}\, \chi (t)\,\left[ \int _{U_j}\gamma _j(y)\,\Pi ^\tau (x_1,y)\, \left[ P^\tau _t\circ \Pi _{-t}^{\tau }\right] (y,x_2)\,\textrm{d}V_{X^\tau }(y)\right] \,\textrm{d}t.\nonumber \\ \end{aligned}$$

(110)

By definition of $U_1$, the function $y\mapsto \gamma _1(y)\cdot \Pi ^\tau (x_1,y)$ is ${\mathcal {C}}^\infty$ (and depends smoothly on $x_1$); therefore, for $j=1$ the inner integral in (110) is the distributional kernel of the composition of a smoothing kernel with $P^\tau _t$, whence it is itself a smoothing kernel. In other words, it a smooth function of $(x_1,x_2,t)$, uniformly so under the assumption. Therefore, that $\Pi ^\tau _{\chi ,\lambda }(x_1,x_2)_1$ is $O\left( \lambda ^{-\infty }\right)$ then follows by integration by parts.

Similarly, by definition of $U_2$, the function $y\mapsto \gamma _2(y)\cdot \left[ P^\tau _t\circ \Pi _{-t}^{\tau }\right] (y,x_2)$ is ${\mathcal {C}}^\infty$ (and depends smoothly on $x_2$), whence $\Pi ^\tau _{\chi ,\lambda }(x_1,x_2)_2= O\left( \lambda ^{-\infty }\right)$ by a similar argument. $\square$

Assume from now on $\textrm{dist}_{X^\tau }(x_1,x_2)< 3\,c\,\epsilon$, with c as in (108). Let us define

$$\begin{aligned} U'_1:= & {} \left\{ y\in X^\tau :\,\textrm{dist}_X(x_1,y)< 2\,\epsilon \right\} ,\nonumber \\ U'_2:= & {} \left\{ y\in X^\tau :\,\textrm{dist}_X(x_1,y)>\epsilon \right\} . \end{aligned}$$

(111)

Then ${\mathcal {U}}':=\{U_1',U_2'\}$ is an open cover of $X^\tau$; let $\gamma _1'+\gamma _2'=1$ be a partition of unity subordinate to ${\mathcal {U}}'$. Thus

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)\sim \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)'_1+ \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)'_2, \end{aligned}$$

where $\Pi ^\tau _{\chi ,\lambda }(x_1,x_2)'_j$ is defined as in (110), with $\gamma _j'$ in place of $\gamma _j$. For $y\in U_2'$, the function $y\mapsto \Pi ^\tau (x_1,y)$ is ${\mathcal {C}}^\infty$, and an adaptation of the previous argument implies that $\Pi ^\tau _{\chi ,\lambda }(x_1,x_2)'_2=O\left( \lambda ^{-\infty } \right)$. Thus

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)\sim \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)'_1, \end{aligned}$$

(112)

where integration in y is now over a small neighborhood of $x_1$.

We may assume that $x_1,x_2$ and every y in the support of the integrand in $\Pi ^\tau _{\chi ,\lambda }(x_1,x_2)'_1$ belong to a Heisenberg coordinate neighborhood centered at some $x\in X^\tau$. Without altering the asymptotics, $\Pi ^\tau$ may be represented as a Fourier integral operator (73), and apply Lemma 56 and (103). Then (107) may be rewritten

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)\nonumber \\{} & {} \quad \sim \frac{1}{\sqrt{2\,\pi }}\,\int _0^{+\infty }\, \textrm{d}u\,\int _0^{+\infty }\,\textrm{d}v\, \int _{X^\tau }\,\textrm{d}V_{X^\tau }(y) \int _{-\epsilon }^{+\epsilon }\,\textrm{d}t\nonumber \\{} & {} \qquad \left[ e^{\imath \,[u\,\psi ^\tau (x_1,y) +v\,\psi ^\tau (\Gamma ^\tau _{-t}(y),x_2 ) -\lambda \,t]}\,\gamma _1'(y)\, \chi (t)\,s^\tau (x_1,y,u)\, r^\tau _t\left( y,x_2,v\right) \right] . \end{aligned}$$

(113)

With the rescaling $u\rightsquigarrow \lambda \,u$ and $v\rightsquigarrow \lambda \,v$, (113) becomes

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }(x_1,x_2)\nonumber \\{} & {} \quad \sim \frac{\lambda ^2}{\sqrt{2\,\pi }}\,\int _0^{+\infty }\, \textrm{d}u\,\int _0^{+\infty }\,\textrm{d}v\, \int _{X^\tau }\,\textrm{d}V_{X^\tau }(y) \int _{-\epsilon }^{+\epsilon }\,\textrm{d}t \nonumber \\{} & {} \qquad \left[ e^{\imath \,\lambda \,\Psi ^\tau (x_1,x_2;u,v,t,y)}\, A_\lambda ^\tau (x_1,x_2;u,v,t,y) \right] , \end{aligned}$$

(114)

where

$$\begin{aligned} \Psi ^\tau (x_1,x_2;u,v,t,y):= & {} u\,\psi ^\tau (x_1,y) +v\,\psi ^\tau (\Gamma ^\tau _{-t}(y),x_2 ) -t,\end{aligned}$$

(115)

$$\begin{aligned} A_\lambda ^\tau (x_1,x_2;u,v,t,y):= & {} \chi (t)\,\gamma _1'(y)\,s^\tau (x_1,y,\lambda \,u)\, r^\tau _t\left( \Gamma ^\tau _{-t}(y),x_2,\lambda \,v\right) . \end{aligned}$$

(116)

We shall let $y=x+(\theta ,{\textbf{u}})$ in normal Heisenberg local coordinates on $X^\tau$ at x; then $\textrm{d}V_{X^\tau }(y)$ by ${\mathcal {V}}(\theta ,{\textbf{u}})\,\textrm{d}\theta \,\textrm{d}{\textbf{u}}$, and by (67)

$$\begin{aligned} {\mathcal {V}}(0,{\textbf{0}}) =\frac{2^{d-1}}{\tau }. \end{aligned}$$

(117)

Integration in $(\theta ,{\textbf{u}},t)$ is compactly supported near the origin. By (115), Proposition 34, Corollaries  45 and 49

$$\begin{aligned} \partial _\theta \Psi ^\tau =v-u+O(\epsilon ),\quad \partial _t\Psi ^\tau =\tau \,v-1+O(\epsilon ). \end{aligned}$$

(118)

It follows by a standard ‘partial integration’  argument in the compactly supported variables $(\theta ,t)$ that the contribution of the locus where $\Vert (u,v)\Vert \gg 0$ contributes negligibly to the asymtptotics. Similarly, if $\epsilon \ll 1$, integration by parts in t shows that the contribution of the locus where $v\ll 1/\tau$ is also negligible. Finally, integration by parts in $\theta$ yields a similar conclusion for u. We thus obtain the following reduction.

Lemma 60

There exists $D\gg 0$ such that the following holds. Let $h\in {\mathcal {C}}^\infty _0\big ((1/(2D),2\,D)\big )$ be such that $h\equiv 1$ on (1/D, D). Then only a negligible contribution to the asymptotics of (114) is lost, if the integrand is multiplied by $h(u)\cdot h(v)$. Hence, integration in (u, v) may be assumed to be compactly supported in $(1/(2D),2\,D)^2$.

Proof of Statement 1) of Theorem 4

There exist constants $0<a\le A$ such that

$$\begin{aligned} a\,\textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x \right) \le \textrm{dist}_{X^\tau }\left( y,\Gamma ^\tau _{t}(x) \right) \le A\,\textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x \right) \end{aligned}$$

for every $t\in (-\epsilon ,\epsilon )$ and $y,\,x\in X^\tau$.

Assume $\textrm{dist}_{X^\tau }\left( x_1,x_2^\chi \right) \ge C\,\lambda ^{\delta -1/2}$, and define

$$\begin{aligned} U^\lambda _1:= & {} \left\{ y\in X^\tau :\,\textrm{dist}_{X^\tau }(y,x_1) <(C/2)\,\lambda ^{\delta -1/2} \right\} ,\\ U^\lambda _2:= & {} \left\{ y\in X^\tau :\,\textrm{dist}_{X^\tau }(y,x_1) >(C/3)\,\lambda ^{\delta -1/2} \right\} . \end{aligned}$$

Then ${\mathcal {U}}^\lambda :=\{U^\lambda _1,\,U^\lambda _2\}$ is an open cover of $X^\tau$.

If $y\in U^\lambda _1$, for any $t\in (-\epsilon ,\epsilon )$ we have

$$\begin{aligned} C\,\lambda ^{\delta -1/2}\le & {} \textrm{dist}_{X^\tau }\left( x_1,,\Gamma ^\tau _{t}(x_2)\right) \le \textrm{dist}_{X^\tau }(x_1,y) +\textrm{dist}_{X^\tau }\left( y,\Gamma ^\tau _{t}(x_2) \right) \\< & {} (C/2)\,\lambda ^{\delta -1/2} +\textrm{dist}_{X^\tau }\left( y,\Gamma ^\tau _{t}(x_2) \right) \\\Rightarrow & {} \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_2 \right) \ge \frac{1}{A}\, \textrm{dist}_{X^\tau }\left( y,\Gamma ^\tau _{t}(x_2) \right) \ge \frac{C}{2\,A}\,\lambda ^{\delta -1/2}. \end{aligned}$$

By Corollary 50, in the same range

$$\begin{aligned} \left| \frac{\partial \Psi ^\tau }{\partial v}\right| = \left| \psi ^\tau \left( \Gamma ^\tau _{-t}(y),x_2 \right) \right| \ge D^\tau \,\left( \frac{C}{2\,A}\,\right) ^2\lambda ^{2\,\delta -1}. \end{aligned}$$

Integrating by parts in v, we obtain that the contribution of $U_1^\lambda$ to the asymptotics of (114) is $O\left( \lambda ^{-\infty }\right)$.

On the other hand, if $y\in U^\lambda _2$ then

$$\begin{aligned} \left| \frac{\partial \Psi ^\tau }{\partial u}\right| = \left| \psi ^\tau \left( y,x_1\right) \right| \ge D^\tau \, \textrm{dist}_{X^\tau }(y,x_1)^2 >\frac{D^\tau \,C^2}{9}\,\lambda ^{2\,\delta -1}. \end{aligned}$$

Integrating by parts in u, we obtain that the contribution of $U_2^\lambda$ is also $O\left( \lambda ^{-\infty }\right)$. $\square$

We focus on statement 2. Let us set

$$\begin{aligned} x_{j\lambda }:=x+\left( \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }} \right) . \end{aligned}$$

(119)

Under the assumptions,

$$\begin{aligned} \textrm{dist}_{X^\tau }(x,x_{j\lambda })\le 2\,C\,\lambda ^{\delta -\frac{1}{2}}. \end{aligned}$$

(120)

Let $h^\tau$ be a Riemannian metric on $X^\tau$ that in a sufficiently small neighborhood of x is given in Heisenberg local coordinates by

$$\begin{aligned} h^\tau =\frac{1}{\tau ^2}(\textrm{d}\theta )^2+ \textrm{d}z'\otimes \textrm{d}{\overline{z}}'+ \textrm{d}{\overline{z}}'\otimes \textrm{d}z'. \end{aligned}$$

Thus $h^\tau _x={\hat{\kappa }}^\tau _x$ by Corollary 35. Let $\widetilde{\textrm{dist}}_{X^\tau }:X^\tau \times X^\tau \rightarrow {\mathbb {R}}$ be the Riemannian distance of $h^\tau$. By the latter remark,

$$\begin{aligned} \widetilde{\textrm{dist}}_{X^\tau }(x,y)/\textrm{dist}_{X^\tau }(x,y) \rightarrow 1 \quad \text {for}\quad y\rightarrow x. \end{aligned}$$

For $r>0$, let $B_x(r)\subseteq X^\tau$ be the open ball centered at x for $h^\tau$. Let r be small enough that $B_x(r)\subset U^\tau$, and consider the open cover of $X^\tau$

$$\begin{aligned} {\mathcal {B}}:=\left\{ B_x(r), \overline{B_x(r/2)}^c\right\} . \end{aligned}$$

Let $(b_1,b_2)$ be a partition of unity subordinate to ${\mathcal {B}}$. For some fixed $R>0$ and any $\lambda \gg 1$, let $b_j^\lambda \in {\mathcal {C}}^\infty (X^\tau )$ be defined in Heisenberg local coordinates by

$$\begin{aligned} b_j^\lambda \left( (\theta _0,z')\right) := b_j\left( \frac{r}{12\,C}\, \lambda ^{1/2-\delta } \,(\theta _0,z') \right) . \end{aligned}$$

Thus $\left\{ b_1^\lambda ,b_2^\lambda \right\}$ is a partition of unity subordinate to the rescaled open cover ${\mathcal {B}}^\lambda := \left\{ B_x\left( 12\,C\, \lambda ^{\delta -1/2} \right) , \overline{ B_x\left( 6\,C\, \lambda ^{\delta -1/2} \right) } ^c\right\}$. For $y\in \textrm{supp}\left( b_2^\lambda \right)$ and $\lambda \gg 0$,

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( x, y\right) \ge \frac{1}{2}\,\widetilde{\textrm{dist}}_{X^\tau }\left( x, y\right) \ge 3\,C\,\lambda ^{\delta -1/2}. \end{aligned}$$

(121)

The asymptotics of $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })$ are given by (114) with $(x_1,x_2)$ replaced by $(x_{1\lambda },x_{2\lambda })$.

Lemma 61

Only a negligible contribution to the asymptotics of $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })$ is lost, if the integrand in (114) is multiplied by $b_1^\lambda (y)$.

Proof

For $y\in \textrm{supp}\left( b_2^\lambda \right)$ and $\lambda \gg 0$,

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( x, y\right) \ge \frac{1}{2}\,\widetilde{\textrm{dist}}_{X^\tau }\left( x, y\right) \ge 3\,C\,\lambda ^{\delta -1/2}. \end{aligned}$$

(122)

Hence where $b_1^\lambda (y)= 0$ in view of (120)

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( x_{1\lambda }, y\right)\ge & {} \textrm{dist}_{X^\tau }\left( x, y\right) -\textrm{dist}_{X^\tau }\left( x, x_{1\lambda }\right) \\\ge & {} 3\,C\,\lambda ^{\delta -1/2}-2\,C\,\lambda ^{\delta -1/2} =C\,\lambda ^{\delta -1/2}. \end{aligned}$$

Recalling (115), with $x_j$ replaced by $x_{j\lambda }$, the claim follows arguing as in the proof of statement 1. (integrate by parts in u). $\square$

We conclude from (114) and Lemma 61 that

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })\nonumber \\{} & {} \quad \sim \frac{\lambda ^2}{\sqrt{2\,\pi }}\,\int _{1/(2\,D)}^{2\,D}\, \textrm{d}u\,\int _{1/(2\,D)}^{2\,D}\,\textrm{d}v\, \int _{-\infty }^{+\infty }\,\textrm{d}\theta \,\int _{{\mathbb {R}}^{2\,d}}\,\textrm{d}{\textbf{u}}\, \int _{-\epsilon }^{+\epsilon }\,\textrm{d}t\nonumber \\{} & {} \qquad \left[ e^{\imath \,\lambda \,\Psi ^\tau \big (x_{1\lambda },x_{2\lambda };u,v,t,y(\theta ,{\textbf{u}})\big )}\, b_1^\lambda \big (y(\theta ,{\textbf{u}})\big )\, A_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };u,v,t,y(\theta ,{\textbf{u}})\big )\,{\mathcal {V}}(\theta ,{\textbf{u}}) \right] .\nonumber \\ \end{aligned}$$

(123)

On the domain of integration, $(\theta /\tau ,{\textbf{u}})$ ranges in a shrinking ball of radius $O\left( \lambda ^{\delta -1/2}\right)$ centered at the origin in ${\mathbb {R}}^{2d+1}$.

Next we show that integration in $\textrm{d}t$ may be localized to a shrinking neighbourhood of the origin.

Let us fix a constant $C_1>0$ such that for all $\lambda \gg 0$ and $y=y(\theta ,{\textbf{u}})$ on the support of $b_1^\lambda \big (y(\theta ,{\textbf{u}})\big )$

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( x_{2\lambda },y\right) \le \textrm{dist}_{X_\tau }(x_{2\lambda },x)+\textrm{dist}_{X^\tau } (x,y)\le C_1\,\lambda ^{\delta -\frac{1}{2}}. \end{aligned}$$

(124)

Let $\beta \in {\mathcal {C}}^\infty _0({\mathbb {R}})$ be such that $\beta (t)\equiv 1$ on $[-1,1]$, and define $\beta ^\lambda (t):= \beta \left( \frac{1}{3\,C_1}\,\lambda ^{\frac{1}{2}-\delta }\,t \right)$. Then $1-\beta ^\lambda (t)=0$ if $|t|\le 3\,C_1\,\lambda ^{\delta -\frac{1}{2}}$.

We have

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })\sim \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })'+ \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })'', \end{aligned}$$

where $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })'$ and $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })''$ are as in (123), but with the integrand multiplied, respectively, by $\beta ^\lambda (t)$ and $1-\beta ^\lambda (t)$.

Lemma 62

$\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })''= O\left( \lambda ^{-\infty }\right)$.

Proof

Where $1-\beta ^\lambda (t)\ne 0$, we have $|t|> 3\,C_1\,\lambda ^{\delta -\frac{1}{2}}$. In view of (43), if $\epsilon$ is small enough and and $|\epsilon |>|t|> 3\,C_1\,\lambda ^{\delta -\frac{1}{2}}$ then

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),y\right) \ge \frac{t}{2}\ge \frac{3}{2}\,C_1\,\lambda ^{\delta -\frac{1}{2}}. \end{aligned}$$

Therefore, by (124) on the support of the integrand of $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })''$ we have

$$\begin{aligned} \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),x_{2\lambda } \right)\ge & {} \textrm{dist}_{X^\tau }\left( \Gamma ^\tau _{-t}(y),y\right) - \textrm{dist}_{X^\tau }\left( x_{2\lambda },y\right) \ge \frac{C_1}{2}\,\lambda ^{\delta -\frac{1}{2}}. \end{aligned}$$

The claim follows again by the argument in the proof of statement 1, by iterated integration by parts in v. $\square$

With the rescalings $\theta \rightsquigarrow \theta /\sqrt{\lambda }$, ${\textbf{u}}\rightsquigarrow {\textbf{u}}/\sqrt{\lambda }$, $t\rightsquigarrow t/\sqrt{\lambda }$, (123) becomes

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })\nonumber \\{} & {} \quad \sim \frac{\lambda ^{2-d}}{\sqrt{2\,\pi }}\,\int _{1/(2\,D)}^{2\,D}\,\, \textrm{d}u\,\int _{1/(2\,D)}^{2\,D}\,\,\textrm{d}v\, \int _{-\infty }^{+\infty }\,\textrm{d}\theta \,\int _{{\mathbb {R}}^{2\,d}}\,\textrm{d}{\textbf{u}}\, \int _{-\infty }^{+\infty }\,\textrm{d}t\nonumber \\{} & {} \qquad \left[ e^{\imath \,\lambda \, \Psi ^\tau _\lambda \big (x_{1\lambda },x_{2\lambda };u,v,t,\theta ,{\textbf{u}}\big )}\, B_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };u,v,t,\theta ,{\textbf{u}} \big ) \right] , \end{aligned}$$

(125)

where, in view of (115),

$$\begin{aligned}{} & {} \Psi ^\tau _\lambda \big (x_{1\lambda },x_{2\lambda };u,v,t,\theta ,{\textbf{u}}\big )\nonumber \\{} & {} \quad :=\Psi ^\tau \left( x_{1\lambda },x_{2\lambda }; u,v,\frac{t}{\sqrt{\lambda }}, y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}})\right) \right) ,\nonumber \\{} & {} \quad = u\,\psi ^\tau \left( x_{1\lambda }, y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}})\right) \right) +v\,\psi ^\tau \left( \Gamma ^\tau _{-t/\sqrt{\lambda }} \left( y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}}) \right) \right) ,x_{2\lambda } \right) -\frac{t}{\sqrt{\lambda }},\nonumber \\{} & {} B_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };u,v,t,\theta ,{\textbf{u}})\big ) \end{aligned}$$

(126)

$$\begin{aligned}{} & {} \quad :=b_1^\lambda \left( y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}}\right) \right) \, A_\lambda ^\tau \left( x_{1\lambda },x_{2\lambda }; u,v,\frac{t}{\sqrt{\lambda }}, y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}})\right) \right) \cdot {\mathcal {V}}\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}})\right) .\nonumber \\ \end{aligned}$$

(127)

Integration in $(t,\theta ,{\textbf{v}})$ in (125) is over an expanding ball centered at the origin and radius $O\left( \lambda ^\delta \right)$.

We now make explicit the dependence of $\Psi ^\tau _\lambda$ in (126) on the rescaled variables. By Proposition 48,

$$\begin{aligned}{} & {} \imath \,\psi ^\tau \left( x_{1\lambda },y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}}) \right) \right) \nonumber \\{} & {} \quad =\imath \,\frac{\theta _1-\theta }{\sqrt{\lambda }} -\frac{1}{4\,\tau ^2\,\lambda }\,\left( \theta _1-\theta \right) ^2 +\frac{\psi _2^{\omega _x}\left( {\textbf{v}}_1,{\textbf{u}}\right) }{\lambda } +R_3\left( \frac{\theta _1}{\sqrt{\lambda }},\frac{{\textbf{v}}_1}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) .\nonumber \\ \end{aligned}$$

(128)

Furthermore, by Corollary 45 and (105),

$$\begin{aligned}{} & {} \Gamma ^\tau _{-t/\sqrt{\lambda }} \left( y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}}) \right) \right) \nonumber \\{} & {} \quad =x+\left( \frac{1}{\sqrt{\lambda }}\left( \theta +\tau \,t\right) -\frac{t}{\lambda }\,\left( \frac{1}{2\,\tau ^2}\, a_x\,\theta +\langle {\textbf{A}}_x,{\textbf{u}}\rangle \right) + R_3\left( \frac{\tau \,t}{\sqrt{\lambda }},\frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{v}}}{\sqrt{\lambda }}\right) ,\right. \nonumber \\{} & {} \qquad \left. \frac{{\textbf{u}}}{\sqrt{\lambda }} + {\textbf{R}}_2\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }}\right) \right) . \end{aligned}$$

(129)

Therefore, again by Proposition 48,

$$\begin{aligned}{} & {} \imath \,\psi ^\tau \left( \Gamma ^\tau _{-t/\sqrt{\lambda }} \left( y\left( \frac{1}{\sqrt{\lambda }}\,(\theta ,{\textbf{u}}) \right) \right) ,x_{2\lambda } \right) \nonumber \\{} & {} \quad =\frac{\imath }{\sqrt{\lambda }}\,(\theta +\tau \,t-\theta _2) -\frac{\imath }{\lambda }\,t\, \left( \frac{1}{2\,\tau ^2}\, a_x\,\theta +\langle {\textbf{A}}_x,{\textbf{u}}\rangle \right) \nonumber \\{} & {} \qquad -\frac{1}{4\,\tau ^2\,\lambda }\,(\theta +\tau \,t-\theta _2)^2 +\frac{\psi _2^{\omega _x}\left( {\textbf{u}},{\textbf{v}}_2\right) }{\lambda } +R_3\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _2}{\sqrt{\lambda }},\frac{{\textbf{v}}_2}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) .\qquad \end{aligned}$$

(130)

We finally obtain

$$\begin{aligned}{} & {} \imath \,\lambda \, \Psi ^\tau _\lambda \big (x_{1\lambda },x_{2\lambda };u,v,t,\theta ,{\textbf{u}}\big )\nonumber \\{} & {} \quad =\imath \,\sqrt{\lambda }\,\Upsilon ^\tau (t,v,\theta ,u) +S({\textbf{u}},t,v,\theta ,u)+\lambda \,R_3\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) ,\qquad \end{aligned}$$

(131)

where

$$\begin{aligned} \Upsilon ^\tau (t,v,\theta ,u)= & {} \Upsilon ^\tau (\theta _j,{\textbf{v}}_j; t,v,\theta ,u)\nonumber \\:= & {} u\,(\theta _1-\theta )+v\,(\theta +\tau \,t-\theta _2)-t, \end{aligned}$$

(132)

$$\begin{aligned} S({\textbf{u}},t,v,\theta ,u)= & {} S_{\theta _j,{\textbf{v}}_j}({\textbf{u}},t,v,\theta ,u)\nonumber \\:= & {} -\imath \,v\,t\,\left( \frac{1}{2\,\tau ^2}\, a_x\,\,\theta +\langle {\textbf{A}}_x,{\textbf{u}}\rangle \right) \nonumber \\{} & {} -\frac{1}{4\,\tau ^2}\,u\,\left( \theta _1-\theta \right) ^2 -\frac{1}{4\,\tau ^2}\,v\,(\theta +\tau \,t-\theta _2)^2\nonumber \\{} & {} + u\,\psi _2^{\omega _x}\left( {\textbf{v}}_1,{\textbf{u}}\right) +v\,\psi _2^{\omega _x}\left( {\textbf{u}},{\textbf{v}}_2\right) , \end{aligned}$$

(133)

and $R_3$ vanishes to third order at the origin. Notice that $S({\textbf{u}},t,v,\theta ,u)$ is homogenous of degree 2 in the rescaled variables.

If we set $\theta ':=\theta -\theta _1$, $t':=\theta +\tau \,t-\theta _2$, and ${\textbf{u}}':={\textbf{u}}-{\textbf{v}}_1$, then

$$\begin{aligned} \Re \big (S({\textbf{u}},t,v,\theta ,u) \big )\le -b_0\,\Vert (t',\theta ',{\textbf{u}}')\Vert ^2 \end{aligned}$$

(134)

for some $b_0>0$.

In light of (131), we can rewrite (125) as follows:

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda }) \sim \frac{\lambda ^{2-d}}{\sqrt{2\,\pi }}\, \int _{{\mathbb {R}}^{2\,d-2}}\,I_\lambda ({\textbf{u}})\,\textrm{d}{\textbf{u}} \end{aligned}$$

(135)

where

$$\begin{aligned} I_\lambda ({\textbf{u}}):= & {} \int _{-\infty }^{+\infty }\,\textrm{d}t\, \int _{1/(2\,D)}^{2\,D}\, \textrm{d}v\,\int _{-\infty }^{+\infty }\,\textrm{d}\theta \, \int _{1/(2\,D)}^{2\,D}\,\,\textrm{d}u \nonumber \\{} & {} \quad \left[ e^{\imath \,\sqrt{\lambda }\,\Upsilon ^\tau (t,v,\theta ,u)}\, {\tilde{B}}_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };{\textbf{u}},t,v,\theta ,u \big ) \right] \end{aligned}$$

(136)

and, using (74), (116), (117), and (131)

$$\begin{aligned}{} & {} {\tilde{B}}_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };{\textbf{u}},t,v,\theta ,u\big )\nonumber \\{} & {} \quad :=e^{S({\textbf{u}},t,v,\theta ,u)+\lambda \,R_3\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) }\,B_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };{\textbf{u}},t,v,\theta ,u \big ). \end{aligned}$$

(137)

For every $N=1,2,\ldots$, Taylor expansion in the rescaled variables yields for the third order remainder $R_3$ in the exponent in (137)

$$\begin{aligned}{} & {} \lambda \,R_3\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) \nonumber \\{} & {} \quad =\sum _{s=0}^N\,\lambda ^{1-\frac{3+s}{2}}\, P_{3+s}(\theta _j,{\textbf{v}}_j, \theta ,{\textbf{u}})+\lambda \,R_{4+N}\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) , \end{aligned}$$

(138)

where $P_l$ denotes a homogeneous polynomial of degree l in the argument. On the domain of integration, the latter summand is bounded in absolute value by $C_N\,\lambda ^{1-\left( \frac{1}{2}-\delta \right) \,(4+N)}$ for some constant $C_N>0$. Passing to the exponential, we therefore obtain an asymptotic expansion

$$\begin{aligned}{} & {} e^{\lambda \,R_3\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) }=\sum _{k=0}^{+\infty }\frac{\lambda ^k}{k!}\, R_3\left( \frac{\tau \,t}{\sqrt{\lambda }}, \frac{\theta _j}{\sqrt{\lambda }},\frac{{\textbf{v}}_j}{\sqrt{\lambda }}, \frac{\theta }{\sqrt{\lambda }},\frac{{\textbf{u}}}{\sqrt{\lambda }} \right) ^k\nonumber \\{} & {} \quad \sim \sum _{k=0}^{+\infty }\frac{1}{k!}\, \left[ \sum _{s=0}^N\,\lambda ^{1-\frac{3+s}{2}}\, P_{3+s}(\theta _j,{\textbf{v}}_j, \theta ,{\textbf{u}})\right] ^k= \sum _{k=0}^{+\infty }\,\lambda ^{-\frac{k}{2}}\,Q_k (\theta _j,{\textbf{v}}_j, \theta ,{\textbf{u}}), \end{aligned}$$

(139)

where $Q_k$ is a polynomial of degree $\le 3\,k$.

On the other hand, the asymptotic expansion (74) yields

$$\begin{aligned}{} & {} s^\tau (x_{1\lambda },y,\lambda \,u)\sim \sum _{k\ge 0}\,(\lambda \, u)^{d-1-k}\,s^\tau _j(x_{1\lambda },y)\nonumber \\{} & {} \quad =(\lambda \,u)^{d-1}\,s^\tau _0(x,x) +\sum _{k+l\ge 1}\lambda ^{d-1-k-\frac{l}{2}}\, u^{d-1-k}\,S^\tau _{k,l}(\theta _1,{\textbf{v}}_1, \theta ,{\textbf{u}}), \end{aligned}$$

(140)

where $S^\tau _{k,l}$ is homogenous of degree l. Similarly, the asymptotic expansion in Lemma 56 yields

$$\begin{aligned}{} & {} r^\tau _t\left( y,x_{2\,\lambda },\,\lambda \,v\right) \sim \sum _{k\ge 0}\,(\lambda \, u)^{d-1-k}\,r^\tau _{t\,j}(y,x_{2\,\lambda })\nonumber \\{} & {} \quad =(\lambda \,u)^{d-1}\,s^\tau _{0}(x,x) +\sum _{k+l\ge 1}\lambda ^{d-1-k-\frac{l}{2}}\, u^{d-1-k}\,R^\tau _{k,l}(\theta _1,{\textbf{v}}_1, \theta ,{\textbf{u}}), \end{aligned}$$

(141)

where again $R^\tau _{k,l}$ is homogeneous of degree l, and we have used that $r^\tau _{0,\,0}(x,x)=s^\tau _0(x,x)$.

Multiplying (139), (140), (141), and the Taylor expansion of $\chi$ and ${\mathcal {V}}$ at the origin, we obtain an asymptotic expansion

$$\begin{aligned}{} & {} {\tilde{B}}_\lambda ^\tau \big (x_{1\lambda },x_{2\lambda };{\textbf{u}},t,v,\theta ,u \big )\nonumber \\{} & {} \quad \sim \lambda ^{2d-2}\,\frac{2^{d-1}}{\tau }\, \chi (0)\, e^{S({\textbf{u}},t,v,\theta ,u)}\, u^{d-1}\,v^{d-1}\,s^\tau _0(x,x)^2\cdot \beta \left( \lambda ^{-\delta }\,\left( {\textbf{u}}, t,\theta \right) \right) \nonumber \\{} & {} \qquad \cdot \left[ 1+\sum _{k\ge 1}\lambda ^{-k/2}\, B_k(x;{\textbf{u}},\theta _j,{\textbf{v}}_j,t,v,\theta ,u) \right] , \end{aligned}$$

(142)

where $B_k(x;\cdot )$ is a polynomial of degree $\le 3\,k$ in $(\theta _j,{\textbf{v}}_j,{\textbf{u}},t,\theta )$, while $\beta$ is compactly supported and identically equal to 1 in a suitable neighborhood of the origin. The latter is indeed an asymptotic expansion for $\delta \in (0,1/6)$. Furthermore, fractional powers of $\lambda$ arise from Taylor expansion in $(\theta _j,{\textbf{v}}_j,{\textbf{u}})$, while the asymptotic expansion for the amplitude in the Szegö kernel parametrix is by descending integer powers. Hence $P_j$ will be even for j even (corresponding to integer powers of $\lambda$), and odd for j odd (corresponding to fractional powers).

Inserting (142) in (136), we obtain an asymptotic expansion for the integrand which, in view of (134) or the previous remark on the domain of integration, can be integrated term by term. Each term is an oscillatory integral with phase (132) in the parameters $(t,v,\theta ,u)$, and depending parametrically on the other parameters.

Now we remark that the asymptotics of (135) are unaltered, if integration in $(t,\theta )$ is restricted to a suitable compact set. In fact, since $\partial _u\Upsilon ^\tau =\theta _1-\theta$, $\partial _v\Upsilon ^\tau =\theta +\tau \,t-\theta _2$, integration by parts in (u, v) implies the following.

Lemma 63

Only a negligible contribution to the asymptotics of (125) is lost, if the amplitude (137) is multiplied by a compactly supported cut-off function in $(\theta , t)$, identically equal to 1 near $\big (\theta _1,(\theta _2-\theta _1)/\tau \big )$.

We shall leave the latter cut-off implicit in the following, and simply assume henceforth that integration in $(\theta ,t)$ is over a compact neighborhood of $\big (\theta _1,(\theta _2-\theta _1)/\tau \big )$.

The proof of the following is omitted.

Lemma 64

$\Upsilon ^\tau$ in (132) has a unique stationary point $P_s=(t_s,v_s,\theta _s,u_s)$, given by

$$\begin{aligned} P_s^\tau =\left( \frac{\theta _2-\theta _1}{\tau },\,\frac{1}{\tau },\,\theta _1,\,\frac{1}{\tau } \right) . \end{aligned}$$

The critical point is non-degenerate. The Hessian matrix and its inverse at the critical point are

$$\begin{aligned} H(\Upsilon ^\tau )_{P_s^\tau }= \begin{pmatrix} 0&{}\quad \tau &{}\quad 0&{}\quad 0\\ \tau &{}\quad 0&{}\quad 1&{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0&{}\quad -1 \\ 0&{}\quad 0&{}\quad -1&{}\quad 0 \end{pmatrix},\quad H(\Upsilon ^\tau )_{P_s^\tau }^{-1}= \begin{pmatrix} 0&{}\quad 1/\tau &{}\quad 0&{}\quad 1/\tau \\ 1/\tau &{}\quad 0&{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0&{}\quad -1 \\ 1/\tau &{}\quad 0&{}\quad -1&{}\quad 0 \end{pmatrix}. \end{aligned}$$

The Hessian determinant, the Hessian signature, and the critical value are

$$\begin{aligned} \det H(\Upsilon ^\tau )_{P_s^\tau }=\tau ^2,\quad \textrm{sgn}H(\Upsilon ^\tau )_{P_s^\tau }= 0,\quad \Upsilon ^\tau (P_s^\tau )=\frac{\theta _1-\theta _2}{\tau }. \end{aligned}$$

The third order remainder at $P_s$ is zero.

Let us set

$$\begin{aligned} L:=\frac{1}{\tau }\,\left( \frac{\partial ^2}{\partial t\partial u} +\frac{\partial ^2}{\partial t\partial v} \right) -\frac{\partial ^2}{\partial \theta \,\partial u}, \end{aligned}$$

(143)

and apply the Lemma of Stationary Phase to (136) in correspondence to the k-th summand in (142); we obtain an asymptotic expansion whose r-th summand (for $r=0,1,2,\ldots$) is a multiple of

$$\begin{aligned}{} & {} (4\,\pi ^2/\tau )\cdot e^{\imath \,\sqrt{\lambda }\,\frac{\theta _1-\theta _2}{\tau }} \cdot \lambda ^{2d-3-(r+k)/2}\nonumber \\{} & {} \quad \cdot \left. L^r\left( e^{S({\textbf{u}},t,v,\theta ,u)}\, u^{d-1}\,v^{d-1}\,P_k(x;\theta _j,{\textbf{v}}_j,{\textbf{u}},t,v,\theta ,u)\right) \right| _{P_s}, \end{aligned}$$

(144)

where the dependence on $(\theta _j,{\textbf{v}}_j)$ of the exponent is left implicit for brevity. In view of (133), with the notation of Definition 57 the value of $S({\textbf{u}},t,v,\theta ,u)$ at the critical point is

$$\begin{aligned} S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}}):= & {} S_{\theta _j,{\textbf{v}}_j}({\textbf{u}},t_s,v_s,\theta _s,u_s)\nonumber \\= & {} \imath \cdot \left[ \frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x+ \frac{\theta _1-\theta _2}{\tau ^2}\cdot \langle {\textbf{A}}_x,{\textbf{u}}\rangle \right] \nonumber \\{} & {} + \frac{1}{\tau }\,\psi _2^{\omega _x}\left( {\textbf{v}}_1,{\textbf{u}}\right) +\frac{1}{\tau }\,\psi _2^{\omega _x}\left( {\textbf{u}},{\textbf{v}}_2\right) \nonumber \\= & {} \imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x -\frac{\imath }{\tau }\cdot \omega _x\big (J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{u}}\big )\nonumber \\{} & {} + \frac{1}{\tau }\,\psi _2^{\omega _x}\left( {\textbf{v}}_1,{\textbf{u}}\right) +\frac{1}{\tau }\,\psi _2^{\omega _x}\left( {\textbf{u}},{\textbf{v}}_2\right) . \end{aligned}$$

(145)

Thus

$$\begin{aligned} S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})= & {} \imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x \nonumber \\{} & {} +\frac{1}{\tau }\left[ -\imath \,\omega _x\big ( {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{u}}\big ) -\frac{1}{2}\,\left( \Vert {\textbf{v}}_1\Vert ^2+\Vert {\textbf{v}}_2\Vert ^2 \right) \right. \nonumber \\{} & {} \left. -\Vert {\textbf{u}}\Vert ^2 +\langle {\textbf{u}},{\textbf{v}}_1+{\textbf{v}}_2 \rangle \right. \Bigg ]\nonumber \\= & {} \imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x \nonumber \\{} & {} + \frac{1}{\tau }\Bigg [ -\frac{1}{2}\,\left( \Vert {\textbf{v}}_1\Vert ^2+\Vert {\textbf{v}}_2\Vert ^2 \right) +\frac{1}{4}\,\Vert {\textbf{v}}_1 +{\textbf{v}}_2\Vert ^2\nonumber \\{} & {} \left. -\imath \,\omega _x\big ( {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{u}}\big ) -\left\| {\textbf{u}}-\frac{1}{2}\,({\textbf{v}}_1+{\textbf{v}}_2) \right\| ^2\right] . \end{aligned}$$

(146)

In particular, $S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})$ is homogenous of degree 2.

It follows from (133) and (143) that (144) is a linear combination of terms of the form $\lambda ^{2d-3-k/2}\,P_k(x; \theta _j,{\textbf{v}}_j,{\textbf{u}})\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})}$, where $P_k(x;\cdot )$ is a polynomial of degree $\le 3\,k$. Furthermore, using that $S({\textbf{u}},t,v,\theta ,u)$ is homogenous of degree 2 in the rescaled variables, the explicit expression (143) of L, and the linear dependence of $\theta _s$ and $t_s$ on $(\theta _1,\theta _2)$, one verifies that $P_k(x;\cdot )$ has parity k.

Putting all these asymptotic expansions together, we obtain an asymptotic expansion for $I_\lambda ({\textbf{u}})$ of the form

$$\begin{aligned} I_\lambda ({\textbf{u}})\sim & {} e^{\imath \,\sqrt{\lambda }\,\frac{\theta _1-\theta _2}{\tau }} \cdot \frac{\lambda ^{2d-3}}{(2\,\pi ^2\,\tau ^2)^{d-1}} \cdot \chi (0)\, e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})}\nonumber \\{} & {} \cdot \beta _1\left( \lambda ^{-\delta }\, {\textbf{u}}, \right) \left[ 1+\sum _{k\ge 1}\lambda ^{-k/2}\,F_k(x; \theta _j,{\textbf{v}}_j,{\textbf{u}})\right] \end{aligned}$$

(147)

where $F_k(x;\cdot )$ is a polynomial of degree $\le 3\,k$ and parity k, and $\beta _1$ is an appropriate cut-off function identically equal to one near the origin.

The asymptotic expansion (147) may be integrated term by term. In view of the rapidly decreasing exponential $e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})}$, we obtain

$$\begin{aligned}{} & {} \Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda }) =\frac{\lambda ^{2-d}}{\sqrt{2\,\pi }}\, \int _{{\mathbb {R}}^{2\,d-2}}\,I_\lambda ({\textbf{u}})\,\textrm{d}{\textbf{u}}\nonumber \\{} & {} \quad \sim e^{\imath \,\sqrt{\lambda }\,\frac{\theta _1-\theta _2}{\tau }} \cdot \frac{\lambda ^{d-1}}{\sqrt{2\,\pi }}\cdot \frac{1}{(\sqrt{2}\,\pi \,\tau )^{2\,(d-1)}} \cdot \chi (0)\, \int _{{\mathbb {R}}^{2\,d-2}}\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})} \textrm{d}{\textbf{u}}\nonumber \\{} & {} \qquad \cdot \left[ 1+\sum _{k\ge 1}\lambda ^{-k/2}\, \int _{{\mathbb {R}}^{2\,d-2}}\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})} F_k(x; \theta _j,{\textbf{v}}_j,{\textbf{u}})\, \textrm{d}{\textbf{u}} \right] . \end{aligned}$$

(148)

We compute the leading order term using (146). With the change of variable

$$\begin{aligned} {\textbf{w}}:={\textbf{u}}-\frac{1}{2}\,({\textbf{v}}_1+{\textbf{v}}_2), \end{aligned}$$

we have

$$\begin{aligned}{} & {} S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})\nonumber \\{} & {} \quad = \imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x \nonumber \\{} & {} \qquad + \frac{1}{\tau }\left[ -\imath \,\omega _x\left( {\textbf{v}}_1-{\textbf{v}}_2+ J_x({\textbf{a}}),\frac{1}{2}\,({\textbf{v}}_1+{\textbf{v}}_2)\right) -\frac{1}{2}\,\left( \Vert {\textbf{v}}_1\Vert ^2+\Vert {\textbf{v}}_2\Vert ^2 \right) +\frac{1}{4}\,\Vert {\textbf{v}}_1+{\textbf{v}}_2\Vert ^2\right. \nonumber \\{} & {} \qquad \left. -\imath \,\omega _x\left( {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{w}}\right) -\left\| {\textbf{w}}\right\| ^2\right. \Bigg ]\nonumber \\{} & {} \quad = \imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x \nonumber \\{} & {} \qquad + \frac{1}{\tau }\left[ -\imath \,\omega _x\left( {\textbf{v}}_1,{\textbf{v}}_2\right) -\imath \,\omega _x\left( J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),\frac{1}{2}\,({\textbf{v}}_1+{\textbf{v}}_2)\right) -\frac{1}{2}\,\left( \Vert {\textbf{v}}_1\Vert ^2+\Vert {\textbf{v}}_2\Vert ^2 \right) \right. \nonumber \\{} & {} \qquad \left. +\frac{1}{4}\,\Vert {\textbf{v}}_1+{\textbf{v}}_2\Vert ^2-\imath \,\omega _x\left( {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{w}}\right) -\left\| {\textbf{w}}\right\| ^2\right] . \end{aligned}$$

(149)

Let us set ${\textbf{v}}_j':=\frac{1}{\sqrt{\tau }}\, {\textbf{v}}_j$, ${\textbf{a}}':=\frac{1}{\sqrt{\tau }}\, {\textbf{a}}_x(\theta _1,\theta _2)$. With the further change of variable ${\textbf{w}}=\frac{1}{\sqrt{2}}\,{\textbf{r}}$, we obtain

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}^{2\,d-2}}\, e^{\frac{1}{\tau }\,\big [-\imath \,\omega _x\left( {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big ),{\textbf{w}}\right) -\left\| {\textbf{w}}\right\| ^2\big ]} \textrm{d}{\textbf{w}}\nonumber \\{} & {} \quad =\frac{1}{2^{d-1}}\,\int _{{\mathbb {R}}^{2\,d-2}}\, e^{\frac{1}{\tau }\,\left[ -\imath \,\omega _x\left( \frac{1}{\sqrt{2}}\big ( {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big )\big ),{\textbf{r}}\right) -\frac{1}{2}\,\left\| {\textbf{r}}\right\| ^2\right] } \textrm{d}{\textbf{r}}\nonumber \\{} & {} \quad =\frac{1}{2^{d-1}}\,\int _{{\mathbb {R}}^{2\,d-2}}\, e^{-\imath \,\omega _x\left( \frac{1}{\sqrt{2\,\tau }}\big ( {\textbf{v}}_1'-{\textbf{v}}_2'+ J_x({\textbf{a}}')\big ),\frac{{\textbf{r}}}{\sqrt{\tau }}\right) -\frac{1}{2}\,\left\| \frac{{\textbf{r}}}{\sqrt{\tau }}\right\| ^2} \textrm{d}{\textbf{r}}\nonumber \\{} & {} \quad =\left( \frac{\tau }{2}\right) ^{d-1}\,\int _{{\mathbb {R}}^{2\,d-2}}\, e^{-\imath \,\omega _x\left( \frac{1}{\sqrt{2\,\tau }}\big ( {\textbf{v}}_1'-{\textbf{v}}_2'+ J_x({\textbf{a}}')\big ),{\textbf{s}}\right) -\frac{1}{2}\,\left\| {\textbf{s}}\right\| ^2} \textrm{d}{\textbf{s}}\nonumber \\{} & {} \quad =\left( \frac{\tau }{2}\right) ^{d-1}\,(2\,\pi )^{d-1} e^{ -\frac{1}{4\,\tau }\,\left\| {\textbf{v}}_1-{\textbf{v}}_2+ J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big )\right\| ^2}\nonumber \\{} & {} \quad =\left( \tau \,\pi \right) ^{d-1}\cdot e^{ -\frac{1}{4\,\tau }\,\left\| {\textbf{v}}_1-{\textbf{v}}_2\right\| ^2 -\frac{1}{4\,\tau }\,\left\| J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big )\right\| ^2 -\frac{1}{2\,\tau }\,\left\langle {\textbf{v}}_1-{\textbf{v}}_2, J_x\big ({\textbf{a}}_x(\theta _1,\theta _2)\big )\right\rangle }. \end{aligned}$$

(150)

We have

$$\begin{aligned}{} & {} -\frac{1}{2\,\tau }\, \left( \Vert {\textbf{v}}_1\Vert ^2+\Vert {\textbf{v}}_2\Vert ^2 \right) +\frac{1}{4\,\tau }\,\Vert {\textbf{v}}_1+{\textbf{v}}_2\Vert ^2 -\frac{1}{4\,\tau }\,\left\| {\textbf{v}}_1-{\textbf{v}}_2\right\| ^2\nonumber \\{} & {} \quad =-\frac{1}{2\,\tau }\,\left( \Vert {\textbf{v}}_1\Vert ^2+\Vert {\textbf{v}}_2\Vert ^2\right) +\frac{1}{\tau }\,\langle {\textbf{v}}_1,{\textbf{v}}_2\rangle = -\frac{1}{2\,\tau }\,\Vert {\textbf{v}}_1-{\textbf{v}}_2\Vert ^2. \end{aligned}$$

(151)

Hence

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}^{2\,d-2}}\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})}\, \textrm{d}{\textbf{u}}\nonumber \\{} & {} \quad = e^{\imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x} \cdot \left( \tau \,\pi \right) ^{d-1}\, e^{\frac{1}{\tau }\,\left[ -\imath \,\omega _x\left( {\textbf{v}}_1,{\textbf{v}}_2\right) -\frac{1}{2}\,\Vert {\textbf{v}}_1-{\textbf{v}}_2\Vert ^2-\frac{\imath }{2}\,\omega _x\left( J_x({\textbf{a}}),{\textbf{v}}_1+{\textbf{v}}_2\right) \right] }\nonumber \\{} & {} \qquad \cdot e^{-\frac{1}{4}\,\left\| J_x({\textbf{a}})\right\| ^2 -\frac{1}{2}\,\langle {\textbf{v}}_1-{\textbf{v}}_2,J_x({\textbf{a}})\rangle }\nonumber \\{} & {} \quad =e^{\imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x} \cdot \left( \tau \,\pi \right) ^{d-1}\nonumber \\{} & {} \qquad \cdot e^{\frac{1}{\tau }\,\left[ -\imath \,\omega _x\left( {\textbf{v}}_1,{\textbf{v}}_2\right) -\frac{1}{4}\,\Vert {\textbf{v}}_1-{\textbf{v}}_2\Vert ^2 -\frac{1}{4}\,\Vert {\textbf{v}}_1-{\textbf{v}}_2+J_x({\textbf{a}})\Vert ^2 -\frac{\imath }{2}\,\omega _x\left( J_x({\textbf{a}}),{\textbf{v}}_1+{\textbf{v}}_2\right) \right] }. \end{aligned}$$

(152)

Recalling Definition 57, we conclude

$$\begin{aligned} \int _{{\mathbb {R}}^{2\,d-2}}\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})}\, \textrm{d}{\textbf{u}}= e^{\imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x} \cdot \left( \tau \,\pi \right) ^{d-1}\,e^{\frac{1}{\tau }\,\Psi _2\big ((\theta _1,{\textbf{v}}_1),(\theta _2,{\textbf{v}}_2)\big )}. \end{aligned}$$

(153)

Hence the leading order term in the asymptotic expansion (148) is

$$\begin{aligned} \frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\, e^{\imath \,\sqrt{\lambda }\,\frac{\theta _1-\theta _2}{\tau }} \, e^{\imath \,\frac{(\theta _1-\theta _2)\,\theta _1}{2\,\tau ^4}\,a_x} \,\chi (0)\, e^{\frac{1}{\tau }\,\Psi _2\big ((\theta _1,{\textbf{v}}_1),(\theta _2,{\textbf{v}}_2)\big )}. \end{aligned}$$

(154)

Lemma 65

$a_x=0$.

Proof

Let us consider the special case where ${\textbf{v}}_1={\textbf{v}}_2={\textbf{0}}$ and $\theta _2=0$, and set $x_\lambda :=x+(\theta /\sqrt{\lambda },{\textbf{0}})$. By (154), the leading order term for the asymptotic expansion of $\Pi _{\chi ,\lambda }(x_\lambda ,x)$ is

$$\begin{aligned} \frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\, e^{\imath \,\sqrt{\lambda }\,\frac{\theta }{\tau }} \, e^{\imath \,\frac{\theta ^2}{\tau ^4}\,a_x} \,\chi (0)\, e^{-\frac{1}{4\,\tau }\,\Vert J_x({\textbf{a}})\Vert ^2}, \end{aligned}$$

while the one for $\Pi _{\chi ,\lambda }(x,x_\lambda )$ is

$$\begin{aligned} \frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\, e^{-\imath \,\sqrt{\lambda }\,\frac{\theta }{\tau }} \,\chi (0)\, e^{-\frac{1}{4\,\tau }\,\Vert J_x({\textbf{a}})\Vert ^2}. \end{aligned}$$

Since $\Pi _{\chi ,\lambda }^\tau (x,x_\lambda )= \overline{\Pi _{\chi ,\lambda }^\tau (x_\lambda ,x)}$ for any $\theta$, $a_x=0$. $\square$

Lemma 66

${\textbf{A}}_x=0$.

Proof

Given Lemma 43 and Corollary 45,

$$\begin{aligned} \Gamma ^\tau _{\theta /\sqrt{\lambda }}(x)=x+ \left( -\frac{\tau \,\theta }{\sqrt{\lambda }}+R_3\left( \frac{\tau \,\theta }{\sqrt{\lambda }}\right) , {\textbf{R}}_2\left( \frac{\tau \,\theta }{\sqrt{\lambda }}\right) \right) . \end{aligned}$$

Hence, in view of Lemma 65, (148), and (154)

$$\begin{aligned} \Pi ^\tau _{\chi ,\lambda }\left( \Gamma ^\tau _{\theta /\sqrt{\lambda }}(x), x \right)&\asymp&\frac{1}{\sqrt{2\,\pi }}\cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\, e^{-\imath \,\sqrt{\lambda }\,\theta } \,\chi (0)\, e^{\frac{1}{\tau }\,\Psi _2\big ((-\tau \,\theta ,{\textbf{0}}),(0,{\textbf{0}})\big )}\\= & {} \frac{1}{\sqrt{2\,\pi }} \cdot \left( \frac{\lambda }{2\,\pi \tau }\right) ^{d-1}\, e^{-\imath \,\sqrt{\lambda }\,\theta } \,\chi (0)\, e^{-\frac{\theta ^2}{4\,\tau }\,\Vert {\textbf{A}}_x\Vert ^2}, \end{aligned}$$

where $\asymp$ means ‘asymptotic to leading order’. The estimate holds uniformly for $|\theta |\le C\,\lambda ^\delta$.

On the other hand, by Theorem 1.1 of [11] in the same range we also have

$$\begin{aligned} \left| \Pi ^\tau _{\chi ,\lambda }\left( \Gamma ^\tau _{\theta /\sqrt{\lambda }}(x), x \right) \right|&\asymp&C_{d,\tau }'\, \lambda ^{d-1}\,\chi (0), \end{aligned}$$

for some constant $C'_{d,\tau }$, and the claim follows. $\square$

Let us consider the lower order terms. The coefficient of $\lambda ^{d-1-\frac{k}{2}}$ in the expansion (148) is a linear combination of Gaussian integrals of the form

$$\begin{aligned} \theta _j^{l}\cdot {\textbf{v}}_j^{L} \int _{{\mathbb {R}}^{2\,d-2}}\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})} {\textbf{u}}^{L'}\, \textrm{d}{\textbf{u}}, \end{aligned}$$

(155)

where L and $L'$ are multi-indexes, $l+|L|+|L'|\le 3\,j$, and $l+|L|+|L'|$ has the same parity as j. In turn, in view of (149), the Gaussian integral in (155) may be written as a linear combination of summands of the form

$$\begin{aligned} \theta _j^{a}\cdot {\textbf{v}}_j^{B} \,D^{(1)}_{\theta _j,{\textbf{v}}_j}\circ \cdots \circ D^{(|C|)}_{\theta _j,{\textbf{v}}_j} \left[ \int _{{\mathbb {R}}^{2\,d-2}}\,e^{S_c(\theta _j,{\textbf{v}}_j,{\textbf{u}})}\, \textrm{d}{\textbf{u}}\right] , \end{aligned}$$

(156)

where each $D^{(a)}_{\theta _j,{\textbf{v}}_j}$ a first order differential operator with constant coefficients and no zeroth order term in $(\theta _j,{\textbf{v}}_j)$, with $a+|B|+|C|=l+|L|+|L'|$. It then follows from (106) and (153) that the coefficient of $\lambda ^{d-1-\frac{k}{2}}$ has the form

$$\begin{aligned} P_k(x;{\textbf{v}}_j,\theta _j)\,e^{\frac{1}{\tau }\,\Psi _2\big ((\theta _1,{\textbf{v}}_1),(\theta _2,{\textbf{v}}_2)\big )}, \end{aligned}$$

where again $P_k$ is a polynomial of degree $\le 3\,k$ and parity k. $\square$

5 Proof of Theorem 7

5.1 Preliminaries for Theorem 7

In addition to the general setting of Theorem 4, we need the description, also due to Zelditch, of the wave group in the complex domain as a dynamical Toeplitz operator ([48, Proposition 7.1], [44, especially §8–9], [46, §4], see also the discussions in [10] and [11]). This is the analogue of the description of $U_{\sqrt{\rho }}^\tau (t)$ as a dynamical Toeplitz operator recalled in Sect. 3.6.

For $t\in {\mathbb {R}}$ and $\tau >0$ sufficiently small, Zelditch considers the complexified Poisson wave kernel

$$\begin{aligned} U_{{\mathbb {C}}}(t+2\,\imath \,\tau )=P^\tau \circ U(t)\circ {P^\tau }^*, \end{aligned}$$

(157)

where $P^\tau$ is as in (19). The distributional kernel of (157) admits the expansion

$$\begin{aligned} U_{{\mathbb {C}}}(t+2\,\imath \,\tau ,x,y)= \sum _j e^{(-2\,\tau +\imath \,t)\,\mu _j}\, {\tilde{\varphi }}_j(x)\,\overline{{\tilde{\varphi }}_j(y)}. \end{aligned}$$

(158)

Arguing as for (98), one may then rewrite (22) as

$$\begin{aligned} P^\tau _{\chi ,\lambda }(x,y) =\frac{1}{\sqrt{2\,\pi }}\,\int _{-\infty }^{+\infty }\chi (t)\,e^{-\imath \,\lambda \,t}\, U_{{\mathbb {C}}}(t+2\,\imath \,\tau ,x,y)\,\textrm{d}t. \end{aligned}$$

(159)

Alternatively, $U_{{\mathbb {C}}}(t+2\,\imath \,\tau )$ is a Fourier integral operator with complex phase of positive type on $X^\tau$, of degree $-(d-1)/2$; in the terminology of [4], it is in fact a Fourier–Hermite operator adapted to the symplectomorphism $\Sigma ^\tau \rightarrow \Sigma ^\tau$ induced by the homogeneous geodesic flow at time t. More precisely, for every $t\in {\mathbb {R}}$ the real locus of the (complex) canonical relation of $U_{{\mathbb {C}}}(t+2\,\imath \,\tau )$ is as follows.

Let $\gamma _t:T^\vee M{\setminus } M_0\rightarrow T^\vee M{\setminus } M_0$ denote the (genuine) homogeneous geodesic flow; thus $\gamma _t$ gets intertwined by $E^\tau$ with Hamiltonian flow of $\sqrt{\rho }$ on ${\tilde{M}}{\setminus } M$. Furthermore, recall that $\Gamma ^\tau _t:X^\tau \rightarrow X^\tau$ is the restriction of the latter flow of $\upsilon _{\sqrt{\rho }}$ on ${\tilde{M}}{\setminus } M$, and $\alpha ^\tau$ is invariant under $\Gamma ^\tau _t$. Therefore, the cotangent lift of $\Gamma ^\tau _t$ restricts on $\Sigma ^\tau \subset T^\vee X^\tau {\setminus } X_0$ to a flow $\Sigma ^\tau \rightarrow \Sigma ^\tau$ by homogeneous symplectomorphisms, that by abuse of language we shall also denote $\Gamma ^\tau _t$ ($\Sigma ^\tau$ as in (10)).

Let $\iota _\tau :T^\vee M{\setminus } M_0\rightarrow \Sigma ^\tau$ be given by

$$\begin{aligned} \iota _\tau (m,\beta ):=\left( E^\tau \left( m,\tau \,\frac{\beta }{\Vert \beta \Vert }\right) , \Vert \beta \Vert \,\alpha _{E^\tau \left( x,\tau \,\frac{\beta }{\Vert \beta \Vert }\right) }\right) . \end{aligned}$$

(160)

Then $\iota _\tau$ is a homogeneous symplectomorphism, and intertwines $\gamma _t$ with $\Gamma ^\tau _t$. Then the wave front of $P^\tau$ is (see e.g. [48])

$$\begin{aligned} \textrm{WF}'\left( P^\tau \right) = \left\{ \big (\iota _\tau (m,\beta ),\,(m,\beta )\big ):\, (m,\beta )\in T^\vee M{\setminus } M_0 \right\} . \end{aligned}$$

(161)

On the other hand, the wave front of U(t) is (see e.g. [12])

$$\begin{aligned} \textrm{WF}'\big (U(t)\big )= \left\{ \big (\gamma _t (m,\beta ),\,(m,\beta )\big ):\, (m,\beta )\in T^\vee M{\setminus } M_0 \right\} . \end{aligned}$$

(162)

Given (157) and the composition law for wave fronts we conclude

$$\begin{aligned} \textrm{WF}'\big ( U_{{\mathbb {C}}}(t+2\,\imath \,\tau ) \big )= & {} \left\{ \left( \Gamma ^\tau _t \left( x,\xi \right) , (x,\xi )\right) :\, (x,\xi )\in \Sigma ^\tau \right\} . \end{aligned}$$

(163)

This is however the same wave front of the composition $\Pi ^\tau \circ \Pi ^\tau _{-t}$, whence of any composition $\Pi \circ Q\circ \Pi ^\tau _{-t}$, with Q a pseudodifferential operator which is elliptic on a conic neighourhood of $\Sigma ^\tau$. Hence, for any such Q, $U_{{\mathbb {C}}}(t+2\,\imath \,\tau )$ and $\Pi \circ Q\circ \Pi ^\tau _{-t}$ are both Fourier integral operators of Hermite type with the same real canonical relation; it follows that they are associated to the same complex Lagrangian. This is the basis for the following analogue of Theorem 55 (notation is as in Sect. 3.6).

Theorem 67

(Zelditch) There exist a polyhomogeneous classical symbol on $X^\tau \times {\mathbb {R}}_+$ of the form

$$\begin{aligned} \gamma ^\tau _t(x,r)\sim \sum _{j\ge 0}\gamma _{t,j}^\tau (x)\, r^{-\frac{d-1}{2}-j}, \end{aligned}$$

and a pseudo-differential operator $Q^\tau _t \sim \gamma ^\tau _t(x,D_{\sqrt{\rho }}^\tau )$ of degree $-(d-1)/2$ on $X^\tau$, such that up to smoothing operators

$$\begin{aligned} U_{{\mathbb {C}}}(t+2\,\imath \,\tau )\sim \Pi ^\tau \circ Q^\tau _t\circ \Pi ^\tau _{-t}= \Pi ^\tau \circ {\mathcal {Q}}^\tau _t, \end{aligned}$$

(164)

where ${\mathcal {Q}}^\tau _t:= Q^\tau _t\circ \Pi _{-t}^{\tau }$.

The coefficients $\gamma _{t,j}^\tau$ depend on the choice of volume form. We shall determine $\gamma _{0,0}^\tau$ a posteriori by deriving a local Weyl law for the complexified eigenfunctions and comparing it to the one in Proposition 3.8 of [46].

Remark 68

Up to smoothing operators that do not affect the asymptotics, the composition (164) only depends on the behaviour of $Q^\tau _t$ in a small conic neighborhood of $\Sigma ^\tau$, where $D_{\sqrt{\rho }}^\tau$ may be assumed to be microlocally elliptic.

Using known results on the composition of pseudodifferential and Fourier integral operators, in view of (95) and Corollary 49 one obtains from Theorem 67 the following analogue of Lemma 56.

Lemma 69

Up to smoothing terms, the Schwartz kernel of ${\mathcal {Q}}^\tau _t$ has the form

$$\begin{aligned} {\mathcal {Q}}^\tau _t(x_1,x_2)\sim \int _0^{+\infty } e^{\imath \,u\,\psi ^\tau \left( \Gamma ^\tau _{-t}(x_1),x_2 \right) }\, q^\tau _t\left( x_1,x_2,u\right) \,\textrm{d}u, \end{aligned}$$

(165)

where

$$\begin{aligned} q^\tau _t\left( x_1,x_2,u\right) \sim \sum _{j\ge 0}\,u^{\frac{d-1}{2}-j}\,q^\tau _{t\,j}(x_1,x_2), \end{aligned}$$

with

$$\begin{aligned} q^\tau _{0\,0}(x_1,x_2)= \frac{1}{\tau ^{\frac{d-1}{2}}}\cdot \gamma _{0,0}^\tau (x)\, s^\tau _0\left( \Gamma ^\tau _{t}(x_1),x_2\right) . \end{aligned}$$

5.2 Proof of Theorem 7

Proof

By the considerations in Sect. 5.1, the analysis of $P^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })$ (notation as in (119)) parallels the one for $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })$ in Theorem 4, with the following change.

The leading order term of the amplitude has been multiplied by a factor $\gamma _{0,0}^\tau (x)\cdot (u\,\tau )^{-\frac{d-1}{2}}$. In view of the rescaling $u\mapsto \lambda \,u$ in (114), this change entails an additional factor $\gamma _{0,0}^\tau (x)\cdot \lambda ^{-\frac{d-1}{2}}$ in front of the resulting asymptotic expansion. Furthermore, by Lemma 64 the evaluation of $u\,\tau$ at the stationary point $P_s=(t_s,v_s,\theta _s,u_s)$ of $\Upsilon ^\tau$ is $u_s\,\tau =1$.

Hence, the leading order term of the asymptotic expansion for $P_{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })$ only differs from the one of $\Pi ^\tau _{\chi ,\lambda }(x_{1\lambda },x_{2\lambda })$ by the factor $\gamma _{0,0}^\tau (x)\cdot \lambda ^{-\frac{d-1}{2}}$. $\square$

5.3 The pointwise Weyl law

Proof of Proposition 10

We shall prove (26); the same argument, with obvious adaptations, also proves (27).

Let us choose $\chi \in {\mathcal {C}}^\infty _c\big ((-\epsilon ,\epsilon )\big )$ with ${\hat{\chi }}>0$. Define $f:{\mathbb {R}}\times {\mathbb {R}}\rightarrow [0,+\infty )$ by

$$\begin{aligned} f_\lambda (t,s):={\hat{\chi }}(t)\,H(\lambda -s-t), \end{aligned}$$

where H is the Heaviside function.

Let us consider the following positive measures ${\mathcal {L}}$ and ${\mathcal {T}}_x^\tau$ on ${\mathbb {R}}$. First, ${\mathcal {L}}$ is the Lebesgue measure. Second,

$$\begin{aligned} {\mathcal {T}}_x^\tau :=\sum _{j\ge 1}\, \Pi _j^\tau (x,x)\, \delta _{\lambda _j}. \end{aligned}$$

(166)

Let us endow ${\mathbb {R}}\times {\mathbb {R}}$ with the product measure ${\mathcal {L}}\times {\mathcal {T}}$.

By the Fubini Theorem (see e.g. Ch. 8 of [34]),

$$\begin{aligned} \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {T}}_x(s)\, \left[ \int _{{\mathbb {R}}}\,f_\lambda (t,s)\, \,\textrm{d}{\mathcal {L}}(t) \right] = \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {L}}(t)\, \left[ \int _{{\mathbb {R}}}\,f_\lambda (t,s)\, \,\textrm{d}{\mathcal {T}}_x(s) \right] ; \end{aligned}$$

(167)

the claim will follow by comparing both sides of (167).

The former integral in (167) is

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {T}}_x(s) \, \left[ \int _{{\mathbb {R}}}\,f_\lambda (t,s) \,\textrm{d}{\mathcal {L}}(t) \right] = \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {T}}_x(s) \,\left[ \int _{-\infty }^{\lambda -s}\,{\hat{\chi }}(t)\,\textrm{d}t \right] \nonumber \\{} & {} \quad = \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {T}}_x(s) \,\left[ \int _{-\infty }^{\lambda }\,{\hat{\chi }}(t-s)\,\textrm{d}t\right] =\sum _{j\ge 1}\, \Pi _j^\tau (x,x) \cdot \int _{-\infty }^{\lambda }\,{\hat{\chi }}(t-\lambda _j)\,\textrm{d}\,t \nonumber \\{} & {} \quad =\int _{-\infty }^{\lambda }\,\left[ \sum _{j\ge 1}\, \Pi _j^\tau (x,x) \cdot {\hat{\chi }}(t-\lambda _j)\right] \,\textrm{d}\,t= \int _{-\infty }^{\lambda }\,\Pi ^\tau _{\chi ,t}(x,x) \,\textrm{d}\,t; \end{aligned}$$

(168)

on the last line, we have made use of (15) and Theorem 1.27 of [34]. In view of Corollary 5, (168) implies that as $\lambda \rightarrow +\infty$

$$\begin{aligned} \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {T}}_x(s) \, \left[ \int _{{\mathbb {R}}}\,f_\lambda (t,s) \,\textrm{d}{\mathcal {L}}(t) \right] =\frac{\sqrt{2\,\pi }}{d\cdot (2\,\pi )^d}\cdot \frac{\lambda ^d}{\tau ^{d-1}} \cdot \chi (0) +O\left( \lambda ^{d-1}\right) . \end{aligned}$$

(169)

On the other hand, the latter integral in (167) is

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\,\textrm{d}{\mathcal {L}}(t)\, \left[ \int _{{\mathbb {R}}}\,f_\lambda (t,s)\, \,\textrm{d}{\mathcal {T}}_x(s) \right] =\int _{-\infty }^{+\infty } \left[ \sum _j\,\Pi _j^\tau (x,x)\,f_\lambda (t,\lambda _j) \right] \,\textrm{d}\,t\nonumber \\{} & {} \quad = \int _{-\infty }^{+\infty }\left[ \sum _j\,\Pi _j^\tau (x,x)\,H(\lambda -t-\lambda _j) \right] \, {\hat{\chi }}(t)\,\textrm{d}\,t \nonumber \\{} & {} \quad =\int _{-\infty }^{+\infty }\,{\mathcal {W}}_x(\lambda -t)\, {\hat{\chi }}(t)\,\textrm{d}\,t \nonumber \\{} & {} \quad ={\mathcal {W}}_x(\lambda )\,\int _{-\infty }^{+\infty }\, {\hat{\chi }}(t)\,\textrm{d}\,t + \int _{-\infty }^{+\infty }\, \big [{\mathcal {W}}_x(\lambda -t)-{\mathcal {W}}_x(\lambda )\big ]\, {\hat{\chi }}(t)\,\textrm{d}\,t\nonumber \\{} & {} \quad =\sqrt{2\,\pi }\, \chi (0)\cdot {\mathcal {W}}_x(\lambda )+ \int _{-\infty }^{+\infty }\, \big [{\mathcal {W}}_x(\lambda -t)-{\mathcal {W}}_x(\lambda )\big ]\, {\hat{\chi }}(t)\,\textrm{d}\,t. \end{aligned}$$

(170)

$\square$

Lemma 70

For $\lambda \rightarrow +\infty$, we have

$$\begin{aligned} \int _{-\infty }^{+\infty }\, \big [{\mathcal {W}}_x(\lambda -t)-{\mathcal {W}}_x(\lambda )\big ]\, {\hat{\chi }}(t)\,\textrm{d}\,t=O\left( \lambda ^{d-1}\right) . \end{aligned}$$

Proof

It follows from Corollary 5 that for $\lambda \gg 0$

$$\begin{aligned} {\mathcal {W}}_x(\lambda +1)-{\mathcal {W}}_x(\lambda )=\sum _{\lambda \le \lambda _j\le \lambda +1}\, \Pi _j^\tau (x,x)=O\left( \lambda ^{d-1}\right) . \end{aligned}$$

Hence there exist $C_0,\,C_1>0$ such that

$$\begin{aligned} {\mathcal {W}}_x(\lambda +1)-{\mathcal {W}}_x(\lambda )\le C_1\,|\lambda |^{d-1}+C_0\qquad \forall \, \lambda \in {\mathbb {R}}. \end{aligned}$$

Thus for suitable $C',\,C''>0$ for any $\lambda ,\,t\in {\mathbb {R}}$

$$\begin{aligned} \big |{\mathcal {W}}_x(\lambda -t)-{\mathcal {W}}_x(t)\big |\le C'\cdot |t|\,\left[ |\lambda |^{d-1}+ |\lambda -t|^{d-1}\right] +C''. \end{aligned}$$

Therefore for $\lambda \gg 0$

$$\begin{aligned}{} & {} \left| \int _{-\infty }^{+\infty }\, \big [W_x(\lambda -t)-W_x(\lambda )\big ]\, {\hat{\chi }}(t)\,\textrm{d}\,t \right| \\{} & {} \quad \le C'\,\int _{-\infty }^{+\infty }\,|t|\,\left[ |\lambda |^{d-1}+ |\lambda -t|^{d-1}\right] \,{\hat{\chi }}(t)\,\textrm{d}\,t+C''' \le A\,\lambda ^{d-1}+B, \end{aligned}$$

for appropriate constants $A,B>0$. $\square$

Comparing (168) and (170), we conclude that

$$\begin{aligned} \sqrt{2\,\pi }\, \chi (0)\cdot W_x(\lambda )= \frac{\sqrt{2\,\pi }}{d\cdot (2\,\pi )^d}\cdot \frac{\lambda ^d}{\tau ^{d-1}} \cdot \chi (0) +O\left( \lambda ^{d-1}\right) , \end{aligned}$$

whence

$$\begin{aligned} W_x(\lambda )=\frac{\tau }{d}\cdot \left( \frac{\lambda }{2\,\pi \,\tau }\right) ^d +O\left( \lambda ^{d-1}\right) . \end{aligned}$$

This establishes (26). To obtain (27), we need only run over the same argument, with the following changes: first, in (166) replace $\Pi _j^\tau (x,x)$ by $U^\tau _j\left( x, x \right)$ (notation as in (22)); second, in the derivation of (169), invoke Corollary 9 in place of Corollary 5.$\square$