Skip to main content
SpringerLink
Log in

Complex dynamics generated by negative and positive feedback delays of a prey–predator system with prey refuge: Hopf bifurcation to Chaos

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

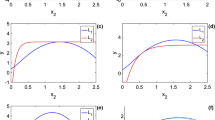
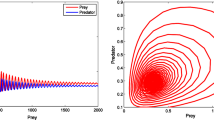
Abstract

Various field and laboratory experiments show that prey refuge plays a significant role in the stability of prey–predator dynamics. On the other hand, theoretical studies show that delayed system exhibits a much more realistic dynamics than its non-delayed counterpart. In this paper, we study a multi-delayed prey–predator model with prey refuge. We consider modified Holling Type II response function that incorporates the effect of prey refuge and then introduce two discrete delays in the model system. A negative feedback delay is considered in the logistic prey growth rate to represent density dependent feedback mechanism and a positive feedback delay is considered to represent the gestation time of the predator. Our study reveals that the system exhibits different dynamical behaviors, viz., stable coexistence, periodic coexistence or chaos depending on the values of the delay parameters and degree of prey refuge. The interplay between two delays for a fixed value of prey refuge has also been determined. It is noticed that these delays work in a complementary fashion. In addition, using the normal form theory and center manifold argument, we derive the explicit formulae for determining the direction of the bifurcation, the stability and other properties of the bifurcating periodic solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Alstad D (2001) Basic populations models of ecology. Prentice Hall Inc., Upper Saddle River

    Google Scholar 

  2. Anderson O (1984) Optimal foraging by largemouth bass in structured environments. Ecology 65:851–861

    Article  Google Scholar 

  3. Anderson TW (2001) Predator responses, prey refuges and density-dependent mortality of a marine fish. Ecology 82(1):245–257

    Article  Google Scholar 

  4. Johnson WD (2006) Predation, habitat complexity and variation in density dependent mortality of temperate reef fishes. Ecology 87(5):1179–1188

    Article  Google Scholar 

  5. Jana D, Ray S (2016) Impact of physical and behavioral prey refuge on the stability and bifurcation of Gause type Filippov prey–predator system. Model Earth Syst Environ 2:1

    Article  Google Scholar 

  6. Lima SL, Dill LM (1990) Behavioral decisions made under the risk of predation: a review and prospectus. Cana J Zool 68:619–640

    Article  Google Scholar 

  7. Bell SS, McCoy ED, Mushinsky HR (1991) Habitat structure: the physical arrangement of objects in space. Chapman and Hall, New York

    Book  Google Scholar 

  8. Lima SL (1998) Stress and decision making under the risk of predation: recent developments from behavioral, reproductive, and ecological perspectives. Adv Study Behav 27:215–290

    Article  Google Scholar 

  9. Brown JS, Kotler BP (2004) Hazardous duty pay and the foraging cost of predation. Ecol Lett 7:999–1014

    Article  Google Scholar 

  10. Caro T (2005) Anti predator defenses in birds and mammals. University of Chicago Press, Chicago

    Google Scholar 

  11. Stankowich T, Blumstein DT (2005) Fear in animals: a meta-analysis and review of risk assessment. Proc R Soc Ser B 272:2627–2634

    Article  Google Scholar 

  12. Cooper WE Jr (2009) Theory successfully predicts hiding time: new data for the lizard Sceloporus virgatus and a review. Behav Ecol 20:585–592

    Article  Google Scholar 

  13. Luckinbill LS (1973) Coexistence in laboratory populations of Paramecium aurelia and its predator Didinium nasutum. Ecology 54:1320–1327

    Article  Google Scholar 

  14. Ray S, Straškraba M (2001) The impact of detritivorous fishes on the mangrove estuarine system. Ecol Model 140:207–218

    Article  Google Scholar 

  15. Roy M, Mandal S, Ray S (2008) Detrital ontogenic model including decomposer diversity. Ecol Model 215:200–206

    Article  Google Scholar 

  16. Sih A et al (1985) Predation, competition, and prey communities, a review of field experiments. Ann Rev Ecol Syst 16:269–311

    Article  Google Scholar 

  17. Savino JF, Stein RA (1982) Predator–prey interaction between largemouth bass and bluegills as influenced by simulated, submersed vegetation. Trans Am Fish Soc 111:255–266

    Article  Google Scholar 

  18. Kar TK (2005) Stability analysis of a preypredator model incorporatinga prey refuge. Commun Nonlinear Sci NumerSimul 10:681691

    Google Scholar 

  19. Jana D (2013) Chaotic dynamics of a discrete predator–prey system with prey refuge. Appl Math Comput 224:848–865

    MATH  MathSciNet  Google Scholar 

  20. Jana D (2014) Stabilizing effect of Prey refuge and Predator’s interference on the dynamics of Prey with delayed growth and generalist Predator with delayed gestation. Int J Ecol 2014(429086):12. doi:10.1155/2014/429086

    Google Scholar 

  21. Jana D, Agrawal R, Upadhyay RK (2015) Dynamics of generalist predator in a stochastic environment: effect of delayed growth and prey refuge. Appl Math Comput 268:1072–1094

    MathSciNet  Google Scholar 

  22. MacDonald M (1989) Biological delay systems: linear stability theory. Cambridge University Press, Cambridge

  23. May RM (1981) Theoretical ecology: principles and applications. Blackwell Scientific Publications, Oxford

    Google Scholar 

  24. XiaoD Ruan S (2001) Multiple bifurcations in a delayed predator-prey system with nonmonotonic functional response. J Differ Equ 176:494–510

    Article  MathSciNet  Google Scholar 

  25. Bairagi N, Jana D (2011) On the stability and Hopf bifurcation of a delay-induced predator–prey system with prey refuge. Appl Math Model 35:3255–3267

    Article  MATH  MathSciNet  Google Scholar 

  26. Jana D, Agrawal R, Upadhyay RK (2014) Top-predator interference and gestation delay as determinants of the dynamics of a realistic model food chain. Chaos Solitons Fractal 69:50–63

    Article  MATH  MathSciNet  Google Scholar 

  27. Yan XP, Chu YD (2006) Stability and bifurcation analysis for adelayed Lotka–Volterra predator–prey system. J Comput Appl Math 196:198–210

    Article  MATH  MathSciNet  Google Scholar 

  28. Song Y, Peng Y, Wei J (2008) Bifurcations for a predatorprey systemwith two delays. J Math Anal Appl 337:466–479

    Article  MathSciNet  Google Scholar 

  29. Nakaoka S, Saito Y, Takeuchi Y (2006) Stability, delay, and chaotic behavior in a Lotka–Volterra predator–prey system. Math Biosci Eng 3:173–187

    MATH  MathSciNet  Google Scholar 

  30. Xu C, Liao M, He X (2011) Stability and Hopf bifurcation analysis for a Lotka–Volterra predator–prey model with two delays. Int J Appl Math Comput Sci 21(1):97–107

    Article  MATH  MathSciNet  Google Scholar 

  31. Liao M, Tang X, Xu C (2012) Bifurcation analysis for a three-speciespredator preysystem with two delays. Commun Nonlinear Sci Numer Simulat 17:183–194

    Article  Google Scholar 

  32. Jana D, Pathak R, Agarwal M (2016) On the stability and Hopf bifurcation of a prey-generalist predator system with independent age-selective harvesting. Chaos Solitons Fractal 83:252–273

    Article  MATH  MathSciNet  Google Scholar 

  33. Yang R, Wei J (2014) Stability and bifurcation analysis of a diffusive prey–predator system in Holling type III with a prey refuge. Nonlinear Dyn 79(1):631–646

    Article  MATH  MathSciNet  Google Scholar 

  34. Yang R, Zhang C (2016) Dynamics in a diffusive predator–prey system with a constant prey refuge and delay. Nonlinear Anal Real World Appl 31:1–22

    Article  MATH  MathSciNet  Google Scholar 

  35. Yang R, Zhang C (2016) The effect of prey refuge and time delay on a diffusive predator–prey system with hyperbolic mortality. Complexity 50(3):105–113

    MathSciNet  Google Scholar 

  36. Freedman HI (1987) Deterministic mathematical models in population ecology. HIFR Consulting Ltd., Edmonton

    MATH  Google Scholar 

  37. Kuang Y (1993) Delay differential equations with applications in population dynamics. Academic Press, New York

    MATH  Google Scholar 

  38. Yang X, Chen L, Chen J (1996) Permanence and positive periodic solution for the single species nonautonomous delay diffusive model. Comput Math Appl 32:109–116

    Article  MATH  MathSciNet  Google Scholar 

  39. Butler G, Freedman HI, Waltman P (1986) Uniformly persistent systems. Proc Am Math Soc 96(3):425–430

    Article  MATH  MathSciNet  Google Scholar 

  40. Freedman HI, Waltman P (1984) Persistence in models of three interacting predator–prey populations. Math Biosci 68:213–231

    Article  MATH  MathSciNet  Google Scholar 

  41. Freedman HI, SO J (1985) Global stability and persistence of simple food chains. Math Biosci 76:69–86

    Article  MATH  MathSciNet  Google Scholar 

  42. Brauer F, Chavez CC (2001) Mathematical models in population biology and epidemiology. Springer, New York

    Book  MATH  Google Scholar 

  43. Gaurd TC, Hallam TG (1979) Persistence in food web-I. Lotka–Voltera chains. Bull Math Biol 41:877–891

    MathSciNet  Google Scholar 

  44. Ruan S, Wei J (2003) On the zeros of transcendental functions with applications to stability of delay differential equations. Dynam Contin Discret Impuls Syst 10:863–874

    MATH  MathSciNet  Google Scholar 

  45. Hassard BD, Kazarinoff ND, Wan YH (1981) Theory and application of Hopf bifurcation. Cambridge University, Cambridge

    MATH  Google Scholar 

  46. Gopalsamy K, He X (1994) Delay-independent stability in bi-directional associative memory networks. IEEE Trans Neural Netw 5:998–1002

    Article  Google Scholar 

Download references

Acknowledgments

M. Lakshmanan acknowledges National Academy of Sciences, India for financial support in the form of a Senior Scientist Platinum Jubilee Fellowship.

Author information

Authors and Affiliations

  1. Department of Mathematics, SRM University, Kattankulathur, Tamil Nadu, 603 203, India

    Debaldev Jana

  2. School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, 613 401, India

    R. Gopal

  3. Centre for Nonlinear Dynamics, School of Physics, Bharathidasan University, Tiruchirapalli, 620 024, India

    M. Lakshmanan

Authors
  1. Debaldev Jana
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Gopal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Lakshmanan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Debaldev Jana.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jana, D., Gopal, R. & Lakshmanan, M. Complex dynamics generated by negative and positive feedback delays of a prey–predator system with prey refuge: Hopf bifurcation to Chaos. Int. J. Dynam. Control 5, 1020–1034 (2017). https://doi.org/10.1007/s40435-016-0267-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-016-0267-5

Keywords

Search

Navigation