Using the extended Melnikov method to study multi-pulse chaotic motions of a rectangular thin plate

Abstract

This paper investigates the multi-pulse global heteroclinic bifurcations and chaotic dynamics for the nonlinear vibrations of a simply supported rectangular thin plate by using an extended Melnikov method in the resonant case. The rectangular thin plate is subjected to spatially and temporally varying transversal and in-plane excitations, simultaneously. The equations of motion for the rectangular thin plate are derived from the von Kármán equation. Applying the method of multiple scales and Galerkin’s approach to the partial differential governing equation, the four-dimensional averaged equation is obtained for the case of 1:2 internal resonance and primary parametric resonance. From the averaged equations obtained, the theory of normal form is used to derive the explicit expressions of normal form with a double zero and a pair of pure imaginary Eigenvalues. Based on the explicit expressions of normal form, the extended Melnikov method is used to analyze the multi-pulse heteroclinic bifurcations and chaotic dynamics of the rectangular thin plate. The contribution of the paper is the simplification of the extended Melnikov method. The extended Melnikov function can be simplified in the resonant case and does not depend on the perturbation parameter. The necessary conditions of the existence for the Shilnikov type multi-pulse chaotic dynamics of the rectangular thin plate are analytically obtained. Numerical simulations also display that the Shilnikov type multi-pulse chaotic motions can occur in the rectangular thin plate. Overall, both theoretical and numerical studies demonstrate that the chaos for the Smale horseshoe sense exists in the rectangular thin plate.

1 Introduction

Due to the high-speed, lightweight and energy-saving requirements in the aerospace and aviation industry, many structures become thinner. Thin plates are widely used as main structures in a large space station, wing skins. In aerospace applications, these thin plates are relatively large structural flexibility, and its flexibility can induce large deformation. Thin plates can exhibit large amplitude vibrations and give rise to non-linear phenomena when these structures are subjected to dynamic loads. Therefore, it is important to investigate large deformation and geometrically nonlinear effects of thin plates in order to effectively control large amplitude vibrations. Since the linear theory is not sufficient to describe the dynamical behaviour of thin plate, nonlinear strain-displacement equations are utilized to include geometrical non-linearities in the local vibration equations which take into account the stretching of the mid-plane of thin plate. However, some problems, such as the Shilnikov type multi-pulse orbits and jumping phenomena for thin plate in the case of large deformation, also are open.

Recently, studies on nonlinear vibrations, bifurcations and chaotic dynamics of thin plates have made some progress. Yang and Sethna [1] investigated Hopf bifurcations and global chaotic phenomena in nonlinear flexural vibrations of a nearly square plate subjected to periodical excitation. Baumgarten and Kreuzer [2] studied periodic motions and chaotic attractor in parametrically excited nonlinear vibrations of shallow cylindrical panels. Elbeyli and Anlas [3] explored nonlinear response of a simple supported rectangular metallic plate subjected to transverse harmonic excitation. Touze et al. [4] applied von Karman theory and the method of multiple scales to examine the forced asymmetric nonlinear vibrations of circular plates with a free edge. Yeh [5] utilized fractal dimension criteria and the maximum Lyapunov exponent to probe into the chaotic motion of a simply supported thermo-mechanically coupled orthotropic rectangular plate. Krysko et al. [6] made use of the Bubnov-Galerkin approach to analyze chaotic motion and bifurcations of flexible plate-strips with non-symmetric boundary conditions. Wang [7] canvassed bifurcations and chaotic vibrations of bimetallic thin circular plates with geometric nonlinearity. Hegazy [8] used the method of multiple scales to investigate nonlinear vibration of a rectangular thin plate under parametric and external excitations. Tang and Chen [9] employed the Hamilton principle and the method of multiple scales to investigate nonlinear free transverse vibrations of in-plane moving plates subjected to plane stresses. Xue et al. [10] exploited the von Karman plate theory to derive the nonlinear partial differential equation for the vibration of a thin orthotropic plate subjected to the transverse magnetic field and the transverse harmonic mechanical excitation.

The global bifurcations and chaotic dynamics of high-dimensional nonlinear systems have been at the forefront of nonlinear dynamics for the past two decades. There are two ways of solutions on Shilnikov type chaotic dynamics of high-dimensional nonlinear systems. One is Shilnikov type single-pulse chaotic dynamics and the other is Shilnikov type multi-pulse chaotic dynamics. Most researchers focused on Shilnikov type single-pulse chaotic dynamics of high-dimensional nonlinear systems. Much research in this field has concentrated on Shilnikov type single-pulse chaotic dynamics of thin plates. Feng and Sethna [11] utilized the global perturbation method to study the global bifurcations and chaotic dynamics of the thin plate under parametric excitation and obtained the conditions in which the Shilnikov type homoclinic orbits and chaos can occur. Tien et al. [12, 13] applied the Melnikov method to investigate the global bifurcation and chaos for the Smale horseshoe sense of a two-degree-of-freedom shallow arch subjected to simple harmonic excitation for the case of 1:2 internal resonance and 1:1 internal resonance. Malhotra and Sri Namachchivaya [14, 15] employed the averaging method and Melnikov technique to canvass the local, global bifurcations and chaotic motions of a two-degree-of-freedom shallow arch subjected to simple harmonic excitation for the case of 1:2 internal resonance and 1:1 internal resonance. The global bifurcations and chaotic dynamics were investigated by Zhang et al. [16, 17] for the simply supported rectangular thin plates subjected to the parametrical-external excitation and the parametrical excitation. Yeo and Lee [18, 19] made use of the global perturbation technique to examine the global dynamics of an imperfect circular plate for the case of 1:1 internal resonance and obtained the criteria for chaotic motions of homoclinic orbits and heteroclinic orbits. Yu and Chen [20] adopted the global perturbation method to explore the global bifurcations of a simply supported rectangular metallic plate subjected to a transverse harmonic excitation for the case of 1:1 internal resonance. Zhang and Li [21] took advantage of exponential dichotomies, an averaging procedure and Melnikov theory to analyze resonant chaotic motions of a simply supported rectangular thin plate with parametrically and externally excitation.

While most of studies are on the Shilnikov type single-pulse global bifurcations and chaotic dynamics of high-dimensional nonlinear systems, there are researchers investigating the Shilnikov type multi-pulse homoclinic and heteroclinic bifurcations and chaotic dynamics. So far, there are two theories of the Shilnikov type multi-pulse chaotic dynamics. One is the extended Melnikov method and the other theory is the energy phase method. Much achievement is made in the former theory of high-dimensional nonlinear systems. In 1996, Kovacic and Wettergren [22] used a modified Melnikov method to investigate the existence of the multi-pulse jumping of homoclinic orbits and chaotic dynamics in resonantly forced coupled pendula. Furthermore, Kaper and Kovacic [23] studied the existence of several classes of the multi-bump orbits homoclinic to resonance bands for completely integral Hamiltonian systems subjected to small amplitude Hamiltonian and damped perturbations. Camassa et al. [24] presented a new Melnikov method which is called as the extended Melnikov method to explore the multi-pulse jumping of homoclinic and heteroclinic orbits in a class of perturbed Hamiltonian systems. Until recently, Zhang and Yao [25, 26] introduced the extended Melnikov method to the engineering field. They came up with a simplification of the extended Melnikov method in the resonant case, and utilized it to analyze the Shilnikov type multi-pulse homoclinic bifurcations and chaotic dynamics for the nonlinear nonplanar oscillations of the cantilever beam. Subsequently, Zhang and Yao [27–29] improved the extended Melnikov method to non-autonomous systems from high-dimensional autonomous systems. They used the extended Melnikov method for non-autonomous nonlinear dynamical systems to examine the global bifurcations and multi-pulse chaotic dynamics of a buckled thin plate and a laminated composite piezoelectric rectangular plate.

The study on the second theory of the Shilnikov type multi-pulse chaotic dynamics were stated by Haller and Wiggins [30]. They presented the energy phase method to investigate the existence of the multi-pulse jumping homoclinic and heteroclinic orbits in perturbed Hamiltonian systems. Up to now, few researchers have made use of the energy phase method to study the Shilnikov type multi-pulse homoclinic and heteroclinic bifurcations and chaotic dynamics of high-dimensional nonlinear systems in engineering applications. Malhotra et al. [31] used the energy-phase method to investigate multi-pulse homoclinic orbits and chaotic dynamics for the motion of flexible spinning discs. Yao and Zhang [32] utilized the energy-phase method to analyze the Shilnikov type multi-pulse heteroclinic orbits and chaotic dynamics in a parametrically and externally excited rectangular thin plate. Yu and Chen [33] made use of the energy-phase method to examine the Shilnikov type multi-pulse homoclinic orbits of a harmonically excited circular plate.

This paper focuses on the Shilnikov type multi-pulse orbits and chaotic dynamics for a simply supported at four-edge, rectangular thin plate subjected to spatially and temporally varying transversal and in-plane excitations, simultaneously. Based on the von Karman type equation, we derive the governing equation of the rectangular thin plate subjected to transversal and in-plane loads. We employ the Galerkin’s approach to obtain a two-degree-of-freedom nonlinear system under combined parametric and external excitations. We apply the method of multiple scales and the theory of normal form to the equations of motions in order to obtain the four-dimensional averaged equation for the case of 1:2 internal resonance and primary parametric resonance-fundamental parametric resonance. We study the heteroclinic bifurcations of the unperturbed system and the characteristic of the hyperbolic dynamics of the dissipative system, respectively. Finally, we employ the extended Melnikov method to analyze the Shilnikov type multi-pulse orbits and chaotic dynamics in the simply supported rectangular thin plate. We present the geometric structure of the multi-pulse orbits in the four-dimensional phase space. The results from numerical simulation show that chaotic motion can occur in nonlinear vibration of the simply supported rectangular thin plate, which verifies the analytical prediction. The Shilnikov type multi-pulse orbits are discovered from the results of numerical simulation. In summary, both theoretical and numerical studies demonstrate that chaos for the Smale horseshoe sense in the motion exists.

2 Equations of motion and perturbation analysis

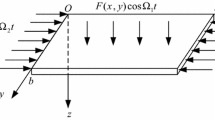
We consider a simply supported at the four-edge, rectangular thin plate, where the edge lengths are $a$ and $b$ and thickness is $h$, respectively. The thin plate is subjected to spatially and temporally varying transversal and in-plane excitations, simultaneously. We establish a Cartesian coordinate system, shown in Fig. 1, such that the coordinate $Oxy$ is located in the middle surface of thin plate. It is assumed that $u, v$ and $w$ represent the displacements of a point in the middle plane of the thin plate in the $x, y$ and $z$ directions, respectively. The excitation in-plane of the thin plate may be described in the form $p=p_0 -p_1 \cos \Omega _2 t$ along the $x$ direction in the Cartesian coordinate system $Oxyz$. From von Karman-type equation for the thin plate obtained by Chia et al. [16, 34], we obtain the equation of motion for the rectangular thin plate as follows

$$\begin{aligned}&D\nabla ^{4}w+\uprho h\frac{\partial ^{2}w}{\partial t^{2}}-\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}{\upphi } }{\partial y^{2}}-\frac{\partial ^{2}w}{\partial y^{2}}\frac{\partial ^{2}{\upphi } }{\partial x^{2}}\nonumber \\&\quad +\, 2\frac{\partial ^{2}w}{\partial x\partial y}\frac{\partial ^{2}{\upphi } }{\partial x\partial y}+\upmu \frac{\partial w}{\partial t}=F(x,y)\cos \Omega _1 t,\end{aligned}$$

(1)

$$\begin{aligned}&\nabla ^{4}{\upphi } =Eh\left[ {\left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right) ^{2}-\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}w}{\partial y^{2}}} \right] , \end{aligned}$$

(2)

where $\uprho$ is the density of thin plate, $D={Eh^{3}}/{(12(1-\nu ^{2}))}$ is the bending rigidity, $E$ is Young’s modulus, $\upnu$ is Possion’s ratio, ${\upphi }$ is the stress function, $\upmu$ is the damping coefficient, and $F(x,y)$ represents the amplitude of transversal excitation for the rectangular thin plate.

Fig. 1

The model of a rectangular thin plate and the coordinate system are given

We assume that the simply supported boundary conditions can be written as

$$\begin{aligned}&\text {at }x=0 \quad \! \text {and}\quad a,w=0,\quad \!\frac{\partial ^{2}w}{\partial x^{2}}=0;\quad \nonumber \\&\text {at }y=0\quad \text {and}\quad b,w=0,\quad \frac{\partial ^{2}w}{\partial y^{2}}=0. \end{aligned}$$

(3)

The boundary conditions satisfied by the stress function ${\upphi }$ may be expressed in the following form

$$\begin{aligned}&u=\int _{0}^{a} {\left[ {\frac{1}{E}\left( {\frac{\partial ^{2}{\phi } }{\partial y^{2}}-\upnu \frac{\partial ^{2}{\phi } }{\partial x^{2}}} \right) -\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \right] } dy={\updelta }_x ,\nonumber \\&\quad \text { and }\quad h=\int _{ 0}^{ b} {\frac{\partial ^{2}{\upphi } }{\partial y^{2}}} dy=p,\text { at } x=0\quad \text { and }\quad a,\end{aligned}$$

(4)

$$\begin{aligned}&v=\int _{ 0}^{ b} {\left[ {\frac{1}{E}\left( {\frac{\partial ^{2}{\upphi } }{\partial x^{2}}-\upnu \frac{\partial ^{2}{\upphi } }{\partial y^{2}}} \right) -\frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right) ^{2}} \right] } dx=0,\quad \text { and } \nonumber \\&\quad \qquad \int _{ 0}^{ a} {\frac{\partial ^{2}{\upphi } }{\partial x^{2}}} dx=0,\text { at }y=0\text { and } b, \end{aligned}$$

(5)

where ${\updelta }_x$ is the corresponding displacement in the $x$ direction at the boundary.

We mainly consider the nonlinear oscillations of a thin plate in the first two modes. There are only the odd-order modes without the presence of even order modes when the thin plate is subjected to uniform transversal and in-plane excitations. Thus, we can not choose (2, 1), (1, 2) and (2, 2) modes. According to the geometry of the structure, we determine modal selection. If the nonlinear oscillations of the square thin plate are considered, the case of 1:1 internal resonance is very likely to occur. We will select (1, 1) mode. But, we study the nonlinear oscillations of the rectangular thin plate in this paper. The case of 1:1 internal resonance is not going to happen, and the case of 1:2 internal resonance may occur in the nonlinear oscillations of the rectangular thin plate. Modal frequency under the case of internal resonance is relatively large since the thin plate is subjected to in-plane excitation. Thus, we choose (3, 1) and (1, 3) modes to investigate the nonlinear oscillations of the thin plate. Thus, we write the $w$ in the form of

$$\begin{aligned} w(x,y,t)&= q_1 (t)\sin \frac{\pi x}{a}\sin \frac{3\pi y}{b}\nonumber \\&+\,q_2 (t)\sin \frac{3\pi x}{a}\sin \frac{\pi y}{b}, \end{aligned}$$

(6)

where $q_i (t)(i=1 ,2)$ represent the amplitudes of two modes, respectively.

For the linear system, it can generate resonance when the external excitation frequency is equal to the natural frequency of the system. It is well known that the amplitude of vibration is the maximum under the case of resonance. The natural frequency of nonlinear continuous system does not exist, and there are only modal functions. It is necessary that the frequency of the external excitation is the same as the modal frequency in order to analyze characteristics of nonlinear vibration for the mode. This can stimulate a mode to produce resonance. In this paper, we study the nonlinear oscillations of a thin plate in (3, 1) and (1, 3) modes. Therefore, we choose the excitations in the same form as these modes. The transverse excitation can be represented as

$$\begin{aligned} F(x,y)&= F_1\sin \frac{\pi x}{a}\sin \frac{3\pi y}{b}\nonumber \\&+\,F_2 \sin \frac{3\pi x}{a}\sin \frac{\pi y}{b}, \end{aligned}$$

(7)

where $F_i (i=1 ,2)$ respectively represent the amplitudes of the transverse forcing excitation matching the two chosen modes.

Substituting Eq. (6) into Eq. (2), considering the boundary conditions (4) and (5) and integrating, we obtain the stress function as follows

$$\begin{aligned} {\upphi } (x,y,t)&= {\upphi }_{20}(t)\cos \frac{2{\uppi }{x}}{a}+{\upphi }_{02}(t)\cos \frac{2{\uppi }y}{b}\nonumber \\&+\,{\upphi } _{60} (t)\cos \frac{6{\uppi }x}{a}+{\upphi }_{06}(t)\cos \frac{6{\uppi }y}{b}\nonumber \\&+\,{\upphi } _{22} (t)\cos \frac{2{\uppi }x}{a}\cos \frac{2{\uppi }y}{b}\nonumber \\&+\,{\upphi } _{24} (t)\cos \frac{2{\uppi }x}{a}\cos \frac{4{\uppi }y}{b}\nonumber \\&+\,{\upphi }_{42} (t)\cos \frac{4{\uppi }x}{a}\cos \frac{2{\uppi } y}{b}\nonumber \\&+\,{\upphi }_{44} (t)\cos \frac{4{\uppi }x}{a}\cos \frac{4{\uppi }y}{b}-\frac{1}{2}py^{2}, \end{aligned}$$

(8)

where the coefficients presented in Eq. (8) are given in Appendix 1.

In order to obtain the dimensionless equations, we introduce the transformations of variables and parameters presented in Appendix 2. By means of the Galerkin’s method, substituting Eqs. (6)–(8) into Eq. (1) and integrating, we obtain the dimensionless equation of motion with two-degree-of- freedom as follows

$$\begin{aligned}&\ddot{q}_1 +{\upvarepsilon } \upmu \dot{q}_1 +({\upomega }_1^2 +2{\upvarepsilon } f_1 \cos \Omega _2 t)q_1\nonumber \\&\quad +\,{\upvarepsilon } ({\upalpha } _1 q_1^3 +{\upalpha } _2 q_1 q_2^2 )={\upvarepsilon } F_1 \cos \Omega _1 t,\end{aligned}$$

(9a)

$$\begin{aligned}&\ddot{q}_2 +{\upvarepsilon } \upmu \dot{q}_2 +({\upomega } _2^2 +2{\upvarepsilon } f_2 \cos \Omega _2 t)q_2\nonumber \\&\quad +\,{\upvarepsilon } ({\upbeta } _1 q_2^3 +{\upbeta } _2 q_1^2 q_2 )={\upvarepsilon } F_2 \cos \Omega _1 t, \end{aligned}$$

(9b)

where the coefficients presented in Eq. (9) are given in Appendix 3.

The above equations include the cubic terms, in-plane excitation and transverse excitation. Equation (9) can describe the nonlinear transverse oscillations of the simply supported rectangular thin plate. We only consider the case of 1:2 internal resonance and primary parametric resonance-fundamental parametric resonance. In this resonant case, there are the following relations

$$\begin{aligned} {\upomega }_1^2&= \frac{1}{4}\Omega _2^2 +{\upvarepsilon } {\upsigma } _1 ,\quad {\upomega }_2^2 =\Omega _2^2 +{\upvarepsilon } {\upsigma } _2,\quad \Omega _1 =\Omega _2,\nonumber \\&2{\upomega } _1 \approx {\upomega } _2, \end{aligned}$$

(10)

where ${\upsigma } _1$ and ${\upsigma } _2$ are the two detuning parameters. For convenience of the study, we let $\Omega _1 =\Omega _2 =2$.

According to the relationship between the parameters in Appendix 1 and 3, we derive the parameter ${\lambda } =1.55$ under the last condition in Eq. (10). The parameter ${\lambda }$ represents the ratio between length and width of rectangular thin plate. Relationships of internal resonance correspond to the structures. Thus, different structures have different internal resonance relationships.

The method of multiple scales [35] is employed to Eq. (9) to find the uniform solutions in the following form

$$\begin{aligned} q_n \left( {t ,{\upvarepsilon } } \right) =q_{n0} \left( {T_0 ,T_1 } \right) +{\upvarepsilon } q_{n1} \left( {T_0 ,T_1 } \right) +\cdots ,\quad n=1 , 2,\nonumber \\ \end{aligned}$$

(11)

where $T_0 =t,T_1 ={\upvarepsilon } t$.

Substituting Eqs. (10) and (11) into Eq. (9), balancing the coefficients of corresponding powers of ${\upvarepsilon }$ on the left-hand and right-hand sides of equations, and eliminating the terms that produce secular terms from equations, the four-dimensional averaged equations in the Cartesian form are obtained as follows

$$\begin{aligned} \frac{dx_1 }{dT_1 }&= -\frac{1}{2}\upmu x_1 -\frac{1}{2}({\upsigma } _1 -f_1 )x_2 -\frac{3}{2}{\upalpha }_1 x_2 \left( x_1^2 +x_2^2\right) \nonumber \\&-\,{\upalpha } _2 x_2 \left( x_3^2 +x_4^2\right) ,\end{aligned}$$

(12a)

$$\begin{aligned} \frac{dx_2 }{dT_1 }&= \frac{1}{2}({\upsigma } _1 +f_1 )x_1 -\frac{1}{2}\upmu x_2 +\frac{3}{2}{\upalpha } _1 x_1 \left( x_1^2 +x_2^2\right) \nonumber \\&+\,{\upalpha } _2 x_1 \left( x_3^2 +x_4^2\right) ,\end{aligned}$$

(12b)

$$\begin{aligned} \frac{dx_3 }{dT_1 }&= -\frac{1}{2}\upmu x_3 -\frac{1}{4}{\upsigma } _2 x_4 -\frac{3}{4}{\upbeta } _1 x_4 \left( x_3^2 +x_4^2\right) \nonumber \\&-\,\frac{1}{2}{\upbeta } _2 x_4 \left( x_1^2 +x_2^2\right) ,\end{aligned}$$

(12c)

$$\begin{aligned} \frac{dx_4 }{dT_1}&= -\frac{1}{8}F_2 +\frac{1}{4}{\upsigma } _2 x_3 -\frac{1}{2}\upmu x_4+\frac{3}{4}{\upbeta } _1 x_3 \left( x_3^2 +x_4^2\right) \nonumber \\&+\,\frac{1}{2}{\upbeta } _2 x_3 \left( x_1^2 +x_2^2\right) . \end{aligned}$$

(12d)

Comparison of Eqs. (9) and (12), it is found that Eq. (9) is non-autonomous ordinary differential equation with two-degree-of-freedom and the four-dimensional averaged Eq. (12) is an autonomous nonlinear system. The variables $x_1$ and $x_2$ in Eq. (12) correspond to the displacement and the speed of mode described by Eq. (9a). The variables $x_3$ and $x_4$ in Eq. (12) agree with the displacement and the speed of mode given by Eq. (9b).

It is necessary to eliminate the secular terms when we derive averaged equations in the Cartesian form. Parameter $F_1$ is eliminated since $F_1$ is included in the secular terms. Thus, there is no $F_1$ in Eq. (12). It is observed from Eq. (12) that it is difficult directly to analyze the singular points and orbits. In order to analyze the Shilnikov type multi-pulse global bifurcations and chaotic dynamics of a simply supported at four-edge, rectangular thin plate subjected to transversal and in-plane excitations simultaneously, we need to reduce Eq. (12) to a normal form. In the next section, we will give normal form of averaged Eq. (12).

3 Computation of normal form

In order to conveniently analyze the Shilnikov type multi-pulse orbits and chaotic dynamics for the simply supported rectangular thin plate subjected to transversal and in-plane excitations, we need to reduce averaged Eq. (12) to a simpler normal form. It is seen that there are $Z_2 \oplus Z_2$ and $D_4$ symmetries in averaged Eq. (12) when these parameters $F_2,\upmu$ and $f_1$ do not exist. Therefore, these symmetries are also held in normal form.

We take into account the exciting amplitude $F_2$ as a perturbation parameter. Amplitude $F_2$ can be considered as an unfolding parameter when the Shilnikov type multi-pulse orbits are investigated. Obviously, when we do not consider the perturbation parameter, Eq. (12) becomes

$$\begin{aligned} \frac{dx_1 }{dT_1}&= -\frac{1}{2}\upmu x_1 -\frac{1}{2}({\upsigma } _1 -f_1 )x_2 -\frac{3}{2}{\upalpha } _1 x_2 \left( x_1^2 +x_2^2\right) \nonumber \\&-\,{\upalpha } _2 x_2 \left( x_3^2+x_4^2\right) ,\end{aligned}$$

(13a)

$$\begin{aligned} \frac{dx_2 }{dT_1 }&= \frac{1}{2}({\upsigma } _1 +f_1 )x_1 -\frac{1}{2}\upmu x_2+\frac{3}{2}{\upalpha } _1 x_1 \left( x_1^2 +x_2^2\right) \nonumber \\&+\,{\upalpha } _2 x_1 \left( x_3^2 +x_4^2\right) ,\end{aligned}$$

(13b)

$$\begin{aligned} \frac{dx_3 }{dT_1 }&= -\frac{1}{2}\upmu x_3 -\frac{1}{4}{\upsigma } _2 x_4 -\frac{3}{4}{\upbeta } _1 x_4 \left( x_3^2 +x_4^2 \right) \nonumber \\&-\,\frac{1}{2}{\upbeta } _2 x_4 \left( x_1^2 +x_2^2\right) ,\end{aligned}$$

(13c)

$$\begin{aligned} \frac{dx_4 }{dT_1 }&= \frac{1}{4}{\upsigma } _2 x_3 -\frac{1}{2}\upmu x_4 +\frac{3}{4}{\upbeta } _1 x_3 \left( x_3^2 +x_4^2 \right) \nonumber \\&+\,\frac{1}{2}{\upbeta } _2 x_3 \left( x_1^2 +x_2^2\right) . \end{aligned}$$

(13d)

Therefore, we can first study normal form of Eq. (13) without perturbation parameter $F_2$. We add the exciting amplitude $F_2$to normal form after we obtain normal form of Eq. (13). It is obviously known that Eq. (13) has a trivial zero solution $\left( {x_1 ,x_2 ,x_3 ,x_4 } \right) =\left( {0 ,0 ,0 ,0} \right)$ at which the Jacobi matrix can be written as

$$\begin{aligned} J=D_x X=\left[ {{\begin{array}{cccc} {-\frac{1}{2}\upmu }&{} {-\frac{1}{2}({\upsigma } _1 -f_1 )}&{} 0&{} 0 \\ {\frac{1}{2}({\upsigma } _1 +f_1 )}&{} {-\frac{1}{2}\upmu }&{} 0&{} 0 \\ 0&{} 0&{} {-\frac{1}{2}\upmu }&{} {-\frac{1}{4}{\upsigma } _2 } \\ 0&{} 0&{} {\frac{1}{4}{\upsigma } _2 }&{} {-\frac{1}{2}\upmu } \\ \end{array} }} \right] \!.\nonumber \\ \end{aligned}$$

(14)

The characteristic equation corresponding to the trivial zero solution is of the form

$$\begin{aligned} (4{\uplambda } ^{2}+4\upmu {\uplambda } +\upmu ^{2}+{\upsigma } _1^2 -f_1^2 )(4{\uplambda } ^{2}+4\upmu {\uplambda } +\upmu ^{2}+\frac{1}{4}{\upsigma } _2^2 )=0.\nonumber \\ \end{aligned}$$

(15)

Let

$$\begin{aligned} {\Delta }_1 =\upmu ^{2}+{\upsigma } _1^2 -f_1^2\quad \text { and }\quad {\Delta }_2 =\upmu ^{2}+\frac{1}{4}{\upsigma } _2^2. \end{aligned}$$

(16)

When $\upmu =0, {\Delta }_1 =0$ and ${\Delta }_2 =\frac{1}{4}{\upsigma } _2^2 >0$ are simultaneously satisfied, Eq. (13) has one non-semisimple double zero and a pair of pure imaginary Eigenvalues

$$\begin{aligned} {\uplambda } _{1,2} =0,\quad {\uplambda } _{3,4} =\pm i{\upomega } , \end{aligned}$$

(17)

where ${\upomega } ^{2}={{\upsigma } _2^2 }/{16}$, non-semisimple double zero is double zero Eigenvalue of non-diagonal matrix.

Generally, there exist two kinds of equilibria in the system. These equilibria are stable equilibrium and the critical stable equilibrium, respectively. The stable equilibria do not change their stability characteristic when they are disturbed. Only critical stable equilibrium may change the properties of equilibrium under the perturbation. Thus, it is the most meaningful that only critical stable equilibrium is studied theoretically. Equation (13) has one non-semisimple double zero and a pair of pure imaginary Eigenvalues at $({0 ,0 ,0 ,0})$. Therefore, the equilibrium at $({0 ,0 ,0 ,0})$ is the critical stable state. The system will change its stability characteristic when the system is disturbed. If there are many equilibria in the system, we must first determine the type of singular points at equilibria. We can calculate the homoclinic orbits and heteroclinic orbits when there are saddle points in the system. Thus, we use the global perturbation methods to investigate dynamical characteristic of the homoclinic orbits and heteroclinic orbits.

Considering $\bar{{{\upsigma } }}_1,\upmu$ and $F_2$ as the perturbation parameters, letting ${\upsigma } _1 =2 \bar{{{\upsigma } }}_1 -f_1$ and setting $f_1 =1$, then, averaged Eq. (13) without the perturbation parameters becomes the following form

$$\begin{aligned} \frac{dx_1 }{dT_1 }&= x_2 -\frac{3}{2}{\upalpha } _1 x_2 \left( x_1^2 +x_2^2 \right) -{\upalpha } _2 x_2 \left( x_3^2 +x_4^2 \right) ,\nonumber \\ \end{aligned}$$

(18a)

$$\begin{aligned} \frac{dx_2 }{dT_1 }&= \frac{3}{2}{\upalpha } _1 x_1 \left( x_1^2 +x_2^2 \right) +\,{\upalpha } _2 x_1 \left( x_3^2 +x_4^2 \right) ,\end{aligned}$$

(18b)

$$\begin{aligned} \frac{dx_3 }{dT_1 }&= -\frac{1}{4}{\upsigma } _2 x_4 -\frac{3}{4}{\upbeta } _1 x_4 \left( x_3^2 +x_4^2 \right) -\frac{1}{2}{\upbeta } _2 x_4 \left( x_1^2 +x_2^2 \right) ,\nonumber \\ \end{aligned}$$

(18c)

$$\begin{aligned} \frac{dx_4 }{dT_1 }&= \frac{1}{4}{\upsigma } _2 x_3 +\frac{3}{4}{\upbeta } _1 x_3 \left( x_3^2 +x_4^2 \right) +\frac{1}{2}{\upbeta } _2 x_3 \left( x_1^2 +x_2^2 \right) \nonumber \\ \end{aligned}$$

(18d)

The difference between Eq. (13) and Eq.  (18) is that Eq. (13) contain the perturbation parameters $\upmu , {\upsigma } _1$ and $f_1$. According to Eq.  (18), we have

$$\begin{aligned} A=\left[ {{\begin{array}{c@{\qquad }c@{\qquad }c@{\qquad }c} 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {-\frac{1}{4}{\upsigma } _2 } \\ 0&{} 0&{} {\frac{1}{4}{\upsigma } _2 }&{} 0 \\ \end{array} }} \right] \!. \end{aligned}$$

(19)

Executing the Maple program given by Zhang et al. [36], the 3rd-order normal form of Eq. (18) is obtained as

$$\begin{aligned} \dot{y}_1&= y_2 ,\end{aligned}$$

(20a)

$$\begin{aligned} \dot{y}_2&= \frac{3}{2}{\upalpha } _1 y_1^3 +{\upalpha } _2 y_1 y_3^2 +{\upalpha } _2 y_1 y_4^2 ,\end{aligned}$$

(20b)

$$\begin{aligned} \dot{y}_3&= -\frac{1}{4}{\upsigma } _2 y_4 -\frac{3}{4}{\upbeta } _1 y_4^3-\frac{1}{2}{\upbeta } _2 y_1^2 y_4 -\frac{3}{4}{\upbeta } _1 y_3^2 y_4 , \end{aligned}$$

(20c)

$$\begin{aligned} \dot{y}_4&= \frac{1}{4}{\upsigma } _2 y_3 +\frac{3}{4}{\upbeta } _1 y_3^3 +\frac{1}{2}{\upbeta } _2 y_1^2 y_3+\frac{3}{4}{\upbeta } _1 y_3 y_4^2. \end{aligned}$$

(20d)

The nonlinear transformation used here is given as follows

$$\begin{aligned} x_1&= y_1 -\frac{1}{4}{\upalpha } _1 y_1^3 -{\upalpha } _2 y_1 y_3^2 -{\upalpha } _2 y_1 y_4^2 ,\end{aligned}$$

(21a)

$$\begin{aligned} x_2&= y_2 +\frac{3}{2}{\upalpha } _1 y_2^3 +\frac{3}{4}{\upalpha } _1 y_1^2 y_2 ,\end{aligned}$$

(21b)

$$\begin{aligned} x_3&= y_3 -\frac{1}{2}{\upbeta } _2 y_1 y_2 y_4 ,\end{aligned}$$

(21c)

$$\begin{aligned} x_4&= y_4 +\frac{1}{2}{\upbeta } _2 y_1 y_2 y_3. \end{aligned}$$

(21d)

The above mentioned nonlinear transformation is computed through the Maple program given Zhang et al. [36], and completely agrees with those presented by Yu et al. [37]. Therefore, a simpler 3rd-order normal form with the parameters for averaged Eq. (12) is obtained as follows

$$\begin{aligned} \dot{y}_1&= -\bar{{\upmu }}y_1 +(1-\bar{{{\upsigma } }}_1 )y_2 ,\end{aligned}$$

(22a)

$$\begin{aligned} \dot{y}_2&= \bar{{{\upsigma } }}_1 y_1 -\bar{{\upmu }}y_2 +\frac{3}{2}{\upalpha } _1 y_1^3 +{\upalpha } _2 y_1 y_3^2 +{\upalpha } _2 y_1 y_4^2 ,\end{aligned}$$

(22b)

$$\begin{aligned} \dot{y}_3&= -\bar{{\upmu }}y_3 -\bar{{{\upsigma } }}_2 y_4 -\frac{3}{4}{\upbeta } _1 y_4^3 -\frac{1}{2}{\upbeta } _2 y_1^2 y_4 -\frac{3}{4}{\upbeta } _1 y_3^2 y_4 ,\nonumber \\\end{aligned}$$

(22c)

$$\begin{aligned} \dot{y}_4&= -\bar{{f}}_2 +\bar{{{\upsigma } }}_2 y_3 -\bar{{\upmu }}y_4+\frac{3}{4}\upbeta _{1} y^3_3+\frac{1}{2} \upbeta _{2} y^2_1y_3 +\frac{3}{4}{\upbeta } _1 y_3 y_4^2 , \end{aligned}$$

(22d)

where the coefficients are $\bar{{\upmu }}=\frac{1}{2}\upmu , \bar{{{\upsigma } }}_2 =\frac{1}{4}{\upsigma } _2$, and $\bar{{f}}_2 =\frac{1}{8}F_2$, respectively.

Further, let

$$\begin{aligned} y_3 =I\cos {\upgamma } \quad \text { and }\quad y_4 =I\sin {\upgamma }. \end{aligned}$$

(23)

Substituting Eq. (23) into Eq. (22) yields

$$\begin{aligned}&\dot{y}_1 =-\bar{{\upmu }}y_1 +\left( {1-\bar{{{\upsigma } }}_1 } \right) y_2 ,\end{aligned}$$

(24a)

$$\begin{aligned}&\dot{y}_2 =\bar{{{\upsigma } }}_1 y_1 -\bar{{\upmu }}y_2 +\frac{3}{2}{\upalpha } _1 y_1^3+{\upalpha } _2 y_1 I^{2},\end{aligned}$$

(24b)

$$\begin{aligned}&\dot{I}=-\bar{{\upmu }}I-\bar{{f}}_2 \sin {\upgamma } ,\end{aligned}$$

(24c)

$$\begin{aligned}&I\dot{{\upgamma }}=\bar{{{\upsigma } }}_2 I+\frac{3}{4}{\upbeta } _1 I^{3}+\frac{1}{2}{\upbeta } _2 Iy_1^2 -\bar{{f}}_2\cos {\upgamma }. \end{aligned}$$

(24d)

In order to get the unfolding of Eq. (24), a linear transformation is introduced

$$\begin{aligned} \left[ {{\begin{array}{c} {y_1 } \\ {y_2 } \\ \end{array} }} \right] =\frac{\sqrt{|{\upalpha } _2 |}}{\sqrt{\left| {\frac{1}{2}{\upbeta } _2 } \right| }}\left[ {{\begin{array}{c@{\qquad }c} {1-\bar{{{\upsigma } }}_1 }&{} 0 \\ {\bar{{\upmu }}}&{} 1 \\ \end{array} }} \right] \left[ {{\begin{array}{c} {u_1 } \\ {u_2 } \\ \end{array} }} \right] . \end{aligned}$$

(25)

Substituting Eq. (25) into Eq. (24), and canceling nonlinear terms including the parameter $\bar{{{\upsigma } }}_1$ yield the unfolding as follows

$$\begin{aligned}&\dot{u}_1 =u_2,\end{aligned}$$

(26a)

$$\begin{aligned}&\dot{u}_2 =-\upmu _1 u_1 -\upmu _2 u_2 +{\upeta } _1 u_1^3 +{\upalpha } _2 u_1 I^{2},\end{aligned}$$

(26b)

$$\begin{aligned}&\dot{I}=-\bar{{\upmu }}I-\bar{{f}}_2 \sin {\upgamma } ,\end{aligned}$$

(26c)

$$\begin{aligned}&I\dot{{\upgamma } }=\bar{{{\upsigma } }}_2 I+{\upeta } _2 I^{3}+{\upalpha } _2 Iu_1^2-\bar{{f}}_2 \cos {\upgamma } , \end{aligned}$$

(26d)

where $\upmu _1 =\bar{{\upmu }}^{2}-\bar{{{\upsigma } }}_1 \left( {1-\bar{{{\upsigma } }}_1 } \right) , \upmu _2 =2\bar{{\upmu }}, {\upeta } _1 =\frac{3{\upalpha } _1 {\upalpha } _2 }{{\upbeta } _2 }$ and ${\upeta } _2 =\frac{3}{4}{\upbeta } _1$.

The scale transformations to be introduced into Eq. (26) are

$$\begin{aligned} {\upmu }_2 \!\rightarrow \! {\upvarepsilon } \upmu _2 ,\bar{{\upmu }}\!\rightarrow \! {\upvarepsilon } \bar{{\upmu }},\bar{{f}}_2 \rightarrow {\upvarepsilon } \bar{{f}}_2 ,{\upeta } _1 \rightarrow {\upeta } _1 ,{\upeta } _2 \rightarrow {\upeta } _2 , \end{aligned}$$

(27)

where ${\upvarepsilon } (0<{\upvarepsilon } <<1)$ is a small perturbation parameter. In this paper, we only consider weak perturbation. Therefore, we introduce the small perturbation parameter ${\upvarepsilon }$ into damping $\upmu _2,\bar{{\upmu }}$ and excitation $\bar{{f}}_2$. Then, normal form (26) can be rewritten in the form with the perturbations

$$\begin{aligned}&\dot{u}_1 =\frac{\partial H}{\partial u_2 }+{\upvarepsilon } g^{u_1}=u_2 ,\end{aligned}$$

(28a)

$$\begin{aligned}&\dot{u}_2 =-\frac{\partial H}{\partial u_1 }+{\upvarepsilon } g^{u_2 }\nonumber \\&\quad =-\upmu _1 u_1 +{\upeta } _1 u_1^3+{\upalpha } _2 u_1 I^{2}-{\upvarepsilon } \upmu _2 u_2,\end{aligned}$$

(28b)

$$\begin{aligned}&\dot{I}=\frac{\partial H}{\partial {\upgamma } }+{\upvarepsilon } g^{I}=-{\upvarepsilon } \bar{{\upmu }}I-{\upvarepsilon } \bar{{f}}_2 \sin {\upgamma },\end{aligned}$$

(28c)

$$\begin{aligned}&I\dot{{\upgamma } }=-\frac{\partial H}{\partial I}+{\upvarepsilon } g^{{\upgamma } }\nonumber \\&\quad =\bar{{{\upsigma } }}_2 I+{\upeta } _2 I^{3}+{\upalpha } _2 Iu_1^2 -{\upvarepsilon } \bar{{f}}_2 \cos {\upgamma }, \end{aligned}$$

(28d)

where the Hamiltonian function $H$ is of the form

$$\begin{aligned} H(u_1 ,u_2 ,I ,{\upgamma } )&= \frac{1}{2}u_2^2 +\frac{1}{2}\upmu _1 u_1^2 -\frac{1}{4}{\upeta } _1 u_1^4\nonumber \\&-\,\frac{1}{2}{\upalpha } _2 I^{2}u_1^2 -\frac{1}{2}\bar{{{\upsigma } }}_2 I^{2}-\frac{1}{4}{\upeta } _2 I^{4}, \end{aligned}$$

(29)

and $g^{u_1}, g^{u_2 }, g^{I}$ and $g^{{\upgamma } }$ are the perturbation terms induced by the dissipative effects

$$\begin{aligned}&g^{u_1 }=0,\quad g^{u_2 }=-\upmu _2 u_2 ,\quad g^{I}=-\bar{{\upmu }}I-\bar{{f}}_2 \sin {\upgamma },\nonumber \\&g^{{\upgamma } }=-\bar{{f}}_2 \cos {\upgamma }. \end{aligned}$$

(30)

4 Unperturbed dynamics

In this section, we focus on studying the nonlinear dynamics characteristic of the unperturbed system. In this paper, we use the global perturbation methods and the extended Melnikov method to investigate the Shilnikov type multi-pulse global bifurcations and chaotic dynamics of the rectangular thin plate. When ${\upvarepsilon } =0$, it can be known that system from Eq. (28) is an uncoupled two-degree-of-freedom nonlinear system. Thus, we can study the nonlinear dynamics characteristic of the unperturbed system and the perturbed system, respectively. Then, we adopt the extended Melnikov method to analyze interactions between the two modes.

The variable $I$ appears in the subspace $(u_1 ,u_2 )$ of Eq. (28) as a parameter since $\dot{I}=0$. Consider the first two decoupled equations of Eq. (28)

$$\begin{aligned} \dot{u}_1&= u_2 ,\end{aligned}$$

(31a)

$$\begin{aligned} \dot{u}_2&= -\upmu _1 u_1 +{\upeta } _1 u_1^3 +{\upalpha } _2 I^{2}u_1. \end{aligned}$$

(31b)

Since ${\upeta } _1 >0$, Eq. (31) can exhibit the heteroclinic bifurcations. Based on studies given by Guckenheimer and Holmes [38], it is obvious from Eq. (31) that when $\upmu _1 -{\upalpha } _2 I^{2}<0$, the only solution to Eq. (31) is the trivial zero solution, $(u_1 ,u_2 )=(0 ,0)$, which is the saddle point. On the curve defined by $\upmu _1 ={\upalpha } _2 I^{2}$, that is,

$$\begin{aligned} \bar{{\upmu }}^{2}=\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )+{\upalpha } _2 I^{2}, \end{aligned}$$

(32)

or

$$\begin{aligned} I_{1 ,2} =\pm \left[ {\frac{\bar{{\upmu }}^{2}-\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )}{{\upalpha } _2 }} \right] ^{\frac{1}{2}}, \end{aligned}$$

(33)

the trivial zero solution bifurcates into three solutions through a pitchfork bifurcation, which are given by $q_0 =(0 ,0)$ and $q_\pm (I)=(B ,0),$ respectively, where

$$\begin{aligned} B=\pm \left\{ {\frac{1}{{\upeta } _1 }\left[ \bar{{\upmu }}^{2}-\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )-{\upalpha } _2 I^{2}\right] } \right\} ^{\frac{1}{2}}. \end{aligned}$$

(34)

From the Jacobian matrix evaluated at the non-zero solutions, it can be found that the singular points $q_\pm (I)$ are the saddle points and the singular point $q_0$ is center point. It is observed that the $I$ and ${\upgamma }$ actually represent the amplitude and phase of the vibrations. Therefore, we assume that $I\ge 0$ and Eq. (33) becomes

$$\begin{aligned} I_1 =0\quad \text { and }\quad I_2 =\left[ {\frac{\bar{{\upmu }}^{2}-\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )}{{\upalpha } _2 }} \right] ^{\frac{1}{2}}, \end{aligned}$$

(35)

such that for all $I\in [I_1 ,I_2 ]$, Eq. (31) has two hyperbolic saddle points, $q_\pm (I)$, which are connected by a pair of heteroclinic orbits, $u_\pm ^h (T_1 ,I)$, that is, $\mathop {\lim }\limits _{T_1 \rightarrow \pm \infty } u_\pm ^h (T_1 ,I)=q_\pm (I)$. Thus, in the full four-dimensional phase space, the set defined by

$$\begin{aligned} M=\left\{ {\left. { (u ,I ,{\upgamma } ) } \right| u=q_\pm (I) ,I_1 \le I\le I_2 ,0\le {\upgamma } <2\uppi } \right\} \nonumber \\ \end{aligned}$$

(36)

is a two-dimensional invariant manifold.

From the results obtained by Kovacic et al. [22–24], it is known that the two-dimensional invariant manifold $M$ is normally hyperbolic. The two-dimensional normally hyperbolic invariant manifold $M$ has three-dimensional stable and unstable manifolds represented as $W^{s}(M)$ and $W^{u}(M)$, respectively. The existence of the heteroclinic orbit of Eq. (31) to $q_\pm (I)=(B ,0)$ indicates that $W^{s}(M)$ and $W^{u}(M)$ intersect non-transversally along a three-dimensional heteroclinic manifold denoted by $\Gamma$, which can be written as

$$\begin{aligned}&\Gamma =\left\{ {(u ,I ,{\upgamma } ) } \right| u=u_\pm ^h (T_1 ,I) ,I_1 <I<I_2,\nonumber \\&{\upgamma }\left. =\int _{ 0}^{ T_1 } {D_I H(u_\pm ^h (T_1,I) ,I)ds+{\upgamma } _0 } \right\} . \end{aligned}$$

(37)

We analyze the dynamics of the unperturbed system of Eq. (28) restricted to $M$. Considering the unperturbed system of Eq. (28) restricted to $M$ yields

$$\begin{aligned}&\dot{I}=0,\end{aligned}$$

(38a)

$$\begin{aligned}&I\dot{{\upgamma } }=D_I H(q_\pm (I) ,I), \quad I_1 \le I\le I_2 , \end{aligned}$$

(38b)

where

$$\begin{aligned} D_I H(q_\pm (I) ,I)&= -\frac{\partial H(q_\pm (I) ,I)}{\partial I}\nonumber \\&= \bar{{{\upsigma } }}_2 I+{\upeta } _2 I^{3}+{\upalpha } _2 Iq_\pm ^2 (I). \end{aligned}$$

(39)

From the results obtained by Kovacic et al. [22–24], it is known that if $D_I H(q_\pm (I) ,I)\ne 0, I=\text {constant}$ is called a periodic orbit, and if $D_I H(q_\pm (I) ,I)=0, I=$ constant is known as a circle of the singular points. Any value of $I\in [I_1 ,I_2 ]$ at which $D_I H(q_\pm (I) ,I)=0$ is a resonant value $I$ and these singular points are resonant singular points. We denoted a resonant value by $I_r$ such that

$$\begin{aligned} D_I H(q_\pm (I) ,I)&= \bar{{{\upsigma } }}_2 I_r +{\upeta } _2 I_r^3 +\frac{{\upalpha } _2 }{{\upeta } _1 }\left[ \bar{{\upmu }}^{2}\right. \nonumber \\&\left. -\,\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )-{\upalpha } _2 I_r^2\right] I_r =0. \end{aligned}$$

(40)

Then, we obtain

$$\begin{aligned} I_r =\pm \left\{ {\frac{\bar{{{\upsigma } }}_2 {\upeta } _1 +{\upalpha } _2 [\bar{{\upmu }}^{2}-\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )]}{{\upalpha } _2^2 -{\upeta } _1 {\upeta } _2 }} \right\} ^{\frac{1}{2}}. \end{aligned}$$

(41)

The geometry structure of the stable and unstable manifolds of $M$ in the full four-dimensional phase space for the unperturbed system of Eq. (28) is given in Fig. 2. Since ${\upgamma }$ represents the phase of oscillations, when $I=I_r$, the phase shift ${\Delta }{\upgamma }$ of oscillations is defined by

$$\begin{aligned} {\Delta }{\upgamma } ={\upgamma } (+\infty ,I_r )-{\upgamma } (-\infty ,I_r ). \end{aligned}$$

(42)

The physical interpretation of the phase shift is the phase difference between the two end points of the orbit. In the subspace $(u_1 ,u_2 )$, there exists a pair of the heteroclinic orbits connecting to the two saddles. Therefore, the homoclinic orbit in the subspace $(I ,{\upgamma } )$ is, in fact, a heteroclinic connecting in the full four-dimensional space $(u_1 ,u_2 ,I ,{\upgamma } )$. The phase shift denotes the difference of the value ${\upgamma }$ when a trajectory leaves and returns to the basin of attraction of $M$. We will use the phase shift in subsequent analysis to obtain the condition for the existence of the Shilnikov-type multi-pulse orbit. The phase shift will be calculated later in the heteroclinic orbit analysis.

Fig. 2

The geometric structure of manifolds $M, W^{\text {s}}(M)$ and $W^{u}(M)$ is given in the full four-dimensional phase space

We consider the heteroclinic orbits of equation (31). Let ${\upvarepsilon } _1 =\upmu _1 -{\upalpha } _2 I^{2}$ and $\upmu _2 ={\upvarepsilon } _2$, Eq. (31) can be rewritten as

$$\begin{aligned} \dot{u}_1&= u_2 ,\end{aligned}$$

(43a)

$$\begin{aligned} \dot{u}_2&= -{\upvarepsilon } _1 u_1 +{\upeta }_1 u_1^3 -{\upvarepsilon } {\upvarepsilon } _2 u_2. \end{aligned}$$

(43b)

Set ${\upvarepsilon } =0$. Equation (43) is a system with the Hamiltonian function

$$\begin{aligned} \bar{{H}}(u_1 ,u_2 )=\frac{1}{2}u_2^2 +\frac{1}{2}{\upvarepsilon } _1 u_1^2 -\frac{1}{4}{\upeta } _1 u_1^4. \end{aligned}$$

(44)

When $\bar{{H}}={{\upvarepsilon } _1^2 }/{(4{\upeta } _1 )}$, there is a heteroclinic loop $\Gamma ^{0}$ which consists of the two hyperbolic saddles $q_\pm$ and a pair of heteroclinic orbits $u_\pm (T_1 )$. In order to calculate the phase shift and the extended Melnikov function, we obtain the equations of a pair of heteroclinic orbits

$$\begin{aligned} u_1 (T_1)&= \pm \sqrt{\frac{{\upvarepsilon } _1 }{{\upeta } _1 }}\tanh \left( {\frac{\sqrt{2{\upvarepsilon } _1 }}{2}T_1 } \right) \!,\end{aligned}$$

(45a)

$$\begin{aligned} u_2 (T_1 )&= \pm \frac{{\upvarepsilon } _1 }{\sqrt{2{\upeta } _1 }}\text {sech}^{2}\left( {\frac{\sqrt{2{\upvarepsilon } _1 }}{2}T_1 } \right) \!. \end{aligned}$$

(45b)

We turn our attention to the computation of the phase shift. Substituting the first equation of Eq. (45) into the fourth equation of the unperturbed system of Eq. (28) yields

$$\begin{aligned} \dot{{\upgamma } }&= \bar{{{\upsigma } }}_2 +{\upeta } _2 I^{2}+\frac{{\upalpha } _2 {\upvarepsilon } _1 }{{\upeta } _1 }\tanh ^{2}\left( {\frac{\sqrt{2{\upvarepsilon } _1 }}{2}T_1 } \right) . \end{aligned}$$

(46)

Integrating Eq. (46) yields

$$\begin{aligned} {\upgamma } (T_1 )&= {\upomega } _r T_1 -\frac{{\upalpha } _2 \sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }\tanh \left( {\frac{\sqrt{2{\upvarepsilon } _1 }}{2}T_1 } \right) +{\upgamma } _0 , \end{aligned}$$

(47)

where ${\upomega } _r =\bar{{{\upsigma } }}_2 +{\upeta } _2 I^{2}+\frac{{\upvarepsilon } _1 {\upalpha } _2 }{{\upeta } _1 }$.

At $I=I_r$, there is ${\upomega } _r \equiv 0$. Therefore, the phase shift may be expressed as

$$\begin{aligned} {\Delta }{\upgamma }&= \left[ {-\frac{2{\upalpha } _2 \sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right] _{I=I_r } \nonumber \\&= -\frac{2{\upalpha } _2 }{{\upeta } _1 }\sqrt{2\left[ \bar{{\upmu }}^{2}-\bar{{{\upsigma } }}_1 (1-\bar{{{\upsigma } }}_1 )-{\upalpha } _2 I_r^2 \right] }. \end{aligned}$$

(48)

5 Existence of multi-pulse orbits

After obtaining detailed information on the nonlinear dynamic characteristics of the subspace $(u_1 ,u_2 )$ for the unperturbed system from Eq. (28), the next step is to examine the effects of small perturbation terms $(0<{\upvarepsilon } \ll 1)$ on the unperturbed system from Eq. (28). The extended Melnikov method developed by Kovacic et al. [22–24] is utilized to discover the existence of the Shilnikov type multi-pulse orbits and chaotic dynamics of the nonlinear vibration for the simply supported rectangular thin plate. We start by studying the influence of such small perturbations on the manifold $M$. The objective of the research is to identify the parameter regions where the existence of the multi-pulse orbits is possible in the perturbed phase space. The main aim is to verify whether these parameters satisfy the transversality condition of multi-pulse chaotic dynamics. It will be shown that these multi-pulse orbits can occur in the Hamilton system with dissipative perturbations if the parameters meet the transversality condition. The existence of such multi-pulse orbits provides a robust mechanism for the existence of the complicated dynamics in the perturbed system. In this section, the emphasis is put on the application aspects of the extended Melnikov method to Eq. (28).

5.1 Dissipative perturbations

We analyze dynamics of the perturbed system and the influence of small perturbations on $M$. Based on the analysis by Kovacic et al. [22–24], we know that $M$ along with its stable and unstable manifolds are invariant under small, sufficiently differentiable perturbations. It is noticed that the singular points $q_\pm (I)$ in Eq. (31) maintains the characteristic of the hyperbolic singular point under small perturbations, in particular, $M\rightarrow M_{\upvarepsilon }$.Therefore, we obtain

$$\begin{aligned}&M=M_{\upvarepsilon } =\left\{ \left. {(u ,I ,{\upgamma } )} \right| u=q_\pm (I) ,\right. \nonumber \\&\quad \left. I_1 \le I\le I_2 ,0\le {\upgamma } <2\uppi \right\} \!. \end{aligned}$$

(49)

Considering the last two equations of Eq. (28) yields

$$\begin{aligned} \dot{I}&= -\bar{{\upmu }}I-\bar{{f}}_2 \sin {\upgamma } ,\end{aligned}$$

(50a)

$$\begin{aligned} \dot{{\upgamma } }&= \bar{{{\upsigma } }}_2 +{\upeta } _2 I^{2}+{\upalpha } _2 u_1^2 -\frac{\bar{{f}}_2 }{I}\cos {\upgamma }. \end{aligned}$$

(50b)

It is known from the above analysis that the last two equations of Eq. (28) are of a pair of pure imaginary Eigenvalues. Therefore, the resonance can occur in Eq. (50). Also introduce the scale transformations

$$\begin{aligned} \bar{{\upmu }}\rightarrow {\upvarepsilon } \bar{{\upmu }}, \quad I=I_r +\sqrt{{\upvarepsilon } }h, \quad \bar{{f}}_2 \rightarrow {\upvarepsilon } \bar{{f}}_2,\quad T_1 \rightarrow \frac{T_1 }{\sqrt{{\upvarepsilon }}}.\nonumber \\ \end{aligned}$$

(51)

Substituting the above transformations into Eq. (50) yields

$$\begin{aligned} \dot{h}&= -\bar{{\upmu }}I_r -\bar{{f}}_2 \sin {\upgamma } -\sqrt{{\upvarepsilon } }h\bar{{\upmu }},\end{aligned}$$

(52a)

$$\begin{aligned} \dot{{\upgamma } }&= -\frac{2{\updelta }}{{\upeta } _1 }I_r h-\sqrt{{\upvarepsilon } }\left( {\frac{{\updelta }}{{\upeta } _1 }h^{2}+\frac{\bar{{f}}_2 }{I_r }\cos {\upgamma } } \right) \!, \end{aligned}$$

(52b)

where ${\updelta }={\upalpha } _2^2 -{\upeta } _1 {\upeta } _2$.

When ${\upvarepsilon } =0$, Eq. (52) becomes

$$\begin{aligned} \dot{h}&= -\bar{{\upmu }}I_r -\bar{{f}}_2 \sin {\upgamma } ,\end{aligned}$$

(53a)

$$\begin{aligned} \dot{{\upgamma } }&= -\frac{2{\updelta }}{{\upeta } _1 }I_r h. \end{aligned}$$

(53b)

The unperturbed system from Eq. (53) is a Hamilton system with the function

$$\begin{aligned} \hat{{\mathrm{H}}}_D (h,{\upgamma } )&= -\bar{{\upmu }}I_r {\upgamma } +\bar{{f}}_2 \cos {\upgamma }+\frac{{\updelta }}{{\upeta } _1 }I_r h^{2}. \end{aligned}$$

(54)

The singular points of Eq. (53) are given as

$$\begin{aligned} P_0&= (0 ,{\upgamma } _c )=\left( {0 ,-\arcsin \frac{\bar{{\upmu }}I_r }{\bar{{f}}_2 }} \right) \!, \nonumber \\ Q_0&= (0 ,{\upgamma } _s )=\left( 0 ,\uppi +\arcsin \frac{\bar{{\upmu }}I_r }{\bar{{f}}_2 } \right) \!. \end{aligned}$$

(55)

Based on the characteristic equations evaluated at the two singular points $P_0$ and $Q_0$, we can know the stabilities of these singular points. Therefore, it is known that the singular point $P_0$ is a center point. The singular point $Q_0$ is a saddle which is connected to itself by a homoclinic orbit. The phase portrait of system for Eq. (53) is shown in Fig. 3a.

Fig. 3

Dynamics on the normally hyperbolic manifold is described; a the unperturbed case; b the perturbed case

It is found that for the sufficiently small parameter ${\upvarepsilon }$, the singular point $Q_0$ remains a hyperbolic singular point $Q_{\upvarepsilon }$ of the saddle stability type. For small perturbations, the singular point $P_0$ becomes a hyperbolic sink $P_{\upvarepsilon }$. The phase portrait of the perturbed system from Eq. (52) is depicted in Fig. 3b.

Using the function (54), at $h=0$, the estimate of the basin of attractor for ${\upgamma } _{\min }$ is obtained as

$$\begin{aligned} -\bar{{\upmu }}I_r {\upgamma } _{\min } +\bar{{f}}_2 \cos {\upgamma } _{\min } =-\bar{{\upmu }}I_r {\upgamma } _s +\bar{{f}}_2 \cos {\upgamma } _s. \end{aligned}$$

(56)

Substituting ${\upgamma } _s$ in Eq. (55) into Eq. (56) yields

$$\begin{aligned} {\upgamma } _{\min } -\frac{\bar{{f}}_2 }{\bar{{\upmu }}I_r }\cos {\upgamma } _{\min } =\uppi +\arcsin \frac{\bar{{\upmu }}I_r }{\bar{{f}}_2 }+\frac{\sqrt{\bar{{f}}_2^2 -\bar{{\upmu }}^{2}I_r^2 }}{\bar{{\upmu }}I_r }.\nonumber \\ \end{aligned}$$

(57)

Define an annulus $A_{\upvarepsilon }$ near $I=I_r$ as

$$\begin{aligned}&A_{\upvarepsilon } =\left\{ {(u_1 ,u_2 ,I ,{\upgamma } )} \Big |u_1 =B , \ u_2 =0,\right. \nonumber \\&\left. \qquad \quad \quad \Big | I-I_r \Big |<\sqrt{{\upvarepsilon }}C ,{\upgamma } \in T^{l} \right\} , \end{aligned}$$

(58)

where $C$ is a constant and is sufficiently large so that the unperturbed homoclinic orbit is enclosed within the annulus.

It is noticed that three-dimensional stable and unstable manifolds of $A_{\upvarepsilon }$, denoted as $W^{s}(A_{\upvarepsilon } )$ and $W^{u}(A_{\upvarepsilon } )$, are the subsets of $W^{s}(M_{\upvarepsilon } )$ and $W^{u}(M_{\upvarepsilon } )$, respectively. We will indicate that for the perturbed system, the saddle focus $P_{\upvarepsilon }$ on $A_{\upvarepsilon }$ has the multi-pulse orbits which come out of the annulus $A_{\upvarepsilon }$ and can return to the annulus in the full four-dimensional space. These orbits, which are asymptotic to some invariant manifolds in the slow manifold $M_{\upvarepsilon }$, leave and enter a small neighborhood of $M_{\upvarepsilon }$multiple times, and finally return and approach an invariant set in $M_{\upvarepsilon }$ asymptotically, as shown in Fig. 4. In Fig. 4, this is an example of the three-pulse jumping orbit which depicts the formation mechanism of the multi-pulse orbits.

Fig. 4

The Shilnikov type three-pulse homoclinic orbits is obtained

5.2 The k-pulse Melnikov function

The extended Melnikov method was first presented by Kovacic et al. [22–24], which is an extension of the global perturbation method used by Feng et al. [11–21]. Kovacic et al. [22–24] gave the detail procedure of mathematical proof on the extended Melnikov method, which unifies several disjoint perturbation theoretical methods. This method can be also utilized to detect the Shilnikov type multi-pulse orbits to the slow manifolds of four-dimensional near-integrable Hamilton systems or higher-dimensional, nonlinear systems. The extended Melnikov function is different from the usual Melnikov function, and describes slow dynamics of the multi-pulse orbits on the hyperbolic manifold. The extended Melnikov function is computed by a recursion procedure from the usual one-pulse Melnikov function, and depends on the small perturbation parameter ${\upvarepsilon }$ through a logarithmic function which calculates the asymptotic in the particularly delicate small ${\upvarepsilon }$ limit.

We use the extended Melnikov method described by Kovacic et al. [22–24] to find the Shilnikov type multi-pulse orbits for nonlinear vibration for the simply supported rectangular thin plate. We search for the multi-pulse excursions to find the non-degenerate zeroes of the extended Melnikov function $M_k ({\upvarepsilon } ,I ,{\upgamma } _0 ,\bar{{\upmu }})$ with the certain combination of parameters ${\upvarepsilon },I, {\upgamma } _0$ and $\bar{{\upmu }}$, which we name the $k$-pulse Melnikov function.

It is important to obtain the detailed expression of the $k$-pulse Melnikov function. We compute the one-pulse Melnikov function based on the formula obtained by Kovacic et al. [22–24] at the resonant case $I=I_r$. The one-pulse Melnikov function $M_1 ({\upvarepsilon },I_r,{\upgamma } _0,\bar{{\upmu }})$ coincides with the standard Melnikov function $M(I_r,{\upgamma } _0 ,\bar{{\upmu }})$. The one-pulse Melnikov function $M(I_r ,{\upgamma } _0 ,\bar{{\upmu }})$ on both manifolds $W^{s}(\mathrm{M})$ and $W^{u}(\mathrm{M})$ is given as follows

$$\begin{aligned}&M(I_r ,{\upgamma } _0 ,\bar{{\upmu }},{\upeta } _1,{\upalpha } _2 ,{\upvarepsilon } _1 )=\int _{-\infty }^{+\infty } {\left\langle {\mathbf{n}(p^{h}(t)) ,\mathbf{g}(p^{h}(t) ,\upmu ,0)} \right\rangle } dT_1\nonumber \\&\quad =\int _{-\infty }^{+\infty } {\left( {\frac{\partial H}{\partial u_1 }g^{u_1 }+\frac{\partial H}{\partial u_2 }g^{u_2 }+\frac{\partial H}{\partial I}g^{I}+\frac{\partial H}{\partial {\upgamma } }g^{{\upgamma } }} \right) } dT_1\nonumber \\&\quad =-\frac{2\sqrt{2}\upmu _2 }{3{\upeta } _1 }{\upvarepsilon } _1^{3/2} -2\sqrt{2}{\upalpha } _2 \bar{{\upmu }}I_r^2 \frac{{\upvarepsilon } _1^{1/2} }{{\upeta } _1 }\nonumber \\&\qquad \,\,-\,\bar{{f}}_2 I_r \left[ \cos \left( {{\upgamma } _0 -{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) -\cos \left( {\upgamma } _0+{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }\right) \right] \!.\nonumber \\ \end{aligned}$$

(59)

Based on the results given by Kovacic et al. [22–24], it is known that the $k$-pulse Melnikov function $M_k ({\upvarepsilon } ,I_r ,{\upgamma } _0 ,\bar{{\upmu }}) (k=1 ,2 ,\ldots )$ is defined as

$$\begin{aligned} M_k ({\upvarepsilon },I_r,{\upgamma } _0,\bar{{\upmu }})&= \sum _{j=0}^{k-1} M(I_r,j{\Delta }{\upgamma } (I_r )\nonumber \\&+\,\Gamma _j ({\upvarepsilon },I_r , {\upgamma } _0 ,\bar{{\upmu }})+{\upgamma } _0 ,\bar{{\upmu }}), \end{aligned}$$

(60)

where

$$\begin{aligned} \Gamma _j ({\upvarepsilon } ,I_r ,{\upgamma } _0 ,\bar{{\upmu }})=\frac{\Omega (\bar{{x}}_0 (I_r ),I_r )}{{\uplambda } (I_r )}\sum _{r=1}^j {\log \left| {\frac{\varsigma (I_r )}{{\upvarepsilon } M_r ({\upvarepsilon } ,I_r , {\upgamma } _0,\bar{{\upmu }})}} \right| } ,\nonumber \\ \end{aligned}$$

(61)

for $j=1 ,\ldots ,k-1$ and $\Gamma _0 ({\upvarepsilon } ,I_r , {\upgamma } _0,\bar{{\upmu }})=0$.

It is noticed that the angle function $\Gamma _j ({\upvarepsilon } ,I_r , {\upgamma } _0 ,\bar{{\upmu }})$ is the complex formula where $M_k ({\upvarepsilon } ,I_r ,{\upgamma } _0 ,\bar{{\upmu }})$ appears as the argument of a logarithm. When resonance occurs, the periodic orbit corresponding to the value $I_r$ degenerates into a circle of equilibria. In this case, there exist roots of parameters $I_r, {\upgamma } _0$ and $\bar{{\upmu }}$ for $\Gamma _j ({\upvarepsilon } ,I_r , {\upgamma } _0 ,\bar{{\upmu }})=0,\,(j=0 ,1 ,\ldots ,k-1)$. Based on the expression obtained by Kovacic et al. [22–24], the $k$-pulse Melnikov function can be shown as

$$\begin{aligned}&M_k (I_r,{\upgamma } _0,\bar{{\upmu }}, {\upeta } _1,{\upalpha } _2 , {\upvarepsilon } _1 )\nonumber \\&\quad =\sum _{j=0}^{k-1} {M(I_r },{\upgamma } _0+j{\Delta }{\upgamma } (I_r ), \bar{{\upmu }} ,{\upeta }_1 ,{\upalpha } _2 ,{\upvarepsilon }_1 )\nonumber \\&\quad =-\,\bar{{f}}_2 I_r \left[ \cos \left( {{\upgamma } _0 -{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) \!-\!\cos \left( {\upgamma } _0+{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 } \right) \right] \nonumber \\&\qquad \,-\frac{2\sqrt{2}\upmu _2 }{3{\upeta } _1 }{\upvarepsilon } _1^{3/2}-2\sqrt{2}{\upalpha } _2 \bar{{\upmu }}I_r^2 \frac{{\upvarepsilon } _1^{1/2} }{{\upeta } _1 }\nonumber \\&\qquad \,-\bar{{f}}_2 I_r \left[ \cos \left( {{\upgamma } _0 -{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }-2{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) \right. \nonumber \\&\qquad \,\left. -\,\cos \left( {{\upgamma } _0 +{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }-2{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) \right] \nonumber \\&\qquad \,-\,\frac{2\sqrt{2}\upmu _2 }{3{\upeta } _1 }{\upvarepsilon } _1^{3/2} -2\sqrt{2}{\upalpha } _2 \bar{{\upmu }}I_r^2 \frac{{\upvarepsilon } _1^{1/2} }{{\upeta } _1 }+\cdots \cdots \nonumber \\&\qquad \,-\,\bar{{f}}_2 I_r \left[ \cos \left( {{\upgamma } _0 -{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }-2(k-1){\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) \right. \nonumber \\&\qquad \,\left. -\,\cos \left( {{\upgamma } _0 +{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1}}{{\upeta } _1 }-2(k-1){\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) \right] \nonumber \\&\qquad \,-\frac{2\sqrt{2}\upmu _2 }{3{\upeta } _1 }{\upvarepsilon } _1^{3/2} -2\sqrt{2}{\upalpha } _2 \bar{{\upmu }}I_r^2 \frac{{\upvarepsilon } _1^{1/2} }{{\upeta } _1 }\nonumber \\&\quad =-\,\bar{{f}}_2 I_r \left[ \cos \left( {{\upgamma } _0 -{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }-2(k-1){\upalpha } _2\frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }} \right) \right. \nonumber \\&\qquad \,\left. -\,\cos \left( {{\upgamma } _0 +{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1}}{{\upeta } _1 }}\right) \right] -\frac{2\sqrt{2}k\upmu _2 }{3{\upeta } _1 }{\upvarepsilon } _1^{3/2}\nonumber \\&\qquad \,-\,2\sqrt{2}k\bar{{\upmu }}I_r^2 {\upalpha } _2 \frac{{\upvarepsilon } _1^{1/2} }{{\upeta } _1 }. \end{aligned}$$

(62)

If we set ${\Delta }{\upgamma } =-2{\upalpha } _2 \frac{\sqrt{2{\upvarepsilon } _1 }}{{\upeta } _1 }$ and ${\upgamma } _{k-1} ={\upgamma }_0 +(k-1)\frac{{\Delta }{\upgamma } }{2}$, Eq. (62) is rewritten as follows

$$\begin{aligned}&M_k (I_r,{\upgamma } _0 ,\bar{{\upmu }} ,{\upeta } _1,{\upalpha } _2 ,{\upvarepsilon } _1 )\nonumber \\&\quad =M_k (I_r,{\upgamma } _{k-1}-(k-1)\frac{\Delta {\upgamma } }{2},\bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 )\nonumber \\&\quad =\bar{{f}}_2 I_r \left[ {\cos \left( {\upgamma } _{k-1} -\frac{1}{2}k\Delta {\upgamma } \right) -\cos \left( {\upgamma } _{k-1} +\frac{1}{2}k{\Delta }{\upgamma } \right) } \right] \nonumber \\&\qquad +\,\frac{k\upmu _2 {\upvarepsilon } _1 }{3{\upalpha } _2 }{\Delta }{\upgamma } +2\bar{{\upmu }}I_r^2 \left( {\frac{1}{2}k{\Delta }{\upgamma } } \right) \nonumber \\&\quad =2\bar{{f}}_2 I_r \sin {\upgamma } _{k-1} \sin \left( {\frac{1}{2}k{\Delta }{\upgamma } } \right) \nonumber \\&\qquad +\,\frac{2\upmu _2 {\upvarepsilon } _1 }{3{\upalpha } _2 }\left( {\frac{1}{2}k{\Delta }{\upgamma } } \right) +2\bar{{\upmu }}I_r^2 \left( {\frac{1}{2}k{\Delta }{\upgamma } } \right) . \end{aligned}$$

(63)

Based on Proposition 3.1 given by Kovacic et al. [22–24], the nonfolding condition is always satisfied in the resonant case. We obtain the following two conditions

$$\begin{aligned}&\left| {\frac{\frac{1}{2}k{\Delta }{\upgamma } }{\sin \left( {\frac{1}{2}k{\Delta }{\upgamma } } \right) }\frac{(\upmu _2 {\upvarepsilon }_1 +3{\upalpha } _2 \bar{{\upmu }}I_r^2 )}{3{\upalpha } _2 \bar{{f}}_2 I_r }} \right| <1\quad \! \text {and}\!\quad \!\frac{1}{2}k{\Delta }{\upgamma } \ne n\uppi ,\nonumber \\&\quad n=0,\pm 1 ,\pm 2 ,\ldots . \end{aligned}$$

(64)

The main aim of the following analysis focuses on identifying simple zeroes of the $k$-pulse Melnikov function. Define a set that contains all such simple zeroes to be

$$\begin{aligned} Z_-^n =\left\{ {\left. { (I_r ,{\upgamma } _{k-1} ,\bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 ) } \right| M_k =0 ,D_{{\upgamma } _0 } M_k \ne 0} \right\} \!.\nonumber \\ \end{aligned}$$

(65)

The $k$-pulse Melnikov function has two simple zeroes in the interval ${\upgamma } _{k-1} \in \left[ {0 ,\uppi } \right]$

$$\begin{aligned} \bar{{{\upgamma } }}_{k-1 ,1}&= -\arcsin \frac{\frac{1}{2}k\Delta {\upgamma } }{\sin \left( {\frac{1}{2}k{\Delta }{\upgamma } } \right) }\frac{(\upmu _2 {\upvarepsilon } _1 +3{\upalpha } _2 \bar{{\upmu }}I_r^2 )}{(3{\upalpha } _2 \bar{{f}}_2 I_r )}\quad \text { and } \nonumber \\ \bar{{{\upgamma } }}_{k-1 ,2}&= \uppi +\bar{{{\upgamma } }}_{k-1 ,1}. \end{aligned}$$

(66)

5.3 Geometric structure of the multi-pulse orbits

Based on the above analysis, we obtain the following conclusions. When the parameters of $k, \upmu _2, {\upvarepsilon } _1 ,\bar{{\upmu }},{\upalpha } _2$ and $\bar{{f}}_2$ satisfy condition (64), the $k$-pulse Melnikov function (63) has simple zeroes at ${\upgamma } _{k-1} =\bar{{{\upgamma } }}_{k-1 ,1}$ and ${\upgamma } _{k-1} =\bar{{{\upgamma } }}_{k-1 ,2} =\uppi +\bar{{{\upgamma } }}_{k-1 ,1}$. For $i=1$ or $i=2$, when the $j$-pulse Melnikov function $M_j (I_r,\bar{{{\upgamma } }}_{0,i} ,\bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 )$ have no simple zeroes, the stable and unstable manifolds $W^{s}(\mathrm{M}_{\upvarepsilon })$ and $W^{u}(\mathrm{M}_{\upvarepsilon } )$ intersect transversely along a symmetric pair of the two-dimensional, $k$-pulse surfaces $\sum _{ \pm ,{\upvarepsilon } }^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,i} } )$. This signifies that the presence of the Shilnikov type $n$-pulse orbits leads to chaotic dynamics in the sense of the Smale horseshoes for nonlinear vibration for the simply supported rectangular thin plate. In the phase space of the unperturbed system from Eq. (28), this symmetric pair of the two-dimensional, $k$-pulse surfaces breaks down smoothly onto a pair of limiting $k$-pulse surfaces, $\sum _{ \pm ,0}^{ \bar{{\upmu }},{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,i}})$, parametrized by Eqs. (45) and (47) with $I=I_r,{\upgamma } _0 =\bar{{{\upgamma } }}_{k-1, i} -(k-1)({{\Delta }{\upgamma } }/2)+j\Delta {\upgamma }$, and an arbitrary $h$. The sign in Eq. (45) is determined by the sign of the corresponding $j$-pulse Melnikov function$M_j (I_r,\bar{{{\upgamma } }}_{0, i},\bar{{\upmu }}, {\upeta } _1,{\upalpha } _2,{\upvarepsilon } _1 )$.

From the discussion given by Kovacic et al. [22–24], it is easily found that for $\bar{{{\upgamma } }}_{0,i} =\bar{{{\upgamma } }}_{k-1,i} -(k-1)({{\Delta }{\upgamma } }/2)+j{\Delta }{\upgamma }$ ($i=1$ or $i=2)$, the values of the $j$-pulse Melnikov functions $M_j (I_r ,\bar{{{\upgamma } }}_{0,i} ,\bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 )$ are not zero for all $j=1 ,\ldots ,k-1$, and all $j$have the same sign. It is known that this sign is negative for $\bar{{{\upgamma } }}_{0 ,1}$ and positive for $\bar{{{\upgamma } }}_{0 ,2}$. Therefore, the $k$-pulse surfaces $\sum _{ \pm ,{\upvarepsilon } }^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,1} } )$ and $\sum _{ \pm ,{\upvarepsilon } }^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,2} } )$ indeed exist, and the limiting $k$-pulse surfaces $\sum _{ \pm ,0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,1} } )$ and $\sum _{ \pm ,0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,2} } )$ also exist when ${\upvarepsilon } =0$. Since the regions enclosed by the stable and unstable manifolds $W^{s}(\mathrm{M})$ and $W^{u}(\mathrm{M})$ are both convex, and the normal vector

$$\begin{aligned} \mathbf{n}=\left( {\left( -\upmu _1 u_1 +{\upeta } _1 u_1^3 +{\upalpha } _2 I^{2}u_1 \right) ,-u_2 ,0 ,0} \right) \end{aligned}$$

is known to point out of these manifolds, it demonstrates that the orbits forming each of the surfaces $\sum _{ \pm ,0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,1} } )$ are parametrized by Eqs. (45) and (47) with the alternating signs, and the orbits forming each of the surfaces $\sum _{ \pm ,0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,2} } )$ are parametrized by Eqs. (45) and (47) with the same signs.

For the parameter $\upmu =\bar{{\upmu }}$, there exist $N-1$ orbit segments $O_i (\bar{{\upmu }}) \quad (i=2 ,\ldots ,N)$ on the annulus $M$, where the end points of the segments $O_i (\bar{{\upmu }})$ are $d_i (\bar{{\upmu }})$ and $c_i (\bar{{\upmu }})$, respectively. The trajectories of Eq. (53) on the segments $O_i (\bar{{\upmu }})$ travel from the end points $d_i (\bar{{\upmu }})$ to $c_i (\bar{{\upmu }})$ in forward time. Therefore, the end points $d_i (\bar{{\upmu }})$ and $c_i (\bar{{\upmu }})$ are respectively referred to as the departure and landing points of the jumping $\Gamma _i$. In addition, the line ${\upgamma } =\bar{{{\upgamma } }}_{0 ,i} (I_r ,\bar{{\upmu }})-{\Delta }{\upgamma } ^{-}(I_r )$ transversely intersects the segments $O_i (\bar{{\upmu }})$ at the end point $c_i (\bar{{\upmu }})$ for $i=2 ,\cdots ,N$, while the line ${\upgamma } =\bar{{{\upgamma } }}_{0 ,i} (I_r ,\bar{{\upmu }})+{\Delta }{\upgamma } ^{+}(I_r )$ transversely intersects the segments $O_{i+1} (\bar{{\upmu }})$ at the end point $d_{i+1} (\bar{{\upmu }})$ when $i=1 ,\ldots ,N-1$. For all $i=2 ,\ldots ,N-1$, the difference in the coordinates $h$ of two end points $c_i (\bar{{\upmu }})$ and $d_{i+1} (\bar{{\upmu }})$ is zero, namely,

$$\begin{aligned} h(c_i (\bar{{\upmu }}))-h(d_{i+1} (\bar{{\upmu }}))=0. \end{aligned}$$

(67)

For each $i=2 ,\ldots ,N-1$, one of the orbits represented by $\Gamma _i$ and contained in the limiting surfaces $\sum _{ 0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{0,i} } )$ at the value $\upmu =\bar{{\upmu }}$, connects two intersection points $c_i (\bar{{\upmu }})$ and $d_{i+1} (\bar{{\upmu }})$. Therefore, an orbit $\Gamma _1$ on the limiting surfaces $\sum _{ 0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{0 ,1} } )$ connects the certain point $c_1 (\bar{{\upmu }})$ on the annulus $M$ to the end point $d_2 (\bar{{\upmu }})$ on the segment $O_2 (\bar{{\upmu }})$. It is also known that an orbit $\Gamma _N$ on the limiting surfaces $\sum _{ 0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{0,N} } )$ connects the end point $c_N (\bar{{\upmu }})$ on the segments $O_N (\bar{{\upmu }})$ to the certain point $d_{N+1} (\bar{{\upmu }})$ on the annulus $M$. According to the study of Kovacic et al. [22–24], there exists an $n$-bump singular transition orbit or a modified $N$-bump singular transition orbit. The three-bump jumping orbit depicted in Fig. 5 consists of the orbits $\Gamma _i \quad (i=1 ,2 ,3)$ on the limiting surfaces $\sum _{ 0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2 ,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{0,i} } ) \quad (i=1 ,2 ,3)$ at the parameter $\upmu =\bar{{\upmu }}$ and the orbit segments $O_1 (\bar{{\upmu }})$ and $O_2 (\bar{{\upmu }})$ of Eq. (53). It is known from the above analysis that the orbit segments $O_i (\bar{{\upmu }})(i=2 ,\ldots ,N)$ intersect transversely with the lines ${\upgamma } =\bar{{{\upgamma } }}_{0 ,i} (I_r ,\bar{{\upmu }})+{\Delta }{\upgamma } ^{+}(I_r )$ and ${\upgamma } =\bar{{{\upgamma } }}_{0 ,i} (I_r ,\bar{{\upmu }})-{\Delta }{\upgamma } ^{-}(I_r )$.

Fig. 5

The three-bump orbit with the single-pulse is depicted

The two-bump singular surface shown in Fig. 6 is composed of two single-pulse singular intersection surfaces $\sum _{ 0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,1} } )$ and $\sum _{ 0}^{ \bar{{\upmu }} ,{\upeta } _1 ,{\upalpha } _2,{\upvarepsilon } _1 } {(\bar{{{\upgamma } }}_{k-1 ,2} } )$. This surface connects the singular points of Eq. (53) that lie on the line ${\upgamma } =\bar{{{\upgamma } }}_{0 ,1} -{\Delta }{\upgamma } ^{-}$ to those of Eq. (53) that lie on the line ${\upgamma } =\bar{{{\upgamma } }}_{0 ,1} -{\Delta }{\upgamma } ^{+}$ on the annulus $M$.

Fig. 6

The two-pulse singular surfaces $\sum {(\bar{{{\upgamma } }}_{0 ,1} ,\bar{{{\upgamma }}}_{0 ,2} )}$ is depicted

We obtain a countable infinity of the singular jumping orbits as follows. Each orbit starts along one branch of the manifold $W(Q_0 )$ of the saddle $Q_0$ on the annulus $\mathrm{M}$. Then, the singular jumping orbit departs from the annulus $\mathrm{M}$, goes along one of the singular $k$-pulse orbits $\Gamma _k$, and lands back at a point on the separatrix that connects the saddle $Q_0$ to itself on the annulus $\mathrm{M}$. After traveling along the separatrix for a while, the singular jumping orbit takes off again along the singular $l$-pulse orbit $\Gamma _l$, and continues such process. Eventually, the singular jumping orbit lands back on the separatrix.

Therefore, it is concluded that the multi-pulse orbits of Eq. (28) consist of several portions of the slow time scale on the hyperbolic manifold $\mathrm{M}_{\upvarepsilon }$ and many fast time scale pulses leaving from the manifold $\mathrm{M}_{\upvarepsilon }$, and these multi-pulse orbits form a consecutive and recurrence process.

6 Numerical results of chaotic motions

Based on the above qualitative analysis for the multi-pulse orbits and chaotic dynamics of the simply supported rectangular thin plate, the conditions of the chaotic motion in the sense of the Smale horses are obtained. The heteroclinic bifurcations of Eq. (12) appear when ${\upeta } _1 >0$. Therefore, the above theoretical analysis is focused on the situation which the heteroclinic bifurcations of Eq. (12) exist. The parameter ${\upeta } _1$ is the combination of the parameters ${\upalpha } _1,{\upalpha } _2$ and ${\upbeta } _2$, where ${\upeta } _1 =(3{\upalpha } _1 {\upalpha } _2 )/{\upbeta } _2$. In this section, we have only performed numerical simulations of the multi-pulse chaotic motions of the simply supported rectangular thin plate under heteroclinic bifurcations in order to further verify the theoretical analysis. Consequently, the parameters ${\upalpha } _1,{\upalpha } _2$ and ${\upbeta } _2$ are chosen to satisfy ${\upeta } _1 >0$.

The chaotic and periodic responses of nonlinear dynamical system can be identified by several conventional criteria such as waveform, phase portraits and Poincare map. In this section, we use these mathematical tools to detect the existence of chaotic motions in the simply supported rectangular thin plate. For the periodic motions, Poincare map is of several separate points. For a chaotic motion, the Poincare map consists of a number of points on the limited Poincare section. Therefore, it can be observed that chaotic motion of the simply supported rectangular thin plate appear from Poincare map. We choose the averaged Eq. (12) to conduct numerical simulations. The averaged Eq. (12) is obtained under the case of 1:2 internal resonance and primary parametric resonance-fundamental parametric resonance. A numerical approach through the computer software Matlab is utilized to explore the existence of the Shilnikov type multi-pulse chaotic motions in the simply supported rectangular thin plate subjected to transversal and in-plane excitations.

Figure 7 demonstrates the existence of the multi-pulse chaotic motion of the simply supported rectangular thin plate when the in-plane and transversal excitations are $f_1 =90$, and $F_2 =210.6$. Other parameters and initial conditions are chosen as $\upmu =0.1, {\upsigma } _1 =1.0, {\upsigma } _2 =1.75, {\upalpha } _1 =1.6, {\upalpha } _2 =2.55, {\upbeta } _1 =-1.35, {\upbeta } _2 =3.15, x_{10} =0.1385, x_{20} =0.55, x_{30} =0.35, x_{40} =-0.180$. Figure 7a and c represent the phase portraits on the planes $(x_1 ,x_2 )$ and $(x_3 ,x_4 )$, respectively. Figure 7b and d give the waveforms on the planes $(t ,x_1 )$ and $(t,x_3 )$, respectively. Figure 7e and f are the three-dimensional phase portrait in the space $(x_1 ,x_2 ,x_3 )$ and the Poincare map on the plane $(x_1 ,x_2 )$, respectively. There are two kinds of chaotic motions during numerical simulations. One is the transient chaotic motion, the other is steady chaotic motion. There has been steady chaos and transient chaos will disappear when time increase. In this paper, numerical simulations start from 1000 seconds since we mainly investigate steady chaotic motion of the rectangular thin plate.

Fig. 7

The multi-pulse chaotic motion is obtained when $f_1 =90, F_2 =210.6,\upmu =0.1, {\upsigma } _1 =1.0,{\upsigma } _2 =1.75, {\upalpha } _1 =1.6, {\upalpha } _2 =2.55, {\upbeta } _1 =-1.35,{\upbeta } _2 =3.15, x_{10} =0.1385, x_{20} =0.55, x_{30} =0.35, x_{40} =-0.180$, a the phase portrait on the plane $\left( {x_1 ,x_2 } \right)$; b the waveform on the plane $\left( {t ,x_1 } \right)$; c the phase portrait on the plane $\left( {x_3 ,x_4 } \right)$; d the waveform on the plane $\left( {t ,x_3 } \right)$; e the phase portraits in the three-dimensional space$(x_1,x_2,x_3 )$; f Poincare map on the plane $\left( {x_1 ,x_2 } \right)$

Figure 8 indicates that the multi-pulse chaotic motion of the simply supported rectangular thin plate occurs when the in-plane and transversal excitations, parameters and initial conditions respectively are $f_1 =70, F_2 =531.1, \upmu =0.01, {\upsigma } _1 =2.0,{\upsigma } _2 =6.5, {\upalpha } _1 =-1.6, {\upalpha } _2 =1.1, {\upbeta } _1 =-5.7, {\upbeta } _2 =-2.3, x_{10} =1.4, x_{20} =0.55, x_{30} =2.35$ and $x_{40} =1.8$. Comparing with Figs. 7 and 8, it is found that there are differences in the phase portraits, the waveforms and the Poincare map, respectively. From the phase portrait on the plane $(x_1 ,x_2 )$, waveform on the plane $(t ,x_1 )$, the three-dimensional phase portrait and Poincare map in Fig. 8, we can see that the obvious multi-pulse jumping phenomenon exists.

Fig. 8

The multi-pulse chaotic motion is obtained when $f_1 =70,F_2 =531.1,\upmu =0.01, {\upsigma } _1 =2.0,{\upsigma } _2 =6.5, {\upalpha } _1 =-1.6, {\upalpha } _2 =1.1, {\upbeta } _1 =-5.7,{\upbeta } _2 =-2.3, x_{10} =1.4, x_{20} =0.55, x_{30} =2.35, x_{40} =1.8$, a the phase portrait on the plane $\left( {x_1 ,x_2 } \right)$; b the waveform on the plane $\left( {t ,x_1 } \right)$; c the phase portrait on the plane $\left( {x_3 ,x_4 } \right)$; d the waveform on the plane $\left( {t ,x_3 } \right)$; e the phase portraits in the three-dimensional space$(x_1,x_2,x_3 )$; f Poincare map on the plane $\left( {x_1 ,x_2 } \right)$

In the following numerical simulations, several different sets of parameters and initial conditions are given in order to investigate the different shapes of the multi-pulse chaotic motion. When we respectively change the in-plane and transversal excitations, parameters and initial conditions to $f_1 =62, F_2 =222.2, \upmu =0.03, {\upsigma }_1 =2.0,{\upsigma } _2 =35, {\upalpha } _1 =-3.2, {\upalpha } _2 =-5.1, {\upbeta } _1 =-2.7,{\upbeta } _2 =6.3,x_{10} =0.14, x_{20} =0.55, x_{30} =0.35$ and $x_{40} =-0.180$, we can see that there is another shape for the multi-pulse chaotic motion from Fig. 9. It is found that the shapes of these two phenomena depicted in Figs. 8 and 9 are completely different.

Fig. 9

The multi-pulse chaotic motion is obtained when $f_1 =62, F_2 =222.2,\upmu =0.03, {\upsigma } _1 =2.0, {\upsigma } _2 =35, {\upalpha } _1 =-3.2, {\upalpha } _2 =-5.1, {\upbeta } _1 =-2.7, {\upbeta } _2 =6.3, x_{10} =0.14, x_{20} =0.55, x_{30} =0.35$ and $x_{40} =-0.180$, a the phase portrait on the plane $\left( {x_1 ,x_2 } \right)$; b the waveform on the plane $\left( {t ,x_1 } \right)$; c the phase portrait on the plane $\left( {x_3 ,x_4 } \right)$; d the waveform on the plane $\left( {t ,x_3 } \right)$; e the phase portraits in the three-dimensional space$(x_1,x_2,x_3 )$; f Poincare map on the plane $\left( {x_1 ,x_2 } \right)$

In Fig. 10, the multi-pulse chaotic motion of the rectangular thin plate is discovered when the detuning parameter ${\upsigma } _2$ is changed to ${\upsigma } _2 =45$, and other parameters and initial conditions are the same as those in Fig. 9. In contrast to Figs. 9 and 10, it can be seen that the phase portraits, the waveforms and the Poincare map are not like each other. Figure 11 is obtained when the detuning parameter ${\upsigma } _2$ is selected as ${\upsigma } _2 =34$. In this case, other parameters and initial conditions are the same as those in Fig. 10. From the three-dimensional phase portraits of Figs. 9, 10 and 11, it is observed that the multi-pulse chaotic motions exist in nonlinear vibration of the simply supported rectangular thin plate. The above analysis proves that parameters make a great impact on the occurrence of the multi-pulse chaotic motions of the simply supported rectangular thin plate.

Fig. 10

The multi-pulse chaotic motion is obtained when ${\upsigma } _2 =45$, a the phase portrait on the plane $\left( {x_1 ,x_2 } \right)$; b the waveform on the plane $\left( {t ,x_1 } \right)$; c the phase portrait on the plane $\left( {x_3 ,x_4 } \right)$; d the waveform on the plane $\left( {t ,x_3 } \right)$; e the phase portraits in the three-dimensional space$(x_1,x_2,x_3 )$; f Poincare map on the plane $\left( {x_1 ,x_2 } \right)$

Fig. 11

The multi-pulse chaotic motion is obtained when ${\upsigma } _2 =34$, a the phase portrait on the plane $\left( {x_1 ,x_2 } \right)$; b the waveform on the plane $\left( {t ,x_1 } \right)$; c the phase portrait on the plane $\left( {x_3 ,x_4 } \right)$; d the waveform on the plane $\left( {t ,x_3 } \right)$; e the phase portraits in the three-dimensional space$(x_1,x_2,x_3 )$; f Poincare map on the plane $\left( {x_1 ,x_2 } \right)$

7 Conclusions

In this paper, the nonlinear vibrations of the simply supported rectangular thin plate are studied by applying the theories of the global bifurcations and chaotic dynamics for high-dimensional nonlinear systems. The multi-pulse orbits and chaotic dynamics are investigated using the extended Melnikov method for the case where the averaged equations have one non-semisimple double zero and a pair of pure imaginary Eigenvalues. Analysis of the multi-pulse orbits in the rectangular thin plate demonstrates that such an analysis is a typical singular perturbation problem in which there are two different time scales. Dynamics on the hyperbolic manifold $M_{\upvarepsilon }$ is of the slow time scale and the multi-pulse jumping orbits taking off from this manifold are of the fast time scale. It is shown that the transfer of energy between the different modes occurs through the multi-pulse jumping orbits. The studies have led to the following conclusions:

• (1) There exist the Shilnikov type multi-pulse chaotic motions in the nonlinear vibrations of the simply supported rectangular thin plate. The geometric interpretation of the $k$-pulse Melnikov function is a signed distance measured along the normal to a manifold, which gives the more delicate local estimates near the hyperbolic manifold. In the resonant case, the $k$-pulse extended Melnikov function $M_k (I ,{\upgamma } _0 ,\upmu )$ does not depend on the small perturbation parameter $0<{\upvarepsilon } \ll 1$, and the non-folding condition is automatically satisfied, resulting in the angle function $\Gamma _j ({\upvarepsilon } ,I_r,\uptheta _0 ,\upmu )(j=0 ,1 ,\ldots ,k-1)$ being zero. Therefore, the computing procedure of the extended Melnikov function can be simplified.

• (2) Based on the theoretically qualitative analysis, it is found that parameters $\bar{{\upmu }}$ and $\bar{{f}}_2$ play an important role in the multi-pulse chaotic motions of the simply supported rectangular thin plate. Parameters $\bar{{\upmu }}$ and $\bar{{f}}_2$ have relationships with the parameters $\upmu$ and $F_2$, respectively, where $\bar{{\upmu }}=\frac{1}{2}\mu$, $\bar{{f}}_2 =\frac{1}{2}F_2$. Parameter $\upmu$ is the damping coefficient of nonlinear system from the simply supported rectangular thin plate. Parameter $F_2$ describes the transverse excitation of the simply supported rectangular thin plate. Thus, the above analysis proves that the transverse excitation $F_2$ and the damping coefficient $\upmu$ make a great impact on the occurrence of the multi-pulse chaotic motions of the simply supported rectangular thin plate.

• (3) There exist different shapes of the chaotic motions in nonlinear vibration of the simply supported rectangular thin plate under different excitation, parameters, and initial conditions. It is found from numerical simulations that the shapes of the chaotic motions are completely different. Therefore, parameters and initial conditions impact on the shapes of the multi-pulse chaotic motions.

• (4) There exist multi-pulse chaotic motions in the averaged equations. It is well known that the multi-pulse chaotic motions in the averaged equations can lead to the multi-pulse amplitude modulated chaotic vibrations in the original system under certain conditions. Therefore, the multi-pulse amplitude modulated chaotic motions occur in the simply supported rectangular thin plate.

Appendices

Appendix 1

The coefficients presented in Eq. (8) are as follows

$$\begin{aligned}&{\upphi } _{20} (t)=\frac{9Eh}{32{\uplambda } ^{2}}q_1^2,\quad {\upphi }_{02} (t)=\frac{9{\uplambda } ^{2}Eh}{32}q_2^2 ,\nonumber \\&{\upphi }_{60}(t)=\frac{Eh}{288{\uplambda } ^{2}}q_2^2 ,\nonumber \\&{\upphi } _{06} (t)=\frac{{\uplambda } ^{2}Eh}{288}q_1^2,\quad {\upphi } _{22} (t)=-\frac{{\uplambda } ^{2}Eh}{\left( {{\uplambda } ^{2}+1} \right) ^{2}}q_1 q_2,\nonumber \\&{\upphi } _{24} (t)=\frac{25{\uplambda } ^{2}Eh}{16\left( {{\uplambda } ^{2}+4} \right) ^{2}}q_1 q_2 ,\nonumber \\&{\upphi } _{42} (t)=\frac{25{\uplambda }^{2}Eh}{16\left( {4{\uplambda } ^{2}+1} \right) ^{2}}q_1 q_2 ,\nonumber \\&{\upphi }_{44} (t)=-\frac{{\uplambda } ^{2}Eh}{16\left( {{\uplambda } ^{2}+1} \right) ^{2}}q_1 q_2,\quad {\uplambda } =\frac{b}{a}. \end{aligned}$$

(68)

Appendix 2

In order to obtain the dimensionless equations, we introduce the transformations of variables and parameters

$$\begin{aligned}&\bar{{q}}_i =\frac{\left( {ab} \right) ^{1/2}}{h^{2}}q_i (i=1,2), \quad \bar{{F}}_i =\frac{\left( {ab} \right) ^{7/2}}{\uppi ^{4}Eh^{7}}F_i (i=1,2), \nonumber \\&\bar{{p}}=\frac{b^{2}}{\uppi ^{2}D}p, \quad \bar{{t}}=\frac{\uppi ^{2}}{ab}\left( {\frac{D}{\uprho h}} \right) ^{1/2}t,\nonumber \\&\bar{{\Omega }}_k =\frac{ab}{\uppi ^{2}}\left( {\frac{\uprho h}{D}} \right) ^{1/2}\Omega _k(k=1,2), \quad {\upvarepsilon } =\frac{12\left( {1-\upnu ^{2}} \right) h^{2}}{ab}, \nonumber \\&\bar{{\upmu }}=\frac{a^{2}b^{2}}{\uppi ^{2}h^{4}}\left( {\frac{1}{12\left( {1-\upnu ^{2}} \right) \uprho E}} \right) ^{1/2}\upmu , \end{aligned}$$

(69)

where ${\upvarepsilon }$ is a small parameter. For simplicity, we drop the overbars in the following analysis.

Appendix 3

The coefficients presented in Eq. (9) are as follows

$$\begin{aligned}&{\upalpha }_1 =\frac{{\uplambda } ^{2}+81}{16{\uplambda }^{2}}, \quad {\upbeta } _1 =\frac{1}{16}\left( {81{\uplambda } ^{2}+\frac{1}{{\uplambda } ^{2}}} \right) ,\nonumber \\&{\upalpha } _2={\upbeta } _2 =\frac{17{\uplambda } ^{2}}{\left( {1+{\uplambda } ^{2}} \right) ^{2}}+\frac{625{\uplambda } ^{2}}{16\left( {4+{\uplambda } ^{2}} \right) ^{2}}+\frac{625{\uplambda } ^{2}}{16\left( {1+4{\uplambda } ^{2}} \right) ^{2}},\nonumber \\&{\upomega } _k^2 =\left( \left( {\upomega } _k^{*} \right) ^{2}-h_k p_0\right) \text { and }\nonumber \\&h_k =\left\{ {{\begin{array}{l@{\quad }l} 1 ,&{} k=1,\\ 9 ,&{} k=2,\\ \end{array} }} \right. \quad p_1^{*} ({\upomega } _1^{*} )^{2}=\frac{\left( {9+{\uplambda } ^{2}} \right) ^{2}}{{\uplambda } ^{2}},\nonumber \\&p_2^{*} =({\upomega } _2^{*} )^{2}=\frac{\left( {9{\uplambda } ^{2}+1} \right) ^{2}}{{\uplambda } ^{2}},\quad f_k =\frac{1}{2}h_k p_1 \nonumber \\&\quad \text {and}\quad k=1,2 , \end{aligned}$$

(70)

where ${\upomega }_k (k=1,2)$ are two linear natural frequencies of the thin plate, $p_k^{*} (k=1,2)$ are the critical forces corresponding to two buckling modes at which thin plate looses its stability, ${\upomega }_k^{*} (k=1,2)$ are the natural frequencies of the two buckling modes, and $f_k (k=1,2)$ are the amplitudes of parametric excitation.