A novel model of dipteran flight mechanism

Abstract

In this paper, a novel model for the mechanism of dipteran flight motor is proposed and a flight dynamics is explored by nonlinear dynamics techniques. This model comprises a lumped mass, a pair of inclined rigid bars and a pair of horizontal springs. Even the springs are linear, this system is irrationally nonlinear which causes difficulty for classical nonlinear analysis. We investigate the original irrational equation by direct numerical simulation avoiding Taylor’s expansion to retain the intrinsic character of dipteran flight. This enables us to reveal the bounded characteristics of depteran flight including “click”, bursting and the “complex” flight patterns. Equilibrium analysis demonstrates the “click” mechanism and the “non-click” condition for the unperturbed system. While for the perturbed system, Poincaré section and basin analysis are carried out to demonstrate the bursting behaviour, transitions between different flight modes and their coexistence. The results obtained herein reveal that the complex bifurcations of equilibria, periodic behaviours and the chaotic motions of the presented system associate respectively with “resting”, “calm” and “complex” flight. All the results related to the perturbed system are obtained by the fourth order Runge–Kutta method which ensures the accuracy of the computation. This study provides an additional insight into the understanding of various flight dynamics of insects and bridges a gap between the nonlinear dynamics and the biology.

1 Introduction

Much attention has been paid on the mechanism of the dipteran flight motor to explorer the complex insect manoeuvres, see [1–4] for example. Majority of investigations are focussed on the mechanism of “click” which has been studied extensively over 50 years [5–8], while some others interested in the “complex” flight patterns incorporated with insect flight manoeuvres or the flight patterns [9]. The early investigations on the flight motor [10] was based upon the observation of the insect flight in the laboratory and also the examination of their anatomy. The sinusoidal input force may result in non-sinusoidal stroke and then the peak velocity on the downward merged in the stroke could be gained to achieve a greater lift. A topological model to understand the mechanism of the dipteran flight was proposed in [11, 12]. Later studies has been attempted to develop mathematical tool for the qualitative analysis of insect flight. A mathematical model, $\epsilon \dot{x}=-(x^3-3x+b)$ was introduced in [13] to study this mechanism based on the catastrophe theory to illustrate this sudden change. However, the initial effects was not considered. Miyan gave a mechanical model for the flight mechanism [14] and contended that the “click” had been caused by anaesthetic administered to a dipteran in laboratory studies but this did not contain “click” mechanism [15]. Other researchers, seen [16, 17], conjectured that the flight mechanism is a resonant system without being identified theoretically. Recently, a dynamic analysis for the “click” mechanism of motor dipteran flight was given in [8], in which a simplified mathematical model, $u^{\prime \prime }+\gamma u^{\prime }-\frac{1}{2}u(1-u^2)=F\cos \Omega \tau ,$ is developed based upon the work in [13] to investigate the “click” mechanism. However, all the studies reviewed above were based upon the standard Duffing equation [18–21] truncated from the Taylor series to the third order, which may not reflect the real characteristics of the flight behaviours due to the limitations using the conventional mathematical approach where the bounded characteristic was lost.

The motivations and the contributions of this paper are (i) to provide a new and more effective mathematical model for flight mechanism of dipteran flight motor with irrational nonlinearity which currently attracted much attention, see [22–30] for example, (ii) to develop the nonlinear analysis techniques to remove the barrier raised from the irrationality avoiding Taylor expansion to a truncated Duffing system, and (iii) to bridge the gap between the nonlinear dynamics and the biology through the detailed analysis of the novel system to gain a deeper understanding of dipteran flight mechanism.

This paper is organised as follows. In Sect. 2, the mathematical model for the bio-inspired system is developed. The governing equation is derived, which is an irrational nonlinear dynamic system due to the geometrical configuration. In the following section, Sect. 3, the irrational equation is directly analysed without using Taylor expansion and the “click” mechanism is revealed from the viewpoint of nonlinear dynamics and the “non-click” switch off condition is provided. While in Sect. 4, the “complex” flight behaviour of bursting and various flight patterns including “clam”, “resting” and also the hybrid “complex” flights are observed through the analysis of nonlinear characteristics. Finally we summarise the conclusions and provide the further challenge researches.

2 Proposed model and the governing equation

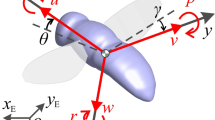
We propose a novel model comprising a lump mass $m,$ a pair of rigid bars of length $l$ and a pair of springs of stiffness $k,$ as shown in Fig. 1a for the depteran flight mechanism, which is evolved from the model given in [13] shown in Fig. 2a–c. The mechanism of the flight motor is described by the deformations of the simple triangle ABC shown in Fig. 2a1–c1 corresponding to the three successive positions illustrated in Fig. 2a–c, respectively. In this model, Fig. 1a, the mass $m$ represents hinge lumped at A corresponding to the first axillary sclerite (ax1 in Fig. 2c), to which the driven force is applied; the pair of bars (AB $=$ AC $= l$) represent the wing articulating at AB and AC and the pair of springs model the pleurosternal muscle stiffness added to B and C, respectively.

Fig. 1

a The proposed model of mass–bar–spring system for the depteran flight motor, b equilibrium bifurcation diagram of system (3)

Fig. 2

a–c Adopted from [13], three successive positions of the wing articulation in the course of a beat, from the up position (al) to the down position (cl). The key to the anatomy is as follows: $a\times 1,$ $a\times 2$-axillary sclerites 1 and 2; $n$ notum; $p$ parascutum; $pm$ pleurosternal muscle; $pn$ anterior notal process; $pw$ wing process; $rv$ base of radial vein; $sl$ section through tip of scutellar level, and (a1)–(c1) the corresponding simplifications to the “click” mechanism

Based upon the physical model described above, the governing equation of free vibration is derived as

$$\begin{aligned} m Y^{\prime \prime }-2kY\left( 1-\displaystyle \frac{B}{\sqrt{l^2-Y^{2}}}\right) =0, \quad B>0, \;|Y|<l, \end{aligned}$$

(1)

where $Y$ is the instantaneous vertical displacement of the mass and $B$ is the half length between the ends of the springs at their equilibrium positions with $B\ge 0.$ Different combinations of the parameters $l,B$ and $k$ can represent a variety of depteran insects.

Now supposing the system (1) is perturbed by a viscous damping and an external harmonic excitation of amplitude $F_{0}$ and frequency $\Omega ,$ this leads to the following equation,

$$\begin{aligned} m Y^{\prime \prime }+\delta Y^{\prime }-2kY\left( 1-\displaystyle \frac{B}{\sqrt{l^{2}-Y^{2}}}\right) =F_{0}\cos \Omega t. \end{aligned}$$

(2)

System (1) can be made dimensionless to the following form by re-scaling $y=lY,$ $b=\frac{B}{l}$ and letting $\omega ^2_0=\frac{2k}{m}.$

$$\begin{aligned} \ddot{y}-\omega ^2_0 y\left( 1-\displaystyle \frac{b}{\sqrt{1-y^{2}}}\right) =0, \quad b>0,\; |y|<1, \end{aligned}$$

(3)

and similarly, system (2) can be written in a dimensionless form by letting $\tau =\omega _{0}t,$ $f_{0}=\frac{F_{0}}{2mk},$ $\xi =\frac{\delta }{2m\omega _{0}}$ and $\omega =\frac{\Omega }{\omega _{0}},$

$$\begin{aligned} \ddot{y}+2\xi \dot{y}-\omega ^2_0y\left( 1-\displaystyle \frac{b}{\sqrt{1-y^{2}}}\right) =f_{0}\cos \omega \tau , \end{aligned}$$

(4)

where “$\cdot$” denotes differentiation with respect to $\tau .$

It is worth noting that although the springs themselves are linear, this system is strongly nonlinear having irrational restoring force due to the geometrical configuration, i.e. the nonlinear restoring force $F(y)=\omega _0^2y\left( 1-\frac{b}{\sqrt{1-y^{2}}}\right)$ with the definition of $y$ bounded within $|y|< 1.$ The nonlinear forces and the corresponding potentials are plotted in Fig. 3a and b, respectively, for different value of parameter $b.$

Fig. 3

a Nonlinear irrational restoring forces, and b the corresponding potentials (the solid curves indicate the case for $b=0.01,$ the dotted for $b=\frac{1}{3},$ the dashed for $b=\frac{2}{3}$ and the thick solid for $b=1,$ respectively)

In the following analysis, we will analyse the irrational equation directly avoiding Taylor expansion to reflect the truth flight dynamics, which is one of the distinguished characteristic of this research in comparison with the previous studies. In addition, various flight mechanism will be revealed from the viewpoint of nonlinear dynamics.

3 Unperturbed system and “click” mechanism

In this section, the unperturbed dynamics are analyzed directly for the original equation with irrational nonlinearity, rather than truncating to the conventional Duffing system, to examine the “click” mechanism, “resting” flight and the “non-click” condition.

3.1 The equilibria and the “resting”

The unperturbed system (3) can be written as a two-dimensional one

$$\begin{aligned} \left\{ \begin{array}{lc}\dot{y}=u, &{} \\ \dot{u}=y\left( 1-\displaystyle \frac{b}{\sqrt{1-y^{2}}}\right) ,\quad b> 0,\; |y|<1.&{}\end{array}\right. \end{aligned}$$

(5)

here and thereafter $\omega _0^2=1$ is always assumed without loss of the generality.

The equilibria of system (5) can be obtained as

$$\begin{aligned} (y_{0},u_0)=(0,0), (y_{1,2},u_{1,2})=(\pm \sqrt{1-b^{2}},0), \quad b>0, \end{aligned}$$

whose Jacobian matrix of the unperturbed system (5) at $(0,0)$ can be derived as

$$\begin{aligned} J\left( \begin{array}{c} y \\ u \end{array}\right) _{(0,0)}= \left( \begin{array}{l@{\quad }l} 0 &{} 1 \\ 1-b&{} 0 \end{array}\right) , \end{aligned}$$

whose eigenvalues are $\lambda _{1,2}=\pm \sqrt{1-b} .$ Thus the equilibrium $(0,0)$ is a saddle point for $0\le b<1$ and a centre point for $b>1$; while for $b=1$ it is a bifurcation point.

Similarly, the Jacobian matrix of the unperturbed system at ($\pm \sqrt{1-b^{2}},0$) can be obtained as

$$\begin{aligned} J\left( \begin{array}{c} y \\ u \end{array}\right) _{(\pm \sqrt{1-b^{2}},0)}= \left( \begin{array}{l@{\quad }l} 0 &{} 1 \\ -\frac{1}{b^2}(1-b^{2})&{} 0 \end{array}\right) , \end{aligned}$$

whose eigenvalues $\lambda _{1,2}=\pm i \frac{1}{b}\sqrt{1-b^{2}}$ for $0<b<1$ and the equilibria $(\pm \sqrt{1-b^{2}},0)$ are centre points and for the case of $b\ge 1$ these equilibria merge into $(0,0),$ which has been discussed previously.

Equilibria bifurcation diagram of system (3) is plotted for $y$ versus parameter $b$ in Fig. 1b. When $0<b<1,$ the dashed line denotes the unstable one which implies the “click” behaviour and the solid curves mark two stable branches, which indicates two possible “resting” status of the dipteran flight. While $b>1$ there exists “no-click”, but a unique “resting” phenomenon occurs. Therefore the “non-click” condition is found when $b=1.$

3.2 Hamiltonian function

Following the above discussions from the equilibrium status to “click” mechanism, we then analyse the mechanism from energy view point by employing one of the nonlinear techniques through Hamiltonian. Therefore, multiplying both sides of the second equation by the first in (5) leads to

$$\begin{aligned} u\dot{u}=y\left( 1-\displaystyle \frac{b}{\sqrt{1-y^{2}}}\right) \dot{y}. \end{aligned}$$

(6)

Integrating both sides of (6) yields the Hamiltonian function as follows,

$$\begin{aligned} H(y,u)=\displaystyle \frac{1}{2}u^{2}-\displaystyle \frac{1}{2}y^{2} +b\left( 1-\sqrt{1-y^{2}}\right) . \end{aligned}$$

(7)

With the help of the Hamiltonian (7), the phase structure of system (5) can be sketched and analysed for different values of the Hamiltonian $H(y,u)=E,$ as shown in Fig. 4, to reveal the multiple flight modes. When $0<b<1,$ as shown in Fig. 4a ($b=0.75$), $E=0$ represents the homoclinic orbit, which contains the saddle point $(0,0)$ implying “click” and separates the periodic status (“clam” flight, as described in [9] at different energy levels. Both cases of $\frac{1}{2}(b-1)<E<0$ and $E>0$ denote the periodic status which corresponds to the “clam” flights at different energy levels. While $E=\frac{1}{2}(b-1)$ indicates the pair of centres around which bistable flight statu sustains. Similarly for $b\ge 1,$ as shown in Fig. 4b ($b=1.0$), the phase structure comprises a family of periodic orbits for $E>0$ centred at the unique equilibrium $(0,0)$ for $E=0.$ Accordingly, there exists “no-click” but “resting” and “clam” flights.

Fig. 4

“Click” mechanism demonstrated by phase portraits: a bistable and “click” status exhibited by the double-well dynamics for $b=0.75$: $E=0$ represents the homoclinic orbit, $E<0$ a pair family of periodic orbits and $E>0$ the periodic orbits; b the “non-click” condition associated with the bounded single well dynamics for $b=1.0$

More importantly, this analysis reveals correctly the characteristics of the bounded ($|y|<1$) flight mechanism attributed by the irrational nonlinearity in the proposed model. This existing phenomenon could not be explained by the previous simplified models, such as the standard Duffing system used by many [8, 11, 13].

4 Perturbed dynamics and multiple flight patterns

In this section, numerical analysis is carried out to further investigate the nonlinear dynamics and to explore the multiple flight patterns of the perturbed system subjected to both damping and the external harmonic excitations. All the numerical results in the following sections are given by the fourth order Runge–Kutta method which can ensure the accuracy of computation for the perturbed system.

4.1 Dissipative flight

In this subsection, the flight behaviour of the dissipative system without input is investigated first. For the case when $\xi \ne 0$ and $f_0=0,$ Eq. (4) takes form

$$\begin{aligned} y^{\prime \prime }+2\xi y^{\prime }-y\left( 1-\displaystyle \frac{b}{\sqrt{1-y^{2}}}\right) =0, \end{aligned}$$

(8)

Damping ratio $\xi$ is always assumed to be small, $\xi <1.$ The equilibria of this damped system are the same as that of the system (5). The equilibria $(\pm \sqrt{1-b^{2}},0)$ of system (8) are stable with the eigenvalues having negative real parts, $\lambda _{1,2}=-\xi \pm i \frac{1}{b}\sqrt{1-b^2}.$ The property of the saddle singularity $(0,0)$ remains unchanged as that of system (5). The basin of attractions of the stable singularities $(\pm \sqrt{1-b^{2}},0)$ are shown in Fig. 5a and the basin boundary is plotted in Fig. 5b. The point $(0,0)$ is located in the basin boundary. This boundary is the stable manifold for the point $(0,0).$ It is the separatrix curve to separate the basin of attractions of equilibria $(\pm \sqrt{1-b^{2}},0).$ It can be seen that from both Fig. 5a, b that without external excitation (input), the flights remains a “resting” stage due to the energy exhausted.

Fig. 5

Damping effect on flight behaviour for $\xi =0.2$ and $f_0=0.0$: a the basins of attractions are shown in yellow for the point $(\sqrt{1-b^{2}},0)$ and in blue for $(-\sqrt{1-b^{2}},0),$ b the separatrix on the border of the basin of attractions is the stable manifold tending to saddle point (0,0) as time $t\rightarrow \infty$. (Color figure online)

4.2 Low frequency excitation and bursting phenomena

The system responses to external harmonic input to the flight motor are examined via time history series, as seen in Fig. 6a–d for $\xi =0.1,$ $f_0=0.125$ and $b=0.85.$ It is observed that high frequency bursting phenomena are detected by applying low frequency excitations. As the excitation frequency decreases, the flight bursting phenomena becomes more pronounced. Figure 6 also shows the transition from spiking, as shown in Fig. 6a, at higher frequency of $\omega =0.35$ to bursting, as shown in Fig. 6b–d, at lower exciting frequencies of $\omega =0.2, 0.1$ and $\omega =0.05,$ respectively. This results are in agreement with both analytical and experimental results given in [9, 31–33].

Fig. 6

Flight bursting mechanism described by the time histories when $\xi =0.1,$ $f_0=0.125$ and $b=0.85$ and for frequencies: a $\omega =0.35,$ b $\omega =0.2,$ c $\omega =0.1$ and d $\omega =0.05$

From the dynamical analyse point of view, the process of bursting behaviour can also been clearly demonstrated by phase portrait and the corresponding Poincaré sections which will be marked by “*” for periodic solutions in the following discussions without mentioning. Parameters taken as $\xi =0.1,$ $f_0=0.125$ and $b=0.85$ in Fig. 7 to show the bursting behaviours of the flights. For example, no subharmonic response occurs in the phase portrait shown in Fig. 7a for $\omega =0.35,$ which means no bursting as evidenced in the time history in Fig. 6a. Higher frequency bursting appears as the exciting frequency decreases, as seen in Fig. 7b–d for $\omega =0.2, 0.1$ and $\omega =0.05,$ respectively. These bursting phenomena correspond to the subharmonic resonances of $(3:1),$ $(7:1)$ and higher ones, respectively.

Fig. 7

Flight bursting mechanism characterised by phase portraits for, both trajectories and the corresponding Poincaré sections for the same parameters as in Fig. 6

4.3 Multiple flight modes and “complex” flights

In this subsection, we investigate the multiple flight modes affected by the amplitude of the external excitation from the nonlinear dynamics point of view. It is found that there coexists period doubling leading to the coexisted of chaos, which merge into a large chaotic motion as the parameter varies, which indicate the transition from the co-existing “clam” modes to “complex” [9] flight patterns. In all Figs. 8, 9 and 10, the periodic solutions are marked with “*”s and the chaotic attractors are colored blue.

Fig. 8

Transitions between different flight modes affected by the amplitude $f_0$ versus $y,$ $\xi =0.1, b=0.85$: a bifurcation diagrams: starting from a pair of period solutions marked blue and black respectively. b Lyapunov exponents; co-existing period doubling to chaos and merged to a new chaotic attractor: c co-existing period one solutions for $f_0=0.05,$ d co-existing period two solutions for $f_0=0.085$. (Color figure online)

Fig. 9

Continued from Fig. 8c, d, the co-existing period doubling for $\xi =0.1$ and $b=0.85$: a co-existing period four solutions for $f_0=0.088,$ b co-existing period eight solutions for $f_0=0.091$; which lead to the co-existing chaotic solutions and then these co-existing chaos will be merged into a new chaotic attractor: c co-existing chaotic solutions $f_0=0.1,$ and d the merged chaotic motion $f_0=0.15$

Fig. 10

Multiple flight modes with different beating frequencies demonstrated by the process from period three doubling to a chaotic attractor for $\xi =0.1$ and $b=0.85$: a a sudden change at $f_0=0.15$ from the merged chaos to period three motion as $f_0$ increases, b period doubling to period six $f_0=0.175,$ c a three winged chaotic motion, for $f_0=0.183$ and d the chaotic attractors $f_0=0.19$

4.3.1 Complex flight influenced by the amplitude of external excitation

Bifurcation diagrams are given for displacement $y$ versus the amplitude $f_0$ of the external excitation with $\xi =0.1, b=0.85$ in Fig. 8a, and corresponding Lyapunov exponent bifurcation is also given in Fig. 8b to reflect the degree of complexity of the flight behaviour. The bifurcation diagrams are plotted from the different initial conditions with blue and black respectively, from which the existence of a pair of period doubling series can be seen from the bifurcation diagram, Fig. 8a.

The series co-existed pair of period doublings, seen in Fig. 8c for $f_0=0.05,$ Fig. 8d for $f_0=0.085$; Fig. 9a for $f_0=0.088$ and Fig. 9b for $f_0=0.091,$ lead to the respective chaotic attractors, as shown in Fig. 9c when $f_0=0.10$, which then can merge into a single chaotic attractor, as presented in Fig. 9d when $f_0$ increases to $f_0=0.125.$ The Poincaré sections for both periodic and the chaotic solutions are plotted in the corresponding figures.

Similarly, as $f_0$ further increases, the process of a periodic three doubling leading to chaos can be observed from Fig. 8a, as well as from the periodic three solution shown in Fig. 10a for $f_0=0.15$ bifurcating to periodic six in Fig. 10b for $f_0=0.175$ to the corresponding chaotic branches in Fig. 10c for $f_0=0.183$ and finally to the chaotic attractor in Fig. 10d for $f_0=0.19.$

These nonlinear analysis explains the transition mechanism of the depteran flight from simple “calm” flight to “complex” flight patterns when subjected to an increasing external excitation force. It should be noted that when decreasing excitation forces the “complex” flight mode can also transit back to a simple “calm” or to another “complex” flight as clearly demonstrated from bifurcation diagram Fig. 8a.

4.3.2 Multiple flight modes affected by damping

In this subsection, flight patterns affected by viscous damping are discussed and the “complex” flight modes are also presented for $\omega =1.0, f_0=0.125$ and $b=0.85.$ Bifurcation diagram and the corresponding Lyapunov exponents to parameter $\xi$ are plotted in Fig. 11a and b respectively. There also exits transitions to “complex” flight from the period doubling when $\xi$ varies from $\xi =0.2$–$0.11$ and the sudden change happens as damping $\xi$ decreases to $\xi =0.082,$ which leads to a “calm” flight of period three from the “complex” flight mode. Similarly, this flight pattern repeats as $\xi$ decreases further.

Fig. 11

Transitions between different flight modes influenced by damping $\xi$ demonstrated by bifurcation diagram, Lyapunov exponent, trajectories and the corresponding Poincaré sections for the responses to the viscous damping $\xi$ for $\omega =1.0, f_0=0.125$ and $b=0.85$: a bifurcation diagram for $\xi$ versus $u,$ b the corresponding Lyapunov exponents, c a period five solution for $\xi =0.1095$ and d the co-existing periodic attractors for $\xi =0.057$: the pair of period five, marked with black and blue, and the larger amplitude vibration, marked with red. (Color figure online)

In addition to complex flight behaviours, periodic windows for “clam” flight can also be found from the bifurcation diagram, Fig. 11a. A period five window near $\xi =0.1095$ and a periodic window for a pair of period five near $\xi =0.057$ are clearly displayed in the bifurcation diagram and the corresponding the trajectories are also plotted in Fig. 11c and d respectively. It is found that this pair of period five solutions, marked with blue and black respectively, coexist with another larger amplitude motion of which the Poincaré section is marked with red.

4.3.3 Basin analysis of co-existing flight patterns

In this subsection basin analysis of the co-existing flight patterns of “calm” flight and “complex” flights are carried out. Figure 12 shows the Poincaré sections or the stroboscopic mappings and the corresponding basins for $\omega =1.0, f_0=0.125,$ $\xi =0.057$ and different values of $b,$ in which the area coloured black means undefined.

Fig. 12

Basin analysis for the co-existing flight patterns using Poincré sections for $\omega =1.0, f_0=0.125,$ $\xi =0.057$: a for $b=1.25,$ b for $b=0.85,$ c for $b=0.75$ and d for $b=0.5,$ respectively

The analysis shows that for $b\ge 1$ there exits a pair of stable periodic solutions, or two possible “clam” flight modes, one with a small and the other with a large amplitude, see for example, for $b= 1.25$ as shown in Fig. 12a, where the light grey is the basin of the solution with larger amplitude marked yellow, while blue is the basin of the smaller one marked red.

Figure 12b for $b=0.85$ shows the basins, coloured red, blue and light grey, of the associated co-existed solutions or the flight modes of a pair of period five, marked green and white, and yellow, respectively. A Wada fractal basin boundary [34–37] can be clearly shown from Fig. 12b that any point that is on the boundary of the basin for the periodic one solution is also simultaneously on the boundary of the basins of the pair of periodic five solutions. If decreasing $b$ to $0.75,$ there co-exists a chaotic attractor or “complex” flight as well as a period one solution or a “clam” flight, which are plotted blue and yellow, respectively in Fig. 12c and their basins are colored red and light grey. While further decreasing $b$ to $0.5,$ the basin is also reduced and there only exist two possible “clam” flights corresponding to periodic one solutions, as marked yellow and grey, and the their basins are plotted in blue and red, respectively.

It can be seen from the above basin analysis that the “clam” flight mode with a larger amplitude in Fig. 12a disappears as parameter $b$ decreases and the other one bifurcates into a pair of period five type, then a complex mode and finally a pair of periodic one type as $b$ deceases further.

In general, the basins of the co-existing modes vanish when parameter $b$ decreases to zero. However, the periodic solutions with smaller amplitudes always exist regardless parameter $b$ changes.

5 Conclusions and discussion

In this paper, a novel model inspired by the mechanism of dipteran flight motor has been proposed to investigate the flight mechanism from the nonlinear dynamics point of view. This evolved model has irrational nonlinear term due to the geometrical configuration of the inclined bars linked with springs and mass. The technique of nonlinear dynamical analysis to the bio-inspired irrational nonlinear system has been developed, which enables us to reveal correctly the characteristics of the bounded ($|y|<1$) flight mechanism and variety of flight patterns associated with the profound dynamical behaviours of the nonlinear system. The main findings are surmised as follows:

• 1. The bounded flight mechanism in depteran flight motor has been analysed and could not be characterised by the classical Duffing type systems.

• 2. “Click” transition behaviour has been clearly modelled by parameter $b$ termed as a switch value, i.e. the “click” occurs only when $0<b<1,$ while the “click” switches off at $b=1.$

• 3. High frequency flight bursting phenomena induced by low frequency excitation have been found and illustrated using both phase portraits and time history series.

• 4. Multiple flight patterns, such as “resting”, “calm” and “complex” modes have been observed using energy method analytically as well as nonlinear dynamics numerically.

• 5. Complex co-existing flight modes are revealed using basin analysis and the behaviours demonstrated by the shrinking of basins as $b$ decreases and will vanish when parameter $b$ tends to zero. However, the periodic solutions with smaller amplitudes always exist regardless $b$ changes.

Further researches have been actively undertaken by the current authors in the following directions: (i) to develop the methodologies for the irrational nonlinear system to derive the dynamic responses under perturbations; (ii) to determine the analytical measures e.g., the construction of Melnikovian to predict the border of chaos; (iii) to investigate the energy transmission mechanism [38–40] using power flow approach for the irrational nonlinear dynamic systems.