Skip to main content
Springer Nature Link
Log in

Contact modeling of heterogeneous materials of the machine tool bed–foundation interface based on the gradient of contact stress distribution

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

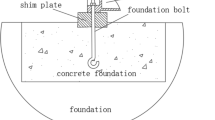
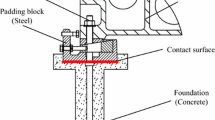
The machine tool bed and concrete foundation of heavy machine tools are typically connected by anchor bolts. The dynamic characteristics of the bolted joint's bed and foundation contact surfaces have an important influence on the machining accuracy and service life of the machine tool. This paper proposes a virtual material model based on the gradient of contact stress distribution for modeling the contact interfaces between the heterogeneous material of the machine tool bed and the foundation. An expression for the equivalent elastic modulus of the metal-concrete contact surface is derived by considering the nonlinear properties of concrete. Concrete crushing is assumed, and the evaluation basis of critical deformation parameters of asperity is established. Based on Fractal theory and Hertz contact theory, theoretical models of the elastic moduli, Poisson's ratios, densities, and thicknesses of the virtual material are established. Due to the uneven distribution of contact stress, a gradient equation with virtual material parameters is obtained according to the contact stress distribution curve. Then, the contact surface is stratified based on the virtual material parameters. The theoretical model was verified by simulations and experiments. The first-order natural frequency error was found to be 1.3%. The proposed method provides a new approach for modeling the contact between heterogeneous materials of the machine tool bed–foundation interface.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data availability

The authors declare that all data and material support their published claims and comply with field standards;

Code availability

Not applicable.

References

  1. Greenwood J, Williamson J (1966) Contact of nominally flat surfaces [J]. Proc R Soc Lond 295(1442):300–319

    Google Scholar 

  2. Guo X, Ma B, Zhu Y (2017) A magnification-based multi-asperity (MBMA) model of rough contact where the Greenwood-Williamson and Persson theories meet

  3. Wang W, Wu J, Gao Z et al (2018) A calculation model for tangential contact damping of machine joint interfaces. Chin J Theor Appl Mech 50(003):633–642

    Google Scholar 

  4. Hu S, Huang W, Shi X et al (2019) Review on mechanical seals using a bi-Gaussian stratified surface theory. J Mech Eng 55(01):103–117

    Article  Google Scholar 

  5. Persson B (2007) Theory of rubber friction and contact mechanics. J Chem Phys 115(8):3840–3861

    Article  Google Scholar 

  6. Zhao Y, Xu J, Cai L et al (2016) Stiffness and damping model of bolted joint based on the modified three-dimensional fractal topography. Proc Inst Mech Eng Part C 231(2):1

    Google Scholar 

  7. Yuan Y, Chen J, Zhang L (2018) Loading-unloading contact model between three-dimensional fractal rough surfaces. AIP Adv 8(7):115–124

    Article  Google Scholar 

  8. Liang A, Bian Y, Chen Q, et al (2019) Fractal prediction model for the contact of friction surface and simulation analysis. In: 2019 8th International Conference on Industrial Technology and Management (ICITM)

  9. Liu Z, Jiang K, Zhang C et al (2019) A stiffness model of a joint surface with inclination based on fractal theory. Precis Eng 1:1

    Google Scholar 

  10. Wei S, Tan L, Wu N (2018) Static hysteresis behavior analysis and stiffness and damping identification of bolted joints. J Northeastern Univ (Nat Sci) 1:1

    Google Scholar 

  11. Puchaa K, Szymczyk E, Jachimowicz J (2015) About mechanical joints desing in metal-composite structure. J Kones 19(3):381–390

    Google Scholar 

  12. Han R, Li G, Gong J et al (2019) Equivalent method of joint interface based on persson contact theory: virtual material method. Materials 12(19):1

    Article  Google Scholar 

  13. Zhao Y, Yang C, Cai L et al (2016) Surface contact stress-based nonlinear virtual material method for dynamic analysis of bolted joint of machine tool. Precis Eng 43:230–240

    Article  Google Scholar 

  14. Yang Y, Cheng H, Liang B et al (2020) A novel virtual material layer model for predicting natural frequencies of composite bolted joints. Chin J Aeronaut 1:1

    Google Scholar 

  15. Sun Q, Huang Q, Sun Z et al (2018) Interface parameter identification of bolted connections based on gradient virtual material. J Mech Eng 054(011):102–109

    Article  Google Scholar 

  16. Liao J, Zhang J, Yu D et al (2016) Modeling method of bolted joint interface based on gradient virtual materials. J Jilin Univ (Eng Technol Ed) 46(4):1149–1155

    Google Scholar 

  17. Zhang J, Han Y, Han J, et al. (2014) Cement hydration based model to predict the mechanical properties of precast concrete. Mag Concret Res

  18. Ruiz M, Muttoni A, Gambarova P (2007) Relationship between nonlinear creep and cracking of concrete under uniaxial compression. J Adv Concr Technol 5(3):383–393

    Article  Google Scholar 

  19. Salari A, Ghadami J et al (2016) Stress-strain behavior of freshly compressed concrete under axial compression with a practical equation. Constr Build Mater 1:1

    Google Scholar 

  20. Yuan Y, Chen J, Zhang L (2018) Loading-unloading contact model between three-dimensional fractal rough surfaces. AIP Adv 8(7):1

    Article  Google Scholar 

  21. Ciulli E, Ferreira L, Pugliese G et al (2008) Rough contacts between actual engineering surfaces—Part I. Simple models for roughness description. Wear 264(11):1105–1115

    Article  Google Scholar 

  22. Komvopoulos K, Ye N (2001) Three-dimensional contact analysis of elastic-plastic layered media with fractal surface topographies. J Tribol 123(1):632–640

    Article  Google Scholar 

  23. Majumdar A, Bhushan B (1990) Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J Tribol 112(2):205–216

    Article  Google Scholar 

  24. Tian H, Li B, Liu H et al (2011) A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools. Int J Mach Tools Manuf 51(3):239–249

    Article  Google Scholar 

  25. Zhao Y, Yang C, Cai L et al (2016) Stiffness and damping model of bolted joint with uneven surface contact pressure distribution. J Mech Eng 62(11):665–677

    Article  Google Scholar 

  26. Ye H, Huang Y, Li P et al (2016) Virtual material parameter acquisition based on the basic characteristics of the bolt joint interfaces. Tribol Int 95:109–117

    Article  Google Scholar 

  27. Cao J, Zhang Z (2019) Finite element analysis and mathematical characterization of contact pressure distribution in bolted joints. J Mech Sci Technol 33(2):1

    Google Scholar 

  28. Liao J, Zhang J, Feng P et al (2016) Interface contact pressure-based virtual gradient material model for the dynamic analysis of the bolted joint in machine tools. J Mech Sci Technol 30(10):4511–4521

    Article  Google Scholar 

  29. Miguel F, Aurelio M, Pietro G et al (2007) Relationship between nonlinear creep and cracking of concrete under uniaxial compression. J Adv Concr Technol 5(3):383–393

    Article  Google Scholar 

  30. Fu W, Lou L, Gao Z et al (2017) Theoretical model for the contact stiffness and damping of mechanical joint surface. J Mech Eng 53(9):73–82

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (52075012);

Author information

Authors and Affiliations

  1. Institute of Advanced Manufacturing and Intelligent Technology, Beijing University of Technology, Beijing, 100124, China

    Nana Niu, Yongsheng Zhao, Ying Li, Kui Chen & Xin Li

  2. Beijing Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing, 100124, China

    Nana Niu, Yongsheng Zhao & Ying Li

  3. Machinery Industry Key Laboratory of Heavy Machine Tool Digital Design and Testing Technology, Beijing University of Technology, Beijing, 100124, China

    Kui Chen & Xin Li

  4. College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing, 100124, China

    Yongsheng Zhao

Authors
  1. Nana Niu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yongsheng Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ying Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Kui Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Xin Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors on this list have contributed to this article.

Corresponding author

Correspondence to Yongsheng Zhao.

Ethics declarations

Conflict of interest

The authors declare no potential conflicts of interest with respect to the research, authorship, and publication of this article.

Consent to participate

The authors declare that they consent to participate in this paper.

Consent to publish

The authors declare that they consent to publish this paper.

Additional information

Technical Editor: Ehsan Noroozinejad Farsangi.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Niu, N., Zhao, Y., Li, Y. et al. Contact modeling of heterogeneous materials of the machine tool bed–foundation interface based on the gradient of contact stress distribution. J Braz. Soc. Mech. Sci. Eng. 44, 594 (2022). https://doi.org/10.1007/s40430-022-03910-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-022-03910-3

Keywords