Introduction

TA6V is the most widely used titanium alloy because it shows excellent mechanical properties at high temperatures [1, 2]. TA6V is commonly used in industrial applications such as aeronautics and aerospace equipment [3] and in biomechanical applications such as implants and prostheses [4, 5]. Although TA6V can be assembled from a variety of welding processes, laser welding presents a practical option owing to its high heat input and flexibility [6], which lead to small heat-affected zones and high welding velocities. Several physical phenomena can occur during laser welding, causing part of the energy to be lost. Such energy losses can reduce the efficiency of laser welding.

It is important to develop numerical techniques in order to simulate the thermal consequences of laser welding because experimental investigations can be difficult, impractical, time-consuming, and prohibitively expensive. Several works have focused on numerical analyses of welding [7]; the obtained numerical results can be used to optimize welding parameters and to explain the physics of some phenomena that occur during welding. Thus, numerical modeling is a powerful tool for understanding welding conditions and parameters.

Davis et al. [8] used numerical model to study laser welding of different metals. They found correlations between various welding parameters without considering energy losses. Abderrazak et al. [9] used also numerical model to analyze the formation of pools of molten metal during laser welding without considering energy losses.

Bannour et al. [10] have studied the temperature dependence of physical properties during welding, and they have considered convection losses. Several authors have shown that energy dissipates on surface by convection and radiation [11, 12]. Belhadj et al. [13] considered surface convection losses; they assumed the losses by radiation are on surfaces irradiated with the laser beams. They develop a model for simulating thermal history during laser welding. Abderrazak et al. [14] estimated both thermal convection and radiation phenomena in welding areas to develop a thermal model for predicting the different parameters expected during the welding of magnesium alloys. We point out that some researchers prefer using a single heat loss equation in which they combine the effects of radiation and convection into a single heat transfer coefficient [15,16,17].

In our knowledge, there is a paucity of research on calculating of the energy rate due to convection and radiation during welds; therefore, the present paper aims to quantify the amount of energy lost by convection and by radiation during the CO2 laser welding of thin plates of TA6V.

Mathematical model and numerical method

The laser welding of a thin plate results in uniform properties in depth. Therefore, the welding temperatures were assumed to be identical at all penetration depths under the welding conditions used in this study. For simplicity, we assumed that energy lost though the surface by radiation and by convection could be treated by two-dimensional model without loss of generality.

Heat source model

The power density, Q, produced by a focused beam is very intense, thereby allowing the melting of metal. A keyhole will be formed to transmit the energy to the metal. During welding laser, the keyhole was maintained directly under the laser beam. For laser velocity V and laser beam radius R, a Gaussian surface distribution was used and it is expressed as follows:

$$ Q_{ (r,t )} = \left\{ {\begin{array}{*{20}l} {Q_{0} \exp \left( {\frac{{ - r^{2} (t)}}{{R^{2} }}} \right)} \hfill & {r \le 2R} \hfill \\ 0 \hfill & {r > 2R} \hfill \\ \end{array} } \right. $$
(1)

with: r2(t) = x2 + (y − Vt)2.

Note that Q0 is chosen to have the total laser power P. The power density is Q(R, t) = exp (− 1)Q0 = 0.37Q0 for r = R, and it is Q(2R, t) = exp (− 4)Q0 = 0.02Q0 for r = 2R; the energy distribution is practically around R.

Assumptions and governing equations

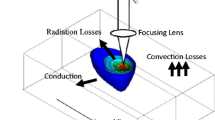
The geometrical configuration of the problem and the corresponding Cartesian coordinate system are shown in Fig. 1. The mathematical formulation of the model was based on the following assumptions:

Fig. 1
figure 1

Presentation of the problem

Full size image
  1. 1.

    The initial temperature of the work piece was T0 = 300 K;

  2. 2.

    The laser beam was moved at a constant velocity, V;

  3. 3.

    A perfect contact joint was welded between two identical parts;

  4. 4.

    The thermal analysis was only performed on half the assembly;

  5. 5.

    Energy was assumed to be lost only by radiation and by convection.

The governing equation for energy is the heat equation. It is expressed as follows:

$$ \rho C_{\text{P}} \left[ {\frac{\partial T}{\partial t}} \right] = \lambda {\text{div}}({\text{grad}}T) + Q - Q{}_{\text{W}} $$
(2)

An important temperature gradient was produced from the beginning to the end of laser welding, so the TA6V could transit from solid to liquid. Since the characteristics of metals are temperature dependent, we assumed that each phase would show different average thermal conductivity, density, specific heat, and emissivity.

Heat distribution in the solid phase obeys the following equation:

$$ \rho_{\text{s}} C_{\text{ps}} \frac{{\partial T_{(x,y,t)} }}{\partial t} = \lambda_{\text{s}} \nabla^{2} T_{(x,y,t)} + Q_{(x,y,t)} - \sigma \varepsilon_{\text{S}} \left( {T_{(x,y,t)}^{4} - T_{0}^{4} } \right) - h\left( {T_{(x,y,t)} - T_{0} } \right) $$
(3)

Heat distribution in the liquid phase obeys the following equation:

$$ \rho_{\text{L}} C_{\text{pL}} \frac{{\partial T_{(x,y,t)} }}{\partial t} = \lambda_{L} \nabla^{2} T_{(x,y,t)} + Q_{(x,y,t)} - \sigma \varepsilon_{L} \left( {T_{(x,y,t)}^{4} - T_{0}^{4} } \right) - h\left( {T_{(x,y,t)} - T_{0} } \right) $$
(4)

To account for the transition between the solid phase and liquid phase, we computed the amount of energy, dφ, accumulated in an elementary volume [18] and we compared with the enthalpy of fusion. We assumed that the welding temperature varied linearly during the phase transition.

$$ {\text{d}}\varphi = \left( {\lambda_{\text{SL}} {\text{grad}}T_{(x,y,t)} \cdot \vec{n}.{\text{d}}s - \sigma \varepsilon_{\text{SL}} {\text{d}}s\left( {T_{(x,y,t)}^{4} - T_{0}^{4} } \right) - h{\text{d}}s\left( {T_{(x,y,t)} - T_{0} } \right)} \right){\text{d}}t + Q(x,y,t) $$
(5)

Numerical model and boundary condition

For the numerical model, the finite difference method (FDM) was used to simulate thermal behavior. The principal idea is to replace the partial differential equations by an equivalent and approximate set of algebraic equations. Equations 3, 4, and 5 are discretized in space and time; they can be written as:

$$ \alpha_{1} T_{{\left( {i - 1,j} \right)}}^{n + 1} - \alpha_{2} T_{{\left( {i,j} \right)}}^{n + 1} + \alpha_{1} T_{{\left( {i + 1,j} \right)}}^{n + 1} = T_{{\left( {i,j} \right)}}^{n} - \alpha_{3} \left( {T_{i,j - 1)}^{n + 1} + T_{{\left( {i,j + 1} \right)}}^{n + 1} } \right) - \alpha_{4} Q_{{\left( {i,j} \right)}} - \beta_{1} $$
(6)
$$ \alpha_{5} T_{{\left( {i - 1,j} \right)}}^{n + 1} - \alpha_{6} T_{{\left( {i,j} \right)}}^{n + 1} + \alpha_{5} T_{{\left( {i + 1,j} \right)}}^{n + 1} = T_{{\left( {i,j} \right)}}^{n} - \alpha_{7} \left( {T_{i,j - 1)}^{n + 1} + T_{{\left( {i,j + 1} \right)}}^{n + 1} } \right) - \alpha_{8} Q_{{\left( {i,j} \right)}} - \beta_{2} $$
(7)
$$ {\text{d}}\varphi_{{\left( {i,j} \right)}} = 2\gamma_{1} T_{{\left( {i + 1,j)} \right)}}^{n + 1} - \gamma_{2} T_{{\left( {i - 1,j} \right)}}^{n + 1} + 2\gamma_{1} T_{{\left( {i,j + 1} \right)}}^{n + 1} + \gamma_{3} $$
(8)

where i and j are space steps for, respectively, x- and y-axis (for mesh indexes), n is the time step, and parameters αk, γk, and βk are constants and parameters related to physical properties and numerical values of the discretized system.

We developed a FORTRAN-based computer program. The Gauss–Seidel iterative algorithm was used to solve the equations. The time step and mesh construction depended on the laser beam dimension and the welding velocity; a dense mesh was used near the weld bead.

Boundary conditions are as follows (shown in Fig. 2):

Fig. 2
figure 2

Geometry, mesh, and boundary conditions

Full size image
  1. 1.

    Along the axe y = 0: (∂T/∂y)y=0 = 0

  2. 2.

    On y = Ly: \( \left( {\partial T/\partial y} \right)_{{y = L_{y} }} = 0 \)

  3. 3.

    On x = Lx; T(Lx, y) = T0

  4. 4.

    Along the axe of symmetry (x = 0), we assumed a zero heat flux on the contact between two parts to be assembled.

The general scheme of calculation, for a time step n, is as follows:

  • For a j value:

    1. (a)

      Identification of nodes phase (solid, liquid, phase transition) of meshes for all values i,

    2. (b)

      Calculation of elements of matrix A and B for values i,

    3. (c)

      Calculation of the temperature Tn(i,j), at time n, by Gauss–Seidel iterative method,

    4. (d)

      Repeat calculation (a)–(c) for other value j = j+1.

  • Verification of convergence and stability of solution Tn(i,j) for the same time step n for all i and j values,

  • Calculation for the next step time n + 1 if the convergence is verified.

With this scheme, the calculation, for the proposed time of welding and for the dimension of the two parts and laser beam power, will be stable and will not affect the generality of result.

Material properties

Unalloyed titanium consists of two allotropes. At ambient temperature, titanium shows the hexagonal-close-packed (hcp) (α) crystal structure. Near the β-transus temperature, Tβ= 1155 K [19], titanium allotropically transforms into the body-centered-cubic (bcc) (β) phase. Therefore, titanium alloys are classified according to their favored structure (usually α, β, or α–β) under ambient conditions.

TA6V, the most commonly used of α–β titanium alloy, is composed of 6% of aluminum, 4% of vanadium, and residual elements. The β-transus temperature range of TA6V is Tβ≈ 1253–1268 K [20], which is important for determining the TA6V structure. In this work, TA6V melted in the range 1913–1933 K. An average temperature of Tf = 1923 K was used as melting point, as previously has been used by many authors [2, 21, 22].

Titanium exhibits some excellent characteristics for fusion welding [23]. Since an important temperature gradient was produced during laser welding, the physical characteristics of the material must be temperature dependent. Boiniveau et al. [3] investigated the effect of welding temperature on the physical properties of solid and liquid TA6V, which are published elsewhere in the literature [2, 21]. Table 1 presents physical properties of TA6V; we exploited these values and others in this work. The heat transfer coefficient, h = 50 Wm−2 K−1 [2], was temperature independent. The used absorption coefficient is η = 0.34 [2].

Table 1 Physical properties of TA6V titanium alloy
Full size table

Results and discussion

Geometry dimensions were Lx= 0.050 m in length and Ly= 0.006 m in width. With an average velocity of V = 0.060 m/s, the time required to weld a distance of 0.006 m is 0.1 s. Laser beam radius was R = 0.30 mm. Temperature distribution was calculated as a function of welding time and position during the laser welding. To get a stable calculation, the maximum value of time step is Δt = 4 × 10−5 s with an irregular mesh sizes (Δx = variable and Δy = 5.10−5 m). If we want to increase the accuracy of the calculations, we must check Δt ≤ 10−5 s under the welding conditions used in this study. The mesh sizes vary, and the time step size is usually determined by the smallest mesh sizes (Δx = 5 × 10−5 m and Δy = 5.10−5 m). For a better presentation of the results and their analyses, we will present the lengths x, y and R in mm in the rest of this section.

Figure 3 illustrates temperature evolution for P = 2500 W of laser power and different welding velocities at the point (x = 0 mm, y = 3.0 mm). A similar trend of temperature evolution was observed for different welding velocities. It is clearly seen that the peak welding temperature was increased by decreasing the welding velocity. It can be noted that for a welding velocity V ≤ 0.060 m/s the temperature can reach the melting point on the weld bead. With well-studied conditions, we have looked for the appropriate welding conditions. These results were in good agreement with the experimental results of Caiazzo et al. [24] and Ahn et al. [20]. The results are presented in Table 2.

Fig. 3
figure 3

Temperature evolution for P = 2500 W of laser power and different welding velocities at (x = 0 mm, y = 2.0 mm)

Full size image
Table 2 Appropriate welding conditions
Full size table

Figure 4 gives temperature evolution during laser welding at different positions (x = 0.0, y = 3.0 mm), (x = 0.0, y = 3.5 mm), and (x = 0.0, y = 4.0 mm) on the weld bead for P = 2500 W of and V = 0.060 m/s. The same shape can be observed as other curves in the literature [11, 22]. It is known that when there is convection heat transfer, the temperature profile approaches slightly to ambient temperature. This trend can be clearly observed in Figs. 3, 4.

Fig. 4
figure 4

Temperature evolution during laser welding at different positions on the weld bead (P = 2500 W, V = 0.060 m/s)

Full size image

The variation of the temperature is presented in Fig. 5 as a function of the position x during welding for P = 2500 W and V = 0.060 m/s at t = 0.1 s. This figure shows that during laser welding there is an important thermal gradient near x = 0. The temperature may vary between 400 K and 1500 K at a distance less than 0.4 mm from the weld bead, to note that R = 0.30 mm.

Fig. 5
figure 5

Variation of the temperature as a function of the position x (P = 2500 W, V = 0.060 m/s, t = 0.1 s)

Full size image

Temperatures values were calculated on the weld bead at the point (x = 0 mm, y = 2.5 mm) for P = 2500 W and V = 0.040 m/s with and without losses. The results are reported in Table 3. We can note that the variations of temperature ΔT/T do not exceed 0.2% after 0.20 s.

Table 3 Variations of temperature with and without lost energy
Full size table

Figures 6, 7 show the energy lost by radiation and convection as function of time for V = 0.060 m/s and P = 2500 W. It can be seen that during welding, the energy lost by radiation or convection varies according to time and it is greater near the weld bead. The maximum value of energy lost by radiation (about 2.52 × 10−4 J) is greater than the maximum value of energy lost by convection (about 1.67 × 10−4 J). The energy lost by radiation is less than to the energy lost by convection in a duration time. We can see also that the energy lost by radiation is less than to the energy lost by convection in space function. So there is a competition between the two phenomena radiation and convection. As the laser beam radius R = 0.3 mm, these two last conclusions confirm the hypothesis taken by Belhadj et al. [13], where they assumed the loss by radiation is on the irradiated surface by laser beam. These results confirm our choice for the form of power density (Q(2R, t) = exp (− 4)Q0 = 0.02Q0), outside 2R the energy lost by convection and radiation are negligible.

Fig. 6
figure 6

Energy lost by radiation as a function of time at different positions x

Full size image
Fig. 7
figure 7

Energy lost by convection as a function of time at different positions x

Full size image

For R = 0.30 mm, P = 2500 W and V = 0.060 m/s, the energy lost from one plate at different zones during welding (0.1 s) is shown in Table 4. Results show the loss in and near the weld bead is important per unit area, but the total energy lost, especially by convection, is most important on all the surface of the plate.

Table 4 Lost energy during welding from one plate
Full size table

Energy lost at y = 2.0 mm as a function of position x for different laser powers is illustrated in Fig. 8.We notice that along x losses decrease. At every time, it can be observed that the lost energy was increased by increasing the laser power.

Fig. 8
figure 8

Energy lost as a function of positions x for different laser powers

Full size image

It is clear that the energy lost near and on the weld bead is greater than the energy lost in the rest of the plate. The temperatures can reach the β-transus temperature on the weld bead and near the weld bead. The exact calculation of the temperatures in those positions is required. Therefore, it is necessary to take into account energy losses on the weld bead and near the weld bead. The study of the influence of the results on the structure of the materials would require a more computation on the volume of the materials.

The amount of energy lost by convection and radiation for both plates of TA6V represented 2.5% of the energy balance during 0.10 s and 7% during 0.20 s. In a previous work [14], both thermal convection and radiation in the welding area of magnesium alloy have been estimated to be about 20% of the laser power. This difference is probably due to several parameters such as physical properties, welding parameters, cooling rate, or calculation models.

Conclusion and perspectives

A numerical model has been used to determine temperature distribution as a function of welding time and position during the laser welding of two identical thin plates of TA6V. The amount of energy lost by radiation and convection could be calculated at any instant during welding. According to the results, the main conclusions are summarized as follows:

  • The temperature evolutions produced by different welding velocities showed similar trends.

  • The peak welding temperature was increased by decreasing the welding velocity.

  • The numerical results obtained using the appropriate welding conditions were in good agreement with previous published experimental data.

  • The energy loss depended on the position and power and the welding velocity and time.

  • Under the welding conditions used in this study, variations in temperature ΔT/T did not exceed 0.2% after 0.20 s, and the amount of energy lost by convection and radiation represented 7% of the energy balance.

  • It is necessary to take into account energy losses in the welding area to improve laser welding efficiency.

As a perspective, it would be interesting to study metal vaporization and its impact on the welding area. Further, it would be interesting to study exactly how lost energy affects material structures. These last need a calculation in the volume of materials, in and near the weld bead, with an appropriate formulation of the laser power.