Introduction

The study of propagation properties of nonlinear solitary waves in different plasma environments (e.g., magnetized/unmagnetized multicomponent dusty/complex plasmas) is an important area of research in modern plasma physics. For the last many years, various types of nonlinear structures such as solitary waves, shocks, double layers and vortices have been studied theoretically as well as experimentally under different plasma conditions. When dispersion of the medium is completely balanced by nonlinearity, the dissipative effects can be negligible and solitary waves are formed. However, when the dissipative effects are more dominant than dispersion of medium, this leads to the formation of shock structures. The dissipation can be caused by fluid viscosity, inter-particle collision, Landau damping or can be due to nonadiabatic dust charge fluctuations. The dynamics of shock waves in a magnetized plasma are governed by KdV–Burgers equation whose solution has the form of shock structures. The shock structures play very important role in understanding astrophysical plasmas, e.g., supernova explosions [1], cosmic ray generation [2], bow shock region [3] and nonlinear dynamics of solar wind [4].

Over the last three decades, research activities in dusty plasmas have been witnessed in a number of studies with different velocity distributions of the charged particles [5, 6]. This is not only due to the omnipresence of dust but may also be due to the broad range applications of dusty plasmas in understanding the different collective processes in astrophysical and space environments [7,8,9], as well as in laboratory experiments [10]. The presence of dust particles (micron to submicron sized) is common in different plasma environments, e.g., magnetosphere of Earth, solar winds, ionosphere and planetary rings of Saturn [9, 11]. Charging of dust (positive or negative) depends upon the charging processes (e.g., photoionization, secondary electron emission, thermionic emission or by electron ion bombardments on surface of dust particles). The presence of charged dust in a plasma generates new eigenmodes such as dust acoustic (DA) waves [12], dust ion-acoustic DIA waves [13, 14], dust acoustic shock waves [15] and dust lattice waves [16].

A large number of investigations have been reported for the study of shock structures in plasmas both theoretically [15, 17,18,19,20,21,22] and experimentally [23,24,25,26]. Dust acoustic shock waves for two temperature ions in unmagnetized dusty plasma were investigated by Zhang and Wang [17]. Shock waves in an unmagnetized dusty plasma consisting of charged adiabatic dust fluid and Boltzmann-distributed electrons and ions have been studied by Rahman and Mamun [18] and only negative potential shocks were observed. It was also noticed that the effect of dust fluid temperature modifies the basic properties of shock structures. El-Hanbaly et al. [21] derived the modified KdV–Burgers equation in a dusty plasma consisting of Boltzmann-distributed electrons and trapped ions obeying vortex-like distribution and studied the shock solution in a dissipative space plasma. Recently, Tansim et al. [22] have studied dust acoustic shock waves in a four-component unmagnetized dusty plasma consisting of cold dust fluid, Boltzmann-distributed electrons and two temperature ions obeying q-nonextensive and Cairns distribution respectively. They have studied the combined effects of both nonextensive and nonthermal distribution of ions on the properties of dust acoustic shocks.

A number of observations and in situ measurements have confirmed the presence of excess superthermal population of charged particles in astrophysical and space plasmas, e.g., in the magnetospheres of Earth, Mercury, Saturn, Uranus and the solar wind [27,28,29,30]. Superthermal plasma behavior was also observed in various experimental plasma contexts, such as laser–matter interactions or plasma turbulence [31]. Such plasmas are best modeled by generalized Lorentzian (kappa) distribution rather than Maxwellian. The presence of excess superthermal charged particles population due to velocity space diffusion may lead to inverse power law distribution at a velocity much higher than the electron thermal speeds [32,33,34,35,36].

We shall use a three-dimensional \(\kappa\)-distribution function as [37]

$$\begin{aligned} f_k(v)=\frac{n_0}{(\pi \kappa \theta ^2)^{3/2}} \frac{\Gamma (\kappa +1)}{\Gamma (\kappa -\frac{1}{2})} \left( 1+\frac{v^2}{\kappa \theta ^2}\right) ^{-(\kappa +1)}. \end{aligned}$$
(1)

The effective thermal speed \(\theta\) = \((\frac{\kappa -3/2}{\kappa })^{1/2}v_\text{th}\) is related to thermal velocity \(v_\text {th}=(2K_BT/m)^{1/2}\), m is species mass and T is the characteristic kinetic temperature. The spectral index \(\kappa\) is a measure of the slope of the energy spectrum of the superthermal particles forming the tail of the velocity distribution function. A small value of \(\kappa\) means particles are more superthermal and energy spectrum is hard. In the limit \(\kappa \rightarrow \infty\), the kappa distribution approaches the Maxwellian limit. By integrating the distribution function given by Eq. (1) in the presence of electrostatic potential \(\phi\), one can obtain the number density of electrons/ions.

A number of investigations of solitary structures and shock waves in plasma with kappa-distributed electrons/ions have been reported by numerous authors in different kinds of plasma systems. Shahmansouri and Astaraki [38] investigated the properties of ion-acoustic solitary structures in a plasma system containing inertial ions and superthermal electrons and positrons which are assumed to be inertialess. Kundu et al. [39] studied the shock waves in unmagnetized dusty plasma where electrons are superthermally distributed. Burgers equation was derived using standard reductive perturbation method and it was concluded that shock waves are modified by the presence of positively and negatively charged dust particles and superthermal nature of kappa-distributed electrons/ions. Shahmansouri and Alinejad [40] studied the effect of superthermality of ions/electrons and dust charge fluctuation on dust acoustic shock waves.

It is a well-known fact that the propagation properties of electrostatic solitary structures can be modified under the influence of external magnetic field. Since most of the space and astrophysical plasmas are permeated by magnetic field, the effect of external magnetic field on electrostatic solitary waves in different kinds of plasma environments has been studied by various authors [41,42,43,44,45,46,47,48,49,50,51,52,53]. The obliquely propagating ion-acoustic (IA) solitons in a magnetized and weakly relativistic warm plasma have been investigated by deriving KdV equation and it was inferred that the soliton energy is lowered by stronger magnetic field and the solitons become narrower [41]. Furthermore, the effect of ion temperature and dust charging on characteristics of ion-acoustic (IA) solitons in a magnetized inhomogenous plasma has been reported by Malik [43] and Kumar et al. [44] respectively. The propagation properties of compressive solitons were analyzed by Malik and Malik [47] in a dusty plasma comprising of electrons, positrons and dust grains of either positive or negative charge. They derived the KdV equation and reported that the amplitude of a compressive soliton remains larger in case of positively charged dust grains as compared to dust grains having negative charge. Tomar et al. [48] studied the evolution and reflection of ion-acoustic solitary waves in an inhomogenous magnetized dusty plasma consisting of ions, electrons having two temperature and dust grains with varying charge. The evolution of solitons has also been studied by Tomar et al. [49] by deriving a modified KdV equation in a plasma having ions, two temperature electrons and negatively charged dust grains. Dust acoustic shock waves in magnetized homogenous dusty plasma have been investigated by Zhang and Xue [50]. In the past, ion-acoustic shock waves in magnetized plasma have been studied by Bains and Tribeche [51] and the effects of nonextensivity of electrons on the characteristics of shock structures have been analyzed. Shahmansouri and Mamun [52] studied the dust acoustic shock waves in magnetized nonthermal dusty plasma. Zaghbeer et al. [53] reported the study of dust acoustic shocks in magnetized dusty plasma with nonextensive electrons and ions. The KdV–Burgers equation was derived by using reductive perturbation method and found that DA shocks are significantly modified by the combined effects of dust fluid viscosity, external magnetic field and obliqueness.

Motivation of the present investigation is to study the combined influence of superthermality of charged particles, strength of magnetic field and other plasma parameters on the characteristics of shock structures in a homogenous dusty plasma. To the best of our knowledge, the properties of dust acoustic shocks in a magnetized dusty plasma with superthermal electrons and ions have not been investigated so far. In this study, our target is to investigate the effects of dust concentration, kinematic viscosity, superthermality of electrons and ions and the strength of ambient magnetic field on the characteristics of dust acoustic shocks. In the framework of \(\kappa\)-distribution, we shall develop a comprehensive formulation for three-dimensional dust acoustic shock waves projecting in a magnetized dusty plasma consisting of dust fluid, superthermal electrons and ions. The dust fluid viscosity will be responsible for dissipative effects. A nonlinear evolution equation known as KdV–Burgers equation is derived by using reductive perturbation method, and we shall analyze that the influence of various physical parameters modifies the width and amplitude of DA shocks due to dependence of nonlinear, dispersion and dissipative terms on such parameters.

The paper is structured as follows: In Sect. 2, the fluid model equations are described for DA shock waves. In Sect. 3, employing a reductive perturbation method, KdV–Burgers equation is derived and its solution is discussed. Sections 4 and 5 are devoted to parametric analysis and concluding remarks of present study respectively.

The fluid equations

We consider a plasma system consisting of negatively charged massive dust as inertial fluid, inertialess ions and electrons are considered to follow superthermal distribution. The dynamics of dust acoustic waves can be described by following set of normalized continuity, momentum and Poisson’s equations as

$$\frac{\partial n_d}{\partial t}+\nabla \cdot \left( n_d\mathbf {u_d}\right) = 0,$$
(2)
$$\frac{\partial \mathbf {u_d}}{\partial t}+ (\mathbf {u_d} \cdot \nabla ){\mathbf {u_d}} =\nabla \phi -(\mathbf {u_d} \times \mathbf {\mathbf {\Omega _d}})+\eta \nabla ^2 \mathbf {u_d},$$
(3)
$$\nabla ^2\phi=(n_d+\mu _e n_e-\mu _i n_i).$$
(4)

The equilibrium condition is \(n_{i0}= n_{e0} + Z_{d} n_{d0}\), which reduces to \(\mu _i=\mu _e +1\), where \(\mu _{e}=\frac{n_{e0}}{Z_{d0}n_{d0}}\) and \(\mu _{i}=\frac{n_{i0}}{Z_{d0}n_{d0}}\). \(\mathbf{u_d}=u \hat{x}+v \hat{y}+w \hat{z}\) where, u, v and w represent the dust particles velocities in x, y and z directions normalized by the dust acoustic speed \(C_d = (Z_{d}T_{i}/m_{d})^{1/2}\), \(\phi\) represents the electrostatic potential normalized by \(T_{i}/e\). The space and time coordinates are normalized by the dust Debye length \(\lambda _{Dd} = ( T_{i}/4 \pi e^2 Z_{d} n_{d0})^{1/2}\) and the inverse of the dust plasma frequency \(\omega _{pd}^{-1} =(\frac{4\pi e^2 {Z_{d}}^2 n_{d0}}{m_{d}})^{-1/2}\) , respectively. \(\eta\) is dust kinematic viscosity normalized by \(\lambda _{Dd}^2 n_{d0} m_d \omega _{pd}\). The magnetic field is assumed to be along z-direction, i.e., \(\mathbf {B}=B_0 \hat{\mathbf {k}}\) and \(\mathbf {\Omega _{d}}=\frac{\omega _{cd}}{\omega _{pd}}\), where \(\omega _{cd}=\frac{Z_d e\mathbf{B}}{m_d}\) is dust cyclotron frequency. The ion and electron densities obtained by integrating Eq. (1) are represented in normalized form as

$$\begin{aligned} n_{e}= & {} \left( 1- \frac{\sigma _{i} \phi }{\kappa _{e}-3/2}\right) ^{-\kappa _{e}+1/2} \nonumber \\ n_{i}= & {} \left( 1+ \frac{\phi }{\kappa _{i}-3/2}\right) ^{-\kappa _{i}+1/2}, \end{aligned}$$
(5)

where \(\sigma _{i}=T_i/T_e\). The parameters \(\kappa _e\) and \(\kappa _i\) are significant in the present case and hold a physical meaning when \(\kappa _s>3/2\), where s=i, e for ions and electrons, respectively. In the limit \(\kappa _e,\kappa _i\rightarrow \infty\), Eq. (5) agrees with the Maxwellian case expressions. The power law in Eq. (5) makes the Poisson’s equation (4) intractable analytically. This difficulty is removed by assuming that any disturbance of the electrostatic potential is small (i.e., \(\phi<<1\)) in this regime, a Taylor expression of Eq. (4) around this parameter can be preferred and densities of electrons and ions are expressed as

$$\begin{aligned} n_j=1\pm c_{j1} \phi + c_{j2}\phi ^2\pm O(\phi ^3)+\cdots, \end{aligned}$$
(6)

where \(j=e,i\) and lower sign (negative sign) is for ions. Truncating the expression at third order, Eq. (4) can be written as

$$\begin{aligned} \frac{\partial ^2 \phi }{\partial x^2}+ \frac{\partial ^2 \phi }{\partial y^2}+\frac{\partial ^2 \phi }{\partial z^2}= n_{d} -1 +C_{1}\phi + C_{2}\phi ^2+C_3 \phi ^3, \end{aligned}$$
(7)

the coefficients \(C_1\) and \(C_2\) are defined as

$$\begin{aligned} C_{1}= \mu _e c_{e1} + \mu _i c_{i1}, \end{aligned}$$
(8)
$$\begin{aligned} C_{2}= \mu _e c_{e2}-\mu _i c_{i2}, \end{aligned}$$
(9)
$$\begin{aligned} C_{3}= \mu _e c_{e3}+\mu _i c_{i3}, \end{aligned}$$
(10)

where \(c_{e1}=\frac{\sigma _{i} (\kappa _e-1/2)}{(\kappa _e-3/2)},\ c_{i1}=\frac{(\kappa _i-1/2)}{(\kappa _i-3/2)}\), \(c_{e2}=\frac{\sigma _{i}^2 (\kappa _e^2-1/4)}{2(\kappa _e-3/2)^2}, c_{i2}=\frac{(\kappa _i^2-1/4)}{2(\kappa _i-3/2)^2}\), \(c_{e3}=\frac{{\sigma _i}^3(\kappa _e^2-1/4)(\kappa _e+3/2)}{6(\kappa _e-3/2)^3}, c_{i3}=\frac{(\kappa _i^2-1/4)(\kappa _i+3/2)}{6(\kappa _i-3/2)^3}\).

Derivation of KdV–Burgers equation

To investigate the dynamics of DA shock waves in a magnetized superthermal dusty plasma, we shall derive the KdV–B equation in the frame work of reductive perturbation method [54]. The stretched coordinates are introduced in the following form:

$$\begin{aligned} \xi =\epsilon ^{1/2}(l_x x+l_y y+l_z z-V_0 t), \qquad \tau =\epsilon ^{3/2}t \end{aligned}$$
(11)

where \(\epsilon,\) is a small parameter characterizing the nonlinearity. \(l_x\), \(l_y\) and \(l_z\) are respectively the direction cosines of wave vector k along x-, y- and z-axis so that \(l_x^2+l_y^2+l_z^2=1\). \(V_0\) is the DA phase speed normalized by \(C_d\). In a weak damping situation, the dust ion kinematic viscosity can be considered small but finite. This leads us to assume that

$$\begin{aligned} \eta \approx \epsilon ^{1/2}\eta _{0} \end{aligned},$$
(12)

where \(\eta _{0}\) is a finite parameter. The expansion of dependent variables \(n_d\), u, v, w and \(\phi\) around their equilibrium values in a power series is given as [55, 56]:

$$\begin{aligned} n_d=\, & {} 1+\epsilon n_{d1}+\epsilon ^2 n_{d2}+\cdots \nonumber \\ u= \,& {} \epsilon ^{3/2}u_{1}+\epsilon ^2 u_{2}+\cdots\nonumber \\ v=\, &{} \epsilon ^{3/2}v_{1}+\epsilon ^2 v_{2}+\cdots\nonumber \\ w= \,&{} \epsilon w_{1}+\epsilon ^2 w_{2}+\cdots \nonumber \\ \phi=\, &{} \epsilon \phi _{1}+\epsilon ^2 \phi _{2}+\cdots\end{aligned}$$
(13)

It is pertinent to mention here that the higher is the power of \(\epsilon\), the lower is the magnitude of perturbation of that physical quantity. It is a well-known fact that the solitons evolve in a homogenous plasma if the physical quantities have a slow time variation in comparison with their space variation, which leads to the balance between nonlinearity and dispersion in a given plasma medium. On the other hand, if the variation in nonlinearity is of the same order as dissipation in a given medium, then the nonlinear effects are balanced by dissipative effects and shock waves are formed. The dissipative effects are realized through kinematic viscosity of dust particles in a given plasma medium. The stretching in space and time variables is given by Eq. (11) where \(\xi\) is the space-like coordinate and \(\tau\) is the time-like coordinate, whereas the stretching in kinematic viscosity is given by Eq. (12). The variation in other physical quantities such as density, velocity and potential is presented by Eq. (13). The Lorentz force acts only in the direction perpendicular to the ambient magnetic field, which is in the z- direction in present case. Hence, the magnitude of perturbation in \(v_x\) and \(v_y\) is taken to be lower than the perturbation in \(v_z.\) Using Eqs. (11)–(12) in Eqs. (2)–(4) and Eq. (7) and equating different powers of \(\epsilon\), the lowest order of \(\epsilon\) leads to

$$\begin{aligned} n_{d1}= & {} \frac{-{l_{z}}^2 \phi _1}{{V_0}^2}, \end{aligned}$$
(14)
$$\begin{aligned} w_1= & {} -\frac{l_z \phi _1}{V_0},\end{aligned}$$
(15)
$$\begin{aligned} V_0= & {} {\frac{l_z}{\sqrt{ \mu _e c_{e1} + \mu _i c_{i1} }}}. \end{aligned}$$
(16)

On the other hand, the lowest order of \(\epsilon\), x- and y-components of momentum equation is reduced to

$$\begin{aligned} u_1= -\frac{l_y}{\Omega _d}\frac{\partial \phi _1 }{\partial \xi }, \qquad v_1= \frac{l_x}{\Omega _d}\frac{\partial \phi _1}{\partial \xi }. \end{aligned}$$
(17)

Next higher order in \(\epsilon\) leads to the following set of evolution equations

$$\begin{aligned} \frac{\partial n_{d1}}{\partial \tau }-V_0 \frac{\partial n_{d2}}{\partial \xi }+\frac{\partial }{\partial \xi }(l_x u_2+l_y v_2 + l_z w_2+l_z n_{d1} w_1)=0, \end{aligned}$$
(18)
$$\begin{aligned} \frac{\partial w_1}{\partial \tau }-V_0 \frac{\partial w_2}{\partial \xi }+l_z w_1\frac{\partial w_1}{\partial \xi }= l_z \frac{\partial \phi _2}{\partial \xi }+ \eta _0 \frac{\partial ^2 w_1}{\partial \xi ^2}, \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial ^2 \phi _1}{\partial \xi ^2}= C_1 \phi _2+ C_2 \phi ^2 +n_{d2}, \end{aligned}$$
(20)
$$\begin{aligned} u_2=-\frac{V_0 l_x}{\Omega _d^2}\frac{\partial ^2 \phi _1}{\partial \xi ^2}, \end{aligned}$$
(21)
$$\begin{aligned} v_2=-\frac{V_0 l_y}{\Omega _d^2}\frac{\partial \phi _1}{\partial \xi ^2}. \end{aligned}$$
(22)

Using Eqs. (14)–(22) and eliminating the second-order perturbed quantities, we find the following KdV–Burgers equation

$$\begin{aligned} \frac{\partial \phi _1}{\partial \tau }+ A \phi _1 \frac{\partial \phi _1}{\partial \xi }+ B \frac{\partial ^3 \phi _1}{\partial \xi ^3}= C \frac{\partial ^2 \phi _1}{\partial \xi ^2}. \end{aligned}$$
(23)

Equation (23) describes the nonlinear evolution of obliquely propagating DA shock waves in a magnetized superthermal plasma where the nonlinear, dispersion and dissipation coefficients A, B and C are respectively given by

$$\begin{aligned} A=-\biggr (\frac{3 l_z^2}{2 V_0}+\frac{V_0^3 C_2}{l_z^2}\biggr ), \end{aligned}$$
(24)
$$\begin{aligned} B= \biggr (1+\frac{1-l_z^2}{\Omega _d^2}\biggr )\frac{V_0^3}{2 l_z^2}, \end{aligned}$$
(25)
$$\begin{aligned} C= \frac{\eta _0}{2}. \end{aligned}$$
(26)

It can be observed easily that the obliqueness (\(l_z\)) and superthermality of ions/electrons (\(\kappa _i/\kappa _e\)) influence the nonlinear coefficient A and dispersion coefficient B. However, dissipation coefficient C depends only on kinematic viscosity \(\eta _0\). The dispersion coefficient B is always positive and the nonlinear coefficient A remains negative for the given set of parameters. Thus, it is clear that only negative potential DA shocks are observed in the present study. If superthermality parameters \(\kappa _e,\kappa _i\rightarrow \infty\), we get the same results as that of [52] for \(\beta _e,\beta _i\rightarrow 0\) (i.e., the ions/electrons obey Maxwellian distribution).

Solution of KdV–Burgers equation

To find the shock-like solution of KdV–B equation (23), we will adopt a reference frame moving with the shock speed. The spatial \((\xi )\) and temporal \((\tau )\) coordinates are expressed as \(\zeta =\alpha (\xi -V\tau )\) and \(\tau =\tau\), here V is the shock speed and \(\alpha ^{-1}\) physically represents the shock width. The values of \(\alpha\) account for spatially extended shock profile and vice versa. With new variables, transformed Eq. (23) reads as

$$\begin{aligned} -V \frac{d\phi _1}{d \zeta }+ A \phi _{1} \frac{d \phi _1}{d\zeta } + B {\alpha ^2}\frac{d^3 \phi _{1}}{d\zeta ^3}={C}{\alpha }\frac{d^2\phi _{1}}{d\zeta ^2}. \end{aligned}$$
(27)

Integrating Eq. (27) once and using appropriate boundary conditions, \(\phi _1\rightarrow 0\), \(\frac{d \phi _1}{d \zeta }\rightarrow 0\) and \(\frac{d^2 \phi _1}{d \zeta ^2}\rightarrow 0\) for \(\zeta \rightarrow \infty\), we obtain

$$\begin{aligned} -V\phi _{1}+\frac{A}{2}(\phi _{1})^2+{B}{\alpha ^2}\frac{d^2 \phi _{1}}{d\zeta ^2}=C\alpha \frac{d\phi _{1}}{d\zeta }. \end{aligned}$$
(28)

Using hyperbolic tangent (tanh) method [57], we shall determine the analytical stationary solution of Eq. (23). Substituting \(\phi _1=U(Y)\), where, \(Y=Tanh(\zeta )\), and \(U(Y)=\Sigma _{n=0}^{\infty }a_n Y_n\), followed by balancing procedure, we get N = 2. Equating various powers of Y in Eq. (28), the shock solution of KdV–Burgers equation is determined as

$$\begin{aligned} \phi _{1}(\xi ,\tau )=\phi _{max}\biggr (1-\frac{1}{4} \biggr [1+\tanh \biggr (\frac{\xi -V\tau }{W}\biggr )\biggr ]^2\biggr ), \end{aligned}$$
(29)

where \(\phi _{max}=12 C^2/25 A B\) represents the shock amplitude, \(W (=\alpha ^{-1})=10 B/C\) is the shock width and \(V=6C^2/25B\) is the shock speed.

Parametric analysis of dust acoustic shock structures

As obvious from the KdV–B equation (23), the nonlinear, dispersion and dissipation coefficients are functions of superthermality parameter of ions (\(\kappa _{i}\)) and electrons (\(\kappa _e\)), strength of magnetic field (via \(\Omega _{d}\)), obliqueness (via \(l_{z}\)) and viscosity (via \(\eta _{0}\)). These parameters will effect the shock amplitude, width and velocity. Since the coefficient B is always positive, the nature of the shock structures depends upon the sign of the nonlinear coefficient (A). Positive sign of (\(A>0\)) supports positive potential shocks, while negative sign (\(A<0\)) corresponds to negative potential shocks. Figure 1 depicts the variation of nonlinear coefficient A with superthermality of ions (via \(\kappa _i\)) for different values of electron-to-dust density ratio (\(\mu _e\)) and obliqueness (\(l_z\)). It is seen that for all chosen set of parameters, the coefficient A is always negative, and thus, only negative potential shock waves are formed. However, the absolute value of nonlinear coefficient A increases with increase in superthermality of ions (decrease in \(\kappa _i\)) and for a particular value of superthermality parameter the nonlinearity increases with increase in electron-to-dust density ratio. It is also observed that small obliqueness increases the nonlinearity in the system. Hence, it is concluded that absolute value of nonlinear coefficient A is enhanced with increase in superthermality of ions, electron-to-dust-density ratio and decrease in obliqueness. It is noteworthy to mention here that even in the case of dust acoustic solitary waves in an unmagnetized plasma with kappa-distributed electrons and ions, only negative potential nonlinear structures were reported if the dust is negatively charged [58].

Fig. 1
figure 1

(color online) Variation of nonlinear Coefficient A with \(\kappa _i\) at different obliqueness (via \(l_z\)) and electron-to-dust-density ratio (via \(\mu _e\)). Solid curve is for \(\mu _e=0.2, \kappa _e=3.5, l_z=0.7,\sigma _i=0.01\). Dotted (Black) curve: \(l_z=0.8\), Dashed (Blue) curve: \(\mu _e=0.3\)

Full size image
Fig. 2
figure 2

(color online) Variation of velocity of shock waves with superthermality of ions at different values of magnetic field (via \(\Omega _d\)) and kinematic viscosity (via \(\eta _0\)). Solid curve is for \(\mu _e=0.2, \kappa _e=3.5, l_z=0.7,\sigma =0.01,\Omega _d=1,\eta _0=0.8\). Dotted (Black) curve: \(\eta _0=1\), Dashed (Blue) curve: \(\Omega _d=0.5\)

Full size image
Fig. 3
figure 3

(color online) 3D graph showing variation of width of shock structure with viscosity (via \(\eta _0\)) and superthermality of ions (via \(\kappa _i\)) for \(\mu _e=0.2, \kappa _e=3.5, l_z=0.7, \sigma =0.01, \Omega _d=1\)

Full size image
Fig. 4
figure 4

(color online) Shock wave profile at different values of superthermality of ions (via \(\kappa _i\)) with values \(\mu _e=0.2, \kappa _e=3.5, l_z=0.7, \sigma =0.01, \Omega _d=1, \eta _0=0.8\). Solid (Red) curve: \(\kappa _i=4\), Dotdashed (Blue) curve: \(\kappa _i=5\), Dashed (Green) curve: \(\kappa _i=6\), Dotted (Black) curve: \(\kappa _i=25\)

Full size image
Fig. 5
figure 5

(color online) Variation of 3D shock wave profile with superthermality of ions (via \(\kappa _i\)) for \(\mu _e=0.2, \kappa _e=3.5, l_z=0.7, \sigma =0.01, \omega _d=1, \eta _0=0.8\)

Full size image
Fig. 6
figure 6

(color online) Shock wave profile at different values of kinematic viscosity (via \(\eta _0\)) for \(\mu _e=0.2, \kappa _e=3.5, \kappa _i=4, l_z=0.7, \sigma =0.01, \Omega _d=1\). Solid (Red) curve: \(\eta _0=0.4\), Dotted (Black) curve: \(\eta _0=0.6\), Dashed (Blue) curve: \(\eta _0=0.8\), Dotdashed (Green) curve: \(\eta _0=1\)

Full size image
Fig. 7
figure 7

(color online) Shock wave profile at different value of obliqueness (via \(l_z\)), electron-to-dust-density ratio (via \(\mu _e\)) and magnetic field (via \(\Omega _d\)). Solid curve is \(\mu _e=0.2, \kappa _e=3.5, \kappa _i=4, l_z=0.7, \sigma =0.01, \Omega _d=0.5, \eta _0=0.8\). Dotted (Black) curve: \(\mu _e=0.4\), Dashed (Green) curve: \(l_z=0.8\), Dotdashed (Blue) curve: \(\Omega _d=0.6\)

Full size image
Fig. 8
figure 8

(color online) Variation of 3D Shock wave profile with magnetic field (via \(\Omega _d\)) for \(\mu _e=0.2, \kappa _e=3.5, \kappa _i=4, l_z=0.7, \sigma =0.01, \eta _0=0.8\)

Full size image

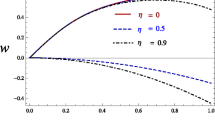
To study the effect of various physical parameters on the profile of DA shock structures, we have studied numerically the stationary solutions of KdV–Burgers equation. Since nonlinear, dissipation and dispersion coefficients are dependent on the various physical parameters, it is important to trace the influence of such parameters on the characteristics of dust acoustic shock waves through the variations in various coefficients. We have displayed the numerical results in Figs. 2–8 depicting the influence of physical parameters on the profile of DA shocks governed by KdV–Burgers equation. The effect of superthermality on the speed and width of shock structures is depicted in Figs. 2 and 3. Figure 2 illustrates the variation of velocity of shocks with superthermality of ions for different values of magnetic field and viscosity. It is clear that the speed of shock waves is enhanced with increase in superthermality of ions (i.e., decrease in value of \(\kappa _i\)), but it has opposite effect on the width of the shock waves, i.e., the width of shock structures decreases with increase in superthermality of ions (see Fig. 3). The combined effects of superthermality of ions and kinematic viscosity on the width of shock structures affirm that a less viscous fluid is more attuned to superthermality parameter and support narrower shocks for more superthermal ions. The variation of shock profile with superthermality of ions is displayed in Fig. 4. It is observed that more superthermal ions lead to higher amplitude shock structures. It has also been asserted by Malik [43] for the case of ion-acoustic solitons that the amplitude of nonlinear structures increases with increase in temperature of ions. Overall, the amplitude and velocity of shock waves are enhanced with increase in superthermality (i.e., decrease in \(\kappa _i\)) and it is very sensitive for low range of \(\kappa _i\). Thus, highly superthermal ions make the shocks taller, narrower and faster. This inference is further illustrated in 3D plot shown in Fig. 5, where more superthermal ions result in the formation of more abrupt shocks. Similar kind of variation of DA shock structures with superthermality of ions is observed in an unmagnetized electron-depleted dusty plasma environment containing two temperature superthermal ions [59].

Figure 6 presents the shock wave profile at different values of kinematic viscosity (via \(\eta _0\)). It is obvious from the graphs that higher values of kinematic viscosity support the shock structures with larger amplitude and smaller width. The results are in agreement as reported for the study of dust acoustic shock waves in a magnetized nonthermal dusty plasma [52]. The similar results are obtained for variation of magnetic field (via \(\Omega _d\)) and ratio of electron to dust concentration (via \(\mu _e\)), i.e., increase in \(\Omega _d\) and \(\mu _e\) makes the shocks more abrupt and faster as shown in Fig. 7 which are also consistent with the results reported by Shahmansouri and Mamun [52]. On the other hand, the decrease in obliqueness (increase in \(l_Z\)) results in shocks of smaller amplitude, whereas stronger is the magnetic field more spiky are the shock structures. This is due to the fact that the effect of magnetic field on shock structures is realized through dispersion coefficient B in KdV–Burgers equation. The value of dispersion coefficient decreases with increase in strength of magnetic field. Since the amplitude of shocks is inversely proportional to the dispersion coefficient, the shock structures become taller with increase in strength of magnetic field. The opposite effect is observed by Malik [43] on the propagation properties of ion-acoustic (IA) solitons in a magnetized plasma where it is observed that the strength of magnetic field reduces the amplitude of ion-acoustic solitons. On the other hand, since the width of shock structures is directly proportional to the dispersion coefficient, the increase in strength of magnetic field tends to decrease the width of shocks structures and makes them narrower. Similar kind of behavior was observed by Kumar et al. [44]. Figure 8 illustrates the variation of shock structures with magnetic field in 3D. It is seen that magnetic field has a great influence on the shocks so formed such that the vanishing of magnetic field may even lead to disappearance of shock structures governed by the solution of KdV–Burgers equation.

Conclusions

We have examined the dust acoustic shocks in magnetized dusty plasma with superthermal electrons and ions. By employing reductive perturbation technique, KdV–Burgers equation has been derived. The role of various plasma parameters (viz. superthermality of ions (via \(\kappa _i\)), electron-to-dust density ratio (via \(\mu _e\)), dust kinematic viscosity of medium (via \(\eta _0\)), strength of magnetic field (via \(\Omega _d\)) and obliqueness of magnetic field (via \(l_z\))) on the characteristics of DA shock structures has been highlighted in the present study. Only negative potential shock structures are observed. The amplitude of shock structures increases with increase in superthermality of ions, dust concentration and increase in strength of magnetic field. On the other hand, width of shock structures decreases with increase in superthermality of ions.

For Cairns distribution (nonthermal distribution) in the presence of magnetic field, both polarities DA shock structures were obtained by Shahmansouri and Mamun [52], but under the influence of superthermality of charged particles and magnetic field, only negative potential DA shock structures are observed.

The findings of this investigation should be useful for wider understanding of the formation of dust acoustic shock structures in solar wind, Earth’s magnetosphere, Earth’s polar cap region and Saturn’s rings where superthermal electrons/ions and dust particles are present along with an ambient magnetic field. These results may also be applicable in the laboratory experiments for laser–plasma interaction, where dust acoustic shocks may be observed in the presence of dust grains and superthermal particles.