Introduction

Very recently many authors have studied the nonlinear propagation of ion-acoustic (IA) solitary waves (SWs) [1–4] dust-ion-acoustic (DIA) SWs [5–9], dust-acoustic (DA) SWs [10–14] in a multi-ion plasmas, as negative ions can be found in space [15, 16] and laboratory [17–19] as well as positive ions. In multi-ion plasmas, there exist fast and slow mode. In fast mode, positive and negative ions oscillate out of phase (\(180^{\circ }\)) where as positive and negative ions oscillate in phase. In the case of low temperature plasmas, both in space (the Earth’s ionosphere, planetary rings, interstellar clouds, planetary atmospheres, interstellar media, protostellar disks, interstellar and circumstellar clouds, asteroid zones, cometary tails and nebula) and laboratory (plasma processing and plasma crystal) some micron or sub-micron sized dust particles might be present. Due to the size effect on secondary emission [20], the dust particles can have the opposite polarity. Larger particles are found to be negatively charged and smaller ones are positively charged [20]. These opposite polarity ions and opposite polarity dusts [10–14] can significantly modify the basic properties of linear and nonlinear DIA SWs and DA SWs. The anomalous dissipation in complex plasmas, which originates from the dust charging process, makes possible the existence of a new kind of shock wave [21–25]. When the dissipation is weak or absent at the characteristic dynamical time scales of the system, the balance between nonlinearity and dissipation is weak at the characteristic dynamical time scales of the system, the balance between nonlinearity and dissipation effects can result in the formation of a symmetrical SWs.

The non-thermal particle distributions turn out to be a characteristic feature in space plasmas, as in auroral zone [26]. The observation of non-thermal electrons made by the Swedish Viking satellite [27] and Freja satellite [28] have shown electrostatic solitary structures in the magnetosphere with density depression. This non-thermal electron populations might be distributed isotropically in velocities or possess a net streaming motion. Cairns et al. [29] considered the influence of non-thermal electrons on the existence conditions of ion-acoustic (IA) solitary structures. The presence of non-thermal electrons allows for the existence of both positive and negative density perturbations. The non-thermal electron distribution of Cairns et al. [29] is a more general class of the electron distribution including a population of fast or energetic electrons. The non-thermal electron \(n_e\) can be written as

$$\begin{aligned} n_e=\left[ 1-\frac{4\alpha }{1+3\alpha }\psi (1-\psi )\right] e^\psi , \end{aligned}$$
(1)

where \(\alpha\) is a parameter determining the fast particles present in this plasma model and \(\psi\) is the wave potential.

Sayed et al. [9] have studied dust-ion-acoustic (DIA) solitary structures in unmagnetized plasmas containing positive and negative ions with positive and negative dust and Maxwellian distributed electrons. This mode is only valid if a complete depletion of the background electrons and ions is possible, and both positive and negative dust fluids are cold. However, in real dusty plasma, the effect of finite ion temperature cannot be neglected and the electron behavior can be strongly modified by non-linear potential of the localized DIA structures by generating a population of fast energetic electrons [30]. Gill et al. [1] have studied double layered IA SWs containing positive and negative ions of two different temperatures and non-thermal electrons by deriving K-dV and mK-dV equations. Mannan et al. [3] have studied nonplanar (cylindrical and spherical) Gardner solitons and double layers (DLs) in an unmagnetized plasma composed of positive and negative ions, and non-thermal electrons. Mamun and Shukla [4] have studied the effects of the non-thermal distribution of electrons as well as the polarity of the net dust-charge number density on nonplanar DIA SWs. It is found from the different observations that most of the plasmas in reality are magnetized, and it can change its characteristics according to the wave direction.

Haider [5] studied the DIA SWs by deriving K-dV equation, associated with a plasma system containing opposite polarity ions, opposite polarity dusts and non-thermal electrons where restoring forces are provided by the plasma thermal pressure of electrons and the inertia is due to the ion mass. But the instability criterion and growth rate is steel unknown. To do this, Zakharov-Kuznetsov (ZK) equation has derived employing reductive perturbation method [31] and using its constant instability criterion and growth rate has been studied by small-k perturbation technique in a magnetized dusty plasma consisting of ions with opposite polarity (negatively andy positively charged), dusts with opposite polarity (negatively and positively charged) and non-thermal electrons following Cairn distribution [29]. The manuscript is organized as follows. The basic equations are given in Sect. 2. The Zakharov-Kuznetsov (ZK) equation in Sect. 3. The solitary-wave solution of the ZK equation is obtained in Sect. 4. Instability criterion with growth rate is in Sect. 5 and a brief discussion is finally given in Sect. 6.

Basic equations

The propagation of DIA SWs have been studied, in the present work, in a collisionless magnetized dusty plasma consist of

  1. (i)

    opposite polarity (negatively and positively charged) mobile ions,

  2. (ii)

    opposite polarity stationary dust, and

  3. (iii)

    non-thermal electrons.

It is also considered that there is an external static magnetic field \(\mathbf{B_0}\) acting along the z-direction (\(\mathbf{B_0}=\hat{k}{} { B_0}\)), where \(\hat{k}\) is the unit vector along the z-direction which is very strong that the electrons and dusts are moving along the magnetic field direction very fast, i.e. the response of electrons and dusts look like as that in the unmagnetized plasma. The nonlinear dynamics of the DIA SWs propagating in such a multi-component dusty plasma is governed by

$$\begin{aligned}&\frac{\partial n_s}{\partial t}+\nabla \cdot (n_s {\mathbf{u}} _s)=0\end{aligned}$$
(2)
$$\frac{\partial {\mathbf{u}}_n}{\partial t}+({\mathbf{u}}_n\cdot \nabla ){\mathbf{u}}_n=\nabla \phi -\omega _{cn} {\mathbf{u}}_n\times \hat{k}$$
(3)
$$\frac{\partial {\mathbf{u}}_p}{\partial t}+({\mathbf{u}}_p\cdot \nabla ){\mathbf{u}}_p=-\beta \nabla \phi +\beta \omega _{cn} {\mathbf{u}}_p\times \hat{k}$$
(4)
$$\begin{aligned}\bigtriangledown ^2\phi =\mu _0n_e+n_n-\mu _pn_p-j\mu _d \end{aligned}$$
(5)

where \(n_s\) (\(n_n\)/\(n_p\)) is the ion number density (negative/positive) normalized by its equilibrium value \(n_{s0}\), \(u_n\) (\(u_p\)) is the negative (positive) ion fluid speed normalized by \(C_n=(k_BT_e/m_n)^{1/2}\), with \(k_B\) is the Boltzmann constant, \(T_e\) is the temperature of electrons and \(m_n\) being the rest mass of negative ions. \(\phi\) is the DIA wave potential normalized by \(k_BT_e/e\), with e being the magnitude of the charge of an electron. \(\omega _{cn}\) is the negative ion cyclotron frequency \((eB_0/m_{nc})\) normalized by plasma frequency \(\omega _{pn}=(4\pi n_{n0}e^2/m_n)^{1/2}\) with c being the speed of light. The time variable (t) is normalized by \({\omega _{pn}}^{-1}\), the space variables are normalized by Debye radius \(\lambda _D=(k_BT_e/4 \pi n_{n0}e^2)^{1/2}\).

At equilibrium we have

$$\begin{aligned} n_{p0}+jn_{d0}=n_{e0}+n_{n0}\nonumber \end{aligned}$$

where, \(jn_{d0}=n_{d+}-n_{d-}\) with \(n_{d+}\) being the positive dust number density and \(n_{d-}\) being the number density of negative dust. \(j=1\) for the condition \(n_{d+}>n_{d-}\) and \(j=-1\) for the condition \(n_{d+}<n_{d-}\), i.e. the value of j dependents on net charge of dust grain and \(\beta\) is the mass ratio of negative ion to positive ion (\(m_n/m_p\)). We can also write

$$\begin{aligned} \mu _0=\mu _p+j\mu _d-1 \end{aligned}$$
(6)

where, \(\mu _0 = n_{e0}/n_{n0}\), \(\mu _p = n_{p0}/n_{n0}\) and \(\mu _d = n_{d0}/n_{n0}\).

Derivation of ZK equations

To derive a dynamical equation for the nonlinear propagation of the electrostatic waves in a dusty plasma, under consideration, have to employed in Eqs. (1–5). To do so, the following stretched coordinates [31–37] are introduced

$$\begin{aligned} \left. \begin{array}{l} X=\epsilon ^{1/2}x\\ Y=\epsilon ^{1/2}y\\ Z=\epsilon ^{1/2}({z-V_0t})\\ \tau =\epsilon ^{3/2}t\ \end{array} \right\} \end{aligned}$$
(7)

where \(\epsilon\) is a smallness parameter (\(0 < \epsilon < 1\)) measuring the weakness of the dispersion and \(V_0\) is the Mach number (the phase speed normalized by \(C_n\)). \(n_s\), \(u_s\) and \(\phi\) can be expanded about their equilibrium values in a power series of \(\epsilon\), viz.,

$$\begin{aligned} \left. \begin{array}{l} n_s=1+\epsilon n_s^{(1)}+\epsilon ^2n_s^{(2)}+ \cdot \cdot \cdot \\ u_{sx}=\epsilon ^{3/2} u_{sx}^{(1)}+\epsilon ^2u_{sx}^{(2)}+\cdot \cdot \cdot \\ u_{sy}=\epsilon ^{3/2} u_{sy}^{(1)}+\epsilon ^2u_{sy}^{(2)}+\cdot \cdot \cdot \\ u_{sz}=\epsilon u_{sz}^{(1)}+\epsilon ^2u_{sz}^{(2)}+\cdot \cdot \cdot \\ \phi =\epsilon \phi ^{(1)}+\epsilon ^{2}\phi ^{(2)}+\cdot \cdot \cdot \ \end{array} \right\} \end{aligned}$$
(8)

where s represents the species (n for negative ions and p for positive ions).

Using the stretched coordinates and Eq. (8) into Eqs. (2–5) and (1), one can develop equations in various powers of \(\epsilon\). To the lowest order of \(\epsilon\) is

$$\begin{aligned} \left. \begin{array}{l} u_{sx}^{(1)}=-\frac{1}{\omega _{cn}}\frac{\partial \phi ^{(1)}}{\partial Y},\quad u_{sy}^{(1)}=\frac{1}{\omega _{cn}}\frac{\partial \phi ^{(1)}}{\partial X}\\ u_{nz}^{(1)}=-\frac{1}{V_0}\phi ^{(1)}, \quad u_{pz}^{(1)}=\frac{\beta }{V_0}\phi ^{(1)}\\ n_n^{(1)}=-\frac{1 }{V_0^2}\phi ^{(1)},\quad n_p^{(1)}=\frac{1 }{V_0^2}\phi ^{(1)}\end{array} \right\} \end{aligned}$$
(9)

Equating the coefficients of \(\epsilon\) from Poissons equation, we get

$$\begin{aligned} 0=\mu _0\left[ \phi ^{(1)}-\frac{4\alpha }{1+3\alpha }\phi ^{(1)}\right] +n_n^{(1)}-\mu _pn_p^{(1)} \end{aligned}$$
(10)

Using the value of \(n_n^{(1)}\) and \(n_p^{(1)}\) from Eq. (9) into Eq. (10), we can get the linear dispersion relation

$$\begin{aligned}&V_0=\sqrt{\frac{(1+\beta \mu _p)(1+3\alpha )}{\mu _0 (1-\alpha )}} \end{aligned}$$
(11)

Again, following the same procedure, one can obtain the next higher order continuity equation and the z- component of momentum equation as

$$\begin{aligned}&\frac{\partial n_s^{(1)} }{\partial \tau }-V_0\frac{\partial n_s^{(2)} }{\partial Z }+\frac{\partial u_{sx}^{(2)}}{\partial X}+\frac{\partial u_{sy}^{(2)}}{\partial Y}+\frac{\partial u_{sz}^{(2)}}{\partial Z}\nonumber \\&\quad +\frac{\partial }{\partial Z}\left[ n_s^{(1)}u_{sz}^{(1)}\right] =0\end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial u_{nz}^{(1)} }{\partial \tau }-V_0\frac{\partial u_{nz}^{(2)}}{\partial Z }+u_{nz}^{(1)}\frac{\partial u_{nz}^{(1)}}{\partial Z }-\frac{\partial \phi ^{(2)}}{\partial Z}=0\end{aligned}$$
(13)
$$\begin{aligned}&\frac{\partial u_{pz}^{(1)} }{\partial \tau }-V_0\frac{\partial u_{pz}^{(2)}}{\partial Z }+u_{pz}^{(1)}\frac{\partial u_{pz}^{(1)}}{\partial Z }+\beta \frac{\partial \phi ^{(2)}}{\partial Z}=0 \end{aligned}$$
(14)

To the next higher order of \(\epsilon\), i.e., equating the coefficients of \(\epsilon ^2\), we can express \(x-\) and \(y-\)components of the momentum equations for both negative and positive ions, and Poisson’s equation as

$$\begin{aligned}&u_{nx}^{(2)}=-\frac{V_0}{\omega _{cn}^2}\frac{\partial ^2\phi ^{(1)}}{\partial Z\partial X}, \quad u_{ny}^{(2)}=-\frac{V_0}{\omega _{cn}^2}\frac{\partial ^2\phi ^{(1)}}{\partial Y\partial Z}\end{aligned}$$
(15)
$$\begin{aligned}&u_{px}^{(2)}=\frac{V_0}{\beta \omega _{cn}^2}\frac{\partial ^2\phi ^{(1)}}{\partial Z\partial X}, \quad u_{py}^{(2)}=\frac{V_0}{\beta \omega _{cn}^2}\frac{\partial ^2\phi ^{(1)}}{\partial Y\partial Z}\end{aligned}$$
(16)
$$\begin{aligned}&\left( \frac{\partial ^2}{\partial {X}^2}+\frac{\partial ^2}{\partial {Y}^2} +\frac{\partial ^2}{\partial {Z}^2}\right) \phi ^{(1)}-\mu _0\left( \frac{1-\alpha }{1+3\alpha }\right) \phi ^{(2)}\nonumber \\&\quad -\frac{\mu _0}{2}\left[ \phi ^{(1)}\right] ^2+\mu _pn_p^{(2)}-n_n^{(2)}=0 \end{aligned}$$
(17)

Now, using (9–17), we can readily obtain

$$\begin{aligned}&\frac{\partial \phi ^{(1)}}{\partial \tau }+A B\phi ^{(1)}\frac{\partial \phi ^{(1)}}{\partial Z}+\frac{1}{2}A\frac{\partial }{\partial Z}\left[ \frac{\partial ^2}{\partial Z^2} \right. \nonumber \\&\quad \left. +\,D\left( \frac{\partial ^2}{\partial X^2}+\frac{\partial ^2}{\partial Y^2}\right) \right] \phi ^{(1)}=0 \end{aligned}$$
(18)

where

$$\begin{aligned}&A=\frac{V_0}{\mu _0}\left( \frac{1+3\alpha }{1-\alpha }\right) \nonumber \\&B=\frac{3}{2}\frac{(\beta \mu _p-1)}{V_0^4}-\frac{\mu _0}{2}\\&D=1+\frac{1}{\omega _{cn}^2}\left(1+\frac{\mu _p}{\beta }\right)\nonumber \end{aligned}$$
(19)
Fig. 1
figure 1

Variation of of the phase velocity \(V_0\) of DIA SW with \(\mu _p\) and \(\mu _d\) for \(\alpha =0.1\), \(\beta =1\), \(j=1\) (lower surface) and \(j=-1\) (upper surface)

Full size image
Fig. 2
figure 2

Variation of the potential \(\phi _m\) of DIA SW with \(\delta\) for \(u_0=0.1\), \(\beta =1\), \(\mu _p=2\), \(\mu _d=0.2\), \(\alpha =0.1\) for \(j=1\) (solid curve) and \(j=-1\) (dotted curve)

Full size image
Fig. 3
figure 3

Variation of the potential \(\phi _m\) of DIA SW with \(\mu _p\) and \(\mu _d\) for \(u_0=0.1\), \(\delta =60^0\), \(\alpha =0.1\), \(\beta =1\) and \(j=1(-1)\) lower (upper) surface

Full size image
Fig. 4
figure 4

Variation of the width \(\Delta\) of DIA SW with \(\delta\) for \(u_0=0.1\), \(\alpha =0.1\), \(\beta =1\), \(\mu _p=2\), \(\mu _d=0.2\). The solid curve is for the value of \(j=1\) and dotted curve is for the value of \(j=-1\) with \(\omega_{cn} =0.1\) (red curve), \(\omega_{cn} =0.3\) (green curve), \(\omega_{cn} =0.5\) (blue curve)

Full size image
Fig. 5
figure 5

Variation of the width \(\Delta\) of DIA SW with \(\mu _p\) and \(\mu _d\) for \(u_0=0.1\), \(\delta =10^0\), \(\omega_{cn} =0.5\), \(\alpha =0.1\), \(\beta =1\), and \(j=1(-1)\) lower (upper) surface

Full size image

SW solution of the ZK equation

To study the properties of the solitary waves propagating in a direction making an angle \(\delta\) with the Z-axis, i.e., with the external magnetic field and lying in the (Z–X) plane, we first rotate the coordinate axes (X, Z) through an angle \(\delta\), keeping the Y-axis fixed. Thus, we transform our independent variables to

$$\begin{aligned} \left. \begin{array}{l} \rho =X\cos \delta -Z\sin \delta , \\ \xi =X\sin \delta +Z\cos \delta ,\\ \eta =Y. \end{array} \right\} \end{aligned}$$
(20)

This transformation of these independent variables allows us to write the ZK equation in the form

$$\begin{aligned}&\frac{\partial \phi ^{(1)}}{\partial t}+\delta _1{\phi ^{(1)}}\frac{\partial \phi ^{(1)}}{\partial \xi }+\delta _2\frac{\partial ^3\phi ^{(1)}}{\partial \xi ^3}+\delta _3{\phi ^{(1)}}\frac{\partial \phi ^{(1)}}{\partial \rho } \nonumber \\&\quad +\delta _4\frac{\partial ^3\phi ^{(1)}}{\partial \rho ^3}+\delta _5\frac{\partial ^3\phi ^{(1)}}{\partial \xi ^2\partial \rho }+\delta _6\frac{\partial ^3\phi ^{(1)}}{\partial \xi \partial \rho ^2} \nonumber \\&\quad +\delta _7\frac{\partial ^3\phi ^{(1)}}{\partial \xi \partial \eta ^2} +\delta _8\frac{\partial ^3\phi ^{(1)}}{\partial \rho \partial \eta ^2}=0 \end{aligned}$$
(21)

where

$$\begin{aligned}&\delta _1=A B\cos \delta \nonumber \\&\delta _2=\frac{1}{2}A(\cos ^3\delta +D\sin ^2\delta \cos \delta )\nonumber \\&\delta _3=-A B\sin \delta \nonumber \\&\delta _4=-\frac{1}{2}A(\sin ^3\delta +D\sin \delta \cos ^2\delta )\nonumber \\&\delta _5=A\left[ D\bigg (\sin \delta \cos ^2\delta -\frac{1}{2}\sin ^3\delta \bigg ) -\frac{3}{2}\sin \delta \cos ^2\delta \right] \\&\delta _6=-A\left[ D\bigg (\sin ^2\delta \cos \delta -\frac{1}{2}\cos ^3\delta \bigg ) -\frac{3}{2}\sin ^2\delta \cos \delta \right] \nonumber \\&\delta _7=\frac{1}{2}A D\cos \delta \nonumber \\&\delta _8=-\frac{1}{2}A D\sin \delta \nonumber \end{aligned}$$
(22)

We now look for a steady state solution of this ZK equation in the form

$$\begin{aligned} \phi ^{(1)}=\phi _0(Z) \end{aligned}$$
(23)

where

$$\begin{aligned} Z=\xi -u_0t\nonumber \end{aligned}$$

in which \(u_0\) is a constant speed normalized by the ion-acoustic speed \((C_i)\). Using this transformation we can write this ZK equation in steady state form as

$$\begin{aligned}&-u_0\frac{d\phi _0}{dZ}+\delta _1{\phi _0}\frac{d\phi _0}{dZ} +\delta _2\frac{d^3\phi _0}{dZ^3}=0 \end{aligned}$$
(24)

Now, using the appropriate boundary conditions, viz., \(\phi ^{(1)}\rightarrow 0\), \((d\phi ^{(1)}/dZ)\rightarrow 0\), \((d^2\phi ^{(1)}/dZ^2)\rightarrow 0\) as \(Z\rightarrow \pm \infty\), the SWs solution of this equation is given by

$$\begin{aligned} \phi _0(Z)=\phi _m\mathrm{sech}^2 (\kappa Z) \end{aligned}$$
(25)

where \(\phi _m=3u_0/\delta _1\) is the amplitude and \(\kappa =\sqrt{u_0/4\delta _2}\) is the inverse of the width of the solitary waves. As \(u_0>0\), it is clear from (11), (19), and (22) that depending on the sign of B, the solitary waves will be associated with either positive potential \((\phi _m>0)\) or negative potential \((\phi _m<0)\). Therefore, there exists solitary waves associated with positive (negative) potential when \(B > 0\) \((B<0)\). Figure 1 represents the variation of the phase speed \(V_0\) of DIA SWs with \(\mu _p\) and \(\mu _d\) for positive as well as negatively charged stationary dust particles. This figure indicates that the phase speed is larger for negatively charged dust (upper surface) than for positively charged dust (lower surface). It is also found from this figure that the phase speed decreases with increasing the number density of both positive ions and dust particles in our present dusty plasma system. Figures 2,3 represent the variations of the potential \(\phi _m\) of DIA SWs with various parameters. From Fig. 2, it has been found that the SWs associated with negative potential only for propagation angle (\(\delta \rightarrow 0^\circ\)–\(90^\circ\)) and it associated with positive potential for the propagation angle (\(\delta \rightarrow 90^\circ\)–\(180^\circ\)). That means below the propagation angle \(90^\circ\) the solitary wave structure associates with dip shape and above this value the solitary wave structure associates with hump shape. Figure 3 indicates that the potential of the SW decreases with increasing the number density of both positive ions and dust particles but the potential is larger for negatively charged dust (upper surface) than for positively charged dust particles. Figures 4 and 5 show the variation of the width of SWs with propagation angle \(\delta\), \(\mu _p\) and \(\mu _d\) respectively. From Fig. 4, it has been found that for lower limit of the angle \((0^\circ\)–\(50^\circ )\) the width increases with it and decreases for higher limits of the angle \((50^\circ\)–\(90^\circ )\) for both positively and negatively charged dust particles. It is also clear from this figure that the external magnetic field leads to a decrease in the potential width, i.e., a stronger magnetic field leads to steeper and thus narrower soliton profiles. Similar observations are found in the work of Haider [5] and the work of Sabetkar and Dorranian [11, 12, 14] while studying the DIA and DA SWs with the presence of magnetic field. The width of the SWs is lower for positive dust grains than for negative dust grains, thus the positive dust grains makes the soliton profile more steeper. Figure 5 shows how the width changes with \(\mu _p\) and \(\mu _d\) and this figure indicate that the width decreases with increasing the value of both the number density of positive ions and dust particles as found in the work of Haider [5]. From the above analysis we have seen that the magnetic field has an effect only on the width of the SW but it has no effect on the amplitude of the waves.

Instability analysis

We now study the instability of the obliquely propagating SWs, discussed in the previous section, by the method of small-k perturbation expansion technique [33–38]. We first assume that

$$\begin{aligned}&\phi ^{(1)} (\mathcal{Z}, \zeta , \eta , \tau )=\phi _0(\mathcal{Z})+\psi (\mathcal{Z}, \zeta , \eta , \tau ) \end{aligned}$$
(26)

where \(\phi _0(\mathcal{Z})\) is defined by (25), and for a long-wavelength plane wave perturbation in a direction with direction cosines \((l_\zeta , l_\eta , l_\xi )\), \(\psi (\mathcal{Z}, \zeta , \eta , \tau )\) is given by

$$\begin{aligned}&\psi (\mathcal{Z}, \zeta , \eta , \tau )=\varphi (\mathcal{Z})e^{-i\omega \tau +ik(l_\zeta \zeta +l_\eta \eta +l_\xi \mathcal{Z})} \end{aligned}$$
(27)

in which \(l_\zeta ^2+l_\eta ^2+l_\xi ^2=1\), and for small k, \(\varphi (\mathcal{Z})\) and \(\omega\) can be expanded as

$$\begin{aligned}&\varphi (\mathcal{Z})=\varphi _0(\mathcal{Z})+k\varphi _1(\mathcal{Z})+k^2\varphi _2(\mathcal{Z})+\cdot \cdot \cdot \end{aligned}$$
(28)
$$\begin{aligned}&\omega =k\omega _1+k^2\omega _2+\cdot \cdot \cdot \end{aligned}$$
(29)

Now, substituting (26) into (21), and linearizing with respect to \(\psi\), we can express the linearized ZK equation in the form

$$\begin{aligned}&\frac{\partial \psi }{\partial \tau }-u_0\frac{\partial \psi }{\partial \mathcal{Z}}+\delta _1\phi _0\frac{\partial \psi }{\partial \mathcal{Z}}+\delta _1\psi \frac{\partial \phi _0}{\partial \mathcal{Z}} +\delta _2\frac{\partial ^3\psi }{\partial \mathcal{Z}^3}\nonumber \\&\quad +\delta _3\phi _0\frac{\partial \psi }{\partial \zeta } +\delta _4\frac{\partial ^3\psi }{\partial \zeta ^3} +\delta _5\frac{\partial ^3\psi }{\partial \mathcal{Z}^2\partial \zeta }+\delta _6\frac{\partial ^3\psi }{\partial \mathcal{Z}\partial \zeta ^2}\nonumber \\&\quad +\delta _7\frac{\partial ^3\psi }{\partial \mathcal{Z}\partial \eta ^2} +\delta _8\frac{\partial ^3\psi }{\partial \zeta \partial \eta ^2}=0 \end{aligned}$$
(30)

Our main objective is to find \(\omega _1\) by solving the zeroth-, first-, and second-order equations obtained from (27–30). zeroth-order equation can be written, after integration, as

$$\begin{aligned}&[-u_0+\delta _1\phi _0]\varphi _0(\mathcal{Z})+\delta _2\frac{d^2\varphi _0(\mathcal{Z})}{d\mathcal{Z}^2}=C \end{aligned}$$
(31)

where C is an integration constant. It is clear from (24) that the homogeneous part of this equation has two linearly independent solutions, namely

$$\begin{aligned}&f=\frac{d\phi _0}{d Z},\end{aligned}$$
(32)
$$\begin{aligned}&g=f\int ^Z\frac{d Z}{f^2}. \end{aligned}$$
(33)

Therefore, the general solution of this zeroth-order equation can be written as

$$\begin{aligned}&\varphi _0=C_1f+C_2g-Cf\int ^\mathcal{Z}\frac{g}{\delta _2}d \mathcal{Z} +Cg\int ^\mathcal{Z}\frac{f}{\delta _2}d \mathcal{Z} \end{aligned}$$
(34)

where \(C_1\) and \(C_2\) are two integration constants, and \(\delta _2\) is defined in (22). Now, evaluating all integrals, the general solution of this zeroth-order equation, for \(\varphi _0\) not tending to \(\pm \infty\) as \(\mathcal{Z}\rightarrow \pm \infty\), can finally be simplified to

$$\begin{aligned} \varphi _0(\mathcal{Z})=C_1 f \end{aligned}$$
(35)

The first-order equation, i.e.,, the equation with terms linear in k, obtained from (27–30) and (35), can be expressed, after integration, as

$$\begin{aligned}&[-u_0+\delta _1\phi _0]\varphi _1(\mathcal{Z})+\delta _2\frac{d^2\varphi _1(\mathcal{Z})}{d\mathcal{Z}^2}\nonumber \\&\quad =iC_1(\alpha _1 +\beta _1\tanh ^2\kappa \mathcal{Z})\phi _0+K \end{aligned}$$
(36)

where K is another integration constant, and \(\alpha _1\) and \(\beta _1\) are given by

$$\begin{aligned}&\alpha _1=(\omega _1+l_\xi u_0) -\frac{1}{2}\phi _m\mu _1+2\kappa ^2\mu _2\nonumber \\&\beta _1=\frac{1}{2}\phi _m\mu _1-6\kappa ^2\mu _2\\&\mu _1=\delta _1l_\xi +\delta _3l_\zeta, \quad \mu _2=3\delta _2l_\xi +\delta _5l_\zeta \nonumber \end{aligned}$$
(37)
Fig. 6
figure 6

Plot of \(S_i=0\) surface plot (i.e., variation of \(\omega _{cn}\) with \(l_\xi\) and \(l_\eta\) for \(\beta =1\), \(\mu _p=1\) and \(\delta =10^0\)) above which the solitary waves become unstable and below which the SWs become stable

Full size image
Fig. 7
figure 7

Showing the variation of growth rate \(\Gamma\) with \(\delta\) and \(\omega _{cn}\) for \(u_0=0.1\), \(\mu _p =1\), \(l_\xi =0.5\), \(\beta =1\) and \(l_\eta =0.5\)

Full size image
Fig. 8
figure 8

Showing the variation of growth rate \(\Gamma\) with \(l_\eta\) and \(l_\xi\) for \(u_0=0.1\), \(\mu _p =1\), \(\delta =10^0\), \(\beta =1\) and \(\omega _{cn}=0.5\)

Full size image

Now, following the same procedure, the general solution of this first-order equation, for \(\varphi _1(\mathcal{Z})\) not tending to \(\pm \infty\) as \(\mathcal{Z}\rightarrow \pm \infty\), can be written as

$$\begin{aligned}&\varphi _1(\mathcal{Z})=K_1f+\frac{iC_1}{8\delta _2\kappa ^2}\left[ \alpha \mathcal{Z}+\frac{2}{3}(3\alpha _1+\beta _1)\phi _0\right] \end{aligned}$$
(38)

Where \(\alpha =\alpha _1+\beta _1\). The second-order equation, i.e., the equation with terms involving \(k^2\) obtained from (30) after substituting (27–29), can be written as

$$\begin{aligned}&\left[ -u_0\frac{d}{d\mathcal{Z}}+\delta _1\frac{d}{d\mathcal{Z}}\psi _0 +\delta _2\frac{d^3}{d\mathcal{Z}^3}\right] \varphi _2(\mathcal{Z})= i\omega _2\varphi _0(\mathcal{Z})\nonumber \\&\quad +i[\omega _1+l_\xi u_0]\varphi _1(\mathcal{Z})-i\mu _1\psi _0\varphi _1(\mathcal{Z}) \nonumber \\&\quad +\mu _3\frac{d\varphi _0(\mathcal{Z})}{d\mathcal{Z}} -i\mu _2\frac{d^2\varphi _1(\mathcal{Z})}{d\mathcal{Z}^2} \end{aligned}$$
(39)

where

$$\begin{aligned}&\mu _3=3\delta _2l_\xi ^2+2\delta _5l_\zeta l_\xi +\delta _6l_\zeta ^2+\delta _7 l_\eta ^2 \end{aligned}$$
(40)

The solution of this second-order equation exists if the right-hand side is orthogonal to a kernel of the operator adjoint to the operator

$$\begin{aligned}&-u_0\frac{d}{d\mathcal{Z}}+\delta _1\frac{d}{d\mathcal{Z}} \phi _0+\delta _2\frac{d^3}{d\mathcal{Z}^3} \end{aligned}$$
(41)

This kernel, which must tend to zero as \(\mathcal{Z}\rightarrow \pm \infty\), is \(\phi _0=\phi _m\mathrm{sech}^2(\kappa \mathcal{Z})\). Thus, we can write the following equation determining \(\omega _1\):

$$\begin{aligned}&\int ^\infty _{-\infty }\phi _0\bigg[i\omega _2\varphi _0(\mathcal{Z})+i[\omega _1+l_\xi u_0]\varphi _1(\mathcal{Z})-i\mu _1\phi _0\varphi _1(\mathcal{Z})\nonumber \\&\quad +\mu _3\frac{d\varphi _0(\mathcal{Z})}{d\mathcal{Z}} -i\mu _2\frac{d^2\varphi _1(\mathcal{Z})}{d\mathcal{Z}^2}\bigg]d\mathcal{Z}=0 \end{aligned}$$
(42)

Now, substituting the expressions for \(\varphi _0(\mathcal{Z})\) and \(\varphi _1(\mathcal{Z})\) given by (35) and (38), respectively, and then performing the integration, we arrive at the following dispersion relation:

$$\begin{aligned} \omega _1=\Omega -l_\xi U_0+(\Omega ^2-\Upsilon )^{1/2} \end{aligned}$$
(43)

this equation is valid only for first order approximation, i.e., \(\omega =k\omega _1\), where

$$\begin{aligned} \Omega =\frac{2}{3}(\phi _m\mu _1-2\mu _2\kappa ^2) \end{aligned}$$
(44)
$$\begin{aligned} \Upsilon =\frac{16}{45}(\phi _m^2\mu _1^2-3\phi _m\mu _1\mu _2\kappa ^2 -3\mu _2^2\kappa ^4+12\delta _2\mu _3\kappa ^4) \end{aligned}$$
(45)

It is clear from the dispersion relation (43) that there is always instability if \((\Upsilon -\Omega ^2)>0\). Thus, using (19), (22), (37), (40), (44), and (45), we can express the instability criterion as

$$\begin{aligned} S_i>0 \end{aligned}$$
(46)

with

$$\begin{aligned}&S_i=l_\eta ^2\left[ \omega _{cn}^2+Y \sin ^2\delta \right] +l_\zeta ^2\left[ \omega _{cn}^2-\frac{5}{3}(\omega _{cn}^2+Y)\tan ^2\delta \right] \end{aligned}$$
(47)
$$\begin{aligned}&Y=1+\frac{\mu _p}{\beta } \end{aligned}$$
(48)

We have graphically obtained the parametric regimes (values of \(\delta\), \(\omega _{cn}\), \(\mu _p\), \(l_\zeta\), and \(l_\eta\)) for which the SWs become stable and unstable. This is shown in Fig. 6, which indicates that for the parameters above (below) the surface the SWs become unstable (stable). This figure represents \(S_i =0\) surface plot showing the variation of \(\omega _{cn}\) with \(l_\eta\) and \(l_\zeta\) for \(\mu _p=1\), \(\beta =1\) and \(\delta =10^\circ\). This figure shows that the values of \(\omega _{cn}\) increases with increasing the values of \(l_\zeta\) and it decreases with increasing the values of \(l_\eta\).

If this instability criterion \(S_i>0\) is satisfied, the growth rate \(\Gamma =(\Upsilon -\Omega ^2)^{1/2}\) of the unstable perturbation of these SWs is given by

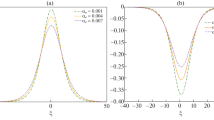
$$\begin{aligned}&\Gamma =\frac{2}{\sqrt{15}}\frac{u_0\sqrt{(\omega _{cn}^2+Y)S_i}}{\omega _{cn}^2+Y\sin ^2\delta } \end{aligned}$$
(49)

The Eq. (49) represents that the growth rate \((\Gamma )\) of the unstable perturbation is a linear function of IA wave speed \(u_0\), but a nonlinear function of propagating angle \((\delta )\), negative ion-cyclotron frequency \((\omega _{cn})\), the ratio of equilibrium positive ion density to negative number density \(\mu _p\), the mass ratio of negative ion to positive ion \(\beta\) and direction cosines (\(l_\zeta\), and \(l_\eta\)). To study instability/stability and growth rate of SWs after ZK equation, some perturbation techniques (ordinary, multi-scale about \(k=0\) and \(k^2=5\), small-k for \(k\ll \cos \alpha\) and \(k>\cos \alpha\)) discussed in the work of Allen and Rowlands [39, 40] based on different cases. Using these techniques Williams and Kourakis [41] studied stability analysis with growth rate of solitary structures. The instability analysis using small-k perturbation technique and process of obtaining growth rate in present form is very suitable to understand, because it express instability criterion and growth rate in terms of basic plasma parameters like ratio of number density, cyclotron frequency, direction cosine etc. which are used to describe the concern plasma situation. Many authentic authors have studied instability criterion as well as growth rate using this perturbation technique [36–38, 42] as it is a well established technique. The nonlinear variations of \(\Gamma\) with \(\delta\), \(\omega _{cn}\), \(l_\eta\), and \(l_\zeta\) are shown in Figs. 7 and 8. Figure 7 shows how \(\Gamma\) changes with \(\delta\) and \(\omega _{cn}\) for \(u_0=0.1\), \(l_\eta =0.5\), \(l_\zeta =0.5\) and \(\mu _p=2\), and Fig. 8 shows the variation of \(\Gamma\) with \(l_\eta\) and \(l_\zeta\) for \(u_0=0.2\), \(\delta =10^\circ\), \(\omega _{cn}=0.3\) and \(\mu _p=0.1\). These figures represent that the growth rate \((\Gamma )\) of the unstable perturbation changes proportionally with direction cosine (\(l_\eta\), \(l_\zeta\)) but inversely with \(\delta\) and \(\omega _{ci}\).

Results and discussions

Here a magnetized dusty plasma system consisting of non-thermal electrons, cold mobile positive as well as negative ions, and opposite polarity stationary dust has been considered. The ZK equation by using the reductive perturbation method has been derived. Then their multi-dimensional instability by the small-k perturbation expansion technique have analyzed. The results, which have been found in this investigation may be pointed out as follows:

  1. (1)

    The effects of non-thermal negative ions have been found to modify the nature of the DIA SWs structures in a dusty plasma.

  2. (2)

    The nonlinear DIA solitary wave structure associated with positive as well as negative potential depending on constant coefficient A and B.

  3. (3)

    The phase velocity of the SWs becomes slower with increasing the values of positive ions and with dust grains. On the other hand phase velocity of the SWs becomes faster with increasing the values of both \(\alpha\) and \(\beta\). But the magnitude of phase velocity is larger for negative dust grains than for positive dust grains.

  4. (4)

    The magnitude of the external magnetic field \(B_0\) has no effect on the solitary wave amplitude. However, it has a direct effect on the width of the SWs, and it is found that the width of the waves decreases as the magnitude of magnetic field \(B_0\) increases, i.e. the magnetic field makes the solitary structures more spiky.

  5. (5)

    The width of the SWs increase for the lower range of \(\delta\), i.e., from \(0^\circ\) to about \(50^\circ\), but decrease for its higher range, i.e., from about \(50^\circ\) to \(90^\circ\). As \(\delta \rightarrow 90^\circ\), the width goes to 0 and the amplitude goes to \(\infty\). It is likely that for large angles the assumption that the waves are electrostatic is no longer valid, and one should look for fully electromagnetic structures.

  6. (6)

    It has found that the values of \(\alpha\) has no other effect whether the SWs are stable or unstable. However, stability strongly depend on the external magnetic field and the propagation directions of both the nonlinear wave and its perturbation mode.

  7. (7)

    It has been found that the value of \(\omega _{cn}\) for which the SWs become unstable increases with increasing the values of \(\alpha\) and \(\mu _p\). On the other hand it decreases with both of \(l_\zeta\) and \(l_\eta\).

  8. (8)

    The growth rate \(\Gamma\) of the unstable perturbation decreases with increasing the value of \(\delta\) and \(\omega _{cn}\) and it increases with both of \(l_\zeta\) and \(l_\eta\) which is shown in Figs. 7 and 8, respectively.

However, our theory is valid for small but finite amplitude solitary waves long wavelength perturbations, but not for large amplitude solitary waves and short wavelength perturbation modes. We, therefore, propose a more exact theory for stability analysis of arbitrary amplitude SWs and arbitrary wavelength perturbation modes, through a generalization of this work. The results which we obtained may be useful for understanding the localized electrostatic disturbances in some space (viz. auroral plasma, Saturns E- and F-rings, etc.) [42–45] and laboratory [45–47] dusty plasmas.