Introduction

Understanding sheath formation between plasma and an absorbing wall or electrode is necessary for many plasma devices as well as plasma processing. The transition layer between plasma and conducting wall can be separated into two sub regions as presheath and sheath. The presheath which is close to the plasma core determines the ion flux and the sheath determines the energy of the ions. In ion sources and for extracted ions from the core of ion source, it is important to predict the kinetic energy and the current of the ions through plasma. The formation of a sheath adjacent to the surrounding wall of the plasma is necessary if the wall is at a different potential from the quasi-neutral plasma. The potential of plasma surrounding wall is negative with respect to the plasma potential and therefore, the number of negative and positive species in the sheath region is different and consequently a space charge forms. Indeed, the positive space charge is responsible to maintain the plasma potential. Understanding the space charge formation and its mechanism is necessary for plasma surface interaction as well as plasma diagnostics such as of Langmuir probe [1–7].

In the sheath region, which is in contact to the wall, because of the absence of the ionizing collisions, the positive ion flux velocity remains constant. In the presheath region which is located between sheath and center of discharge, there are inelastic collisions such as ionizing collisions which leads to flux of the ions and increases toward the wall. The size of the sheath is very small in comparison with the presheath and the typical extension of the sheath is given by electron Debye length \( \lambda_{\text{D}} \). Therefore, in the sheath region, the inelastic collisions can be ignored. In other word, for the asymptotic case \( \frac{{\lambda_{\text{D}} }}{L} \to 0 \), the ionizing collisions can be ignored where \( L \) is the plasma dimension which is usually in the order of ionizing length ([2] and references therein). However, the presence of elastic collisions between the accelerated ions and the neutral atom in the background sheath region can significantly influence the plasma-sheath characteristics. The collision frequency depends on the working pressure and degree of ionization of the plasma. Many papers have investigated the sheath and presheath regions in the presence of such collisions [8–11].

In addition, in most cases of interest such as plasma fusion device or plasma spray, the temperature of positive ions reaching the electrode cannot be ignored and its temperature should be included in the governing equations. The Refs. [12–15] consider the transition layer by including the ion temperature and obtaining the space charge characteristics in the sheath-presheath region.

Furthermore, the presence of the negative ions results some new features in plasma-sheath characteristics. The negative ions in plasmas have the positive effect of improving the performance of dry etching. An example is the cancelation of positive charge accumulated on the wafer. It is known that the accumulation of positive charge can induce serious damage and abnormal etching shapes [15–18]. Moreover, the sheath formation near the negatively biased surface of electrode that interfaces an insulator can act as lens, which focuses the ions to distinct location on the electrode surface [19, 20].

In our previous study, we focused on the influence of the positive ion collisions on the electronegative plasma sheath in the presence of cold positive ions [21]. For many plasma applications in industries and laboratories, the temperature of the positive ion cannot be ignored and the temperature of negative and positive ions is comparable. Therefore, we have to consider the temperature of the positive ion. Here, we concentrate on the collisional space-charge sheath in the presence of negative ion by including the temperature of the positive ions. Moreover, the net current passing through the sheath and positive ion kinetic energy in different conditions are obtained and the influences of the negative ion as well as the positive ion temperature on the sheath characteristic are investigated. The outline of the paper is as follows. In Sect. 2, a plasma-sheath model is introduced using the fluid equations for positive ions and Boltzmann distribution for negative species and the initial boundary conditions are introduced. The results of the model are presented in two subsections of Sect. 3 for collisionless and collisional cases. The conclusion remarks are given in Sect. 4.

The sheath model

In our model, because of high mobility, electrons are assumed to be thermalized and obey the Boltzmann distribution. In addition, it is assumed that the negative ions are isothermal. Therefore, the distribution of electrons and negative ions can be written as

$$ n_{\text{e}} = n_{{{\text{e}}0}} \exp \left( {\frac{e\phi }{{T_{\text{e}} }}} \right) $$
(1)
$$ n_{ - } = n_{ - 0} \exp \left( {\frac{e\phi }{{T_{ - } }}} \right) $$
(2)

where, \( \phi \) is the electrostatic potential, \( T_{\text{e}} \) and \( T_{ - } \) are the electron and negative ion temperatures and \( n_{{{\text{e}}0}} \,,\,n_{ - 0} ,n_{{{\text{i}}0}} \) being the electron, negative ion and positive ion densities, at the beginning of the sheath.

In writing the above equations we assume that each negative ion has one electron charge. The quasi-neutrality condition in the electronegative discharge at the sheath edge expresses that

$$ n_{{{\text{i}}0}} - n_{ - 0} - n_{{{\text{e}}0}} = 0\,\,\,\,\,\, $$
(3)

where the \( n_{{{\text{i}}0}} \) is positive ion density at the sheath edge.

To treat the cold positive ions, the continuity and momentum transfer equations are employed.

$$ \nabla \cdot \left( {n_{\text{i}} V_{\text{i}} } \right)\, = \,0 $$
(4)
$$ m_{\text{i}} n_{\text{i}} (V_{\text{i}} \cdot \nabla )V_{\text{i}} \, = \, - en_{\text{i}} \nabla \phi - \nabla P_{\text{i}} \, - \,m_{\text{i}} n_{\text{i}} \nu \,V_{\text{i}} . $$
(5)

where the hypothesis of a constant positive ion flux in the sheath region has been employed in Eq. (4). Here \( m_{\text{i}} \) and \( V_{\text{i}} \) are the mass and flow velocity of positive ions,\( \nu \) is the positive ion-neutral collision frequency, \( n_{\text{i}} \) is the positive ion density and \( P_{\text{i}} \) is the positive ion pressure. To close the set of fluid equations, one should introduce a state equation. In the current study we assume that \( P_{\text{i}} = n_{\text{i}} kT \), where \( T \) is the positive ion temperature and \( k \) is the Boltzmann constant.

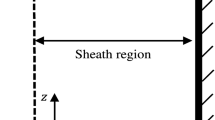
In our model, a slab geometry is considered along with the assumption that all parameters depend on coordinate \( z \), directed from the sheath edge at \( z\, = \,0 \), towards the wall and the \( z\, \) axis is normal to the wall. Thus, the continuity and momentum transfer equations can be written as

$$ n_{\text{i}} V_{{{\text{i}}z}} = n_{{{\text{i}}0}} V_{{{\text{i}}z0}} $$
(6)
$$ m_{\text{i}} V_{{{\text{i}}z}} \frac{{{\text{d}}V_{{{\text{i}}z}} }}{{{\text{d}}z}} = - e\frac{{{\text{d}}\phi }}{{{\text{d}}z}} - \frac{1}{{n_{\text{i}} }}\frac{{{\text{d}}P_{\text{i}} }}{{{\text{d}}z}}\, - \,m_{\text{i}} \nu \,V_{{{\text{i}}z}} $$
(7)

And the Poisson’s equation becomes

$$ \frac{{{\text{d}}^{2} \phi }}{{{\text{d}}z^{2} }}\, = \, - \frac{e}{{\varepsilon_{0} }}(n_{\text{i}} - n_{\text{e}} - n_{ - } ) $$
(8)

where \( \varepsilon_{0} \) is vacuum permittivity. It is useful to normalize the quantities used in this model by the following dimensionless parameters.

$$ \begin{aligned} \,\delta_{ - } = \frac{{n_{ - 0} }}{{n_{{{\text{i}}0}} }};\quad \eta \, = \, - \frac{e\phi }{{T_{\text{e}} }};\quad \,\gamma = \frac{{T_{\text{e}} }}{{T_{ - } }};\quad \xi = \frac{z}{{\lambda_{\text{De}} }}\,;\quad \lambda_{\text{De}} = \sqrt {\frac{{\varepsilon_{0} T_{\text{e}} }}{{n_{{{\text{e}}0}} e^{2} }}} ;\,\, \hfill \\ N_{\text{i}} = \,\frac{{n{}_{\text{i}}}}{{n_{{{\text{i}}0}} }};\quad N_{\text{e}} \, = \,\frac{{n_{\text{e}} }}{{n_{{{\text{e}}0}} }};\quad N_{ - } = \frac{{n_{ - } }}{{n_{ - 0} }};\quad u = \frac{V}{c};\quad M = \frac{{V_{{{\text{i}}z0}} }}{c};\,\quad c = \sqrt {\frac{{T_{\text{e}} }}{{m_{\text{i}} }}} ;\,\quad \alpha \, = \,\lambda_{\text{De}} \frac{\nu }{c} \hfill \\ \end{aligned} $$

where we have scaled \( z \) to Debye length, which is appropriate for the sheath region.

Including the Poisson’s equation, a closed set of coupled differential equations is obtained, which describes the sheath structure. Vanishing the right hand side of Eq. (8) implies a presheath solution, not considered here.

$$ N_{\text{e}} = \exp ( - \eta ) $$
(9)
$$ N_{ - } \, = \,\exp ( - \gamma \eta ) $$
(10)
$$ N_{\text{i}} u_{z} = M $$
(11)
$$ u_{z} \frac{{{\text{d}}u_{z} }}{{{\text{d}}\xi }} = \,\,\frac{{{\text{d}}\eta }}{{{\text{d}}\xi }} - \,\,\alpha \,u_{z} - \frac{T}{{N_{i} }}\frac{{{\text{d}}N_{i} }}{{{\text{d}}\xi }} $$
(12)

The above equation can be written as

$$ \frac{{{\text{d}}u_{z} }}{{{\text{d}}\xi }} = \frac{{u_{z} }}{{u_{z}^{2} - T}}\,\,\left( {\frac{{{\text{d}}\eta }}{{{\text{d}}\xi }}\, - \,\alpha \,u_{z} } \right) $$
(13)

Finally, the poison’s equation becomes

$$ \frac{{{\text{d}}^{2} \eta }}{{{\text{d}}\xi^{2} }} = \frac{{\left( {\frac{M}{{u_{z} }} - \delta_{ - } \exp ( - \gamma \eta ) - (1 - \delta_{ - } )\exp ( - \eta )} \right)}}{{\left( {1 - \delta_{ - } } \right)}} $$
(14)

According to the Ref. [22], by the Sagdeev potential and some algebra it can be shown that the ion velocity should satisfy the below inequality to enter the sheath

$$ M \ge \left[ {\sqrt {\frac{{\eta_{0}^{'} + T(1 - \delta (1 - \gamma ))\eta_{0}^{'} }}{{(1 - \delta (1 - \gamma ))\eta_{0}^{'} }} + \frac{{\alpha^{2} }}{{4\left[ {1 - \delta (1 - \gamma )} \right]^{2} \eta_{0}^{'2} }}} - \frac{\alpha }{{2\eta_{0}^{'} [1 - \delta (1 - \gamma )]}}} \right] $$
(15)

The inequality 15, states that the required flux velocity of positive ions at the sheath edge strongly depends on the number of negative ions and their temperature. For \( \gamma = 1 \), in which the two negative species are indistinguishable, we have the usual Bohm criterion. We have chosen the minimum value of the Eq. (15) for initial boundary condition of the ion velocity.

In the next section we attempt to solve the foregoing sets of equations according to the boundary conditions and acquire numerical results, considering the generalized Bohm criterion.

Results and discussion

Numerical solution in the collisionless case

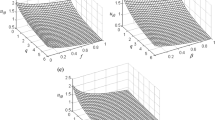
The examples of the calculated space-charge in a pure electropositive plasma in the sheath region are shown in Fig. 1 where \( \xi = 0 \) coincides with plasma-sheath interface.

Fig. 1
figure 1

The space-charge profile in the absence of collisions and negative ions for three values of positive ion temperature

Full size image

In the vicinity of the plasma-sheath edge, there is a peak which is the main characteristic of the sheath region. In the case of hot positive ion, the ions can penetrate more into the sheath and therefore, the profile of the space-charge amplitude increases. According to Eq. (4), the flux of the positive ions is an invariant quantity, hence by accelerating those ions through the sheath, the number density decreases. In addition, as the plasma potential is positive with respect to the plasma surrounding wall, the negative species repel from the wall. Therefore, the space-charge becomes low far from the wall.

As pointed out in the introduction, adding the negative ions in the plasma leads to great variation in the plasma-sheath characteristics. In Fig. 2, the profiles of the space-charge are drawn for a wide range of electronegativity without considering the thermal effects of the positive ions. From this figure, it can be seen that, adding the negative ions results in damping the profiles of the space-charge profile and furthermore, due to the attraction of the positive ions by low temperature negative ions, the main peak of the space-charge moves towards the plasma-sheath edge. It can be observed that in high and low electronegativity, the peak takes higher values with respect to the intermediate electronegativity. In addition, in high electronegativity, the width of the main peak becomes narrower. However, as shown in Fig. 3, in the case of thermal positive ions, raising the temperature of the positive ions leads to the enhancement of the space-charge. The interesting point is that the thermal effect of the positive ions is more pronounced in high electronegativity. In the case of the low concentration of the negative ions, increasing the positive ion temperature has no great influence on the increase of amplitude of the space-charge peak compared with the high electronegativity case. In addition, contrary to the case of cold positive ion, it is observed that the space-charge peak in high electronegativity is higher with respect to the low electronegativity.

Fig. 2
figure 2

The space-charge profile for different values of electronegativity in collisionless case for cold positive ions and \( \gamma = 10 \)

Full size image
Fig. 3
figure 3

The space-charge profile for different values of electronegativity in collisionless case for thermal positive ions and \( \gamma = 10 \)

Full size image

The competition between the positive and negative ion temperature can determine the sheath characteristics and a twofold feature appears. In Fig. 4, the space-charge profiles are presented for different values of negative ion temperature and in the case of the collisionless cold positive ion condition. Far from the plasma wall, increase of \( \gamma \) leads to the decrease of the space charge. However, one can observe that for low enough negative ion temperature, twofold behavior of the space-charge emerges. This result is similar to the results of the Ref. [23] which has investigated the non-thermal electronegative plasma sheath. According to Fig. 5, by increasing the positive ion temperature, the difference between peak and dip of the space charge reduces and far from the sheath edge, the influence of negative ion temperature on the amount of the space-charge becomes negligible. In addition, in the presence of the hot positive ions, the space charge becomes stronger near the sheath edge.

Fig. 4
figure 4

The 3D space-charge profile for different values of negative ion temperature in the presence of cold positive ions and \( \delta = 0.5 \) in collisionless case

Full size image
Fig. 5
figure 5

The 3D space-charge profile for different values of negative ion temperature in the presence of thermal positive ions \( T = 0.4 \) and \( \delta = 0.5 \) in collisionless case

Full size image

The sheath solution in the collisional case

Now, we focus on the influence of the positive ion temperature on the sheath space-charge in the presence of collisions between positive ions and the neutral background. In Fig. 6, the space-charge profiles are presented for three values of positive ion temperature in the absence of negative ions.

Fig. 6
figure 6

The space-charge profile in the absence of negative ions for three values of positive ion temperature in collisional case \( \alpha = 0.25 \)

Full size image

By comparing Fig. 6 with the results of the collisionless case presented in Fig. 1, it can be deduced that apart from the positive ion temperature, the collisions lead to higher amplitude for the space-charge peak and does not change its position significantly.

Figures 7 and 8 show the dependence of the space-charge on the negative ion concentration in the presence of collisions for cold and hot positive ions cases. In the presence of collisions, as illustrated previously, the peak amplitude increases and in high electronegativity, the peaks become shrunk slightly for both cold and hot positive ions cases.

Fig. 7
figure 7

The space-charge profile for different values of electronegativity in collisional case for cold positive ions \( \alpha = 0.25 \) and \( \gamma = 10 \)

Full size image
Fig. 8
figure 8

The space-charge profile for different values of electronegativity in collisional case for thermal positive ions \( T = 0.4 \), \( \alpha = 0.25 \) and \( \gamma = 10 \)

Full size image

The collisions between the positive ions and neutral background result in decrease of positive ion velocity; consequently raises the space-charge which is confirmed by comparison of Fig. 9 with Fig. 4.

Fig. 9
figure 9

The 3D space-charge profile for different values of negative ion temperature in the presence of cold positive ions and \( \delta = 0.5 \) in collisional case

Full size image

As shown in Fig. 10 increasing the positive ion temperature, the ions can penetrate more in the sheath region and result in increasing the space charge profiles, which is more pronounced in the vicinity of the sheath edge. Decreasing the negative ion temperature leads to the damping of space charge which can be a consequence of attraction of the positive ion by the cold negative ions. However, it can be seen from Fig. 10, the temperature of the positive ions decrease the dependency of the space charge damping on the negative ion temperature.

Fig. 10
figure 10

The 3D space-charge profile for different values of negative ion temperature in the presence of thermal positive ions \( T = 0.5 \) and \( \delta = 0.5 \) in collisional case

Full size image

The interesting point is that, in the presence of hot positive ions, the twofold feature starts at lower values of \( \gamma \) which is more pronounced in collisional case.

The kinetic energy of the accelerated ion and net current passing through the sheath

As mentioned in the introduction, one of the important quantities for plasma processing is the kinetic energy of the accelerated ion reaching the cathode. In Fig. 11, the kinetic energies of the positive ions reaching the wall versus the collision frequency are presented.

Fig. 11
figure 11

The dependence of kinetic energy of positive ions on collision frequency

Full size image

Cases considered are for electropositive and electronegative plasmas for two values of \( \gamma \) in the presence of cold and hot positive ion. As can be seen, for all conditions, the collisions lead to a reduction in the positive ion kinetic energy. However, presence of the negative ions gives rise to more reduction in low collisionality while in high collision frequency, the kinetic energy of the positive ions increases. By decreasing the negative ion temperature, due to attraction by massive negative ions, the positive ions decelerate and, therefore, the kinetic energy reduces and finally by including the positive ion pressure in the force balance Eq. (5), the kinetic energy increases.

Now, we focus on the net current reaching the surrounding wall. In the current case, the net current can be defined as:

$$ J_{\text{n}} = J_{\text{i}} - J_{\text{e}} - J_{ - } = en_{\text{i}} V_{{{\text{i}}z}} - \frac{1}{4}en_{\text{e}} V_{\text{the}} - \frac{1}{4}en_{ - } V_{{{\text{th}} - }} $$
(16)

where \( V_{\text{the}} = \sqrt {\frac{{8T_{\text{e}} }}{{\pi m_{\text{e}} }}} \) and \( V_{{{\text{th}} - }} = \sqrt {\frac{{8T_{ - } }}{{\pi m_{ - } }}} \) are the electron and negative ion thermal speeds, \( m_{\text{e}} \) and \( m_{ - } \) are the masses of electron and negative ion, respectively. The thermal effects of the positive ions in the electric current are included in the first term of the left hand side of Eq. (17). The dimensionless net current scaled by \( en_{{{\text{e}}0}} c_{\text{s}} \) [21] is

$$ j_{\text{n}} = \frac{1}{1 - \delta }\left( {N_{\text{i}} u_{z} - (1 - \delta )\sqrt {\frac{{m_{\text{i}} }}{{2\pi m_{\text{e}} }}} N_{\text{e}} - \delta \sqrt {\frac{{m_{\text{i}} }}{{2\pi \gamma m_{ - } }}} N_{ - } } \right) $$
(17)

The oxygen and argon gasses are considered as the source of negative and positive atoms in the plasma.

In Fig. 12, we show the net electric current passing through the space-charge region in different conditions. It can be seen that the sheath thickness is sensitive to the presence of the negative ion concentration which leads to decrease of the sheath thickness. Decreasing the negative ion temperature leads to increments in the net current through the sheath and broadening the sheath thickness and furthermore, by increasing the positive ion temperature, sheath thickness decreases. In addition, the collisions result in decreasing the net current and finally, the presence of hot positive ion leads to decrease of the sheath thickness.

Fig. 12
figure 12

The profile of net electric current across the sheath

Full size image

Conclusion

The characteristic features of space-charge region for thermal electronegative plasma are investigated in both collisionless and collisional cases by the set of fluid equations. The Bohm criterion for the positive ions entering the sheath is extracted using the Sagdeev potential method. In addition the profiles of the space-charge in the presence of the hot and cold positive ions are obtained for different electronegativity and negative ion temperature. It is shown that, increasing the positive ion temperature leads to enhancement of the space-charge amount and the influence of the thermal positive ion on the space-charge peak is more pronounced in high electronegativity. However, it is observed that the positive ion temperature has no influence on the peak position. Raising the positive ion temperature causes the effect of the negative ion temperature far from the sheath edge disappears. Moreover, the collisions does not change the peak position and twofold feature of the space-charge and in the presence of the hot positive ions, the twofold feature starts at lower values of relative temperature of electron to negative ion. In addition, the positive ion temperature leads to a decrease in the net current as well as the sheath thickness.