Introduction

Graphene is a monoatomic layer of graphite densely packed into a two-dimensional (2D) honeycomb lattice, \( sp^{2} \) bonded, with two nonequivalent triangular sublattices. Graphene sheet was first fabricated by Novoselov et al. [1–4]. Charge carriers, i.e., electrons and holes close to the Dirac points \( K \) and \( K^{{\prime }} \), in graphene are described by the massless Dirac equation where Fermi velocity (\( v_{\text{F}} \approx 10^{6} \;{\text{m/s}} \)) plays the role of speed of light [2, 5]. The Fermi velocity in graphene is almost 100 times the velocity in normal metal and thus the coulomb interaction is surely negligible comparing to kinetic energy in graphene [6, 7]. Due to the massless Dirac equation for charge carriers in graphene, tunneling through a barrier in graphene is described by Klein tunneling mechanism [8–11]. Graphene exhibits numerous novel electronic and transport properties, for example, half-integer and unconventional quantum hall effect [4], ultrahigh carrier mobility [3], optical effect [12, 13], finite minimal electrical conductivity [4, 14, 15], special Andreev reflection [16] and so on.

The charge carriers in clean bilayer graphene have parabolic energy spectrum, which means they are massive quasiparticle, similar to the conventional nonrelativistic electrons. Based on the arrangement of layers, a bilayer graphene can be categorized into two types of AA and AB. In AA arrangement, both graphene layers are stacked directly on top of each other which yield a metastable configuration [11], whereas AB arrangement in which the two layers are stacked alternatively is more stable structure. One of the most important phenomena in monolayer graphene is the Klein tunneling (KT) that exhibits perfect transmission through the classically forbidden region for normal incident. It occurs due to required conservation of pseudospin [12, 13]. KT causes the monolayer graphene not to be so useful for the electronic devices based on the monolayer graphene materials. The KT can be avoided if a gap is induced in the electronic spectrum. A gap in the spectrum of monolayer graphene can be induced by controlled structural modification of the graphene channel [14], by interaction of the sample with the substrate [15] and by patterning it into nanoribbons [16]. Nevertheless, these ways are expensive and it may not be possible to scale up the processes to mass production level. On the other hand, the absence of the KT, presence of the very high carrier mobility and easy to induce an energy gap in a bilayer graphene make it to have a great potential for application in nano-material electronic device.

In 1970, the superlattice was proposed by Esaki and Tsu [17], which was attracted a great deal of researches over the past decades years on the transport properties of the superlattice. Transport properties in several superlattices have been studied and lots of interesting results have been achieved [18–28]. The transport properties in graphene superlattice structure were first studied in Ref. [23] the authors found that the conductivity of the graphene superlattice depends on the superlattice structural parameters. The conductance of a disordered graphene superlattice was investigated in Ref. [24], and the authors found that the conductance vanishes when the sample size becomes very large. In Ref. [27], the spin transport properties of magnetic graphene superlattice in the presence of Rashba spin–orbit interaction was studied and found that the magnetoresistance ratio shows a strong dependence on the number of magnetic barriers. In all mentioned works the transport properties in graphene superlattice were studied in absence of the external electric field. Therefore, it would be worthwhile to investigate the electrical transport properties in monolayer and bilayer graphene superlattices modulated by a homogeneous electric field. We show that angular range of the transmission through graphene superlattice can be efficiently controlled by the bias voltage and the number of barriers. Our probes show that for bilayer system unlike monolayer structure the value of current density can be zero.

The rest of the paper is organized as follows. Model and theory are present in “Model and method” section, the results are discussed in “Numerical result and discussion” section, and finally we end the paper with a brief “Summary” section.

Model and method

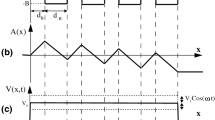
In the present study, we consider two kinds of systems, MGS and BGS. Where MGS and BGS indicate monolayer and bilayer graphene superlattices, respectively. Each system includes N square barriers modulated by a homogeneous electric field. The schematic of the structures in the presence of an external electric field \( (E^{{\prime }} ) \) applied between \( x = l_{(1)} \) and \( x = l_{(2N)} \) as shown in Fig. 1. The potential profile of the systems along the growth direction (the x-axis) has the multiple quantum well structure which is given by:

$$ V^{{\prime }} (x) = \left\{ {\begin{array}{*{20}l} {V_{0} - eE^{{\prime }} x} \hfill & {\quad {\text{for}}\;{\text{barrier}}} \hfill \\ { - eE^{{\prime }} x} \hfill & {\quad {\text{elsewhere,}}} \hfill \\ \end{array} } \right. $$

where, \( V_{0} \) represents height of the potential barrier.

Fig. 1
figure 1

The potential profile for the graphene superlattice with N electrostatic barriers of width b, (N − 1) wells of width w, and the system length of \( l_{(2N)} = (L). \)  a Without electric field and b under the applied electric field

Full size image

To neglect the strip edges, we focus on the case where the width of the graphene strip in the y-direction is much larger than the width of barriers, namely b.

Tunnelign in MGS

The charge carriers in graphene superlattice are described by the Dirac equation in which Homiltonian of carriers is written as \( \hat{H} = \hat{H}_{0} + V^{{\prime }} (x) \), where \( \hat{H}_{0} = \hbar v_{\text{F}} \hat{\sigma } \cdot \vec{k} \). \( \vec{k} \) represents wave vector of quasiparticles, \( \hat{\sigma } \) is 2D Pauli matrix and \( v_{\text{F}} \approx 10^{6} \) m/s is Fermi velocity. To study the transport problem in a monolayr graphene superlattice, we shall first solve the Dirac equation. For this purpose, we suppose that incident electron with energy E, propagates at angle \( \phi \) along x-axis. General solution to the Hamiltonian \( \hat{H} = \hat{H}_{0} + V^{{\prime }} (x) \) in the ith strip can be written in the following form [22–25].

$$ \begin{aligned} \psi_{1}^{i} & = \left( {a_{i} e^{{ik_{ix} x}} + b_{i} e^{{ - ik_{ix} x}} } \right)e^{{ik_{y} y}} , \\ \psi_{2}^{i} & = s_{i} \left( {a_{i} e^{{ik_{ix} x + i\phi_{i} }} + b_{i} e^{{ - ik_{ix} x - i\phi_{i} }} } \right)e^{{ik_{y} y}} . \\ \end{aligned} $$
(2)

Here \( \psi_{1}^{i} \) and \( \psi_{2}^{i} \) are the components of the Dirac spinor, \( a_{i} \) and \( b_{i} \) are the transmission and reflection coefficients, respectively; \( k_{x} \) and \( k_{y} \) are the wave vectors along x and y-direction, respectively can be read as follows

$$ K_{ix} = \left\{ {\begin{array}{*{20}l} {q_{x} = \frac{{E - V_{0} + eE^{{\prime }} x}}{{\hbar v_{\text{F}} }}\cos \theta ,} \hfill & {{\text{for}}\;{\text{barrier,}}} \hfill \\ {k_{x} = \frac{{E + eE^{{\prime }} x}}{{\hbar v_{\text{F}} }}\cos \varphi ,} \hfill & {{\text{elsewhere}} .} \hfill \\ \end{array} } \right. $$
(3)
$$ K_{iy} = \left\{ {\begin{array}{*{20}l} {q_{y} = \frac{{E - V_{0} + eE^{{\prime }} x}}{{\hbar v_{\text{F}} }}\sin \theta ,} \hfill & {{\text{for}}\;{\text{barrier}}} \hfill \\ {k_{y} = \frac{{E + eE^{{\prime }} x}}{{\hbar v_{\text{F}} }}\sin \varphi ,} \hfill & {\text{elsewhere}} \hfill \\ \end{array} } \right. $$
(4)
$$ s_{i} = \text{sgn} (E - V^{{\prime }} (x)) $$
(5)

where, \( \theta = \tan^{ - 1} (k_{y} /q_{x} ) \) is angle of refraction, i.e., the corresponding angle inside the barriers. Since the system used in this modeling is homogeneous along y-direction, the momentum parallel to y-axis is conserved [29].

By applying continuity of wave function at boundaries for the system consisting of N barriers, \( b_{1} \) and \( a_{(2N + 1)} \) are obtained which represent reflection and transmission coefficients, respectively. Angular dependent transmission probability can be evaluated by:

$$ T(\phi ) = \frac{{\cos \phi_{n} }}{\cos \phi }\left| {a_{(2N + 1)} } \right|^{2} . $$
(6)

Note that \( \varphi_{n} \) is emergence angle of the electron from the right side in graphene superlattice, which is different from the incident angle (\( \varphi \)).

Tunnelign in BGS

In low energy regime, the charge carriers in bilayer graphene are described by an off-diagonal Hamiltonian like below [3].

$$ \hat{H} = \frac{{\hbar^{2} }}{{2m^{*} }}\left( {\begin{array}{*{20}l} 0 \hfill & {\quad (k_{x} - ik_{y} )^{2} } \hfill \\ {(k_{x} + ik_{y} )^{2} } \hfill & {\quad 0} \hfill \\ \end{array} } \right), $$
(7)

which yields a gapless semiconductor with chiral electrons and holes having a finite mass osf \( m^{*} \). Here \( m^{*} \) is \( 0.035\;m_{\text{e}} , \) where \( m_{\text{e}} \) is the mass of bare electron. Thus, it would be possible to describe the Hamiltonian of charge carriers in the BGS under the applied electric field as follows:

$$ \hat{H} = \frac{{\hbar^{2} }}{{2m^{*} }}\left( {\begin{array}{*{20}l} 0 \hfill & {\quad (k_{x} - ik_{y} )^{2} } \hfill \\ {(k_{x} + ik_{y} )^{2} } \hfill & {\quad 0} \hfill \\ \end{array} } \right) + V^{\prime } (x). $$
(8)

General solution to Eq. (8), for the ith strip can be expressed by the following formulation [8, 23, 30]

$$ \begin{aligned} \psi_{1}^{i} (x,y) & = \left( {a_{i} e^{{ik_{x\sigma } x}} + b_{i} e^{{ - ik_{x\sigma } x}} + c_{i} e^{{\kappa_{ix\sigma } x}} + d_{i} e^{{ - \kappa_{ix\sigma } x}} } \right)e^{{ik_{iy\sigma } y}} , \\ \psi_{2}^{i} (x,y) & = s_{i} \left( {a_{i} e^{{ik_{x\sigma } x + 2i\phi_{i} }} + b_{i} e^{{ - ik_{x\sigma } x - 2i\phi_{i} }} - c_{i} h_{i} e^{{\kappa_{ix\sigma } x}} - \frac{{d_{i} }}{{h_{i} }}e^{{ - \kappa_{ix\sigma } x}} } \right)e^{{ik_{iy\sigma } y}} , \\ \end{aligned} $$
(9)

where \( a_{i} \), \( b_{i} \), \( c_{i} \), and \( d_{i} \) are the transmission amplitudes, and

$$ \begin{aligned} \hbar k_{ix\sigma } & = \sqrt {2m^{*} |E - V^{{\prime }} (x)|} \cos \,\phi_{i} , \\ \hbar k_{iy\sigma } & = \sqrt {2m^{*} |E - V^{{\prime }} (x)|} \sin \,\phi_{i} , \\ \kappa_{ix\sigma } & = \sqrt {k^{2}_{ix\sigma } + 2k^{2}_{iy\sigma } } , \\ h_{i} & = (\sqrt {1 + \sin^{2} \phi_{i} } - \sin \,\phi_{i} )^{2} , \\ s_{i} & = \text{sgn} (V^{{\prime }} (x) - E). \\ \end{aligned} $$
(10)

One significant difference in wave function between monolayer and bilayer graphenes is that there are four possible solutions in the latter case as shown in Eq. (9). By appling continuity of wave function as well as their derivatives at the boundaries for a system consisting of N barriers and using the transfer-matrix method, one can obtain the angular dependent transmission probability in BGS.

Using transmission probability, the current density (I) in MGS and BGS due to a bias voltage \( (V_{\text{b}} = E^{{\prime }} L) \) along the x-direction is given by [31–34].

$$ I = - \frac{{2ev_{\text{F}} }}{{h^{2} }}\int\limits_{ - \pi /2}^{\pi /2} {T(\phi )[f(E) - f(E + eV_{\text{b}} )]E\,{\text{d}}E\;\cos (\phi ){\text{d}}\phi ,} $$
(11)

Where f(E) is the Fermi function, for low temperatures, the function \( [f(E) - f(E + eV_{\text{b}} )] \) can be approximated by \( - eV_{\text{b}} \delta (E - E_{\text{F}} ) \). Thus, one can find the expression for the low temperature current density as

$$ I = \lambda V_{\text{b}} \int\limits_{ - \pi /2}^{\pi /2} {T(\phi )E\,{\text{d}}E\;\cos (\phi ){\text{d}}\phi ,} $$
(12)

where \( \lambda = 2e^{2} E_{\text{F}} v_{\text{F}} /h^{2} \) and \( E_{\text{F}} \) is the Fermi energy.

Numerical results and discussion

In this section, we present our numerical results using the methods described in the previous section. In all the cases, the energy E of the incident electron, barrier height \( V_{0} \), well width w, and barrier width b are taken to be 80, 200 meV, 5 and 10 nm, respectively for MGS, while these parameters are chosen 17, 50 meV, 5 and 10 nm for BGS, unless otherwise specified. At first, the transmission probability of charge carriers T as a function of incident angle \( \phi \) and bias voltage \( (V_{\text{b}} = E^{{\prime }} L) \) are plotted in Figs. 2 and 3 for MGS and BGS, respectively.

Fig. 2
figure 2

The transmission probability as a function of bias voltage and incident angle for monolayer graphene superlattice. a For N = 2; b N = 4 and c N = 6

Full size image
Fig. 3
figure 3

The transmission probability as a function of bias voltage and incident angle for bilayer graphene superlattice. a For N = 2, b N = 4 and c N = 6

Full size image

As it is obvious in Fig. 2, perfect transmission with \( T_{\sigma } = 1 \) at normal incident i.e., \( \phi = 0 \) is observed for monolayer structure. This is due to the massless Dirac fermions and directly attributed to Klein tunneling. It can be seen from Fig. 3, for a small external field, i.e., bias voltage lower than height of barrier, a perfect reflection (T = 0) is observed at normal incident due to chiral symmetry in the bilayer graphene superlattice. This is completely different from the behavior observed for monolayer graphene superlattice. Further, some resonant peaks appear in Figs. 2 and 3. Resonant peaks originate from interference of incident and scattered waves in the barrier and well regions. Also, the number of the resonant peaks increases by increasing the number of barriers. This indicates that the number of barriers plays a key role in transmission for the graphene superlattice. But for high external field \( (V_{\text{b}} \times b/w) > (N \times V_{0} - 2E) \), the transmission probability is raised by increasing the bias voltage. Because in the high regime of the external field, the x component of electron wave vector in the barrier (\( q_{x} \)) is a real value for most incident angles, which is proportional to the propagated wave inside the barrier. However, transmitting window for the incident angles is limited with the condition that \( q_{x} \) is real. According to the abovementioned discussions, it is clear that one can control the transmission probability in graphene superlattice by the external electric field.

Figure 4 depicts the current density as a function of bias voltage \( (V_{\text{b}} = E^{{\prime }} L) \) for MGS at different values of Fermi energy. As can be seen from Fig. 4 the current density is an oscillating function of \( V_{\text{b}} \). It is because the transmission probability T for incident angles \( \phi \ne 0 \) is an oscillating function of \( q_{x} \), while \( q_{x} \) is determined from \( V^{{\prime }} (x) \) (see Eq. (4)). For instance, at the limit of high barrier \( \left| {V_{0} } \right| >> E \), for monolayer graphene superlattice with single barrier this equation is suggested: \( T_{{}} = \cos^{2} \phi /[1 - \cos^{2} (q_{x} b)\;\sin^{2} \phi ] \). It is also evident from Fig. 4 that the oscillation amplitude of the current density increases by reducing the Fermi energy. Different values of Fermi energy can be selected by n doping [35]. However, the current density increases monotonically by decreasing the external electric field. This is quite expectable since the transmission probability is increased by increasing the external field. The presence of Klein tunneling causes the minimum current density in MGS to be always greater than zero. However, Klein tunneling makes the monolayer graphene materials not so useful for nanoelectronic devices. On the other hand, absence of the Klein tunneling and presence of the very high carrier mobility in a bilayer graphene, make it of a great potential for applications in nanoelectronic tunneling devices.

Fig. 4
figure 4

Current density (in unit of \( \lambda \)) as a function of the bias voltage \( V_{\text{b}} \) (in Volt) for monolayer graphene superlattice. a For N = 2, b N = 4 and c N = 6. Blue solid line, red-dashed line and green dot line correspond to E = 80, 70 and 60 meV, respectively

Full size image

Figure 5 shows the current density as a function of the bias voltage for BGS at different values of the Fermi energy. Same as MGS, the current density for BGS is also an oscillating function of \( V_{\text{b}} \). Meanwhile, the current density increases monotonically by decreasing the external field. Furthermore, zero value of current density can occur in BGS, which means that for all incident angles the transmission probability is zero. In the discussions above and from Fig. 5 it is clear that the current density has a gap, which increases when E is decreasing. This is due to the evanescent wave in the barrier region. This means that bilayer graphene is a native quantum switch of ballistic electrons.

Fig. 5
figure 5

Current density (in unit of \( \lambda \)) as a function of the bias voltage \( V_{b} \) (in Volt) for bilayer graphene superlattice. a For N = 2, b N = 4 and c N = 6. Blue solid line, red-dashed line and green dot line correspond to E = 17, 15 and 13 meV, respectively

Full size image

A comparison between the results for MGS and BGS indicate that the presence of the Klein tunneling makes the transmission probability and the current density in the MGS do not zero. But in the BGS these parameters can be zero under suitable conditions due to the absence of the Klein tunneling. This means that BGS is a native quantum switch of ballistic electrons.

The most striking feature of Figs. 4 and 5 is that in some ranges of the external field, the current density is decreased by increasing the external field, which means that the graphene superlattice displays a negative differential resistance for some ranges of the external field.

Summary

Based on the transfer-matrix technique, the transport properties of charge carriers are investigated through monolayer and bilayer graphene superlattices modulated by a homogeneous electric field. It has been shown that the transmission probability and the current density sensitively depend on external field as well as Fermi energy and number of barriers. This means that both the transmission probability and the current density in monolayer and bilayer graphene superlattices can be controlled by modification of bias voltage and structure parameter. In addition, current density has an oscillatory behavior with the external electric field. This finding suggests that the structures have a negative differential resistance. Author of this paper hope that their theoretical result can stimulate some interests in experimental efforts to design electronic devices based on graphene materials.