Introduction

The investigation of exact solutions to the higher dimensional space nonlinear evolution differential equation plays an important role in the understanding many of nonlinear physical phenomena than one-dimensional equation.

The standard two-dimensional KP equation in the normalized form follows

$$ \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t} + \alpha u\frac{\partial u}{\partial x} + \beta \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) + \gamma \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0 , $$
(1)

Here, u(x, y, t) is a scalar function of two spatial coordinates x, y and one temporal coordinates t, whereas α, β and γ are three real-valued constants. γ = ±1 measures the positive and negative transverse dispersion effect. The KP equation is widely used in various branches of physics, such as plasma physics, fluid physics and quantum field theory. In addition, it describes the dynamics of solitons and nonlinear waves in plasma and super fluids [1]. This equation is derived in various physical contexts assuming that the solitary wave is moving along x- and all changes in y- directions are slower than in the direction of motion. Also, the integrability of this equation is verified by means of inverse scattering method [2].

Here, we shall deal with the generalized KP (GKP) equation instead of the standard one. The GKP in the normalized form is

$$ \frac{\partial }{\partial x}\left[ {\frac{\partial u}{\partial t} + \beta \frac{\partial k(u)}{\partial x} + \alpha \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right] + \gamma \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0 , $$
(2)

with an arbitrary nonlinear term k(u). It is observed that the GKP equation includes, as special cases, considerably interesting one-dimensional equation such as KdV equation and mKdV equation. This means that the GKP equation is the two-dimensional analog of KdV or mKdV or the combined KdV–mKdV equations. In addition, there are many versions of the KP equations according to different forms of k(u) that are related to various physical phenomena. For instance, if k(u) = un, the corresponding KP equations with power law nonlinearity dictated by the exponent n have been used to describe and investigate the flow of shallow water waves [1]. This version of KP equation is considered by Biswas et al. [3] and they obtained one soliton solution by means of solitary wave ansatz. Recently, Pandir et al. [4] classified some of exact solutions of KP equation with generalized evolution by means of the trial equation method.

In the case of k(u) = u2/2, the corresponding equation models the propagation of dust acoustic wave in the dusty plasma in both spherical and cylindrical KP equations. Very recently, El-Wakil et al. [5, 6] derived this type of KP equation based on the reductive perturbation method to study ion-acoustic solitary wave forms and calculate the energy of electron-acoustic soliton at critical ion density. If the exponent parameter n = 3/2, the associated KP equation arises in the case of unmagnetized collision less plasma physics with vortex-like hot electron [7, 8]. Another interesting feature of solitary wave solution is associated with k(u) = u3 where the solitary waves associated with k(u) = u3/3 have finite amplitude at the critical density while it diverges if k(u) = u2/2 [9].

Moreover, in the case of inhomogeneous magnetized warm plasma the KP equation has also an important role in understanding the behavior of nonlinear solitary waves at critical and non-critical densities [10–13].

From the above, we are interested to deal with GKP equation with an arbitrary nonlinearity since the above-mentioned cases are obviously appeared as particular cases from GKP equation.

Since the GKP equation can be regarded as universal integrable equation, it is still used as classical model for developing and testing of new mathematical technique. So, a large number of effective mathematical methods have been proposed to solve KP equations [14–21]. Among those, the Lie symmetries are considered as one of the most powerful technique for solving either partial differential equation or nonlinear coupled system of integro-differential equation [22–28].

For a given k(u), the symmetries group of KP equation is investigated by many authors. Recently, the symmetries of the (3 + 1)-dimensional KP equation with k(u) = u2/2 are obtained and some of similarity reductions and similarity solutions are discussed by Khalique and Adem [29].

In this article, we aim to extend the analysis of Lie point symmetries to GKP equation with arbitrary nonlinearity to obtain and classify the allowed symmetry group that leaves GKP equation invariant. By means of the Lie symmetries method, the similarity reduction of GKP equation can be obtained and it will be investigated by performing the bifurcations and phase portrait analysis.

This paper is organized as follows: in “Lie symmetries of GKP equation”, the symmetry analysis of GKP equation is presented. “Bifurcation and phase portrait of GKP equation” is devoted to study the topology of both phase portrait and potential curves of the reduced GKP equation for different cases of k(u) and also the explicit solutions for each case are obtained. Final section is “Conclusions and remarks”.

Lie symmetries of GKP equation

Since the Lie point symmetry approach is considered as one of the most powerful technique, we are here interested to use such technique for obtaining the similarity solutions of GKP equation. Generally, this technique is, however, based on the study of the invariance property of the differential equations under one-parameter Lie group of point transformations [13, 14]. Since we restrict ourselves to Lie point symmetries, the Lie algebra of the symmetry group of GKP Eq. (2) will be generated by vector fields of the form

$$ \chi = \tau (x,y,t,u)\frac{\partial }{\partial t} + \xi (x,y,t,u)\frac{\partial }{\partial x} + \eta (x,y,t,u)\frac{\partial }{\partial y} + \varphi (x,y,t,u)\frac{\partial }{\partial u} , $$
(3)

where τ, ξ, η, φ are infinitesimal transformations of Lie group variables (independent and dependent variables) that have to be determined later. Following the algorithm of Lie [14], we aim to determine the functions τ, ξ, η, φ and hence the form of the vector field χ. Usually, the determining equations of the functions τ, ξ, η, φ are over-determined set of linear partial differential equations. After lengthy calculations and many algebraic manipulations, the set of equations can be solved and yield

$$ \tau (t) = 3a_{4} t + a_{1} , $$
(4a)
$$ \eta (y,t) = 2a_{4} y + a_{3} (t) , $$
(4b)
$$ \xi (x,y,t) = a_{4} x - \frac{1}{2\gamma }\frac{{\partial a_{3} (t)}}{\partial t}y + a_{2} (t) , $$
(4c)
$$ \varphi (u,y,t) = a_{5} u + A_{3} (y,t) , $$
(4d)

with

$$ \alpha [a_{5} u + A_{3} (y,t)]\frac{{{\text{d}}^{2} k(u)}}{{{\text{d}}u^{2} }} + 2\alpha a_{4} \frac{{{\text{d}}k(u)}}{{{\text{d}}u}} - \frac{\text{d}}{{{\text{d}}t}}\left[ {a_{2} (t) - \frac{1}{2\gamma }\frac{{\partial a_{3} (t)}}{\partial t}} \right] = 0 , $$
(5)

where a1, a4 are arbitrary constants whereas a2(t), a3(t), A3(y, t) are three arbitrary functions of their arguments. Now, one can obviously see that by applying Lie point symmetries on GKP Eq. (2) the function k(u) is no longer arbitrary function of u but it must satisfy the condition (5) for existence Lie point symmetries.

The advantage of the presence of the condition (5) is that one can check it case by case to provide a quick answer of whether GKP equation admits Lie symmetry or not. The condition (5) can be viewed in two different ways:

  1. (1)

    This condition can be viewed as a determining equation for k(u) and this of course implies that the coefficients of different derivatives of k(u) as well as the free term in (5) should be functions of u only otherwise there exists a contradiction. This will put further constraints on the functions A3(y, t), a3(t) and a2(t).

  2. (2)

    For a given k(u), this condition can also be viewed as compatibility condition for A3(y, t), a3(t), a2(t), a4 and a5.

Anyway, the two ways lead us to the same symmetry group. However, we list in Table 1 the complete symmetries and vector fields of GKP equation associated with different classes of k(u).

Table 1 The symmetries and vector fields of GKP equation associated with different classes of \( k(u) \)
Full size table

Now, one can see that the obtained Lie symmetries, listed in Table 1, of GKP equations are of infinite dimensional since they contain two arbitrary functions namely; a2(t), a3(t).

The importance of the presence of these arbitrary functions is twofold:

  • On one hand, the existence of an infinity dimensional symmetry group makes it possible to obtain large classes of similarity solutions.

  • On the other hand, the existence of these arbitrary functions in the symmetry group is very useful for solving initial or boundary value problems.

It is noted that the corresponding symmetries of the case k(u) = u2/2 are equivalent to those obtained previously by Khalique and Adem [29] whereas the other cases in Table 1 are appeared as new symmetries group. Also, three new classes of k (u) that are related to logarithmic and exponential KP equations are discovered.

With the knowledge of Lie point symmetries of GKP Eq. (2) associated with different classes of k(u), the similarity variables s, z and similarity solution u(s, z) can be obtained by integrating the corresponding characteristic equations

$$ \frac{{{\text{d}}t}}{\tau (x,y,t,u)} = \frac{{{\text{d}}x}}{\xi (x,y,t,u)} = \frac{{{\text{d}}y}}{\eta (x,y,t,u)} = \frac{{{\text{d}}u}}{\varphi (x,y,t,u)} . $$
(6)

Inserting the obtained forms of the similarity variables and solutions into GKP Eq. (2), the reduced GKP equation is obtained in terms of the two similarity variable s, z.

Bifurcation and phase portrait of GKP equation

In this section, we aim to identify various types of solutions of the GKP equation by studying the topology of phase portraits and potential diagrams. Since we have wide classes of GKP equations according to different forms of k(u), we restrict our analysis to the case in which k(u) is an arbitrary function while the other cases can be done in a forthcoming work. Integrating the corresponding characteristic equations yields the reduced GKP equation

$$ - \left( {\frac{{\partial^{2} u}}{{\partial s^{2} }} + \frac{{\partial^{2} u}}{\partial s\partial z}} \right) + \alpha \frac{{d^{2} k}}{{du^{2} }}\left( {\frac{\partial u}{\partial s}} \right)^{2} +\, \alpha \frac{dk}{du}\frac{{\partial^{2} u}}{{\partial s^{2} }} + \beta \frac{{\partial^{4} u}}{{\partial s^{4} }} + \gamma \frac{{\partial^{2} u}}{{\partial z^{2} }} = 0, $$
(7)

where the similarity variables are s = x − t, z = y − t and u = u(s, z).

This equation can be rewritten in the following form

$$ \left( {q^{2} \gamma - pw} \right)\frac{{{\text{d}}^{2} u}}{{{\text{d}}\zeta^{2} }} + \alpha p^{2} \frac{{{\text{d}}^{2} }}{{{\text{d}}\zeta^{2} }}k(u) + \beta p^{4} \frac{{{\text{d}}^{4} u}}{{{\text{d}}\zeta^{4} }} = 0, $$
(8)

where ζ = ps + qz = px + qy − wt and upon integrating twice with respect to ζ, Eq. (8) becomes

$$ \frac{{{\text{d}}^{2} u}}{{{\text{d}}\zeta^{2} }} = \frac{h}{{\beta p^{4} }}u - \frac{\alpha }{{\beta p^{2} }}k(u) + m_{0} \zeta + m_{1} , $$
(9)

where h = pw − q2γ and m0, \( m_{1} \) are integration constants. Setting m0 = m1 = 0, this equation can be rewritten in the form of energy conservation law

$$ \frac{1}{2}\left( {\frac{{{\text{d}}u}}{{{\text{d}}\zeta }}} \right)^{2} + V(u) = E, $$
(10)

where E is the integration constant and represents the total energy and V(u) is the potential function. In terms of the arbitrary function k(u), the potential energy is given by

$$ V(u) = {\alpha \mathord{\left/ {\vphantom {\alpha {\left( {\beta p^{2} } \right)}}} \right. \kern-0pt} {\left( {\beta p^{2} } \right)}}\int {{\text{d}}u} k(u) - {{hu^{2} } \mathord{\left/ {\vphantom {{hu^{2} } {\left( {2\beta p^{4} } \right)}}} \right. \kern-0pt} {\left( {2\beta p^{4} } \right)}} $$
(11)

Here, one may obviously conclude that solving GKP equation is now equivalent to solve the equation of motion of a particle in a conservative field with the potential energy (11). In addition, the exact solutions of GKP equation can be obtained by integrating

$$ {\text{d}}\zeta = \pm \frac{{{\text{d}}u}}{{\sqrt {{{{{hu^{2} } \mathord{\left/ {\vphantom {{hu^{2} } {\left( {\beta p^{4} } \right)}}} \right. \kern-0pt} {\left( {\beta p^{4} } \right)}} - 2\alpha } \mathord{\left/ {\vphantom {{{{hu^{2} } \mathord{\left/ {\vphantom {{hu^{2} } {\left( {\beta p^{4} } \right)}}} \right. \kern-0pt} {\left( {\beta p^{4} } \right)}} - 2\alpha } {\left( {\beta p^{2} } \right)}}} \right. \kern-0pt} {\left( {\beta p^{2} } \right)}}\int {{\text{d}}u} k(u) + 2E} }} , $$
(12)

Now dealing with GKP equation with an arbitrary nonlinear coefficient k(u), there are some important points to make here:

Firstly, one can see from Eqs. (11), (12) that the nonlinear term k(u) plays a crucial role for constructing different forms of potential functions and explicit solutions of GKP equation.

Secondly, the explicit forms of both potential functions and the corresponding solutions of GKP equation can be obtained in terms of quadrature by integrating (11) and (12) that can only be done for given explicit forms of k(u). For example, if

$$ k(u) = \frac{{c_{1} }}{m + 1}u^{m + 1} + \frac{{c_{2} }}{n + 1}u^{n + 1} . $$
(13)

The corresponding potential function is given by

$$ V(u) = \frac{\alpha }{{\beta p^{2} }}\left( {\frac{{c_{1} }}{(m + 1)(m + 2)}u^{m + 2} + \frac{{c_{2} }}{(n + 1)(n + 2)}u^{n + 2} } \right) - \frac{h}{{2\beta p^{4} }}u^{2} , $$
(14)

where c1, c2, m and n are constants. In the field of the plasma physics, this type of the potential V(u) is called Sagdeev potential. This potential plays an important role for investigating the stability condition of the obtained solution. However, stable solitonic solution can be recognized when the Sagdeev potential satisfies the condition ∂2V(u)/∂u2 < 0 at u = 0, otherwise stable solutions do not exist.

With the knowledge of the explicit form of the Sagdeev potential, the general solution of GKP equation can be obtained by integrating Eq. (12).

As a particular case, if c1 = c2 and m = n, the explicit solitary wave solution of GKP goes to the one obtained by Dai et al. [30]

$$ u = \pm \left( {\frac{{(m + 1)(m + 2)h\sec h^{2} \left( {\frac{m}{2}\zeta \sqrt {\frac{h}{{\beta p^{4} }}} } \right)}}{{2\alpha p^{2} }}} \right)^{\frac{1}{m}} , $$
(15)

using auxiliary and homogenous method. Clearly, this type of solution depends mainly on the values of the exponent m of the power law nonlinearity. Therefore, five particular cases of physical interest are considered.

Case 1: m = n = 2, c1 = c2 = 1/2

In this case k(u) = \( {{u^{3} } \mathord{\left/ {\vphantom {{u^{3} } 3}} \right. \kern-0pt} 3} \) and the corresponding GKP equation reads

$$ \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t} + \alpha \frac{\partial }{\partial x}\left( {\frac{1}{3}u^{3} } \right) + \beta \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) + \gamma \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0, $$
(16)

This class of the KP equation has been used to describe the propagation of dust acoustic solitary waves in dusty plasma at critical density [9]. Upon integrating (11), the corresponding potential function is

$$ V(u) = \frac{\alpha }{{12\beta p^{2} }}u^{4} - \frac{h}{{2\beta p^{4} }}u^{2} . $$
(17)

In terms of the similarity variably ζ, the KP Eq. (16) reads

$$ \frac{{{\text{d}}u}}{{{\text{d}}\zeta }} = \pm \sqrt {2E + \frac{h}{{\beta p^{4} }}u^{2} - \frac{\alpha }{{6\beta p^{2} }}u^{4} } . $$
(18)

To furnish bifurcation and phase portrait in this case, Eqs. (17) and (18) should be used.

Under the conditions \( \alpha > 0 \), \( \beta > 0 \) and \( h > 0 \), as shown in Fig. 1, the potential diagram has three fixed points in a pitchfork bifurcation with two symmetric wells. This means that the potential curve has two pits and a hump. The corresponding phase portrait (\( u \),\( {{{\text{d}}u} \mathord{\left/ {\vphantom {{{\text{d}}u} {{\text{d}}\zeta }}} \right. \kern-0pt} {{\text{d}}\zeta }} \)) is shown Fig. 2 and it obviously has two centers and saddle equilibrium state on the phase portrait of Eq. (16). It can be seen that there exist a series of periodic orbits around the points (\( {{3h} \mathord{\left/ {\vphantom {{3h} {(\alpha p^{2} )}}} \right. \kern-0pt} {(\alpha p^{2} )}} \), 0) and (\( - {{3h} \mathord{\left/ {\vphantom {{3h} {(\alpha p^{2} )}}} \right. \kern-0pt} {(\alpha p^{2} )}} \), 0). These trajectories refer to a periodic travelling wave solutions. Also as shown from the topology of the phase portrait, the particular trajectories going from a saddle and retuning to it referred to as separatrix closed loops (homoclinic loops). These trajectories refer to existence of solitary wave solutions of GKP equation with such type of potential. This type of solution can be obtained by integrating (12) and yields

Fig. 1
figure 1

The potential \( V(u) \) for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
Fig. 2
figure 2

Phase portrait for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
$$ u = \pm\,\; u_{0} \sec h\left( {\frac{\zeta }{W}} \right), $$
(19)

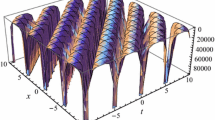
where \( u_{0} = \sqrt {{{6h} \mathord{\left/ {\vphantom {{6h} {(\alpha p^{2} )}}} \right. \kern-0pt} {(\alpha p^{2} )}}} \) is the amplitude and \( W = \sqrt {{{\beta p^{4} } \mathord{\left/ {\vphantom {{\beta p^{4} } h}} \right. \kern-0pt} h}} \) is the width of the soliton. It is noted that this solution is a special case from (15) if \( m = 2 \) and its behavior in terms of the original variables is shown in Fig. 3. This solution was obtained previously by Pakzad and Javiden [9]. Also, it is stable solitonic solution since the stability condition \( {{\partial^{2} V(u)} \mathord{\left/ {\vphantom {{\partial^{2} V(u)} {\partial u^{2} < 0}}} \right. \kern-0pt} {\partial u^{2} < 0}} \) at \( u = 0 \) is satisfied.

Fig. 3
figure 3

The solution with \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image

Case 2:\( m \) = \( n \) = 1, \( c_{1} \) = \( c_{2} \) = 1/2

In this case \( k(u) \) = \( {{u^{2} } \mathord{\left/ {\vphantom {{u^{2} } 2}} \right. \kern-0pt} 2} \) and GKP equation reads

$$ \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t} + \alpha \frac{\partial }{\partial x}\left( {\frac{1}{2}u^{2} } \right) + \beta \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) + \gamma \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0. $$
(20)

This is the most familiar type of the KP equation and it has many applications in various field of physics. With this choice, the corresponding potential function is

$$ V(u) = \frac{\alpha }{{6\beta p^{2} }}u^{3} - \frac{h}{{2\beta p^{4} }}u^{2} , $$
(21)

In terms of the similarity variable \( \zeta \), the reduced KP equation is

$$ \frac{{{\text{d}}u}}{{{\text{d}}\zeta }} = \pm \sqrt {2E + \frac{h}{{\beta p^{4} }}u^{2} - \frac{\alpha }{{3\beta p^{2} }}u^{3} } . $$
(22)

Under the condition \( \alpha > 0 \), \( \beta > 0 \) and \( h > 0 \), the profile of the potential function and phase portrait are shown in Figs. 4 and 5, respectively. In this case, the potential well has one hump and a pit that correspond to a saddle point at (0, 0) and a center point at (\( {h \mathord{\left/ {\vphantom {h {(\alpha p^{2} )}}} \right. \kern-0pt} {(\alpha p^{2} )}} \), 0) in the phase portrait. An explicit solution of GKP equation can be obtained by integrating (12) and yields the well-known stable solitary wave solution

$$ u = \pm u_{0} \sec h^{2} \left( {\frac{\zeta }{W}} \right), $$
(23)

where \( u_{0} = {{3h} \mathord{\left/ {\vphantom {{3h} {(\alpha p^{2} )}}} \right. \kern-0pt} {(\alpha p^{2} )}} \) is the amplitude and \( W = 2\sqrt {{{\beta p^{4} } \mathord{\left/ {\vphantom {{\beta p^{4} } h}} \right. \kern-0pt} h}} \) is the width of the soliton solution.

Fig. 4
figure 4

The potential \( V(u) \) for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
Fig. 5
figure 5

Phase portrait for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image

If \( m = 1\), one can see that this solution is a special case from the general one (15) and in terms of the original coordinates the obtained solution is shown in Fig. 6.

Fig. 6
figure 6

The solution for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image

Case 3:\( m = n =1/2\), \( c_{1} = c_{2} = 1/2\)

In this case \( k(u) \) = \( 2{{u^{3/2} } \mathord{\left/ {\vphantom {{u^{3/2} } 3}} \right. \kern-0pt} 3} \) and GKP equation reads

$$ \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t} + \alpha \frac{\partial }{\partial x}\left( {\frac{2}{3}u^{\frac{3}{2}} } \right) + \beta \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) + \gamma \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0. $$
(24)

This class of KP equation has been considered to study both electron and ion-acoustic waves in a plasma in the case of positive and negative dispersion [7, 8].

In this case, the corresponding potential function is

$$ V(u) = \frac{4\alpha }{{15\beta p^{2} }}(u)^{\frac{5}{2}} - \frac{h}{{2\beta p^{4} }}u^{2} , $$
(25)

and the portrait follows the equation

$$ \frac{{{\text{d}}u}}{{{\text{d}}\zeta }} = \pm \sqrt {2E + \frac{h}{{\beta p^{4} }}u^{2} - \frac{8\alpha }{{15\beta p^{2} }}.u^{\frac{5}{2}} } . $$
(26)

Under the condition \( \alpha > 0 \), \( \beta > 0 \) and \( h > 0 \), the profile of the potential function and phase portrait are shown in Figs. 7 and 8, respectively. In this case, the potential well has one hump and a pit and this correspond to a saddle point at (0, 0) and a center point at (\( {{[3h} \mathord{\left/ {\vphantom {{[3h} {(2\alpha p^{2} )}}} \right. \kern-0pt} {(2\alpha p^{2} )}}]^{2} \), 0) in the phase portrait. These trajectories refer to existence of solitary wave solution and are given by integrating (12) in the following form

Fig. 7
figure 7

The potential \( V(u) \) for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
Fig. 8
figure 8

Phase portrait for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
$$ u = \pm \; u_{0} \sec h^{4} \left( {\frac{\zeta }{W}} \right), $$
(27)

where \( u_{0} = {{[15h} \mathord{\left/ {\vphantom {{[15h} {(8\alpha p^{2} )}}} \right. \kern-0pt} {(8\alpha p^{2} )}}]^{2} \) is the amplitude and \( W = 4\sqrt {{{\beta p^{4} } \mathord{\left/ {\vphantom {{\beta p^{4} } h}} \right. \kern-0pt} h}} \) is the width of the soliton solution. If \( m \) = 1/2, one can see that this solution is a special case from the general one (15) and in terms of the original coordinates the obtained solution is shown in Fig. 9. This type of solution is stable since the stability condition is satisfied. It is noted that this type of solitonic solution has been obtained previously by Mamun et al. [31].

Fig. 9
figure 9

The solution for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image

Case 4:\( m \) = 2, \( n \) = 1

In this case \( k(u) = {{c_{1} u^{3} } \mathord{\left/ {\vphantom {{c_{1} u^{3} } 3}} \right. \kern-0pt} 3} + {{c_{2} u^{2} } \mathord{\left/ {\vphantom {{c_{2} u^{2} } 2}} \right. \kern-0pt} 2} \) and GKP equation reads

$$ \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t} + \alpha \frac{\partial }{\partial x}\left( {\frac{{c_{1} }}{3}u^{3} + \frac{{c_{2} }}{2}u^{2} } \right) + \beta \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) + \gamma \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0. $$
(28)

This class of KP equation is very important in the field of nonlinear physics, since it is the generalization of the combined one-dimensional KdV–mKdV equations.

The corresponding potential function follows

$$ V(u) = - \frac{h}{{2\beta p^{4} }}u^{2} + \frac{\alpha }{\beta p2}\left( {\frac{{c_{2} }}{6}u^{3} + \frac{{c_{1} }}{12}u^{4} } \right), $$
(29)

and the portrait follows in this case the equation

$$ \frac{{{\text{d}}u}}{{{\text{d}}\zeta }} = \pm \sqrt {2E + \frac{h}{{2\beta p^{4} }}u^{2} - \frac{\alpha }{\beta p2}\left( {\frac{{c_{2} }}{6}u^{3} + \frac{{c_{1} }}{12}u^{4} } \right)} . $$
(30)

As shown in Figs. 10 and 11, the potential well has one hump and two pits that correspond to saddle and two centers equilibrium state in the phase plane of GKP equation. The corresponding solution in this case is

Fig. 10
figure 10

The potential \( V(u) \) for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
Fig. 11
figure 11

Phase portrait for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
$$ u = \pm \frac{1}{{a_{1} + a_{2} \sinh^{2} \left( {\frac{\zeta }{W}} \right)}}, $$
(31)

where \( a_{1} = {{p^{2} [c_{2} + \sqrt {c_{2}^{2} + {{6c_{1} h} \mathord{\left/ {\vphantom {{6c_{1} h} {p^{2} }}} \right. \kern-0pt} {p^{2} }}} ]} \mathord{\left/ {\vphantom {{p^{2} [c_{2} + \sqrt {c_{2}^{2} + {{6c_{1} h} \mathord{\left/ {\vphantom {{6c_{1} h} {p^{2} }}} \right. \kern-0pt} {p^{2} }}} ]} {(6h)}}} \right. \kern-0pt} {(6h)}} \), \( a_{2} = {{p^{2} [\sqrt {c_{2}^{2} + {{6c_{1} h} \mathord{\left/ {\vphantom {{6c_{1} h} {p^{2} }}} \right. \kern-0pt} {p^{2} }}} ]} \mathord{\left/ {\vphantom {{p^{2} [\sqrt {c_{2}^{2} + {{6c_{1} h} \mathord{\left/ {\vphantom {{6c_{1} h} {p^{2} }}} \right. \kern-0pt} {p^{2} }}} ]} {(3h)}}} \right. \kern-0pt} {(3h)}} \), \( W = 2\sqrt {{{\beta p^{4} } \mathord{\left/ {\vphantom {{\beta p^{4} } h}} \right. \kern-0pt} h}} ] \). The behavior of this solution in terms of the original coordinates is shown graphically in Fig. 12.

Fig. 12
figure 12

The solution for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image

Case 5: In this case, we consider the GKP equation with \( k(u) = u\ln (\left| u \right|) + {u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0pt} 2} \) that yields the following logarithmic potential function

$$ V(u) = - \frac{h}{{2\beta p^{4} }}u^{2} + \frac{\alpha }{2\beta p2}u^{2} \ln \left( {\left| u \right|} \right). $$
(32)

This type of potential appears in the problem of studying propagation of Alfven waves in compressible fluid in the presence of an external magnetic field [28], and the portrait follows the equation

$$ \frac{{{\text{d}}u}}{{{\text{d}}\zeta }} = \pm \sqrt {2E + \frac{h}{{\beta p^{4} }}u^{2} - \frac{\alpha }{\beta p2}u^{2} \ln \left| u \right|} . $$
(33)

The potential diagram Fig. 13 has three fixed points in a pitchfork bifurcation with two symmetric wells. This means that the potential curve has two pits and a hump and the corresponding phase portrait has obviously two centers and saddle equilibrium state on the phase portrait of (32). The topology of potential curves and phase portrait are, respectively, shown in Figs. 13, 14 and GKP equation with the logarithmic nonlinear coefficient \( k(u) \) admits the following solution

Fig. 13
figure 13

The potential \( V(u) \) for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
Fig. 14
figure 14

Phase portrait for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image
$$ u = \exp \left( {a_{1} + a_{2} \xi^{2} } \right) , $$
(34)

where \( a_{1} = {h \mathord{\left/ {\vphantom {h {(\alpha p^{2} )}}} \right. \kern-0pt} {(\alpha p^{2} )}} \), \( a_{2} = {{ - \alpha } \mathord{\left/ {\vphantom {{ - \alpha } {(4\beta p^{2} )}}} \right. \kern-0pt} {(4\beta p^{2} )}} \). This type of solution is shown in Fig. 15 in terms of the original variables.

Fig. 15
figure 15

The solution for \( \alpha = 1,\beta = 0.05,p = 0.93,\gamma = 2 \)

Full size image

Conclusions and remarks

In this paper, we considered GKP equation with an arbitrary nonlinear term \( k(u) \). Based on the Lie symmetry method, we derived a very important condition on \( k(u) \) that must satisfy for the existence of Lie symmetries. The advantage of this condition is that one can get a quick answer of whether GKP equation admits Lie symmetries or not. Also with the aid of this condition, we able to specify three new classes of \( k(u) \) associated with new symmetries. These classes are related to the logarithmic and exponential nonlinearity. As shown in Table 1, the obtained symmetry groups are of infinite dimensional since they contain two arbitrary functions of time. This type of symmetry is very useful for solving initial and boundary value problem. In addition, this gives an impression that the GKP equation with infinite symmetry group admits wide classes of similarity solutions.

In the frame work of bifurcation and phase portrait, different classes of solutions are predicted and the explicit solitary wave solutions are obtained for different forms of the nonlinear coefficient \( k(u) \). All the obtained solutions are similarity solutions and correspond to time and coordinate translation. The solutions associated with other types of symmetries will be done in forthcoming work.

When the inhomogeneous media are considered, the GKP equation with variable coefficients becomes more realistically than GKP Eq. (2). Studying the behavior of solutions of inhomogeneous case merits a separate investigation using tools of soliton theory, which is our future task. The application of our results might be particularly interesting in the investigations in homogeneous and inhomogeneous space and laboratory plasma [32–36].