Introduction

One of the greatest challenges for modern electronic science is miniaturizing electronic devices packed in IC chips towards an atomic scale. From fundamental quantum theories supported by elaborate experiments, it is well known that quantum effects are prominent as the transport dimension becomes small beyond the Fermi wavelength [1, 2]. Hence, the understanding of quantum characteristics of nano systems is important in order for developing future technologies in the electronic industry relevant to nano dimension. As the scale of metallic electronic devices, whose electron-energy levels are continuous, reaches a nanometer, the energy levels may no longer be allowed to remain continuous but become discrete instead. Then, the devices may look like a low dimensional quantum systems in parts.

While the time behavior of charges in ideal electronic circuits, such as an LC circuit, is represented by a simple harmonic oscillator, a large part of intricate nanoelectronic circuits may belong to time-varying systems that are described by time-dependent Hamiltonians [3–5]. Rigorous mathematical techniques are crucial for exact treatment of time-dependent Hamiltonians. In a previous research [2], Choi et al. have investigated displaced squeezed number states of a two-dimensional nanoelectronic circuit. The extension of such research to superposed quantum states may not only be interesting but also has many useful applications in science [6–10]. According to this, superposition states composed of two displaced number states (DNSs) with an opposite or an arbitrary phase difference for quantum nanoelectronic circuits will be studied in this work. We consider a series RLC nanoelectronic circuit driven by a time-dependent power source. One may possibly treat a general series RLC nanoelectronic circuit, where R, L, and C vary with time. However, for the difficulty of mathematical treatment of such a complicated system, we regard the case that only the capacitance C is an arbitrary time function while R and L are constants. As well as it is more easier to vary the capacitance than to vary resistance and/or inductance, the electronic circuits that involve a time-varying capacitance have several applications in science and technology [11–15].

At first, quantum characteristics of the system will be studied regarding the displacement of number states. Then, the superposition of two DNSs [16] of the system will be investigated. Energy eigenvalues in number states for a quantized RLC nanoelectronic circuit are discrete and the corresponding energies dissipate like a classical state due to the existence of a resistor R which roles as a damping factor [17]. A class of interesting quantum states for a harmonic oscillator is superpositions (Schrödinger’s cat states) of two DNSs of the same amplitude with opposite phases. A novel application of DNSs is their use as a resource for establishing (single) qubit operations in quantum computations [18]. Displaced number states can also be implemented to realizing an irreversible analog of quantum gates, such as the Hadamard gate, and to optimizing such gates [19]. The DNSs follow sub-Poissonian statistics [20] and exhibit several pure quantum effects, such as the revival-collapse phenomenon [21] and the interference in the phase space [22].

The success of experimental setups of superposition states [23] provides evidence for a remarkable fact that a particular system could take two or several separate quantum states simultaneously. In general, superposition states exhibit nonclassical characters. Such characters can be potentially exploited to be essential resources in various quantum information processing, such as quantum computation [6], quantum teleportation [7], quantum communication [8], quantum cryptography [9], and dense-coding [10]. All these applicabilities of the nonclassical states are important in future technology of information science. However, there is a difficulty for maintaining such nonclassicality of a system due to the appearance of decoherence of states [24]. Various quantum properties of the system including nonclassicality associated with DNSs will be investigated here.

Due to the time-dependence of the Hamiltonian of the system, a conventional technique for quantizing the system, which is the separation of variables method, is unapplicable in this case. Hence, special techniques for quantizing the system in the superposition states are necessary. The invariant operator method and the unitary transformation method will be adopted for this purpose. The underlying idea for the invariant operator method is that the Schrödinger solutions of a time-varying system is represented in terms of the eigenstates of an invariant operator [25]. For this reason, it is necessary to derive eigenstates of the invariant operator in order to study quantum features of the system. We will introduce a quadratic invariant operator that can be obtained from its fundamental definition. The original invariant operator may be not a simple form due to the time-dependence of the system. For this reason, we will transform the original invariant operator to a simple form that does not contain time functions by adopting a unitary transformation technique. Then, the eigenstates of the transformed invariant operator may be easily identified due to their simplicities. The eigenstates of the transformed invariant operator will be inversely transformed to those in the original system in order to obtain the full wave functions in the superposition state. This is the main strategy that we will adopt in this work.

Results and discussion

Hamiltonian dynamics

We consider the series RLC nanoelectronic circuit driven by a time-dependent electromotive force \(\mathcal {E} (t)\) and assume that the capacitance in the circuit varies with time. A common example of a varying capacitance can be seen from the turning of a radio dial for the purpose of receiving a particular radio wave. The equation of amount for charge stored in the capacitor can be derived by applying Kirchhoff’s law in the circuit. Then, the corresponding Hamiltonian can be easily identified from basic Hamiltonian dynamics. By replacing classically represented variables of the Hamiltonian with the counterpart quantum operators, we have quantum Hamiltonian of the system, that is given in the form

$$\begin{aligned} \hat{H} = e^{-(R/L)t} \frac{\hat{p}^2}{2L} + \frac{1}{2}e^{(R/L)t} \left[ \frac{1}{C(t)} \hat{q}^2 - 2 \mathcal {E} (t) \hat{q} \right] , \end{aligned}$$
(1)

where canonical variables \(\hat{q}\) and \(\hat{p}\) represent charge stored in the capacitor and canonical current defined as \(\hat{p} = -i\hbar \partial / \partial q \), respectively.

The energy operator of a time-dependent Hamiltonian system (TDHS) is different from the Hamiltonian itself. The role of the Hamiltonian in the TDHS is limited to be the only one in that it generates the classical equation of motion [26]. For the present system, the energy operator is represented as [27]

$$\begin{aligned} \hat{E}_\mathrm{op} = e^{-(2R/L)t}\frac{\hat{p}^2}{2L} + \frac{1}{2C(t)} \hat{q}^2. \end{aligned}$$
(2)

As you can see, the Hamiltonian given in Eq. (1) is a time-dependent form. It is known that quantum solutions of a TDHS is represented in terms of classical solutions of the system (or of a system similar to the given one) [25]. The classical definition of canonical current is \({p} = L e^{(R/L)t} \mathrm d { q}/ \mathrm{d}{} { t}\) and the classical equations of motion for charge and current are

$$\begin{aligned} \ddot{q} + \frac{R}{L} \dot{q} + \frac{1}{LC(t)} q = \frac{\mathcal {E} (t)}{L}, \end{aligned}$$
(3)
$$\begin{aligned} \ddot{p} + \bigg (\frac{\dot{C}(t)}{C(t)}-\frac{R}{L}\bigg ) \dot{p} + \frac{1}{LC(t)} p = e^{(R/L)t} \bigg (\frac{\dot{C}(t)}{C(t)} \mathcal {E} (t) +\dot{\mathcal {E}} (t)\bigg ) . \end{aligned}$$
(4)

If we denote general classical solutions of Eqs. (3) and (4) as Q(t) and P(t), respectively, they are in general represented as \(Q(t)=Q_{c}(t) +Q_p(t)\) and \(P(t)=P_{c}(t) +P_p(t)\), where \(Q_{c}(t)\) and \(P_{c}(t)\) are complementary functions and \(Q_{p}(t)\) and \(P_{p}(t)\) are particular solutions.

When investigating a quantum system that is described by a time-dependent Hamiltonian, it is useful to introduce an invariant operator [25] as mentioned previously. From \(\mathrm{d}\hat{I}/\mathrm{d}t =\partial \hat{I} /\partial t + [\hat{I}, \hat{H}]/(i\hbar )=0\), we obtain a quadratic invariant operator for the system as

$$\begin{aligned} \hat{I} =\; &{} \frac{L \rho _0^2 \Omega _0^2}{2 \rho ^2 (t)} [\hat{q}-Q_p(t)]^2 \\&+ \frac{1}{2\rho _0^2 L} \left\{ \rho (t) [\hat{p}-P_p(t)] - e^{(R/L)t} L \dot{\rho }(t) [\hat{q}- Q_p(t)] \right\} ^2, \end{aligned}$$
(5)

where \(\Omega _0 = 1/\sqrt{LC(0)}\) and \({\rho } (t)\) is a function of time which satisfies the differential equation

$$\begin{aligned} \ddot{\rho } (t) + \frac{R}{L} \dot{\rho } (t)+ \frac{1}{LC(t)} \rho (t) - \Omega _0^2 e^{-2(R/L)t} \frac{\rho _0^4}{\rho ^3(t)} =0 . \end{aligned}$$
(6)

Here \(\rho _0\) is an arbitrary real constant which has the same dimension with \(\rho (t)\). Equation (6) is a modified form of the Milne–Pinney equation [28–30].

Because the invariant operator given in Eq. (5) is somewhat complicated, it is necessary to simplify it for the convenience for further treatment. For this purpose, we use the unitary transformation technique. We introduce a suitable unitary operator which is [31]

$$\begin{aligned} \hat{U} =\hat{U}_1 \hat{U}_2 \hat{U}_3, \end{aligned}$$
(7)

where

$$\begin{aligned} \hat{U}_1=\; & {} e^{iP_p(t) \hat{q} /\hbar }e^{-iQ_p(t) \hat{p} /\hbar }, \end{aligned}$$
(8)
$$\begin{aligned} \hat{U}_2=\; & {} \exp \left( \frac{i L \dot{\rho }(t) e^{(R/L) t} \hat{q}^2}{2\hbar \rho (t) }\right) , \end{aligned}$$
(9)
$$\begin{aligned} \hat{U}_3=\; & {} \exp \left[ -\frac{i}{4\hbar } (\hat{q}\hat{p}+\hat{p}\hat{q}) \ln \left( \frac{\rho ^2(t)}{\rho _0^2} \right) \right] . \end{aligned}$$
(10)

Then, the unitary transformation of \(\hat{I}\) and \(\hat{H}\) can be fulfilled as

$$\begin{aligned} \hat{I}'= & {} \hat{U}^{-1} \hat{I} \hat{U}, \end{aligned}$$
(11)
$$\begin{aligned} \hat{H}'= & {} \hat{U}^{-1} \hat{H} \hat{U} - i \hbar \hat{U}^{-1} \frac{\partial \hat{U}}{\partial t}. \end{aligned}$$
(12)

We easily see through a standard evaluation using Eqs. (7)–(10) that this transformation yields

$$\begin{aligned} \hat{I}'(q,p)= {} \frac{\hat{p}^2}{2L} + \frac{1}{2} {L} \Omega _0^2 \hat{q}^2, \end{aligned}$$
(13)
$$\begin{aligned} \hat{H}'(q,p,t)= {} \frac{\rho _0^2 }{\rho ^2 (t)} e^{-(R/L)t} \hat{I}' + \mathcal {L}_p (t), \end{aligned}$$
(14)

where \(\mathcal {L}_p (t)\) is a time function of the form

$$\begin{aligned} \mathcal {L}_p (t) = e^{-(R/L)t} \frac{P_p^2(t)}{2L} - \frac{1}{2} e^{(R/L)t} \frac{1}{C(t) } Q_p^2(t). \end{aligned}$$
(15)

The transformed Hamiltonian \(\hat{H}'\) is very simple and represented in terms of the Hamiltonian of the simple harmonic oscillator. But \(\hat{H}'\) is still dependent on time. By performing a basic algebra with the use of Eq. (14), we see that the classical equations of motion for charge and current in the transformed system are given by

$$\begin{aligned}&\ddot{q} + \bigg ( 2\frac{\dot{\rho }(t)}{\rho (t)}+ \frac{R}{L} \bigg ) \dot{q} + \frac{\rho _0^4}{\rho ^4(t)} e^{-2(R/L)t} \Omega _0^2 q = 0 , \end{aligned}$$
(16)
$$\begin{aligned}&\ddot{p} + \bigg ( 2\frac{\dot{\rho }(t)}{\rho (t)}+ \frac{R}{L} \bigg ) \dot{p} + \frac{\rho _0^4}{\rho ^4(t)} e^{-2(R/L)t} \Omega _0^2 p = 0 . \end{aligned}$$
(17)

Because these equations do not involve driving power source terms, the classical solutions in the transformed system consist of only complementary functions. Let us denote them as \(Q_{\mathrm{t},c}(t)\) and \(P_{\mathrm{t},c}(t)\), respectively for charge and current. The quantum description in the transformed system can also be carried out in terms of these solutions.

Now, let us consider the following Schrödinger equations in the transformed system

$$\begin{aligned} i\hbar \frac{\partial \psi _{n}' ({q},t)}{\partial t} = \hat{H}' \psi _{n}'({q},t) . \end{aligned}$$
(18)

From this equation, we easily confirm that the Schrödinger solutions at initial time are given by

$$\begin{aligned} \psi _{n}' ({q},0) = \left( \frac{L \Omega _0}{\hbar \pi }\right) ^{1/4} \frac{1}{\sqrt{2^nn!}} H_n \left[ \left( \frac{L \Omega _0}{\hbar }\right) ^{1/2} {q}\right] \exp \left( -\frac{L \Omega _0}{2\hbar } {q}^2\right) , \end{aligned}$$
(19)

where \(H_n\) are Hermite polynomials of order n. In Eq. (19), it is assumed for convenience that the global phase at initial time is zero. The annihilation and the creation operators in the transformed system is represented as

$$\begin{aligned} \hat{a}= {} \sqrt{\frac{L \Omega _0}{2\hbar }}\hat{q} + \frac{i\hat{p}}{\sqrt{2\hbar L \Omega _0}} , \end{aligned}$$
(20)
$$\begin{aligned} \hat{a}^\dagger= {} \sqrt{\frac{L \Omega _0}{2\hbar }}\hat{q} - \frac{i\hat{p}}{\sqrt{2\hbar L \Omega _0}}, \end{aligned}$$
(21)

which correspond to those of the simple harmonic oscillator.

It may be worthy to find quantum states that oscillate with time like classical ones. These states correspond to a class of a displaced state and are obtained by displacing number states with a displacement operator. We can put the displacement operator in terms of \(\hat{a}\) and \(\hat{a}^\dagger \), at initial time, in the form

$$\begin{aligned} \hat{D} (\alpha ) = \exp (\alpha \hat{a}^\dagger - \alpha ^* \hat{a}), \end{aligned}$$
(22)

where \(\alpha \) is an eigenvalue of \(\hat{a}\) and is given by

$$\begin{aligned} \alpha = \sqrt{\frac{L \Omega _0}{2\hbar }} Q_{\mathrm{t},c}(0) + \frac{i P_{\mathrm{t},c}(0)}{\sqrt{2\hbar L \Omega _0}}. \end{aligned}$$
(23)

Using Eqs. (20) and (21), it is possible to show that Eq. (22) is represented in terms of \(\hat{q}\) and \(\hat{p}\). Then, after decoupling the exponential function into \(\hat{q}\)- and \(\hat{p}\)-terms, we have [32]

$$\begin{aligned} \hat{D} (\alpha ) = & {} \exp \left( -i\frac{Q_{\mathrm{t},c}(0)P_{\mathrm{t},c}(0)}{2\hbar }\right) \exp \left( i\frac{P_{\mathrm{t},c}(0) \hat{q}}{\hbar }\right) \\ & \times \exp \left( -i\frac{{Q}_{\mathrm{t},c} (0) \hat{p}}{\hbar }\right) . \end{aligned} $$
(24)

With the use of this operator, the initial wave functions can be made to be displaced. Then, we have a DNS which oscillates like a classical state. By acting a time evolution operator on the wave functions of such displaced states, one can find the time evolution of the wave functions. The degree of displacement is determined by the scale of \(\alpha \), i.e., the values of \(Q_{\mathrm{t},c}(0)\) and \(P_{\mathrm{t},c}(0)\). In the next subsection, we will investigate the time behavior of superposition of two individual DNSs.

Superposition of displaced number states

It is interesting to study superpositions of two different quantum states on account of their widely acknowledged nonclassical properties. Amplitude interference that appears in the superposition states (Schrödinger cat states) is one of the most novel characteristics of quantum mechanics that has no analogue in classical mechanics. While superpositions of pure number states seldom share the coherence properties that are necessary in both fundamental experiments and practical implementations applicable to science and technology, a superposition of DNSs exhibits coherence properties and other interesting quantum statistical properties such as unusual oscillations in the quantum number distribution [33].

Consider a superposition of two DNSs, \(\hat{D} (\alpha ) \psi _{n}' ({q},0)\) and \(\hat{D} (-\alpha ) \psi _{n}' ({q},0)\):

$$\begin{aligned} \psi _{\mathrm{c},n}'^\epsilon ({q},0) \equiv \lambda _\mathrm{c}^\epsilon [\hat{D} (\alpha )+ \epsilon \hat{D} (-\alpha )] \psi _{n}' ({q},0), \end{aligned}$$
(25)

where \(\epsilon = |\epsilon | e^{i\varphi }\) and \(\lambda _\mathrm{c}^{\epsilon }\) is a normalization constant of the form

$$\begin{aligned} |\lambda _\mathrm{c}^{\epsilon }|^2 = [1+ |\epsilon |^2 +2 |\epsilon | \exp (-2|\alpha |^2 ) L_n (4|\alpha |^2) \cos \varphi ]^{-1}, \end{aligned}$$
(26)

where \(L_n\) are Laguerre polynomials of order n. In the earlier work of Cahill and Glauber, we can find the idea of the definition of DNS, where they have considered it as the eigenstate of \(\hat{D}(\alpha )\) [34]. For the methods of generating DNSs and how to reconstruct them, one can refer to Ref. [35]. The generation of superposition of DNSs given in Eq. (25) is given in Ref. [36]. For \(\epsilon =\pm 1\) with \(n=0\), Eq. (25) becomes even and odd coherent states respectively [24].

Using Eq. (24), we can easily evaluate Eq. (25) to be

$$\begin{aligned} \psi _{\mathrm{c},n}'^\epsilon ({q},0) =\lambda _\mathrm{c}^\epsilon [\psi _{\mathrm{c},n,+}' ({q},0) + \epsilon \psi _{\mathrm{c},n,-}' ({q},0)], \end{aligned}$$
(27)

where

$$\begin{aligned} \psi _{\mathrm{c},n,\pm }' ({q},0)= \left( \frac{L\Omega _0}{\hbar \pi }\right) ^{1/4} \frac{1}{\sqrt{2^nn!}} H_n \left[ \left( \frac{L\Omega _0}{\hbar }\right) ^{1/2} [{q} \mp Q_{\mathrm{t},c}(0)]\right] \nonumber \\\quad \times \exp \left( -i\frac{Q_{\mathrm{t},c}(0)P_{\mathrm{t},c}(0)}{2\hbar } \pm i\frac{P_{\mathrm{t},c}(0)q}{\hbar } \right)\times \exp \left( -\frac{L\Omega _0}{2\hbar } [{q} \mp Q_{\mathrm{t},c}(0)]^2 \right) . \end{aligned}$$
(28)

Now, let us consider the following time evolution operator defined in the transformed system

$$\begin{aligned} \hat{T}'(\hat{q},\hat{p},t) = \exp \left( - \frac{i }{\hbar }\int _0^t \hat{H}'(\hat{q}, \hat{p}, \tau ) \mathrm d \tau \right) . \end{aligned}$$
(29)

If we use a useful identity that is given in Eq. (A1) in Appendix A, the time evolution operator becomes

$$\begin{aligned} \hat{T}'= {} \frac{1}{\sqrt{\cos \Omega (t)}} \exp \left[ -\frac{iL \Omega _0}{2\hbar }\hat{q}^2 \tan \Omega (t) \right] \exp \left[ -\frac{i}{\hbar } \hat{q} \hat{p}\ln [\cos \Omega (t)] \right] \nonumber \\\times \exp \left[ -i \frac{1}{2L\Omega _0 \hbar }\hat{p}^2 \tan \Omega (t) \right] \exp \left[ -\frac{i}{\hbar } \int _0^t {\mathcal L}_{p} (\tau ) \text{d}\tau \right] , \end{aligned}$$
(30)

where \(\Omega (t)\) is given by

$$\begin{aligned} \Omega (t) = \rho _0^2 \Omega _0 \int _0^t \frac{e^{-(R/L)\tau }}{\rho ^2 (\tau )} \mathrm d\tau . \end{aligned}$$
(31)

The time evolution of the wave functions in the transformed system is obtained by acting \(\hat{T}'\) on Eq. (27), i.e.,

$$\begin{aligned} \psi _{\mathrm{c},n}'^\epsilon ({q},t) = \hat{T}' \psi _{\mathrm{c},n}'^\epsilon ({q},0). \end{aligned}$$
(32)

Using Eq. (30) with the relations given in Eqs. (A2) and (A3) in Appendix A, we see that Eq. (32) is easily evaluated to be

$$\begin{aligned} \psi _{\mathrm{c},n}'^\epsilon ({q},t) = \lambda _\mathrm{c}^\epsilon [ \psi _{\mathrm{c},n,+}' ({q},t) + \epsilon \psi _{\mathrm{c},n,-}' ({q},t)], \end{aligned}$$
(33)

where

$$\begin{aligned}\psi _{\mathrm{c},n,\pm }' ({q},t) &= \root 4 \of {\frac{L \Omega _0}{\hbar \pi }} \frac{1}{\sqrt{2^nn!}} H_n \bigg [\sqrt{\frac{L \Omega _0}{\hbar }}({q} \mp Q_{\mathrm{t},c}(t) )\bigg ] \nonumber \\& \quad \times \exp \bigg [-\frac{L \Omega _0}{2\hbar } \bigg ( ({q} \mp Q_{\mathrm{t},c}(t) )^2 \mp 2iq \frac{P_{\mathrm{t},c}(t)}{L \Omega _0} + i Q_{\mathrm{t},c}(t) \frac{P_{\mathrm{t},c}(t)}{L \Omega _0} \bigg ) \bigg ] \nonumber \\& \quad \times \exp \bigg [ -i\Omega (t) \left( n+\frac{1}{2}\right) -\frac{i}{\hbar } \int _0^t {\mathcal L}_{p} (\tau ) \text{d}\tau \bigg ] . \end{aligned}$$
(34)

Notice that the time evolutions of \(Q_{\mathrm{t},c}(t)\) and \(P_{\mathrm{t},c}(t)\) that appeared in Eq. (34) are given by

$$\begin{aligned} Q_{\mathrm{t},c}(t)&= Q_{\mathrm{t},c}(0) \cos \Omega (t) + \frac{P_{\mathrm{t},c}(0)}{L \Omega _0} \sin \Omega (t) , \end{aligned}$$
(35)
$$\begin{aligned} P_{\mathrm{t},c}(t)&= {P_{\mathrm{t},c}(0)} \cos \Omega (t) - {L \Omega _0} Q_{\mathrm{t},c}(0)\sin \Omega (t) . \end{aligned}$$
(36)

Thus, we have identified the complete quantum solutions associated to the DNS in the transformed system. We see from Eqs. (35) and (36) that, if the initial condition, \((Q_{\mathrm{t},c}(0),P_{\mathrm{t},c}(0))\), is determined and the time evolution of \(\Omega (t)\) is known, we can easily deduce the time evolutions of \(Q_{\mathrm{t},c}(t)\) and \(P_{\mathrm{t},c}(t)\).

From the inverse transformation of the solutions given in Eq. (33), it is also possible to obtain the complete solutions in the original system:

$$\begin{aligned} \psi _{\mathrm{c},n}^\epsilon ( {q},t) = \hat{U} \psi _{\mathrm{c},n}'^\epsilon ( {q},t). \end{aligned}$$
(37)

Hence, using Eq. (7), we now have

$$\begin{aligned} \psi _{\mathrm{c},n}^\epsilon ( {q},t) =\; \lambda _\mathrm{c}^\epsilon [\psi _{\mathrm{c},n,+} ({q},t) + \epsilon \psi _{\mathrm{c},n,-} ({q},t)], \end{aligned}$$
(38)

where

$$\begin{aligned} \psi _{\mathrm{c},n,\pm } ({q},t)= & {} \root 4 \of {\frac{L\Omega _0}{\hbar \pi }} \sqrt{ \frac{\rho _0}{\rho (t)} } \frac{1}{\sqrt{2^{n}n!}} H_n [\xi _{\pm }(q,t) ] \exp \left( \frac{i}{\hbar } P_{p}(t) {q} \right) \nonumber \\&\times \exp \bigg ( \frac{i L \dot{\rho }(t)e^{(R/L)t}}{2\hbar \rho (t)} [q - Q_{p}(t)]^2 \bigg ) \exp \bigg \{- \frac{\xi _{\pm }^2 (q,t)}{2} \nonumber \\&- \frac{1}{2\hbar }\bigg [ iQ_{\mathrm{t},c}(t) P_{\mathrm{t},c}(t) \mp 2i \frac{\rho _0}{\rho (t)} P_{\mathrm{t},c}(t) [q - Q_{p}(t)] \bigg ]\bigg \} \nonumber \\&\times \exp \left[ -i\Omega (t) \left( n+\frac{1}{2}\right) -\frac{i}{\hbar } \int _0^t {\mathcal L}_{p} (\tau ) \text{d}\tau \right] , \end{aligned}$$
(39)

with

$$\begin{aligned} \xi _{\pm }(q,t) = \sqrt{\frac{L\Omega _0}{\hbar }} \bigg ( \frac{\rho _0}{\rho (t)} [{q}- Q_{p}(t) ] \mp Q_{\mathrm{t},c}(t) \bigg ). \end{aligned}$$
(40)

Although we have chosen \(\rho _0\) as an arbitrary constant, the magnitude of \(\rho _0\) does not affect to the results. If we represent \(\rho (t)\) as \(\rho _0 f(t)\) without loss of generality, all \(\rho _0\) in Eqs. (39) and (40) are canceled out and, as a consequence, the final results are independent of \(\rho _0\).

The full wave functions, Eq. (38) with Eqs. (39) and (40), are very useful for studying the superposition properties of DNSs in the original system. It is well known that the wave function is a probability function that enables us to understand the characteristics of the nanoscale world and its concept constitutes the heart of quantum mechanics. We can estimate subsequent time behavior of charge carriers of the nanoelectronic circuit using the wave functions with some degree of certainty as far as quantum mechanics allows.

To see the time behavior of the state given in Eq. (38), let us consider a solvable case that the time-dependence of the capacitance and the electromotive force is given by

$$\begin{aligned} C(t)&= C_0 (1+\beta t)^4 , \end{aligned}$$
(41)
$$\begin{aligned} {\mathcal E}(t)&= {\textsf {Q}}\left( \frac{1}{C_0(1+\beta t)^4}-\omega _1^2 L\right) \sin (\omega _1 t ), \end{aligned}$$
(42)

where \(C_0[=C(0)]\), \(\beta \), \({\textsf {Q}}\), and \(\omega _1\) are real constants, and we put \(R=0\) in this example for simplicity. Then, it is easily verified that the solutions of Eqs. (6) and (31) are given by

$$\begin{aligned} \rho (t)=\; & {} \rho _0 (1+\beta t), \end{aligned}$$
(43)
$$\begin{aligned} \Omega (t)= & {} \frac{1}{\sqrt{LC_0}} \frac{t}{1+\beta t}, \end{aligned}$$
(44)

and the particular solutions of Eqs. (3) and (4) are given by

$$\begin{aligned} Q_p(t)=\; & {} {\textsf {Q}} \sin (\omega _1 t), \end{aligned}$$
(45)
$$\begin{aligned} P_p(t)=\; & {} L{\textsf {Q}}\omega _1 \cos (\omega _1 t). \end{aligned}$$
(46)

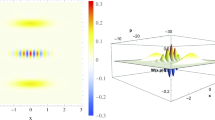
It is important to note that the superposition state composed of the two DNSs exhibits very distinct characteristics compared to those shown by their components. The probability density, \(|\psi _{\mathrm{c},n}^\epsilon ( {q},t)|^2\) which is the absolute square of Eq. (38), is plotted in Fig. 1 as a function of q and t under the same choice of parameters as given from Eq. (41) to Eq. (44) without considering a power source. We see from this figure that the effects of displacement become more conspicuous as the displacing parameters \(Q_{\mathrm{t},c}(0)\) and \(P_{\mathrm{t},c}(0)\) grow. Hence, the amplitude of the oscillation of each component increases as the initial values \(Q_{\mathrm{t},c}(0)\) and \(P_{\mathrm{t},c}(0)\) become large. We can confirm from Fig. 1c, which reveals the highest displacement among Fig. 1a–c, that there appear interference structures when the two components of packets meet together. This is a signature of the nonclassicality of the system. The effects of the sinusoidal power source on charge can be identified from Fig. 2. The comparison of this figure with Fig. 1 reveals that the wave packets are distorted somewhat significantly by the driving power source. Figure 2a is the case of a higher driving frequency while Fig. 2c is that of a relatively low driving frequency. The effects of a higher value of \(\beta \) on packets are shown in Fig. 3. As \(\beta \) increases, the displacing of packets becomes less prominent.

Fig. 1
figure 1

Probability density \(|\psi _{\mathrm{c},n}^\epsilon ({q},t)|^2\) [the absolute square of Eq. (38)] for the system that has parameters illustrated between Eqs. (41) and (46), plotted as a function of q and t. Here, the driving electromotive force is not considered [\(({\textsf {Q}},\omega _1)=(0,0)\)]. Displacing parameters \((Q_{\mathrm{t},c}(0), P_{\mathrm{t},c}(0))\) are (1,1) for a, (2,2) for b, and (5,5) for c. Other values taken here are \(L=1\), \(C_0 = 1\), \(\Omega _0=1\), \(\epsilon =(1+i)/\sqrt{2}\), \(\hbar =1\), \(\beta =0.1\), and \(n=3\). All values are taken to be dimensionless for the sake of convenience. This convention will also be used in all subsequent figures.

Full size image
Fig. 2
figure 2

The same as Fig. 1c, but for the case that the driving electromotive force is not zero. The parameters \(({\textsf {Q}}, \omega _1)\) associated with the electromotive force are (0.3, 15) for a, (1, 3) for b, and (10, 0.3) for c.

Full size image
Fig. 3
figure 3

The effects of large values of \(\beta \) on time evolution of probability density \(|\psi _{\mathrm{c},n}^\epsilon ({q},t)|^2\) illustrated in Figs. 1 and 2. The values of \((\beta , {\textsf {Q}}, \omega _1)\) are (0.25, 0, 0) for a, (0.25, 10, 0.3) for b, and (0.50, 10, 0.3) for c. Other values taken here are \(L=1\), \(C_0 = 1\), \(\Omega _0=1\), \(\epsilon =(1+i)/\sqrt{2}\), \(Q_{\mathrm{t},c}(0)=5\), \(P_{\mathrm{t},c}(0)=5\), \(\hbar =1\), and \(n=3\), which are in fact the same as those of Figs. 1c or 2.

Full size image

Conclusion

A series RLC nanoelectronic circuit driven by an arbitrary power source was considered, where its capacitance is allowed to vary with time. The Hamiltonian of the system is constructed from Kirchhoff’s law and the corresponding quadratic invariant operator is introduced in order to study quantum characteristics of the system. As you can see from Eq. (5), the invariant operator is a somewhat complicated form to manage. In this case, we need to simplify it for further treatment using unitary transformation or canonical transformation. For this purpose, a unitary operator is introduced as shown in Eq. (7) with Eqs. (8)–(10). The transformed invariant operator \(\hat{I}'\) is the same as the Hamiltonian of the simple harmonic oscillator. Because the transformed Hamiltonian is represented in terms of \(\hat{I}'\), we easily identified the quantum solutions in number states in the transformed system. Superposition of DNSs at initial time is considered as given in Eq. (25). The time evolution of DNS in the transformed system is given in Eq. (33). Through inverse transformation of this, the DNS in the original system is evaluated [see Eq. (38) with Eqs. (39) and (40)].

To promote the understanding of our consequence, our results are applied to a particular system that the time dependence of the capacitance is given by Eq. (41). The wave packet is somewhat distorted when a sinusoidal power source is exerted on the system. The corresponding probability densities are illustrated in Figs. 1, 2, and 3 for several values of displacing parameters \((Q_{\mathrm{t},c}(0), P_{\mathrm{t},c}(0))\). When displacing parameters are small (Fig. 1a), the distortion of the wave packet is not so significant and its form is near to that of the original number state. As the values of the displacing parameters increase (Fig. 1b), the distortion of the packet become more or less significant. From Fig. 1c, we see the effects of the strong displacement on the wave function. By comparing Fig. 2c with Fig. 2a, we can make out the difference of time evolution of the wave packet between the cases that angular frequency of the power source is small and large. The effects of displacement become less significant as the value of \(\beta \) increases. All RLC circuits with time-dependent capacitance C(t) and power source \(\mathcal {E}(t)\), founded in an electronic laboratory, may have this quantum nature under the same situation.

From Figs. 1, 2, and 3, you can see interference structures that appear when the two components of the state meet together. This quantum interference is inherent to superposition states and is strong evidence for the signature of nonclassicality of the system, that we cannot find any analogous effects from classical systems [37, 38]. A scheme for observing quantum interference via phase-sensitive amplification of a superposition state using a two-photon CEL (correlated emission laser) amplifier has been suggested by Zubairy and Qamar [39]. Superposition states are vulnerable to external interventions caused from the environment; hence, they can be easily corrupted by noisy or dissipative forces. This is a stumbling-block for achieving robust quantum computations on the basis of nonclassical features of superposition states through encoding logical qubits with a treatment of the states [40, 41]. A number of proposals to overcome this major hurdle in quantum computing has been suggested so far [42–44]. The development of techniques for protecting quantum information from decoherence is crucial for realizing universal quantum computation.

Author's contribution statement

J.R.C. wrote the paper and approved it.