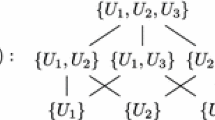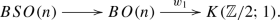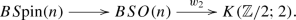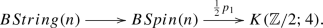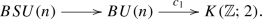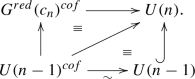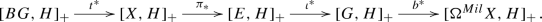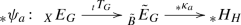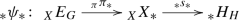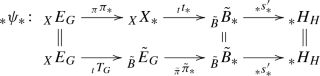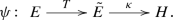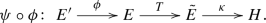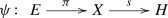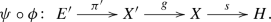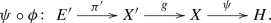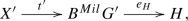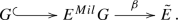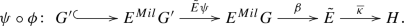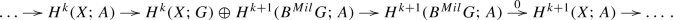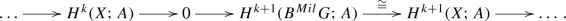Characteristic classes as complete obstructions

Abstract

In the first part of this paper, we propose a uniform interpretation of characteristic classes as obstructions to the reduction of the structure group and to the existence of an equivariant extension of a certain homomorphism defined a priori only on a single fiber of the bundle. Afterwards, we define a family of invariants of principal bundles that detect the number of group reductions that a principal bundle admits. We prove that they fit into a long exact sequence of abelian groups, together with the cohomology of the base space and the cohomology of the classifying space of the structure group.

1 Introduction

By a classical result [3, 32], every principal G-bundle E over a CW-complex X is classified up to equivalence by the homotopy class of a map $X\rightarrow BG$, where BG is the classifying space of the group. Having fixed an abelian group of coefficents $A$, one can look at $\chi _k:H^k(BG;A)\rightarrow H^k(X;A)$, the map induced in cohomology in degree k. The elements of $H^k(BG;A)$ are referred to as universal characteristic classes, and depend only on the topological group G. On the other hand, their images in the cohomology of the base space $H^k(X;A)$ are invariants of the bundle E, known as characteristic classes [22].

It is known that certain characteristic classes measure the obstruction to specific geometric features of the principal bundle. For example, when $k=1$, $A={\mathbb {Z}}/2$ and $G=O(n)$, the generator of the group $H^1(BO(n);{\mathbb {Z}}/2)\cong {\mathbb {Z}}/2$ is the first Stiefel-Whitney class$w_1\in H^1(BO(n);{\mathbb {Z}}/2)$, which measures obstruction to orientability. The orientability of an O(n)-bundle can be expressed by saying that the structure group can be reduced to SO(n) or, equivalently, by saying that the choice of a sign on a distinguished fiber can be extended coherently to the whole bundle. This is encoded precisely in the following theorem [22].

Classical Theorem. For E an O(n)-bundle over a CW-complex X, the following are equivalent.

• (A) There exists an SO(n)-bundle ${\hat{E}}$ over X such that ${\hat{E}}\otimes _{SO(n)}O(n)\cong E$.

• (B) The first Stiefel–Whitney class $w_1$ of E vanishes, i.e., $w_1(E)=0\in H^1(X;{\mathbb {Z}}/2)$.

• (C) The map $\det :O(n)\rightarrow O(1)\cong {\mathbb {Z}}/2$ extends to an O(n)-equivariant map $E\rightarrow {\mathbb {Z}}/2$.

While the different flavors of characteristic classes are often studied separately, in this paper we develop a uniform treatment that can be applied in great generality. We first prove that every characteristic class measures the obstruction to two features of a principal bundle: the possibility of reducing the structure group, and the possibility of extending an interesting quantity to the whole bundle (being a priori only defined on a single fibre). The general approach gives a global explanation of the fact that so many examples of characteristic classes were already known to measure obstruction to group reduction. Afterwards, we define the plus-cohomology groups of a principal bundle: invariants that detect the number of interesting group reductions that the bundle admits. We prove that the plus-cohomology groups fit into a long exact sequence together with the cohomology groups of the base space and of the classifying space of the structure group.

The first contribution of this paper is an analog of this theorem for any universal characteristic class $c\in H^k(BG;A)$, where G is any topological group whose homotopy groups are countable (e.g. a Lie group) and $A$ is a countable abelian group. To this end, we first construct a topological group $G^{red}(c)$ and a homomorphism of topological groups $\gamma :G^{cof}:=\Omega ^{Mil}BG\rightarrow M^{k-1}A$, which will play for $c\in H^k(BG;A)$ the roles played for the first Stiefel–Whitney class $w_1\in H^1(X;{\mathbb {Z}}/2)$ in the theorem above by SO(n) and by the determinant map, respectively. These constructions rely on Milnor’s model $\Omega ^{Mil}X$ of the based loop space for a countable CW-complex X from [16] and on Milgram’s model of classifying space $MH$ of an abelian topological group $H$ from [19].

While the precise definitions of $\gamma$ and $G^{red}(c)$ require some work, their homotopical behaviour can be described as follows. If we regard the universal characteristic class c as a map $c:BG\rightarrow K(k;A)$, then $\gamma$ is a homomorphism of topological groups homotopy equivalent to $\Omega c:G\simeq \Omega BG\rightarrow K(k-1;A)$, and $G^{red}(c)$ is a topological group which gives a model for the homotopy fiber of $\Omega c$. In particular, the homotopy groups of $G^{red}(c)$ are the same as G, except possibly in degrees $k-2$ and $k-1$, where the values depend on c according to an exact sequence of the following form:

Although the reduction group $G^{red}(c)$ and the delooping homomorphism $\gamma$ are only unique in a homotopical sense, which is explained after the constructions, they succeed at detecting the vanishing of the characteristic class c for G-bundles. This idea is summarized by the following result, that is a combination of Theorems 2.15 and 2.18.

Main Result 1. Let G be a topological group whose homotopy groups are countable, $A$ a countable abelian group, $k>1$ and $c\in H^k(BG;A)$ a universal characteristic class. For E a G-bundle over a CW-complex X, the following are equivalent.

• (A) There exists a $G^{red}(c)$-bundle ${\hat{E}}$ over X such that ${\hat{E}}\otimes _{G^{red}(c)}G\cong E$.

• (B) The characteristic class c of E vanishes, i.e., $c(E)=0\in H^k(X;A)$.

• (C) The homomorphism of topological groups $\gamma :G^{cof}\rightarrow M^{k-1}A$ extends to a $G^{cof}$-equivariant continuous map $E^{cof}\rightarrow M^{k-1}A$.

Here, $G^{{cof}}$ and $E^{{cof}}$ are fattened-up versions of G and E, which are introduced in Construction 1.17 and do not change the homotopy type of G and E, and $M^{k-1}A$ is the $(k-1)$-fold Milgram delooping from [19]: an Eilenberg-Maclane space of type $K(A;k-1)$ that is also a group.

The equivalence between statements of type (A) and (B) is well-known for groups appearing in the Whitehead tower of the orthogonal group O(n) and certain characteristic classes. For instance, the second Stiefel–Whitney class measures the obstruction to admitting a spin structure, the first fractional Pontryagin class measures the obstruction to admitting a string structure, and the second fractional Pontryagin class measures the obstruction to admitting a Fivebrane structure [30]. These cases are recovered and strengthened by the fact that the reduction of the structure group is expressed not only by a lift of the classifying map, but by an honest tensor product with a topological group. The general construction $G^{red}(c)$ might still look different from some of the explicit groups that are known for specific examples. However, there is a homomorphism of topological groups from $G^{red}(c)$ to the classical model, which is also a weak equivalence. For instance, in the case of the first Stiefel–Whitney class, there is a map of topological groups $G^{red}(w_1)\rightarrow SO(n)$ that is also a weak equivalence. As a further application, the construction $G^{red}(c)$ can also be used to build a Whitehead tower [34] of G, where every layer is a topological group (and the maps homomorphisms of such).

On the other hand, for an arbitrary universal characteristic class $c\in H^k(BG;A)$, the equivalence between conditions analogous to (B) and (C) is not as evident in the literature. Even for well-studied examples of characteristic classes (e.g. Chern classes), there is no obvious choice of homomorphism for which the characteristic class measures the obstruction to a coherent extension.

While the first part of the paper explains how characteristic classes are related to the existence of group reductions of a fixed bundle, one can then wonder about the uniqueness of such group reductions, or more generally look for quantitative analogs of the first result. For instance, when $c:=w_2\in H^2(BSO(n);{\mathbb {Z}}/2)$ is the second Stiefel–Whitney class, the problem translates to counting how many spin structures (up to a suitable equivalence relation) an orientable bundle admits. In the second part of the paper we develop some tools in order to answer these kinds of questions. More precisely, we give a quantitative explanation of the equivalence between (B) and (C) for a universal characteristic class $c\in H^k(BG;A)$ represented by a homomorphism $\gamma$ of topological groups. Indeed, given a G-bundle E over X, the vanishing of the characteristic class c(E) can be expressed by saying that c is in the kernel of the characteristic map $\chi _k:H^k(BG;A)\rightarrow H^k(X;A)$ of E, whereas the extension of the homomorphism $\gamma$ can be expressed by saying that $\gamma$ is in the image of a certain map. Compactly, this phenomenon is governed by an exact sequence of abelian groups. In order to describe the maps that form such a sequence, we need to describe the setup.

We first define a category ${{{\mathcal {B}}un}_*}$ of pointed bundles that contains topological groups as bundles over a point, and pointed spaces as bundles with a trivial structure group. In this category lives in particular the Nomura-Puppe sequence (following the terminology of [6]) of any G-bundle E over X,

As described in Remark 3.5. this sequence is obtained by including the structure group G as a distinguished fiber of E, by projecting E onto the base space X, and by adding on one side the usual classifying map $X\rightarrow BG$, and on the other side the classifying map $\Omega ^{Mil}X\rightarrow G$, which is the homomorphism of topological groups constructed in a previous paper [26]. We explain that any topological abelian group, and in particular the Milgram delooping $M^kA$, is an abelian group object in the category ${{\mathcal {B}}un}_*$, and thus the homset ${{{\mathcal {B}}un}_*}(E,M^kA)$ becomes an abelian group, when endowed with pointwise multiplication. We define on it a compatible equivalence relation $\simeq _+$, and focus on the plus-cohomology group of E:

$$\begin{aligned} H_+^k(E;A):={{{\mathcal {B}}un}_*}(E^{cof},M^kA)/ {}_{\simeq _+}. \end{aligned}$$

When the input is a discrete bundle X, namely a pointed space, or a codiscrete bundle G, namely a topological group, the plus-cohomology groups recover the ordinary cohomology groups (of the classifying space), i.e.,

$$\begin{aligned} H^k_+(X;A)\cong H^k(X;A)\text { and }H^k_+(G;A)\cong H^{k+1}(BG;A). \end{aligned}$$

More generally, the plus-cohomology of a trivial bundle $X\times G$ gives the sum of the two, and the plus-cohomology of a contractible bundle EG is trivial, i.e.,

$$\begin{aligned} H^k_+(X\times G;A)\cong H^k(X;A)\oplus H^{k+1}(BG;A)\text { and }H^k_+(EG;A)\cong 0. \end{aligned}$$

As the equivalence relation $\simeq _+$ is not totally well behaved with respect to precomposition of maps, the assignment $E\mapsto H^k_+(E;A)$ will not define a functor on the category ${{{\mathcal {B}}un}_*}$. However, the assignment acts on the Nomura-Puppe sequence of a bundle E, which leads to the following result appearing later as Theorem 3.23.

Main Result 2. Let G be a topological group whose homotopy groups are countable. For every G-bundle E over a CW-complex X, there is a long exact sequence of abelian groups

of which the connecting map can be identified with the characteristic map $\chi _k:H^k(BG;A)\rightarrow H^k(X;A)$ induced by the classifying map of E.

From the long exact sequence, one can extract a lot of geometric information about the bundle. The exactness at $H^k(BG;A)$ reflects the fact that characteristic classes are obstructions to the extension of the delooping homomorphism to the whole bundle, incorporating part of the previous theorem. The exactness at $H^k_+(E;A)$ says that the plus-cohomology group is a non-trivial extension of the kernel of the characteristic map in degree $k+1$, and the cokernel of the characteristic map in degree k:

They carry, respectively, information about the characteristic classes of the bundles in degree k and $k+1$. This is an indication of some surprising interaction between characteristic classes in different degrees.

The existence of such a long exact sequence suggests the existence of (and is used in the author’s Ph.D. thesis [27] to construct) an unexpected isomorphism

$$\begin{aligned} H_+^k(E;A)\cong H^{k+1}({\mathrm{cof}}(t);A) \end{aligned}$$

between the plus-cohomology groups of E and the ordinary cohomology groups of the homotopy cofiber ${\mathrm{cof}}(t)$ of the classifying map t of E. This yields an alternative definition of the plus-cohomology groups, which has a homotopical flavor and does not require any further assumption on the structure group G. On the other hand, the original definition is the one that allows us to extract the geometric information of the bundle. For instance, we explain how the plus-cohomology groups of a bundle can be used to counting the group reductions with respect to a fixed structure group, e.g., counting the spin structures of an orientable bundle or enumerate the string structures of a spin bundle.

In Sect. 1 we set up the framework for the structure group G the theory applies to. We start by stating useful properties of countable CW-groups, which are very special topological groups. We then study topological groups that are equivalent to countable CW-groups in a suitable sense, and prove that they coincide with topological groups whose homotopy groups are countable. In Sect. 2 we construct from every universal characteristic class a reduction group and a delooping homomorphism, and prove that they both detect the vanishing of that universal characteristic class. In Sect. 3 we define the plus-cohomology groups of principal bundles. We prove that they fit into a long exact sequence, and explain what features of a bundle they detect.

2 Framework for the structure group

2.1 Recollection of prior results

We refer the reader to [3, 32] for the general theory of principal bundles. In this section, we recall the preliminary results that are needed in the paper. Unless specified otherwise, in this paper all bundles are supposed to be principal bundles.

Notation 1.1

Let X be a topological space and G a topological group.

• A G-bundle over X consists of a space E, together with a map $E\rightarrow X$ and a right G-action $E\times G\rightarrow E$, such that E is locally trivial, i.e., there exists an open cover $\{U\}$ of X and G-homeomorphisms $E|_U\cong U\times G$ compatible with the projection over X. The group G is called structure group, and the space X is called base space. We denote by ${}_X{{\mathcal {B}}un}_G$ the class of principal G-bundles over X. Two G-bundles E and $E'$ over X are equivalent if there exists an equivalence of bundles$\Phi :E\rightarrow E'$, i.e., a map G-equivariant continuous map that respects the projection over X. Equivalence of bundles defines an equivalence relation, because the G-action guarantees that any equivalence is bijective with continuous inverse, and we write $E\cong E'$ if E and $E'$ are equivalent.

• If $a:G\rightarrow G'$ is a map of topological groups, it endows $G'$ with a G-action, and we denote by $a_*E$ the tensor product $E\otimes _GG'$, which is a $G'$-bundle over X and comes with a canonical map $E\cong E\otimes _GG\rightarrow E\otimes ^a_GG'=a_*E$. Dually, if $f:X'\rightarrow X$ is a continuous map, we denote by $f^*E$ the pullback $X'\times _XE$ of E along f, which is a $G'$-bundle over $X'$ and comes with a canonical map $f^*E=X'\times _XE\rightarrow X\times _XE\cong E$. Given $f':X'\rightarrow X$ another continuous map and $a':G'\rightarrow G''$ another map of topological groups, there are canonical equivalences of $G''$-bundles over $X''$:

  $$\begin{aligned} (f\circ f')^*(E)\cong f'^*f^*(E),\quad a_*f^*(E)\cong f^*a_*(E)\quad \text {and}\quad (a'\circ a)_*(E)\cong a'_*a_*(E). \end{aligned}$$

The following property is easy to verify.

Proposition 1.2

Let $a:G\rightarrow G'$ be a map of topological groups and $f:X\rightarrow X'$ a continuous map. Let E be a G-bundle over X and $E'$ a $G'$-bundle over $X'$. Any a-equivariant map $\psi :E\rightarrow E'$ that induces $f:X\rightarrow X'$ also induces an equivalence $a_*E\cong f^*E'$ of $G'$-bundles over X. $\square$

Recall that, if E is a G-bundle over B and E is contractible, we say that E is a universalG-bundle for G and B is a classifying space for G.

Theorem 1.3

[17, §3]. Let G be a topological group. There exists a universal G-bundle EG with corresponding classifying space BG. The constructions EG and BG are functorial on topological groups.

We recall the universal property of universal G-bundles and classifying spaces, which determines the weak homotopy type of the classifying space of G.

Theorem 1.4

[3]. Let E be a universal G-bundle with base space B. For every CW-complex X, the pullback construction induces a natural bijection

$$\begin{aligned} (-)^*(E):{{\mathcal {T}}op}_*(X,B)/ {}_{\simeq }\ \cong {}_B{{\mathcal {B}}un}_G/ {}_{\cong }. \end{aligned}$$

Remark 1.5

It is easy to see that any topological group G admits a model of classifying space that is also a CW-complex. Indeed, given a weak equivalence $B\rightarrow BG$ with B a CW-complex, the pullback $(B\rightarrow BG)^*(EG)$ is a universal G-bundle with base space the CW-complex B. However, it is often convenient to have at one’s disposal models of classifying spaces or universal bundles that have further topological or algebraic properties.

Recall from [16] that a countable CW-complex is a CW-complex with countably many attaching cells. Recall from [17] that a countable CW-group is a countable CW-complex with a structure of a topological group such that the multiplication and the inversion are cellular. Countable CW-groups should not be confused with G-CW-complexes from equivariant homotopy theory (for instance treated in [1, 12, 14]).

For countable CW-groups, there are special models of classifying spaces that enjoy further properties.

Theorem 1.6

[17, §5]. Let G be a countable CW-group. There exists a universal G-bundle such that the total space $E^{Mil}G$ and the base space $B^{Mil}G$ are countable CW-complexes. The constructions $E^{Mil}G$ and $B^{Mil}G$ are functorial on countable CW-groups (and maps of topological groups between such).

Remark 1.7

Given a countable CW-group G, the spaces EG and $E^{Mil}G$ from [17] are both defined. They share the same underlying G-set (given by the fat realization of the bar construction of G), but $E^{Mil}G$ is endowed with what Milnor calls the weak topology (that is the usual topology on a fat geometric realization), whereas EG is endowed with what he call the strong topology (which is the initial topology with respect to a certain class of maps). Using the explicit descriptions of these topologies from [17, Section 2], one can see that the identity ${{\mathrm{d}}}:E^{Mil}G\rightarrow EG$ defines a continuous map. The corresponding classifying spaces BG and $B^{Mil}G$ also carry (a priori) different topologies. The identity map ${{\mathrm{d}}}:B^{Mil}G\rightarrow BG$ defines however a weak equivalence (because the identity ${{\mathrm{d}}}:E^{Mil}G\rightarrow EG$ is a weak equivalence and is compatible with the G-action). Both models are needed in this paper (e.g. in the proof of Proposition 1.14). On the one hand, BG is always defined and used when G is an arbitrary group. On the other hand, when restricting to the case of G being a countable CW-group, $B^{Mil}G$ is defined and gives a model of classifying space that admits the structure of a countable CW-complex.

The emphasis on countable CW-complexes is also due to the following theorem of Milnor.

Theorem 1.8

(Milnor). Let X be a connected countable CW-complex. There exists a countable CW-group $\Omega ^{Mil}X$ and a universal $\Omega ^{Mil}X$-bundle $P^{Mil}X$ over X, with the property that $(-)_*(P^{Mil}X)$ induces for every topological group G a surjection

$$\begin{aligned} (-)_*(P^{Mil}X):{{\mathcal {G}}p}({{\mathcal {T}}op})(\Omega ^{Mil}X,G)\twoheadrightarrow {}_X{{\mathcal {B}}un}_G/ {}_{\cong }. \end{aligned}$$

Proof

Suppose at first that X is a countable connected simplicial complex. Then, modulo a change of notation, the constructions of the topological group $\Omega ^{Mil}X$ and of the $\Omega ^{Mil}X$-bundle $P^{Mil}X$ over X are from [16, Theorem 3.1]. Still in [16, Theorem 3.1], Milnor endows $\Omega ^{Mil}X$ with the structure of a countable CW-complex, which makes $\Omega ^{Mil}X$ into a countable CW-group, as mentioned in the first paragraph of [17, Section 5]. Finally, the surjection of $(-)_*(P^{Mil}X)$ is from [16, Theorem 5.1].

When, more generally, X is a connected countable CW-complex, Milnor explains in [16, Corollary 3.7] how to obtain the topological group $\Omega ^{Mil}X$ and the $\Omega ^{Mil}X$-bundle $P^{Mil}X$. Namely, given a homotopy equivalence $s:X\rightarrow S$, where S is a countable connected simplicial complex, one can take $\Omega ^{Mil}X:=\Omega ^{Mil}S$ and $P^{Mil}X:=s^*P^{Mil}S$. Since s is a homotopy equivalence, the surjection of $(-)_*(P^{Mil}S)$ implies the surjection of $(-)_*(P^{Mil}X)$. $\square$

Milnor’s model of classifying space ${\tilde{B}}$ will be used to identify maps of topological groups, in the sense of the following definition.

Definition 1.9

Let G and $G'$ be countable CW-groups. We say that two maps $a,b:G\rightarrow G'$ of topological group are algebraically equivalent if there exists a homotopy ${\tilde{B}}a\simeq {\tilde{B}}b:B^{Mil}G\rightarrow B^{Mil}G'$. In this case we write $a\equiv b:G\rightarrow G'$.

Algebraic equivalence is indeed an equivalence relation, and detects the kernel of the surjection above, as made precise by the following theorem from a previous paper.

Theorem 1.10

[26]. Let X be a connected countable CW complex and G a countable CW-group. Then the assignments $(-)_*(P^{Mil}X)$ and $(-)^*(E^{Mil}G)$ induce bijections

$$\begin{aligned} {{\mathcal {G}}p}({{\mathcal {T}}op})(\Omega ^{Mil}X,G)/ {}_{\equiv }\ \cong \ {}_X{{\mathcal {B}}un}_G/ {}_{\cong }\ \cong \ {{\mathcal {T}}op}(X,B^{Mil}G)/ {}_{\simeq }. \end{aligned}$$

Remark 1.11

If a map of topological groups $a:\Omega ^{Mil}X\rightarrow G$ and a continuous map $g:B^{Mil}G\rightarrow X$ correspond to each other as in Theorem 1.10, i.e., there is an equivalence $a_*P^{Mil}X\cong g^*E^{Mil}G$ of G-bundles over X, then a is a weak equivalence if and only if g is a weak equivalence. Indeed, the map $\Phi$ induced by a and g

$$\begin{aligned}&\Phi :P^{Mil}X\rightarrow P^{Mil}X\otimes _{\Omega ^{Mil}X}G=a_*P^{Mil}X\cong g^*E^{Mil}G\\&\quad =X\times _{B^{Mil}G}E^{Mil}G\rightarrow E^{Mil}G \end{aligned}$$

is a weak equivalence (because its source and target are contractible), induces $g:X\rightarrow B^{Mil}G$ at the level of base spaces and restricts to $a:\Omega ^{Mil}X\rightarrow G$ on every fiber. It follows that a is a weak equivalence if and only if g is one.

We state one last property of countable CW-complexes that will be needed later. The proof is elementary but technical, and is therefore postponed until the appendix.

Proposition 1.12

Let E be a fiber bundle over X with fiber F. If X and F admit the structure of countable CW-complexes, so does E.

Many of the constructions that have been recalled involve countable CW-groups. It is in general hard to understand whether a given topological group endowed with a CW-structure is indeed a countable CW-group. We collect here the main known examples.

Example 1.13

• All discrete countable groups are countable CW-groups.

• For every connected countable CW-complex X, the group $\Omega ^{Mil}X$ is a countable CW-group.

• Finite products of countable CW-groups are countable CW-groups.

• It is possible but unclear whether the usual matrix groups (e.g., the orthogonal group O(n), the unitary group U(n), and the simplectic group Sp(n)) are (countable) CW-groups. A finite CW-structure for O(n), U(n), and Sp(n) (seen as degenerate Stiefel manifolds) is given, for instance, in [22, Theorem 6.4] or [31, Theorem IV.2.1]. By reading through the definition of the cells, one could investigate by direct inspection whether the multiplication and the inversion maps are cellular. While it is easy to treat the case $n=1$, addressing the question for general n becomes very quickly computationally involved.

The reader should not be discouraged by the fact that the condition of being a countable CW-group is highly restrictive. Indeed, the next section is devoted to relaxing this notion in order to include the majority of relevant examples (e.g. all Lie groups).

2.2 Groups that admit a countable CW-replacement

Thanks to the following proposition, we see that many groups are at least equivalent to a countable CW-group in a precise sense. The theory developed in the later sections of this paper applies to such larger class of topological groups. Recall from Remark 1.7 that for every countable CW-group G the identity maps ${{\mathrm{d}}}:E^{Mil}G\rightarrow EG$ and ${{\mathrm{d}}}:B^{Mil}G\rightarrow BG$ are weak equivalences.

Proposition 1.14

For a topological group G, the following are equivalent.

• (1) There exists a countable CW-group ${\tilde{G}}$ and a map of topological groups $\epsilon :{\tilde{G}}\rightarrow G$ that is also a weak equivalence.

• (2) There exists a classifying space ${\tilde{B}}$ for G that is a countable CW-complex.

• (3) All homotopy groups of G are countable.

Proof

We prove $(1)\Rightarrow (2)$. Suppose we are given a countable CW-group ${\tilde{G}}$ and a map of topological groups $\epsilon :{\tilde{G}}\rightarrow G$ that is a weak equivalence. By applying the functorial model of classifying space from Theorem 1.3 we obtain a weak equivalence $B{\tilde{G}}\rightarrow BG$. Recall from Remark 1.7 that the identity is a weak equivalence ${{\mathrm{d}}}:B^{Mil}{\tilde{G}}\rightarrow B{\tilde{G}}$. Therefore, $B\epsilon :B^{Mil}{\tilde{G}}\rightarrow B{\tilde{G}}\rightarrow BG$ is a weak equivalence. By pulling back $EG\rightarrow BG$ along this map we obtain a new universal G-bundle of which the base space is the countable CW-complex $B^{Mil}{\tilde{G}}.$

We prove $(2)\Rightarrow (1)$. Let ${\tilde{E}}$ be a universal G-bundle with a countable CW-complex ${\tilde{B}}$ as base space. By Theorem 1.8, there exists a map of topological groups $\epsilon :\Omega ^{Mil}B^{Mil}\rightarrow G$ such that $\epsilon _*(P^{Mil}{\tilde{B}})\cong {\tilde{E}}$. The map induced by $\epsilon$

$$\begin{aligned} P^{Mil}{\tilde{B}}\cong P^{Mil}{\tilde{B}}\otimes _{\Omega ^{Mil}{\tilde{B}}}\Omega ^{Mil}{\tilde{B}}\rightarrow P^{Mil}{\tilde{B}}\otimes ^\epsilon _{\Omega ^{Mil}{\tilde{B}}}G=\epsilon _*(P^{Mil}{\tilde{B}})\cong {\tilde{E}} \end{aligned}$$

is a weak equivalence, as the source and the target are weakly contractible spaces, and is compatible with the projection over ${\tilde{B}}$. It follows that the restriction to the fiber, which can be computed to be

$$\begin{aligned} \epsilon :\Omega ^{Mil}{\tilde{B}}\cong \Omega ^{Mil}{\tilde{B}}\otimes _{ \Omega ^{Mil}{\tilde{B}}} \Omega ^{Mil}{\tilde{B}}\rightarrow \Omega ^{Mil}{\tilde{B}}\otimes ^\epsilon _{\Omega ^{Mil}{\tilde{B}}}G\cong G, \end{aligned}$$

is therefore a weak equivalence, too.

We prove $(2)\Leftrightarrow (3)$. Let B be a classifying space for G that admits the structure of a CW-complex, which exists by Remark 1.5. Observe that the homotopy groups of G are countable if and only if the homotopy groups of B are countable. By [13, Theorem 6.1, Page 137], the homotopy groups of B are countable if and only if B is homotopy equivalent to a countable CW-complex ${\tilde{B}}$, which is necessarily a classifying space for G, too. $\square$

The proposition motivates the following terminology.

Definition 1.15

If G is a topological group satisfying either of the equivalent conditions of Proposition 1.14, we say that Gadmits a countable CW-replacement or that it admits a good classifying space. Referring to the notation from Proposition 1.14, the group ${\tilde{G}}$ is a countable CW-replacement for G, the space ${\tilde{B}}$ is a good classifying space for G and the group $\Omega ^{Mil}{\tilde{B}}$ is a good countable CW-replacement for G. Since the good countable CW-replacement of a group behaves in many ways as a cofibrant replacement for that group, we let us be inspired by the model categorical terminology and denote it by

$$\begin{aligned} G^{cof}:=\Omega ^{Mil}{\tilde{B}}. \end{aligned}$$

The emphasis on $\Omega ^{Mil}{\tilde{B}}$, as opposed to the more general ${\tilde{G}}$, is due to the fact that we have a good control on maps of topological groups defined on $\Omega ^{Mil}{\tilde{B}}$, thanks to Theorem 1.8. Note also that all choices of ${\tilde{B}}$ lead to equivalent groups $G^{cof}$.

The notion of a topological group that admits a countable CW-replacement widely generalizes that of countable CW-group.

Example 1.16

• Using [13, Theorem 6.1, Page 137], we obtain that any topological group whose underlying topological space is homotopy equivalent to a countable CW-complex has countable homotopy groups, and therefore admits a countable CW-replacement.

• Using [18, Corollary 1], we obtain that any finite-dimensional Lie group admits a countable CW-replacement, since the underlying manifold is separable.

• For many interesting (orientable) manifolds M, the (orientation-preserving) diffeomorphism group ${\mathrm{Diff}}(M)$ has countable homotopy groups and therefore admits a countable CW-replacement. For instance, this is true when when $M=S^2$ (since ${\mathrm{Diff}}(S^2)\simeq O(3)$ by the a theorem of Smale [29], when M is an orientable surface of genus $g\ge 2$ such that $\pi _0({\mathrm{Diff}}(M))$ is countable (since by [4, Theorem 1(c)] every connected component of ${\mathrm{Diff}}(M)$ is contractible), when $M=S^3$ (since ${\mathrm{Diff}}(S^3)\simeq O(4)$ by the Smale Conjecture proven by Hatcher in [10]), when $M=S^1\times S^2$ (since ${\mathrm{Diff}}(S^1\times S^2)\simeq O(2)\times O(3)\times \Omega O(3)$ by [9]), and when M is a hyperbolic manifold of dimension 3 (as a consequence of [8, Theorem 1.2]).

• Finite products of topological groups that admit a countable CW-replacement admit a countable CW-replacement.

If a topological group G admits a countable CW-replacement, the good replacement $G^{cof}$ is enough to recover the theory of G-bundles. Recall from Remark 1.7 that for every countable CW-group G the identity maps ${{\mathrm{d}}}:E^{Mil}G\rightarrow EG$ and ${{\mathrm{d}}}:B^{Mil}G\rightarrow BG$ are weak equivalences.

Proposition 1.17

Let X be a countable CW-complexes and G a topological group that admits a countable CW-replacement. A good CW-replacement $\epsilon :G^{cof}\rightarrow G$ for G induces a bijection

$$\begin{aligned} {\epsilon }_*:{}_X{{{\mathcal {B}}un}}_{G^{cof}}/ {}_{\cong }\rightarrow {}_X{{{\mathcal {B}}un}}_{G}/ {}_{\cong }. \end{aligned}$$

Proof

Using the fact that, by Proposition 1.2 applied to the map $E\epsilon :EG^{cof}\rightarrow EG$, there is an equivalence $(B\epsilon )^*(EG)\cong \epsilon _*(EG^{cof})$ of $G^{cof}$-bundles over BG, one can check that the map $\epsilon _*$ fits into the following commutative diagram:

We conclude that $\epsilon _*$ induces a bijection because the vertical maps are bijections by Theorem 1.4, and the top horizontal map is a weak equivalence because $B\epsilon$ is a weak equivalence and X is a CW-complex. $\square$

Notation 1.18

Given G a topological group with a good CW-replacement $\epsilon :G^{cof}\rightarrow G$, denote by $(-)^{cof}$ the inverse of the map $\epsilon _*$ from Proposition 1.17:

$$\begin{aligned} (-)^{cof}:{}_X{{{\mathcal {B}}un}}_{G}/ {}_{\cong }\rightarrow {}_X{{{\mathcal {B}}un}}_{G^{cof}}/ {}_{\cong }. \end{aligned}$$

3 Characteristic classes as obstructions

Given a topological group G that admits a countable CW-replacement and a countable abelian group $A$, the aim of this section is to construct a topological group $G^{red}(c)$ and the homomorphism of topological groups $\gamma :G^{cof}\rightarrow M^{k-1}A$ associated to a universal characteristic class $c\in H^k(BG;A)$, and prove that they both detect the vanishing of the characteristic class c for a G-bundle.

3.1 The delooping homomorphism

Milgram constructed in [19] a model of classifying space for abelian topological groups, that inherits the structure of a topological abelian group. We will need the following properties of Milgram’s classifying space. Recall Milnor’s model $B^{Mil}$ from Theorem 1.6.

Theorem 2.1

Let $H$ be an abelian countable CW-group.

• (1) For any abelian countable CW-group $H$, there exists a functorial classifying space $MH$ that is an abelian countable CW-group.

• (2) There is a natural homotopy equivalence $\tau _H:B^{Mil}H\rightarrow MH$.

Proof

All the ingredients to prove (1) are from [19]. The construction of the topological abelian group $MH$ follows from [19, Corollary 1.7]. In [19, Theorem 2.3], a cell decomposition for $MH$ is constructed. When $H$ is a countable CW-complex, the cell decomposition constructed in [19, Theorem 2.3] recovers the topology, so $MH$ is a CW-complex. By reading through the definition of the cells, we see that the cells can be enumerated by finite collections of cells of $H$, and therefore there are countably many. Therefore $MH$ is a countable CW-complex. Moreover, it is proven in [19, Section 2] that the multiplication on $MH$ defined in [19, Corollary 1.7] is continuous and cellular. The fact that the inversion is cellular is straightforward, based on the explicit formula for inverses, in the proof of [19, Corollary 1.7]. So $MH$ is an abelian countable CW-group.

For (2), one can read from [19] and [17] the explicit constructions of $MH$ and $B^{Mil}H$, and see that they coincide respectively with the neat realization $|{\mathrm{Bar}}(H)|$ and the fat realization $||{\mathrm{Bar}}(H)||$ of the bar construction ${\mathrm{Bar}}(H)$. We take $\tau _H$ to be the Bousfield-Kan map

$$\begin{aligned} \tau _H:B^{Mil}H=||{\mathrm{Bar}}(H)||\rightarrow |{\mathrm{Bar}}(H)| = MH, \end{aligned}$$

which is natural. As the unit of $H$ is a vertex and $H^n$ is a CW-complex (because $H$ is a countable CW-complex), the simplicial space ${\mathrm{Bar}}(H)$ is good (according to [28, Definition A.4]), and therefore $\tau _H$ is a weak equivalence by [28, Proposition A.1(iv)]. $\square$

We are interested in iterating this construction.

Notation 2.2

Let $A$ be a discrete countable abelian group and $k\ge 0$. We denote by $M^kA$ the topological abelian group given by

$$\begin{aligned} M^kA:=\underbrace{M\circ \dots \circ M}_{k\text { times}}(A). \end{aligned}$$

It can be seen by induction on $n\ge 0$ that $M^kA$ has the homotopy type of an Eilenberg–Maclane space of type $(A;k)$. Since $M^kA$ is also an abelian topological group, by [25, Theorem 1.2.4], for any topological space X, the set of homotopy classes $[X,M^kA]$ becomes an abelian group when endowed with pointwise multiplication.

Proposition 2.3

Let $A$ be a countable abelian group and $k\ge 0$. For any CW-complex X there is a natural isomorphism of abelian groups

$$\begin{aligned} H^k(X;A)\cong [X,M^kA]. \end{aligned}$$

Proof

Recall from [11] that the ordinary cohomology $H^k(X;A)$ can be identified with $[X,K(A;k)]$ as a set, and with $[X,\Omega K(A;k+1)]$ as a group, where the notation should emphasize that the group structure on $[X,\Omega K(A;k+1)]$ is induced by the H-space structure of the loop space $\Omega K(A;k+1)$. Using [19, Section 5] there is a weak equivalence

$$\begin{aligned} M^{k}A{\mathop {\longrightarrow }\limits ^{\simeq }}\Omega M^{k+1}A\end{aligned}$$

that is also maps of H-spaces, where $M^kA$ is endowed with the abelian group structure and the H-space structure on $\Omega M^{k+1}A$ is given by concatenation. This map is in fact a homotopy equivalence, because $M^kA$ and $\Omega M^{k+1}A$ are both CW-complexes using [7, Corollary 5.3.7]. Therefore, this map induces the desired isomorphism of abelian groups

$$\begin{aligned}{}[X,M^{k}A]\cong [X,\Omega M^{k+1}A]\cong [X,\Omega K(A;k+1)]\cong H^k(X;A). \end{aligned}$$

$\square$

Recall that for any topological group G with classifying space BG the elements of $H^k(BG,A)$ are called universal characteristic classes. We refer the reader to [22] for more details on this account.

Construction 2.4

Let G be a topological group that admits a countable CW-replacement, ${\tilde{B}}$ a classifying space for G that has the homotopy type of a countable CW-complex, $A$ a discrete countable abelian group and $k>0$. By Proposition 2.1(2) and Theorem 1.10, the cohomology of ${\tilde{B}}$ can be identified with a quotient of ${{\mathcal {G}}p}({{\mathcal {T}}op})(G^{cof},M^{k-1}A)$ as follows:

$$\begin{aligned} H^k({\tilde{B}};A)\cong & {} {{\mathcal {T}}op}({\tilde{B}},M^kA)/ {}_{\simeq }\cong {{\mathcal {T}}op}({\tilde{B}},B^{Mil}M^{k-1}A)/ {}_{\simeq }\\= & {} {{\mathcal {G}}p}({{\mathcal {T}}op})(G^{cof},M^{k-1}A)/ {}_{\equiv }. \end{aligned}$$

Note that a different choice for ${\tilde{B}}$ would lead to a compatible identification. In particular, every characteristic class $c\in H^k({\tilde{B}};A)$ in positive degree $k>0$ is represented by a homomorphism of topological groups

$$\begin{aligned} \gamma :G^{cof}\rightarrow M^{k-1}A, \end{aligned}$$

which is determined up to algebraic equivalence. Note that $\gamma$ determines the cohomology class c completely, as c is represented by the homotopy class of

We therefore refer to $\gamma$ as the delooping homomorphism¹ of c.

The delooping homomorphism of the first Stiefel–Whitney map is essentially the determinant map.

Example 2.5

Let $k=1$, $A={\mathbb {Z}}/2$, $G=O(n)$ and $c:=w_1\in H^1(BO(n);{\mathbb {Z}}/2)$ the first universal Stiefel-Whitney class. We construct (a representative for) the delooping homomorphism $\omega _1:O(n)^c\rightarrow M^0({\mathbb {Z}}/2)={\mathbb {Z}}/2$ associated to $w_1$ as follows. Notice that the real Stiefel manifold $V({\mathbb {R}}^\infty ;n)$ is an O(n)-universal bundle with corresponding classifying space the real Grassmannian $Gr({\mathbb {R}}^\infty ;n)$, that admits the structure of a countable CW-complex. Use Theorem 1.10 to assert the existence of a homomorphism of topological groups $O(n)^{cof}=\Omega ^{Mil}Gr({\mathbb {R}}^\infty ;n)\rightarrow O(n)$ such that

$$\begin{aligned}&(\Omega ^{Mil}Gr({\mathbb {R}}^\infty ;n)\rightarrow O(n))_*P^{Mil}Gr({\mathbb {R}}^\infty ,n)\cong V({\mathbb {R}}^\infty ,n)\\&\quad \cong ({{\mathrm{d}}}:Gr({\mathbb {R}}^\infty ,n)\rightarrow Gr({\mathbb {R}}^\infty ,n))^*V({\mathbb {R}}^\infty ,n). \end{aligned}$$

Such a map $O(n)^{cof}\rightarrow O(n)$ is necessarily a weak equivalence by Remark 1.11. Then the homomorphism $\omega _1$ can be taken to be the composite

3.2 The reduction group

The following proposition exhibits a convenient model for the homotopy fiber of $B^{Mil}\gamma :B^{Mil}G^{cof}\rightarrow B^{Mil}M^{k-1}A$. Recall the notation for the tensor product $\alpha _* E =E\otimes ^{\alpha }_GH$.

Proposition 2.6

Let $\alpha :G\rightarrow H$ be a homomorphisms of countable CW-groups.

• (1) The space $\alpha _* E^{Mil}G$ is a countable CW-complex.

• (2) The space $\alpha _* E^{Mil}G$ is the homotopy fiber of $B^{Mil}\alpha :B^{Mil}G\rightarrow B^{Mil}H$.

• (3) The space $\alpha _* E^{Mil}G$ is connected if and only if $\alpha$ is $\pi _0$-surjective.

Proof of Proposition 2.6

The space $\alpha _* E^{Mil}G =E^{Mil}G\otimes _GH$ is an $H$-bundle over $B^{Mil}G$. By applying Proposition 1.12 to $\alpha _* E^{Mil}G$, we conclude that $\alpha _* E^{Mil}G$ is a countable CW-complex, which proves (1).

The argument for (2) is a variant of the one used in [20, Proof of Theorem 10.1]. The tensor product $E^{Mil}G\otimes _G E^{Mil}H$, obtained by coequalizing the actions of G on $E^{Mil}H$ and $E^{Mil}G$, is a fiber bundle over the countable CW-complex $B^{Mil}H$ with fiber the space $E^{Mil}G\otimes _GH$, which admits the structure of a countable CW-complex by (1). Again by Proposition 1.12, $E^{Mil}G\otimes _G E^{Mil}H$ admits therefore the structure of a countable CW-complex. We then consider the map

$$\begin{aligned} ( E^{Mil}G,E^{Mil}\alpha ):E^{Mil}G\rightarrow E^{Mil}G\times E^{Mil}H, \end{aligned}$$

a morphism of right G-spaces (where the action on $E^{Mil}G\times E^{Mil}H$ is on both factors), which are in fact G-bundles. The morphism $( E^{Mil}G,E^{Mil}\alpha )$ induces therefore a map at the level of quotients:

$$\begin{aligned} \overline{( E^{Mil}G,E^{Mil}\alpha )}:B^{Mil}G\rightarrow E^{Mil}G\otimes _G E^{Mil}H. \end{aligned}$$

Moreover $( E^{Mil}G,E^{Mil}\alpha )$ is a weak homotopy equivalence (since its source and target are contractible), and restricts to a homeomorphism on the distinguished fibers because of the equivariance condition. By naturality of the homotopy long exact sequence induced by a fibration, the induced map $\overline{( E^{Mil}G,E^{Mil}\alpha )}$ is also a weak equivalence. As $B^{Mil}G$ and $E^{Mil}G\otimes _G E^{Mil}H$ are (countable) CW-complexes, this map is in fact a homotopy equivalence. Since the following diagram commutes

the homotopy fiber of $B^{Mil}\alpha$ is equivalent to the (homotopy) fiber of the bundle projection $E^{Mil}G\otimes _G E^{Mil}H\rightarrow B^{Mil}H$, which is $E^{Mil}G\otimes _GH= \alpha _* E^{Mil}G$, as desired.

For (3), we observe that, using the homotopy long exact sequence induced by fibrations, there is an exact sequence (of pointed sets)

$\square$

We can now define the reduction group associated to a universal characteristic class.

Definition 2.7

Let $\alpha :G\rightarrow H$ be a $\pi _0$-surjective homomorphisms of countable CW-groups. The reduction group of $\alpha$ is the countable CW-group

$$\begin{aligned} G^{red}(\alpha ):=\Omega ^{Mil}(\alpha _*E^{Mil}G ). \end{aligned}$$

It comes with a map of topological groups $j:G^{red}(\alpha )\rightarrow G$, which is determined up to algebraic equivalence, obtained by adjoining the projection $\alpha _\star (E^{Mil}G)\rightarrow B^{Mil}G$ according to Theorem 1.10. Note that the condition of $\pi _0$-surjectivity for $\alpha$ is automatically satisfied when $H$ is connected.

We now focus on reduction groups produced by delooping homomorphisms associated to universal characteristic classes.

Definition 2.8

Let G be a topological group that admits a countable CW-replacement, $A$ a countable abelian group and $k>0$. Let $c\in H^k(BG;A)$ be a universal characteristic class represented by a $\pi _0$-surjective delooping homomorphism $\gamma :G^{cof}\rightarrow M^{k-1}A$ (as in Construction 2.4). The reduction group of c is the countable CW-group

$$\begin{aligned} G^{red}(c):=G^{red}(\gamma )=\Omega ^{Mil}(\gamma _*E^{Mil}G^{cof} ). \end{aligned}$$

It comes with a homomorphism $G^{red}(c){\mathop {\rightarrow }\limits ^{j}}G^{cof}{\mathop {\rightarrow }\limits ^{\epsilon }}G$, where $\epsilon$ is the countable CW-replacement, and the map j is from Definition 2.7. Note that $\gamma :G^{cof}\rightarrow M^{k-1}A$ is $\pi _0$-surjective if and only if the cohomology class $c:B^{Mil}G^{cof}\rightarrow K(A;k)$ is $\pi _1$-surjective, which is automatically satisfied when $k>1$.

The reduction group of a map $\alpha$ has a sort of universal property.

Proposition 2.9

Let $\alpha :G\rightarrow H$ be a $\pi _0$-surjective homomorphisms of countable CW-groups.

• (1) The classifying space of $G^{red}(\alpha )$ is the homotopy fiber of $B^{Mil}\alpha :B^{Mil}G\rightarrow B^{Mil}H$.

• (2) If $G'$ is another topological group whose classifying space is the homotopy fiber of $B^{Mil}\alpha :B^{Mil}G\rightarrow B^{Mil}H$, there exists a homomorphism of topological groups $G^{red}(\alpha )\rightarrow G'$ that is also a weak equivalence.

Proof

For (1), we note that $P^{Mil}(\alpha _*E^{Mil}G)$ is by Theorem 1.8 a universal $\Omega ^{Mil}(\alpha _*E^{Mil}G)$-bundle, i.e., a universal $G^{red}(\alpha )$-bundle, with base space $\alpha _*E^{Mil}G$. Therefore, $\alpha _*E^{Mil}G$ is a classifying space for $G^{red}(\alpha )$, and is therefore equivalent to $B^{Mil}G^{red}(\alpha )$, which was proven in Proposition 2.6 to be the homotopy fiber of $B^{Mil}\alpha$.

For (2), we suppose that $G'$ is a topological group with a classifying space $B'$ that is the homotopy fiber of $B^{Mil}\alpha$. Without loss of generality, we can assume that $B'$ is a CW-complex, and is therefore homotopy equivalent to $\alpha _*E^{Mil}G$. Let $h:\alpha _*E^{Mil}G\rightarrow B'$ be a homotopy equivalence. Let $E'$ be a universal $G'$-bundle whose base space is $B'$. Then $h^*E'$ is a universal $G'$-bundle, with base space $\alpha _*E^{Mil}G$. By Theorem 1.8, there exists a homomorphism of topological groups $a:G^{red}(\alpha )=\Omega ^{Mil}(\alpha _*E^{Mil}G)\rightarrow G'$ such that $h^*E'\cong a_*P^{Mil}(\alpha _*E^{Mil}G)$. Using (a variant of) Remark 1.11, we conclude that a is a weak equivalence, as desired. $\square$

This proposition can be used to check that the general construction $G^{red}(c)$ recovers certain important topological groups. In particular, for certain interesting characteristic classes c, the reduction group $G^{red}(c)$ is equivalent to a Lie group.

Example 2.10

• When $k=1$, $A={\mathbb {Z}}/2$, $G=O(n)$ and $c=w_1$ is the first Stiefel–Whitney class, it is known that the classifying space of the special orthogonal group BSO(n) of SO(n) fits into a homotopy fiber sequence

  

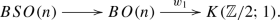
  By Proposition 2.9(2), there exists a homomorphism of topological groups $G^{red}(w_1)\rightarrow SO(n)$ which is also a weak equivalence.

• When $k=2$, $A={\mathbb {Z}}/2$, $G=SO(n)$ and $c=w_2$ is the second Stiefel–Whitney class, it is known that the classifying space $BS\text {pin}(n)$ of the spin group $S\text {pin}(n)$ fits into a homotopy fiber sequence

  

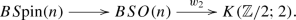
  By Proposition 2.9(2), there exists a homomorphism of topological groups $G^{red}(w_2)\rightarrow Spin(n)$ which is also a weak equivalence.

• When $k=4$, $A={\mathbb {Z}}/2$, $G=Spin(n)$ and $c=\frac{1}{2}p_1$ is the first fractional Pontryagin class, it is known that the classifying space BString(n) of the string group String(n) fits into a homotopy fiber sequence

  

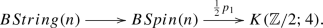
  By Proposition 2.9(2), there exists a homomorphism of topological groups $G^{red}(\frac{1}{2}p_1)\rightarrow String(n)$ which is also a weak equivalence.

• When $k=2$, $A={\mathbb {Z}}$, $G=U(n)$ and $c=c_1$ is the first Chern class, it is known that the classifying space of the special unitary group BSU(n) of SU(n) fits into a homotopy fiber sequence

  

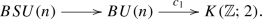
  By Proposition 2.9(2), there exists a homomorphism of topological groups $G^{red}(c_1)\rightarrow SU(n)$ which is also a weak equivalence.

• When $k=2n$, $A={\mathbb {Z}}$, $G=U(n)$ and $c=c_n$ is the top Chern class, by Proposition 2.9(1) $B^{Mil}G^{red}(c_n)$ is the homotopy fiber of $c_n$. Using the standard identification of the cohomology of complex grassmannians with polynomial algebras, one can prove that the composite $B^{Mil}U(n-1)\rightarrow B^{Mil}U(n){\mathop {\rightarrow }\limits ^{c_n}} K({\mathbb {Z}};2n)$ represents a trivial cohomology class in $H^{2n}(B^{Mil}U(n-1),{\mathbb {Z}})$. Therefore $B^{Mil}U(n-1)\rightarrow B^{Mil}U(n)$ lifts up to homotopy to $B^{Mil}G^{red}(c_n)$,

  

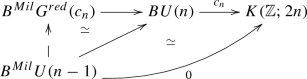
  By adjoining (according to Theorem 1.10) the homotopy commutative triangle to the left, with a little work one can build a diagram of topological groups of the following form, which commutes up to algebraic equivalence:

  

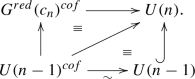
  This can be rephrased by saying that, modulo replacing $U(n-1)$ with $U(n-1)^{cof}$, the standard inclusion $U(n-1)\hookrightarrow U(n)$ factors through the reduction group $G^{red}(c_n)$ of the top Chern class. This gives an indication of how $G^{red}(c_n)$ is related to $U(n-1)$.

The following remark gives a fair description of the homotopy groups of reduction groups associated to universal characteristic classes: the homotopy groups of $G^{red}(\gamma )$ coincide with the homotopy groups of G except possibly in degree $k-1$ and $k-2$.

Remark 2.11

Let $A$ be a countable abelian group, G a countable CW-group and $k\ge 1$. Let $\alpha :G\rightarrow M^{k-1}A$ be a $\pi _0$-surjective homomorphisms. We know by Proposition 2.6 that $B^{Mil}G^{red}(\gamma )$ fits into a homotopy fiber sequence

and that $B^{Mil}M^{k-1}A$ is an Eilenberg-MacLane space of type $K(A;k)$. This implies that

$$\begin{aligned} \pi _i(G^{red}(\gamma ))\cong \pi _i(G)\text { for }i\ne k-1,k-2, \end{aligned}$$

and the remaining homotopy groups fit into an exact sequence of the form

This fact can be used to build a Whitehead tower [34] of any topological group G whose homotopy groups are countable (e.g. Lie groups).

It is known that every layer of the Whitehead tower of an H-space is itself an H-space, and a result in a similar direction is also [5, Theorem 3.A.2]. We now promote this result to the framework of topological groups and continuous homomorphisms, by showing that the topological group G admits a Whitehead tower made by topological groups (and homomorphisms of such).

Construction 2.12

Let G be a topological group that admits a countable CW-replacement ${\tilde{G}}$. We inductively define a countable CW-group $G^{(n)}$ together with maps

$$\begin{aligned} j_n:G^{(n)}\rightarrow G^{(n-1)}\rightarrow \dots \rightarrow G^{(0)}\rightarrow G \end{aligned}$$

that induce isomorphisms

$$\begin{aligned} \pi _i(G^{(n)})\cong \pi _i(G^{(n-1)})\cong \dots \cong \pi _i(G^{(0)})\cong \pi _i(G)\text { for }i\ge n. \end{aligned}$$

and such that

$$\begin{aligned} \pi _i(G^{(n)})\cong 0\text { for }i<n. \end{aligned}$$

We first set $G^{(0)}:={\tilde{G}}$, together with the map $\epsilon :{\tilde{G}}\rightarrow G$ that gives the countable CW-replacement. Suppose then $n>0$ and that $G^{(n-1)}$ and the map $j_{n-1}:G^{(n-1)}\rightarrow G$ have been constructed. By the universal coefficient theorem for cohomology and the Hurewicz Theorem, there is an isomorphism of abelian groups

$$\begin{aligned} \left[ B^{Mil}(G^{(n-1)}),K\left( \pi _{n}(BG),n\right) \right]\cong & {} H^{n}\left( B^{Mil}(G^{(n-1)});\pi _{n}(BG)\right) \\\cong & {} {\mathrm{Hom}}\left( H_{n}(B^{Mil}(G^{(n-1)});{\mathbb {Z}}),\pi _{n}(BG))\right) \\\cong & {} {\mathrm{Hom}}\left( \pi _{n}(B^{Mil}(G^{(n-1)})),\pi _{n}(BG))\right) \\\cong & {} {\mathrm{Hom}}\left( \pi _{n-1}(G^{(n-1)}),\pi _{n-1}(G))\right) . \\ \end{aligned}$$

One can check that the isomorphism above is precisely induced by applying $\pi _{n-1}$. One of the elements of ${\mathrm{Hom}}\left( \pi _{n-1}(G^{(n-1)}),\pi _{n-1}(G))\right)$ is the isomorphism $\pi _n(j_{n-1}):\pi _{n-1}(G^{(n-1)})\cong \pi _{n-1}(G)$ induced by the map $j_{n-1}:G^{(n-1)}\rightarrow G$. Let $c_n:B^{Mil}(G^{(n-1)})\rightarrow K(\pi _n(BG),n)$ be the element in $H^n(B^{Mil}(G^{(n-1)});\pi _n(BG))$ corresponding to $\pi _n(j_{n-1})$. We then set $G^{(n)}:=G^{red}(c_n)$, together with the map $j_n:G^{(n)}=G^{red}(c_n)\rightarrow G^{(n-1)}{\mathop {\longrightarrow }\limits ^{j_{n-1}}} G$.

Theorem 2.13

Let G be a topological group that admits a countable CW-replacement. The tower of groups

$$\begin{aligned} \dots \rightarrow G^{(n+1)}\rightarrow G^{(n)}\rightarrow G^{(n-1)}\rightarrow \dots \rightarrow G^{(0)}\rightarrow G \end{aligned}$$

from Construction 2.12 is a Whitehead tower for G.

Proof

The map $j_0:=\epsilon :{\tilde{G}}=G^{(0)}\rightarrow G$ is a weak equivalence by definition. By construction, the exact sequence Remark 2.11 (with $k=n$, $A=\pi _n(BG)\cong \pi _{n-1}(G)$ and $\gamma =c_n$) becomes of the following form:

which implies the vanishing of the homotopy groups of $G^{(n)}$ in degree $i=n-1,n-2$:

$$\begin{aligned} \pi _{n-2}(G^{(n)})\cong \pi _{n-2}(G^{(n-1)})\cong 0\quad \text { and }\quad \pi _{n-1}(G^{(n)})\cong 0. \end{aligned}$$

On the other hand, by Remark 2.11, we know that the homotopy groups in degree $i\ne n-2,n-1$ are given by

$$\begin{aligned} \pi _i(G^{(n)})= & {} \pi _i(G^{red}(c_n))\cong \pi _i(G^{(n-1)})\\= & {} \left\{ \begin{array}{ll} 0&{}\text { if }i<n-2\\ \pi _i(G^{(n-1)})\cong \dots \cong \pi _i(G^{(0)})\cong \pi _i(G).&{}\text { if }i>n-1 \end{array} \right. \end{aligned}$$

We therefore conclude that $\left( G^{(n)}\right) _{n\ge 0}$ is a Whitehead tower for G. $\square$

3.3 Characteristic classes as obstructions to group reduction

Given G a topological group whose homotopy groups are countable (e.g., a Lie group) and a universal characteristic class c, we constructed its reduction group $G^{red}(c)=G^{red}(\gamma )$, together with a map $j:G^{red}(\gamma )\rightarrow G$. In this section we prove that it detects the vanishing of the characteristic class c for a G-bundle. The first step is the following proposition.

Proposition 2.14

Let $\alpha :G\rightarrow H$ be a $\pi _0$-surjective homomorphisms of countable CW-groups. For E a G-bundle over a CW-complex X classified by a map $t:X\rightarrow B^{Mil}G$, the following are equivalent.

• (a) There exists a $G^{red}(\alpha )$-bundle ${\hat{E}}$ over X such that ${\hat{E}}\otimes _{G^{red}(\alpha )}G=j_*{\hat{E}}\cong E$.

• (b) The map $B^{Mil}\alpha \circ t:X\rightarrow B^{Mil}H$ is nullhomotopic.

Proving Theorem 2.14 from Proposition 2.6 is a standard argument, that we briefly recall.

Proof

Condition (b) says that t is killed by $B^{Mil}\alpha$, which is equivalent to saying that t factors up to homotopy through the homotopy fiber $B^{Mil}G^{red}(\alpha )$ via a map ${\hat{t}}:X\rightarrow B^{Mil}G^{red}(\alpha )$, as displayed

Note that, by Proposition 1.2, the map $E^{Mil}j:E^{Mil}G^{red}(\gamma )\rightarrow E^{Mil}G$ induces an equivalence

$$\begin{aligned} j_*E^{Mil}G^{red}(\alpha )\cong (B^{Mil}j)^*E^{Mil}G. \end{aligned}$$

Finally, if we then let ${\hat{E}}:={\hat{t}}^*E^{Mil}G^{red}(\alpha )$, we have that

$$\begin{aligned} j_*{\hat{E}}\cong & {} j_*{\hat{t}}^* E^{Mil}G^{red}(\alpha )\cong {\hat{t}}^* j_* E^{Mil}G^{red}(\alpha )\\\cong & {} {\hat{t}}_* (Bj)^* E^{Mil}G\cong (B^{Mil}j\circ {\hat{t}})^* E^{Mil}G. \end{aligned}$$

So t is homotopic to $Bj\circ {\hat{t}}$ if and only if $j_* {\hat{E}}\cong t^* EG\cong E$, namely Condition (a). $\square$

We are interested in applying the previous proposition to a homomorphism $\gamma :G^{cof}\rightarrow M^{k-1}A$ that represents a universal characteristic class c, as in Construction 2.4. The following result shows that the universal characteristic class c measures the obstruction to the reduction to a $G^{red}(c)$-bundle. Recall the map $\epsilon \circ j:G^{red}(c)\rightarrow G^{cof}\rightarrow G$ from Definition 2.8.

Theorem 2.15

Let G be a topological group that admits a countable CW-replacement, $A$ a countable abelian group and $k>0$. Let $c\in H^k(BG;A)$ be a $\pi _1$-surjective universal characteristic class. For E a G-bundle over a CW-complex X, the following are equivalent.

• (A) There exists a $G^{red}(c)$-bundle ${\hat{E}}$ over X such that ${\hat{E}}\otimes _{G^{red}(\gamma )}G=(\epsilon \circ j)_*{\hat{E}}\cong E$.

• (B) The characteristic class c of E vanishes, i.e., $c(E)=0\in H^k(X;A)$.

Proof

By applying Proposition 2.14 to $E^{\text {c}}$ (classified by a map $t:X\rightarrow B^{Mil}G^{cof}$ with respect to the universal bundle $E^{Mil}G^{cof}$) and to the delooping homomorphism $\gamma :G^{\text {c}}\rightarrow M^{k-1}A$ associate to c as in Construction 2.4, we obtain that the following are equivalent.

• (a) There exists a $G^{red}(c)$-bundle ${\hat{E}}$ over X and an equivalence $j_*{\hat{E}}\cong E^{\text {c}}$ of $G^{\text {c}}$-bundles over X.

• (b) The map $B^{Mil}\gamma \circ t:X\rightarrow B^{Mil}G^{cof}\rightarrow B^{Mil}M^{k-1}A$ is nullhomotopic.

The conditions (A) and (a) are equivalent by Proposition 1.17. Indeed condition (a) is obtained from condition (A) by applying $(-)^{cof}$, and (A) is obtained from (a) by applying ${\epsilon }_*$.

The conditions (b) and (B) are equivalent because the cohomology class c(E) is represented by $B^{Mil}\gamma \circ t:X\rightarrow B^{Mil}M^{k-1}A$. Indeed, the same $t:X\rightarrow B^{Mil}G^{cof}$ is also a classifying map for E (with respect to the universal G-bundle $(B\epsilon :B^{Mil}G^{cof}\rightarrow BG^{cof}\rightarrow BG)^*(EG)$, and $B^{Mil}\gamma$ represents the cohomology class of the universal characteristic class c (by Construction 2.4). $\square$

We use this theorem to recover and strengthen certain classical statements (cf. [22]). Recall that certain matrix groups $G'$ have been identified in Example 2.10 with the reduction groups $G^{red}(c)$ associated to certain characteristic classes c, via a map $G^{red}(c)\rightarrow G'$ which is also a weak equivalence. By Proposition 1.17, such a map induces a bijection between the set of equivalence classes of $G'$-bundles over X and the set of equivalence classes of $G^{red}(c)$-bundles over X.

Example 2.16

• As an application of Theorem 2.15, the first Stiefel–Whitneyclass $w_1(E)$ of an O(n)-bundle E vanishes if and only if there exists an SO(n)-bundle ${\hat{E}}$ such that $E\cong {\hat{E}}\otimes _{SO(n)}O(n)$, which coincides with one of the standard notions of orientability.

• As an application of Theorem 2.15, the second Stiefel–Whitneyclass $w_2(E)$ of an SO(n)-bundle E vanishes if and only if there exists a Spin(n)-bundle ${\hat{E}}$ such that $E\cong {\hat{E}}\otimes _{Spin(n)}SO(n)$, which is equivalent the usual notion of existence of a spin structure.

• As an application of Theorem 2.15, the first fractional Pontryagin class $\frac{1}{2}p_1(E)$ of a Spin(n)-bundle E vanishes if and only if there exists a String(n)-bundle ${\hat{E}}$ such that $E\cong {\hat{E}}\otimes _{String(n)}Spin(n)$, which refines (but is equivalent to) the usual notion of existence of a string structure.

• As an application of Theorem 2.15, the first Chern class $c_1(E)$ of a U(n)-bundle E vanishes if and only if there exists an SU(n)-bundle ${\hat{E}}$ such that $E\cong {\hat{E}}\otimes _{SU(n)}U(n)$.

• As an application of Theorem 2.15, the top Chern class $c_n(E)$ of a U(n)-bundle E vanishes if and only if there exists a $G^{red}(c_n)$-bundle ${\hat{E}}$ such that $E\cong {\hat{E}}\otimes _{G^{red}(c_n)}U(n)$.

• If E is the frame bundle of a complex vector bundle ${\mathcal {E}}$ of rank n, we observe that ${\mathcal {E}}$ admits a nowhere vanishing section if and only if there exists a $U(n-1)$-bundle ${\hat{E}}'$ such that $E\cong {\hat{E}}'\otimes _{U(n-1)}U(n)$ (see [2, Theorem 2.27]). In this case, by setting ${\hat{E}}:={\hat{E}}'\otimes _{U(n-1)}G^{red}(c_n)$ and recalling from Example 2.10 that the inclusion of $U(n-1)\hookrightarrow U(n)$ essentially factors through $G^{red}(c_n)$, we obtain that

  $$\begin{aligned} E\cong & {} {\hat{E}}'\otimes _{U(n-1)}U(n)\cong {\hat{E}}'\otimes _{U(n-1)}G^{red}(c_n)\otimes _{G^{red}(c_n)}U(n)\\= & {} {\hat{E}}\otimes _{G^{red}(c_n)}U(n). \end{aligned}$$

  In this case, Theorem 2.15 tells us that the top Chern class $c_n(E)=c_n({\mathcal {E}})$ vanishes. This argument (re)proves that well-known fact that the top Chern class (i.e., the Euler class) of a complex vector bundle is an obstruction to the existence of a nowhere vanishing section. The fact that it is not the only obstruction is a symptom of the fact that $G^{red}(c_n)$ is not homotopy equivalent to $U(n-1)$.

3.4 Characteristic classes as obstructions to the extension of the delooping homomorphism

Given G a topological group whose homotopy groups are countable (e.g., a Lie group) and a universal characteristic class c, we constructed its delooping homomorphism $\gamma$. In this section we prove that $\gamma$ detects the vanishing of the characteristic class c for a G-bundle. The first step is the following proposition.

Proposition 2.17

Let $\alpha :G\rightarrow H$ be a $\pi _0$-surjective homomorphisms of countable CW-groups. For E a G-bundle over a CW-complex X classified by a map $t:X\rightarrow B^{Mil}G$, the following are equivalent.

• (b) The map $B^{Mil}\alpha \circ t:X\rightarrow B^{Mil}H$ is nullhomotopic.

• (c) The map of topological groups $\alpha :G\rightarrow H$ extends (along any G-equivariant inclusion $G\rightarrow E$) to an $\alpha$-equivariant map $E\rightarrow H$.

• (d) The bundle $\alpha _*E^{Mil}G$ is trivial, i.e, $\alpha _* E\cong X\times H$.

Proof

We prove $[(b)\Leftrightarrow (d)]$. Using Proposition 1.2 on the map $E^{Mil}a:E^{Mil}G\rightarrow E^{Mil}H$, we obtain equivalences of $H$-bundles over X:

$$\begin{aligned} (B^{Mil}a\circ t)^*E^{Mil}H\cong t^*(B^{Mil}a)^*E^{Mil}H\cong t^* a_*E^{Mil}G\cong a_* t^*E^{Mil}G\cong a_* E. \end{aligned}$$

By Theorem 1.10, the map $B^{Mil}a\circ t$ is nullhomotopic if and only if $a_* E$ is equivalent to the trivial bundle.

We prove $[(c)\Rightarrow (d)]$. If there exists an $\alpha$-equivariant map $\kappa :E\rightarrow H$, then

$$\begin{aligned} (\pi ,\kappa ):E\rightarrow X\times H\end{aligned}$$

is an $\alpha$-equivariant map over X, which induces by Proposition 1.2 an equivalence of $H$-bundles

$$\begin{aligned} \overline{(\pi ,\kappa )}:\alpha _* E\cong X\times H. \end{aligned}$$

We prove $[(d)\Rightarrow (c)]$. Given an equivalence $\phi :\alpha _* E\cong X\times H$ of $H$-bundles over X, we use it to construct the $\alpha$-equivariant map

which can be checked to extend $\alpha$. $\square$

Again, we are interested in applying the previous proposition to the delooping homomorphism $\gamma :G^{cof}\rightarrow M^{k-1}A$ associated to a universal characteristic class c, as in Construction 2.4. The following result shows that the $\pi _1$-surjective characteristic class c measures the obstruction to the equivariant extension of $\gamma$ to the whole bundle $E^{cof}$.

Theorem 2.18

Let G be a topological group that admits a countable CW-replacement, $A$ a countable abelian group and $k>0$. Let $c\in H^k(BG;A)$ be a $\pi _1$-surjective universal characteristic class with delooping homomorphism $\gamma :G^{cof}\rightarrow M^{k-1}A$. For E a G-bundle over a CW-complex X, the following are equivalent.

• (B) The characteristic class c(E) of E vanishes, i.e., $c(E)=0\in H^k(X;A)$.

• (C) The map $\gamma :G^{cof}\rightarrow M^{k-1}A$ extends to a $\gamma$-equivariant map $E^{cof}\rightarrow M^{k-1}A$.

Proof

By applying Proposition 2.17 to $E^{\text {c}}$ (classified by a map $t:X\rightarrow B^{Mil}G^{cof}$ with respect to the universal bundle $E^{Mil}G^{cof}$) and to the delooping homomorphism $\gamma :G^{cof}\rightarrow M^{k-1}A$ associate to c as in Construction 2.4, we obtain that the following are equivalent.

• (b) The map $B^{Mil}\gamma \circ t:X\rightarrow B^{Mil}G^{cof}\rightarrow B^{Mil}M^{k-1}A$ is nullhomotopic.

• (C) The map $\gamma :G^{cof}\rightarrow M^{k-1}A$ extends to a $\gamma$-equivariant pointed map $E^{{cof}}\rightarrow M^{k-1}A$.

The equivalence between (b) and (B) was already established in the proof of Theorem 2.15. $\square$

The theorem recovers another characterization of orientability.

Example 2.19

We apply the theorem, and use the fact that the delooping homomorphism of the fist Stiefel–Whitneyclass has been identified with the determinant map in Example 2.5. We obtain that the first Stiefel–Whitney class $w_1(E)$ of an O(n)-bundle E vanishes if and only if there exists an $O(n)^{cof}$-equivariant function $E^{cof}\rightarrow {\mathbb {Z}}/2$ that extends $O(n)^{cof}\rightarrow {\mathbb {Z}}/2$. Since the topology of ${\mathbb {Z}}/2$ is discrete, this is equivalent to asking for the existence of a ${\mathbb {Z}}/2$-equivariant function $\pi _0(E)\cong \pi _0(E^{cof})\rightarrow {\mathbb {Z}}/2$, that extends the canonical isomorphism $\pi _0(O(n))\cong \pi _0(O(n)^{cof})\cong {\mathbb {Z}}/2$. This is in turn equivalent to asking for the existence of an O(n)-equivariant function $E\rightarrow {\mathbb {Z}}/2$ that extends the determinant map $O(n)\rightarrow {\mathbb {Z}}/2$. This argument (re)proves that well-known fact that the first Stiefel–Whitney class vanishes if and only if there exists a coherent choice of sign for the bundle E, which is one of the usual definitions of orientability.

4 The plus-cohomology groups of a principal bundle

Given a topological group G whose homotopy groups are countable, $A$ a countable abelian group, and E a G-bundle, we exploit from Theorems 2.15 and 2.18 the idea that equivariant maps $E^{cof}\rightarrow M^{k-1}A$ correspond to the group reductions of a certain bundle E with respect to some universal characteristic class in $H^k(BG;A)$, and define an invariant that implements this point of view.

4.1 The category of pointed bundles

This section provides the correct framework to study the equivariant maps $E^{cof}\rightarrow M^{k-1}A$.

We say that a G-bundle E over a pointed space X is pointed if E is endowed with a base point that makes the projection $E\rightarrow X$ pointed. Given E and $E'$ two pointed G-bundles over X, we write $E\cong _*E'$ if there exists a pointed equivalence of G-bundles over X between them. This clearly defines an equivalence relation.

The following is a variant of Theorem 1.10 that takes into account the base points. The proof of the improved statement can be found in [27]. Given maps of countable CW-groups $a,b:G\rightarrow G'$ we say that they are pointed algebraically equivalent if there is a pointed homotopy $B^{Mil}a\simeq _*B^{Mil}b:B^{Mil}G\rightarrow B^{Mil}G'$. In this case we write $a\equiv _*b$.

Theorem 3.1

[27]. Let X be a connected countable CW complex pointed in a vertex and G a countable CW-group. Then the assignments $(-)_*(P^{Mil}X)$ and $(-)^*(E^{Mil}G)$ induce bijections

$$\begin{aligned} {{\mathcal {G}}p}({{\mathcal {T}}op})(\Omega ^{Mil}X,G)/ {}_{\equiv _*}\ \cong \ {}_X{{\mathcal {B}}un}_G/ {}_{\cong _*}\ \cong \ {{\mathcal {T}}op}(X,B^{Mil}G)/ {}_{\simeq _*}. \end{aligned}$$

Definition 3.2

We denote by ${{\mathcal {B}}un}_*$ the category of pointed principal bundles.

• An object consists of a triple (X, G, E), where X is a pointed topological space, G is a topological group and E is a pointed G-bundle over X. The space X is the base space, the group G is the structure group and the space E is the total space. We denote this object by ${}_XE_G$, or just by E when there is no risk of confusion.

• A morphism ${}_XE_G\rightarrow {}_{X'}E'_{G'}$ consists of a triple $(\psi ,g,a)$, where $g:X\rightarrow X'$ is a pointed map, $a:G\rightarrow G'$ is a homomorphism of topological groups, and $\psi :E\rightarrow E'$ is a pointed map that is a-equivariant and g-coequivariant. The pointed map g is called the geometric information, the homomorphism a is called algebraic information, and the pointed map $\psi$ is called total information. We denote this object by ${}_g\psi _a$, or just $\psi$ when there is no risk of confusion.

• Composition and identity are defined in the obvious way.

Restricting ourselves to pointed bundles allows a better interaction between the category of bundles and the categories of groups and spaces we work with. For instance, if E is a pointed G-bundle over X, there is a canonical G-equivariant inclusion $G\rightarrow E$ determined by sending the identity of G to the base point of E.

Remark 3.3

For every pointed bundle ${}_XE_G$, the canonical inclusion $\iota$ of the structure group and the projection $\pi$ on the base space are morphisms in ${{\mathcal {B}}un}_*$, as displayed:

Every morphism of bundles of the form ${}_X\psi _a:{}_XE_G\rightarrow {}_{X'}E'_{G'}$ induces a on the distinguished fibers and g on the base spaces, namely, there is a commutative diagram in ${{\mathcal {B}}un}_*$:

Using Remark 3.3, one can check that topological groups and pointed spaces embed fully faithfully into pointed bundles.

Proposition 3.4

• (1) The assignment $X\mapsto {}_XX_*,$ which interprets a pointed space as a discrete bundle over itself with trivial structure group, induces a fully faithful inclusion ${{\mathcal {T}}op}_*\hookrightarrow {{\mathcal {B}}un}_*$.

• (2) The assignment $G\mapsto {}_* G_G$, which interprets a topological group as a codiscrete G-bundle over a point, induces a fully faithful inclusion ${{\mathcal {G}}p}({{\mathcal {T}}op})\hookrightarrow {{\mathcal {B}}un}_*$.

Remark 3.5

Let E be a pointed G-bundle over X, with X a countable CW-complex pointed in a vertex and G a countable CW-group. By Theorem 3.1, there exist pointed classifying maps

$$\begin{aligned} t:X\rightarrow B^{Mil}G\text { and }b:\Omega ^{Mil}X\rightarrow G \end{aligned}$$

that yield pointed equivalences of G-bundle over X

$$\begin{aligned} t^*E^{Mil}G\cong _*E\cong _*b_*P^{Mil}X. \end{aligned}$$

The maps t and b are unique up to pointed homotopy and pointed algebraic equivalence, respectively. Having chosen two such maps b and t, we can build the Nomura-Puppe sequence of the bundle

which, thanks to Proposition 3.4, lives in the category ${{\mathcal {B}}un}_*$ as

Using an Eckmann-Hilton argument, one can check that, for any abelian topological group $H$, the codiscrete $H$-bundle over a point $H\mapsto {}_* H_H$ is an abelian group object in ${{\mathcal {B}}un}_*$. As a consequence, for any topological abelian group $H$ the assignment ${}_XE_G\mapsto {{{\mathcal {B}}un}_*}({}_XE_G,{}_* H_H)=:{{{\mathcal {B}}un}_*}(E,H)$ defines a contravariant functor in abelian groups

$$\begin{aligned} {{{\mathcal {B}}un}_*}(-,H):{{{\mathcal {B}}un}_*}^{\text {op}}\rightarrow {{\mathcal {A}}b}, \end{aligned}$$

where the group structure is given by pointwise multiplication. By applying the functor ${{\mathcal {B}}un}_*(-,H)$ to the Nomura-Puppe sequence from Remark 3.5, we obtain a diagram of abelian groups,

which needs not be exact, and not even a complex of abelian groups.

We will define an equivalence relation $\simeq _+$ on ${{{\mathcal {B}}un}_*}(E,H)$ with the following properties.

• The plus-homgroup$[E,H]_+$, defined as the quotient

  $$\begin{aligned} {[}E,H]_+:={{{\mathcal {B}}un}_*}(E,H)/ {}_{\simeq _+}, \end{aligned}$$

  is an abelian group with respect to pointwise multiplication.

• When $H=M^kA\simeq K(A;k)$ is a k-fold Milgram delooping and $E=X$ is a discrete bundle or $E=G^{\text {c}}$ is a codiscrete bundle, the plus-homgroup recovers the ordinary cohomology (of the classifying space):

  $$\begin{aligned} {[}X,M^kA]_+\cong H^k(X;A)\quad \text { and }\quad [G^{\text {c}},M^kA]_+\cong H^{k+1}(B^{Mil}G;A). \end{aligned}$$

• There is an exact sequence of abelian groups obtained by quotienting the diagram above,

  

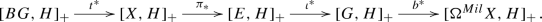
Remark 3.6

Let G be a topological group, and ${\tilde{E}}$ a pointed universal bundle for G over the pointed space ${\tilde{B}}$, and E a pointed G-bundle over a CW-complex X pointed in a vertex. By a pointed variant of Theorem 1.4 that takes into account the base point (and can be found in [27]), there exists a pointed classifying map $t:X\rightarrow {\tilde{B}}$ that induces a pointed equivalence $t^*{\tilde{E}}\cong _* E$. Such a map t is unique up to pointed homotopy. The map t determines further data. More precisely, the following data are equivalent.

• (1) A pointed map $t:X\rightarrow {\tilde{B}}$ together with an equivalence $t^*{\tilde{E}}\cong E$;

• (2) A pointed G-equivariant map $T:E\rightarrow {\tilde{E}}$;

• (3) A pullback diagram of pointed spaces

  

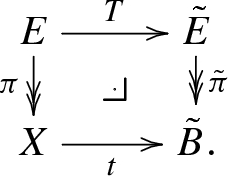
In this case, we refer to the map $T:E\rightarrow {\tilde{E}}$ as a universal map for E and to the map $t:X\rightarrow {\tilde{B}}$ as a pointed classifying map for E (with respect to ${\tilde{E}}$). Note that both maps live in ${{\mathcal {B}}un}_*$, as displayed

$$\begin{aligned} {}_tT_G:{}_XE_G\rightarrow {}_{{\tilde{B}}}{\tilde{E}}_G\text { and }{}_tt_*:{}_{{\tilde{B}}}{\tilde{B}}_*\rightarrow {}_{X}X_*. \end{aligned}$$

4.2 Some distinguished classes of maps

We now identify certain classes of maps in ${{\mathcal {B}}un}_*$ which will play a fundamental role in defining the plus-cohomology groups. Most of these maps of bundles will be nullhomotopic when regarded as maps of spaces.

Definition 3.7

Let X be a CW-complex pointed in a vertex, G a countable CW-group, E a pointed G-bundle over X, and $H$ a topological abelian group.

• A morphism $\psi :E\rightarrow H$ in ${{\mathcal {B}}un}_*$ is of type U if it factors through a universal map $T:E\rightarrow {\tilde{E}}$ in ${{\mathcal {B}}un}_*$, where ${\tilde{E}}$ is a pointed G-bundle over a CW-complex ${\tilde{B}}$ pointed in one of its vertices such that ${\tilde{E}}$ admits the structure of a countable CW-complex and is contractible. Explicitly, this means that $\psi$ factors as

  

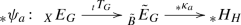
  for some $\kappa :{\tilde{E}}\rightarrow H$ in ${{{\mathcal {B}}un}_*}$.

• A morphism $\psi :E\rightarrow H$ in ${{\mathcal {B}}un}_*$ is of type P if it factors though the projection $\pi :E\rightarrow X$ in ${{\mathcal {B}}un}_*$, or equivalently if the algebraic information is the constant map at the neutral element $e_H$ of $H$. Explicitly, this means that that $\psi$ factors as

  

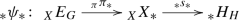
  for some $s:X\rightarrow H$ in ${{{\mathcal {B}}un}_*}$.

• A morphism $\psi :E\rightarrow H$ in ${{\mathcal {B}}un}$ is of type UP if it factors through ${\tilde{\pi }}\circ T=t\circ \pi :E\rightarrow {\tilde{B}}$ in ${{{\mathcal {B}}un}_*}$, where ${\tilde{\pi }}:{\tilde{E}}\rightarrow {\tilde{B}}$ the projection of a pointed universal bundle that admits the structure of a countable CW-complex, ${\tilde{B}}$ is a good classifying space, $T:E\rightarrow {\tilde{E}}$ is a universal map and $t:X\rightarrow {\tilde{B}}$ is the corresponding pointed classifying map. Explicitly, this means that that $\psi$ factors as

  

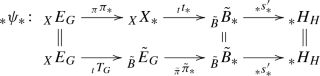
  for some $s':{\tilde{B}}\rightarrow H$ in ${{{\mathcal {B}}un}_*}$. As proven in Proposition 3.9(4), this is equivalent to saying that $\psi$ is of type U and of type P, which justifies the terminology.

• A morphism $\psi :E\rightarrow H$ in ${{\mathcal {B}}un}$ is weakly of type UP or of type wUP if it is of type P and the factor $s:X\rightarrow H$ occurring in the factorization $\psi =s\circ \pi$ factors up to pointed homotopy through a pointed classifying map $t:X\rightarrow {\tilde{B}}$, where ${\tilde{B}}$ is good pointed classifying space. In particular, this means that $\psi$ factors (up to pointed homotopy) as

  

  for some $s:X\rightarrow H$ and $s':{\tilde{B}}\rightarrow H$. As pointed out in Proposition 3.9(3), this is a weaker condition than being of type UP, which justifies the terminology.

Remark 3.8

Every map of type U factors through a contractible space, and every map of type wUP is homotopic to a map of type UP, which factors through a contractible space. It follows that maps of types U and wUP are nullhomotopic when the bundle structure is disregarded and they are considered maps of spaces.

We now prove useful closure properties of these distinguished classes of maps.

Proposition 3.9

Let X be a CW-complex pointed in a vertex, G a countable CW-group, E a pointed G-bundle over X and $H$ an abelian topological group. Let $\psi$ and $\psi '$ be morphisms $E\rightarrow H$ in ${{\mathcal {B}}un}_*$, and $\psi \cdot \psi '$ their pointwise multiplication.

• (1) If $\psi$ and $\psi '$ are of type U, then $\psi \cdot \psi '$ is of type U.

• (2) If $\psi$ and $\psi '$ are of type wUP, then $\psi \cdot \psi '$ is of type wUP.

• (3) If $\psi$ is of type UP, then $\psi$ is of type wUP.

• (4) $\psi$ is of type UP if and only if it is of type P and of type U.

Proof

We prove (1). As $\psi$ and $\psi '$ are of type U, by definition they factor through pointed universal bundles ${\tilde{E}}$ and ${\tilde{E}}'$ that admit the structures of countable CW-complexes, as displayed:

Then the product $\psi \cdot \psi '$ factors through ${\tilde{E}}\times {\tilde{E}}'$, as displayed

We note that the pointed space ${\tilde{E}}\times {\tilde{E}}'$ is a pointed universal bundle for G that admits the structure of a countable CW-complex. Indeed, it is contractible, and is a pointed G-bundle over ${\tilde{E}}\otimes _G{\tilde{E}}'$, which is a bundle over ${\tilde{B}}$ with fiber ${\tilde{E}}'$. Then ${\tilde{E}}\otimes _G{\tilde{E}}'$ is a countable CW-complex by Proposition 1.12, and ${\tilde{E}}\times {\tilde{E}}'$ is a countable CW-complex because it is a product of countable CW-complexes.

We prove (2). As $\psi$ and $\psi '$ are of type wUP, by definition they factor through the base space X, as displayed:

Then the product $\psi \cdot \psi '$ factors through X, as displayed

Moreover, without loss of generality, s and $s'$ factor up to pointed homotopy through some good classifying space ${\tilde{B}}$, as displayed:

As ${\tilde{E}}$ is a G-bundle and ${\tilde{E}}'$ is a universal bundle for G, there exists a pointed map $\tau :{\tilde{B}}\rightarrow {\tilde{B}}'$ such that

$$\begin{aligned} \tau ^*{\tilde{E}}'\cong _*{\tilde{E}}. \end{aligned}$$

We then have the following pointed equivalences of G-bundles over X:

$$\begin{aligned} (\tau \circ t)^*{\tilde{E}}'\cong _*t^*\tau ^*{\tilde{E}}'\cong _*t^*{\tilde{E}}\cong _*E\cong _*t'^*{\tilde{E}}', \end{aligned}$$

which implies that

$$\begin{aligned} t'\simeq _*\tau \circ t. \end{aligned}$$

In other words, up to pointed homotopy, $s':X\rightarrow H$ also factors through ${\tilde{B}}$, as

Then the product $s\cdot s'$ factors up to pointed homotopy through ${\tilde{B}}$, as

It follows that $\psi \cdot \psi '$ is of type wUP.

The statement (3) is straightforward from the definitions. We prove (4). The direct implication is straightforward. We prove the inverse direction. As $\psi$ is of type U, by definition $\psi$ factors through a universal bundle ${\tilde{E}}$ that admits the structure of a countable CW-complex as displayed

Then, as $\psi$ is of type P, the algebraic information $a(\kappa )$ of $\kappa$ vanishes, and we have that

$$\begin{aligned} 0=a(\psi )=a(\kappa \circ T)=a(\kappa )\circ a(T)=a(\kappa )\circ {{\mathrm{d}}}{}_G=a(\kappa ). \end{aligned}$$

So the map $\kappa$ is of type P, and factors therefore through the quotient ${\tilde{E}}/G={\tilde{B}}$. Thus we can write $\psi$ as follows

and see that it factors through the classifying space ${\tilde{B}}$. It follows that $\psi$ is of type UP. $\square$

4.3 The plus-cohomology groups

In this section, we define the plus-cohomology-groups of a bundle. Denote by $\psi ^{-1}$ and by $\psi \cdot \psi '$ the pointwise inverse and the pointwise multiplication of maps $E\rightarrow H$, respectively.

Definition 3.10

Let X be CW-complex pointed in a vertex, G a countable CW-group, E a pointed G-bundle over X and $H$ an abelian topological group.

• A UP-decomposition of $\psi :E\rightarrow H$ in ${{{\mathcal {B}}un}_*}$ consists of a morphism $\psi _U:E\rightarrow H$ of type U and a morphism $\psi _P:E\rightarrow H$ of type P such that

  $$\begin{aligned} \psi =\psi _U\cdot \psi _P\in {{{\mathcal {B}}un}_*}(E,H). \end{aligned}$$

• A UW-decomposition of $\psi :E\rightarrow H$ in ${{{\mathcal {B}}un}_*}$ consists of a morphism $\psi _U:E\rightarrow H$ of type U and a morphism $\psi _W:E\rightarrow H$ of type wUP such that

  $$\begin{aligned} \psi =\psi _U\cdot \psi _W\in {{{\mathcal {B}}un}_*}(E,H). \end{aligned}$$

• Two morphisms $\psi ,\psi ':E\rightarrow H$ in ${{{\mathcal {B}}un}_*}$ are plus-equivalent, and we write $\psi \simeq _+\psi '$, if and only if $\psi \cdot \psi '^{-1}:E\rightarrow H$ admits a UW-decomposition

  $$\begin{aligned} \psi \cdot \psi '^{-1}=\psi _U\cdot \psi _W\in {{{\mathcal {B}}un}_*}(E,H). \end{aligned}$$

Note that he relation $\simeq _+$ is an equivalence relation. Indeed, it is easily verified to be reflexive and symmetric, and is transitive as a consequence of Proposition 3.9 (1) and (2) and of the fact that $H$ is abelian. It is also a compatible with pointwise multiplication, again thanks to Proposition 3.9 (1) and (2).

Notation 3.11

We denote by $[\psi ]_+$ the class of $\psi :E\rightarrow H$ with respect to the relation $\simeq _+$, and by $[E,H]_+$ the quotient

$$\begin{aligned}{}[E,H]_+:={{{\mathcal {B}}un}_*}(E,H)/ {}_{\simeq _+}, \end{aligned}$$

which is an abelian group with respect to pointwise multiplication.

Recall the notation $E^{cof}$ is from Notation 1.18. If $A$ is a countable abelian group and $k\ge 0$, we define the plus-cohomology group$H^k_+(E;A)$ by

$$\begin{aligned} H^k_+(E;A):=[E^{\text {c}},M^kA]_+. \end{aligned}$$

Remark 3.12

Let X be a connected space pointed in $x_0$, and E an unpointed bundle over X. Given two points $e_0$ and $e_0'$ in the fiber $E|_{x_0}$, there exists a pointed equivalence

$$\begin{aligned} (E,e_0)\cong _*(E,e_0'), \end{aligned}$$

which can be realized as follows. If $g_0$ is the element of G such that $e_0'=e_o\cdot g_0$, then the map

is an equivalence and maps $e_0$ to $e_0'$. Therefore, the pointed equivalence class of E does not depend on the chosen base point. In particular, it makes sense to talk about the plus-cohomology of E without specifying any base point for E.

The notion of plus-equivalence generalizes both the notions of pointed algebraic homotopy for pointed maps and of pointed algebraic equivalence for homomorphisms of topological groups. If $H$ is a topological group we denote by $e_H$ both the neutral element of $H$ and any map into $H$ constant at the value $e_H$.

Proposition 3.13

Let $H$ be an abelian countable CW-group.

• (1) Given a CW-complex X pointed in a vertex, and pointed maps $s,s':X\rightarrow H$ we have that

  $$\begin{aligned} s\simeq _+s':X\rightarrow H\text { if and only if }s\simeq _* s':X\rightarrow H. \end{aligned}$$

• (2)q Given a countable CW-group G, and maps of topological groups $a,a':G\rightarrow H$ we have that

  $$\begin{aligned} a\simeq _+a':G\rightarrow H\text { if and only if }a\equiv _* a':G\rightarrow H. \end{aligned}$$

The following lemma is preliminary to Proposition 3.13.

Lemma 3.14

For a map of topological groups $a:G\rightarrow H$ between countable CW-groups the following are equivalent.

• (1) The homomorphism a extends to an a-equivariant pointed map $\kappa :E^{Mil}G\rightarrow H\text { in }{{\mathcal {B}}un}_*$.

• (2) There is a pointed equivalence $a_*E^{Mil}G\cong _*B^{Mil}G\times H$ of $H$-bundles over $B^{Mil}G$.

• (3) The homomorphism a is pointed equivalent to the constant map, i.e., $a\equiv _* e_H:G\rightarrow H$.

Proof of Lemma 3.14

Recall that every pointed $H$-equivariant map between $H$-bundles over $B^{Mil}G$ that is compatible with the projection onto $B^{Mil}G$ is a pointed equivalence of $H$-bundles over $B^{Mil}G$.

We prove $[(1)\Rightarrow (2)]$. Since $\kappa$ is a-equivariant, it induces an $H$-equivariant map ${\overline{\kappa }}:a_*E^{Mil}G\rightarrow H$ and factors through $a_*E^{Mil}G$ as displayed:

Moreover, the projection of $a_* E^{Mil}G$ gives a map $\pi :a_* E^{Mil}G\rightarrow B^{Mil}G$. Combining $\pi$ and ${\overline{\kappa }}$, we obtain a pointed equivalence of $H$-bundles over $B^{Mil}G$

We prove $[(1)\Leftarrow (2)]$. Given a pointed equivalence $\phi :a_* E^{Mil}G\cong _*B^{Mil}G\times H$ of $H$-bundles over $B^{Mil}G$, the following map $\kappa$ is equivariant and extends the map a:

We prove $[(2)\Leftrightarrow (3)]$. By Theorem 3.1 there is a pointed equivalence between $B^{Mil}G\times H={e_H}_*E^{Mil}G$ and $a_*E^{Mil}G$ if and only if a is pointed equivalent to the constant homomorphism $e_H:G\rightarrow H$. $\square$

We can now prove the proposition.

Proof of Proposition 3.13

• (1) We prove the direct implication. If $s\simeq _* s':X\rightarrow H$, then$s'\cdot s^{-1}\simeq _* e_H:X\rightarrow H$ factors up to pointed homotopy through a point, therefore $s'\cdot s^{-1}$ is of type wUP in ${{{\mathcal {B}}un}_*}(X,H)$. So $s\simeq _+ s'$.

  We prove the inverse implication. If $s\simeq _+ s':X\rightarrow H$, then $s'\cdot s^{-1}=\psi _U\cdot \psi _W$ where $\psi _U:X\rightarrow H$ is of type U and $\psi _W:X\rightarrow H$ is of type wUP in ${{{\mathcal {B}}un}_*}(X,H)$. By Remark 3.8, all maps of type U and all maps of type wUP are pointed homotopic to the constant pointed map, and therefore

  $$\begin{aligned} s'\cdot s^{-1}=\psi _U\cdot \psi _W\simeq _* e_H\cdot e_H=e_H:X\rightarrow H. \end{aligned}$$

  It follows that $s\simeq _* s'$.

• (2) We prove the direct implication. If $a\equiv _* a':G\rightarrow H$, then $a'\cdot a^{-1}\equiv _* e_H:G\rightarrow H$. By Lemma 3.14, $a'\cdot a^{-1}$ factors through $E^{Mil}G$, and is therefore of type U in ${{{\mathcal {B}}un}_*}(G,H)$. It follows that $a\simeq _+a'$.

  We prove the inverse implication. If $a\simeq _+ a':G\rightarrow H$, then $a'\cdot a^{-1}=\psi _U\cdot \psi _W$ where $\psi _U:G\rightarrow H$ is of type U and $\psi _W:G\rightarrow H$ is of type wUP in ${{{\mathcal {B}}un}_*}(G,H)$. As $\psi _U$ is of type U, it factors through some classifying space ${\tilde{E}}$ for G. As $E^{Mil}G$ is a G-bundle and ${\tilde{E}}$ is a universal bundle for G, there exists a G-equivariant pointed map $EG\rightarrow {\tilde{E}}$. Then $\psi _U$ also factors through EG, as displayed

  

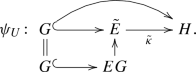
  By Lemma 3.14, $\psi _U$ is then pointed algebraic equivalent to the constant homomorphism. On the other hand, $\psi _W$ is constant because it factors through the base space of G, which is a point. Therefore

  $$\begin{aligned} a'\cdot a^{-1}=\psi _U\cdot \psi _W=\psi _U\cdot e_H=\psi _U\equiv _*e_H:G\rightarrow H. \end{aligned}$$

  It follows that $a\equiv _* a'$.$\square$

When $E=X$ is a discrete bundle, or $E=G^{\text {c}}$ is a codiscrete bundle, the plus-cohomology group recovers ordinary (group) cohomology.

Proposition 3.15

Let X be a CW-complex pointed in a vertex, G a topological group that admits a countable CW-replacement, and $H$ an abelian countable CW-group. The following isomorphisms of abelian groups hold.

$$\begin{aligned} \begin{array}{lrcl} (1) &{} [{}_XX_*,{}_* H_H]_+&{}{}\cong {}&{}[X,H]_*\\ (2) &{} [{}_* G^{\text {c}}_{G^{\text {c}}},{}_* H_H]_+&{}{}\cong {}&{}[BG,MH]_*\\ (3) &{} [{}_X{X\times G^{\text {c}}}_{G^{\text {c}}},{}_X H_H]_+&{}{}\cong {}&{}[X,H]_*\oplus [BG,MH]_*\\ (4) &{}[{}_{B^{Mil}G}E^{Mil}G_{G},{}_X H_H]_+&{}{}\cong {}&{}0 \end{array} \end{aligned}$$

We need a preliminary lemma to prove (2).

Lemma 3.16

For every abelian countable CW-group $H$ and any connected countable CW-complex X pointed in a vertex there is an isomorphism of abelian groups

Proof of Lemma 3.16

Let $\tau :B^{Mil}H\rightarrow MH$ be the natural pointed homotopy equivalence of Theorem 2.1, and let $\eta _X:X\rightarrow {\tilde{B}}\Omega ^{Mil}X$ be the classifying map of $P^{Mil}X$ over the universal bundle ${\tilde{E}}\Omega ^{Mil}X$. One can check that the map

$$\begin{aligned} \tau \circ {\tilde{B}}-\circ \eta _X:[\Omega ^{Mil}X,H]_+\rightarrow [X,MH]_+ \end{aligned}$$

realizes the bijection

$$\begin{aligned} {[}\Omega ^{Mil}X,H]_+\cong & {} {{\mathcal {G}}p}({{\mathcal {T}}op})(\Omega ^{Mil}X,H)/ {}_{\equiv }\cong {{\mathcal {T}}op}(X,B^{Mil}H)/ {}_{\simeq }\\\cong & {} {{\mathcal {T}}op}(X,MH)/ {}_{\simeq }\cong [X,MH]_+, \end{aligned}$$

obtained by means of Proposition 3.13, Theorems 1.10, and 2.1. The map is also a group homomorphism. Indeed, for any $a,a':\Omega ^{Mil}X\rightarrow H$, the following diagram commutes up to pointed homotopy:

$\square$

We can now prove the proposition. Note that the proofs of (1), (2) and (4) follow from previous results. However, there is no elementary proof of (3). We here give two arguments, but they both use results that will appear later in the paper.

Proof

Statement (1) is a consequence of Proposition 3.13 and Statement (2) is a consequence of (1) and Lemma 3.16. Statement (4) is a consequence of the fact that, by definition, every map $EG\rightarrow H$ is of type U, and therefore plus-equivalent to the trivial map.

We prove (3). By Lemma 3.19, the assignments $(s:X\rightarrow H)\mapsto (s\circ {{\mathrm{pr}}}{}_1:X\times G\rightarrow H)\text { and }(a:G\rightarrow H)\mapsto (a\circ {{\mathrm{pr}}}{}_2:X\times G\rightarrow H)$ induce maps $[X,MH]_+\rightarrow [X\times G,H]_+\text { and }[G,H]_+\rightarrow [X\times G,H]_+.$ They can be combined into a map $[X,MH]_+\oplus [BG,MH]_+\rightarrow [X\times G,H]_+$ which is given by $(s:X\rightarrow H,a:G\rightarrow H)\mapsto ((s\circ {{\mathrm{pr}}}{}_1)\cdot (a\circ {{\mathrm{pr}}}{}_2):X\times G\rightarrow H).$ One can prove directly that the map is a bijection. Alternatively, by using Theorem 3.21 we obtain a short exact sequence of abelian groups

which splits because the mentioned above map $[G,H]_+\rightarrow [X\times G,H]_+$ is a section. $\square$

By specializing the last proposition to the case $H=M^kA$, we obtain the following.

Corollary 3.17

Let X be a CW-complex pointed in a vertex, G a group that admits a countable CW-replacement, $A$ a countable abelian group, and $k>0$. The following isomorphisms of abelian groups hold.

$$\begin{aligned} \begin{array}{lrcl} 1) &{} H^k_+({}_XX_*,A)_+&{}{}\cong {}&{}H^k(X;A)\\ 2) &{}H^k_+({}_* G_{G},A)&{}{}\cong {}&{}H^{k+1}(BG;A)\\ 3) &{}H^k_+({}_X X\times G_{G},A)&{}{}\cong {}&{}H^{k+1}(BG;A)\oplus H^k(X;A)\\ 4) &{}H^k_+({}_{BG} EG_{G},A)&{}{}\cong {}&{}0 \end{array} \end{aligned}$$

As a consequence of Remark 3.8, if two maps of bundles are plus-equivalent, they they are also pointed homotopic as pointed maps of pointed spaces. This can be summarized by the following fact.

Remark 3.18

For every pointed G-bundle E over X, the identity yields a homomorphism of abelian groups

$$\begin{aligned}{}[{}_XE_G,{}_* H_H]_+\rightarrow [E,H]_*. \end{aligned}$$

By specializing to the case of $H=M^kA$, and using the fact that the construction $(-)^{cof}$ does not change the homotopy type, the map becomes

$$\begin{aligned} H^k_+(E;A)\rightarrow H^k(E^{\text {c}};A)\cong H^k(E;A). \end{aligned}$$

This map is an isomorphism if $E=X$ is a discrete bundle. However it will not be in general, not even when the bundle is codiscrete.

We now discuss the functoriality of the assignment $E\mapsto [E,H]_+$. Although the group ${{\mathcal {B}}un}_*(E,H)$ is functorial in E before taking the quotient modulo $\simeq _+$, the property for a map to be of type U is not a priori compatible with precomposition of maps. This prevents us from considering $[E,H]_+$ as a functor in $E\in {{\mathcal {B}}un}_*$. However, the assignment $[-,H]_+$ can act on at least three kinds of maps: G-equivariant morphisms of G-bundles, maps between codiscrete bundles, and maps to a discrete bundle X, as stated by the following lemma. Note that the property (3) is counterintuitive.

Lemma 3.19

Let X and $X'$ be CW-complexes pointed in vertices, G and $G'$ countable CW-groups, E a pointed G-bundle over X, $E'$ a pointed $G'$-bundle over $X'$ and $H$ an abelian topological group. Let $\phi :E'\rightarrow E$ and $\psi :E\rightarrow H$ be morphisms in ${{\mathcal {B}}un}_*$.

• (1) When $G=G'$, if $\psi$ is of type U, then $\psi \circ \phi$ is of type U.

• (2) When $G=G'$, if $\psi$ is of type wUP, then $\psi \circ \phi$ is of type wUP.

• (3) When $E=X$, if $\psi$ is of type U, then $\psi \circ \phi$ is of type wUP.

• (4) When $E=X$, if $\psi$ is of type wUP, then $\psi \circ \phi$ is of type wUP.

• (5) When $E=G$ and $E'=G'$, if $\psi$ is of type U, then $\psi \circ \phi$ is of type wUP.

• (6) When $E=G$ and $E'=G'$, if $\psi$ is of type wUP, then $\psi \circ \phi$ is of type wUP.

Proof

• (1) As $\psi$ is of type U, it factors through a universal bundle ${\tilde{E}}$ for G, as displayed:

  

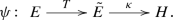
  Then $\psi \circ \phi$ factors through ${\tilde{E}}$, as displayed

  

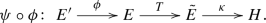
  It follows that $T\circ \phi$ is a universal map and $\psi \circ \phi$ is of type U.

• (2) As $\psi$ is of type wUP, it factors through the base space X, as displayed:

  

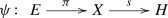
  If $\pi ':E'\rightarrow X'$ is the projection of $E'$ and $g:X\rightarrow X'$ is the geometric information of $\phi$, then $\psi \circ \phi$ factors through $\pi \circ \phi =g\circ \pi '$ as displayed:

  

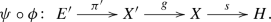
  This proves that $\psi \circ \phi$ is of type P. Moreover, since $\psi$ is of type wUP, the map s factors up to pointed homotopy through a classifying space ${\tilde{B}}$ of G, as displayed

  

  where t is a classifying map for E with respect to a universal bundle ${\tilde{E}}$. Then the map $s\circ g$ factors up to pointed homotopy through the classifying space ${\tilde{B}}$ of G, as displayed

  

  where $t\circ g$ happens to be a classifying map for $E'$ with respect to ${\tilde{E}}$. Indeed, using Proposition 1.2 on $\phi :E\rightarrow E'$, we obtain pointed equivalences of G-bundles over $X'$:

  $$\begin{aligned} E'\cong _* g^* E\cong _* g^* t^* {\tilde{E}}\cong _*(t\circ g)^*{\tilde{E}}. \end{aligned}$$

  It follows that $\psi \circ \phi$ is of type wUP.

• (3) As $\psi$ is of type U, it is pointed homotopic to a constant map by Remark 3.8. Now, if $\pi ':E'\rightarrow X'$ is the projection of $E'$ and $g:X\rightarrow X'$ is the geometric information of $\phi$, then $\psi \circ \phi$ factors through the base space $X'$ as displayed:

  

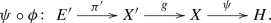
  This proves that $\psi \circ \phi$ is of type P. Moreover the map $\psi \circ g$ is pointed homotopic to the trivial map because $\psi$ is. So $\psi \circ g$ factors up to pointed homotopy through the classifying space $B^{Mil}G'$ of $G'$, as displayed

  

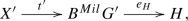
  It follows that $\psi \circ \phi$ is of type wUP.

• (4) As $\psi$ is of type wUP, it is pointed homotopic to a constant map by Remark 3.8. The same argument used in (3) applies. It follows that $\psi \circ \phi$ is of type wUP.

• (5) As $\psi$ is of type U, it factors through some universal map ${\overline{\kappa }}:{\tilde{E}}\rightarrow H$ as

  

  As $E^{Mil}G$ is a G-bundle and ${\tilde{E}}$ is a universal bundle for G, there exists a G-equivariant pointed map $\beta :E^{Mil}G\rightarrow {\tilde{E}}$ and the inclusion $G\hookrightarrow {\tilde{E}}$ factors through it as

  

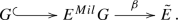
  In conclusion, $\psi \circ \phi$ factors through $E^{Mil}G'$, as displayed

  

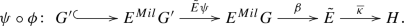
  It follows that $\psi \circ \phi$ is of type U.

• (6) As $\psi$ is of type wUP, it factors through a singleton, and is therefore constant. Then $\psi \circ \phi$ is constant and is in particular of type wUP.

$\square$

The first consequence of Lemma 3.19 is that the assignment $E\mapsto [E,H]_+$ defines a functor on the (non-full!) subcategory ${{{\mathcal {B}}un}_*}_G$ of ${{\mathcal {B}}un}_*$ given by of pointed G-bundles and G-equivariant maps.

Proposition 3.20

Let X be a CW-complex pointed in a vertex, G a countable CW-group, E a pointed G-bundle over X and $H$ an abelian countable CW-group. Then the assignment

$$\begin{aligned} E\mapsto \mathcal [E,H]_+:={{{\mathcal {B}}un}_*}(E,H)/ {}_{\simeq _+} \end{aligned}$$

defines a contravariant functor of G-bundles into abelian groups

$$\begin{aligned} {[}-,H]_+:{{{\mathcal {B}}un}_*}_G^{\text {op}}\rightarrow {{\mathcal {A}}b}. \end{aligned}$$

Proof

By Lemma 3.19(1) and (2), plus-equivalence is compatible with precomposition. $\square$

The second consequence of Lemma 3.19 is that the assignment $E\mapsto [E,H]_+$ acts on the Nomura-Puppe sequence of Remark 3.5 and produces a sequence of abelian groups,

which will be proven to be exact in the next section. When $H=M^kA$, this sequence becomes

4.4 The long exact sequence

In this section we prove that the sequence above is exact and can be extended to be a long exact sequence.

Proposition 3.21

Let X be a countable CW-complex pointed in a vertex, G a countable CW-group, E a pointed G-bundle over X and $H$ an abelian countable CW-group. There is an exact sequence of abelian groups

We need a preliminary lemma. Recall the notion of algebraic equivalence $\equiv _*$ from Definition 1.9.

Lemma 3.22

Let X be a CW-complex pointed in a vertex, G a countable CW-group, E a pointed G-bundle over X and $H$ an abelian countable CW-group. Every a-equivariant pointed morphism $\psi :E\rightarrow H$ such that $a\equiv _* e_H:G\rightarrow H$ admits a UP-decomposition.

In the proof, if $\psi :E\rightarrow H$ is a map of bundles, we denote by $\psi ^{-1}:E\rightarrow H$ the map obtained by inverting pointwise in $H$ the map $\psi$.

Proof of Lemma 3.22

We first fix a G-equivariant pointed map $T:E\rightarrow E^{Mil}G$, that induces a classifying map $t:X\rightarrow B^{Mil}G$. In particular there is a commutative diagram

As $a\equiv _* e_H$, by Lemma 3.14a extends to a pointed a-equivariant map $\kappa :E^{Mil}G\rightarrow H$. Recalling the proof of Lemma 3.14, we see that $\kappa$ factors through $a_* E^{Mil}G$, as displayed

The map $\overline{\kappa }$ induces pointed equivalence of $H$-bundles over $B^{Mil}G$ and X

$$\begin{aligned} ({\tilde{\pi }},{\overline{\kappa }}):a_* E^{Mil}G\rightarrow B^{Mil}G\times H\text { and }(\pi ,{\overline{\kappa }}\circ a_*T):a_*E\rightarrow X\times H\end{aligned}$$

which fits into a commutative diagram

On the other hand, since $\psi$ is a-equivariant, it induces an $H$-equivariant map ${\overline{\psi }}:a_*E\rightarrow H$ and factors through $a_* E$ as displayed

Using the equivalence $a_*E\cong _* X\times H$, $\psi$ factors through $X\times H$, too. The map $X\times H\rightarrow H$ occurring in such a factorization for $\psi$ is obtained by composing the inverse of $({\overline{\pi }},{\overline{\kappa }}\circ a_* T)$ and ${\overline{\psi }}$, which are both $H$-equivariant. So the composite is also $H$-equivariant, and thus it must be of the form

where $s:X\rightarrow H$ is a pointed map. There is therefore a commutative diagram

There is no reason for $s\cdot H$ to factor further through $B^{Mil}G\times H$. Using the fact that both $\psi$ and $(s\circ \pi )^{-1}$ both factor through $a_* E$ and $X\times H$, we write a diagram similar to the one above for

$$\begin{aligned} \psi _U:=\psi \cdot (s\circ \pi )^{-1}:E\rightarrow H\end{aligned}$$

instead of $\psi$. The key fact is that $\psi _U$ is designed such that the map $X\times H\rightarrow H$ occurring in the factorization of $\psi _U$ is now just a projection on the second factor. In particular $\psi _U$ factors through $B^{Mil}G\times H$, as displayed

As a consequence $\psi _U$ factors through the universal bundle $E^{Mil}G$ for G, and is therefore of type U.

We then set

$$\begin{aligned} \psi _P:=s\circ \pi :E\rightarrow H, \end{aligned}$$

which is of clearly type P, and the desired factorization of $\psi$ follows:

$$\begin{aligned} \psi =(s\circ \pi )\cdot (\psi \cdot (s\circ \pi )^{-1})=\psi _P\cdot \psi _U. \end{aligned}$$

$\square$

We can now prove the proposition.

Proof of Proposition 3.21

We prove the exactness at $[X,H]_+$: In order to show that ${{\mathrm{im}}}(t^*)\subset {{\mathrm{ker}}}(\pi ^*)$, take $[s:B^{Mil}G\rightarrow H]_+$. As $s\circ t\circ \pi$ clearly factors through $B^{Mil}G$ as

it is of type UP and

$$\begin{aligned} \pi ^*(t^*([s]_+))=[s\circ t\circ \pi ]_+=[e_H]_+, \end{aligned}$$

namely $t^*([s]_+)\in {{\mathrm{ker}}}(\pi ^*)$. In order to show that ${{\mathrm{im}}}(t^*)\supset {{\mathrm{ker}}}(\pi ^*)$, take $[s:X\rightarrow H]_+\in {{\mathrm{ker}}}(\pi ^*)$. Then

$$\begin{aligned} {[}e_H]_+=\pi ^*([s]_+)=[s\circ \pi ]_+. \end{aligned}$$

Then there exists $\psi _W:E\rightarrow H$ of type wUP and $\psi _U:E\rightarrow H$ of type U such that $s\circ \pi =\psi _W\cdot \psi _U$. As $\psi _U$ is of type U, it factors through a universal bundle ${\tilde{E}}$ for G as

As $\psi _W$ is of type wUP, in factors through X as

Since $s\circ \pi$ and $\psi _W$ both factor through $\pi$, their algebraic information maps $a(s\circ \pi )$ and $a(\psi _W)$ are trivial. It follows that also the algebraic information $a(\psi _U)$ of $\psi _U$ is also trivial, since

$$\begin{aligned} a(\psi _U)=a((s\circ \pi )\cdot \psi _W^{-1})=a(s\circ \pi )\cdot a(\psi _W)^{-1}=e_H\cdot e_H=e_H. \end{aligned}$$

Thus $\kappa$ factors through the quotient ${\tilde{B}}={\tilde{E}}/G$, as

Define $g_U$ as the composite of t and $s_U$, as displayed:

Since $\psi _W$ is of type wUP, the map $g_W$ occurring in its factorization factors up to pointed homotopy through any classifying space for G, and in particular through ${\tilde{B}}$, as displayed

Therefore

$$\begin{aligned} s\circ \pi =\psi _U\cdot \psi _W=(g_U\circ \pi )\cdot (g_W\circ \pi )=(g_U\cdot g_W)\circ \pi . \end{aligned}$$

and, since $\pi$ is surjective,

$$\begin{aligned} s=g_U\cdot g_W=(s_U\circ t)\cdot g_W\simeq _*(s_U\circ t)\cdot (s_W\circ t)=(s_U\cdot s_W)\circ t. \end{aligned}$$

Finally

$$\begin{aligned} {[}s]_+=[(s_U\cdot s_W)\circ t]_+=t^*([s_U\cdot s_W]_+)\in {{\mathrm{im}}}(t^*). \end{aligned}$$

We prove the exactness at $[E,H]_+$. In order to show that ${{\mathrm{im}}}(\pi ^*)\subset {{\mathrm{ker}}}(\iota ^*)$, take $[s:X\rightarrow H]_+\in [X,H]_+$ and remark that $\pi \circ \iota$ is constant. Therefore

$$\begin{aligned} \iota ^*(\pi ^*([s]_+))=[s\circ \pi \circ \iota ]_+=[s\circ e_H]_+=[e_H]_+, \end{aligned}$$

namely $\pi ^*[s]\in {{\mathrm{ker}}}(\iota ^*)$. In order to show that ${{\mathrm{ker}}}(\iota ^*)\subset {{\mathrm{im}}}(\pi ^*)$, take $[\psi :E\rightarrow H]_+\in {{\mathrm{ker}}}(\iota ^*)$. Then the algebraic information of $\psi$ is plus-equivalent to the trivial homomorphism, since

$$\begin{aligned}{}[e_H]_+=\iota ^*([\psi ]_+)=[\iota \circ \psi ]_+=[a(\psi )]_+. \end{aligned}$$

By Lemma 3.22, there exists $\psi _P:E\rightarrow H$ of type P, and $\psi _U:E\rightarrow H$ of type U such that $\psi =\psi _P\cdot \psi _U$. As $\psi _P$ is of type P, it factors through the base space X

Moreover, $\psi _U\simeq _+e_H$ and

We prove the exactness at $[G,H]_+$. In order to show that ${{\mathrm{im}}}(\iota ^*)\subset {{\mathrm{ker}}}(b^*)$, take $[\psi :E\rightarrow H]_+$. By Theorem 1.10, there exists a classifying map $b:\Omega ^{Mil}X\rightarrow G$ and an a-equivariant map $B:P^{Mil}X\rightarrow E$. In particular there is a commutative diagram

It follows that $\psi \circ \iota \circ b$ factors through the universal bundle $P^{Mil}X$ for $\Omega ^{Mil}X$,

Then $\psi \circ \iota \circ b$ is of type U and

$$\begin{aligned} b^*(\iota ^*([\psi ]_+))=[\psi \circ \iota \circ b]_+=[e_H]_+. \end{aligned}$$

Therefore $\iota ^*([\psi ]_+)\in {{\mathrm{ker}}}(b^*)$. In order to show that ${{\mathrm{ker}}}(b^*)\subset {{\mathrm{im}}}(\iota ^*)$, take $[a:G\rightarrow H]_+\in {{\mathrm{ker}}}(b^*)$. Then

$$\begin{aligned}{}[e_H]_+=b^*([a]_+)=[a\circ b]_+, \end{aligned}$$

and, by Proposition 3.13(2), $a\circ b\equiv _* e_H$. There are then pointed equivalences of $H$-bundles over X

$$\begin{aligned} a_* E\cong _*a_* b_*P^{Mil}X\cong _*(a\circ b)_*P^{Mil}X\cong _*{e_H}_*P^{Mil}X=X\times H\end{aligned}$$

that we use to construct the map $\psi :E\rightarrow a_*E\cong X\times H\rightarrow H$, whose algebraic information can be computed to be $a:G\rightarrow H$. This means that

$$\begin{aligned} {{\mathrm{im}}}(\iota ^*)\ni \iota ^*([\psi ]_+)=[\psi \circ \iota ]_+=[a(\psi )]_+=[a]_+. \end{aligned}$$

$\square$

If we specialize the exact sequence to the case $H=M^kA$ we obtain the following long exact sequence, which can be regarded as a dual of the homotopy long exact sequence of a fibration.

Theorem 3.23

Let X be a connected countable CW-complex (pointed in a vertex), G a topological group whose homotopy groups are countable, E a G-bundle over X, and $A$ a countable abelian group. There is a long exact sequence of abelian groups

where the map $\chi _k$ is induced by the classifying map of E.

Proof

Let $t:X\rightarrow B^{Mil}G^{cof}$ be a classifying map for $E^{cof}$. We first notice that by Theorem 3.1 there exists a map of topological groups $\Omega ^{Mil}t:\Omega ^{Mil}X\rightarrow G^{\text {c}}$ such that $E^{\text {c}}\cong _* (\Omega ^{Mil}t)_*P^{Mil}X$. By applying Proposition 3.21 to $E^{\text {c}}$ with $k>0$ and $H:=M^kA$ we obtain a sequence of abelian groups with five terms:

By Lemma 3.16, there is a commutative diagram

Therefore the connecting map to the right in degree k,

$$\begin{aligned} -\circ \Omega ^{Mil}t:[G^{\text {c}},M^kA]_+\rightarrow [ \Omega ^{Mil}X,M^kA]_+, \end{aligned}$$

can be identified with the connecting map map to the left in degree $k+1$,

$$\begin{aligned} -\circ t:[B^{Mil}G,M^{k+1}A]_+\rightarrow [ X,M^{k+1}A]_+, \end{aligned}$$

which can further be identified with the map induced in cohomology by t in degree $k+1$,

$$\begin{aligned} \chi _{k+1}:H^{k+1}(B^{Mil}G;A)\rightarrow H^{k+1}(X;A). \end{aligned}$$

Starting with $k=0$ we can extend the sequence to the right infinitely many times, and obtain the desired long exact sequence. $\square$

We specialize the sequence above to two extreme cases and use Corollary 3.17 to simplify it.

Example 3.24

Let X be a connected countable CW-complex (pointed in a vertex), G a topological group whose homotopy groups are countable, E a G-bundle over X, and $A$ a countable abelian group.

• If $E=X\times G$ is the trivial bundle, the long exact sequence of Theorem 3.23 splits

  

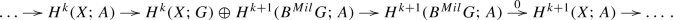
• If $E=EG$ is a universal bundle, the long exact sequence of Theorem 3.23 degenerates to

  

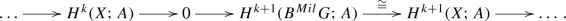
4.5 Applications

We collect here some interesting consequences of Theorem 3.23, that allow us to compare the plus-cohomology groups with ordinary cohomology groups and with an instance of the twisted cohomology from [24]. The detailed proofs can be found in the author’s thesis [27].

For any G-bundle E, the fiber inclusion $\iota :G\hookrightarrow E$ is a Hurewicz cofibration. By [25, Theorem 3.2.1], if we let the ordinary cohomology groups act on the cofiber sequence of $\iota :G\hookrightarrow E$, , we obtain a cohomology long exact sequence

This sequence can be compared to the sequence of Theorem 3.23.

Proposition 3.25

[27]. Let X be a connected countable CW-complex (pointed in a vertex), G a topological group whose homotopy groups are countable, E a G-bundle over X, and $A$ a countable abelian group. The comparison map of Remark 3.18 induces a morphism of long exact sequences of abelian groups

It was pointed out by Jeffrey Carlson (personal communication, November 15, 2016) that there is a different way to produce a long exact sequence involving the characteristic map. Indeed, the cofiber sequence induces a long exact sequence

The fact that the plus-cohomology group $H^k_+(E;A)$ and the ordinary cohomology group $H^{k+1}({\mathrm{cof}}(t);A)$ of the cofiber ${\mathrm{cof}}(t)$ of the classifying map $t:X\rightarrow BG$ both fit into long exact sequences suggests that one can hope for a comparison. In [27], a comparison map

$$\begin{aligned} H^{k+1}({\mathrm{cof}}(t);A)\rightarrow H^k_+(E;A) \end{aligned}$$

is constructed, and proven to be an isomorphism using Theorem 3.23 together with standard techniques of homological algebra. This is summarized by the following theorem.

Theorem 3.26

[27]. Let X be a connected countable CW-complex (pointed in a vertex), G a topological group whose homotopy groups are countable, E a G-bundle over X, and $A$ a countable abelian group. There is an isomorphism

$$\begin{aligned} H_+^k(E;A)\cong H^{k+1}({\mathrm{cof}}(t);A) \end{aligned}$$

that induces an isomorphism of long exact sequences of abelian groups

This isomorphism gives an interpretation of the plus-cohomology groups in purely homotopical terms, and does not involve any assumption of countability for the (CW-structure of the) structure group G. The geometric definition in terms of plus-cohomology groups, however, highlights better the role played by the bundle structure. For instance, the plus-cohomology groups of a bundle E can be used to detect the number of structures of a fixed type on a bundle, e.g. the number of reductions of the structure group to a specific one, as we now explain.

Given X a connected countable CW-complex, G a topological group whose homotopy groups are countable, E a G-bundle over X, $A$ a countable abelian group, and $c\in H^k(BG;A)$ a universal characteristic class, one can be interested in counting the number of $G^{red}(c)$-reductions of G. For instance, when $c:=w_2\in H^2(BSO(n);{\mathbb {Z}}/2)$ is the second Stiefel–Whitney class, and E is an SO(n)-bundle E over X, the question translates to counting the number of spin structures on E (up to a suitable equivalence relation). Combining Theorems 2.15 and 2.18, we see that there exists a $G^{red}(c)$-reduction for a G-bundle E if and only if the fiber

$$\begin{aligned} H^{k-1}_+(E;A)_c:={\mathrm{fib}}_c\left( \iota ^*:H^{k-1}_+(E;A)\rightarrow H^{k-1}_+(G;A)\cong H^k(BG;A)\right) \end{aligned}$$

of $\iota ^*$ over $c\in H^k(BG;A)$ is not empty. This suggests that such fiber could be an indication of how many such reductions there are. On the other hand, in the literature the $G^{red}(c)$-reductions of a bundle E are often enumerated by means of $\pi _0(\Gamma ^h(Bj;t))$, i.e., the set of connected components of the space of homotopy liftings of the classifying map $t:X\rightarrow BG$ of E along the map $Bj:BG^{red}(c)\rightarrow BG$. This is an instance of twisted cohomology (as in [24]). The link between twisted cohomology and plus-cohomology is made precise by the following theorem.

Theorem 3.27

[27]. Let X be a connected countable CW-complex, G a topological group whose homotopy groups are countable, E a G-bundle over X, $A$ a countable abelian group, and $c\in H^k(BG;A)$ a universal characteristic class. There is a transitive action of $H^{k-1}(BG;A)$ on the twisted cohomology $\pi _0(\Gamma ^h(Bj;t))$, such that

$$\begin{aligned} H^{k-1}_+(E;A)_c\cong \pi _0(\Gamma ^h(Bj;t))/ {}_{H^{k-1}(BG;A)}. \end{aligned}$$

The isomorphism is built by making explicit use of the construction of the plus-cohomology groups. The action, together with the isomorphism, provides useful information on the cardinality of the twisted cohomology, namely on the number of structures of a specific kind on a bundle.

Very often the action is trivial, and the fiber $H^{k-1}_+(E;A)_c$ therefore coincides with the twisted cohomology $\pi _0(\Gamma ^h(Bj;t))$. This happens, for instance, when the cohomology of BG vanishes in certain degrees. Here is an application that exploits this idea.

Example 3.28

Recall from Construction 2.12 the Whitehead tower $(O(n)^{(k)})_{k\ge 0}$ of the orthogonal group O(n). We first observe that, by the universal coefficient theorem for cohomology and the Hurewicz Theorem,

$$\begin{aligned} H^{k-1}(BO(n)^{(k)};{\mathbb {Z}}/2)\cong & {} {\mathrm{Hom}}(H_{k-1}(BO(n)^{(k)};{\mathbb {Z}}),{\mathbb {Z}}/2)\\\cong & {} {\mathrm{Hom}}(\pi _{k-1}(BO(n)^{(k)}),{\mathbb {Z}}/2)\\\cong & {} {\mathrm{Hom}}(0,{\mathbb {Z}}/2)\cong 0.\\ \end{aligned}$$

The induced map $H^k(BO(n);{\mathbb {Z}}/2)\rightarrow H^k(BO(n)^{(k)};{\mathbb {Z}}/2)$ allows us to think of the kth universal Stiefel–Whitney class $w_k\in H^k(BO(n);{\mathbb {Z}}/2)$ as a characteristic class living in $H^k(BO(n)^{(k)};{\mathbb {Z}}/2)$. Now, given an O(n) bundle E over X, by Theorem 3.27, the (possibly empty) fiber $H^0_+(E;{\mathbb {Z}}/2)_{w_1}$ counts the SO(n)-reductions of E, namely the orientations of E. If this set is not empty, there exists a bundle $E^{(1)}$ such that $E\cong E^{(1)}\otimes _{SO(n)}O(n)$. By Theorem 3.27, the (possibly empty) fiber $H^1_+(E^{(1)};{\mathbb {Z}}/2)_{w_2}$ coincides with twisted cohomology, and counts the Spin(n)-reductions of $E^{(1)}$, namely the spin structures of $E^{(1)}$. If this set is non-empty, there exists a bundle $E^{(2)}$ such that $E^{(1)}\cong E^{(2)}\otimes _{Spin(n)}SO(n)$. Inductively, if there exists an $O(n)^{(k)}$-bundle $E^{(k)}$ such that $E^{(k-1)}\cong E^{(k)}\otimes _{G^{(k-1)}}G^{(k)}$, by Theorem 3.27, the (possibly empty) fiber $H^{k-1}_+(E^{(k-1)};{\mathbb {Z}}/2)_{w_k}$ counts the $G^{(k)}$-reductions of $E^{(k-1)}$.

Appendix: Proof of Proposition 1.12

In this section we prove Proposition 1.12, which is needed for Propositions 2.6 and 3.9. The proof uses certain properties of compactly generated weakly Hausdorff spaces. Recall that a space X is weakly Hausdorff if for every compact Hausdorff space K and continuous map $f:K\rightarrow X$ the image f(K) is closed. A function $f:X\rightarrow Y$ between topological spaces is k-continuous if for any compact Hausdorff space C the precomposition $f\circ j:C\rightarrow Y$ of f with a continuous map $j:C\rightarrow X$ is continuous (cf. [33, Proposition 1.11]). The space X is compactly generated if every k-continuous function $f:X\rightarrow Y$ is continuous. It is shown in [15, §5.2] and [33] that compactly generated weakly Hausdorff spaces and continuous maps form a category CGWH of convenient topological spaces, i.e., the category CGWH contains all CW-complexes, is bicomplete and is cartesian closed.

Remark 4.1

The category CGWH of compactly generated weakly Hausdorff spaces is reflective in the category CG of compactly generated topological spaces, and the category CG is coreflective in the category ${{\mathcal {T}}op}$ of all spaces. The left adjoint $h:CG\rightarrow CGWH$ (described e.g. in [33, Proposition 2.22]) and the right adjoint $k:{{\mathcal {T}}op}\rightarrow CG$ (defined in [33, Definition 1.1]) are called h-fication and k-fication respectively. These functors help construct (co)limits in CGWH.

• (1) Colimits in CGWH are constructed by h-fying the colimits in ${{\mathcal {T}}op}$, as proven in [33, Corollary 2.23]. In formulas,

  $$\begin{aligned} {\mathrm{colim}}_i^{CGWH}C_i\cong h({\mathrm{colim}}_i^{{{\mathcal {T}}op}}C_i). \end{aligned}$$

  In particular, if a colimit in ${{\mathcal {T}}op}$ of a diagram of CGWH spaces is a CGWH space, then it coincides with the colimit in CGWH.

• (2) Products in CGWH are constructed by k-fying the products in ${{\mathcal {T}}op}$, because the inclusion of CGWH in CG is a right adjoint and products in CG are constructed by k-fying the products in ${{\mathcal {T}}op}$ [33, Proposition 2.4]. In formulas,

  $$\begin{aligned} C\times _{CGWH}C'\cong k(C\times _{{{\mathcal {T}}op}}C'). \end{aligned}$$

  In particular, if a product in ${{\mathcal {T}}op}$ of two CGWH spaces is a CGWH space, then it coincides with the product in CGWH.

We now prove two closure properties of CGWH spaces.

Lemma 4.2

• (1) Every open subset of a CW-complex is a CGWH space.

• (2) Every fiber bundle whose base space is a CW-complex and whose fiber is a CW-complex is a CGWH space.

Proof of Lemma 4.2

We prove (1). As CW-complexes are normal spaces [11, Proposition A.3.], they are in particular regular. Whence, by [23, Lemma 2.1(a)], every open neighborhood of a point contains a closed neighborhood of the same point. In particular, for every U open subset of a CW-complex, each point of U has a closed neighborhood in U. By [15, Chapter 5, Problem 1] this is enough for U to be a CGWH space.

We prove (2). Let E be a bundle over the countable CW-complex X and with fiber the countable CW-complex F. We prove that E is Hausdorff. Let $e,e'$ be two distinct points in E. If $\pi (e)\ne \pi (e')$, then there exist U and $U'$ disjoint neighborhoods of $\pi (e)$ and $\pi (e')$ in X. So $E|_U$ and $E|_{U'}$ are disjoint neighborhoods of e and $e'$. If $\pi (e)=\pi (e')$, then there exist W a trivialization open that contains $\pi (e)$. As $E|_W\cong W\times F$, which is a product of Hausdorff spaces, the points e and $e'$ can be separated in the open $E|_W$ by two disjoint open neighborhoods.

We prove that E is compactly generated. Let $f:E\rightarrow Y$ be a k-continuous function between topological spaces. Let e be a point of E, and U a trivialization open containing $\pi (e)$. The space $E|_U\cong U\times F$ is (homeomorphic to) an open subset of $X\times F$, which is a product of countable CW-complexes, and therefore a CW-complex. By (1), $E|_U$ is a CGWH space, and $f|_{E|U}$ is k-continuous, so $f|_{E|U}$ is continuous. Since the open subsets of the form $E|_U$ form a cover of E, it follows that f is continuous, and E is a CGWH space. $\square$

We can now prove Proposition 1.12.

Proof of Proposition 1.12

If $\sigma$ is a closed cell of X and U is a trivializing open subset of X, the following spaces are CGWH: the spaces X, F and $\sigma$, as they are CW-complexes, the space E, as proven in Lemma 4.2(2), the spaces $X\times F$ and $\sigma \times F$, as they are products of countable CW-complexes, and therefore CW-complexes by [11, Theorem A.6], the spaces U, $U\cap \sigma$, $U\cap \sigma \times F$, and $U\times F$, as they are open subsets of CW-complexes, and therefore CGWH spaces by Lemma 4.2(1), and the space $E|_U$, as it is homeomorphic to $U\times F$, and therefore a CW-complex.

By Remark 4.1(1), colimits of diagrams involving these spaces coincide, be they taken in the category ${{\mathcal {T}}op}$ of all spaces or in the category CGWH of CGWH spaces.

We prove that the topological space E is a colimit of its restrictions $E|_{\sigma }$ to closed cells $\sigma$ of X. If $\sigma$ varies over the closed cells of X (and inclusions of those) and U varies over the trivialization open subsets of X for E (and inclusion of those), we have the following homeomorphisms

Now, every piece $\sigma \times F$ is a countable CW-complex, because it is the product of two countable CW-complexes. We therefore conclude that E is a countable CW-complex. $\square$