1 Introduction

Blood transfusion plays a critical role in the provision of medical care for some large-scale sudden-onset disasters due to human-made and natural hazards (Hess and Thomas 2003; Mujeeb and Jaffery 2007; Abolghasemi et al. 2008; Liu et al. 2010; Ibrion et al. 2015). Overburdened with the influx of injured people, a blood center in the affected area will call for urgent collection and transshipment of blood units from some nearby blood centers, and a considerable number of blood products for emergency surgery are usually gathered at the affected blood center. Subsequently, an appropriate blood allocation is required to replenish the blood inventory of each blood bank that is within the service area of the blood center, which is essential for emergency medical services in disaster relief operations. For example, the 2003 Bam Earthquake resulted in 108,985 donated blood units and 21,347 units were actually distributed (Abolghasemi et al. 2008). After the 2008 Wenchuan Earthquake, a total of 107,911 units of blood products were gathered and ultimately 70,415 units were distributed (Ma et al. 2015). Therefore, exploring emergency blood allocation approach to alleviate blood shortage after a large-scale sudden-onset disaster has great practical significance.

Emergency blood allocation is different from the allocation of general relief materials because blood has some remarkable features, such as limited shelf life, multiple kinds of blood products (for example, red blood cells (RBCs), plasma, and platelets), and multiple blood groups with complex ABO/Rh(D) compatibility. In the existing literature on blood allocation, each kind of blood product is regarded as a single material and thus the problem is degenerated into a transportation problem (Gregor et al. 1982; Hemmelmayr et al. 2009; Ganesh et al. 2014). There are eight blood groups for each kind of blood product. Moreover, ABO/Rh(D)-compatible blood substitution is allowed in cases of blood shortage during emergencies, that is, each kind of blood product with a specific group not only can satisfy its own demand, but also can be used as a substitute for the same product with other compatible groups. ABO/Rh(D)-compatible blood substitution is a recourse action that offers incredible alternatives to meet demand when supply of a specific blood is restricted in emergencies (NHS 2012). There are specific and complicated substitution rules for different blood products. Figure 1 shows all possible compatible substitutions among eight ABO/Rh(D) blood groups for red blood cell (that is, each blood group can only be substituted by the blood group whose arrow points directly or indirectly at it). For example, blood group AB+ can be substituted by all other seven blood groups, and O− can substitute all other blood groups (Lang 2010; Duan and Liao 2014). As shown in Table 1, blood demand should first be satisfied by the exact ABO/Rh(D) match so that preference order “1” stands for the highest priority, preference order “2” stands for the possible compatible substitutions for red blood cells, and “∞” means not feasible.

Fig. 1
figure 1

ABO/Rh(D)-compatible blood substitution graph of red blood cell (RBC)

Full size image
Table 1 Possible ABO/Rh(D)-compatible substitutions for red blood cell (RBC)
Full size table

ABO/Rh(D)-compatible blood substitution further complicates the emergency blood allocation problem in disaster relief operations. In recent years, some researchers such as Zahiri and Pishvaee (2017) and Osorio et al. (2018) have considered the compatible substitution for the problems of blood supply chain design and blood fractionation. However, the blood allocation problem with ABO/Rh(D) compatibility has not been well investigated yet. First, allocation should try to control the ratio of allotypic transfusion and adopt homotype transfusion as much as possible (BSMS 2003). Thus, decision makers are faced with the dilemma of creating a solution with less shortage and less substitution in the allocation solution.

Moreover, the substitution rules are not identical among different blood products. The preference order of possible ABO/Rh(D)-compatible substitutions are also not same, but currently there is no research report clarifying it. Although one blood group can be substituted by other blood groups, doctors will choose a suitable blood group for substitution transfusion according to their clinical experience.

Therefore, this study aimed to develop a decision-making framework for the multi-product, multi-group emergency blood allocation problem in disaster relief operations. Furthermore, we evaluate the influence of an ABO/Rh(D)-compatible substitution policy for emergency blood allocation decision making. The primary contributions of this study include:

  • Propose a mixed integer programming model for the multi-product multi-group emergency blood allocation problem in disaster relief operations, which considers the complex ABO/Rh(D) compatibilities among blood groups.

  • Consider the substitution rate as well as substitution preference order, which enhances the practicality of the developed model.

  • Propose a greedy heuristic algorithm to determine the near-optimal scheme of the emergency blood allocation problem in disaster relief operations.

  • Quantify the effect of an ABO/Rh(D)-compatible substitution policy on emergency blood allocation in disaster relief operations under different substitution relations and preference orders of different blood products.

The remainder of this article is organized as follows. In Sect. 2, the related literature is reviewed. In Sect. 3, a multi-product multi-group emergency blood allocation model for disaster relief operations is developed based on a mixed integer programming method. In Sect. 4, a greedy heuristic algorithm is proposed to solve the model. In Sect. 5, a numerical example is presented to verify the proposed model and algorithm. Finally, the results are concluded in Sect. 6, and research implications and managerial insights are also discussed.

2 Literature Review

Operations management in blood supply chain has attracted much attention focusing mainly on blood inventory management of hospital blood banks or regional blood centers (Nahmias 1982; Prastacos 1984; Pierskalla 2005; Karaesmen et al. 2011; Bakker et al. 2012; Beliën and Forcé 2012; Osorio et al. 2015). However, the blood allocation problem has not been well investigated quantitatively by scholars. Prastacos (1981) proposed an optimal allocation policy to minimize both expected average shortages and expected average expirations in a region where a perishable product (for example, blood) is periodically produced and allocated among several locations. Sapountzis (1984) developed an integer programming model to allocate blood from a regional blood transfusion service center to local hospitals according to the characteristics of the blood. Federgruen et al. (1986) presented an allocation model for distributing a perishable product (for example, blood) from a regional center to a given set of locations with random demands. They considered the combined problem of allocating the available inventory at the center while deciding how these deliveries should be performed. Atkinson et al. (2012) studied the issue of whether transfusing fresher blood can be achieved without jeopardizing blood availability and proposed a novel allocation strategy for blood transfusions, which focuses on the tradeoff between the age and availability of transfused blood. Olusanya and Adewumi (2014) presented the use of meta-heuristic techniques to optimize the blood assignment problem in a blood bank to minimize the total amount of blood resources imported from outside. All the above studies aimed at solving the blood allocation problem under the routine conditions and did not consider the effect of ABO/Rh(D)-compatible substitution.

Currently there is a growing research interest in the emergency blood supply problem, such as post-disaster location analysis of regional blood centers (Sahin et al. 2007; Sharma et al. 2017), robust design of emergency blood supply networks (Jabbarzadeh et al. 2014), supply chain design for blood supply in disasters (Ensafian and Yaghoubi 2017; Fahimnia et al. 2017; Fazli-Khalaf et al. 2017; Khalilpourazari and Khamseh 2017; Samani et al. 2018), and an age-based policy for blood transshipment during blood shortage (Wang and Ma 2015). But the emergency blood allocation problem in disaster relief operations has never been discussed.

Specifically, one important feature of blood is possible ABO/Rh(D)-compatible substitutions among the eight blood groups—if the exact ABO/Rh(D) match is unavailable, an ABO/Rh(D)-compatible match can be sought by following ABO/Rh(D) compatibility (Lang 2010; Duan and Liao 2014). ABO/Rh(D)-compatible blood substitution is an important way to ensure an adequate blood supply, especially when blood is in shortage or under emergency conditions. ABO/Rh(D)-compatible blood substitution has only been considered in recent years, and we list the literature in Table 2.

Table 2 Recent studies on blood substitution
Full size table

In the studies listed in Table 2, blood substitution has only been considered in a routine blood collection and supply problem, where most objectives are based on cost, and the effects of substitution rate constraint are ignored. Emergency blood allocation problem is quite different from the studies in Table 2—it should consider the constraint of substitution rate. Our objective was to lessen both shortage and substitution in an allocation solution. Moreover, the problem also has scenarios under preference order of possible substitutions.

In the above literature, emergency blood allocation problem considering ABO/Rh(D)-compatible substitution has not been studied yet. To fill this gap and cater to the practical demand in disaster relief operations, this study developed a mixed integer programming model for emergency blood allocation considering ABO/Rh(D) compatibilities among blood groups, and a heuristic algorithm was proposed to explore the performance of an emergency blood allocation policy with ABO/Rh(D)-compatible substitution.

3 Model Framework

This section describes the emergency blood allocation problem in disaster relief operations and its mathematical formulation.

3.1 Problem Description

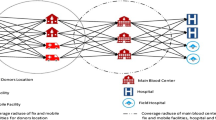
This study considered the emergency blood allocation problem after a large-scale disaster. Figure 2 illustrates emergency blood collection and transshipment from some nearby blood centers after a disaster has caused heavy casualties and a batch of blood products has been gathered at the regional blood center in the affected area. In this kind of emergency situation, the blood products are then in need of timely allocation to the affected blood banks within the service area of the blood center, so as to meet the local demand for blood transfusions in emergency relief.

Fig. 2
figure 2

Emergency blood allocation problem in disaster relief operations

Full size image

The volume of blood products is smaller than other emergency relief goods, and the distance between a blood center and its affiliated blood banks is often not very far—in general, one car can transport all the allocated blood products from a blood center to a blood bank within a day. So for this kind of urgent allocation problem in post-disaster blood management, our research focused on allocation rather than inventory or transportation decision problem. The main aim was to minimize the total unmet demand of blood products of the affected blood banks while optimizing the ABO/Rh(D)-compatible substitution scheme. Based on the above prerequisites, the following assumptions were made to rationalize the proposed model.

  1. (1)

    The total amount of blood products to be allocated at the blood center is sufficient to satisfy the total demand from all blood banks in the affected region. But the supply of blood products with a specific blood group does not always match the total demand for this kind of blood product at all blood banks. The remaining lifetime of these products is assumed longer than the period of blood demand for emergency relief.

  2. (2)

    According to the equity principle, the shortage or substitution amount of each kind of blood product is apportioned among the blood banks according to their demand proportions.

  3. (3)

    Since homotype blood transfusion has the best curative effect, the maximum ABO/Rh(D)-compatible substitution rate should be set when ABO/Rh(D)-compatible blood substitution is inevitable in emergencies. Moreover, to improve the clinical efficiency of emergency blood transfusions, ABO/Rh(D)-compatible blood substitutions among different blood groups should follow the principle that the higher the substitution priority, the better.

3.2 Model Formulation

The notations used throughout the remainder of this article are as follows.

3.2.1 Parameter

\(K\) :

Set of all blood groups, that is, \(K = \left\{ {{\text{A}} + ,{\text{B}} + ,{\text{AB}} + ,{\text{O}} + ,{\text{A}} - ,{\text{B}} - ,{\text{AB}} - ,{\text{O}} - } \right\}\).

\(E\) :

Set of all arcs of a directed graph \(G = \{ K,E\}\), and represents ABO/Rh(D)-compatible blood substitutions, where \(E \subseteq K \times K\). A directed arc \([i,k]{\kern 1pt} {\kern 1pt} {\kern 1pt} (i,k \in K{\kern 1pt} {\kern 1pt} )\) denotes that blood group \(k\) can be substituted by blood group \(i\).

\(U_{i}\) :

Set of blood groups that can be substituted by blood group \(i\), that is, \(U_{i} = \left\{ {k|[i,k] \in E} \right\}\) and \(U_{i} \subseteq K\).

\(V_{i}\) :

Set of blood groups that can substitute blood group \(i\), that is, \(V_{i} = \left\{ {k|[k,i] \in E} \right\}\) and \(V_{i} \subseteq K\).

\(J\) :

Set of blood banks in the affected area.

\(P\) :

Set of blood products (such as whole blood, plasma, and RBCs).

\(W\) :

Set of priority weights of ABO/Rh(D)-compatible blood substitution.

\(w_{ik}\) :

Priority weight of substituting blood group \(k\) with blood group \(i\). For any blood group \(k\), blood group \(i\) with a smaller \(w_{ik}\) has a higher substitution priority, \(\forall {\kern 1pt} w_{ik} \in W{\kern 1pt} ,{\kern 1pt} {\kern 1pt} i \in K,{\kern 1pt} {\kern 1pt} k \in U_{i}\).

\(s_{kp}\) :

Available blood product \(p\) with blood group \(k\) at the local blood center, \(\forall k \in K,p \in P\).

\(d_{kp,j}\) :

Demand for blood product \(p\) with blood group \(k\) at blood bank \(j\), \(\forall k \in K,p \in P,j \in J\).

\(\delta\) :

Maximum ABO/Rh(D)-compatible substitution rate among different blood groups, that is, the maximum ratio of substitution amount to total demand of each blood product.

\(\rho\) :

Per-unit penalty on the blood shortage.

3.2.2 Decision variables

\(x_{kp,j}\) :

Amount of blood product \(p\) with blood group \(k\) allocated to blood bank \(j\), \(\forall k \in K,p \in P,j \in J\).

\(y_{ikp,j}\) :

Amount of blood group \(i\) that is used to substitute blood group \(k\) for blood product \(p\) at blood bank \(j\), \(\forall i \in K,k \in U_{i} ,p \in P,j \in J\).

\(z_{kp,j}\) :

Shortage of blood product \(p\) with blood group \(k\) at blood bank \(j\), \(\forall k \in K,p \in P,j \in J\).

To solve the emergency blood allocation problem considering ABO/Rh(D)-compatible substitution, a mixed integer programming model is developed as follows:

$$\hbox{min} F = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho \sum\limits_{p \in P} {\sum\limits_{k \in K} {\sum\limits_{j \in J} {z_{kp,j} } } } + \sum\limits_{k \in K} {\sum\limits_{{i \in V_{k} }} {\left( {w_{ik} \times \sum\limits_{j \in J} {\sum\limits_{p \in P} {y_{ikp,j} } } } \right)} }$$
(1)

s.t.

$$\rho \ge {\kern 1pt} \hbox{max} (w_{ik} ), \, \forall i \in V_{k} ,k \in K$$
(2)
$$w_{kk} \le {\kern 1pt} w_{ik} , \, \forall i \in V_{k} ,k \in K$$
(3)
$$x_{kp,j} + \sum\limits_{{i' \in V_{k} }} {y_{i'kp,j} } - \sum\limits_{{i \in U_{k} }} {y_{kip,j} } = d_{kp,j} {\kern 1pt} - z_{kp,j} ,\quad \forall k \in K,p \in P,j \in J{\kern 1pt}$$
(4)
$$\sum\limits_{j \in J} {x_{kp,j} } \le s_{kp} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \forall k \in K,p \in P$$
(5)
$$z_{kp,j} \le \left\lceil {\sum\limits_{j \in J} {z_{kp,j} } \times \left( {d_{kp,j} /\sum\limits_{j \in J} {d_{kp,j} } } \right)} \right\rceil ,\quad \forall k \in K,p \in P,j \in J$$
(6)
$$\sum\limits_{{i \in U_{k} }} {y_{kip,j} {\kern 1pt} } \le x_{kp,j} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \forall k \in K,p \in P,j \in J$$
(7)
$$\sum\limits_{k \in K} {\sum\limits_{{i \in V_{k} }} {y_{ikp,j} } } \le \delta \sum\limits_{k \in K} {d_{kp,j} } ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \forall p \in P,j \in J$$
(8)
$$y_{ikp,j} \le \left\lceil {\sum\limits_{j \in J} {y_{ikp,j} } \times \left( {d_{kp,j} /\sum\limits_{j \in J} {d_{kp,j} } } \right)} \right\rceil ,\quad \forall k \in K,i \in V_{k} ,p \in P,j \in J$$
(9)
$$z_{kp,j} ,y_{ikp,j} {\kern 1pt} ,{\kern 1pt} x_{kp,j} \ge 0\,{\text{and}}\,{\text{ all}}\,{\text{ of}}\,{\text{ them}}\,{\text{are}}\,{\text{integers}},\,\forall i \in V_{K} ,k \in K,p \in P,j \in J$$
(10)

There are actually two targets in the problem—the first is to minimize shortage and the second is to get the best substitution solution under the substitution priority order. Initially, we preferred to build a bi-level programming model or a dual objective function model for this problem. But the bi-level programming model and the dual objective function model were also difficult to develop efficient algorithms to solve. Eventually we chose the single objective nonlinear mixed integer programming model to directly solve the two targets under some special constraints.

Constraint 2 ensures that the shortage weight \(\rho\) is larger than the largest priority weight of substituting \(w_{ik}\) between any blood group \(i\) and \(k\). Constraint 3 ensures that the homotype allocation is preferred than the allotypic allocation. As lower weight among blood groups stands for higher substitution priority, we can use the min-sum function to express the two targets in one formula with the above two constraints. So the objective function 1 is to minimize the sum of the total priority weight of ABO/Rh(D)-compatible blood substitutions and the total shortage of all blood products at all blood banks in the affected area.

Constraint 4 denotes the formula relation among the supply, the demand, and the shortage. The demand of blood product \(p\) with blood group \(k\) at blood bank \(j\) is satisfied by the same group product and substitutions of other blood groups, and the unsatisfied demand will be the shortage. Constraint 5 ensures that the total demand for any type of blood product may not exceed its supply. Constraint 6 denotes that the shortage of each type of blood product is allocated among all blood banks according to their demand proportions. Constraint 7 denotes the limitation on the substitution amount of each blood group at each blood bank. Constraint 8 represents the total substitution amount of each blood product at each blood bank under the limitation of substitution rate. Constraint 9 denotes that the substitution amount of each blood product is allocated among all blood banks according to their demand proportions. Constraint 10 defines the domain of decision variables.

4 Model Solution

The proposed model is nonlinear due to constraints 6 and 9. But there is no existing algorithm for this allocation problem considering the priorities of ABO/Rh(D)-compatible substitution. Due to the complexity of ABO/Rh(D)-compatible substitution rules, the above mixed integer programming model is a high-dimensional optimization problem. To solve the model efficiently, in this study we applied a greedy heuristic algorithm in which a judgment matrix that includes ABO/Rh(D)-compatible blood substitution relations was used to reduce the computational complexity.

As shown in Fig. 3, a judgment matrix of ABO/Rh(D)-compatible blood substitution was first built to denote the ABO/Rh(D) compatibility for each blood product. Then, the judgment matrix was simplified according to the total supply and demand of blood products with each blood group. Next, two lemmas on ABO/Rh(D)-compatible substitution were used to obtain the optimal substitution amounts of those blood products with blood groups that satisfy the lemmas. Afterwards, the greedy rule was used to optimize the remaining optimal substitution amounts and obtain the substitution amounts and shortages of blood products with different blood groups. Finally, the shortages and substitutions of blood products were allocated among blood banks.

Fig. 3
figure 3

Flowchart of the greedy heuristic algorithm

Full size image

Before the detailed steps of the greedy heuristic algorithm are presented, we first explore the quantitative properties of ABO/Rh(D)-compatible blood substitution. Let \(y_{ikp}^{ * }\) be the optimal amount of blood product \(p\) with blood group \(k\) substituted by blood group i in consideration of blood substitution priority, \(\forall i \in K,k \in U_{i} ,p \in P,j \in J\). Based on Lemmas 1 and 2, we can determine \(y_{ikp}^{ * }\) among eligible blood groups.

Lemma 1

Assume that the supply of blood product \(p\) with blood group \(k\) is superfluous, if \((\sum\nolimits_{j} {d_{ip,j} - s_{ip} ) > 0}\) for \(i \in U_{k}\) , we can get

$$y_{kip}^{ * } = \hbox{min} \left\{ {s_{kp} - \sum\limits_{j} {d_{kp,j} {\kern 1pt} ,\sum\limits_{j} {d_{ip,j} - s_{ip} {\kern 1pt} {\kern 1pt} } } } \right\},\,{\text{when}}\quad |U_{k} | = = 1\quad {\text{and}}\quad w_{ki} = \hbox{min} \{ w_{ki} |w_{ki} \in W\} .$$

Lemma 1 implies that for blood product \(p\), if the supply of blood group \(k\) is superfluous and only group \(i\) is in shortage among all those blood groups that can be substituted with blood group \(k\), then we can determine the optimal value of \(y_{kip}^{ * }\) when \(w_{ki}\) equals the minimum priority weight of blood substitution.

Lemma 2

Assume that blood product \(p\) with blood group \(k\) is inadequate, if \((s_{ip} {\kern 1pt} - \sum\limits_{j} {d_{ip,j} ) > 0}\) for \(i \in V_{k}\), we can get \(y_{ikp}^{ * } = \hbox{min} \left\{ {\sum\limits_{j} {d_{kp,j} - s_{kp} {\kern 1pt} ,s_{ip} - \sum\limits_{j} {d_{ip,j} {\kern 1pt} } } } \right\}\) when \(|V_{k} | = = 1\) and \(w_{ik} = = \hbox{min} \{ w_{ik} |w_{ik} \in W\}\).

Lemma 2 implicates that for blood product \(p\), if the supply of blood group \(k\) is inadequate and only group \(i\) is in surplus among all those blood groups that can substitute group \(k\), then we can determine the optimal value of \(y_{ikp}^{ * }\) when \(w_{ik}\) equals the minimum priority weight of blood substitution. On these bases, the process of the greedy heuristic algorithm is as follows:

  1. (1)

    Initialization

  • Step 1: Input the data of blood supply \(s_{kp}\) and blood demand \(d_{kp,j}\), and set the priority weights of blood substitution \(w_{ik}\) and the maximum ABO/Rh(D)-compatible substitution rate \(\delta\). Initialize the optimal total allocation amount \(x_{kp}^{ * }\), the optimal total substitution amount \(y_{ikp}^{ * }\), and the optimal total shortage \(z_{kp}^{ * }\) as 0-matrices.

  • Step 2: Obtain the total demand for each blood product with each blood group \(D_{kp} = \sum\nolimits_{j \in J} {d_{kp,j} }\) and its initial allocation \(xa_{kp} = \hbox{min} (s_{kp} ,D_{kp} )\). Thus, the initial shortage is \(za_{kp} = D_{kp} - xa_{kp}\), or the initial surplus is \(sa_{kp} = s_{kp} - xa_{kp}\). Let \(x_{kp}^{ * } = xa_{kp}\).

  1. (2)

    Simplifying the judgment matrix of ABO/Rh(D)-compatible blood substitution

  • Step 3: Obtain the judgment matrix of ABO/Rh(D)-compatible blood substitution \(UV\_now\) according to ABO/Rh(D) compatibility as well as the supply and demand of blood products with each blood group.

    Step 3.1: Obtain a priority weight matrix of blood substitution \(UV\) according to ABO/Rh(D) compatibility.

    Step 3.2: Initialize \(UV\_now\) as a \({\kern 1pt} \left| K \right| \times \left| K \right| \times {\kern 1pt} \left| P \right|\) 0-matrix, and let \(i = 1\).

    Step 3.3: Let \(UV\_now_{:,:,i} = UV\), where \(:,:,i\) denotes all the columns and rows on page \(i\) of the judgment matrix, that is, the ith 2-D matrix in \(UV\_now\) whose size is \(\left| K \right| \times \left| K \right|\), similarly hereinafter. Let \(j = 2\), and \(k = 1\).

  • Step 3.3.1: If the initial surplus \(sa_{ij} = = 0\), then \(UV\_now_{j,:,i} = 0.\)

  • Step 3.3.2: If the initial shortage \(za_{ik} = = 0\), then \(UV\_now_{:,k,i} = 0.\)

  • Step 3.3.3: Let \(j = j + 1\) and \(k = k + 1\); repeat Steps 3.3.1 and 3.3.2 until \(j = = \left| K \right|\) and \(k = = \left| K \right| - 1\).

  • Step 3.4: Let \(i = i + 1\), repeat Step 3.3 until \(i = = \left| P \right|\).

Figure 4 shows the transformation process of \(UV\_now\) in Step 3. Let the priority weights of ABO/Rh(D)-compatible blood substitution be equal to the values listed in Table 1; thus \(\hbox{min} (W) = 2\), and \(\hbox{max} (W) = 8\). We can get a priority weight matrix \(UV\), as shown in Fig. 4a, where 0 denotes that there is no need to consider its corresponding row and column in optimizing ABO/Rh(D)-compatible blood substitution. \(UV_{2,1} = 2\) denotes that when a blood product with blood group AB+ is in shortage, the same type of blood product with AB− has the highest substitution priority. Similarly, \(UV_{2,8} = 8\) denotes that when a blood product with blood group AB+ is in shortage, the same type of blood product with blood group O− has the lowest substitution priority.

Fig. 4
figure 4

Transformation of the judgment matrix of ABO/Rh(D)-compatible blood substitution

Full size image

For blood product \(i\), if the surplus supply of blood group \(j\) is equal to zero, that is, \(sa_{ij} = = 0\), then blood group \(j\) cannot be used to substitute other blood groups. Thus, all the values of row \(j\) in matrix \(UV\_now_{:,:,i}\) should be zero, and it is unnecessary to consider ABO/Rh(D) compatibility between this row and all the columns during the optimization process. The simplification process of rows in matrix \(UV\_now\), as shown in Fig. 4b, demonstrates the computation process in Step 3.3.1.

Similarly, for blood product \(i\), if the surplus supply of group \(k\) is equal to zero, that is, \(za_{ik} = = 0\), then group \(k\) is of no need to be substituted by other blood groups. Thus, all the values of column \(k\) in matrix \(UV\_now_{:,:,i}\) should be 0, and it is unnecessary to consider ABO/Rh(D) compatibility between this column and all the rows during the optimization process. The simplification process of columns in matrix \(UV\_now\), as shown in Fig. 4c, demonstrates the computation process in Step 3.3.2.

In conclusion, the matrix \(UV\_now\) established in Step 3 not only can denote the substitution priority among different blood groups, but also can denote ABO/Rh(D) compatibility according to the actual supply and demand of blood, which reduces non-zero values in the matrix and then simplifies the subsequent computation process.

  1. (3)

    Computing the optimal substitution amounts based on ABO/Rh(D) compatibility

  • Step 4: Obtain the maximum substitution amount of each blood product \(ym_{p}\) according to the maximum ABO/Rh(D)-compatible substitution rate \(\delta\)

  • Step 5: Obtain the optimal substitution amounts of each blood product with each blood group that satisfies Lemmas 1 and 2.

  • Step 5.1: Let \(i = 1\).

  • Step 5.2: Let \(j = 2\) and use Lemma 1.

  • Step 5.2.1: If \(sum(UV\_now_{j,:,i} ) = = \hbox{min} \{ w_{ik} |w_{ik} \in W\}\), then let the sequence number of the corresponding column in \(UV\_now\) be \(g\) and \(y_{jgi}^{ * } = \hbox{min} (sa_{ij} ,za_{ig} )\); otherwise, go to Step 5.2.4.

  • Step 5.2.2: If \(y_{jgi}^{ * } = = sa_{ij}\), then \(UV\_now_{j,:,i} = 0\); otherwise, \(UV\_now_{:,g,i} = 0\).

  • Step 5.2.3: Let \(sa_{ij} = sa_{ij} - y_{jgi}^{ * }\), \(za_{ig} = za_{ig} - y_{jgi}^{ * }\), \(x_{ji}^{ * } = x_{ji}^{ * } + y_{jgi}^{ * }\), and \(ym_{i} = ym_{i} - y_{jgi}^{ * }\).

  • Step 5.2.4: Let \(j = j + 1\) and repeat Steps 5.2.1 to 5.2.3 until \(j = = \left| K \right|\).

  • Step 5.3: Let \(k = 1\) and use Lemma 2.

  • Step 5.3.1: If \(sum(UV\_now_{:,k,i} ) = = \hbox{min} \{ w_{ik} |w_{ik} \in W\}\), then let the sequence number of the corresponding row in \(UV\_now\) be \(g\) and \(y_{gki}^{ * } = \hbox{min} (sa_{ig} ,za_{ik} )\); otherwise, go to Step 5.3.4.

  • Step 5.3.2: If \(y_{gki}^{ * } = = sa_{ig}\), then \(UV\_now_{g,:,i} = 0\); otherwise, \(UV\_now_{:,k,i} = 0\).

  • Step 5.3.3: Let \(sa_{ig} = sa_{ig} - y_{gki}^{ * }\), \(za_{ik} = za_{ik} - y_{gki}^{ * }\), \(x_{gi}^{ * } = x_{gi}^{ * } + y_{gki}^{ * }\), and \(ym_{i} = ym_{i} - y_{gki}^{ * }\).

  • Step 5.3.4: Let \(k = k + 1\) and repeat Steps 5.3.1 to 5.3.3 until \(k = = \left| K \right| - 1\).

  • Step 5.4: Let \(i = i + 1\) and repeat Steps 5.2 and 5.3 until \(i = = \left| P \right|\).

In Step 5, we not only use Lemmas 1 and 2 to optimize the computation process, but also to further simplify the matrix \(UV\_now\) for the subsequent computation. For example, in Step 5.2.2, if \(y_{jgi}^{ * } = = sa_{ij}\), there will be no supply of blood product \(i\) with blood group \(j\) and all the values of column \(j\) in the matrix \(UV\_now_{:,:,i}\) should be zero; otherwise, \(y_{jgi}^{ * } = = za_{ig}\), which denotes that there exists no shortage of blood product \(i\) with blood group \(g\), and all the values of row \(g\) in the matrix \(UV\_now_{:,:,i}\) should be zero. Similarly, we can judge the value of \(y_{gki}^{ * }\) in Step 5.3.2 to simplify the matrix \(UV\_now\) further.

  1. (4)

    Compute the remaining optimal substitution amounts based on greedy criterion.

    Let \(i = 1\).

    Step 6.2: Obtain a vector \({\kern 1pt} wn\) by sorting the non-zero values of matrix \(UV\_now_{:,:,i}\) in ascending order. Let \({\kern 1pt} row\) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} col\) be the vector of row numbers and the vector of column numbers of each non-zero element in vector \({\kern 1pt} wn\), respectively. Let \({\kern 1pt} j = 1:length(wn)\).

    Step 6.2.1: If \(ym_{i} > 0\), then let \({\kern 1pt} k = row_{j}\), \({\kern 1pt} g = col_{j}\), and \(y_{kgi}^{ * } = \hbox{min} (ym_{i} ,sa_{ik} ,za_{ig} )\); otherwise, go to Step 6.2.4.

    Step 6.2.2: If \(y_{kgi}^{ * } = = sa_{ik}\), then \(UV\_now_{k,:,i} = 0\); If \(y_{kgi}^{ * } = = za_{ig}\), then \(UV\_now_{:,g,i} = 0\); otherwise, \(UV\_now_{k,g,i} = 0\).

    Step 6.2.3: Let \(sa_{ik} = sa_{ik} - y_{kgi}^{ * }\), \(za_{ig} = za_{ig} - y_{kgi}^{ * }\), \(x_{ki}^{ * } = x_{ki}^{ * } + y_{kgi}^{ * }\), and \(ym_{i} = ym_{i} - y_{kgi}^{ * }\).

    Step 6.2.4: Let \(j = j + 1\) and repeat Steps 6.2.1 to 6.2.3 until \({\kern 1pt} j = = length(wn)\).

Step 6.3: Let \(i = i + 1\) and repeat Step 6.2 until \(i = = \left| P \right|\).

  1. (5)

    Allocating the substitution amounts and shortages of each blood product

Step 7: The optimal amount of shortage \(z_{kp}^{ * }\) is equal to \(za_{kp}^{ * }\). The substitution amount \(y_{ikp,j}\) and the shortage \(z_{kp,j}\) of each blood product can be allocated respectively to each blood bank according to constraints 4 and 7. Calculate the allocation amount of each blood product with each blood group \(x_{kp,j}\) according to constraint 2 and the objective function value \({\kern 1pt} F_{{}}^{*}\).

In the above steps of the proposed heuristic method, we introduced a matrix \(UV\_now\) to represent the selection process of substitutions, the final value of the matrix can be used to validate the correctness of the substitution process. For example, for product \({\kern 1pt} i\), if \(UV\_now_{g,j,i} > 0\) in the final stage, it denotes that product \({\kern 1pt} i\) with blood group \({\kern 1pt} g\) still has surplus to substitute group \({\kern 1pt} j\), so we check the allocation solution to verify whether the substitution process is completed.

5 Simulation Experiments

This study took the emergency blood supply scenario after the Wenchuan Earthquake on 12 May 2008 as an example. The blood products gathered urgently at the Sichuan Blood Center had to be allocated to four blood banks in the affected area: Chengdu (CD), Deyang (DY), Mianyang (MY), and Guangyuan (GY).

Referring to Ma et al. (2015), we estimated the total emergency blood demand of the affected area after the earthquake and then apportioned it among the four blood banks in proportion to their covered population and blood groups. The proportions of blood groups O, A, B, and AB were approximately 36%, 32%, 24%, and 8%, respectively, while the proportions of blood groups Rh+ and Rh- were approximately 99.65% and 0.35%, respectively. The allocation of RBCs is shown in Table 3; the remaining lifetime of these blood products was assumed to be at least more than 20 days. The demand for red blood cells at each blood bank in the affected area in the 2 weeks after the Wenchuan Earthquake is listed in Table 4.

Table 3 Red blood cells with each blood group to be allocated at the Chengdu Blood Center after the Wenchuan Earthquake (U)
Full size table
Table 4 Red blood cell demand from each blood bank in the Wenchuan Earthquake affected area (U)
Full size table

5.1 Computational Results of Allocation

To get the solution with the least shortage, the per-unit penalty on blood shortage \(\rho\) should be greater than the maximum priority weight of blood substitution. Let \(\rho\) be 10,000 and we set priority weights of ABO/Rh(D)-compatible blood substitution \(w_{ik}\) according to the values listed in Table 1. All priority weights follow the preference order.

The proposed greedy heuristic algorithm was implemented by the Matlab software on a PC platform with an Intel i5 CPU, 8 GB memory, and Windows XP operating system. Table 5 shows the optimal emergency blood allocation scheme when the maximum ABO/Rh(D)-compatible substitution rate \(\delta\) equals to 5%.

Table 5 Optimal emergency blood allocation scheme for the studied case after the Wenchuan Earthquake (\(\delta = 5\%\))
Full size table

In the column of substitution amounts of Table 5, “B+ →AB+ 278” denotes that 278 units of AB+ product are substituted with B+ product, while in the column of shortages, “AB− 2” denotes the shortage of AB− product is 2 units.

The results show that when \(\delta = 5\%\), there existed ABO/Rh(D)-compatible substitutions among different blood groups of each blood product at each blood bank. Moreover, the substitution scheme followed the order of ABO/Rh(D)-compatible blood substitution, as shown in Table 1. In Table 5, the substitutions of each blood group among all blood banks are allocated according to their demand proportions, as well as the homotype allocations and shortages of each blood group at each blood banks are all generated under this principle.

The other blood products that are mainly used in disaster relief are whole blood and plasma. As shown in Tables 6 and 7 (Oneblood 2018), the substitution relations of these two products are quite different from the possible compatible substitutions for red blood cell.

Table 6 Possible ABO/Rh(D)-compatible substitutions for whole blood.
Full size table
Table 7 Possible ABO/Rh(D)-compatible substitutions for plasma.
Full size table

With regard to the ABO/Rh(D)-compatible substitutions for whole blood, Tables 3 and 4 were used as the data of the supply and demand of whole blood for the experiment. As all Rh(D)- products of whole blood have no possible substitution, ABO type products only are substituted by Rh(D)- products with same ABO type, the substitution relations of whole blood are remarkably less than RBCs. According to the testing result, the total shortage increases to 1655 units, and the total substitutions are only 10 units.

With regard to the ABO/Rh(D)-compatible substitutions for plasma, Tables 3 and 4 were used as the data of the supply and demand of plasma for a new experiment. According to this testing result, the total shortage increases to 1651 units, and the total substitutions are also only 10 units. The substitutions of plasma are quite different from the compatible substitutions for red blood cells, blood group O+/O− can be substituted by all other seven blood groups, and AB+/AB− can substitute all other blood groups. However, there are more surplus O+ products in the experiment data, so there are very few substitutions in the allocation solution.

In the above experiments for whole blood and plasma, if we had collected these blood products with different groups at the same proportion as red cells, there would be severe shortages in the allocation solution. Different blood products have different substitution rules, so it is suggested to collect more of these blood products with the blood groups that can substitute other blood groups to cause less shortages.

Through the above experiments, the feasibility of the heuristic algorithm we proposed is confirmed. By checking the relation between the values of matrix \(UV\_now\) and the allocation solution, the correctness of the algorithm is validated. The computation time of the heuristic method for these scenarios is within 2 s. During the above experiments, we also found that the allocation solutions are not unique as the possible substitution weights are the same values when substitutions happen.

5.2 Sensitivity Analysis of Substitution Rate

To further investigate the effect of an ABO/Rh(D)-compatible blood substitution policy, we performed a sensitivity analysis with change in the maximum ABO/Rh(D)-compatible substitution rate \(\delta\) and obtained the corresponding total substitution amounts and shortages, as shown in Fig. 5.

Fig. 5
figure 5

Total substitution amounts and shortages with the change in the maximum compatible substitution rate

Full size image

When ABO/Rh(D)-compatible blood substitution is not allowed, the total shortage of blood products within each blood group at the four blood banks reaches 1665 units. As the maximum ABO/Rh(D)-compatible substitution rate \(\delta\) increases, the total shortage decreases while the total substitution amount increases. When \(\delta \ge 10\%\), both the total substitution amount and the total shortage remain constant due to the maximum possibility of ABO/Rh(D)-compatible blood substitution.

The result shows that an ABO/Rh(D)-compatible substitution policy can significantly reduce the unmet rate of emergency blood demand and enhance the emergency blood supply level in disaster relief operations. With the increase of the maximum ABO/Rh(D)-compatible substitution rate among different blood groups, the total shortage of blood products decreases while the total substitution amount increases. Setting an appropriate maximum ABO/Rh(D)-compatible substitution rate, however, is a thorny problem for the decision maker. We should get a balance between less unmet demand and fewer allotypic transfusions since allotypic transfusions with blood substitutions are riskier than homotype transfusions.

5.3 Priorities of ABO/Rh(D)-Compatible Substitution

In practice, doctors may have their own preferences for substitution transfusion according to their clinical experience. For decision makers of emergency blood allocation, it is important to understand the impact of priorities of ABO/Rh(D)-compatible substitution on allocation solution.

In Table 8 we list a meticulous blood type preference order for substitution for red blood cells that was assumed by Lang (2010): Blood demand should first be satisfied by the exact ABO/Rh(D) match—lower substitution weight among blood groups stands for higher priority, so “1” stands for the highest priority, “8” stands for the lowest priority, and “∞” means not feasible. If the exact match is not available, an ABO/Rh(D)-compatible match could be sought according to the substitution priority.

Table 8 Assumed preference order of possible ABO/Rh(D)-compatible substitutions for red blood cells.
Full size table

We used the priority weight for ABO/Rh(D)-compatible substitutions in Table 8 and the supply and demand data from Sect. 5.1 for a new experiment and the testing results are shown in Table 9. The total shortage is 802 units, and the total substitutions are 863 units. These amounts for shortage and substitutions are the same as in Table 5, but substitutions among blood groups are different.

Table 9 Optimal emergency blood allocation scheme of red blood cells under preference order for substitution (\(\delta = 5\%\))
Full size table

For example, if RBCs with the AB− group are in shortage but RBCs with the A− group and O− group are both in surplus, then the A− group will be selected as the substitute because of its higher priority. Comparing Table 9 with Table 5, as A+ products are in shortage, O+ products are only selected to substitute A+ products in Table 5 (384 units) for blood bank CD; however, under the preference order for substitution, O+ products are less often selected to substitute A+ products in Table 9 (373 units). In the allocation solution for CD in Table 9, at higher priority (lower priority weight), 8 units of A− products are selected to substitute A+ products, and 3 units O− products are selected to substitute B− products. The priority weight of O+ for A+ is 3, but the priority weight of A− for A+ is 2 and O− for B− is 2, so these higher priority substitutions are considered first before lower priority substitutions.

In the solution for other blood banks, the priority substitutions also happen, so the allocation has the best value of the objective function. The result shows that considering the preference order of substitution will remarkably enhance the practical application of the proposed model under the scenario in which doctors can set the preference for substitution transfusion according to their clinical experience.

6 Discussions

The findings of this study provide the following research implications:

  • This study contributes to the understanding of emergency blood allocation problem in disaster relief operations. Particularly, we consider possible ABO/Rh(D)-compatible substitutions among different blood groups. The priority weights of ABO/Rh(D)-compatible blood substitution were used to represent possible substitution priorities among different blood groups. Then, a mixed integer programming model was developed for the emergency blood allocation problem in disaster relief operations with consideration of complex ABO/Rh(D) compatibility. To the best of our knowledge, this is the first study to investigate the emergency blood allocation problem in disaster relief operations, especially considering ABO/Rh(D) compatibility.

  • In view of the complexity of ABO/Rh(D) compatibility and the high-dimensional optimization task, this study proposed a greedy heuristic algorithm to solve the developed model. The greedy rules improves the optimization capability efficiently. Except for its advantages in real-time computing and adaptability to different scales, the heuristic algorithm used in the study can also deal with any type of objective function model as well as output the optimal solution of the model just by adding a few steps to the procedure.

  • The proposed model is able to adapt to a variety of substitution preference order, which will remarkably enhance the practical application of this research. If we set the order values of possible compatible substitutions for other blood groups the same, the allocation solution is not unique. The experiments in Sect. 5.1 also can verify this.

  • This study quantifies the effect of an ABO/Rh(D)-compatible substitution policy on emergency blood allocation. The result shows in Sect. 5.2 that the unmet rate of emergency blood demand can be decreased significantly by using an ABO/Rh(D)-compatible substitution policy, especially with a high maximum compatible substitution rate.

This study not only offered a general decision-making framework for emergency blood allocation in disaster relief operations, but also revealed the following managerial insights:

  • Based on the simulation experiments of Sect. 5, we can conclude that allowing ABO/Rh(D)-compatible blood substitution in emergency blood allocation can decrease the shortages of blood products significantly and keep the shortage rate within an acceptable level. Accordingly, the satisfaction degree of emergency blood demand can be improved remarkably.

  • Blood product collection scheme should be adjusted based on its possible ABO/Rh(D)-compatible substitution in emergency management. The more a blood group can substitute other blood groups, the larger amount the products with this kind of blood group should be collected. We should recognize that the possible ABO/Rh(D)-compatible substitution relations among the different blood products are not the same. The tests in Sect. 5.1 show that, if there is no particular consideration of different possible compatible substitutions during different blood product collection, there may be severe shortages in the allocation solution.

  • The higher the substitution rate, the less the shortage rate. As the result in Sect. 5.2 shows, theoretically we can narrow the gap between the demand and supply of blood products with each blood group by increasing the maximum ABO/Rh(D)-compatible substitution rate. But in practice, allotypic transfusion only accounts for approximately 5% of routine clinical medical treatments (BSMS 2003). Setting an upper limit on the substitution rate can help avoid potential domino effect caused by ABO/Rh(D)-compatible blood substitution, that is, when one group of blood product is used to substitute other groups in the current period, this group of blood product may be in shortage and must be substituted by other groups in the subsequent periods.

  • In addition, preference order of possible ABO/Rh(D)-compatible substitutions influences the allocation solution. As the experiments in Sect. 5.3 show, for the decision makers of emergency blood allocation, setting the substitution order in advance according to the preference of local doctors is important to reaching a suitable allocation solution.

7 Conclusion

Motivated by the practice of emergency blood supply in disaster relief operations, in this study we examined a multi-product multi-group emergency blood allocation problem considering ABO/Rh(D)-compatible blood substitution. Based on the restriction and priority of possible ABO/Rh(D)-compatible blood substitutions, a mixed integer programming model was developed to address the emergency blood allocation problem in disaster relief operations, which was solved by a greedy heuristic algorithm. Finally, a numerical example is presented to verify the model and algorithm and analyze the effect of an ABO/Rh(D)-compatible blood substitution policy on emergency blood allocation. The proposed model can help decision makers to design appropriate emergency blood allocation schemes with consideration of ABO/Rh(D)-compatible blood substitution, to alleviate the dilemma of blood supply in a disaster affected area.

ABO/Rh(D)-compatible blood substitution is undoubtedly an effective way to decrease blood shortage in emergency blood allocation. We should collect blood products with different blood groups based on their possible ABO/Rh(D)-compatible substitution in emergency. Collecting more blood products with the blood groups that can substitute other blood groups will reduce shortages. It is also suggested to set an upper limit to the ABO/Rh(D)-compatible substitution rate among different blood groups.

Although this study contributes to the exploration of the multi-group emergency blood allocation problem in disaster relief operations and has important implications for practice, some opportunities exist for further research, which may include: (1) develop a multi-period decision-making framework for emergency blood allocation considering the uncertainties of supply and demand in disaster relief operations; (2) evaluate how to set an appropriate ABO/Rh(D)-compatible substitution rate among blood groups at different disaster relief stages to reduce the unmet blood demand and prevent the domino effect caused by ABO/Rh(D)-compatible blood substitution; (3) consider the age of blood products; and (4) extend our model to cover other relevant decisions in addition to allocation decision, such as location-allocation model, inventory-allocation decision model, among others.