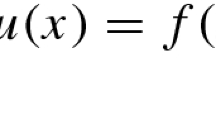Abstract
This article investigates the existence and properties of ground state solutions to the following nonlocal Hamiltonian elliptic system:
where \((-\Delta )^\frac{1}{2}\) is the square root Laplacian operator, \(V_0 >0\) and f, g have critical exponential growth in \(\mathbb R\). Using minimization technique over some generalized Nehari manifold, we show that the set \(\mathcal S\) of ground state solutions is non empty. Moreover for \((u,v) \in \mathcal S\), u, v are uniformly bounded in \(L^\infty (\mathbb R)\) and uniformly decaying at infinity. We also show that the set \(\mathcal S\) is compact in \(H^\frac{1}{2}(\mathbb R) \times H^\frac{1}{2}(\mathbb R)\) up to translations. Furthermore under locally lipschitz continuity of f and g we obtain a suitable Pohožaev type identity for any \((u,v) \in \mathcal S\). We deduce the existence of semi-classical ground state solutions to the singularly perturbed system
where \(\epsilon >0\) and \(V \in C(\mathbb R)\) satisfy the assumption (V) given below (see Sect. 1). Finally as \(\epsilon \rightarrow 0\), we prove the existence of minimal energy solutions which concentrate around the closest minima of the potential V.
Similar content being viewed by others
References
Alves, C.O., Do Ó, J.M., Miyagaki, O.H.: Concentration phenomena for fractional elliptic equations involving exponential critical growth. Adv. Nonlinear Stud. 16(4), 843–861 (2016)
Ambrosio, V.: Concentration phenomena for critical fractional Schrödinger systems. Commun. Pure Appl. Anal. 17(5), 2085–2123 (2018)
Benci, V., Fortunato, D.: Variational Methods in Nonlinear Field Equations, Springer Monographs in Mathematics. Springer, Basel (2014)
Benci, V., Rabinowitz, P.H.: Critical point theorems for indefinite functionals. Invent. Math. 52(3), 241–273 (1979)
Brasco, L., Lindgren, E., Parini, E.: The fractional Cheeger problem. Interfaces Free Bound. 16, 419–458 (2014)
Brasco, L., Mosconi, S., Squassina, M.: Pohožaev identity for the fractional \(p\)-Laplacian on \({\mathbb{R}}^n\). http://cvgmt.sns.it/media/doc/paper/3292/BMS-GlobalPohozaev.pdf
Bueno, H.P., Caqui, E.H., Miyagaki, O.H.: Critical fractional elliptic equations with exponential growth. J. Elliptic Parabol. Equ. 7, 75–99 (2021)
Caffarelli, L.A.: Nonlocal equations, drifts and games. Nonlinear Partial Differ. Equa. Abel Symp. 7, 37–52 (2012)
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32, 1245–1260 (2007)
Cassani, D., Zhang, J.: A priori estimates and positivity for semiclassical ground states for systems of critical Schrödinger equations in dimension two. Commun. Partial Differ. Equ. 42(5), 655–702 (2017)
Chen, W., Deng, S.: The Nehari manifold for a fractional \(p\)-Laplacian system involving concave convex nonlinearities. Nonlinear Anal. Real World Appl. 27, 80–92 (2016)
Clément, P., de Figueiredo, D.G., Mitidieri, E.: Positive solutions of semilinear elliptic systems. Commun. Partial Differ. Equ. 17(5–6), 923–940 (1992)
Costa, A.C.R., Maia, B.B.V., Miyagaki, O.H.: On existence and concentration of solutions for Hamiltonian systems involving fractional operator with critical exponential growth. Math. Nachr. 295, 1–33 (2022)
de Albuquerque, J.C., Do Ó, J.M.: Coupled elliptic systems involving the square root of the Laplacian and Trudinger–Moser critical growth. Differ. Integr. Equ. 31(5/6), 403–434 (2018)
de Figueiredo, D.G., Do Ó, J.M., Ruf, B.: Critical and subcritical elliptic systems in dimension two. Indiana Univ. Math. J. 53, 1037–1054 (2004)
de Figueiredo, D.G., Do Ó, J.M., Zhang, J.: Ground state solutions of Hamiltonian system in dimension two. Proc. R. Soc. Edinburg Sect. A 150(4), 1737–1768 (2020)
de Figueiredo, D.G., Felmer, P.L.: On superquadratic elliptic systems. Trans. Am. Math. Soc. 343(1), 99–116 (1994)
Do Ó, J.M., Giacomoni, J., Mishra, P.K.: Nonautonomous fractional Hamiltonian system with critical exponential growth. Nonlinear Differ. Equ. Appl. 26, 1–25 (2019)
de Souza, M., Do Ó, J.M.: Hamiltonian elliptic systems in \({\mathbb{R}}^2\) with subcritical and critical exponential growth. Ann. Mat. 195, 935–956 (2016)
Di Nezza, E., Palatucci, G., Valdinoci, E.: Hitchhiker’s Guide to the fractional Sobolev spaces. Bull. Sci. Math. 136, 521–573 (2012)
Ekeland, I.: On the variational principle. J. Math. Anal. Appl. 47, 324–353 (1974)
Giacomoni, J., Mishra, P., Sreenadh, K.: Critical growth fractional systems with exponential nonlinearity. Nonlinear Anal. 136, 117–135 (2016)
Giacomoni, J., Mishra, P., Sreenadh, K.: Critical growth problems for \(\frac{1}{2}\)- Laplacian in \({\mathbb{R} }\). Differ. Equ. Appl. 8(3), 295–317 (2016)
He, X., Squassina, M., Zou, W.: The Nehari manifold for fractional systems involving critical nonlinearites. Commun. Pure Appl. Anal. 15(4), 1286–1308 (2016)
Hulshof, J., van der Vorst, R.: Differential systems with strongly indefinite variational structure. J. Funct. Anal. 114(1), 32–58 (1993)
Iannizzotto, A., Squassina, M.: \(1/2\)-Laplacian problems with exponential nonlinearity. J. Math. Anal. Appl. 414, 372–385 (2014)
Iula, S., Maalaoui, A., Martinazzi, L.: A fractional Moser–Trudinger type inequality in one dimension and its critical points. Differ. Integr. Equ. 29(5–6), 455–492 (2016)
Lam, N., Lu, G.: Elliptic equations and systems with subcritical and critical exponential growth without the Ambrosetti–Rabinowitz condition. J. Geom. Anal. 24(1), 118–143 (2014)
Li, G., Yang, J.: Asymptotically linear elliptic systems. Commun. Partial Differ. Equ. 29(5–6), 925–954 (2004)
Lions, P.L.: The concentration-compactness principle in the calculus of variations, the locally compact case, parts I and II. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(2), 109–145 (1984)
Mengesha, T., Schikorra, A., Yeepo, S.: Calderon–Zygmund type estimates for nonlocal PDE with Hölder continuous kernel. Adv. Math. 383, 107692 (2021)
Ozawa, T.: On critical cases of Sobolev’s inequalities. J. Funct. Anal. 127, 259–269 (1995)
Pankov, A.: Periodic nonlinear Schrödinger equation with application to photonic crystals. Milan J. Math. 73, 259–287 (2005)
Qin, D., Tang, X., Zhang, J.: Ground states for planar Hamiltonian elliptic systems with critical exponential growth. J. Differ. Equ. 308, 130–159 (2022)
Sirakov, B.: On the existence of solutions of Hamiltonian elliptic systems in \({\mathbb{R} }^n\). Adv. Differ. Equ. 5(10–12), 1445–1464 (2000)
Sirakov, B., Soares, S.H.M.: Soliton solutions to systems of coupled Schrödinger equations of Hamiltonian type. Trans. Am. Math. Soc. 362(11), 5729–5744 (2010)
Szulkin, A., Weth, T.: The method of Nehari manifold. In: Gao, D.Y., Motreanu, D. (eds.) Handbook of Nonconvex Analysis and Applications, pp. 597–632. International Press, Boston (2010)
Zhang, J., Do Ó, J.M., Squassina, M.: Fractional Schrödinger–Poisson systems with a general subcritical or critical nonlinearity. Adv. Nonlinear Stud. 16(1), 15–30 (2016)
Acknowledgements
G. C. Anthal thanks the CSIR(India) for financial support in the form of a Senior Research Fellowship, Grant Number 09/086(1406)/2019-EMR-I. J. M. Do Ó is partially funded by IFCAM (Indo-French Centre for Applied Mathematics) IRL CNRS 3494. We thank the anonymous referee for a careful reading of our manuscript and valuable comments that help us to improve the quality of our paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Anthal, G.C., Do Ó, J.M., Giacomoni, J. et al. Fractional Hamiltonian type system on \(\mathbb R\) with critical growth nonlinearity. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 118, 12 (2024). https://doi.org/10.1007/s13398-023-01511-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13398-023-01511-w
Keywords
- Nonlocal Hamiltonian system
- Schrödinger system
- Trudinger–Moser inequality
- Critical exponential growth
- Ground state solutions
- Pohožaev identity
- Concentration phenomena