Variety enhancement of PUF responses using the locations of random outputting RS latches

Abstract

Physical Unclonable Functions (PUFs) are expected to represent an important solution for secure ID generation and authentication etc. In general, manufactured PUFs are considered to be more secure when the pattern of outputs (the variety of responses) is larger, i.e., the response bit length is longer (e.g., 192-bit response is more secure than 128-bit one). However, the actual bit length is reduced because some response bits are inconsistent (random) for repeated measurements, which are regarded as unnecessary for ID generation and discarded. Latch-based PUFs with $N$ RS latches, for example, generate ideally $2^{N}$ responses depending on binary values output from RS latches (0/1). However, some RS latches output random responses which are inconsistent and cannot be used for reliable ID generation, so the variety of responses becomes smaller than $2^{N}$. In this paper, we propose a novel Latch-based PUF structure, which outputs larger variety of responses by utilizing location information of the RS latches outputting the random responses. Differently from random responses themselves, this location information is determined during a manufacturing process, so almost fixed once PUFs are manufactured. The proposed PUF generates $3^{N}\approx 2^{1.58N}$ responses by considering random responses as the third stable value: using ternary values (0/1/random). We estimate the variety of responses generated by the proposed PUFs. According to our experiment with 40 FPGAs, a Latch-based PUF with 128 RS latches can improve it from $2^{116}$ to $2^{192.7}$, this being maximized when the 128 latches outputs 0s, 1s, or random outputs with equal probability. We also show the appropriate RS latch structure for satisfying this condition, and validate it using two kinds of different Xilinx FPGAs: Spartan-3E and Spartan-6. The average error rate of responses is only 5.3 % when the core voltage is changed within the rated voltage range of the FPGAs. Our proposed PUF using ternary values enhances dramatically the variety of responses while keeping the reliability.

1 Introduction

Secure identification/authentication technology using Integrated Circuit (IC) chips is very important for secure information infrastructure. It is used for anticounterfeiting devices on medical supplies, prepaid cards and public ID cards such as passports and driver’s licenses. The IC card is a well-known solution for this kind of application. Counterfeiting is prevented by storing a secret key on the IC card and using a secure cryptographic protocol to make the key invisible from outside. In theory, however, the possibility of counterfeiting still remains if its design is revealed and reproduced by the counterfeiter. Naturally, this is difficult because current IC cards are equipped with several highly developed tamper-proofing technologies. However, further anticounterfeiting technologies are desirable to meet future developments in reverse-engineering techniques.

Recently, interest has been focused on Physical Unclonable Functions (PUFs) as a solution [17]. In a PUF, the output value (response) to the input value (challenge) is unique for each individual IC. This uniqueness is provided by the process variations of each individual IC [5, 6]. It is expected that PUFs will represent breakthrough in technology for anticounterfeiting devices, through its use for ID generation, key generation and authentication protocol, which make cloning impossible even when the design is revealed.

The PUFs on ICs are classified into two categories: memory-based PUFs and delay-based PUFs [15]. Memory-based PUFs use the characteristics of memory cells such as SRAM-PUFs [7, 9], Butterfly PUFs [11], Flip-flop PUFs [13] and Latch PUFs (LPUFs) [20, 21]. Delay-based PUFs use the characteristics of delay variations such as Arbiter PUFs [12], Glitch PUFs [19, 23] and Ring Oscillator PUFs [22]. SRAM-PUFs are based on the unstable power-up values of SRAM cells on ICs such as ASIC. However, a device power-up operation is required for the generation of every response. To counter this drawback, Butterfly PUFs are composed of cross-coupled latches which behave similarly to an SRAM cell. The output of the Butterfly PUF is triggered by a clock edge signal applied to the latches, without an actual device power up. Flip-flop PUFs were proposed in order to solve the problem that the power-up values of SRAM cells on FPGAs were automatically initialized to fixed values. Flip-flop PUFs uses the power-up values of flip-flops instead of SRAM cells. LPUFs are very similar to SRAM-PUFs and Butterfly PUFs. LPUFs generate each response using a metastable value of a latch composed of cross-coupled logic gates. LPUFs can be implemented on both ASIC and FPGA, and generate responses without an actual device power up. Arbiter PUFs have an arbiter circuit that generates a response determined by the difference in the signal delay between two paths, which is mixed by a challenge. However, a machine learning attack can predict responses of Arbiter PUFs using a number of challenge–response pairs [18]. The Glitch PUF [19, 23] was proposed to solve this problem of ease of prediction. It generates a one-bit response using the parity of the number of glitches obtained from an 8-bit AES S-Box used as a glitch generator. Since the responses to challenges behave like a non-linear function, machine learning attacks are prevented. Ring Oscillator PUFs derive responses from the difference in oscillator frequencies. In [10], the performances of five types of PUFs (Arbiter, Ring Oscillator, SRAM, Flip-flop and Latch PUFs) are evaluated on ASIC implementations.

Today, memory-based PUFs are some of the most feasible and secure technique because there have already been implementations of error correcting codes (ECCs) and universal hash functions [2] for randomness extraction optimized for the PUFs, which are needed for Fuzzy Extractors [4]. Especially, error corrections utilizing soft decision decoding techniques are optimized for memory-based PUFs in [14, 24]. LPUFs implemented in ASIC seem to have many advantages over SRAM-PUFs, such as not requiring a power-up operation. This paper therefore focuses on LPUFs, which generate $N$-bit responses based on $N$ outputs from $N$ RS latches.

The responses from PUFs need to have extremely high uniqueness. This paper defines uniqueness as the independence among multiple PUFs of responses to the same challenge. In order to prevent clones of cryptographic hardware, it is important for manufacturers to make sure that multiple PUFs with the same challenge–response pairs do not exist. However, this is very difficult in terms of cost because there are a huge number of manufactured PUFs and challenge–response pairs. Therefore, one of the most practical solutions is to increase variety: the number/pattern/range of responses in manufactured PUFs as much as possible. For example, 192-bit responses are obviously more secure and unpredictable than 128-bit responses. 192-bit responses have $2^{192}$ variety ideally. However, the actual variety of the responses is much less than the ideal $2^{192}$ variety if 192-bit responses obtained from multiple PUFs are almost the same. Consequently, we must note that a large number of response bits are not necessarily equivalent to a large actual variety of responses: a high level of the Shannon entropy in those responses. PUFs that output responses with high entropy are capable of generating completely unpredictable responses. Consequently, the probability of multiple PUFs that output unpredictable responses having the same challenge–response pairs is extremely small. Hence, it is important for PUFs to increase not only variety but also entropy of responses so as to have extremely high uniqueness.

In addition, the response needs to have high reliability. This paper defines reliability as the consistency of PUF challenge–response pairs for repeated measurements. That is, ideally, a PUF always generates the same response to a given challenge. However, the LPUF has some RS latches that generate inconsistent (random) numbers (i.e., “random latches”). This randomness causes a problem in that the reliability of the response is reduced. This is because the values of the response corresponding to the random latches change every time a response is generated. Hence, PUFs need to eliminate random responses in order to generate stable responses. For example, the Glitch PUF can generate relatively stable responses because it selects only available challenges to output consistent responses for repeated measurements through a masking process. However, as pointed out by the designers of the Glitch PUF, the masking process reduces the number of responses since random responses are eliminated. Also in LPUFs, the response bits become lower as the number of random latches increases, which reduces the variety and entropy of responses. In such a conventional approach, in order to maintain the reliability of responses, the outputs of the random latches are not used to generate stable responses. However, in this paper we make efficient use of the random outputs.

1.1 Our contributions

This paper proposes a novel PUF structure for generating high-entropy responses using randomness. Note that our proposed methods can be applied to any PUFs. As an example, our paper focuses on an LPUF with random latches. The use of random latches dramatically increases variety and entropy of responses. Also, the construction can maintain the reliability of responses even if random latches are used for the generation of responses. In specific terms, responses are generated based on the location information of the random latches. The proposed LPUF with $N$ RS latches generates approximately $3^{N}$ responses by considering random responses as the third stable value: using ternary values (0/1/random). However, the actual variety of responses is less than $3^{N}$ because $3^{N}$ is the total variety of responses: all the possible combinations of the ternary values. The variety of random latches is almost fixed and determined by the kind of PUF device. Consequently, $3^{N}$ is not accurate, but is intuitively easy to understand, so an accurate evaluation for the actual variety of responses is given below. The actual variety of responses takes on its maximum value when the frequency of each ternary value (0/1/random) is equal. Hence, we also propose suitable RS latch structures to satisfy this equality condition to the maximum extent. The proposed structures are optimized for two types of Xilinx FPGAs: Spartan-3E (SP3E) and Spartan-6 (SP6), which have different FPGA architectures. We evaluate the performance of the proposed PUF with both types of FPGAs. Using 40 SP3E FPGAs, an LPUF with 128 RS latches based on our RS latch construction increases the average number of random latches from 12 to 32, approaching around 43 (=128/3). The proposed PUF with ternary values improves the variety of responses from $2^{116}$ to $2^{196}$ theoretically. From the actual responses generated by 40 PUFs, the entropy of responses is experimentally evaluated as 192.7 bits, which indicates that the proposed PUF has extremely high entropy. Additionally, we develop an experiment system with SP6 FPGAs, which can change the supply voltage within the rated voltage range of the FPGAs (1.14–1.26 V). The average error rate of responses is about 5.3 %, which indicates that the proposed PUF using ternary values has high reliability.

1.2 Organization of the paper

The rest of the paper is organized as follows: Section 2 gives an outline of the LPUF with RS latches, and the conventional methods for implementing RS latches on FPGAs. Section 3 proposes our original LPUF, which generates responses using the location information of the random latches. In addition, new methods of implementing RS latches are proposed that maximize the performance of our PUF. Sections 4 and 5 evaluate the performance of our PUF using SP3E and SP6 FPGAs, respectively. Section 6 discusses the applicability of proposed methods to other kinds of PUFs than LPUFs. Finally, in Sect. 7, we give a summary and comment on future directions.

Part of the content of our proposal has been published in [26]. This paper proposes the appropriate RS latch structure optimized for Xilinx Spartan-6 FPGAs in Sect. 3.2.2. We evaluate the PUF performance on Spartan-6 and discuss the voltage resistance in Sect. 5. We also discuss the applicability of proposed methods to various kinds of PUFs in Sect. 6.

2 Conventional methods

2.1 Conventional method (1): generation of responses from an LPUF

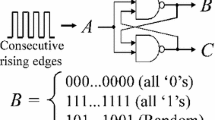
This paper focuses on an LPUF using RS latches. First, we describe the circuit and behavior of an RS latch created from two NAND gates, shown in Fig. 1. NOR gates are used in [20, 21], but this difference does not influence the LPUF performance. An RS latch is in a stable state with output $(B,C)=(1,1)$ when input $A=0$. When input $A$ changes from 0 to 1 (= rising edge), the RS latch temporarily enters a metastable state. It then enters a stable state with either output $(B,C)=(1,0)$ or $(B,C)=(0,1)$. Ideally, the probability of transition to either of these states is equal. In fact, however, many RS latches have a high probability of entering one specific state. This is because the drive capabilities of the two NAND gates or the wire length between them are not exactly the same. Hence, the output $B$ from RS latches fall into three patterns: all 0s, all 1s, or a mixture of 0s and 1s (=random number) when a clock signal is applied to input $A$.

Fig. 1

NAND-based RS latch

We now describe the LPUF, shown in Fig. 2. Challenges to the LPUF are equivalent to choosing $M(\le N)$ RS latches from $N$ implemented RS latches. The LPUF can generate $M$-bit responses corresponding to ${}_N \mathrm C _M$ challenges. Here, ${}_N \mathrm C _M$ is defined as the number of combinations of $N$ elements taken $M$ at a time. The LPUF in Fig. 2 generates an $N$-bit response: $\text{ RES}[N-1:0]$ when $M$ is set equal to $N$. Note that, in order to simplify discussion in this paper, the more significant bits of the response correspond to the outputs of RS latches with bigger latch labels. LPUFs, which generate only a response, can be used for applications such as authentication as shown in Fig. 3. A random number $S$ is sent from an authentication server to a PUF as a new challenge, and a response $R$ is newly defined by equation $R=F(S\parallel {\text{ RES}})$. Here, $F()$ indicates a mixing function, such as a hash function. The operation $\parallel$ means a concatenation of two variables. The value of response $R$ changes depending on the challenge $S$, so LPUFs provide security when used for this application. The PUF in Fig. 2 has some RS latches that generate random numbers such as ${\text{ LATCH}_{2}}$ and ${\text{ LATCH}_{{ N}-2}}$. These random numbers cause a problem in that the reliability of the response RES is reduced since its value changes every time it is generated.

Fig. 2

Latch PUF

Fig. 3

LPUF-based authentication protocol

There are two widely known conventional approaches to response generation aimed at solving this problem. In the first approach [“conventional method (1-A)”], random latches are not used for the generation of responses. This approach maintains the reliability of responses, but reduces response bits and the variety of responses. It also requires a mechanism to detect random latches. Suppose that the LPUF with 128 RS latches ($N=128$) in Fig. 2 has $T$ random latches. The conventional method (1-A) generates $2^{N-T}$ responses, so the variety and entropy of responses decrease as the number of random latches increases. Hence, it is necessary to implement extra RS latches in the PUF in accordance with the number of random latches. This PUF is, however, not suitable for embedded systems with limited hardware resources such as smart cards because, while also maintaining the variety of responses, it is necessary for PUFs in embedded systems to have an RS latch area size and peripheral circuit that are as small as possible.

In the second approach [“conventional method (1-B)”], ECCs are used to correct the inconsistency in the responses resulting from the random latches. This approach requires larger redundant data for response correction as the number of random latches increases. In addition, it also suffers from the disadvantage of necessitating increased hardware resources and processing time for the ECCs. An LPUF with 128 RS latches generates no more than $2^{128}$ responses even if ECCs are used. From the above, it can be seen that the first approach, in which random latches are not used for responses, is not suitable. Furthermore, it is not sufficient to use only ECCs, as in the second approach. In Sect. 3, we propose a method for generating responses based on the locations of random latches. The proposed method maintains the reliability of responses and dramatically improves their variety and entropy.

2.2 Conventional method (2): implementation of RS latches on FPGAs

A method for implementing RS latches as a physical random number generator on Xilinx Virtex-4 FPGAs [“conventional method (2-A)”] is proposed in [8]. The implementing method can be also applied to Xilinx SP3E FPGAs because they have the almost same architecture as Virtex-4 FPGAs. We focus on SP3E FPGAs since our experiment uses this kind of FPGA. Flip-flops (FFs) are positioned in front of the two NAND gates, as shown in Fig. 4. This minimizes the difference in signal arrival time between the two gates, enabling the RS latch to enter the metastable state more readily and improving the probability of the RS latches outputting random numbers. An SP3E FPGA consists of a matrix of configurable logic blocks (CLBs) including four slices. A slice includes two pairs of LookUp Tables (LUTs) and FFs. The right and left slices of the CLB are different. The right slice (SliceL) is available only for logic, while the left one (SliceM) is for both memory and logic. Two types of implementation for an RS latch are reported in [8]. In one type [“conventional method (2-B1)”], two RS latches are implemented on two CLBs, as shown in Fig. 5a. In the other [“conventional method (2-B2)”], only one RS latch is implemented on two CLBs, as shown in Fig. 5b. Both methods implement the NAND gates of an RS latch using the same kind of slice (SliceL in Fig. 5) on different CLBs. The conventional method (2-B1) uses two CLBs per two RS latches, leading to reasonable circuit efficiency. However, it is pointed out in [8] that multiple RS latches which have NAND gates implemented on the same CLB, as shown in Fig. 5a, have a low probability of outputting random numbers. RS latches based on conventional method (2-B2) have some probability of generating random numbers, but result in low circuit efficiency because an RS latch requires two CLBs. To the best of our knowledge, any methods for implementing RS latches applied to an SP6 FPGA, a later generation of SP3E, have not been proposed. The next section proposes an implementation method applied to SP3E FPGAs that gives the RS latches a high probability of outputting random numbers. In addition, the proposed method gives higher circuit efficiency than in the conventional methods. We also first propose an implementation method suitable for SP6 FPGAs.

Fig. 4

Conventional method (2-A): RS latch circuit [8]

Fig. 5

Implementation of RS latches on Xilinx Spartan-3/Virtex-4 family FPGAs [8]

3 Proposed methods

3.1 Proposed method (1): use of the location information of random latches

The conventional LPUF in Fig. 2 generates responses based only on RS latches outputting fixed numbers such as 0s or 1s (i.e., “fixed latches”). Our proposed LPUF uses the location information of random latch $X$, rather than the random numbers from the random latches. If an LPUF with $N$ RS latches has $T$ random latches, then the number of locations of random latches equals to ${}_N\mathrm C _T$, which increases the number of different representation of LPUFs. Hence, the PUF based on our method utilizes the entropy derived from the locations of random latches in order to increase the variety of responses. However, this kind of LPUF requires complex controls to associate the location of RS latch $X$ with the output number, which leads to a large circuit size. In this paper, we propose a simple and efficient method [“proposed method (1)”] of solving this problem. Proposed method (1) considers the three types of output patterns from the RS latches (0s, 1s, and random numbers) as ternary values (00/11/10), respectively. Our method can generate responses with much larger patterns than conventional approaches. We describe the details of the proposed method with reference to Fig. 6. When a clock signal is applied to the inputs of the RS latches in our LPUF, they generate three types of outputs: 0s, 1s, and random numbers. The PUF based on our method has new detection circuits (shown in Fig. 7) located after the RS latches which distinguish these three types. The detection circuit $i$ outputs a 2-bit unique value $S_i[1:0] ({=}00/11/10)$ depending on the output of the RS latch $i$ (0s/1s/random numbers). If the output stream of RS latch $i$ includes a transition from 0(1) to 1(0), detection circuit $i$ considers RS latch $i$ as a random latch, and from that point onwards continues outputting the 2-bit value ‘10’ regardless of RS latch $i$’s subsequent output stream. Stated more precisely, let RES$[2N-1:0]$ be the $2N$-bit response of our LPUF. Then

$$\begin{aligned}&\text{ RES}[2N-1:0]\nonumber \\&= S_{N-1} \parallel S_{N-2} \parallel \cdots \parallel S_{i} \parallel \cdots \parallel S_{1} \parallel S_{0}. \end{aligned}$$

(1)

The gate size of the detection circuit, shown in Fig. 7, is estimated to be around 28 gates, which is definitely compact enough for embedded systems. Here, we use the equivalencies 1 FF = 12 NAND gate, 1 AND = 1.5 NAND gate, 1 OR = 1.5 NAND gate, and 1 INV = 0.5 NAND gate, introduced in [1]. Naturally, in order to distinguish three types of outputs, CPU-based software approach is able to be used instead of the detection circuit. The reason why we propose the detection circuit as hardware approach is that it is essential when our proposed PUF is implemented on ASIC.

Fig. 6

Proposed method (1)

Fig. 7

Proposed detection circuit

Next, for the PUF based on our proposed method, we theoretically estimate the variety (number) of responses. Let $N$ be the number of implemented RS latches, and $T$ be the number of random latches. The PUF based on the proposed method generates ternary values (00/11/10), so the total variety of responses is ideally $3^{N}$. We define this total number as “ideal upper bound” of responses, which is estimated in consideration of all the possible combinations of the ternary values. Concretely, the ideal upper bound includes the cases when random latches are few or many. However, the value of $T$ is in fact almost fixed because it is determined by the kind of PUF device and the way in which the RS latches are implemented. Therefore, the manufactured PUFs generate less than $3^{N}$ responses. The following theoretically estimates the variety of responses for a given value of $T$. The variety of responses arising from the fixed latches is $2^{N-T}$, while the variety of responses arising from the random latches is ${}_N\mathrm C _T$. Therefore, the variety of responses for a given value of $T$ is estimated to be $2^{N-T} \cdot {}_N\mathrm C _T$. This value is obviously less than $3^{N}$ because the variety of responses for given $T$ corresponds to the $T$-th term of the binomial expansion of $3^{N}=(2+1)^{N}$, which is $2^{N-T} \cdot {}_N\mathrm C _T$, the same as the above estimate. We define this variety of responses for a given value of $T$ as “theoretical bound” of responses. Figure 8 shows a comparison between the theoretical bound of responses for the conventional method (1-A) without random latches and the theoretical bound of responses using our proposed method with various $T$ and given $N ({=}128)$ values. The conventional method (1-A) generates $2^{N-T}$ responses, so the theoretical bound of responses decreases as the number of random latches increases. Even conventional method (1-B), which uses ECCs, generates no more than $2^{128}$ responses. In contrast, the proposed method (1) dramatically increases the theoretical bound of responses. The theoretical bound of responses takes on its maximum value (${\approx } 2^{203}$) when $T$ is around 43 (${\approx } 128/3$). Hence, the proposed method dramatically improves the theoretical bound of responses.

Fig. 8

Theoretical bound of responses against the number of random latches (Estimate)

Section 4.4 experimentally evaluates the average value of $T$ based on PUF implementations on SP3E. Section 4.5 calculates the theoretical bound of responses using this experimental value of $T$. However, this theoretical bound is calculated on the strong assumption that the value of $T$ is fixed, which means that all of PUF implementations have $T$ random latches strictly. We experimentally evaluate the variety of responses in consideration of further calculations: the ratios of RS latches outputting 0s, 1s.

3.2 Proposed method (2): increasing the number of random latches

3.2.1 Optimization for Spartan-3E

This section proposes new methods for SP3E FPGAs [“proposed methods (2-A) and (2-B)”] to give a higher probability of RS latches outputting random numbers than those obtained with the conventional methods in Sect. 2.2. These proposed methods increase the number of random latches to 1/3 of the total number of RS latches, which improves the effectiveness of the proposed method (1).

In proposed method (2-A), a shared FF is positioned in front of two NAND gates, as shown in Fig. 9. This FF sharing between two NAND gates eliminates clock skew in FFs. Consequently, the signal arrival times for the two NAND gates are much closer, allowing the RS latches to become metastable more easily, and increasing the probability of the RS latches outputting random numbers. Proposed method (2-A) also reduces the FF gate size per RS latch by FF sharing.

In proposed method (2-B), one RS latch is implemented on a CLB in an SP3E FPGA, as shown in Fig. 10. In [8], an RS latch is implemented on two different CLBs, as described in Fig. 5, because FPGA synthesis tools cannot implement two NAND gates of an RS latch on ‘different’ kinds of slices (SliceM and SliceL) on the same CLB. To avoid this problem, proposed method (2-B) implements two NAND gates using the ‘same’ kinds of slices on the same CLB. Proposed method (2-B) uses only one CLB (two slices) per RS latch, giving high circuit efficiency. In addition, it is anticipated that the probability of RS latches becoming metastable and outputting random numbers would increase since the signal arrival times for the two NAND gates are much closer due to shortening of the wire length between the gates. The concepts behind proposed methods (2-A) and (2-B) can be applied not only to FPGAs but also to ASICs.

Fig. 9

Proposed method (2-A): RS latch circuit

Fig. 10

Proposed method (2-B): Implementation of RS latches on SP3E

3.2.2 Optimization for Spartan-6

This section first proposes an implementation method suitable for SP6 enabling RS latches to output random numbers. An SP6 FPGA consists of a matrix of CLBs including only two slices, differently from an SP3E FPGA with four slices. These two slices are of different types. Hence, it is impossible to implement two NAND gates of an RS latch using the ‘same’ kinds of slices on a CLB like the proposed method (2-B) shown in Fig. 10. Due to constraints of FPGA synthesis tools, we also cannot implement an RS latch not only on different kinds of slices, but also on two pairs of LUTs and FFs on a slice as shown in Fig. 11a and b, respectively. To solve this problem, we propose the method [“proposed method (2-C)”] to implement an RS latch using two pairs of LUTs and FFs on two vertically neighboring CLBs as shown in Fig. 12. Here, we use not horizontally but vertically neighboring CLBs because horizontally neighboring CLBs are of different types: SliceM and SliceL. In SP6 FPGAs, each column of CLBs contains two slice columns. One column alternates between SliceMs and SliceLs, the other column includes SliceXs which have a similar structure to SliceLs except for some logic functions. The use of the completely same type of slices for implementing two NAND gates gives a higher probability of RS latches being metastable and outputting random numbers.

Fig. 11

Impossible implementation of RS latches on SP6

Fig. 12

Proposed method (2-C): Implementation of RS latches on SP6

4 Performance evaluation on Spartan-3E

4.1 Experimental environment

Figure 13 shows our experimental evaluation system, which uses a starter kit board [25] with a Xilinx SP3E FPGA (XC3S500E-4FG320C). A 50-MHz clock signal generated by an on-board oscillator is applied to a Digital Clock Manager (DCM) primitive, which divides it into a 2.5-MHz clock signal that is applied to 128 RS latches. The output stream from each RS latch is switched by a multiplexer (MUX) and stored into a block RAM through a FF. Finally, the raw stream data from all the RS latches are transmitted to the PC through an RS232C port. In our evaluation, a software on the PC detects whether or not the streams contain random numbers rather than this being done with detection circuits. We consider that the detection technique does not influence PUF performance because the latter depends only on the output of the RS latches. We implement 128 RS latches on a 16 $\times$ 8 matrix of FPGA CLBs in accordance with proposed methods (2-A) and (2-B), this being done manually with the FPGA synthesis tools in Xilinx ISE Design Suite 11.1. We consider one FPGA board as four virtual boards, since the RS latches are implemented at four completely different locations in the CLB matrixes for each FPGA. The evaluation uses 10 actual FPGA boards, but in the following discussion, we take the number of FPGA boards to be 40.

Fig. 13

Experimental evaluation system using SP3E

4.2 Reliability and uniqueness

Before we represent an evaluation of the effectiveness of proposed methods, we show the basic performance of our LPUF, reliability and uniqueness. Our LPUF with 128 RS latches—based on proposed methods (2-A) and (2-B)—gives the results for reliability and uniqueness shown in Figs. 14 and 15, respectively. In our experiment, the PC is used to measure a 1,000-bit output stream from each RS latch. The 2-bit partial response generated by each RS latch is ‘00(11)’ if the 1,000-bit bitstream is identically zero (one), or ‘10’ if it includes a transition from 0(1) to 1(0). As a result, our LPUF with 128 RS latches can generate a 256-bit response. The reliability evaluation generates 40 responses using only a single specific FPGA selected at random. Figure 14 shows a histogram of normalized Hamming distance between two arbitrary responses among the 40 responses (i.e., ${}_{40}\mathrm C _{2}=780$ combinations). The average error rate is approximately 2.4 % with a standard deviation (SD) of 0.75 %, which is much less than the 15 % assumed in [14] for stable responses based on a Fuzzy Extractor with a reasonable size of redundant data. Hence, our PUF gives responses that are of high reliability. Next, the uniqueness evaluation generates a total of 40 responses using all 40 FPGAs (one response per FPGA). Figure 15 shows a histogram of normalized Hamming distance between two arbitrary responses among the 40 responses. This evaluation is a general way of showing the extent to which the responses of the chips are different. The difference in the responses of two arbitrary PUFs is approximately 46 % with an SD of 3.8 %. Note that the ideal difference is not 50 % but around 44.4 %. This is because our proposed PUF do not generate ‘01’ for 2-bit partial responses. The line graph in Fig. 15 represents the ideal normalized Hamming distance obtained from a simulation. The simulation generates 40 responses using a pseudorandom number generator [16]. Our experimental result follows the ideal simulation result. Hence, our PUF gives responses with a high level of uniqueness.

Fig. 14

Reliability on SP3E (Mean = 2.4 %, SD = 0.75 %)

Fig. 15

Uniqueness on SP3E (Mean = 46 %, SD = 3.8 %)

4.3 Cost

Table 1 indicates the gate size and processing time of our PUF evaluation system, shown in Fig. 13. In the FPGA evaluation system, a software on the PC is used instead of detection circuits. Our PUF (not including detection circuits) uses only 5 % of the total slices in a FPGA, and the gate size is expected to be very small in ASICs. However, our PUF implemented in ASICs requires 128 detection circuits, and the gate size is estimated to be about 5.4 K gates, using the gate equivalencies introduced in [1]. The gate size of our PUF is comparable to that of compact hardware for common key block ciphers such as AES. Hence, our PUF is sufficiently small to be implemented in embedded systems. The gate size can be reduced by a shared detection circuit switched by an MUX. The processing time is around 0.4 ms, this being the total time taken to generate a response. One way of improving the processing time is to reduce the bitstream length for detection (1,000 bits in our experiment). However, too short a length may result in misdetection. For example, RS latches outputting a large number of 0s and very few 1s might be detected not as random, but as fixed latches. This misdetection leads to the loss of reliability, so our PUF makes a tradeoff between reliability and processing time. Our proposed PUF has advantages in terms of low noise because RS latches are allowed to become non-metastable through RS latch clock gating except when generating responses. In addition, our PUF can generate responses at anytime, unlike SRAM PUFs which can only generate them during power activation.

Table 1 Gate size and processing time of our PUF (not including detection circuits)

4.4 Evaluation of proposed method (2): number of random latches

Before we represent an evaluation of proposed method (1), we show the effectiveness of proposed methods (2-A) and (2-B). Figure 16 represents a histogram showing the number of random latches per FPGA. The results show that the proposed methods increase the number of random latches. This is because these methods allow the RS latches to become readily metastable and increase their probability of outputting random numbers. In proposed method (1), the variety of responses for 128 RS latches takes its maximum value when the number of random latches is around 43. Hence, the proposed methods (2-A) and (2-B) are expected to improve the variety of responses by increasing the number of random latches to as close to 43 as possible.

Fig. 16

Histogram for the number of random latches per FPGA

4.5 Evaluation of proposed method (1): variety and Shannon entropy of responses

4.5.1 Review of our concept

Table 2 shows the average number of random latches calculated using Fig. 16. The theoretical bounds of responses for various implementation methods are also calculated based on this average number of random latches and Fig. 8. The theoretical bound is estimated to be $2^{116} ({=}2^{128-12})$ when PUFs implemented by conventional method (2-B1) generate responses without 12 random latches. The PUFs based on proposed method (1) can generate $2^{170} ({\approx } 2^{128-12} \cdot {}_{128}\mathrm C _{12})$ responses using the location information entropy of 12 random latches. Moreover, PUFs based on both proposed methods (1) and (2-B) generate approximately $2^{196} ({\approx } 2^{128-32} \cdot {}_{128}\mathrm C _{32})$ responses with 32 random latches. Our proposed methods therefore dramatically increase the theoretical bound of responses.

This theoretical bound of responses estimated in Table 2 is based on the strong assumption that the value of $T$ is the same on every FPGA, which means that all of PUF implementations have $T$ random latches strictly. However, the value of $T$ varies depending on individual FPGAs, as shown in Fig. 16. Since only fixed value of $T$ is not sufficient for a discussion on the variety of responses, the next section takes into account further calculations: the ratios of RS latches outputting 0s, 1s, and random numbers. This enables us to experimentally confirm the validity of the theoretical upper bound on the variety of responses under fixed value of $T$: $2^{N-T} \cdot {}_{N}\mathrm C _{T}$.

Table 2 Average number of random latches and variety of responses

4.5.2 Experimental evaluation

The theoretical upper bound on the Shannon entropy of responses is defined as the binary logarithm of the theoretical bound: $\log _{2}(2^{N-T} \cdot {}_{N}\mathrm C _{T})$. In contrast, this section experimentally calculates the Shannon entropy of responses derived from manufactured PUFs, i.e., 40 PUFs implemented on SP3E FPGAs. Concretely, the Shannon entropy is calculated as the sum of each entropy experimentally derived from each latch. This Shannon entropy is more accurate than the above binary logarithm of the theoretical bound because the each entropy is calculated in consideration of detailed experimental results: the ratios of RS latches outputting 0s, 1s and random numbers. We will show later that this experimental entropy is equal to the theoretical upper bound, $\log _{2}(2^{N-T} \cdot {}_{N}\mathrm C _{T})$, under the ideal condition that fixed latches output 0s or 1s with equal probability. By following the two steps below, we can accurately calculate the experimental entropy of responses from our PUFs using the experimental results with 40 SP3E FPGAs.

In the first step, we show the ratios of RS latches outputting 0s, 1s, and random numbers, shown in Fig. 17. We explain how to read the figure with the specific example in Fig. 18, as follows. First, the 40 RS latches at the same physical CLB location (e.g., ${\text{ LATCH}_{0}}$) on the 40 FPGAs are called “a latch group”. Hence, in our experiment, there are 128 latch groups corresponding to the range from ${\text{ LATCH}_{0}}$ to ${\text{ LATCH}_{127}}$. Suppose that the 40 RS latches labeled as ${\text{ LATCH}_{0}}$ include 15 latches outputting 0s, 20 outputting 1s, and 5 outputting random numbers. The ratios are therefore 0.375, 0.500 and 0.125, respectively. A plot of ${\text{ LATCH}_{0}}$ is obtained by relating the ratios to the three sides of a triangle, and 128 plots are obtained, corresponding to the 128 latch groups in Fig. 17. A plot is located at the central point of the triangle if the ratios are equal, which is the ideal. It is therefore desirable that a large proportion of plots located in the small central triangle are illustrated by thick line. If the plot is in the small triangle, the three ratios fall within a range of 0.20–0.60. In conventional method (2-B1), it can be seen that all of the RS latches in each latch group have a low probability of outputting random numbers since many of the plots are located on the right side of the triangle. In addition, most RS latches in each latch group have a one-sided probability of outputting 0s or 1s since many of the plots are located throughout the whole of the right side. Conventional method (2-B2) improves the ratios, making them roughly equal, but requires a large number of CLBs to implement the RS latches shown in Fig. 5. In addition, there are not so many random latches (around 26 in Table 2), so the variety of responses is not very large. In contrast, proposed method (2-B) improves the ratios such that they are almost equal since as many as 93 plots are located in the small central triangle. Furthermore, no latch groups have RS latches outputting ternary values at a high $({>}0.9)$ or low $({<}0.1)$ probability. The number of plots in the small triangle is significantly higher than with conventional methods, which implies that the proposed method makes many of the RS latches readily metastable, so that the ratios become almost equal as a favorable side effect. Hence, using the proposed methods, the experimental variety of responses is expected to be close to the theoretical bound shown in Table 2.

Fig. 17

Ratios of RS latches outputting 0s, 1s, or random numbers in 128 latch groups

Fig. 18

How to read Fig. 17

In the second step, we accurately calculate the Shannon entropy of responses based on the ratios discussed in the first step. The Shannon entropy derived from ${\text{ LATCH}_{0}}$ to ${\text{ LATCH}_{127}}$ are given as $\sum _{i=0}^{n-1} E_{i}$, where $n=128$ and $E_{i}$ derived from ${\text{ LATCH}_{i}}$ is defined as

$$\begin{aligned} E_{i}&= -P_i(0) \cdot \log _{2}P_i(0)-P_i(1) \cdot \log _{2}P_i(1)\nonumber \\&-P_i(R) \cdot \log _{2}P_i(R). \end{aligned}$$

(2)

Let the ratios of the RS latches labeled as ${\text{ LATCH}_{{ i}}}$ outputting 0s, 1s, or random numbers be $P_i(0)$, $P_i(1)$ and $P_i(R)$, respectively (e.g., $P_0(0)$ = 0.375, $P_0(1)$ = 0.500 and $P_0(R)$ = 0.125 in Fig. 18). In the following, we discuss the relation between the Shannon entropy: $\sum _{i=0}^{n-1} E_{i}$ and the theoretical bound on the entropy: $\log _{2}(2^{N-T} \cdot {}_{N}\mathrm C _{T})$. Here, we assume that RS latches operate independently from each other, so the Shannon entropy are calculated by the sum of $E_{i}$. We also assume ideal conditions that each of all 40 PUFs has $t$ random latches out of $n$ implemented RS latches, and the remaining $n-t$ fixed latches output 0s or 1s with equal probability. To be specific, $P_i(R)=t/n$ and $P_i(0)=P_i(1)=\frac{1}{2}(1-t/n)$ ($0 \le i \le n-1$). Based on these assumptions, each $E_{i}$ is identical, so $\sum _{i=0}^{n-1} E_{i}=n \cdot E_{i}$. $\sum _{i=0}^{n-1} E_{i}$ can be calculated as follows:

$$\begin{aligned} \sum _{i=0}^{n-1} E_{i}&= n \cdot E_{i}\nonumber \\&= n \cdot \{ -P_i(0) \cdot \log _{2}P_i(0) -P_i(1) \cdot \log _{2}P_i(1) \nonumber \\&-P_i(R) \cdot \log _{2}P_i(R) \}\nonumber \\&= n \cdot \left\{ - \frac{1}{2} \cdot \frac{n-t}{n} \cdot \log _{2} \left( \frac{1}{2} \cdot \frac{n-t}{n} \right) \right.\nonumber \\&\left. - \frac{1}{2} \cdot \frac{n-t}{n} \cdot \log _{2} \left(\frac{1}{2} \cdot \frac{n-t}{n} \right) \right.\nonumber \\&\left. - \frac{t}{n} \cdot \log _{2} \frac{t}{n} \right\} \end{aligned}$$

(3)

which is equal to $(n-t) + n h(t/n)$ where $h(\cdot )$ is the binary entropy defined as $h(x) = -x\log _2 x -(1-x) \log _2(1-x)$ for $0 \le x \le 1$. It is well known that $\log _2 {}_n\mathrm C _t=n h(t/n)+o(1)$ holds for arbitrary integers $t$ and $n$ such that $t \le n$ (for instance, see [3, Example 11.1.3]). Hence, we have

$$\begin{aligned} (n-t) + n h(t/n)&= (n-t) + \log _2 {}_n\mathrm C _t +o(1) \nonumber \\&\approx \log _2 (2^{n-t} \cdot {}_n\mathrm C _t). \end{aligned}$$

(4)

If the number of FPGAs are sufficiently large, $t/n$ means the probability that each latch outputs random numbers. Then, it holds that $t/n \approx T/N$, which implies that Eq. (4) is equal to our theoretical bound: $\log _{2}(2^{N-T} \cdot {}_{N}\mathrm C _{T})$. Therefore, in consideration of the ratios of RS latches outputting 0s, 1s, and random numbers in first step, the experimental variety of responses can be accurately calculated from $\sum _{i=0}^{n-1} E_{i}$. Table 3 shows the Shannon entropy of responses experimentally calculated from $\sum _{i=0}^{n-1} E_{i}$. A PUF with 128 RS latches based on conventional method (2-B1) generates $2^{126.6}$ responses even if proposed method (1) is applied. This is because the number of random latches is small, and the ratios are not equal. In contrast, the PUF based on proposed method (2-B) generates $2^{192.7}$ responses, which is almost the same as the upper bound in Table 2 and is larger than for PUFs based on conventional methods. Hence, a PUF based on both proposed methods reduces circuit size and dramatically improves the variety and entropy of responses.

The entropy derived from an unit area (gate size) of proposed method (1) is expected to be higher than that of conventional methods (1-A) and (1-B). Both proposed and conventional methods (1-A) requires a mechanism to detect random latches, so their area sizes are almost the same, while the entropy of proposed method (1) is higher from Table 3. In contrast, conventional method (1-B) does not require the mechanism, so the area size is smaller than proposed method (1). The entropy of conventional method (1-B) seems to be higher by implementing more RS latches. In fact, however, conventional method (1-B) needs to correct the variation resulting from all the random latches, which requires larger redundant data for stable responses. In contrast, proposed method (1) considers random numbers as the third stable value, which leads to a suitable size of redundant data for embedded systems. Therefore, in consideration of the area size for redundant data, the proposed method is expected to generate higher entropy per unit area.

Table 3 Shannon entropy of responses

4.6 Temperature resistance

This section evaluates the robustness of our PUF against temperature variation – the reliability of responses when temperature is changed within the rated temperature of the SP3E FPGAs (0–85 $^\circ$C). In this evaluation, one 256-bit response is generated as the reference at the standard temperature of 25 $^\circ$C, and the other response is generated for analysis at 0 or 85 $^\circ$C. Figure 19 shows histograms of normalized Hamming distances between the reference response and the analysis one [i.e., 1 $\times$ 40(chips) = 40 elements]. Due to space constraints, we show the results at the lower temperature 0 $^\circ$C and at the higher temperature 85 $^\circ$C. At 0 and 85 $^\circ$C, the average error rate is approximately 2.4 and 5.0 % with an SD of 0.95 and 1.2 %, respectively. The bigger the temperature difference from 25 $^\circ$C—as the standard temperature—the higher the error rate. The error rate is less than around 15 % regardless of temperature, so stable responses are generated based on a Fuzzy Extractor with a reasonable size of redundant data [14]. Hence, our PUF has sufficient robustness against temperature variation.

Fig. 19

Reliability at 0 and 85 $^\circ$C

5 Performance evaluation on Spartan-6

This section evaluates the performance of our PUF using SP6 FPGA. The reason why we use not only SP3E but also SP6 is to confirm the effectiveness of our variety enhancement on a different architecture. In addition, we evaluate the robustness of our PUF against voltage variation—the reliability of responses when changing the supply voltage to FPGAs.

5.1 Experimental environment

Figure 20 shows our experimental evaluation system, which uses a custom-made expansion board with a Xilinx SP6 FPGA (XC6SLX16-2CSG324C). We cannot control the core voltage of an SP3E because a regulator on the starter kit board makes it 1.20 V forcibly. In contrast, the core voltage of an SP6 chip can be easily changed by 0.01 V using a stabilized power supply. The expansion board is connected to the SP3E board. We implement manually 128 RS latches in accordance with proposed method (2-C). We implement the RS latches on an SP6 FPGA, and other peripheral circuits on an SP3E FPGA. Such configuration enables us to change only the core voltage of the SP6 chip on which the PUF is implemented. The voltage change does not impact the peripheral circuits, which enhances the confidence of our experimental results. The data acquisition process is the same as when using only SP3E except the method of sending the data to the PC. The values of the block RAM are sent to a SD write module, and written into a micro SD card. The PC can obtain the data through the micro SD card faster than through an RS232C port. This difference does not influence PUF performance. The evaluation uses 20 actual SP6 chips, but we take the number of chips to be 40 since we implement manually the RS latches at two completely different locations.

Fig. 20

Experimental evaluation system using SP6

5.2 Reliability and uniqueness

The reliability and uniqueness results are shown in Figs. 21 and 22, respectively. In the reliability evaluation at normal operating condition (room temperature and standard supply voltage of 1.20 V), 101 256-bit responses are generated per SP6 FPGA chip. One response is used as the reference, and the remaining are used for analysis. Figure 21 shows a histogram of normalized Hamming distances between the reference response and each repeated one [i.e., 100 $\times$ 40(chips) = 4,000 elements]. The average error rate is approximately 0.86 % with an SD of 0.54 %. Hence, our result shows that our PUF on SP6 yields highly reliable responses. Next, in order to evaluate the uniqueness, a total of 40 256-bit responses using all 40 FPGAs (one response per FPGA) is generated. Figure 22 shows a histogram of normalized Hamming distances between every combination of two responses, i.e., ${}_{40}\mathrm C _{2}=780$ combinations, in the same way as the evaluation on SP3E. The difference in the responses of two arbitrary PUFs is approximately 49 % with an SD of 3.9 %. Our PUF gives responses with a high level of uniqueness. Here, this difference is a little larger than the ideal 44.4 %, as mentioned in Sect. 4.2. This is because the average number of random latches is 14, which is smaller than 43 (=128/3). Consequently, most of the 2-bit partial responses are ‘00’ or ‘11’, so the difference approaches 50 % similar to the conventional PUF using binary values (0/1). According to Fig. 8, PUFs on SP6 using both proposed methods (1) and (2-C) is estimated to generate approximately $2^{175}$ responses with 14 random latches. Finally, the Shannon entropy of the responses is $2^{167.9}$ based on the same steps in Sect. 4.5. A PUF based on our proposed methods improves the entropy of responses on various architectures.

Fig. 21

Reliability on SP6 (Mean = 0.86 %, SD = 0.54 %)

Fig. 22

Uniqueness on SP6 (Mean = 49 %, SD = 3.9 %)

5.3 Voltage resistance

In this section, we evaluate the robustness of our PUF against voltage variation—the reliability of responses when a supply voltage is changed within the rated voltage range of SP6 FPGAs (1.14–1.26 V). In this evaluation, one response is generated as the reference at the standard voltage of 1.20 V, and the remaining 100 responses are generated at 1.14 or 1.26 V. Figures 23 and 24 show histograms of normalized Hamming distances between the reference response and each repeated one (4,000 elements). Due to space constraints, we show the results at the lower voltage 1.14 V and at the higher voltage 1.26 V. At 1.14 and 1.26 V, the average error rate is approximately 5.3 and 4.8 % with an SD of 1.3 and 1.6 %, respectively. This error rate is much less than the 15 % assumed in [14] for stable responses based on a Fuzzy Extractor with a reasonable size of redundant data. Hence, our PUF has sufficient robustness against voltage variation.

Fig. 23

Reliability at 1.14 V (Mean = 5.3 %, SD = 1.3 %)

Fig. 24

Reliability at 1.26 V (Mean = 4.8 %, SD = 1.6 %)

6 Applicability of proposed methods to delay-based PUFs

The above section discusses the applicability of our proposed methods to LPUFs, one of the most feasible memory-based PUFs. The proposed methods can be also applied to delay-based PUFs such as Arbiter PUFs, Glitch PUFs and Ring Oscillator PUFs as shown in Fig. 25. The delay-based PUFs generate a one-bit response corresponding to an $\omega$-bit challenge. If a challenge $CHA_{i}$(0 $\le$ $i$ $\le$ $N-1$) is input to the PUFs repeatedly for $p$ times ($p$ = 1,000 in this ork), a $p$-bit output bitstream is obtained. The detection circuit outputs a 2-bit partial response $S_i[1:0]$(=00/11/10) based on the bitstream in the same way as mentioned in Sect. 3.1. Like memory-based PUFs, delay-based PUFs using our proposed methods also output a $2N$-bit response RES$[2N-1:0]$ satisfying Eq. (1) when inputting $N$ patterns of challenges. Hence, our proposed methods are expected to improve the variety and entropy of responses regardless of the kinds of PUFs.

Fig. 25

Applying our proposed methods to delay-based PUFs

7 Conclusion

This paper proposed a method for generating responses from an LPUF based on the location information of RS latches outputting random numbers. Our proposed detection circuit generates ternary values (00/11/10) in accordance with the three types of output bitstream from RS latches. This dramatically increases the variety of responses from $2^{N}$ to $2^{N-T} \cdot {}_{N}\mathrm C _{T}$ with $N$ implemented RS latches and $T$ random latches. In addition, with its small circuit size, the new implementation method increases the number of random latches and equalizes the ratios of RS latches outputting 0s, 1s, and random numbers, thereby enhancing the effectiveness of the proposed method. According to our experiment with FPGAs, an LPUF with 128 RS latches based on the proposed methods is able to generate responses with 193-bit Shannon entropy, which is larger than the 116-bit Shannon entropy achieved by conventional methods. Our LPUFs also have high robustness against temperature and voltage variation. The proposed methods can be applied to other delay-based PUFs, such as the Arbiter PUF. Inconsistent (random) outputs from the PUF can be used for generating highly unique responses without the necessity of selecting available challenges. Future work will include discussion of performance evaluations on ASICs.