The enumerative geometry of cubic hypersurfaces: point and line conditions

Abstract

The set of smooth cubic hypersurfaces in ${{\mathbb {P}}}^n$ is an open subset of a projective space. A compactification of the latter which allows to count the number of smooth cubic hypersurfaces tangent to a prescribed number of lines and passing through a given number of points is termed a 1–complete variety of cubic hypersurfaces, in analogy with the space of complete quadrics. Imitating the work of Aluffi for plane cubic curves, we construct such a space in arbitrary dimensions by a sequence of five blow-ups. The counting problem is then reduced to the computation of five total Chern classes. In the end, we derive the desired numbers in the case of cubic surfaces.

1 Introduction

A famous moduli space in enumerative geometry is the space of complete quadrics. This is a compactification of the set of smooth quadric hypersurfaces in ${{\mathbb {P}}}(W)={{\mathbb {P}}}^n$, where W is an $(n+1)$-dimensional vector space over an algebraically closed field . To construct this space, one starts with $V_0={{\mathbb {P}}}\left( \textrm{Sym}^2\left( W^*\right) \right)$ and considers the sequence of n blow-ups obtained by iteratively blowing up the proper transforms of the loci of symmetric matrices with rank at most i. For details, we refer to [19] and the references therein. This variety has been used to answer the degree 2 case of questions like:

How many smooth degree d hypersurfaces in ${{\mathbb {P}}}^n$ are tangent to $\left( {\begin{array}{c}n+d\\ d\end{array}}\right) -1$ general linear spaces of various dimensions?

The solutions to these problems are classically called characteristic numbers (of the family of degree d hypersurfaces). In the case of quadrics, this question was first answered by Schubert [21], back in 1879. Later this was translated into a problem about the Chow ring of the space of complete quadrics, and beautiful results have been achieved [7, 23, 28]. More recently, the space of complete quadrics has proved useful to study some classical problems in algebraic statistics related to maximum likelihood estimation [19, 20]. Therefore, for quadrics, the problem of computing characteristic numbers is essentially solved. An explicit construction of a space where the above question translates into a cohomological problem is known.

Much less is understood when it comes to higher degree hypersurfaces. To our knowledge, the only cases where all characteristic numbers are known are plane cubics and plane quartics. For the latter, partial results were achieved in [3, 30], and later a full description was given in [29]. When it comes to numbers for cubic plane curves, we have to go back to around 150 years ago, when in the early 1870s Maillard [18] and Zeuthen [31] claimed to have computed them. Unfortunately, their methods were relying on assumptions that were not rigorously justified. It took more than a century to prove these numbers by using rigorous theoretical foundations provided by Fulton–MacPherson intersection theory, as in the works of Kleiman and Speiser [16], and Aluffi [1, 2]. A particularly interesting feature of [1] is that in order to compute the characteristic numbers the author constructs a space of complete plane cubics, which turns out to be the right compactification of the set of reduced plane cubics where to solve the characteristic numbers problem. In a similar fashion as for complete quadrics, the space of complete plane cubics is constructed through a sequence of blow-ups of the projective space parametrizing all cubic forms.

As far as we know, the case of higher-dimensional cubic hypersurfaces has been unexplored. Our aim in this paper is to generalize the space of complete plane cubics in [1] and to construct what we call a variety of 1–complete cubic hypersurfaces, which is the right space where to answer the following question:

What is the number of smooth cubic hypersurfaces in ${{\mathbb {P}}}^n$ passing through $n_p$ general points and tangent to $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -n_p-1$ general lines?

The paper is based on [1], whose construction we find out to be generalizable to higher dimensions in a direct way. We now give an outline of this construction and explain how a 1–complete variety of cubic hypersurfaces can be used to answer the above question.

The set of all cubic hypersurfaces in ${{\mathbb {P}}}(W)$ is naturally parametrized by the projective space ${{\mathbb {P}}}\left( \textrm{Sym}^3\left( W^*\right) \right)$ of dimension $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -1$. The classical theory of discriminants of univariate polynomials shows that the subset of ${{\mathbb {P}}}\left( \textrm{Sym}^3\left( W^*\right) \right)$ of cubics tangent to a given line in ${{\mathbb {P}}}(W)$ is a hypersurface which we call a line condition, see also Remark 2.2. Similarly, a point condition is the hyperplane in ${{\mathbb {P}}}\left( \textrm{Sym}^3\left( W^*\right) \right)$ of all cubics containing a given point in ${{\mathbb {P}}}(W)$. We want to count the finite number of smooth cubics in the intersection of $n_p$ general point conditions and $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -n_p-1$ general line conditions. However, the intersection of such hypersurfaces is not always generically transverse. A central role is indeed played by the locus where all line conditions intersect, which turns out to be the set of non-reduced cubics, i.e., those of the form $\lambda \mu ^2$ for linear forms $\lambda$ and $\mu$. This simple description of the base locus is indeed the reason for our focus on lines rather than higher-dimensional linear spaces. The goal of our construction is to obtain a variety birational to ${{\mathbb {P}}}\left( \textrm{Sym}^3\left( W^*\right) \right)$ but such that in this new space, the proper transforms of the line conditions will no longer intersect. This is what we called earlier a 1-complete variety of cubic hypersurfaces. It turns out that, as in [1], it is enough to blow-up five times along irreducible components of the loci where the proper transforms of the line conditions intersect. The ultimate goal of computing the characteristic numbers is then achieved by subtracting from the bound provided by Bézout’s theorem a certain correction term which can be expressed via certain Chern classes of vector bundles arising in the blow-up process. Let us note that one crucial difference to [1], apart from the natural difficulties when dealing with higher dimensions, is that the center $B_4$ of the fifth blow-up in our case is the projectivization of a vector bundle ${\mathcal {E}}$ of rank $>1$ which is not a priori known explicitly. Its identification and the computation of its Chern classes are difficult tasks and have no analog in [1]. In particular, Proposition 2.25 provides a new proof of the important Lemma 4.2 of [1].

The paper is organized as follows. In Sect. 1 we give the definition of a 1-complete variety of cubic hypersurfaces ${\tilde{V}}$ and Theorem 1.4 proves that the intersection numbers we will compute in this variety coincide with the characteristic numbers we were aiming for.

Section 2 concerns the construction of the 1-complete variety ${\tilde{V}}$ achieved by performing five blow-ups. In each subsection we spell out the details of each blow-up by expressing its equations, the support of the intersection of the proper transforms of the line conditions, and the equations for this intersection. Roughly, this intersection is then taken to be the center of the next blow-up. The construction ends with Corollary 2.23 where we show that the proper transforms of the line conditions no longer intersect.

Section 3 is devoted to the Chow rings of the five centers defined in the previous section and to the computation of the intersection classes needed for the correction term.

In the final Sect. 4, we gather the data computed so far and provide the characteristic numbers for cubic surfaces in projective 3-space. The proof of Theorem 3.14(ii) and Remark 3.15 explain what is missing to determine the characteristic numbers in higher dimensions.

The code used in this work together with computational results is available at

2 First associated hypersurfaces and the Hurwitz map

We fix an integer $d\ge 2$, an algebraically closed field of characteristic 0 or strictly greater than d, and a -vector space W of dimension $n+1$ with $n \ge 2$. We refer to [13, Section 3.2.E] for the notion of higher associated hypersurfaces of a projective variety. Specifically, we are interested in the following case: Let $X {:}{=}{\mathcal {V}}(f) \subseteq {{\mathbb {P}}}(W)$ be an integral projective hypersurface of degree $d\ge 2$, defined by an irreducible homogeneous polynomial f. If X is smooth, its first associated hypersurface ${\mathcal {Z}}_1(X) \subseteq {{\,\textrm{Gr}\,}}(2,W)$ consists of all lines $\ell \subseteq {{\mathbb {P}}}(W)$ such that $\ell$ is tangent to X at some point or, more precisely, $\dim (\ell \cap E T_xX)=1$ for some point $x\in \ell \cap X$, where $E T_xX$ is the embedded tangent space of X at the point x. If instead X is singular, we first consider the lines $\ell$ for which there exists a smooth point satisfying the above conditions and then take the Zariski closure of this set in the Grassmannian ${{\,\textrm{Gr}\,}}(2,W)$.

In [13, Proposition 2.11] it is shown that ${\mathcal {Z}}_1(X)$ is an irreducible hypersurface in ${{\,\textrm{Gr}\,}}(2,W)$. Moreover, if X is smooth, [25, Theorem 1.1] shows that ${\mathcal {Z}}_1(X)$ is defined by an irreducible element ${{\,\textrm{Hu}\,}}_f$ of degree $d(d-1)$ in the projective coordinate ring of ${{\,\textrm{Gr}\,}}(2,W)$, called the Hurwitz form, written as a degree $d(d-1)$ homogeneous polynomial in the Plücker coordinates, uniquely only up to the degree $d(d-1)$ piece of the ideal generated by the Plücker relations. On the open set of ${{\mathbb {P}}}\left( \textrm{Sym}^d(W^*)\right)$ parametrizing smooth degree d hypersurfaces, we can define a morphism sending X to the degree $d(d-1)$ hypersurface ${\mathcal {Z}}_1(X)$ of ${{\,\textrm{Gr}\,}}(2,W)$. The set of hypersurfaces in ${{\,\textrm{Gr}\,}}(2,W)$ of this degree is parametrized by the projective space $|{\mathcal {O}}_{{{\,\textrm{Gr}\,}}(2,W)}(d(d-1))|$.

Hence, we define the Hurwitz map to be the rational map

For instance, if $n=2$, this map is simply the one taking a degree d plane curve into its dual curve. Following [25, Example 2.2], ${{\,\textrm{Hu}\,}}_f$ can be computed as the resultant of the homogeneous polynomials of degree $d-1$ in the variables s and t given by the two partial derivatives of $f(s v_0 + t w_0, \ldots , s v_n + t w_n)$. As a polynomial in s and t, the coefficients of the latter are bihomogeneous of degree (1, d) in the coefficients of f and the variables $v_i, w_i$, respectively. It follows that the polynomial ${{\,\textrm{Hu}\,}}_f$ is bihomogeneous of degree $(2(d-1), 2d(d-1))$ with respect to the aforementioned variables. By [25, Example 2.2], ${{\,\textrm{Hu}\,}}_f$ can even be expressed as a polynomial in the Plücker coordinates $p_{0,1},p_{0,2},\dots ,p_{n-1,n}$ of the Grassmannian ${{\,\textrm{Gr}\,}}(2,W)$ given by the $2 \times 2$ minors $p_{ij} = v_i w_j - v_j w_i$. Hence, ${{\,\textrm{Hu}\,}}_f$ is bihomogeneous of degree $(2(d-1),d(d-1))$ in the coefficients of f and the Plücker coordinates, respectively. Notice that the polynomial obtained in this way makes sense also for non-smooth, reducible and even non-reduced hypersurfaces ${\mathcal {V}}(f)$.

Remark 1.1

The rational map induced by the linear system generated by all line conditions in $H^0({{\mathbb {P}}}(\textrm{Sym}^d(W^*)),{\mathcal {O}}(2(d-1)))$ is closely related to ${{\,\textrm{Hu}\,}}$. Composing the former with a suitable linear embedding into $|{\mathcal {O}}_{{{\,\textrm{Gr}\,}}(2,W)}(d(d-1))|$ gives the latter.

In the same line of [1], we define the point condition $P^p$ and the line condition $L^{\ell }$ as the hypersurfaces in ${{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ consisting of the degree d hypersurfaces, respectively, containing the point p and tangent to the line $\ell$.

Lemma 1.2

The indeterminacy locus of the Hurwitz map ${{\,\textrm{Hu}\,}}$ is precisely the intersection of all line conditions, which in turn set-theoretically agrees with the subset $S_0 \subseteq {{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ of the hypersurfaces defined by degree d homogeneous polynomials divisible by the square of some non-constant polynomial.

Proof

Fixing a line $\ell \in {{\,\textrm{Gr}\,}}(2,W)$, the polynomial ${{\,\textrm{Hu}\,}}_f(\ell )$ is a homogeneous degree $2(d-1)$ polynomial in the coefficients of f. Its vanishing set agrees with $L^{\ell } \subseteq {{\mathbb {P}}}(\textrm{Sym}^d(W^*))$, hence for the first claim it is enough to see that ${{\,\textrm{Hu}\,}}_f(\ell )$, for fixed $\ell$, is irreducible as a polynomial in the coefficients of f. This is clearly a property invariant under the action of ${{\,\textrm{PGL}\,}}_n$, so we can consider the line $\ell = \langle e_0, e_1 \rangle$. Then ${{\,\textrm{Hu}\,}}_f(\ell )$ is precisely the discriminant of the generic homogeneous degree d polynomial in two variables $x_0, x_1$, and this is indeed known to be an irreducible polynomial of degree $2(d-1)$ if .

The indeterminacy locus of ${{\,\textrm{Hu}\,}}$ is the set of [f] such that ${{\,\textrm{Hu}\,}}_f(\ell ) = 0$ for every line $\ell$. In this case, the singular locus of the closed subscheme ${\mathcal {V}}(f) \subseteq {{\mathbb {P}}}(W)$ must have codimension 0, otherwise the general line would intersect ${\mathcal {V}}(f)$ transversally in d distinct smooth points. But the singular locus of ${\mathcal {V}}(f)$ can only have codimension 0 if ${\mathcal {V}}(f)$ has a non-reduced component, so f is divisible by the square of some non-constant polynomial. $\square$

This allows us to present the following definition.

Definition 1.3

A 1-complete variety of degree d hypersurfaces is a morphism $\pi :{\tilde{V}} \rightarrow {{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ from a smooth projective variety ${\tilde{V}}$ which is an isomorphism outside $\pi ^{-1}(S_0)$ resolving ${{\,\textrm{Hu}\,}}$, i.e., such that the proper transforms of all line conditions $L^{\ell }$ in ${\tilde{V}}$ do not intersect:

An analogous construction for tangency with respect to s-dimensional planes instead of lines would lead to the definition of s-complete varieties of degree d hypersurfaces. For $s \ge 2$, however, the intersection of all s-plane conditions set-theoretically agrees with the subset of ${{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ given by all degree d hypersurfaces with singular locus of dimension $\ge n-s$, which to our knowledge is not as easily parametrizable as the set $S_0$ of non-reduced hypersurfaces.

Theorem 1.4

We write $V_0 {:}{=}{{\mathbb {P}}}(\textrm{Sym}^d(W^*))$. Let ${\tilde{V}}$ be a 1-complete variety of degree d hypersurfaces as above and let $F \subseteq V_0 {\setminus } S_0$ be a locally closed subvariety. Denote by ${\tilde{F}} \subseteq {\tilde{V}}$ the proper transform of the closure ${\overline{F}}$ and by ${\tilde{L}}^{\ell }, {\tilde{P}}^p \subseteq {\tilde{V}}$ the line and point conditions of ${\tilde{V}}$, i.e., the proper transforms in ${\tilde{V}}$ of the irreducible hypersurfaces $L^{\ell }, P^p \subseteq V_0$ corresponding to line and point conditions of $V_0$, respectively, for the line $\ell \subseteq {{\mathbb {P}}}(W)$ and the point $p \in {{\mathbb {P}}}(W)$.

• (i) For any finite set of subvarieties $A_1, \ldots , A_r \subseteq {\tilde{V}}$, there exist a point p and a line $\ell$ such that ${\tilde{P}}^p$ and ${\tilde{L}}^{\ell }$ both intersect every $A_i$ properly, i.e., in the expected dimension. In fact, this is the case for a general point and a general line.

• (ii) If $r = \dim (F)$, there exist r lines $\ell _1, \ldots ,\ell _r$ such that the corresponding line conditions in ${\tilde{V}}$ intersect ${\tilde{F}}$ in finitely many points, mapping to F under $\pi$. Again, this is the case for general lines $\ell _1, \ldots , \ell _r$.

• (iii) The number of elements of F, counted with multiplicity, passing through $n_p$ general points and tangent to $n_{\ell }$ general lines such that $n_p + n_{\ell } = \dim (F)$ equals the degree of the 0-cycle ${\tilde{P}}^{n_p} \cdot {\tilde{L}}^{n_{\ell }} \cdot {\tilde{F}} \in \textrm{CH}_0({\tilde{V}})$, where ${\tilde{P}}, {\tilde{L}}$ denote the cycle classes of any point and line condition ${\tilde{P}}^p, {\tilde{L}}^{\ell }$ in ${\tilde{V}}$.

• (iv) Assume 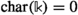. Then for sufficiently general points and lines, the multiplicity of every element of F from (iii) is 1.

Proof

Both (ii) and (iii) follow from (i), the arguments being the same as in [1, Proposition 1]. For (i), we also mimic the strategy of [1, Proposition 1] and assume the conclusion is false, i.e., there are subvarieties $A_1, \ldots , A_r$ such that for every line $\ell$, the line condition ${\tilde{L}}^{\ell }$ intersects non-properly at least one of the $A_i$. As ${\tilde{L}}^{\ell }$ is an irreducible hypersurface and all $A_i$ are irreducible, this means that every line condition in ${\tilde{V}}$ contains at least one of the $A_i$. Pick a point $p_i \in {\widetilde{{{\,\textrm{Hu}\,}}}}(A_i)$ for each $i = 1, \ldots , r$ and denote by $G^{\ell } \subseteq |{\mathcal {O}}_{{{\,\textrm{Gr}\,}}(2,W)}(d(d-1))|$ the hyperplane given by all degree $d(d-1)$ elements of the projective coordinate ring of ${{\,\textrm{Gr}\,}}(2,W)$ vanishing at $\ell$. The coefficients of the linear equation defining $G^{\ell }$ are the monomials of degree $d(d-1)$ in the Plücker coordinates evaluated at the line $\ell$. Now, by construction, ${{\,\textrm{Hu}\,}}(L^{\ell } \setminus S_0) \subseteq G^{\ell }$ and therefore ${\widetilde{{{\,\textrm{Hu}\,}}}}({\tilde{L}}^{\ell }) \subseteq G^{\ell }$. In particular, every hyperplane $G^{\ell }$ contains at least one of the finitely many points $p_i$. Dually, in ${\check{{{\mathbb {P}}}}}(H^0({\mathcal {O}}_{{{\,\textrm{Gr}\,}}(2,W)}(d(d-1))))$ this means that all points corresponding to the hyperplanes $G^{\ell }$ are contained in the finite union of hyperplanes corresponding to the points $p_i$. However, the set of points corresponding to the $G^{\ell }$ is the image of the $d(d-1)$-Veronese embedding ${{\,\textrm{Gr}\,}}(2,W) \rightarrow {\check{{{\mathbb {P}}}}}(H^0({\mathcal {O}}_{{{\,\textrm{Gr}\,}}(2,W)}(d(d-1))))$ and thus irreducible. Hence, this image would have to be contained in a single hyperplane. In other words, switching back to the primal setting, there exists some $p_i$, say $p_1$, that is contained in all hyperplanes $G^{\ell }$. Then $p_1$ corresponds to a non-zero element in the degree $d(d-1)$ part of the projective coordinate ring of ${{\,\textrm{Gr}\,}}(2,W)$ that, as a polynomial in the Plücker coordinates, must vanish at all lines in ${{\mathbb {P}}}(W)$, hence on all of ${{\,\textrm{Gr}\,}}(2,W)$. This, of course, is impossible.

The statement of (iv) follows from [11, Theorem (d), p. 162]. $\square$

3 A 1-complete variety of cubic hypersurfaces

This section is dedicated to our construction of a 1-complete variety of cubic hypersurfaces. We start from the projective space $V_0 {:}{=}{{\mathbb {P}}}(\textrm{Sym}^3 (W^*))$ parametrizing cubic hypersurfaces in ${{\mathbb {P}}}^n={{\mathbb {P}}}(W)$ and blow-up five times along smooth centers. At each level, these are given by an irreducible component of the intersection of all proper transforms of the line conditions. We will also refer to cubic hypersurfaces as cubics.

We saw in the previous section that $S_0$ coincides with the set of cubic hypersurfaces divisible by the square of a non-constant polynomial. Hence, $S_0$ is the image of the morphism

As $\phi _0$ is injective, $S_0$ is a subvariety of ${{\mathbb {P}}}(\textrm{Sym}^3(W^*))$ of dimension 2n. Let $\Delta$ denote the diagonal in ${{\mathbb {P}}}(W^*) \times {{\mathbb {P}}}(W^*)$. We write $B_0$ for the locus $\phi _0(\Delta )$ of triple hyperplanes.

The following result is a direct generalization of [1, Lemma 0.1]. We will often use it without explicit reference. The statement does not depend on the choice of the line $\ell \subseteq {{\mathbb {P}}}^n$, hence can be verified on the equation of any line condition.

Lemma 2.1

Let $L^{\ell }$ be the line condition in ${{\mathbb {P}}}(\textrm{Sym}^3(W^*))$ corresponding to $\ell \subseteq {{\mathbb {P}}}^n$. Then:

• (i) If $c\in L^{\ell }$, then $L^{\ell }$ is smooth at c if and only if c intersects $\ell$ with multiplicity exactly 2 at a point. In particular, the line conditions are generically smooth along the locus $S_0$ of non-reduced cubics.

• (ii) If c intersects $\ell$ with multiplicity 3 at a point, then $L^\ell$ has multiplicity 2 at c. In particular, the line conditions have multiplicity 2 along the locus $B_0$ of triple hyperplanes.

• (iii) The tangent hyperplane to $L^{\ell }$ at a smooth point c consists of the cubics containing the point of tangency of c to $\ell$. The tangent cone in $V_0$ to $L^{\ell }$ at a cubic c intersecting $\ell$ in a triple point p is supported on the hyperplane in $V_0$ consisting of the cubics containing p.

An immediate generalization of Lemma 0.2 in [1] implies that the map $\phi _0$ is an isomorphism onto its image when restricted to ${{\mathbb {P}}}^n \times {{\mathbb {P}}}^n \setminus \Delta$.

The next subsections explain in details the construction of the 1-complete variety of cubic hypersurfaces ${\tilde{V}}$. A schematic overview of this construction and the notation employed is englobed in the following diagram:

The center of each blow-up is denoted by $B_i$, while the blow-ups are called $V_i$. Hence $V_{i+1}$ denotes the blow-up of $V_{i}$ at the center $B_i$ and $\pi _{i+1}:V_{i+1}\rightarrow V_i$ the corresponding blow-up map, for $i=0,\dots ,4$. For $i\le 3$, $S_i$ indicates the proper transform of the locus $S_0$ in $V_i$.

The above diagram is analogous to the one in [1, p. 514]. Our construction of the 1-complete variety of cubic hypersurfaces $V_5$ is indeed a direct generalization to higher dimensions of the one performed by Aluffi for plane cubic curves. In particular, the same number of blow-ups is needed to empty the locus where the proper transforms of the line conditions intersect.

3.1 Space of cubic hypersurfaces

In what follows, let be an algebraically closed field of characteristic $\ne 2, 3$ and W a -vector space of dimension $n+1$ with basis $e_0, \ldots , e_n$. Let us introduce some notation in order to develop the first blow-up. Given a set of multi-indices ${\mathcal {I}}=\{I_1,\dots ,I_n\}$, we denote $(c_I)$ (resp. $[c_I]$) the vector of affine (resp. projective) coordinates $(c_{I_1},\dots ,c_{I_n})$ (resp. $[c_{I_1}:\dots :c_{I_n}]$). In particular, denote by $[a_I] = [a_{(0,0,0)}: \dots : a_{(n,n,n)}]$ the vector of $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right)$ projective coordinates for $V_0$. More explicitly, each $a_{(i,j,k)}$ corresponds to the coefficient of the monomial $x_ix_jx_k$ in the equation for the associate cubic in ${{\mathbb {P}}}^n$, where we assume $i\le j \le k$. We denote by [n] the set of natural numbers between 0 and n and by ${\mathcal {J}}$ the set of multi-indices $(i,j,k)\in [n]^3$ with $i \le j \le k$ and $j\ge 1$. Then in the affine chart $D(a_{(0,0,0)})$, the ideal ${\mathcal {I}}(B_0)$ in $V_0$ determining the locus of triple hyperplanes is generated by the polynomials $f_J$, with $J\in {\mathcal {J}}$, given as follows:

$$\begin{aligned} f_{(0,i,i)} \,&{:}{=}\, 3a_{(0,i,i)}-a_{(0,0,i)}^2{} & {} \ \qquad \text { for } i>0, \nonumber \\ f_{(0,i,j)} \,&{:}{=}\, 3a_{(0,i,j)}-2a_{(0,0,i)}a_{(0,0,j)}{} & {} \ \qquad \text { for } j>i>0, \nonumber \\ f_{(i,i,i)} \,&{:}{=}\, 9a_{(i,i,i)}-a_{(0,0,i)}a_{(0,i,i)}{} & {} \ \qquad \text { for } i>0,\nonumber \\ f_{(i,i,j)} \,&{:}{=}\, 3a_{(i,i,j)}-a_{(0,i,i)}a_{(0,0,j)}{} & {} \ \qquad \text { for } i,j>0, i \ne j, \nonumber \\ f_{(i,j,k)} \,&{:}{=}\, 3a_{(i,j,k)}-a_{(0,i,j)}a_{(0,0,k)}{} & {} \ \qquad \text { for } k>j>i>0. \end{aligned}$$

(2)

These polynomials will be needed to provide equations for the center of the first blow-up. Note that $B_0$ is a smooth complete intersection of codimension $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -1 - n$ inside this open chart. In what follows, when we write the affine coordinates $(a_I)$ we always assume the index $I = (0,0,0)$ to be excluded.

Remark 2.2

A line condition is a degree 4 hypersurface in $V_0$. Indeed, fix the line $\ell ={\mathcal {V}}(x_2, \ldots , x_n)\subseteq {{\mathbb {P}}}^n$. The tangency condition for a cubic to such line is given by the vanishing of the resultant of its derivatives with respect to $x_0$ and $x_1$. Then the equation for the line condition $L^{\ell }$ in $D(a_{(0,0,0)}) \subseteq V_0$ is given by

$$\begin{aligned} \small {a_{(0,0,1)}^2a_{(0,1,1)}^2+18a_{(0,0,1)}a_{(0,1,1)}a_{(1,1,1)}-4a_{(0,1,1)}^3-4a_{(0,0,1)}^3a_{(1,1,1)}-27 a_{(1,1,1)}^2=0. }\quad \end{aligned}$$

(3)

Using the action of ${{\,\textrm{PGL}\,}}_n$, we can recover the equation for $L^{\ell }$ for any line ${\ell } \subseteq {{\mathbb {P}}}^n$.

3.2 First Blow-up

Denote by $V_1$ the blow-up of the space $V_0$ along the center $B_0$, and $L_1$ the proper transform in $V_1$ of a line condition L.

Coordinates I

Let $([a_I],[b_J])$ denote the projective coordinates on $V_0 \times {{\mathbb {P}}}^{r-1}$, where $r=\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -1-n$ is the codimension of $B_0$ as subvariety of $V_0$ and $J\in {\mathcal {J}}$. Then, by [9, Exercise 17.14(b)] the blow-up $V_1$ is a closed subvariety of the affine chart $D(a_{(0,0,0)})$ given by the equations

$$\begin{aligned} f_{J_1} b_{J_2} - f_{J_2} b_{J_1}=0, \end{aligned}$$

where $J_1, J_2\in {\mathcal {J}}$ and the $f_J$’s denote the equations in (2).

We restrict to the affine chart $D(b_{(0,1,1)})$, where $V_1$ can be described by the affine coordinates $(a_{(0,0,1)}, \ldots , a_{(0,0,n)},a',b_J)$, with $J\in {\mathcal {J}}{\setminus } \{(0,1,1)\}$, and the additional variable $a'$ corresponds to the equation $f_{(0,1,1)} = 3a_{(0,1,1)} - a_{(0,0,1)}^2$. The equations for $V_1$ in this affine open set become

$$\begin{aligned} a' - f_{(0,1,1)}=0, \qquad f_J - b_J a'=0, \qquad \hbox {for all} \;\; J\in {\mathcal {J}}\setminus \{(0,1,1)\}. \end{aligned}$$

The equation for the exceptional divisor $E_1$ inside $V_1$ is then $a'=0$, and the $(b_J)$ provide coordinates in the chosen affine chart for the fiber of $E_1$ over a point in $B_0$. In what follows, we will always exclude the index $J=(0,1,1)$ when considering the affine coordinates $(b_J)$. Denote by $N_{{{\mathbb {P}}}(W^*)} {{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ the normal bundle of the d-th Veronese embedding $\nu _d:{{\mathbb {P}}}(W^*) \hookrightarrow {{\mathbb {P}}}(\textrm{Sym}^d(W^*))$, where ${{\mathbb {P}}}(W^*)$ is embedded in ${{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ via $\nu _d$.

Lemma 2.3

Let $e \le d$. Then there is a natural embedding of normal bundles

$$\begin{aligned} \alpha _{e,d}:\, N_{{{\mathbb {P}}}(W^*)} {{\mathbb {P}}}(\textrm{Sym}^{e}(W^*)) \,\,\hookrightarrow \,\, N_{{{\mathbb {P}}}(W^*)} {{\mathbb {P}}}(\textrm{Sym}^d(W^*)), \end{aligned}$$

given by “multiplication by $\lambda ^{d-e}$” in the fiber over $[\lambda ] \in {{\mathbb {P}}}(W^*)$.

Proof

We write . The pullback of the Euler sequence on ${{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ via $\nu _d$ is

$$\begin{aligned} 0 \rightarrow {\mathcal {O}}_{{{\mathbb {P}}}(W^*)} \overset{\nu _d^{*}(\varepsilon )}{\rightarrow } \textrm{Sym}^d(W^*) \otimes {\mathcal {O}}_{{{\mathbb {P}}}(W^*)}(d) \rightarrow T{{\mathbb {P}}}(\textrm{Sym}^d(W^*))|_{{{\mathbb {P}}}(W^*)} \rightarrow 0, \end{aligned}$$

where $\nu _d^{*}(\varepsilon )$ is induced by the graded R-module homomorphism

$$\begin{aligned} R \rightarrow \textrm{Sym}^d(W^*) \otimes _{R} R(d), \ f \mapsto \sum _{|I|=d} \left( {\begin{array}{c}d\\ I\end{array}}\right) e_I \otimes (x^I f) = f \cdot (e_0 \otimes x_0 + \dots e_n \otimes x_n)^d. \end{aligned}$$

The fiber of $\nu _{d}^*(\varepsilon )$ over $\lambda$ is therefore just multiplication by $\lambda ^d = (\lambda _0 e_0 + \ldots + \lambda _n e_n)^d$. More generally, there is a commutative diagram with exact rows

In here, $\alpha _{e,d}$ is induced by the graded R-module homomorphism which is multiplication by $(e_0 \otimes x_0 + \ldots + e_n \otimes x_n)^{d-e}$. It can be checked that $\overline{\alpha _{1,e}} = \textrm{d}\nu _{e}$ is the differential of the e-th Veronese embedding. Then $\alpha _{e,d}$ induces the embedding of normal bundles we are looking for. $\square$

For us, $e=2$, $d=3$. The exceptional divisor is $E_1 \cong {{\mathbb {P}}}(N_{{{\mathbb {P}}}(W^*)} {{\mathbb {P}}}(\textrm{Sym}^3(W^*)))$ and we call $B_1$ the image of ${{\mathbb {P}}}(\alpha _{2,3})$ in $E_1$. The proper transform of $S_0$ in $V_1$ will be denoted by $S_1$.

Proposition 2.4

The intersection of the proper transforms of all line conditions in $V_1$ is contained in the union $S_1 \cup B_1$.

Proof

It is enough to check that the intersection of the proper transforms of all line conditions and $E_1$ lies inside $B_1$. The intersection of the proper transform $L_1$ of a line condition L with the fiber over $[\lambda ^3] \in B_0$ is the image of the tangent cone of L at the point $[\lambda ^3]$ in the projectivized normal bundle ${{\mathbb {P}}}(N_{B_0} V_0)$. By definition of $\alpha _{2,3}$ in Lemma 2.3, the fiber of $B_1$ over $[\lambda ^3]$ consists of all cubics divisible by $\lambda$. Lemma 2.1(iii) implies that the intersection of all tangent cones at $[\lambda ^3]$ of all line conditions is contained in the set of cubics containing the hyperplane $\lambda$. This shows the claim. $\square$

Lemma 2.5

We have a commutative diagram

where $\phi _1$ is an isomorphism. In particular, $S_1$ is smooth.

Proof

We write e for the exceptional divisor of $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$. The map $\phi _0$ lifts to a map $\phi _1: \textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n \rightarrow S_1$ via the universal property of blowing up. Indeed, it can be checked that the pullback of the ideal sheaf ${\mathcal {I}}(B_0)$ via $\phi _0$ is precisely the squared ideal sheaf ${\mathcal {I}}(\Delta )^2$ of the diagonal $\Delta \subseteq {{\mathbb {P}}}^n \times {{\mathbb {P}}}^n$, in particular the pullback of ${\mathcal {I}}(B_0)$ to $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$ is an effective Cartier divisor, as needed. Clearly, $\phi _1$ restricts to an isomorphism of $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n \setminus e$ onto $S_1 {\setminus } E_1$. As $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$ and $S_1$ are projective varieties, $\phi _1$ is a closed map, so surjectivity follows. In order to prove the injectivity of $\phi _1$ we observe that $\phi _0$ is an injective morphism between varieties over an algebraically closed field, hence $\phi _0$ is universally injective. Base-changing $\phi _0$ along the blow-up map $\pi _1:V_1 \rightarrow V_0$ hence gives an injection $({{\mathbb {P}}}^n \times {{\mathbb {P}}}^n) \times _{V_0} V_1 \rightarrow V_1$. The blow-up closure lemma ensures that $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$ is naturally a closed subscheme of $({{\mathbb {P}}}^n \times {{\mathbb {P}}}^n) \times _{V_0} V_1$, and the composition $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n \rightarrow V_1$ agrees with $\phi _1$, showing that $\phi _1$ is injective. By [15, Corollary 14.10], it remains to show that $(d\phi _1)_p: T_p \left( \textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n\right) \rightarrow T_{\phi _1(p)} V_1$ is injective for all p in the exceptional divisor e of $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$. This matter is local and invariant under the ${{\,\textrm{PGL}\,}}_n$-action, so we can assume p to lie in the fiber of $([1:0:\cdots :0],[1:0:\cdots :0]) \in \Delta$. Choose local coordinates

$$\begin{aligned}([1: \lambda _1: \cdots : \lambda _n], [1: \mu _1: \cdots : \mu _n]) \in {{\mathbb {P}}}^n\times {{\mathbb {P}}}^n.\end{aligned}$$

The equations for $\Delta$ are $u_i{:}{=}\lambda _i - \mu _i =0$ for all $i \in \{1,\dots ,n\}$. Thus, $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$ is described by the points $(\mu _1,\dots ,\mu _n,u_1,\dots ,u_n, [s_1,\dots ,s_n])$ such that $u_i s_{j} - u_j s_{i}=0$ for all i, j. In the affine chart $D(s_1)$, the morphism $\phi _1$ is given explicitly in the affine coordinates $(\mu _1,\dots ,\mu _n,u_1,s_2,\dots ,s_n)$ by

$$\begin{aligned} \begin{aligned} a_{(0,0,1)}&=3\mu _1 + u_1,\\ a_{(0,0,i)}&=3\mu _i + s_i u_1 \;\;&\text{ for } i>1,\\ a'&=-u_1^2,\\ b_{(0,i,i)}&=s_i^2 \;\;&\text{ for } i>1,\\ b_{(1,i,i)}&=2\mu _i s_i \;\;&\text{ for } i>1,\\ b_{(1,1,i)}&=2\mu _1 s_i \;\;&\text{ for } i>1, \end{aligned}\qquad \qquad \begin{aligned} b_{(1,1,1)}&=2\mu _1,\\ b_{(0,1,i)}&=2s_i \;\;&\text{ for } i>1,\\ b_{(0,i,j)}&=2s_i s_j \;\;&\text{ for } j>i>1,\\ b_{(i,i,i)}&=2 \mu _i s_i^2 \;\;&\text{ for } i>1,\\ b_{(i,i,j)}&=2\mu _i s_i s_j \;\;&\text{ for } i,j>1, i \ne j,\\ b_{(i,j,k)}&=2s_k\left( \mu _i s_j+\mu _j s_i\right) \;\;&\text{ for } k>j>i>0. \end{aligned} \end{aligned}$$

The exceptional divisor e now has equation $u_1 = 0$. This explicit description of $\phi _1$ allows us to conclude the proof by checking the non-degeneracy of the Jacobian at every point. Indeed, the 2n row vectors in the Jacobian corresponding to $a_{(0,0,i)}$ for $1 \le i \le n$, to $b_{(0,1,i)}$ for $2 \le i \le n$ and to $b_{(1,1,1)}$ are linearly independent. $\square$

Lemma 2.6

The set-theoretic intersection of $B_1$ and $S_1$ is $\phi _1(e)$. Moreover, the proper transforms of the line conditions are generically smooth and tangent to $E_1$ along $B_1$.

Proof

Since $\phi _1$ is an isomorphism, we have $\phi _1(e) = S_1 \cap E_1$ and it suffices to show $\phi _1(e) \subseteq B_1$. By invariance under projective transformations, it suffices to prove the inclusion for the fiber in $E_1$ over $[x_0^3] \in B_0$. Using the coordinates described above, the intersection of this fiber with $B_1$ in $V_1$ is described by the equations $a_{(0,0,i)}=0$ for all $1 \le i \le n$, $a'=0$ and $b_J=0$ for the multi-indices $J\in {\mathcal {J}}$ with first entry being non-zero. The explicit description of $\phi _1$ shows that the image of the fiber of $([1:0:\cdots :0],[1:0:\cdots :0]) \in {{\mathbb {P}}}^n \times {{\mathbb {P}}}^n$ satisfies all these equations, proving the claim.

For the second point, the invariance under the natural action of ${{\,\textrm{PGL}\,}}_n$ on $V_1$, allows us to verify the claim for the line condition corresponding to the line $\ell = {\mathcal {V}}(x_2, \ldots , x_n)$. We can restrict to the affine open $D(a_{(0,0,0)}) \cap D(b_{(0,1,1)})$ where we have local coordinates (see Remark I). The equation for the line condition $L^{\ell }$ in $D(a_{(0,0,0)}) \subseteq V_0$ is given in (3). Plugging in $3a_{(0,1,1)}=a'+a_{(0,0,1)}^2$ and $27a_{(1,1,1)}=3b_{(1,1,1)}a'+a_{(0,0,1)}\left( a'+a_{(0,0,1)}^2\right)$, we get the equation

$$\begin{aligned} (a')^2\left( 12b_{(1,1,1)}a_{(0,0,1)}-4a_{(0,0,1)}^2-4a'-9b_{(1,1,1)}^2\right) =0, \end{aligned}$$

which outside of $E_1$ describes the proper transform $L^{\ell }_1$ of the line condition in the chosen affine chart, whose equation is therefore $-4a'-\left( 3b_{(1,1,1)}-2a_{(0,0,1)}\right) ^2=0$. Since the equation of $E_1$ in the local coordinates is $a'=0$, every point of $E_1$ belonging to the proper transform is indeed a tangency point. Moreover, the equation shows that the proper transform is smooth in this entire affine open. $\square$

Lemma 2.7

The ideal of $B_1 \subseteq V_1$ in the open $D(a_{(0,0,0)})$ is generated by the equations

$$\begin{aligned} \begin{aligned} f_J&= 0{}&{} \;\;&\text{ for } \text{ all } J, \\ f_{(i,i,i)}' \,&{:}{=}\, 3b_{(i,i,i)} - 2a_{(0,0,i)} b_{(0,i,i)} = 0{}&{} \;\;&\text{ for } \text{ all } i>0, \\ f_{(i,i,j)}' \,&{:}{=}\, 3b_{(i,i,j)} - a_{(0,0,i)} b_{(0,i,j)} = 0{}&{} \;\;&\text{ for } \text{ all } i,j>0, \ i \ne j, \\ f_{(i,j,k)}' \,&{:}{=}\, 3b_{(i,j,k)} - a_{(0,0,i)} b_{(0,j,k)} - a_{(0,0,j)} b_{(0,i,k)} = 0{}&{} \;\;&\text{ for } \text{ all } k>j>i>0. \end{aligned} \end{aligned}$$

These equations clearly form a regular sequence, so $B_1$ is a complete intersection in the open chart. In the affine chart $D(b_{(0,1,1)})$, we can moreover replace the first set of conditions by $a'=0$, as above.

Proof

From the commutative diagram in the proof of Lemma 2.3, the fiber over $[\lambda ^3] \in B_0$ of the normal bundle can be naturally identified with the vector space $\textrm{Sym}^3(W^*)/\langle \lambda ^2 x_0, \ldots , \lambda ^2 x_n \rangle$. We want to understand how an element in the latter corresponds to an element of the fiber $E_1|_{[\lambda ^3]}$ if explicitly written in the coordinates from the description of $V_1$ in (I). The answer is provided by the conormal sequence

Any point $k \in \textrm{Sym}^3(W^*)/\langle \lambda ^2 x_0, \ldots , \lambda ^2 x_n \rangle$ can be uniquely represented as a cubic not containing the monomials $x_0^3, x_0^2 x_1, \ldots , x_0^2 x_n$. If we write $k = k_{(0,1,1)} x_0 x_1^2 + \ldots + k_{(n,n,n)} x_n^3$, then k corresponds to the element $\sum _J y_J \overline{f_J}$ in via

$$\begin{aligned} b_{(i,j,k)}&= 3 k_{(i,j,k)} - a_{(0,0,k)} k_{(0,i,j)}{} & {} \hspace{3cm} \qquad \text { for all } k>j>i>0, \\ b_{(i,i,j)}&= 3 k_{(i,i,j)} - a_{(0,0,j)} k_{(0,i,i)}{} & {} \hspace{3cm} \qquad \text { for all } i,j>0, i \ne j, \\ b_{(i,i,i)}&= 9 k_{(i,i,i)} - a_{(0,0,i)} k_{(0,i,i)}{} & {} \hspace{3cm} \qquad \text { for all } i>0, \\ b_{(0,i,j)}&= 3 k_{(0,i,j)}{} & {} \hspace{3cm} \qquad \text { for all } j \ge i > 0. \end{aligned}$$

in the fiber over $[\lambda ^3]\in B_0$ we have $a_{(0,0,i)} = 3\lambda _i$ and it is easy to see that the cubic k is divisible by $\lambda = x_0 + \lambda _1 x_1 + \ldots + \lambda _n x_n$ if and only if k satisfies the equations

$$\begin{aligned} 3 k_{(i,j,k)}&= a_{(0,0,i)} k_{(0,j,k)} + a_{(0,0,j)} k_{(0,i,k)} + a_{(0,0,k)} k_{(0,i,j)}{} & {} \;\; \text { for all } k>j>i>0, \\ 3 k_{(i,i,j)}&= a_{(0,0,j)} k_{(0,i,i)} + a_{(0,0,i)} k_{(0,i,j)}{} & {} \;\;\text { for all } i,j>0, i\ne j, \\ 3 k_{(i,i,i)}&= a_{(0,0,i)} k_{(0,i,i)}{} & {} \;\; \text { for all } i>0. \end{aligned}$$

The claim can be deduced directly from this. $\square$

3.3 Second Blow-up

Let $V_2 {:}{=}\textrm{Bl}_{B_1} V_1$. This is smooth because so is $B_1$. We denote $\pi _2:V_2\rightarrow V_1$ the blow-up map, and respectively $\tilde{E}_1,S_2,P_2,L_2$ the proper transforms of $E_1,S_1,P_1,L_1$. Moreover, we define $B_2 {:}{=}\tilde{E}_1 \cap E_2 = {{\mathbb {P}}}(N_{B_1}E_1)$, where $E_2$ denotes the exceptional divisor in $V_2$.

Coordinates II

Let $(a_{(0,0,1)}, \ldots , a_{(0,0,n)}, a', b_J,[c_a,c_H])$ denote coordinates for the product space $(D(a_{(0,0,0)}) \cap D(b_{(0,1,1)})) \times {{\mathbb {P}}}^{r-1}$, where $r = \left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) +1$ is the codimension of $B_1$ as subvariety of $V_1$ and $J\in {\mathcal {J}}$. More precisely, $c_a$ denotes a single variable and $[c_H]$ stands for the projective variables with multi-indices varying in the set ${\mathcal {H}} = \{(i,j,k)\in [n]^3, \,\, \text {with} \,\, 1\le i\le j\le k\}$.

Thanks to Lemma 2.7, the blow-up $V_2$ in the open chart $D(a_{(0,0,0)}) \cap D(b_{(0,1,1)})$ is a closed subvariety given by the equations

$$\begin{aligned} c_a f_H' - a' c_H = 0, \qquad c_{H_1} f_{H_2}' - c_{H_2} f_{H_1}' = 0, \end{aligned}$$

for $H, H_1, H_2\in {\mathcal {H}}$. We can choose the affine open of $V_2$ given by $D(c_{(1,1,1)})$, then these equations simplify to

$$\begin{aligned} c_a f_{(1,1,1)}' - a' =0, \qquad c_H f_{(1,1,1)}' - f_H'=0, \end{aligned}$$

where $H\in {\mathcal {H}}\setminus \{(1,1,1)\}$. Introducing the new variable $b' {:}{=}f_{(1,1,1)}'$, essentially carrying the same information as $b_{(1,1,1)}$, this affine open of $V_2$ has affine coordinates $(a_{(0,0,i)}, b_{(0,j,k)},b',c_a, c_H)$ with $H \ne (1,1,1)$ subject to no relations. In these coordinates, the equation for $E_2$ in $V_2$ becomes $b' = 0$ and the equation for the proper transform $\tilde{E_1}$ becomes $c_a = 0$. We will always exclude the index $H=(1,1,1)$ when considering the affine coordinates.

Lemma 2.8

Write $N_2 {:}{=}N_{{{\mathbb {P}}}(W^*)} {{\mathbb {P}}}(\textrm{Sym}^2(W^*))$ and $N_3 {:}{=}N_{{{\mathbb {P}}}(W^*)} {{\mathbb {P}}}(\textrm{Sym}^3(W^*))$ and let $p_1: B_1 \rightarrow B_0$ be the restriction of the canonical map from the projective bundle $E_1 = {{\mathbb {P}}}(N_{B_0} V_0)$ to its base $B_0 \cong {{\mathbb {P}}}(W^*)$. Therefore, there is a natural isomorphism

$$\begin{aligned} N_{B_1}E_1&\,\,\cong \,\, p_1^*(N_3/N_2) \otimes _{{\mathcal {O}}_{B_1}} {\mathcal {O}}_{B_1}(1) \\ {}&\,\,\cong \,\, p_1^*\left( \frac{\textrm{Sym}^3(W^*) \otimes {\mathcal {O}}_{{{\mathbb {P}}}(W^*)}(3)}{\textrm{Sym}^2(W^*) \otimes {\mathcal {O}}_{{{\mathbb {P}}}(W^*)}(2)} \right) \otimes {\mathcal {O}}_{B_1}(1) \\ {}&\,\,\cong \,\, p_1^*(\textrm{Sym}^3(T{{\mathbb {P}}}(W^*))) \otimes {\mathcal {O}}_{B_1}(1). \end{aligned}$$

Hence, over a point $(\lambda , q) \in B_1$, the normal space $N_{B_1} {E_1}_{|_{(\lambda ,q)}}$ is naturally identified with $\textrm{Sym}^3(W^*)/(\lambda \cdot \textrm{Sym}^2(W^*))$. Points in $B_2$ can be thought of as triples consisting of a hyperplane $\lambda$ together with a quadric q and a cubic c inside $\lambda$.

Proof

The first isomorphism is given by [8, Proposition 9.13]. The Euler sequences for $T{{\mathbb {P}}}(W^*)$, $T{{\mathbb {P}}}(\textrm{Sym}^2(W^*))$, $T{{\mathbb {P}}}(\textrm{Sym}^3(W^*))$ then give the second and third equality. $\square$

Lemma 2.9

The set-theoretical intersection of all proper transforms of the line conditions in $V_2$ is contained in the union of $S_2$ and the smooth variety $B_2 = \tilde{E}_1 \cap E_2$.

Proof

The variety $S_2$ is clearly a component of the intersection. By Lemma 2.6, the line conditions in $V_1$ are generically tangent to $E_1$, and therefore the tangent space of each line condition is contained in the tangent space of $E_1$. Hence, the intersection of the proper transforms of the line conditions with the exceptional divisor $E_2$ is contained in $\tilde{E_1}$. $\square$

A similar reasoning as in Lemma 2.5 shows also the following.

Lemma 2.10

The lift $\phi _2: \textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n \rightarrow V_2$ of $\phi _1$ is explicitly given by

$$\begin{aligned} \begin{aligned} a_{(0,0,1)}&=3\mu _1 + u_1,\\ a_{(0,0,i)}&=3\mu _i + s_i u_1 \quad&\text{ for } i>1,\\ b_{(0,i,i)}&=s_i^2 \quad&\text{ for } i>1,\\ b_{(0,1,i)}&=2s_i \quad&\text{ for } i>1,\\ b_{(0,i,j)}&=2s_i s_j \quad&\text{ for } j>i>1,\\ b'&=-2u_1, \end{aligned}\qquad \qquad \qquad \begin{aligned} c_a&=u_1 /\,2, \\ c_{(1,1,i)}&= s_i \quad&\text{ for } i>1,\\ c_{(1,i,i)}&= s_i^2 \quad&\text{ for } i>1,\\ c_{(i,i,j)}&= s_i^2 s_j\quad&\text{ for } i, j> 1,\\ c_{(i,i,i)}&= s_i^3\quad&\text{ for } i\ne 0,1,\\ c_{(i,j,k)}&= 2 s_i s_j s_k \quad&\text{ for } k>j>i>0. \end{aligned} \end{aligned}$$

Lemma 2.6 implies that the set-theoretic intersection of $S_1$ with $B_1$ is given by $\phi _1(e)$. It is not hard to see then that $S_2$ is isomorphic to $S_1$, hence to $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$. Abusing notation, we will indicate with e the exceptional divisor of $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$ as well as all its isomorphic images under the maps $\phi _i$.

Lemma 2.11

The following hold:

• (i) $B_2$ intersects $S_2$ along e.

• (ii) The line conditions in $V_2$ are generically smooth along $B_2$.

Proof

First, recall that $S_1$ is tangent to $E_1$ along e. In fact, for any point $p\in e$ we have $T_{\phi _1(p)} S_1 = d\phi _1\left( T_p \left( \textrm{Bl}_{\Delta } {{\mathbb {P}}}^n \times {{\mathbb {P}}}^n\right) \right)$. Working in the chosen affine chart for $V_1$, since the entry relative to $a'$ in the column vectors of the Jacobian is always zero, then $T_{\phi _1(p)} S_1$ is contained in the tangent space of $E_1$. By invariance under projective transformations this is true everywhere. Thus, since $B_1$ intersects $S_1$ along $\phi _1(e)$ we have that $S_2 \cap E_2 \subseteq \tilde{E_1} \cap E_2 = B_2$ because the tangent space of $S_1$ is contained in the tangent space of $E_1$.

For the second claim, observe that the line conditions in $V_1$ are generically smooth along $B_1$. The claim then follows from the blow-up closure lemma and the fact that the blow-up of a smooth variety is again smooth. $\square$

Remark 2.12

A cubic $k \in B_2|_{[\lambda , q]} \cong {{\mathbb {P}}}(\textrm{Sym}^3(W^*)/(\lambda \cdot \textrm{Sym}^2(W^*)))$, whose defining equation can be uniquely written (up to scaling) in the form $k = k_{(1,1,1)} x_1^3 + k_{(1,1,2)} x_1^2 x_2 + \ldots + k_{(n,n,n)} x_n^3$, not containing any monomial divisible by $x_0$, is identified with the projective coordinates $[c_a,c_H]$ in Remark II via $c_a = 0$ and $k_H = 3 c_H$ for all $H \in {\mathcal {H}}$ with at least two entries in $H=(i,j,k)$ being distinct, and $k_{(i,i,i)} = c_{(i,i,i)}$ for all $i \ge 1$. In particular, $S_2 \cap B_2$ consists of all triples $(\lambda , q, k) = (\lambda , g^2, g^3)$ for some hyperplane $g \in {{\mathbb {P}}}(W^*/\lambda )$ as follows from the explicit description of $\phi _2$ in Lemma 2.10.

Proposition 2.13

Let ${\overline{\lambda }}{:}{=}([\lambda ],[q],[k])$ be a point of $B_2$, i.e. a hyperplane $\lambda$ together with a quadric q and a cubic k. Consider the line condition $L_2^{\ell }$ in $V_2$ corresponding to a line $\ell \subseteq {{\mathbb {P}}}(W)$. Then:

• (i) $\ell$ intersects $\lambda$ at the quadric q if and only if $L_2^{\ell }$ is tangent to $E_2$ at ${\overline{\lambda }}$

• (ii) $\ell$ intersects $\lambda$ at the cubic k if and only if $L_2^{\ell }$ is tangent to $\tilde{E_1}$ at ${\overline{\lambda }}$

Proof

We can assume the hyperplane $\lambda$ to be ${\mathcal {V}}(x_0)$ and $\ell$ the line ${\mathcal {V}}(x_1,x_3,\dots , x_n)$. By plugging in the equations $c_{(1,2,2)} b'-3 b_{(2,2,2)}+2 a_{(0,0,2)} b_{(0,2,2)}=0$ and $a'-c_a b'=0$ in the equation of the proper transform of the line condition in $V_1$, we get the equation for $L^{\ell }$ in local coordinates in $V_3$, i.e.

$$\begin{aligned} 4b_{(0,2,2)}^3 c_a + c_{(2,2,2)}^2 b'. \end{aligned}$$

From Lemma 2.7, one has that the quadrics intersecting $\lambda$ at its point of intersection with $\ell$ are given by the equation: $b_{(0,2,2)} = 0$. From Remark 2.12 the cubics intersecting $\lambda$ in $\lambda \cap \ell$ are given by the equation $c_{(2,2,2)} = 0$. The statement on the tangency at $E_2$ and at $\tilde{E}_1$ follows from the direct computation with the equations. $\square$

Remark 2.14

We can notice that if the line $\ell$ does not intersect the quadric q or the cubic k at the point ${\overline{\lambda }}$, then the line condition $L^{\ell }$ is smooth at ${\overline{\lambda }}$. This is clear from the proof of the previous lemma when $\lambda = x_0$ and $\ell ={\mathcal {V}}(x_1,x_3,\dots , x_n)$. The claim follows by invariance under projective transformations.

3.4 Third Blow-up

Let $V_3 {:}{=}\textrm{Bl}_{B_2} V_2$. This is smooth because $B_2$ is. We stick to the notation $\pi _3:V_3\rightarrow V_2$ for the blow-up map and $E_3$ for the exceptional divisor. We denote $L_3$ the proper transform in $V_3$ of the a line condition $L_2\subseteq V_2$, and $S_3$ is the proper transform of $S_2$.

Coordinates III

In the chosen chart for $V_2$ described in Remark II the base locus $B_2$ is given by ${\mathcal {V}}(c_{a},b')$. Consider $(D(a_{(0,0,0)})\cap D(b_{(0,1,1)})\cap D(c_{(1,1,1)}))\times {{\mathbb {P}}}^1$ with coordinates $(a_{(0,0,i)},b_{(0,j,k)},b',c_{a},c_H,[d_{c},d_{b}])$. The blow-up of $B_2$ in the chosen chart of $V_2$ can be described as the subvariety determined by

$$\begin{aligned} b' d_c = d_b c_a. \end{aligned}$$

In the affine chart $D(a_{(0,0,0)})\cap D(b_{(0,1,1)})\cap D(c_{(1,1,1)})\cap D(d_c)$ of $V_3$ we can work with coordinates $(a_{(0,0,i)},b_{(0,j,k)},c_{a},c_H,d_{b})$. The exceptional divisor $E_3$ is cut out by $c_{a}=0$ in this chart.

Remark 2.15

The line condition $L_3^{\ell }$ corresponding to $\ell {:}{=}{\mathcal {V}}(x_1,x_3,\dots , x_n)$ has equation

$$\begin{aligned} 4b_{(0,2,2)}^3 + c_{(2,2,2)}^2 d_b=0. \end{aligned}$$

Therefore, every other line condition obtained from this one by an induced action of the ${{\,\textrm{PGL}\,}}_n$-action preserving this chart will be of type

$$\begin{aligned} 4f(b_{J})^3 + g(c_{H})^2 d_b=0, \end{aligned}$$

where f is a linear function in the $(b_{J})$ coordinates and g is a linear function in the $(c_{H})$ coordinates.

We now prove that the intersection of all line conditions coincides with $S_3$.

Proposition 2.16

The intersection of all line conditions in $V_3$ is supported on the smooth irreducible variety $S_3$.

Proof

The base locus $B_2={{\mathbb {P}}}(N_{B_1}E_1)$ has codimension 2 in $V_2$. The exceptional divisor $E_3={{\mathbb {P}}}(N_{B_2}V_2)$ is then a ${{\mathbb {P}}}^1$-bundle over $B_2$. Let ${\overline{\lambda }}{:}{=}([\lambda ],[q],[k])$ be a fixed point in $B_2$ with $\pi _2\circ \pi _1({\overline{\lambda }})=[\lambda ^3] \in B_0$, i.e., a hyperplane $\lambda$ together with a quadric q and a cubic k lying on $\lambda$. Thanks to Remark 2.14, a general line condition is smooth at ${\overline{\lambda }} \in B_2$, has codimension one, and contains $B_2$. Its proper transform intersects the fiber of ${{\mathbb {P}}}(N_{B_2}V_2)$ over ${\overline{\lambda }}$ at most in one point. We need to check that line conditions in $V_3$ can only intersect in $E_3$ above $B_2\cap S_2$.

The base locus $B_2=E_2\cap \tilde{E_1}$ is smooth of codimension 2 in $V_2$. Therefore, the proper transforms of $\tilde{E_1}$ and $E_2$ in $V_3$ cut the fiber of $E_3$ over any ${\overline{\lambda }}\in B_2$ in different points $r_1$ and $r_2$. From Proposition 2.13 it follows that if a line $\ell$ intersects q, then the line condition $L^{\ell }_3$ contains $r_2$, while if $\ell$ intersects k, then the line condition $L^{\ell }_3$ contains the point $r_1$.

We claim that in order for the line conditions to intersect over ${\overline{\lambda }}$ we must have $q=hg$ and $k=h^2\,g$ where h, g are linear forms on the hyperplane $\lambda$. In fact, suppose there is a point of q which is not in k. Then, we can take a line $\ell$ in ${{\mathbb {P}}}^n$ passing through that point and not contained in $\lambda$. Thanks to Remark 2.14, the line condition $L^{\ell }_2$ is smooth at ${\overline{\lambda }}$ and $L^{\ell }_3$ intersects the fiber over ${\overline{\lambda }}$ in a unique point, necessarily in $r_2$. Take now another line condition $L^{\ell '}_2$ in $V_2$ such that the line $\ell '$ does not intersect the cubic nor the quadric. The line condition $L^{\ell '}_2$ is a hypersurface which is smooth at ${\overline{\lambda }}$ and contains $B_2$. If its proper transform intersects the fiber over ${\overline{\lambda }}$ in $r_2$, then $L^{\ell '}_2$ is tangent to $E_2$, and by Proposition 2.13 it must intersect the quadric.

Similarly, we can show that there is no point of q which is not in k. Hence, we proved that in order for the line conditions to intersect over ${\overline{\lambda }}$ we must have $q=k$ set-theoretically. But this is equivalent to $q=hg$ and $k=h^2\,g$ with h, g linear forms on the hyperplane $\lambda$.

By Remark 2.12, we just have to show that $g=h$. It is enough to show it for $\lambda =x_0$ because the locus $B_2\cap S_2$ is invariant under the induced ${{\,\textrm{PGL}\,}}_n$-action on $V_2$. Consider the point $\overline{x_0}=([x_0^3],[q],[k])$, where

$$\begin{aligned} q=\left( h_1x_1+\dots +h_nx_n\right) \left( g_1x_1+\dots + g_n x_n\right) , \quad k=\left( h_1x_1+\dots +h_nx_n\right) ^2\left( g_1x_1+\dots + g_nx_n\right) \end{aligned}$$

are respectively a quadric and a cubic on the hyperplane $x_0=0$.

We claim there exists an index l such that $\overline{x_0}$ belongs to $D(b_{(0,l,l)})$. First, fix i and j such that $\overline{x_0}$ belongs to the affine chart $D(b_{(0,i,j)})\cap D(c_{(i,i,j)})$. Then, we can work in this affine chart with its coordinates. For , consider the line conditions $L^{x_i+tx_j}_2$ in $V_2$ corresponding to the line given by the vanishing of $x_i+tx_j=0$ and of all coordinates except for $x_0,x_i,x_j$. Their equations in $V_2$ are

$$\begin{aligned} 4(t^2b_{(0,i,i)}+b_{(0,j,j)}-t)^3c_{a}+(t^3c_{(i,i,i)}-3t^2-c_{(j,j,j)}+3tc_{(i,j,j)})^2b'=0 \end{aligned}$$

in the mentioned open chart, where $b'=f_{(i,i,j)}'$ and $a'=f_{(0,i,j)}$. Notice that thanks to Lemmas 2.7 and 2.12, we have a relation between the coordinates and the coefficients of q and k. Suppose $b_{(0,l,l)}(\overline{x_0})=h_lg_l=0$ for all indices. The line conditions $L^{x_i+tx_j}_3$ intersect the fiber over $\overline{x_0}$ in $V_3$ in the points

$$\begin{aligned} \left[ -4t^3,\left( 3t^2-3tc_{(i,j,j)}(\overline{x_0})\right) ^2\right] . \end{aligned}$$

Recall that we are working in a chart such that $h_i^2g_j=c_{(i,i,j)}(\overline{x_0})\ne 0$, therefore $c_{(i,j,j)}(\overline{x_0})=h_j^2g_i=0$ and the points become

$$\begin{aligned} \left[ -4t^3,9t^4\right] =[-4,9t]. \end{aligned}$$

This is absurd because we are assuming these line conditions to intersect over $\overline{x_0}$ and we proved the claim. Without loss of generality, we put $l=1$, and we work in the affine chart $D(a_{(0,0,0)})\cap D(b_{(0,1,1)})\cap D(c_{(1,1,1)})$ of $V_2$, so we can assume $h_1=g_1=1$.

We claim that $h_i$ is zero if and only if $g_i$ is zero for every index i. Suppose there exists an index i such that $h_i=0$ and $g_i\ne 0$ and consider the line conditions $L^{x_i+tx_1}_2$ in $V_2$ with equations

$$\begin{aligned} 4\left( t^2b_{(0,i,i)}+1-tb_{(0,1,i)}\right) ^3 c_{a}+\left( t^3c_{(i,i,i)}-3t^2c_{(i,i,1)}-1+3tc_{(1,1,i)}\right) ^2 b'=0 \end{aligned}$$

in the chosen affine chart. The line conditions $L^{x_i+tx_1}_3$ intersect the fiber over $\overline{x_0}$ in $E_3$ in the points

$$\begin{aligned} \left[ 4\left( 1-t b_{(0,1,i)}(\overline{x_0})\right) ^3,\left( 1-3t c_{(1,1,i)}(\overline{x_0})\right) ^2\right]&=\left[ 4(1-t h_i-tg_i)^3,(1-tg_i)^2\right] \\&=\left[ 4(1-t g_i)^3,(1-t g_i)^2\right] . \end{aligned}$$

Notice that for $g_i\ne 0$, these would give different points for different values of t which is absurd. The same reasoning holds for $g_i=0$ and $h_i\ne 0$ proving then the claim. Finally, if we consider the line condition $L^{x_j}_2$ in $V_2$ corresponding to the line given by the vanishing of all coordinates except for $x_0$ and $x_j$ then this has equation

$$\begin{aligned}4b_{(0,j,j)}^3c_a+c_{(j,j,j)}^2b'=0\end{aligned}$$

in the chosen open chart. If we assume $(b_{(0,j,j)}(\overline{x_0}),c_{(j,j,j)}(\overline{x_0}))\ne (0,0)$, we must have

$$\begin{aligned} \begin{aligned}{}[4,1]=\left[ 4(b_{(0,j,j)}(\overline{x_0}))^3,(c_{(j,j,j)}(\overline{x_0}))^2\right] \Leftrightarrow&(b_{(0,j,j)}(\overline{x_0}))^3=(c_{(j,j,j)}(\overline{x_0}))^2 \\ \Leftrightarrow&g_j^3h_j^3=g_j^4h_j^2, \end{aligned} \end{aligned}$$

and therefore $g_j=h_j$ when $h_j$ is non-zero. $\square$

Since $S_3$ will be the next center for the blow-up, we denote it with $B_3$. From Lemma 2.11 follows that $B_3$ is isomorphic to $S_2$. In particular, the isomorphism map $\phi _2:\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n\rightarrow S_2$ defined in Lemma 2.10 lifts to the following map.

Lemma 2.17

The lift $\phi _3: \textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n \rightarrow V_3$ of $\phi _2$ on the chosen open charts is explicitly given by

$$\begin{aligned} \begin{aligned} a_{(0,0,1)}&=3\mu _1 + u_1,\\ a_{(0,0,i)}&=3\mu _i + s_i u_1 \quad&\text{ for } i>1,\\ b_{(0,i,i)}&=s_i^2 \quad&\text{ for } i>1,\\ b_{(0,1,i)}&=2s_i \quad&\text{ for } i>1,\\ b_{(0,i,j)}&=2s_i s_j \quad&\text{ for } j>i>1,\\ c_a&={u_1}/ \, {2}, \end{aligned}\qquad \qquad \qquad \begin{aligned} c_{(1,1,i)}&= s_i \quad&\text{ for } i>1,\\ c_{(1,i,i)}&= s_i^2 \quad&\text{ for } i>1,\\ c_{(i,i,j)}&= s_i^2 s_j \quad&\text{ for } i, j> 1,\\ c_{(i,j,k)}&= 2 s_i s_j s_k \quad&\text{ for } k>j>i>0, \\ d_b&=-4. \end{aligned} \end{aligned}$$

Remark 2.18

The equations

$$\begin{aligned} \begin{aligned}&d_b+4 \,=\, 0, \\ g_{(0,1,i)}&\,{:}{=}\,b_{(0,1,i)}-2c_{(1,1,i)} = 0 \quad \qquad {}&{} \text{ for } i>1,\\ g_{(0,i,i)}&\,{:}{=}\,b_{(0,i,i)}-c_{(1,1,i)}^2 = 0 \quad \qquad {}&{} \text{ for } i>1,\\ g_{(0,i,j)}&\,{:}{=}\,b_{(0,i,j)}-2c_{(1,1,i)}c_{(1,1,j)} = 0 \quad \qquad {}&{} \text{ for } j>i>1,\\ g_{(1,i,i)}&\,{:}{=}\,c_{(1,i,i)}-c_{(1,1,i)}^2 = 0 \quad \qquad {}&{} \text{ for } i> 1,\\ g_{(i,i,j)}&\,{:}{=}\,c_{(i,i,j)}-c_{(1,1,i)}^2c_{(1,1,j)} = 0 \quad \qquad {}&{} \text{ for } i,j>1,\\ g_{(i,j,k)}&\,{:}{=}\,c_{(i,j,k)}- 2 c_{(1,1,i)}c_{(1,1,j)}c_{(1,1,k)} = 0\quad \qquad {}&{} \text{ for } k>j>i>0. \end{aligned} \end{aligned}$$

cut out $B_3$ in the chosen affine open chart. Notice that the equations form a regular sequence and that $B_3$ is indeed a complete intersection of codimension $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -1-2n$ in the chosen affine chart.

3.5 Fourth Blow-up

Recall that $B_3=S_3$. Let $V_4{:}{=}\textrm{Bl}_{B_3}V_3$. We will write $E_4$ for the exceptional divisor and $\pi _4: V_4 \rightarrow V_3$ for the blow-up map.

Coordinates IV

In the chosen affine chart of $V_3$ the base locus $B_3$ is cut out by the equations in Remark 2.18. Consider $D(a_{(0,0,0)})\cap D(b_{(0,1,1)})\cap D(c_{(1,1,1)})\cap D(d_c)\times {{\mathbb {P}}}^{\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -2n-2}$ with coordinates $(a_{(0,0,i)},b_{(0,j,k)},c_{a},c_H,d_{b},[e_d,e_F])$, where $e_d$ is a new coordinate and the multi-indices F vary in the set ${\mathcal {F}} = \{(i,j,k)\in [n^3], \,\, \text {with} \,\, 0\le i \le j\le k, \,\,1< j\}$. The blow-up of $V_3$ along $B_3$ in the chosen affine chart can be described as the subvariety determined by

$$\begin{aligned}&e_d g_{(i,j,k)} - (d_b+4) e_{(i,j,k)} = 0 \;\;\quad{} & {} \hbox { for } (i,j,k)\in F,\\&e_{(i_1,j_1,k_1)} g_{(i_2,j_2,k_2)} - g_{(i_1,j_1,k_1)} e_{(i_2,j_2,k_2)} = 0 \;\;\quad{} & {} \hbox { for } (i_1,j_1,k_1),(i_2,j_2,k_2)\in F. \end{aligned}$$

In the affine chart $D(a_{(0,0,0)})\cap D(y_{(0,1,1)})\cap D(c_{(1,1,1)})\cap D(d_c)\cap D(e_{(0,1,2)})$ of $V_4$ we can work with coordinates $(a_{(0,0,i)},c_{a},c_{(1,1,2)},..,c_{(1,1,n)},e_d,e_F,e')$ where $e'=g_{(0,1,2)}$ is used as a coordinate and F is the same index set as above but we exclude (0, 1, 2). The exceptional divisor $E_4$ is cut out by $e'=0$ in this chart.

Proposition 2.19

The intersection of all line conditions in $V_4$ is supported on a smooth subvariety $B_4$ of codimension $\left( {\begin{array}{c}n+2\\ 3\end{array}}\right)$ inside $E_4$. More precisely, $B_4={{\mathbb {P}}}({\mathcal {E}})$ where ${\mathcal {E}}$ is a vector subbundle of rank $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ of the normal bundle $N_{B_3} V_3$.

Proof

We generalize the proof of [1, Proposition 4.1]. Let $R_{\mu } \subseteq V_0$ denote the subvariety of cubics containing the hyperplane $\mu$. Clearly, $R_\mu \cong {{\mathbb {P}}}(\textrm{Sym}^2(W^*))$ is smooth. By Lemma 2.1, a line condition $L^{\ell }$ is smooth at $[\lambda \mu ^2] \in S_0 \setminus B_0$ if the line $\ell$ intersects $\mu$ in a single point outside $\lambda$. Clearly, $T_{[\lambda \mu ^2]} R_\mu \subseteq T_{[\lambda \mu ^2]} L^{\ell }$ for every line $\ell$, and Lemma 2.1 shows that

$$\begin{aligned} \bigcap _{\ell \subseteq {{\mathbb {P}}}(W) \text { line}} T_{[\lambda \mu ^2]} L^{\ell } = T_{[\lambda \mu ^2]} R_\mu . \end{aligned}$$

Clearly, finitely many lines suffice for the intersection of the tangent spaces to agree with $T_{[\lambda \mu ^2]} R_\mu$ over every point $[\lambda \mu ^2] \in B_3 \setminus e \cong S_0 \setminus B_0$. By Proposition 2.16, the intersection of the proper transforms $L_{3}^{\ell }$ in $V_3$ for all lines $\ell$ agrees set-theoretically with $S_3 = B_3$. The proper transforms $L^{\ell }_{4}$ in $V_4$ therefore only intersect in the exceptional divisor $E_4$. We claim that their intersection is precisely the projectivization of a vector subbundle ${\mathcal {E}} \subseteq N_{B_3} V_3$. We construct ${\mathcal {E}}$ as the intersection of the images of the tangent sheaves ${\mathcal {T}} L^{\ell }_{3}|_{B_3}$ in $N_{B_3} V_3$ corresponding to finitely many lines $\ell$. The finiteness will ensure that the resulting subsheaf ${\mathcal {E}}$ of $N_{B_3} V_3$ is coherent. First, we pick finitely many lines such that the intersection of the tangent spaces over every point $[\lambda \mu ^2] \in B_3 \setminus e$ agrees with $T_{[\lambda \mu ^2]} R_\mu$. The intersection of the images of the tangent sheaves in $N_{B_3} V_3$ of these line conditions defines a coherent subsheaf ${\mathcal {E}}'$ which restricts to a vector subbundle over $B_3 \setminus e$. Then by Lemma 2.1 and a Zariski closure argument, every other line condition $L^{\ell }_{4}$ contains the projectivization ${{\mathbb {P}}}({\mathcal {E}}'|_{B_3 \setminus e})$, and we have

$$\begin{aligned}{\mathcal {E}}'([\lambda \mu ^2]) \cong T_{[\lambda \mu ^2]} R_{\mu } / T_{[\lambda \mu ^2]} S_0,\end{aligned}$$

where ${\mathcal {E}}'(p)$ denotes the geometric fiber of ${\mathcal {E}}'$ over the point p. The rank of ${\mathcal {E}}'$ over $B_3 \setminus e$ is $r = \left( {\begin{array}{c}n+2\\ 2\end{array}}\right) - 2n - 1 = \left( {\begin{array}{c}n\\ 2\end{array}}\right)$. Next, we fix a point $p \in e = B_3 \cap E_3$ lying in our affine open chart. By Remark 2.15, in the chosen affine chart the equation for $L^{{\ell }}_{3}$ with ${\ell }$ any line passing through the point $[1:0:\cdots :0]$ does not depend on the variable $c_{a}$, and the equation determining $E_3$ in $V_3$ is exactly $c_a = 0$. The transversality of such line conditions can therefore be checked outside of $E_3$ and hence in $S_0 {\setminus } B_0$. This shows at once that there are $\textrm{codim}(R_\mu , V_0) = \left( {\begin{array}{c}n+2\\ 3\end{array}}\right)$ lines ${\ell }_i \subseteq {{\mathbb {P}}}(W)$ such that the line conditions $L^{{\ell }_i}_{3}$ are all smooth and intersect transversally at p. Moreover, employing the ${{\,\textrm{PGL}\,}}_n$-action and using that it acts transitively on e by Lemma 2.24, we obtain finitely many more lines such that the intersection of their tangent spaces at every point of e has dimension at most r. Let ${\mathcal {E}}$ be the intersection of ${\mathcal {E}}'$ with the images of the tangent sheaves in $N_{B_3} V_3$ of these new line conditions. Then ${\mathcal {E}}$ is a coherent subsheaf of $N_{B_3} V_3$ which still restricts over $B_3 \setminus e$ to a vector subbundle of rank r and has rank $\le r$ over every point of e. By upper semi-continuity of the rank, since ${\mathcal {E}}$ is coherent, ${\mathcal {E}}$ is a vector subbundle of $N_{B_3} V_3$ of rank r everywhere. As ${{\mathbb {P}}}({\mathcal {E}})$ is an irreducible closed subset of $V_4$, a Zariski closure argument then shows that it is contained in $L^{\ell }_4$ for every $\ell$, so it is contained in the intersection of all line conditions in $V_4$. Nevertheless, by construction ${{\mathbb {P}}}({\mathcal {E}})$ also contains the intersection of some (and hence of all) line conditions in $V_4$, proving equality. $\square$

3.6 Fifth Blow-up

Let $V_5 {:}{=}\textrm{Bl}_{B_4}V_4$. Denote with $E_5$ the exceptional divisor and let $\pi _5: V_5 \rightarrow V_4$ be the blow-up map. Let $\tilde{E_4}$ be the strict transform of $E_4$.

Lemma 2.20

We have the isomorphism

$$\begin{aligned} N_{B_4} E_4 \cong (\pi _4|_{B_4})^*(N_{B_3} V_3/{\mathcal {E}}) \otimes {\mathcal {O}}_{B_4}(1). \end{aligned}$$

Moreover, over $U{:}{=}B_4 \setminus (\pi _4|_{B_4})^{-1}(e)$ the normal bundle $N_{B_4} E_4$ restricts to

$$\begin{aligned} N_{U} E_4 \cong (\pi _4|_{U})^*\left( \frac{\textrm{Sym}^3(W^*) \otimes {\mathcal {O}}(1,2)}{\textrm{Sym}^2(W^*) \otimes {\mathcal {O}}(1,1)} \right) \otimes {\mathcal {O}}_{U}(1), \end{aligned}$$

where ${\mathcal {O}}(a,b)$ denotes the pullback to ${{\mathbb {P}}}^n \times {{\mathbb {P}}}^n {\setminus } \Delta$. In particular, the fiber of $N_{B_4} E_4$ over some point of $B_4 \setminus \pi _4^{-1}(e)$ mapping to $[\lambda \mu ^2] \in B_3 {\setminus } e$ is given by $\textrm{Sym}^3(W^*)/(\mu \cdot \textrm{Sym}^2(W^*))$.

The proof is similar to that of Lemma 2.8. We can now start to understand the intersection of all line conditions inside $V_4$.

Lemma 2.21

Fix a line $\ell$ of ${{\mathbb {P}}}^n$ and a cubic $\lambda \mu ^2$ such that $\ell$ does not intersect $\lambda \cap \mu$. The strict transform $L_5^{\ell }$ in $V_5$ contains a point p in $E_5\cap {\tilde{E}}_4$ with $(\pi _4 \circ \pi _5)(p)= [\lambda \mu ^2]$ if and only if the line $\ell$ intersects the cubic on $\mu$ associated with p, i.e. the element of $\textrm{Sym}^3(W^*)/(\mu \cdot \textrm{Sym}^2(W^*))$.

Proof

By assumption, $L_3^{\ell }$ and its proper transforms are smooth at every point over $[\lambda \mu ^2] \in B_3$. We have $(L_5^{\ell } \cap {\tilde{E}}_4 \cap E_5)|_{\pi _5(p)} = {{\mathbb {P}}}(N_{B_4} (L_4 \cap E_4)|_{\pi _5(p)})$. Since $L_4 \cap E_4|_{U} = {{\mathbb {P}}}(N_{B_3} L_3|_{U})$ on the smooth locus U of $L_3^{\ell }$ inside $B_3$, we have the canonical isomorphisms

$$\begin{aligned} N_{B_4}(L_4^{\ell }\cap E_4)|_{\pi _5(p)} \cong ((\pi _4|_{B_4})^*(N_{B_3} L_3^{\ell }/{\mathcal {E}}) \otimes {\mathcal {O}}_{B_4}(1))|_{\pi _5(p)} \cong (N_{B_3} L_3^{\ell }/{\mathcal {E}})|_{[\lambda \mu ^2]}. \end{aligned}$$

Knowing that $T_{[\lambda \mu ^2]}L_3^{\ell }$ is given by those cubics containing $\ell \cap \mu$ by Lemma 2.1(iii) and that the fiber of ${\mathcal {E}}$ at $[\lambda \mu ^2]$ is the quotient of the cubics containing $\mu$ by the tangent space of $B_3$ at $[\lambda \mu ^2]$, we conclude that the projective fiber of this bundle over the point $\pi _5(p)$ of $B_4$ is exactly given by those cubics on $\mu$ touching $\ell$. $\square$

Lemma 2.22

There exists a point $[\lambda \mu ^2]$ with $\lambda \ne \mu$ in $B_3$ such that for every point $\overline{\lambda \mu ^2}$ in $B_4$ with $\pi _3(\overline{\lambda \mu ^2}) = [\lambda \mu ^2]$ the intersection of the line conditions in the fiber $(E_5)|_{\overline{\lambda \mu ^2}}$ is contained in the proper transform ${\tilde{E}}_4$ of $E_4$ in $V_5$.

Proof

Consider the chart in $V_3$ given by $D(a_{(0,0,0)}) \cap D(b_{(0,1,1)}) \cap D(c_{(1,1,1)})\cap D(d_a)$. We can now choose any point in $B_3\setminus e$; we will choose our favourite one $P{:}{=}[(x_2+x_0)^2(x_2+x_1+x_0)]$. Notice that this is indeed contained in the chart. We will denote with (P, Q) a point in the fiber of $B_4$ over P, where $Q\in {{\mathbb {P}}}(R_{(x_2+x_0)}/(TB_3)_{P})$ and where $R_{(x_2+x_0)}$ is the space of cubics which are divisible by $(x_2+x_0)$. Points $P_{\epsilon ,q}$ in $R_{(x_2+x_0)}$ can be uniquely written up to constants as $P_{\epsilon ,q}{:}{=}(x_2+x_0)q$ in the projective coordinates $[q_{ij}]_{i,j\in [n]}$ of the quadric q in $(n+1)$ variables. In this coordinates, the tangent space $(TB_3)_{P}$ is given by

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} q_{00}+q_{22}=q_{02}\\ q_{0j}-q_{2j}=0\quad &{} \text{ for } \text{ all } j\ne {0,1,2},\\ q_{ij}=0 \qquad \quad \;\,&{} \text{ for } \text{ all } i,j\ne {0,1,2}. \end{array}\right. } \end{aligned} \end{aligned}$$

Denoting $\pi _P:R_{(x_2+x_0)}\setminus {(TB_3)_P}\rightarrow (B_4)_P$ the quotient map followed by the projectivization, every point (P, Q) can be represented in a non-unique way as $\pi _P([q_{ij}]_{i,j\in [n]})$. We now want to show that for every point $(P,Q)=\pi _P([q_{ij}]_{i,j\in [n]})$ there exists a sequence of line conditions $L_4^m$ in $V_4$ which are smooth at (P, Q) and such that the hyperplanes $(TL_4^{m})_{(P,Q)}$ tend to $(TE_4)_{(P,Q)}$ as vector subspaces of $(TV_{4})_{(P,Q)}$. This proves the lemma, as the intersection of all line conditions in $(E_5)_{(P,Q)}$ will be the same as the intersection of all line conditions and $({\tilde{E}}_4)_{(P,Q)}$.

Before choosing appropriate line conditions, let us compute the projective coordinates $[e_{d},e_{(0,1,2)},\dots ,e_{(0,n,n)}, e_{(1,1,2)}, \dots ,e_{(n,n,n)}]$ for $(P,Q)=\pi _P([q_{ij}]_{i,j\in [n]})$ as functions of $[q_{ij}]$. We get the following coordinates for the point (P, Q):

$$\begin{aligned} \begin{aligned} {e_d}&= 0, \\ {e}_{(0,1,j)}&=0 \,\,&\text{ for } j\ne 0,1,\\ {e}_{(0,2,2)}&=3(q_{02}-q_{00}-q_{22}), \\ {e}_{(0,j,j)}&=-3q_{jj} \,\,&\text{ for } j\ne 0,1,2, \\ {e}_{(0,2,j)}&=3(q_{0j}-q_{2j})\,\,&\text{ for } j\ne 0,1,2,\\ {e}_{(0,i,j)}&=-3q_{ij}\,\,&\text{ for } i,j\ne 0,1,2,\\ {e}_{(1,2,2)}&=\frac{3}{2}(q_{02}-q_{00}-q_{22}), \\ \end{aligned} \qquad \begin{aligned} {e}_{(1,j,j)}&=-\frac{3}{2}q_{jj} \,\,&\text{ for } j\ne 0,1,2, \\ {e}_{(1,2,j)}&=\frac{3}{2}(q_{0j}-q_{2j}) \,\,&\text{ for } j\ne 0,1,2,\\ {e}_{(1,i,j)}&=-\frac{3}{2}q_{ij} \,\,&\text{ for } i,j\ne 0,1,2,\\ {e}_{(i,i,j)}&=0 \,\,&\text{ for } i,j\ne 0,1,\\ {e}_{(j,j,j)}&=0 \,\,&\text{ for } j\ne 0,1.\\ \end{aligned} \end{aligned}$$

Notice that this makes sense as long as $[q_{ij}]_{i,j\in [n]}\notin (TB_3)_P$, which is the case we are interested in.

We will use the notation $L^{j,t}$ for line conditions associated to the lines

$$\begin{aligned} {\mathcal {V}}\left( x_1+tx_j,x_2,\dots ,{\hat{x}}_j,\dots , x_n\right) . \end{aligned}$$

The proper transform $L^{j,t}_3$ of these line conditions in the chosen affine chart for $V_3$ are given by

$$\begin{aligned} 4\left( t^2+b_{(0,j,j)}-tb_{(0,1,j)}\right) ^3+\left( t^3-3t^2c_{(1,1,j)}-c_{(j,j,j)}+3tc_{(1,j,j)}\right) ^2d_b=0. \end{aligned}$$

Notice that the line condition $L^{j,0}_3$ is singular at P for any $j\ne 0,1$, but the line conditions $L^{j,t}_3$ for $t\ne 0$ are not, and therefore the proper transforms $L^{j,t}_4$ in $V_4$ are smooth at every point $(P,Q)\in B_4$. Now consider the proper transform of such line condition in a chart of $V_4$ different from $D(e_d)$ with coordinate $e'$. Notice that we can do that because $e_d(P,Q)=0$ for every choice of Q. Since we are interested in the gradient of the equation evaluated on points in $B_4\subseteq E_4=\{e'=0\}$), we can just look at the gradient of the following equation:

$$\begin{aligned} \bigg (12(t-c_{(1,1,j)})^4\big (e_{(0,j,j)}-t e_{(0,1,j)}\big )+e_d(t-&c_{(1,1,j)})^6- 8(t-c_{(1,1,j)})^3\big (3te_{(1,j,j)}-e_{(j,j,j)})\big )+\\ e'\bigg (12(t-c_{(1,1,j)})^2(e_{(0,j,j)}-te_{(0,1,j)}&)^2+2e_d(t-c_{(1,1,j)})^3\big (3te_{(1,j,j)}-e_{(j,j,j)}\big )-\\ 4\big (3te_{(1,j,j)}&-e_{(j,j,j)}\big )^2\bigg )=0. \end{aligned}$$

If we look at partial derivatives $\partial _{y}$ with respect to variables $y\ne e'$ evaluated at the point (P, Q), we have that $\frac{\partial _{y}}{t^a}=0$ for $a\in \{0,1,2\}$, and this follows from $c_{(1,1,j)}(P)=0$. If we look at partial derivatives $\partial _{e'}$ evaluated at the point $(P,Q)=\pi _P([q_{ij}]_{i,j\in [n]})$, this is given by

$$\begin{aligned} 12t^2\left( e_{(0,j,j)}\right) ^2-4\left( 3te_{(1,j,j)}\right) ^2. \end{aligned}$$

We see that the partial derivative $\frac{\partial _{e}}{t^2}$ is given by

$$\begin{aligned} 12\left( e^2_{(0,j,j)}-3e^2_{(1,j,j)}\right) .\end{aligned}$$

For $j=2$ then this becomes

$$\begin{aligned}27\left( 4\left( q_{02}-q_{00}-q_{22}\right) ^2-3\left( q_{02}-q_{00}-q_{22}\right) ^2\right) =27\left( q_{02}-q_{00}-q_{22}\right) ^2,\end{aligned}$$

and the claim follows from this quantity being non-zero at the point (P, Q).

Suppose instead $q_{02}-q_{00}-q_{22}=0$, then we can look at different line conditions assuming ${e}_{(0,2,2)}(P,Q)={e}_{(1,2,2)}(P,Q)=0$. Take $L_4^{j,t}$ where $j\ne 2$. If we repeat the same reasoning everything remains the same but in the end we get that $\frac{\partial _{e'}}{t^2}$ is given by

$$\begin{aligned}27\left( 4q_{jj}^2-3q_{jj}^2\right) =27q_{jj}^2.\end{aligned}$$

Once again, we obtain the claim if this quantity is different from zero for our (P, Q). If instead $c_{jj}=0$ for every $j\ne 2$, then we can look at different line conditions assuming $e_{(0,j,j)}(P,Q)=e_{(1,j,j)}(P,Q)=0$ for every j. Let us denote with $L^{i,j,t}$ the line conditions associated to the lines ${\mathcal {V}}(x_1+tx_j,x_2,\dots ,{\hat{x}}_j,\dots ,{\hat{x}}_i,x_i+x_j, \dots ,x_n)$ for $i,j\ne 0,1$. The proper transform $L^{i,j,t}_3$ of these line conditions in the chosen affine chart for $V_3$ are given by

$$\begin{aligned}4F_{i,j,t}^3+G_{i,j,t}^2 d_b=0,\end{aligned}$$

where

$$\begin{aligned}F_{i,j,t}=t^2+b_{(0,j,j)}+b_{(0,i,i)}-b_{(0,i,j)}-tb_{(0,1,j)}+tb_{(0,1,i)},\end{aligned}$$

and

$$\begin{aligned} G_{i,j,t}=&\ t^3+c_{(i,i,i)}+3tc_{(1,i,i)}+3t^2c_{(1,1,i)}+3c_{(i,j,j)}\\ {}&-3c_{(i,i,j)}+3tc_{(1,j,j)}-3t^2c_{(1,1,j)}-3tc_{(1,i,j)}-c_{(j,j,j)}. \end{aligned}$$

If we now consider the proper transform of this line condition in a chart of $V_4$ different from ${e}_d\ne 0$, repeating a similar reasoning to before we can see that for partial derivatives $\partial _{y}$ with respect to variables $y\ne e'$ evaluated at the point (P, Q), we have $\frac{\partial _{y}}{t^a}=0$ for $a\in \{0,1,2\}$, and this follows again from the fact that $c_{(1,1,i)}(P)=c_{(1,1,j)}(P)=0$ for our point P. If we look at partial derivatives $\partial _{e'}$ for the variable $e'$ evaluated at the point $(P,Q)=\pi _P([q_{ij}]_{i,j\in [n]})$, this is given by

$$\begin{aligned} 12t^2\left( e_{(0,i,j)}\right) ^2-4\left( 3te_{(1,i,j)}\right) ^2. \end{aligned}$$

But then we see that $\frac{\partial _{e'}}{t^2}$ is given by

$$\begin{aligned} 12\left( e^2_{(0,i,j)}-3e^2_{(1,i,j)}\right) .\end{aligned}$$

If $j=2$ then this becomes

$$\begin{aligned}27\left( 4(q_{0i}-q_{2i})^2-3\left( q_{0i}-q_{2i}\right) ^2\right) =27(q_{0i}-q_{2i})^2\end{aligned}$$

and we obtain the claim if this quantity is different from zero for our (P, Q). If instead we also have $q_{0i}-q_{2i}=0$ for every i, then we can look at different line conditions. Take $L^{i,j,t}$ where $j\ne i\ne \{0,1,2\}$. If we repeat the same reasoning everything remains the same but in the end we get that $\frac{\partial _{e'}}{t^2}$ is given by

$$\begin{aligned}27\left( 4q_{ij}^2-3q_{ij}^2\right) =27q_{ij}^2.\end{aligned}$$

Once again, we obtain the claim if this quantity is different from zero for our (P, Q). Finally, if $q_{ij}=0$ for every ij as before, then this implies $[q_{ij}]_{i,j\in [n]}\in (TB_3)_{P}$, but this is not possible. This concludes the proof. $\square$

Corollary 2.23

The intersection of all line conditions in $V_5$ is empty.

Proof

We need to show that the line conditions do not intersect in $E_5$. Thanks to Remark 2.15 and the fact that the equations in Remark 2.18 do not involve the variable $c_a$, we can show it over fibers corresponding to points in $B_4\setminus (\pi _4|_{B_4})^{-1}(e)$. By the ${{\,\textrm{PGL}\,}}_n$-action we can just look at one single fiber on a point $\overline{\lambda \mu ^2}$ of $B_4$, with $\pi _4(\overline{\lambda \mu ^2})=[\lambda \mu ^2]$. The claim then follows from Lemma 2.22. $\square$

The previous lemma proves that line conditions separate in $V_5$ and that this space is a 1–complete variety of cubic hypersurfaces.

3.7 Identifying the vector bundle ${\mathcal {E}}$ on e

We now give a more explicit description of the bundle ${\mathcal {E}}|_e$, which will be useful for understanding the total Chern class $c({\mathcal {E}})$.

Lemma 2.24

The natural action of ${{\,\textrm{PGL}\,}}_n$ on the exceptional divisor $e \subseteq \textrm{Bl}_{\Delta } {{\mathbb {P}}}^n \times {{\mathbb {P}}}^n$ is transitive.

Proof

We have $e = {{\mathbb {P}}}(N_{\Delta }{{\mathbb {P}}}^n \times {{\mathbb {P}}}^n) = {{\mathbb {P}}}(T\Delta )$ where the isomorphism $N_{\Delta }{{\mathbb {P}}}^n \times {{\mathbb {P}}}^n \cong T\Delta$ is provided by any multiple of the difference of the differentials of the projections, e.g. $d\textrm{pr}_1 - d\textrm{pr}_2$. Fix now two points $[\lambda ], [\mu ] \in \Delta$ and two non-zero normal vectors $(v_1, v_2) \in N_{\Delta }{{\mathbb {P}}}^n \times {{\mathbb {P}}}^n|_{[\lambda ]}$ and $(w_1, w_2) \in N_{\Delta }{{\mathbb {P}}}^n \times {{\mathbb {P}}}^n|_{[\mu ]}$. These two normal vectors are represented by two curves ${\mathbb {A}}^1 \rightarrow {{\mathbb {P}}}^n \times {{\mathbb {P}}}^n, t \mapsto ([\lambda + t v_1],[\lambda + t v_2])$ and $t \mapsto ([\mu + t w_1],[\mu + t w_2])$, respectively. We then only need to find $A \in {{\,\textrm{PGL}\,}}_n = \text {GL}_{n+1}/\sim$ with $A\lambda = \mu$ and $A(v_1 - v_2) = w_1 - w_2$. Such a A exists if $v_1 - v_2$ is not a multiple of $\lambda$ and $w_1 - w_2$ is not a multiple of $\mu$. Both conditions are satisfied by the requirement that $(v_1, v_2)$ and $(w_1, w_2)$ are both non-zero normal vectors. $\square$

Proposition 2.25

We have ${\mathcal {E}}|_e \cong \textrm{Sym}^2(T_{e/\Delta })$.

Remark 2.26

The geometric intuition behind this proposition is as follows. The fiber of $\textrm{Sym}^2(T_{e/\Delta })$ over a point $([\lambda ],[g]) \in e$ is $\frac{\textrm{Sym}^2(W^*/\lambda )}{g \cdot (W^*/\lambda )}$, the quadrics on g. This makes much sense, given that over a point $[\lambda \mu ^2] \in B_3 \setminus e$, the fiber of ${\mathcal {E}}$ is naturally identified with $\frac{\textrm{Sym}^2(W^*)}{(\lambda \cdot W^*+ \mu \cdot W^*)}$, the quadrics on $\lambda \cap \mu$. Fixing $\lambda$, as $\mu$ approaches $\lambda$ along some curve, $\lambda \cap \mu$ can be seen as a sequence of hyperplanes inside $\lambda$ with some limiting hyperplane g inside $\lambda$. Along this sequence, the quadrics on $\lambda \cap \mu$ should indeed approach the quadrics on g.

Remark 2.27

It follows from the relative Euler sequence of the projective bundle e over $\Delta$ that

$$\begin{aligned} \textrm{Sym}^2(T_{e/\Delta }) \cong \frac{\pi _e^*\left( \textrm{Sym}^2(T\Delta )\right) \otimes {\mathcal {O}}_e(2)}{\pi _e^*\left( T\Delta \right) \otimes {\mathcal {O}}_e(1)}, \end{aligned}$$

the total Chern class of which can be computed using the Chern classes of $T\Delta$.

Proof of Proposition 2.25

From the relative Euler sequence for the projective bundles $e = {{\mathbb {P}}}(T\Delta )$ and $B_1 = {{\mathbb {P}}}(\textrm{Sym}^2(T\Delta ))$ we obtain

$$\begin{aligned} N_e B_1 \cong \frac{T_{B_1/B_0}|_e}{T_{e/\Delta }} \cong \textrm{Sym}^2(T_{e/\Delta }). \end{aligned}$$

We now first give an embedding of $N_e B_1$ into $N_{B_3} V_3|_e$. In a second step we show that the image agrees with ${\mathcal {E}}|_e$. For the first step, we observe the chain of natural inclusions of geometric vector bundles

$$\begin{aligned} T_{B_2/B_0}|_e \subseteq TB_2|_e \cong T{{\mathbb {P}}}(N_{B_2} E_2)|_e \subseteq T{{\mathbb {P}}}(N_{B_2} V_2)|_e = TE_3|_e \subseteq TV_3|_e, \end{aligned}$$

(4)

using in the first step that $B_2 = E_2 \cap \tilde{E_1}$, so $N_{B_2} E_2$ is a line bundle and therefore the restriction of $\pi _3$ is an isomorphism ${{\mathbb {P}}}(N_{B_2} E_2) \cong B_2$. In order to embed $T_{B_1/B_0}|_e$ into $T_{B_2/B_0}|_e$, note that $B_2$ is actually a fiber product over $B_0$. To be precise, it follows from Lemma 2.8 that

$$\begin{aligned} B_2 = {{\mathbb {P}}}(N_{B_1} E_1) \cong {{\mathbb {P}}}(p_1^*(\textrm{Sym}^3(T\Delta ))) = {{\mathbb {P}}}(\textrm{Sym}^3(T\Delta )) \times _{B_0} B_1. \end{aligned}$$

The restriction $p_2: B_2 \rightarrow B_1$ of $\pi _2$ agrees under this identification with the projection to the second factor. Under the natural identifications $B_0 = \Delta$ and $B_1 = {{\mathbb {P}}}(\textrm{Sym}^2(T\Delta ))$, the inclusion $e \subseteq B_2$ corresponds to the map

$$\begin{aligned} e = {{\mathbb {P}}}(T\Delta ) \overset{(\nu _3,\nu _2)}{\longrightarrow } {{\mathbb {P}}}(\textrm{Sym}^3(T\Delta )) \times _{\Delta } {{\mathbb {P}}}(\textrm{Sym}^2(T\Delta )), \end{aligned}$$

where $\nu _2$, $\nu _3$ denote the relative second and third Veronese embeddings. On the fiber over $[\lambda ] \in \Delta = {{\mathbb {P}}}(W^*)$, these map a linear form $[g] \in {{\mathbb {P}}}(W^*/\lambda ) = e|_{[\lambda ]}$ to its second respectively third power. Consider now the following diagram (where we omit the pullback signs and identify $B_0 = \Delta$):

The induced dashed maps provide an isomorphism $T_{B_2/B_0} \cong T_{{{\mathbb {P}}}(\textrm{Sym}^3(T\Delta ))/\Delta } \oplus T_{B_1/B_0}$. We define the embedding

by prescribing it to be the identity on the second factor. On the first factor we define it via

given on the fiber over $([\lambda ],[g]) \in e$ (i.e. $[\lambda ] \in \Delta = {{\mathbb {P}}}(W^*)$ and $g \in W^*/\lambda$) by sending a quadric $q \in \textrm{Sym}^2(W^*/\lambda )/(g^2)$ to $\textrm{cst} \cdot g \cdot q \in \textrm{Sym}^3(W^*/\lambda )/(g^3)$, where $\textrm{cst}$ is some non-zero constant still to be specified. (Up to multiplication by $\textrm{cst}$, this is a relative version of the map $\alpha _{2,3}$ from Lemma 2.3.) Denoting by $e_1 \subseteq B_1$ and $e_2 \subseteq B_2$ the images of $\phi _1(e)$ and $\phi _2(e)$, respectively, we want $s(T_{e_1/\Delta }) = T_{e_2/\Delta } \subseteq T_{B_2/B_0}|_{e_2}$. This is achieved precisely for the choice $\textrm{cst} = \frac{3}{2}$. Composing with (4), the embedding $s: T_{B_1/B_0}|_e \hookrightarrow T_{B_2/B_0}|_e$ now provides an embedding of geometric vector bundles $T_{B_1/B_0}|_e \hookrightarrow TV_3|_e$. Composing further with the quotient map $TV_3|_e \rightarrow N_{B_3} V_3|_e$, the kernel is then precisely $T_{e_1/B_0} \subseteq T_{B_1/B_0}|_{e_1}$. Hence, we obtain an embedding of geometric vector bundles

We denote by ${\mathcal {F}} \subseteq N_e E_3 \subseteq N_{B_3} V_3|_e$ its image. It is enough to show ${{\mathbb {P}}}({\mathcal {F}}) = {{\mathbb {P}}}({\mathcal {E}}|_e) = B_4 \cap \pi _4^{-1}(e)$. As the embedding $N_e B_1 \hookrightarrow N_{B_3} V_3|_e$ is ${{\,\textrm{PGL}\,}}_n$-equivariant, it is enough to show the equality ${{\mathbb {P}}}({\mathcal {F}}) = {{\mathbb {P}}}({\mathcal {E}}|_e)$ for the fiber over a single point of e, using that ${{\,\textrm{PGL}\,}}_n$ acts transitively on e by Lemma 2.24. We pick the point $([\lambda ], [g]) = ([x_0], [x_1]) \in e$. In the explicit coordinates of Subsection 2.4, the fiber of $B_4$ over this point is defined (in the affine chart where $e_{(0,1,2)} = 1$) by the equations

$$\begin{aligned} 0&= e',{} & {} \\ 0&= e_d,{} & {} \\ 0&= e_{(0,i,j)} - 2e_{(1,i,j)} \quad{} & {} \text {for all } i,j>1, \\ 0&= e_F \quad{} & {} \text {for all } F \ne (0,i,j), (1,i,j). \end{aligned}$$

This follows from the fact that the same equations hold for the fiber of $B_4$ over the point $[(x_0 + x_1 + x_2)(x_0 + x_2)^2] \in B_3 {\setminus } e$, see the proof of Lemma 2.22. This point has the same $b_{(0,i,j)}$ and $c_{(i,j,k)}$ coordinates as $([x_0], [x_1]) \in e$. By Remark 2.18, the equations for $B_3$ inside $V_3$ only depend on those, and the same is true for the equations of the line conditions from Remark 2.15. Therefore, the fiber of $B_4$ over $([x_0], [x_1]) \in e$ is indeed defined by the same equations in the $(e_F, e_d, e')$-coordinates as the fiber over $[(x_0 + x_1 + x_2)(x_0 + x_2)^2] \in B_3 {\setminus } e$. Finally, the explicit description of the embedding $s: T_{B_1/B_0}|_e \hookrightarrow T_{B_2/B_0}|_e$ above provides a way to check that all points in the chart satisfying the above equations lie inside ${{\mathbb {P}}}({\mathcal {F}}|_{([x_0],[x_1])})$. Namely, if we start with a tangent vector associated to a quadric $q = \sum _{2 \le i \le j} q_{(i,j)} x_i x_j \in T_{B_1/B_0}|_{([x_0],[x_1])}$, it is represented by a curve in our usual affine open chart of $B_2$ given by sending $t \in {\mathbb {A}}^1$ to $b_{(0,i,j)} = q_{(i,j)} \cdot t$, $c_{(1,i,j)} = \frac{\textrm{cst}}{3} \cdot q_{(i,j)} \cdot t$ for all $i,j>1$ and all other coordinates equal to 0. Tracing the proper transform of this curve in $V_3$, we obtain that this tangent vector corresponds to the point in $E_4$ with coordinates $e' = e_d = 0$, $e_{(0,i,j)} = q_{(i,j)}, e_{(1,i,j)} = \frac{\textrm{cst}}{3} \cdot q_{(i,j)}$ and all other $e_F = 0$. This satisfies the above equations exactly for the choice $\textrm{cst} = \frac{3}{2}$. We get that ${{\mathbb {P}}}({\mathcal {F}}|_{([x_0],[x_1])})$ contains a dense open subset of ${{\mathbb {P}}}({\mathcal {E}}|_{([x_0],[x_1])})$ and hence the entire fiber. As their dimensions agree, we obtain equality, and with this we conclude that ${{\mathbb {P}}}({\mathcal {F}}) = {{\mathbb {P}}}({\mathcal {E}}|_e)$. $\square$

4 Intersection rings and Chern classes

In the following subsections we collect details about the Chow rings of the centers of the blow-ups. This is the last step needed to compute the characteristic numbers. In particular, we find generators, describe the degree of the product of those generators, and find the Chern classes $c(N_{B_i}V_i)$ of the normal bundle of $B_i$ inside $V_i$. Recall from the beginning of [1, Section 2] that for a nonsingular variety V of dimension n, and a nonsingular closed subvariety B in V of codimension d, the full intersection class of a pure-dimensional subscheme X in V is defined as:

$$\begin{aligned} B\circ X {:}{=}c(N_BV)\cap s(B\cap X, X) \end{aligned}$$

in the Chow group $A_*(B\cap X)$ of $B\cap X$, with $s(B\cap X, X)$ denoting the Segre class. In the end of this section, we compute the full intersection classes $B_i\circ P_i$ and $B_i\circ L_i$.

Remark 3.1

For $X\subseteq V_i$ being a divisor and $j_i:B_i\hookrightarrow {} V_i$, we have

$$\begin{aligned} B_i \circ X = e_{B_i}X[B_i] + j_i^*[X] \end{aligned}$$

(5)

where $e_{B_i}X$ denotes the multiplicity of X along $B_i$.

4.1 Chow ring of $\varvec{B_0}$

The following results directly generalize from [1]:

Lemma 3.2

The intersection ring of $B_0\simeq {{\mathbb {P}}}^n$ is generated by the hyperplane class h. Moreover, $c(N_{B_0}V_0)=(1+3h)^{\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) }/(1+h)^{n+1}$.

Lemma 3.3

The full intersection classes of point and line conditions in $V_0$ with respect to $B_0$ are

$$\begin{aligned} B_0\circ P=3h \qquad B_0\circ L=2+12h. \end{aligned}$$

4.2 Chow ring of $\varvec{B_1}$

The center of the second blow-up is $B_1$, this was described in Subsection 2.1.

Lemma 3.4

The variety $B_1$ has dimension $\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) -2$.

• (i) The intersection ring of $B_1$ is generated by the pullback h of h via the map $\pi _1:B_1\rightarrow B_0$ and the pullback $\epsilon$ of $[E_1]$ via the inclusion map $j_1:B_1\hookrightarrow V_1$. Consider the sequence $\{a_s\}$ obtained with the following recursion

  $$\begin{aligned}{\left\{ \begin{array}{ll} a_0=1\\ a_s=\left( {\begin{array}{c}n+1\\ s\end{array}}\right) -\displaystyle \sum _{i=1}^{s}2^i\left( {\begin{array}{c}\dim B_1+2\\ i\end{array}}\right) a_{s-i}.\end{array}\right. }\end{aligned}$$

  We get

  $$\begin{aligned} \int _{B_1} h^{s}\epsilon ^{\dim B_1-s}&=0 \qquad{} & {} \hbox { for } s\in [n+1,\dim B_1],\\ \int _{B_1} h^{s}\epsilon ^{\dim B_1-s}&=(-1)^{\dim B_1-s}a_{n-s} \qquad{} & {} \hbox { for } s\in [0,n]. \end{aligned}$$

• (ii) $c(N_{B_1}V_1)=(1+\epsilon )(1+3h-\epsilon )^{\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) }/(1+2h-\epsilon )^{\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) }$.

Proof

The proof is exactly as in [1]. Notice that ${\mathcal {O}}_{E_1}(-1)={\mathcal {O}}_{V_1}(E_1)_{|_{E_1}}$, so that $c_1({\mathcal {O}}_{E_1}(-1))=c_1({\mathcal {O}}_{V_1}(E_1)_{|_{E_1}})=j_1^*([E_1])$. The coefficients in

$$\begin{aligned} s(N_{v_2({{\mathbb {P}}}^n)}{{\mathbb {P}}}^{\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) -1})=\frac{(1+h)^{n+1}}{(1+2h)^{\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) }} = a_0 + a_1 h + \cdots + a_n h^n \end{aligned}$$

are computed by equating the coefficients of the powers of h. From the above expression one gets the relation

$$\begin{aligned} \left( {\begin{array}{c}n+1\\ s\end{array}}\right) = \sum _{i = 0}^s 2^{s-i}\left( {\begin{array}{c}\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) \\ s-i\end{array}}\right) a_i \end{aligned}$$

from which we attain the recursive formula for the $a_i$’s stated above. $\square$

Remark 3.5

($n=3$) In this case we have:

$$\begin{aligned} s(N_{v_2({{\mathbb {P}}}^3)}{{\mathbb {P}}}^9) = 1 - 16 h + 146 h^2 - 996 h^3. \end{aligned}$$

The center $B_1$ has dimension 8 and $\int _{B_1}h^j \epsilon ^{8-j} = 0 \text { when } j \ge 4$, while the other intersection numbers are summarized in Table 1,

Table 1 The intersection number of $\int _{B_1}h^j \epsilon ^{8-j}$ is given in column $h^j$

Lemma 3.6

We have $\pi _1^*(P) = P_1$ and $\pi _1^*(L) = L_1 + 2 E_1$. The full intersection classes of point and line conditions with respect to $B_1$ are:

$$\begin{aligned} B_1 \circ P_1&= 3h,&B_1 \circ L_1&= 1 + 12 h - 2\epsilon .\\ \end{aligned}$$

4.3 Chow ring of $\varvec{B_2}$

The third center of blow-up is $B_2$, which was described in the Subsection 2.2.

Lemma 3.7

$B_2$ is a ${{\mathbb {P}}}^{\left( {\begin{array}{c}n+2\\ 3\end{array}}\right) -1}$-bundle over $B_1$ and it has dimension $\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) -3$.

• (i) Consider $\pi _{2_{|_{B_2}}}: B_2 \rightarrow B_1$ and the inclusion $j_2: B_2 \hookrightarrow V_2$. Then the intersection ring of $B_2$ is generated by the pullback of the classes h and $\epsilon$ along the projection $\pi _2$ and by $\phi$ the pullback of $[E_2]$ along the inclusion $j_2$. Let $\{c_{j,k}\}_{j\in [n],k\in [\dim B_1]}$ be the sequence obtained recursively for $j + k \le \dim B_1$, following the lexicographic order:

  $$\begin{aligned}{\left\{ \begin{array}{ll} c_{0,0}=1 \\ c_{j,k}=(-1)^k 2^j \left( {\begin{array}{c}\dim B_1+2\\ j,k\end{array}}\right) -\displaystyle \sum _{\begin{array}{c} a\le j, b\le k \\ (a,b) \ne (j,k) \end{array}} c_{a,b}\left( {\begin{array}{c}\dim B_2+3\\ j-a,k-b\end{array}}\right) 3^{j-a}(-1)^{k-b}, \end{array}\right. }\end{aligned}$$

  where $\left( {\begin{array}{c}a\\ b,c\end{array}}\right) =\frac{a!}{(a-b-c)! b!c!}$. For $j\in [n], k\in [\dim B_1]$, we get

  $$\begin{aligned}\int _{B_2} h^{j}\epsilon ^k\phi ^{\dim B_2-j-k}=0 \qquad \qquad \end{aligned}$$

  for $j+k\in [\dim B_1+1,\dim B_2]$ and

  $$\begin{aligned}\int _{B_2} h^{j}\epsilon ^{k}\phi ^{\dim B_2-j-k}=(-1)^{\dim B_2-j-k}\sum _{\begin{array}{c} a+b=\dim B_1-j-k \\ a\in [n-j],b\in [\dim B_1] \end{array}}c_{a,b}(-1)^{\dim {B_1}-a-j}a_{n-a-j}\end{aligned}$$

  for $j+k\in [0,\dim B_1]$, where the $a_{i}$ in the sum are the numbers obtained by recursion in Lemma 3.4.

• (ii) Moreover $c (N_{B_2}V_2) = (1 + \phi )(1 + \epsilon - \phi )$.

Proof

Since $B_2={{\mathbb {P}}}(N_{B_1}V_1)$, the first point follows from [12, Example 8.3.4]. Point (ii) in Lemma 3.4 implies

$$\begin{aligned} c(N_{B_1}E_1) = \frac{(1 + 3h - \epsilon )^{\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) }}{(1 + 2h - \epsilon )^{\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) }}. \end{aligned}$$

Hence recalling that $h^{n+1} = 0$ and $\epsilon ^{\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) } = 0$, we have

$$\begin{aligned} s(N_{B_1}E_1) = \frac{(1 + 2h - \epsilon )^{\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) }}{(1 + 3h - \epsilon )^{\left( {\begin{array}{c}n+3\\ 3\end{array}}\right) }} = \sum _{\begin{array}{c} j \in [n],k \in [\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) ] \end{array}} c_{j,k} h^j \epsilon ^k. \end{aligned}$$

Note that this relation allows us to give a recursive formula for the coefficients $c_{j,k}$ (following the lexicographic order on (j, k)). For the second point we have that $B_2 = \tilde{E_1} \cap E_2$ hence $c(N_{B_2}V_2) = c(N_{E_2}V_2)c(N_{\tilde{E_1}}V_2)$. Note that $N_{E_2}V_2$ is a line bundle on $E_2$ and $N_{\tilde{E_1}}V_2$ is a line bundle on $E_1$. Since $N_{E_2}V_2={\mathcal {O}}_{E_2}(-1)$, we get $c(N_{E_2}V_2)=1+\phi$. The isomorphism $N_{\tilde{E_1}}V_2\simeq \pi _1^*(N_{E_1}V_1)\otimes {\mathcal {O}}_{E_2}(-E_2)$ implies $c(N_{\tilde{E_1}}V_2)=1+\epsilon -\phi$. Hence, one concludes that

$$\begin{aligned}c(N_{B_2}V_2) = c(N_{E_2}V_2)c(N_{\tilde{E_1}}V_2) = (1 + \phi )(1 + \epsilon - \phi ).\end{aligned}$$

$\square$

Remark 3.8

($n=3$) In the case of cubic surfaces, $B_2$ has dimension 17 and $\int _{B_2}h^j\epsilon ^k \phi ^{17-j-k} = 0 \text { with } j+k > 8$ or $j > 3$, while the remaining integrals are summarized in Table 2.

Table 2 The intersection number of $\int _{B_2}h^j\epsilon ^k \phi ^{17-j-k}$ is given in row $h^j$ and column $\epsilon ^k$

Lemma 3.9

We have $\pi _2^*(P_1) = P_2$ and $\pi _2^*(L_1) = L_2 + E_2$. The full intersection classes of point and line conditions with respect to $B_2$ are:

$$\begin{aligned} B_2 \circ P_2&= 3h,&B_2 \circ L_2&= 1 + 12 h - 2\epsilon -\phi .\\ \end{aligned}$$

Proof

As divisor classes we have $\pi _2^*(P_1) = P_2$ and $\pi _2^*(L_1) = L_2 + E_2$, because $L_1$ is generically smooth along $B_1$. In the intersection ring of $B_2$ we get $j_2^*(P_2) = 3\,h$ and $j_2^*(L_2) = 12\,h - 2\epsilon -\phi$. The claim follows by Remark 3.1 observing that in our case the divisor $P_2$ does not contain $B_2$ and $L_2$ is smooth along $B_2$. $\square$

4.4 Chow ring of ${\varvec{B}}_3$

Recall from Sect. 2.3 that $B_3$ denotes the fourth center in our sequence of blow-ups, and it is defined as the proper transform in $V_3$ of $S_0$. Moreover, in Lemma 2.17, we described the isomorphism $\phi _3$ of $S_3$ with $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$.

Theorem 3.10

We identify $B_3$ with $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$.

• (i) We have two natural projections of $\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$ onto ${{\mathbb {P}}}^n$. Let l, m be the pullbacks of the hyperplane classes in ${{\mathbb {P}}}^n$ through these projections, and let e denote the exceptional divisor. Consider the sequence $\{d_s\}$ obtained recursively:

  $$\begin{aligned}{\left\{ \begin{array}{ll} d_0=1\\ d_s=-\sum _{i=0}^{s-1}\left( {\begin{array}{c}n+1\\ s-i\end{array}}\right) d_{i}.\end{array}\right. }\end{aligned}$$

  The intersection ring of $B_3$ is generated by l, m, e subject to $em^s=el^s$ for every s, $l^{n+1}=m^{n+1}=0$ and

  $$\begin{aligned}\int _{B_3} m^{n}l^{n}=1, \qquad \qquad \int _{B_3} l^{s}e^{2n-s}=(-1)^{2n-s-1}d_{n-s} \end{aligned}$$

  with $s\in [n]$. All the remaining intersection numbers vanish.

• (ii) ($n=3$) In the case of cubic surfaces, we have

  $$\begin{aligned} c(N_{B_3}V_3)=&1672560l^3m^3 - 66343820m^3e^3 + 36537350m^2e^4 - 10851224m e^5 + 1356403e^6 +\\ {}&209440 l^3 m^2 + 474320 l^2 m^3 + 8045100 m^3 e^2 - 5907690 m^2 e^3 + 2193180 m e^4 - \\ {}&328977 e^5 + 15960 l^3 m + 53560 l^2 m^2 + 81680 l m^3 - 582940 m^3 e + 642110 m^2 e^2 -\\ {}&317840 m e^3 + 59595 e^4 + 560 l^3 + 3720 l^2 m + 8400 l m^2 + 6460m^3 - 42166 m^2 e + \\&31308 m e^2 - 7827 e^3 + 120 l^2 + 536 l m + 610 m^2 - 1880 m e + 705 e^2 + 16 l + 36 m -\\&39 e +1. \end{aligned}$$

Proof

We follow the proof of [1, Theorem III (4)]. Consider the diagram:

By definition we have $s(\Delta ,{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n)=s(N_{\Delta }({{\mathbb {P}}}^n\times {{\mathbb {P}}}^n))$ and

$$\begin{aligned} s_i(N_{\Delta }({{\mathbb {P}}}^n\times {{\mathbb {P}}}^n))=g_{*}((-\zeta )^{n-1+i}) \end{aligned}$$

where $\zeta =c_1({\mathcal {O}}_{{{\mathbb {P}}}(e)}(-1))=j^*(e)$. Hence we get

$$\begin{aligned} s(\Delta ,{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n)=g_{*}\biggl (\sum _{i=0}^{n}(-1)^{n-1+i}(j^*e)^{n-1+i}\biggr ). \end{aligned}$$

However, we can also compute $s(\Delta ,{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n)$ as the inverse of the Chern class of $N_{\Delta }({{\mathbb {P}}}^n\times {{\mathbb {P}}}^n)$. This gives us

$$\begin{aligned} s(\Delta ,{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n)=\frac{1}{(1+k)^{n+1}}=\left( \sum _{i=0}^{n}(-1)^ik^i\right) ^{n+1}. \end{aligned}$$

Applying the projection formula and the above observations we get

$$\begin{aligned} \int _{B_3}f^*(l)^ie^{2n-i}&=\int _{B_3}j_{*}\left( j^*(f^*l^i)j^*(e^{2n-i-1})\right) =\int _{\Delta }k^ig_{*}\left( j^*(e)^{2n-i-1}\right) =\\&=\int _{\Delta }k^i(-1)^{2n-i-1}s(\Delta ,{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n)=(-1)^{2n-i-1}d_{n-i}. \end{aligned}$$

For proving point (ii), we can compute $\phi _3^*(c(TV_3))$ applying [12, Theorem 15.4] multiple times. Notice that to do this, computing $c(TB_1)$ and $c(TB_2)$ is also needed. Hence we observe that

$$\begin{aligned} c(TB_1)=\frac{(i_1\circ j_1)^*c(TV_1)}{c(N_{B_1}V_1)} \end{aligned}$$

and then we can again use [12, Theorem 15.4] to compute the numerator. Finally, $c(TB_3)$ is computed applying [12, Theorem 15.4] considering $B_3=\textrm{Bl}_{\Delta }{{\mathbb {P}}}^n\times {{\mathbb {P}}}^n$. $\square$

Remark 3.11

Notice that in principle it is possible to compute $c(N_{B_3}V_3)$ for any n, using the strategy of the proof. However, this can be computationally difficult. For instance, here is the result for $n=4$:

$$\begin{aligned} c(N_{B_3}V_3) = \ {}&8604607900l^4m^4 + 1511859296400m^4e^4 - 956335227000m^3e^5 + 379626653775m^2e^6- \\ {}&86448428700me^7 + 8644842870e^8 + 699244875l^4m^3 + 1520696100l^3m^4 - \\ {}&107772730500m^4e^3 + 85215404025m^3e^4 - 40592536260m^2e^5 + 10784338950me^6 - \\ {}&1232495880e^7 + 40828725l^4m^2 + 117863200l^3m^3 + 192910550l^2m^4 + 5484228225m^4e^2 - \\ {}&5781808210m^3e^3 + 3442721815m^2e^4 - 1097565900m e^5 + 146342120e^6 + 1525545l^4 m + \\ {}&6578880 l^3 m^2 + 14291235 l^2 m^3 + 15643810 l m^4 - 177497950 m^4 e + 280693735 m^3 e^2 - \\ {}&222848500 m^2 e^3 + 88807250 m e^4 - 14209160 e^5 + 27405 l^4 + 235480 l^3 m + 764065 l^2 m^2 + \\ {}&1109920 l m^3 + 609280 m^4 - 8685470 m^3 e + 10343355 m^2 e^2 - 5495900 m e^3 + 1099180 e^4 + \\ {}&4060 l^3 + 26245 l^2 m + 56940 l m^2 + 41475 m^3 - 306580 m^2 e + 244350 m e^2 - 65160 e^3 +\\ {}&435 l^2 + 1880 l m + 2045 m^2 - 6950 m e + 2780 e^2 + 30 l + 65 m - 76 e + 1. \end{aligned}$$

Remark 3.12

($n=3$) In this case the dimension of $B_3$ is 6 and $\int _{B_3}l^jm^k e^{6-j-k} = 0 \text { with } j > 3$ or $k>3$, $\int _{B_3}l^3\,m^{3} = 1$ while the other integrals are summarised in Table 3, remembering that $\int _{B_3}l^j m^k e^{6-j-k}=\int _{B_3}l^{j+k} e^{6-j-k}$ for $j+k<6$.

Table 3 The intersection number of $\int _{B_3}l^j e^{6-j}$ is given in column $l^j$

Lemma 3.13

We have $\pi _3^*(P_2) = P_3$ and $\pi _3^*(L_2) = L_3 + E_3$. The full intersection classes of point and line conditions with respect to $B_3$ are:

$$\begin{aligned} B_3 \circ P_3&= l+2m,&B_3 \circ L_3&= 1+4l+8m-6e. \end{aligned}$$

Proof

In the intersection ring of $B_3$ we get $j_3^*(P_3) =l+2m$ and $j_3^*(L_3) = 4(l+2m) - 2(2e)-e-e=4l+8m-6e$. The assertion is then proved by noticing that $P_3$ does not contain $B_3$ and $L_3$ is smooth along $B_3$. $\square$

4.5 Chow ring of $\varvec{B_4}$

Table 4 The intersection number of $\int _{B_4}m^j e^{k} z^{8-j-k}$ is given in row $m^j$ and column $e^k$, while $\int _{B_4}m^j l^{k} z^{8-j-k}$ is given in row $l^k$ and column $m^j$

The fifth center we blow-up is $B_4$, which was described in Subsection 2.4. In particular, recall that $B_4={{\mathbb {P}}}({\mathcal {E}})$ and that we have an isomorphism of ${\mathcal {E}}|_e$ given in Proposition 2.25.

Theorem 3.14

We identify $B_4$ with ${{\mathbb {P}}}({\mathcal {E}})$.

• (i) Let l, m, e be the pullbacks of the generators of the Chow ring of $B_3$ through the projection $\pi _4|_{B_4}:B_4 \rightarrow B_3$. The Chow ring of $B_4$ is generated by l, m, e and z where z is the first Chern class of ${\mathcal {O}}_{B_4}(-1)$. The intesection numbers in the case $n=3$ are collected in Table 4.

• (ii) ($n=3$) In the case of cubic surfaces, we have

  $$\begin{aligned} c(N_{B_4}V_4)=&-8540 e^6z^2 - 45500l^2m^2z^4 - 109900lm^3z^4 + 280350m^2e^2z^4 - 325500me^3z^4 \\ {}&+ 106575e^4z^4 + 13440l^2mz^5 + 44800lm^2 z^5 + 47320m^3z^5 - 235200m^2ez^5 + 174720me^2z^5 \\ {}&- 43680e^3z^5 - 1260l^2z^6- 7560lmz^6 - 11620m^2z^6 + 30240mez^6 - 11340e^2z^6 + 480lz^7 \\ {}&+ 1440mz^7 - 1440ez^7 - 75z^8 + 12810e^6z + 251300l^2m^3z^2 + 195650me^4z^2 - 108220e^5z^2 \\ {}&- 45500l^2m^2z^3 - 109900lm^3z^3 + 280350m^2e^2z^3 - 325500me^3z^3 + 106575e^4z^3 + 630l^2z^5\\ {}&+ 3780lmz^5 + 5810m^2z^5 - 15120mez^5 + 5670e^2z^5 - 420lz^6 - 1260mz^6 + 1260ez^6 + 90z^7 \\ {}&- 4270e^6 - 201040l^2m^3z - 156520me^4z + 86576e^5z + 81900l^2m^2z^2 + 197820lm^3z^2 \\ {}&- 504630m^2e^2z^2 + 585900me^3z^2 - 191835e^4z^2 - 13440l^2mz^3 - 44800lm^2z^3 - 47320m^3z^3\\ {}&+ 235200m^2ez^3 - 174720me^2z^3 + 43680e^3z^3 + 630l^2z^4 + 3780lmz^4 + 5810m^2z^4\\ {}&- 15120mez^4 + 5670e^2z^4 - 42z^6 + 50260l^2m^3 + 39130me^4 - 21644e^5 - 45500l^2m^2z \\ {}&- 109900lm^3z + 280350m^2e^2z - 325500me^3z + 106575e^4z + 13440l^2mz^2 + 44800lm^2z^2 \\ {}&+ 47320m^3z^2 - 235200m^2ez^2 + 174720me^2z^2 - 43680e^3z^2 - 1260l^2z^3 - 7560lmz^3 \\ {}&- 11620m^2z^3 + 30240mez^3 - 11340e^2z^3 + 420lz^4 + 1260mz^4 - 1260ez^4 - 42z^5 + 9100l^2m^2 \\ {}&+ 21980lm^3 - 56070m^2e^2 + 65100me^3 - 21315e^4 - 5760l^2mz - 19200lm^2z - 20280m^3z \\ {}&+ 100800m^2ez - 74880me^2z + 18720e^3z + 900l^2z^2 + 5400lmz^2 + 8300m^2z^2 - 21600mez^2 \\ {}&+ 8100e^2z^2 - 480lz^3 - 1440mz^3 + 1440ez^3 + 90z^4 + 960l^2m + 3200lm^2 + 3380m^3 - 16800m^2e\\ {}&+ 12480me^2 - 3120e^3 - 315l^2z - 1890lmz - 2905m^2z + 7560mez - 2835e^2z + 270lz^2 + 810mz^2\\ {}&- 810ez^2 - 75z^3 + 45l^2 + 270lm + 415m^2 - 1080me + 405e^2 - 80lz - 240mz + 240ez + 35z^2\\ {}&+ 10l + 30m - 30e - 9z + 1. \end{aligned}$$

Proof

To compute the intersection numbers, we follow the usual strategy adopted in the previous proofs, using

$$\begin{aligned} s({\mathcal {E}})=(\pi _4|_{B_4})_*\left( \sum _{i=0}^{\dim (B_4)}(-1)^{i}z^i\right) . \end{aligned}$$

The Segre class $s({\mathcal {E}})$ is computed explicitly in the case $n=3$ thanks to Remark 2.27. In fact, we have the Chern Classes $c({\mathcal {E}}|_{B_3\setminus e})$ and $c({\mathcal {E}}|_e)$. The first one is in the Chow ring of $B_3\setminus e$, which thanks to the excision theorem is described by

$$\begin{aligned}\frac{{\mathbb {Z}}[l,m]}{(l^{n+1},m^{n+1},[\Delta ])}\end{aligned}$$

where $[\Delta ]=\sum _{i=0}^{n}l^{n-i} m^i$. Therefore $c({\mathcal {E}}|_{B_3{\setminus } e})=\sum _{d=0}^{2n}\sum _{j=0}^{d}o_{j,d-j}m^jn^{d-j}$.

The second one is an element of the Chow ring of e described by

$$\begin{aligned}\frac{{\mathbb {Z}}[k,\zeta ]}{(k^{n+1},\zeta ^{2n},(n+1)k^{n}+\sum _{i=1}^{n}\zeta ^ik^{n-i}c_{n-i}(T\Delta ))}\end{aligned}$$

where $\zeta$ is just the pullback of the class e through the inclusion of e in $B_3$, and $c_i(T\Delta )$ is the i-th Chern class of the tangent space of the diagonal. Therefore $c({\mathcal {E}}|_{B_3{\setminus } e})=\sum _{d=0}^{2n}\sum _{j=0}^{d}u_{j,d-j}k^j\zeta ^{d-j}$. In general, knowing $c({\mathcal {E}}|_{B_3\setminus e})$ and $c({\mathcal {E}}|_e)$ allows us to reconstruct $c({\mathcal {E}})$ up to degree n. In fact, for $d<n$ we have

$$\begin{aligned}c_d({\mathcal {E}})=\sum _{j=0}^{d}o_{j,d-j}m^jl^{d-j}+\sum _{j=0}^{d-1}u_{j,d-j}m^je^{d-j}.\end{aligned}$$

For $d=n$, call then $\sum _{j=0}^{n}o_{j,n-j}=u_{n,0}+(n+1){w}$ for some ${w}\in {\mathbb {Z}}$ and

$$\begin{aligned}c_n({\mathcal {E}})=\sum _{j=0}^{n}o_{j,n-j}m^jn^{n-j}-w[\Delta ]+\sum _{j=0}^{n-1}u_{j,n-j}k^j\zeta ^{n-j}.\end{aligned}$$

When $n=3$, since rk$({\mathcal {E}})=3$, we get the entire total Chern class.

For proving (ii), we can follow the strategy of [1, Theorem III(ii)] and Lemma 2.20. $\square$

Remark 3.15

We are not able to recover the Chern class $c({\mathcal {E}})$ in the case $n>3$. Indeed, knowing $c({\mathcal {E}}|_e)$ and $c({\mathcal {E}}|_{B_3\setminus e})$ we can recover $c({\mathcal {E}})$ only up to integer multiples of $m^k [\Delta ] = m^{k}(\sum _{i=1}^{n}e^i m^{n-i} c_{n-i}(T\Delta ))$ for $k\ge 1$.

Lemma 3.16

We have $\pi _4^*(P_3) = P_4$ and $\pi _4^*(L_3) = L_4 + E_4$. The full intersection classes of point and line conditions with respect to $B_3$ are:

$$\begin{aligned} B_4 \circ P_4&= l+2m,&B_4 \circ L_4&= 1+4l+8m-6e-z. \end{aligned}$$

5 Characteristic numbers for cubic surfaces, and something more

In this section we gather all information from Sect. 3 in order to compute the characteristic numbers with respect to line conditions for smooth cubic surfaces. Recall that for $n=3$ the moduli space of cubic surfaces is $V_0 = {{\mathbb {P}}}^{19}$ and that in Sect. 2 we constructed a 1-complete space of cubic surfaces denoted $V_5$. Moreover, $V_{i+1}$ is the blow-up of $V_{i}$ with center $B_i$, and $P_i$ and $L_i$ are the proper transforms, in $V_i$, of a point and line condition from $V_0$. Thanks to Theorem 1.4 and [1, Theorem II] we obtain the following.

Lemma 4.1

The number ${\mathcal {N}}(n_p,n_{\ell })$ of smooth cubic surfaces containing $n_p$ given points and tangent to $n_{\ell }$ given lines in general position with $n_p+n_{\ell }=19$ is

$$\begin{aligned}{\mathcal {N}}(n_p,n_{\ell })=4^{n_{\ell }}-\sum _{i=0}^4\int _{B_i}\frac{(B_i\circ P_i)^{n_p}(B_i\circ L_i)^{n_{\ell }}}{c(N_{B_i}V_i)}\end{aligned}$$

Theorem 4.2

We have

$$\begin{aligned} {\mathcal {N}}(n_p,n_{\ell })= {\left\{ \begin{array}{ll} 4^{19-n_p}, &{}n_p\in \{7,8,\dots ,19\},\\ 67107584, &{}n_p=6,\\ 268391296, &{}n_p=5,\\ 1072926016, &{}n_p=4,\\ 4266198896, &{}n_p=3,\\ 16615227040, &{}n_p=2,\\ 61810371328, &{}n_p=1,\\ 213642327616, &{}n_p=0.\\ \end{array}\right. } \end{aligned}$$

Proof

The proof is merely computational.

$$\begin{aligned} \int _{B_0}\frac{(3h)^{n_p}(2+12h)^{n_{\ell }}(1+h)^{4}}{(1+3h)^{20}}= {\left\{ \begin{array}{ll} 1769472, &{}n_p=3\\ 54263808, &{}n_p=2\\ 877658112, &{}n_p=1\\ 9948889088, &{}n_p=0\\ \end{array}\right. } \\ \int _{B_1}\frac{(3h)^{n_p}(1+12h-2\epsilon )^{n_{\ell }}(1+2h-\epsilon )^{10}}{(1+\epsilon )(1+3h-\epsilon )^{20}}= {\left\{ \begin{array}{ll} 434889, &{}n_p=3\\ 13011156, &{}n_p=2\\ 203305944, &{}n_p=1\\ 2199770536, &{}n_p=0\\ \end{array}\right. } \\ \int _{B_2}\frac{(3h)^{n_p}(1+12h-2\epsilon -\phi )^{n_{\ell }}}{(1+\phi )(1+\epsilon -\phi )}= {\left\{ \begin{array}{ll} 17951031, &{}n_p=3\\ 443328300, &{}n_p=2\\ 5677810728, &{}n_p=1\\ 49885157976, &{}n_p=0\\ \end{array}\right. } \\ \int _{B_3}\frac{(l+2m)^{n_p}(1+4l+8m-6e)^{n_{\ell }}}{c(N_{B_3}V_3)}= {\left\{ \begin{array}{ll} 160, &{}n_p=6\\ 6240, &{}n_p=5\\ 130224, &{}n_p=4\\ 1426504, &{}n_p=3\\ 8284040, &{}n_p=2\\ 7701512, &{}n_p=1\\ -337368096, &{}n_p=0\\ \end{array}\right. } \\ \int _{B_4}\frac{(B_4\circ P_4)^{n_p}(B_4\circ L_4)^{n_{\ell }}}{c(N_{B_4}V_4)} = {\left\{ \begin{array}{ll} 1120, &{}n_p=6\\ 37920, &{}n_p=5\\ 685584, &{}n_p=4\\ 7186504, &{}n_p=3\\ 45754840, &{}n_p=2\\ 142629112, &{}n_p=1\\ -460870176, &{}n_p=0\\ \end{array}\right. } \end{aligned}$$

$\square$

Remark 4.3

As explained in Remark 3.15, we cannot have a similar result for $n>3$. Looking at the computations in , it seems that for $n_p\in [n,2n]$ the last correction term is not affected by the ambiguity explained in Remark 3.15 of the Chern class $c({\mathcal {E}})$. We therefore conjecture that, for every n, the numbers given by the code for $n_p\ge n$ are the characteristic numbers.

It is an interesting question whether the characteristic numbers above can be attained by numerical algebraic geometry methods. However, the numbers in Theorem 4.2 increase fast and it could be numerically challenging to compute them. One could try instead to compute the correction term that needs to be subtracted from $4^{19-n_p}$ by numerical software, e.g. HomotopyContinuation.jl [6]. We did not pursue this direction, it would be in any case an interesting problem for experts in numerical algebraic geometry.

5.1 Crumbs of hyperplanes tangency conditions

We stick to the conventions of Sect. 1. In the case of hyperplane tangency conditions for degree d hypersurfaces, the base locus is in general hard to parametrize if compared with the base locus of tangency with respect to lines, where one has obvious maps as in (1). In fact, hyperplane conditions in ${{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ intersect in the locus $B_0^{H}$ of hypersurfaces with positive-dimensional singular locus

$$\begin{aligned} B_0^{H}(d,n) \,=\, \{ [h] \in {{\mathbb {P}}}(\textrm{Sym}^d(W^*)), \,\, | \dim \textrm{Sing}({\mathcal {V}}(h)) \ge 1 \}, \end{aligned}$$

as a Bertini-type argument shows. This set has been studied in [24, 27]. Building on [5], it is shown in [17, Lemma 2.4] that an integral cubic hypersurface in ${{\mathbb {P}}}^n$ which is not normal, i.e., whose singular locus has dimension $n-2$, is necessarily singular exactly along a linear subspace of ${{\mathbb {P}}}^n$ of dimension $n-2$. For $n=3$, this means that the cubic form defining a cubic surface with singular locus of dimension $\ge 1$ is either reducible or the singular locus contains a line in ${{\mathbb {P}}}^3$ (or both). This fact is also known classically [22, p. 144]. It is not hard to see that the first set has dimension 12. The dimension of the second set is 13 because it is birational to

$$\begin{aligned} \left\{ (\ell ,f): (\textrm{grad} f)|_\ell \equiv 0\right\} \,\, \subseteq \,\,{{\,\textrm{Gr}\,}}(2,4) \times {{\mathbb {P}}}(\textrm{Sym}^3(W^*)), \end{aligned}$$

a ${{\mathbb {P}}}^9$-bundle over ${{\,\textrm{Gr}\,}}(2,4)$. We deduce that Slavov’s theorem [24, Theorem 1.1] is also true for cubic surfaces. The work [26] lists the finitely many ${{\,\textrm{PGL}\,}}$-orbits for cubic surfaces with positive-dimensional singular locus and studies containments among their closures.

We can derive some characteristic numbers for hyperplane conditions without any complicated construction.

For a hyperplane $H \subseteq {{\mathbb {P}}}(W)$, we define $L^H$ to be the hypersurface in ${{\mathbb {P}}}(\textrm{Sym}^d(W^*))$ parametrizing all degree d hypersurfaces tangent to H.

Remark 4.4

The variety $L_H$ of all degree d hypersurfaces in ${{\mathbb {P}}}(W)$ tangent to H has degree $n(d-1)^{n-1}$. Indeed, assume $H={\mathcal {V}}(x_0)$ and $g \in {{\mathbb {P}}}(\textrm{Sym}^d(W^*))$. Asking for the hypersurface g to be tangent to H corresponds to the vanishing of the resultant of the polynomials $\partial _{x_i} g(0,x_1,\dots , x_n)$, for $i\in \{1,..,n\}$. This is the resultant of n homogeneous polymonials of degree $d-1$ in n variables, hence it has degree $n(d-1)^{n-1}$.

Knowing the degree of the variety $L^H$, it is immediate to compute some of the characteristic numbers for degree d hypersurfaces in ${{\mathbb {P}}}(W)$.

Lemma 4.5

Let $d = 5$, $d \ge 7$ and n arbitrary or $(d,n)=(3,3)$. If $n_H<n(d-2)+3$, the number ${\mathcal {N}}^H(n_p,n_H)$ of smooth degree d hypersurfaces in ${{\mathbb {P}}}(W)$ tangent to $n_H$ general hyperplanes and passing through $n_p = \left( {\begin{array}{c}n+d\\ d\end{array}}\right) -1-n_H$ general points equals ${\mathcal {N}}^H(n_p,n_H)=\left( n(d-1)^{n-1}\right) ^{n_H}$.

Proof

If we consider $n_H$ hyperplane conditions with $n_H$ strictly less than the codimension of $B_0^{H}(d,n)$, the claim follows from Bézout’s theorem. The codimension of $B_0^{H}(d,n)$ is known for $d=5$ or $d\ge 7$ and arbitrary n by [27, Theorem 1.6] and equals

$$\begin{aligned} \hbox {codim} B_0^{H}(d,n) = n(d-2)+3. \end{aligned}$$

Moreover, this codimension holds true also in the case of cubic surfaces by the above discussion. $\square$