Introduction

Groundwater contamination is one of the serious problems that can affect the environment. Therefore, the researchers developed numerical models for the modeling of flow and contamination transport of groundwater. The traditional methods have restrictions, such as mesh generation process. Due to limitations of mesh-dependent methods, they developed various mesh-free methods for modeling groundwater flow equation in recent years.

AEM is a mesh-free method used for flow modeling. AEM models were used in traditional ways to conduct research on groundwater resources including capture zone delineation or well field modeling (e.g., Badv and Deriszadeh 2005). At present time, the simulation of contaminant transport by the AEM is only done in very limited conditions such as special form of differential equations (Kuhlman 2008; Strack 2009).

There are some studies on the AEM flow model in combination of mesh-dependent methods for contamination transport model. Rumbaugh (1993) presented a simple rectangular Galerkin FEM transport model based on the AEM flow solutions. The model had some problems in mass balance and numerical stability. Grashoff (1994) coupled a 3-D reactive FDM model and a multilayer AEM model. The limitations of the model included low accuracy of numerical flux integrations which causes errors in the transport model. Craig and Rabideau (2006a, b) developed a new method for coupling AEM flow models with FEM and FDM transport models. They obtained good results, but the transport model was still mesh-dependent. Bandilla et al. (2009) provided a mesh-free contamination transport model using streamline method based on the AEM flow solution.

In recent decades, many researchers are trying to solve groundwater contamination problems using mesh-free approach; Li et al. (2003) developed a mesh-free approach utilizing collocation techniques by radial basis function (RBF) to model contamination transport. The model was very simple, easy to use and accurate. Kumar and Dodagoudar (2010) presented a new approach according to the radial point interpolation method (RPIM) to model contamination transport of groundwater in 2D porous media. The results had small oscillations and were sensitive to the Peclet number. Meenal and Eldho (2011) developed a mesh-free groundwater flow model based on the PCM. The model was verified by available numerical and analytical solutions and applied to field problems. The results demonstrate that the simulation preprocessing time could be saved in comparison with the FEM, FDM and boundary elements method. Meenal and Eldho (2012) simulated groundwater flow and contaminant transport based on Kansa’s method and RBF and point collocation techniques. The model was verified by analytical solutions and field data. Singh et al. (2016) simulated the contaminant transport through confined aquifer using a mesh-free radial point collocation method. Results showed that the model accuracy is satisfactory compared with the FEM solution. Zhang et al. (2017) proposed the moving Kriging meshless method based on Monte Carlo integration to deal with the unconfined seepage problem. Yu et al. (2018) numerically investigated the transformation and transport of contaminant through layered soil with large deformation. The numerical approach was implemented based on large-deformation consolidation theory and the advection–diffusion equation of contaminant in saturated porous media. Sämann et al. (2019) introduced a Lagrangian particle-based transport model to obtain the potential contamination paths of solutes in drainage water in an urban region during a pluvial flood event.

The main purpose of this research is to develop contaminant transport model by coupling AEM–PCM mesh-free methods. To achieve this purpose, the AEM model is applied for groundwater flow simulation in an unconfined aquifer, and a mesh-free model of PCM is developed for modeling contamination transport based on solutions of AEM using multi-quadric radial basis function (MQ-RBF). The model has been developed and implemented by Python object-oriented programming (OOP) language. A particle swarm optimization (PSO) algorithm has been also utilized to calibrate the model. In the following part, the numerical formulations and governing equations are presented. Then, the proposed AEM–PCM approach is described. Finally, the present model is calibrated. The developed coupled model is applied for contamination transport modeling of Astaneh-Kuchesfahan groundwater resources in northern of Iran.

Numerical model preprocessing

Analytic element method (AEM)

Groundwater flow can be represented in terms of a complex potential \(\varOmega\) in AEM method, which is defined by the following relation (Strack 1989):

$$\varOmega = \varPhi + i\varPsi$$
(1)

where \(\varPsi\) [L3 T−1] is the stream function, \(\varPhi\) is the discharge potential, and \(i = \sqrt { - 1}\).

The discharge vectors are defined by the discharge potential in the following relations:

$$Q_{x} = - \frac{\partial \varPhi }{\partial x},\quad Q_{y} = - \frac{\partial \varPhi }{\partial y}$$
(2)

where Qx and Qy are the discharge vector components which are the specific flow rate multiplied by the saturated thickness.

In the case of confined/unconfined Dupuit–Forchheimer flow conditions, the hydraulic head h is dependent on discharge potential by the following relation:

$$\varPhi = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}kh^{2} } \hfill & {{\text{where}}\quad h < H\; ( {\text{in}}\;{\text{unconfined}}\;{\text{aquifer}})} \hfill \\ {kHh - \frac{1}{2}kH^{2} } \hfill & {{\text{where}}\quad h > H\;({\text{in}}\;{\text{confined}}\;{\text{aquifer)}}} \hfill \\ \end{array} } \right.$$
(3)

where k is the horizontal hydraulic conductivity and H is the thickness of aquifer.

A series of analytical functions with unknown coefficients are used in the AEM in order to demonstrate the effects of hydrological features on discharge potentials. Such unknown coefficients, which are called “analytic elements,” can be acquired from known local boundary conditions along the borders of each element (e.g., specified heads) by an iterative approach (Craig and Rabideau 2006b).

The discharge potential for a given aquifer is obtained through superposition of each element which shows the effects of one hydrological feature (e.g., river, lake…). The elements are affected the aquifer (Rabideau et al. 2007). By expanding the mathematical equations through Laplace or Poisson equations, a harmonic function is obtained for each element. Some of the functions which are used in this study are provided in support information.

Vertically averaged transport equation

The vertically averaged advection–dispersion equation (VAADE) in steady state by considering the retardation factor as one is applied as the governing transport equation (Wang and Anderson 1995; Bear and Cheng 2010). Therefore, a reliable flow treatment and transport is ensured, where both contamination concentration and hydraulic head are uniform in the vertical direction. VAADE can be presented as follows:

$$\frac{\partial }{\partial x}\left( {D_{xx} \frac{\partial c}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {D_{yy} \frac{\partial c}{\partial y}} \right) - \frac{\partial }{\partial x}\left( {\bar{v}_{x} c} \right) - \frac{\partial }{\partial y}\left( {\bar{v}_{y} c} \right) = 0$$
(4)

where c represents the contamination vertically averaged concentration, \(\bar{v}_{x}\) and \(\bar{v}_{y}\) indicate the seepage velocity components in x and y directions, and Dxx and Dyy denote the tensor components for the dispersion coefficient.

PCM formulation for 2D transport equation

In PCM, a group of points is scattered in the problem domain, which transformed the governing PDEs into algebraic equations. This solution is used for the whole problem and does not need any predefined mesh (Liu and Gu 2005). Since this method does not need time to generate a mesh, the calculation time and costs are saved (Meenal and Eldho 2012). The first step in PCM is definition of the trial solution c(x,y) as the following relation:

$$c(x,y){ = }\sum\limits_{j = 1}^{N} {c_{j} \varphi_{j} (x,y)} .$$
(5)

The RBF \(\varphi_{j} (x,y)\) in MQ is written as (Kansa 1990):

$$\varphi_{j} (x,y) = \left( {r^{2} + d_{s}^{2} } \right)^{0.5} = \sqrt {\left( {x - x_{j} } \right)^{2} + \left( {y - y_{j} } \right)^{2} + d_{s}^{2} }$$
(6)

where x and y represent the point of interest coordinates in the support domain and xj and yj represent the jth node coordinates in this domain. The derivatives are determined as follows with respect to y and x:

$$\frac{{\partial \varphi_{j} (x,y)}}{\partial x} = \frac{{(x - x_{i} )}}{{\varphi_{j} (x,y)}};\quad \frac{{\partial^{2} \varphi_{j} (x,y)}}{{\partial x^{2} }} = \frac{{((y - y_{i} )^{2} + d_{s}^{2} )}}{{\varphi_{j}^{3} (x,y)}}$$
(7a,b)
$$\frac{{\partial \varphi_{j} (x,y)}}{\partial y} = \frac{{(y - y_{i} )}}{{\varphi_{j} (x,y)}};\quad \frac{{\partial^{2} \varphi_{j} (x,y)}}{{\partial y^{2} }} = \frac{{((x - x_{i} )^{2} + d_{s}^{2} )}}{{\varphi_{j}^{3} (x,y)}}$$
(8a,b)

It can be written by substituting Eqs. (5), (6), (7a,b) and (8a,b) into Eq. (4):

$$c_{i} D_{xx} \frac{{\partial^{2} \varphi_{j} (x,y)}}{{\partial x^{2} }} - c_{i} \bar{v}_{x} \frac{{\partial \varphi_{j} (x,y)}}{\partial x} + c_{i} D_{yy} \frac{{\partial^{2} \varphi_{j} (x,y)}}{{\partial x^{2} }} - c_{i} \bar{v}_{y} \frac{{\partial \varphi_{j} (x,y)}}{\partial y} = 0$$
(9)

Here values of \(\varphi_{j} (x,y)\), \(\left( {{{\partial \varphi_{j} (x,y)} \mathord{\left/ {\vphantom {{\partial \varphi_{j} (x,y)} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)\), \(\left( {{{\partial \varphi_{j} (x,y)} \mathord{\left/ {\vphantom {{\partial \varphi_{j} (x,y)} {\partial y}}} \right. \kern-0pt} {\partial y}}} \right)\), \(\left( {{{\partial^{2} \varphi_{j} (x,y)} \mathord{\left/ {\vphantom {{\partial^{2} \varphi_{j} (x,y)} {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }}} \right)\) and \(\left( {{{\partial^{2} \varphi_{j} (x,y)} \mathord{\left/ {\vphantom {{\partial^{2} \varphi_{j} (x,y)} {\partial y^{2} }}} \right. \kern-0pt} {\partial y^{2} }}} \right)\) are calculated for every support domain. After that, they are incorporated in the global matrix of problem domain. Equation (9) can be plotted as a matrix after rearrangement in the following equation:

$$D_{xx} \left[ {{\mathbf{S}}_{{\mathbf{2}}} } \right]\left\{ {c_{i} } \right\} + D_{yy} \left[ {{\mathbf{S}}_{{\mathbf{4}}} } \right]\left\{ {c_{i} } \right\} = \bar{v}_{x} \left[ {{\mathbf{S}}_{{\mathbf{1}}} } \right]\left\{ {c_{i} } \right\} - \bar{v}_{y} \left[ {{\mathbf{S}}_{{\mathbf{3}}} } \right]\left\{ {c_{i} } \right\}$$
(10)

where [S1] and [S2] are the global matrices of the first derivative of RBFs with respect to x, while [S3] and [S4] are the global matrices of the first derivative of RBFs with respect to y. The boundary features should be assigned to boundary nodes with regard to the Neumann or Dirichlet boundary for integrating the boundary conditions. As the model is developed by OOP language, Eq. (10) is solved by linalg.solve function of Python package Numpy (Bakker and Kelson 2009), which facilitates computing functionality (Oliphant 2006).

Numerical model implementation

Development of AEM–PCM coupled model

According to the mentioned formulations, an AEM flow model and a PCM transport model are developed based on the AEM flow solution. In addition, these models are coupled to obtain AEM–PCM for groundwater flow and simulation of contamination transport:

Information on the porosity, dispersivity, hydraulic conductivity and area is collected from the source data. In the AEM flow model, area sink elements are used for rainfall recharge modeling. The flow and specific head boundaries are modeled by line sink elements. The uniform flow and point sink elements are used in the AEM flow model. Finally, the values of water head at all nodes considered in the PCM transport model can be calculated in the AEM flow model. Velocity is obtained in all of the nodes in the PCM, using Darcy’s law described in Eq. (11):

$$v = ki$$
(11)

where v represents velocity, k indicates hydraulic conductivity, and i represents the hydraulic gradient.

In the PCM transport model, the equidistant nodes are placed on boundaries and in the aquifer domain. A support domain is developed for each node (Meenal and Eldho 2011). For each support domain, the RBF \(\varphi_{j} (x,y)\) values, including its derivatives, are measured relative to x and y and integrated in the global matrices for the problem domain.

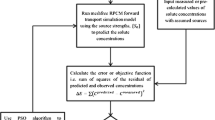
The values of water head are calculated at all nodes in the AEM flow model, and then, velocities at the same nodes are determined based on Eq. (11). In the PCM transport model, by using these velocities, concentration can be measured in the aquifer at all nodes. Figure 1 shows the developed model algorithm.

Fig. 1
figure 1

Flowchart for AEM–PCM coupled flow and transport model

Full size image

Example of practice

To evaluate the capability and applicability of the developed coupled AEM–PCM model for field problems, the contamination transport problem in Astaneh-Kuchesfahan plain’s aquifer, located in Gilan Province, north of Iran, is considered as a case study.

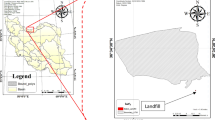
Astaneh-Kuchesfahan plain is one of the agricultural centers in Gilan Province located in north of Iran. The study area is bounded by the Caspian Sea in the north and opening of alluvial fans of Sefid-Rud River in the south. Lahijan–Chaboksar plain defines the eastern boundary and Foman plain defines the western boundary of the study area (Saatsaz et al. 2009). The plain is 35° 34′ 00″–35° 48′ 00″ north latitude and 49° 30′ 00″–50° 15′ 00″ east longitude. The geographical location of Astaneh-Kuchesfahan plain is shown in Fig. 2.

Fig. 2
figure 2

The location of  Astaneh-Kuchesfahan plain (Saatsaz et al. 2013)

Full size image

Conceptual model development

According to the available studies and reviews, Astaneh-Kuchesfahan plain has an unconfined aquifer (GROW 2005). According to Fig. 3, the maximum aquifer thickness is 250 m in the center of the plains and the minimum thickness is 40 m in the northern part of the plains.

Fig. 3
figure 3

The iso-thickness map of the study area (Saatsaz 2012)

Full size image

The model domain is limited by combined Triassic–Jurassic rocks and Cenozoic sedimentary materials on the eastern and western sides. On the other hand, studying the equipotential lines of groundwater makes it clear that the flow direction of water is from south to north. Therefore, the eastern and western parts are no flow boundaries, and they are entered the model by line sink element. The southern boundary is determined by the alluvial fan of Sefid-Rud River with an equipotential line of 40 m; thus, the boundary enters into the model by means of the line sink element with a specific head. The element is also used for the northern boundary that is 50 km along the coastal lines. The boundaries cover an area of about 942 km2 and a circumference of 136 km. The average range of groundwater level is from 40 m above to 25 m below the sea level. Given the significance of Sefid-Rud River, it is taken into the model as the line sink element with specific head. According to pumping test results, the ranges of transmissivity in the plain are from 500 m2 per day in the northern part to 4000 in central parts (Saatsaz et al. 2013).

Developing AEM flow model

After development of conceptual model, the input parameters are given to the present model. Moreover, 16 line sink elements are used for river modeling in the AEM. The flowchart for the developed AEM flow model for the specific case study is shown in Fig. 4.

Fig. 4
figure 4

Development of the flowchart of current AEM flow model

Full size image

To evaluate the present model accuracy, a comparison was made between the hydraulic heads and field hydraulic heads. According to steady-state groundwater modeling in this study, calibration was carried out in the model with respect to the distribution of hydraulic heads from 54 observation wells in March 2010. For calibration, a PSO algorithm was used. During the steady-state calibration, the riverbed conductance and hydraulic conductivity were modified preliminarily via sequential runs. Developing AEM–PSO flowchart for the present model calibration is shown in Fig. 5. Additionally, the coefficient of determination is used for evaluating the calibration results and is computed by the following relation:

Fig. 5
figure 5

Implementation of the AEM–PSO calibration model flowchart

Full size image
$$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {(h_{\text{o}} - h_{\text{c}} )^{2} } }}{{\sum\nolimits_{i = 1}^{N} {(h_{\text{o}} - \bar{h}_{\text{o}} )^{2} } }}$$
(12)

where ho is the observed groundwater level values, hc represents the calculated groundwater level values, \(\bar{h}_{\text{o}}\) represents the mean observed groundwater level values, and N is the total number of observed data.

The calibrated model results demonstrate that the ranges of riverbed conductance of the Sefid-Rud River are between 370 and 1000 m2 per day. According to the assumption of constant hydraulic conductivity for the entire studied area, the value has been estimated 12.75 m per day and also the coefficient of determination was found 0.87.

After calibration, the model was applied for simulating flow in June 2010. During the model verification, the coefficient of determination was found 0.89. These results indicated that the calibrated parameters are acceptable. According to the model results, the equipotential contour lines are shown in Fig. 6. The effects of discharging wells as point sink elements and river as line sink element in hydraulic head contours are clearly specified.

Fig. 6
figure 6

The equipotential contour lines based on the AEM flow model results

Full size image

AEM–PCM contaminant transport model

The contaminant transport model was developed based on the calibrated AEM flow model, discussed in the previous section.

The first stage was to specify the contaminant initial concentration in the model. Chloride anion was used in this study to model solute transport. After the initial concentrations were specified, the variables, containing the ratio of transverse dispersivity to longitudinal dispersivity and initial longitudinal dispersivity, were specified to the model. The ratio of horizontal transverse dispersivity to longitudinal dispersivity was assumed to be 0.1 m, and the effective molecular coefficient was considered 0.0. Considering the extension of the modeled area, it is difficult to determine an appropriate coefficient for longitudinal dispersivity. In a previous study (Saatsaz et al. 2013), the longitudinal dispersivity was set at 70 m.

According to the AEM flow model, the concentration distribution of chloride was considered for June 2010. To compare the calculated concentrations with ones observed, 19 sampling points were considered as concentration observation boreholes throughout the model. The transport model is based on the flow model in steady state, 7 sampling points data used for boundary conditions as specified concentration and other 12 sampling point data used for model verification.

Developing AEM–PCM transport model

Based upon the explanation of model development section, for implementation of the AEM–PCM coupled transport model, the number of considered nodes is 456 and the node number in the square-shaped support domain is 9. Furthermore, it is considered: \(\Delta x = \Delta y = 1500\) m and \(\begin{array}{*{20}c} {\alpha_{c} = 2} & ( \\ \end{array} \alpha_{cx} = \alpha_{cy} = \alpha_{c} )\). Therefore, ds is taken as 3000. Figure 7 shows the nodal arrangement in the problem domain for the AEM–PCM.

Fig. 7
figure 7

Nodal arrangement for the case study (\(\Delta x = \Delta y = 1500\) m)

Full size image

Sensitivity analysis

The developed mesh-free AEM–PCM model for two-dimensional contamination transport is tested for sensitivities of ds values for the field study. According to \(d_{s} = \alpha_{c} d_{c}\), a sensitivity study is conducted for \(\alpha_{c}\) by taking values of 1, 2 and 3 and nodal spacing (dc) is to be constant (Δx = Δy = 1500 m). The model is tested for different ds values of 1500, 3000 and 4500. Here, the nodal arrangement shown in Fig. 7 is considered. According to Table 1, the model results shows a good agreement with the observation field data except for ds = 1500.

Table 1 Coefficient of determination for three difference values of ds
Full size table

From Table 1, it is clear that the simulation result for ds = 3000 and αc = 2 is in reasonable agreement with the observation field data. According to the research of Liu and Gu (2005) by considering \(d_{s} = \alpha_{c} d_{c}\) and if dc is constant, an \(\alpha_{c}\) = 2.0–3.0 leads to good results for many problems. The present model results with αc = 2 and also Cs = 3000 are in agreement with the range of αc proposed by Liu and Gu (2005).

Comparison between the AEM–PCM model results for ds = 1500, 3000 and 4500 and the observed concentration is shown in Fig. 8.

Fig. 8
figure 8

Differences between the observed and calculated concentration by ds = 1500, 3000 and 4500 for 12 sampling points

Full size image

According to Fig. 8, the oscillations of results due to ds = 1500 is more than the oscillations of results due to ds = 3000 and 4500. The best results are calculated by ds = 3000; therefore, this value is considered for modeling in this area. The results of the AEM–PCM contaminant model based on the concentration contour lines are shown in Fig. 9.

Fig. 9
figure 9

The concentration contour lines according to ds = 3000 based on the AEM–PCM transport model results

Full size image

Conclusion

In this study, a mesh-free point collocation method is developed using Kansa’s approach for vertically averaged transport modeling based on continuous steady-state analytic element method flow solution in unconfined aquifers. Python OOP language for implementation and model development has been used. In the case of complex issues such as pumping wells, river and recharge areas, both models are coupled together for the contaminant and flow transport simulation. The developed AEM–PCM model is applied for contaminant and flow transport modeling in the aquifer of Astaneh-Kuchesfahan plain. The PSO algorithm for the AEM flow model calibration is used. The model results were compared with the observed field data, and a good agreement has been found. Moreover, sensitivity analysis was carried out, and the model was found to be sensitive to shape parameter ds. In the AEM flow model, analytic functions were used for groundwater flow modeling, so the solutions are analytically accurate. In the mesh-free PCM model, discretizing the transport-governing equations is straightforward, and there are simple algorithms for implementing these equations. In addition, precise assessment of shape parameter is challenging. The AEM–PCM transport and flow model can be applied for modeling mesh-free contaminant transport, based on the AEM flow solution.