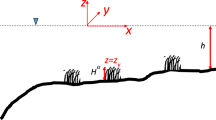
Abstract
A vertical two-dimensional numerical model has been applied to solving the Reynolds Averaged Navier-Stokes (RANS) equations in the simulation of current and wave propagation through vegetated and non-vegetated waters. The k-ɛ model is used for turbulence closure of RANS equations. The effect of vegetation is simulated by adding the drag force of vegetation in the flow momentum equations and turbulence model. To solve the modified N-S equations, the finite difference method is used with the staggered grid system to solver equations. The Youngs’ fractional volume of fluid (VOF) is applied tracking the free surface with second-order accuracy. The model has been tested by simulating dam break wave, pure current with vegetation, solitary wave runup on vegetated and non-vegetated channel, regular and random waves over a vegetated field. The model reasonably well reproduces these experimental observations, the modeling approach presented herein should be useful in simulating nearshore processes in coastal domains with vegetation effects.
Similar content being viewed by others
References
Asano T, Deguchi H, Kobayashi N. 1993. Interaction between water waves and vegetation. In: Edge B L, ed. Proceedings of the Twenty-Third Coastal Engineering Conference. New York: Am Soc of Civil Eng, 2710–2723
Augustin L N, Irish J L, Lynett P. 2009. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coastal Engineering, 56(3): 332–340
Cai Shuqun, Long Xiaomin, Gan Zijun. 2002. A numerical study of the generation and propagation of internal solitary waves in the Luzon Strait. Oceanologica Acta, 25: 51–60
Chen Jie, Jiang Changbo, Hu Shixiong, et al. 2010. Numerical study on the characteristics of flow field and wave propagation near submerged breakwater on slope. Acta Oceanologica Sinica, 29(1): 88–99
Dubi A, Torum A. 1997. Wave energy dissipation in kelp vegetation. In: Edge B L, ed. Proceedings of the Twenty-Fifth Coastal Engineering Conference. NewYork: Am Soc of Civil Eng, 2626–2639
Hieu P D, Katsutoshi T, Ca V T. 2004. Numerical simulation of breaking waves using a two-phase flow model. Applied Mathematical Modelling, 28: 983–1005
Hirt C W, Nichols B D. 1981. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39: 201–225
Huang W R, Xiao H. 2009. Numerical modeling of dynamic wave force acting on Escambia Bay Bridge Deck during Hurricane Ivan. Journal of Waterway, Port, Coastal, and Ocean Engineering, 135(4): 164–175
Iwata K, Kawasaki K, Kim D. 1996. Breaking limit, breaking and post breaking wave deformation due to submerged structures. Proc 25 Intr Conf Coastal Engineering Conference. Orlando, Florida: Am Soc of Civil Eng, 2338–2351
Kawasaki K J. 1999. Numerical simulation of breaking and post-breaking wave deformation process around a submerged breakwater. Coastal Engineering, 41: 201–223
Ketabdari MJ, Nobari M R H, Larmaei MM. 2008. Simulation of waves group propagation and breaking in coastal zone using a Navier Stokes solver with an improved VOF free surface treatment. Applied Ocean Research, 30: 130–143
Kothe D B, Mjolsness R C. 1992. Ripple: a new model for incompressible flows with free surfaces. AIAA Journal, 30(11): 2694–2700
Li C W, Yan K. 2007. Numerical investigation of wave-current-vegetation interaction. Journal of Hydraulic Engineering, 133(7): 794–803
Li C W, Zhang ML. 2010. 3D modelling of hydrodynamics and mixing in a vegetation field under waves. Computer & Fluids, 39(4): 604–614
Lin P, Liu P L F. 1998. A numerical study of breaking waves in the surf zone. Journal of Fluid Mechanics, 359: 239–264
Lopez F, Garcia M. 1997. Open channel flow through simulated vegetation: turbulence modeling and sediment transport. Wetlands Res Program Tech Rep No. WRP-CP 10, Waterw Exp Stn, Vicksburg, Miss
Lovas S M, Torum A. 2001. Effect of the kelp Laminaria hyperborean upon sand dune erosion and water particle velocities. Coastal Engineering, 44: 37–63
Mendez F J, Losada I J. 2004. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coastal Engineering, 53: 103–118
Möller I, Spencer T, French J R. 1996. Wind wave attenuation over salt marsh surfaces: preliminary results from Norfolk England. Journal of Coastal Research, 12(4): 1009–1016
Orlanski I. 1976. Simple boundary-condition for unbounded hyperbolic flows. Journal of Computational Physics, 21(3): 251–269
Ren B, Wang Y X. 2004. Numerical simulation of random wave slamming on structures in the splash zone. Ocean Engineering, 31(5–6): 547–560
Rudman M. 1997. Volume-tracking methods for interfacial flow calculations. International Journal for Numerical Methods in Fluids, 24: 671–691
Synolakis C E. 1987. The runup of solitary waves. Journal of Fluid Mechanics, 185: 523–545
Troch P, Rouck J D. 1999. An active wave generating-absorbing boundary condition for VOF type numerical model. Coastal Engineering, 38: 223–247
Turker U, Yagci O, Kabdaşl M S. 2006. Analysis of coastal damage of a beach profile under the protection of emergent vegetation. Ocean Engineering, 33: 810–828
Wu C H, Yuan H L, Young C C. 2007. Non-hydrostaticmodeling of vegetation effects on wave and flowmotions. Estuarine and Coastal Modeling Congress. Newport, Rhode Island, United States: Am Soc of Civil Eng, 304–321
Xu Z H, Yin B S, Hou Y J. 2011. Response of internal solitary waves to tropical storm Washi in the northwestern South China Sea. Annales Geophysicae, 29: 2181–2187
Youngs D L. 1982 Time-dependent multi material flow with large fluid distortion. In: Morton K, Baines M, eds. Numerical Methods for Fluid Dynamics. New York: Academic Press, 273–285
Author information
Authors and Affiliations
Corresponding author
Additional information
Foundation item: The National Natural Science Foundation of China under contract No. 51279023; the Public Science and Technology Research Funds Projects of Ocean under contract No. 201205023; the Special Funds for Postdoctoral Innovative Projects of Liaoning Province of China under contract No. 2011921018; the Special Funds for Talent Projects of Dalian Ocean University under contract No. SYYJ2011004.
Rights and permissions
About this article
Cite this article
Zhang, M., Hao, Z., Zhang, Y. et al. Numerical simulation of solitary and random wave propagation through vegetation based on VOF method. Acta Oceanol. Sin. 32, 38–46 (2013). https://doi.org/10.1007/s13131-013-0330-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13131-013-0330-4