Kinetic Model of Hydrogen Evolution at an Array of Au-Supported Catalyst Nanoparticles

Abstract

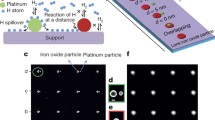
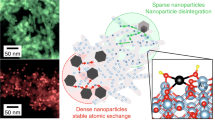
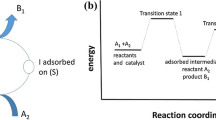
A model is presented for studying the electrocatalytic activity at an array of catalyst nanoparticles that is deposited on a catalytically inactive support material. The objective is to rationalize effects on apparent reactivity of sizes and packing densities of nanoparticles. In the current version, the focus of the model is on the contribution of the spillover effect of adsorbed hydrogen to the overall rate of the hydrogen evolution reaction. For nanoparticles of fixed size, the current density per catalyst surface area exhibits a peculiar maximum as a function of the surface particle density; the optimum particle density varies with the rate of spillover of adsorbed hydrogen from particle to support and with adsorbate surface diffusion. For fixed particle density, the current density per catalyst surface area increases strongly with decreasing particle size. The model was used to fit experimental current densities for different catalyst particle coverage at varying electrode potentials. A good agreement between experimental data and calculated results was found. The fits provide key parameters of surface processes on the catalyst/support system.

Appendix

Using ρ = r/r _R performing a Laplace transformation of Eq. 8 for ν  = 1 gives

$$ s\tilde{\theta }\left( {\rho, s} \right) - \tilde{\theta }\left( {\rho, t = 0} \right) = \frac{1}{\rho }\frac{\partial }{{\partial \rho }}\left[ {\rho \frac{{\partial \tilde{\theta }\left( {\rho, s} \right)}}{{\partial \rho }}} \right] - k_{\rm{s}}^{\rm{d}}\tilde{\theta }\left( {\rho, s} \right) $$

(A1)

The general solution is

$$ s\tilde{\theta }\left( {\rho, s} \right) = A{K_0}\left( {\rho \sqrt {{s + k_{\rm{s}}^{\rm{d}}}} } \right) + B{I_0}\left( {\rho \sqrt {{s + k_{\rm{s}}^{\rm{d}}}} } \right) $$

(A2)

The Laplace transform of the boundary condition at ${\rho_{\rm{c}}} = {{{r_{\rm{c}}}} \mathord{\left/{\vphantom {{{r_{\rm{c}}}} {{r_{\rm{R}}}}}} \right.} {{r_{\rm{R}}}}}$, Eq. 10, is

$$ \begin{array}{*{20}{c}} {{{\left. {\frac{{\partial \tilde{\theta }\left( {\rho, s} \right)}}{{\partial \rho }}} \right|}_{\rho = {\rho_{\rm{c}}}}}}{\begin{array}{*{20}{c}} { = \frac{{k_{\rm{c}}^{\rm{a}}}}{{2s}} + \frac{{k_{\rm{c}}^{\rm{a}} + k_{\rm{c}}^{\rm{d}}}}{2}\tilde{\theta }\left( {{\rho_{\rm{c}}},s} \right)} \\{ = - \sqrt {{s - \alpha }} A{K_1}\left( {\sqrt {{s - \alpha }} {\rho_{\rm{c}}}} \right) + \sqrt {{s - \alpha }} B{I_1}\left( {\sqrt {{s - \alpha }} {\rho_{\rm{c}}}} \right)} \\\end{array} } \\\end{array}, $$

(A3)

where the second step follows from Eq. A2.

The Laplace transform of the boundary condition at ρ = 1, Eq. 13, is

$$ \begin{array}{*{20}{c}} {{{\left. {\frac{{\partial \tilde{\theta }\left( {\rho, s} \right)}}{{\partial \rho }}} \right|}_{\rho = 1}}}{\begin{array}{*{20}{c}} { = 0} \\{ = - \sqrt {{s - \alpha }} A{K_1}\left( {\sqrt {{s - \alpha }} } \right) + \sqrt {{s - \alpha }} B{I_1}\left( {\sqrt {{s - \alpha }} } \right)} \\\end{array} } \\\end{array}, $$

(A4)

From Eqs. A3 and A4, we obtain

$$ \tilde{\theta }\left( {\rho, s} \right) = \frac{{k_{\rm{c}}^{\rm{a}}\left[ {{I_1}\left( {\sqrt {{s - \alpha }} } \right){K_0}\left( {\rho \sqrt {{s - \alpha }} } \right) + {K_1}\left( {\sqrt {{s - \alpha }} } \right){I_0}\left( {\rho \sqrt {{s - \alpha }} } \right)} \right]}}{{s\Delta (s)}} $$

(A5)

where

$$ \begin{gathered} \Delta (s) = 2\sqrt {{s - \alpha }} \left[ { - {I_1}\left( {\sqrt {{s - \alpha }} {\rho_{\rm{c}}}} \right){K_1}\left( {\sqrt {{s - \alpha }} } \right) + {K_1}\left( {\sqrt {{s - \alpha }} {\rho_{\rm{c}}}} \right){I_1}\left( {\sqrt {{s - \alpha }} } \right)} \right] \\+ \left( {k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}} \right)\left[ {{I_0}\left( {\sqrt {{s - \alpha }} {\rho_{\rm{c}}}} \right){K_1}\left( {\sqrt {{s - \alpha }} } \right) + {K_0}\left( {\sqrt {{s - \alpha }} {\rho_{\rm{c}}}} \right){I_1}\left( {\sqrt {{s - \alpha }} } \right)} \right]{ } \\\end{gathered} $$

(A6)

By inverse Laplace transformation of Eq. A5, ${L^{ - 1}}\left\{ {\tilde{\theta }\left( {\rho, s} \right)} \right\}$, we get

$$ \theta \left( {\rho, t} \right) = \frac{1}{{2\pi i}}\int_{\gamma - i\infty }^{\gamma + i\infty } {{e^{st}}} \tilde{\theta }\left( {\rho, s} \right) $$

(A7)

The integrand is a single-valued function of s with a simple pole at s = 0 and simple poles at $\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} = - \alpha_n^2$, where ±α _n are the roots of

$$ \begin{gathered} 2s\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} \left[ {{I_1}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} } \right){K_1}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right) - {K_1}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} } \right){I_1}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right)} \right] + \hfill \\s\left( {k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}} \right)\left[ {{K_1}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} } \right){I_0}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right) + {I_1}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} } \right){K_0}\left( {\sqrt {{s + k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right)} \right] = 0 \hfill \\\end{gathered} $$

(A8)

The residue at the pole s = 0 gives the stationary solution, θ _s(ρ)

$$ \begin{gathered} \hfill \\{\theta_{\rm{s}}}\left( \rho \right) = \frac{{k_{\rm{c}}^{\rm{a}}\left[ {{I_0}\left( {\rho \sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right){K_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right) + {K_0}\left( {\rho \sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right){I_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right)} \right]}}{{2\sqrt {{k_{\rm{s}}^{\rm{d}}}} \left[ { - {I_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right){K_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right) + {I_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right){K_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right)} \right] + \left( {k_{\rm{c}}^{\rm{a}} + k_{\rm{c}}^{\rm{d}}} \right)\left[ {{I_0}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right){K_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right) + {I_1}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} } \right){K_0}\left( {\sqrt {{k_{\rm{s}}^{\rm{d}}}} {\rho_{\rm{c}}}} \right)} \right]}} \hfill \\\end{gathered} $$

(A9)

To find the residues at $s = - \kappa \alpha_{\rm{n}}^2$, we need

$$ \begin{array}{*{20}c} {{\left[ {s\frac{{d\Delta }} {{ds}}} \right]}_{{s = - \kappa \alpha ^{2}_{{\text{n}}} }} = {\left[ {\frac{s} {{2{\sqrt {s + k^{{\text{d}}}_{{\text{s}}} } }}}\frac{{d\Delta }} {{d\mu }}} \right]}_{{\mu = i\alpha }} } \\ { = \frac{{ - \alpha ^{2}_{{\text{n}}} - k^{{\text{d}}}_{{\text{s}}} }} {{2i\alpha }}{\left\{ {\begin{array}{*{20}l} {{\rho _{{\text{c}}} \mu K_{1} {\left( \mu \right)}{\left[ {\mu I_{0} {\left( {\mu \rho _{{\text{c}}} } \right)} - {\left( {k^{{\text{a}}}_{{\text{c}}} + k^{{\text{d}}}_{{\text{c}}} } \right)}I_{1} {\left( {\mu \rho _{{\text{c}}} } \right)}} \right]}} \hfill} \\ {{ + \mu K_{0} {\left( \mu \right)}{\left[ {\mu I_{1} {\left( {\mu \rho _{{\text{c}}} } \right)} - {\left( {k^{{\text{a}}}_{{\text{c}}} + k^{{\text{d}}}_{{\text{c}}} } \right)}I_{0} {\left( {\mu \rho _{{\text{c}}} } \right)}} \right]}} \hfill} \\ {{ - \rho _{{\text{c}}} \mu I_{1} {\left( \mu \right)}{\left[ {\mu K_{0} {\left( {\mu \rho _{{\text{c}}} } \right)} - {\left( {k^{{\text{a}}}_{{\text{c}}} + k^{{\text{d}}}_{{\text{c}}} } \right)}K_{1} {\left( {\mu \rho _{{\text{c}}} } \right)}} \right]}} \hfill} \\ {{ + \mu I_{0} {\left( \mu \right)}{\left[ {\mu K_{1} {\left( {\mu \rho _{{\text{c}}} } \right)} - {\left( {k^{{\text{a}}}_{{\text{c}}} + k^{{\text{d}}}_{{\text{c}}} } \right)}K_{0} {\left( {\mu \rho _{{\text{c}}} } \right)}} \right]}} \hfill} \\ \end{array} } \right\}}} \\ \end{array} _{{\mu = i\alpha _{n} }} $$

(A10)

According to the properties of Bessel function, the recurrence Eq. A8, and the Wronskian relation, we find

$$ \begin{array}{*{20}{c}} {{{\left[ {s\frac{{{\text{d}}\Delta \left( {s + k_{\rm{s}}^{\rm{d}}} \right)}}{{{\hbox{d}}s}}} \right]}_{s + k_{\rm{s}}^{\rm{d}} = - \kappa \alpha_n^2}}}{\begin{array}{*{20}{c}} { = \frac{1}{2}\xi \alpha_n^2 - \frac{1}{{2\xi }}\left[ {\alpha_n^2 + \frac{{\left( {k_{\rm{s}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}} \right)}}{4}} \right]} \\{ = \frac{{F\left( {{\alpha_n}} \right)}}{{2{\alpha_n}{J_1}\left( {{\alpha_n}} \right)\left[ {{\alpha_n}{J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) + \frac{{\left( {k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}} \right)}}{2}{J_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right]}}} \\\end{array} } \\\end{array} $$

(A11)

where

$$ F\left( {{\alpha_n}} \right) = \alpha_n^2{\left[ {{\alpha_n}{J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) + \frac{{k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}}}{2}{J_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right]^2} + \alpha_n^2\left[ {\alpha_n^2 + \frac{{k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}}}{4}J_1^2\left( {{\alpha_n}} \right)} \right] $$

(A12)

Therefore,

$$ \theta \left( {\rho, \tau } \right) = {\theta_{\rm{s}}}\left( \rho \right) - \pi \sum\limits_{n{ = 1}}^\infty {\frac{{{e^{\left( { - k_{\rm{s}}^{\rm{d}} - \alpha_n^2} \right)t}}}}{{1 + \frac{{k_{\rm{s}}^{\rm{d}}}}{{\alpha_n^2}}}}\frac{{{J_0}\left( {\rho {\alpha_n}} \right)\left[ {\frac{{k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}}}{{k_{\rm{c}}^{\rm{a}}}}{Y_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) - \frac{{{\alpha_n}}}{{k_{\rm{s}}^{\rm{a}}}}{Y_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right] - {Y_0}\left( {\rho {\alpha_n}} \right)\left[ {\frac{{k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}}}{{2k_{\rm{c}}^{\rm{a}}}}{J_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) - \frac{{{\alpha_n}}}{{k_{\rm{c}}^{\rm{a}}}}{J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right]}}{{{{\left[ {\frac{{2{\alpha_n}{J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)}}{{k_{\rm{c}}^{\rm{a}}{J_1}\left( {{\alpha_n}} \right)}} + \left( {\frac{{k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}}}{{k_{\rm{c}}^{\rm{a}}}}} \right)\frac{{{J_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)}}{{{J_1}\left( {{\alpha_n}} \right)}}} \right]}^2} - {{\left( {\frac{{2{\alpha_n}}}{{k_{\rm{c}}^{\rm{a}}}}} \right)}^2} - {{\left( {\frac{{k_{\rm{c}}^{\rm{d}} + k_{\rm{s}}^{\rm{d}}}}{{k_{\rm{c}}^{\rm{a}}}}} \right)}^2}}}} $$

(A13)

Using the definition $\xi = \frac{{k_{\rm{c}}^{\rm{a}} + k_{\rm{c}}^{\rm{d}}}}{{k_{\rm{c}}^{\rm{a}}}}$ and $\frac{{k_{\rm{c}}^{\rm{a}} + k_{\rm{s}}^{\rm{d}}}}{{k_{\rm{c}}^{\rm{a}}}} = \frac{{ - 2{\alpha_n}\left[ {{Y_1}\left( {{\alpha_n}} \right){J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) - {J_1}\left( {{\alpha_n}} \right){Y_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right]}}{{k_{\rm{c}}^{\rm{a}}\left[ {{Y_1}\left( {{\alpha_n}} \right){J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) - {J_1}\left( {{\alpha_n}} \right){Y_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right]}} = \frac{{ - 2{\alpha_n}}}{{k_{\rm{c}}^{\rm{a}}}}C\left( {{\alpha_n}} \right)$ in Eq. A13 gives

$$ \theta \left( {\rho, t} \right) = {\theta_{\rm{s}}}\left( \rho \right) - \frac{\pi }{\xi }\sum\limits_{n = 1}^\infty {\frac{{{e^{\left( { - k_{\rm{s}}^{\rm{d}} - \alpha_n^2} \right)t}}}}{{1 + \frac{{k_{\rm{s}}^{\rm{d}}}}{{\alpha_n^2}}}}\frac{{\left[ {{Y_0}\left( {\rho {\alpha_n}} \right){J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) - {J_0}\left( {\rho {\alpha_n}} \right){Y_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right] + \left[ {{Y_0}\left( {\rho {\alpha_n}} \right){J_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right) - {J_0}\left( {\rho {\alpha_n}} \right){Y_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)} \right]}}{{{{\left[ {\frac{{{J_1}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)}}{{{J_1}\left( {{\alpha_n}} \right)}} - \frac{{C\left( {{\alpha_n}} \right){J_0}\left( {{\rho_{\rm{c}}}{\alpha_n}} \right)}}{{{J_1}\left( {{\alpha_n}} \right)}}} \right]}^2} - \left[ {\frac{1}{{C\left( {{\alpha_n}} \right)}} + C\left( {{\alpha_n}} \right)} \right]}}} $$

(A14)

Finally, we obtain Eq. A14 in the form of Eq. 14,

$$ \theta \left( {r,t} \right) = {\theta_{\rm{s}}}(r) - \sum\limits_{n{ = 1}}^\infty {{e^{\left( { - k_{\rm{s}}^{\rm{d}} - \alpha_n^2} \right)t}}f\left( {{J_n}(r){Y_n}(r)} \right)} $$

where the function $f{\left( {J_{n} {\left( r \right)},Y_{n} {\left( r \right)}} \right)}$ is composed of Bessel functions of the first and second kind,

$$ f\left( {{J_n}(r){Y_n}(r)} \right) = \frac{{\left[ {{Y_0}\left( {r{\alpha_n}} \right){J_1}\left( {{r_{\rm{c}}}{\alpha_n}} \right){J_0}\left( {r{\alpha_n}} \right){Y_1}\left( {{r_{\rm{c}}}{\alpha_n}} \right)} \right] + \left[ {{Y_0}\left( {r{\alpha_n}} \right){J_0}\left( {{r_{\rm{c}}}{\alpha_n}} \right) - {J_0}\left( {r{\alpha_n}} \right){Y_0}\left( {{r_{\rm{c}}}{\alpha_n}} \right)} \right]}}{{\left( {1 + \frac{{k_{\rm{s}}^{\rm{d}}}}{{\alpha_n^2}}} \right)\left[ {{{\left( {\frac{{{J_1}\left( {{r_{\rm{c}}}{\alpha_n}} \right)}}{{{J_1}\left( {{\alpha_n}} \right)}} - \frac{{C\left( {{\alpha_n}} \right){J_0}\left( {{r_{\rm{c}}}{\alpha_n}} \right)}}{{{J_1}\left( {{\alpha_n}} \right)}}} \right)}^2} - \left( {\frac{1}{{C\left( {{\alpha_n}} \right)}} + C\left( {{\alpha_n}} \right)} \right)} \right]}} $$

(A15)