1 Introduction

The fluid dynamics problem of boundary layer flow on stretching sheet has paramount importance in broad domains including pipe production with poly vinyl chloride, wiredrawing, metal casting, hot rolling, etc. Sakidas [1, 2] introduce studied for the first time related to the characteristic of boundary layer flow on stretched surface with a constant velocity. Crane [3] investigated further the stretch surface with a varying velocity. Tsou et al. [4]. Few recent applications of computational fluid dynamics addressed with boundary layer flow can be seen in [5,6,7,8,9,10,11,12,13], while the nanofluidic models of paramount interest can be seen in [14,15,16,17,18,19,20,21,22,23]. In boundary layer, flow problem role of heat source and sink becomes essential due to the requirement of the cooling process. Cortell [24] investigated boundary layer flow problem on stretching sheet involving heat source and sink. Dessie and Kishan [25] examined the effect of heat transfer with varying viscosity in a permeable medium on stretching surface involving the heat source and sink. Similarity other related studies conducted by research community Abel et al. [26], Khan et al. [27,28,29], Shafiq [30], Khan et al. [31,32,33]. The computational fluid dynamic problems involving nanofluidic models include thermal consideration in heat pipe involving n-pentane-acetone/methanol binary mixtures [34], microchannel heat sink model [35], turbulent heat transfer in double pipe heat exchanger model [36], magnetic field effect on micro-cross jet injection involving nanoparticle in a channel [37], electroosmosis-induced alterations in peristaltic pumping flow models [38], Navier's slip condition along with magnetic field impacts on unsteady stagnation point nanofluidic flow models [39] and entropy generation and Cattaneo–Christov diffusion model involving micropolar magneto cross nanofluids [40]. Besides these applications, many studies based on deterministic solver like homotopy analysis method [41, 42] are exploited arising in the domain of fluid mechanics governed with boundary layer flow on stretching sheet with heat source and sink are conducted, while artificial intelligence (AI) based computing procedures through supervised/unsupervised neural networks looks to be a promising alternative implemented for these fluidics problems.

Modern AI algorithms-based stochastic methods via neural networks, evolutionary/swarming heuristic procedures and efficient local search methodologies are implemented to variety of linear as well as nonlinear systems represented with integer and non-integer differential models [43, 44]. Recent applications of stochastic solvers include mathematical model in bioinformatics, such as model of heartbeat dynamics, HIV infection dynamics, nonlinear corneal shape model, mosquito dispersion model, nonlinear SITR model for COVID-19 virus spread and heat distribution dynamic of human head; application in physics, such as astrophysics, thermodynamics, atomic physics, plasma, nuclear physics, nonlinear optics, nanotechnology, magnetohydrodynamics and nonlinear circuits; application in fractional-order systems such as Riccati equation, Bagley-Torvik equation, and fractional different equations. Few renewed applications in fluid dynamics such as modeling the thermal conductivity of ZnO-EM with experimental datasets [45], reliable synthesized CuFe2O4/SiO2 nanocomposites models [46], modeling for Fe–CuO/Eg–Water nanofluid [47], refrigeration system [48], optimal thermal conductivity enhancement of nano-antifreeze using carbon nanotubes [49], models for the dynamic viscosity of CuO/water nanofluids [50], modeling of hybrid nanofluidic models [51, 52], measuring thermophysical properties of carbon-based nanofluidic models [53], effects of COOH-MWCNTs on thermal conductivity of antifreeze model [54] and entropy generation of hybrid nanofluidic systems [55]. The aforesaid evidences proved that AI-based solvers are reliable for viable analysis of still nonlinear mathematical model of fluid mechanics representing the dynamics of MHD flow past a stretching surface embedded in porous medium. The contribution and innovative insights into the proposed backpropagated networks-based numerical computing are compactly listed as follows:

  • A novel application of backpropagated neural networks (BNNs)-based computing paradigm is presented for numerical treatment of the dynamics of magnetohydrodynamic nanofluidic model (MHD-NFM) past over a stretching surface embedded in porous medium involving heat source/sink as well as variable viscosity.

  • The ODEs representation of MHD-NFM is derived from governing PDEs by exploitation of suitable similarity transformations.

  • The reference dataset of BNNs is formulated using Adams numerical scheme for variants of MHD-NFM by variation of viscosity, permeability of heat source/sink and magnetic field parameters as well as Prandtl number.

  • The comparative analyses on accuracy and convergence metrics through MSE, histograms, correlation and regression have proven the significance of designed BNNs.

The organization for rest of paper is furnished as follows: The mathematical representation of the MHD-NFM is briefly introduced in Sect. 2, the methodology BNNs to solve system model is narrated in Sect. 3, the outcomes of BNNs with necessary descriptive details are provided in Sect. 4, while the concluding statements are compactly presented in the Sect. 5.

2 Mathematical model of MHD-NFM

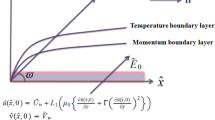
The two-dimensional stretching sheet embedded in a porous medium is considered along with heat generation/absorption. A magnetic force is applied symmetrically in the region y ≥ 0, which is shown in  Fig. 1 as a geometry of the problem. Two forces are applied in the opposite directions against x-axis for stretching of the sheet. The temperature at the free stream region is different for the surface temperature, and the viscosity of the fluid is depending on the variation in the temperature. Lie group transformations in terms of single parametric form are incorporated for the magneto hydrodynamics flow of fluid past a stretching sheet along with heat source/sink and variable viscosity embedded in a porous medium.

Fig. 1
figure 1

Geometry of MHD-NFM consider in the presented study

Full size image

The governing equations of the problem are as follows:

$$\left( {1 + A\left( {1 - \theta } \right)} \right)f^{\prime\prime\prime} + f^{\prime\prime}\left( {f - A\theta^{\prime}} \right) - f^{\prime}\left( {f^{\prime} + M} \right) - k_{1} \left( {1 + A\left( {1 - \theta } \right)} \right)f^{\prime} = 0,$$
(1)
$$\theta^{\prime\prime} + \Pr \left( {\lambda \theta + f\theta^{\prime}} \right) = 0.$$
(2)

The associated boundary conditions for the fluid flow are:

\(f = 0\), \(\theta = 1\) \({\text{when}}\) \(\eta^{ * } = 0\).

$$f^{\prime} \to 0, \theta \to 0, {\text{when}}\, \eta^{ * } \to \infty$$
(3)

,

where, \(A = b\left( {T_{w} - T_{\infty } } \right)\) is the viscosity parameter, \(M = \sigma _{c} B_{0}^{2} /\rho c\) represents magnetic parameter, \(k_{1} = v^{*} /ck\) is the parameter of permeability, \(\lambda = Q_{0} /\rho cC_{P}\) and \(\Pr = v^{*} /k\) shows the Prandtl number.

3 Methodology

The methodology presented here for the proposed BNNs is executed by utilizing ‘nftool,’ which is an effective algorithm in neural networks (NNs) toolbox of MATLAB software package, while weights of network is adopted by Levenberg–Marquardt (LM) approach. The methodology comprises two parts; in the first part, essential description is provided for creation of dataset for LM-NN, while in the second part, implementation procedure implemented for LM-NN is described. The overall process flow of methodology is presented in Fig. 2, while the designed LM-NN through single neuron setup is shown in Fig. 3.

Fig. 2
figure 2

Process workflow of proposed LM-NN for MHD-NFM

Full size image
Fig. 3
figure 3

A structure of a single neuron model

Full size image

The reference solutions, i.e., dataset of LM-NN, is created for inputs between 0 and 10 with time interval of 0.05 by using approach of Adams numerical solver through ‘NDSolve’ program in Mathematica software package for each variant of MHD fluidic system as listed in Table 1.

Table 1 Depiction of scenarios in conjunction with 4 diverse cases of velocity and temperature parameter, respectively, of MHD-NFM
Full size table

4 Numerical experimentation with interpretation of results

Results of numerical investigation with essential explanation for the proposed BNNs via Levenberg are given here for dynamics of viscosity of MHD fluidic system as presented in Eqs. (17–19). The five scenarios of the system model (17–19) by variation of A, λ, K1, Pr, and M are formulated for four cases for both velocity and temperature parameter, respectively, of MHD flow model as tabulated in Table 1.

The reference solutions \(f(\eta )\), \(f^{\prime}(\eta )\) and \(\theta (\eta )\) i.e., dataset of LM-NNs, are estimated with Adams method for η between 0 and 10 for scenarios 1–5, for all four cases of LM-NN model in Eqs. (17–19). The dataset created by Adams method in terms of \(f(\eta )\), \(f^{\prime}(\eta )\) and \(\theta (\eta )\) is used as a reference result throughout in the presented study.

The proposed LM-NN approach is applied for creating the solution for fluid dynamics model of stretchable surface with porous medium involving heat source or sink as well as variable viscosity of MHD flow model Eqs. (17–19) using ‘nftool’ routine. The outcomes of reference solutions for velocity and temperature profile (\(f\), \(f^{\prime}\) and \(\theta\)) in the case of 201 inputs are given for training (70%), validation (15%) and testing (15%) for LM-NN approach using the network presented in Fig. 4. The proposed LM-NN approach is repeated for 5 different scenarios by variety of A, λ, K1, Pr, and M for four different cases for both velocity and temperature parameter, respectively, of MHD-NFM with values as tabulated in Table 1.

Fig. 4
figure 4

LM-NN architecture for MHD-NFM

Full size image

The outcomes of LM-NN for each scenario (4) in terms of performance and states are given in Figs. 5 and 6 and fitting illustration in Figs. 7, 8, 9 and 10. Moreover, histogram plots are shown in Fig. 11, and regression parameters are portrayed in Figs. 12, 13, 14 and 15. Figures 7, 8, 9 and 10 demonstrate fitting plots in terms of solution with error for respective five different cases. Additionally, the convergence achieved in shape of mean square error for training, testing, validation and performance, accomplished epochs, backpropagation operators and time complexity is presented in Tables 2, 3, 4, 5, 6, 7, 8 and 9 for scenarios 1 to 5, respectively, for both variations on velocity and temperature parameter of MHD-NFM.

Fig. 5
figure 5

Performance curves on mean square error for designed LM-NNs for answering MHD-NFM

Full size image
Fig. 6
figure 6

State transition dynamics of LM-NN for answering MHD-NFM

Full size image
Fig. 7
figure 7

Presentation of LM-NN results with outputs of dataset for second case of scenario 1 of magnetohydrodynamics nanofluidic model (MHD-NFM)

Full size image
Fig. 8
figure 8

Presentation of LM-NN results with outputs of dataset for second case of scenario 2 of magnetohydrodynamics nanofluidic model (MHD-NFM)

Full size image
Fig. 9
figure 9

Presentation of LM-NN results with outputs of dataset for second case of scenario 3 of magnetohydrodynamics nanofluidic model (MHD-NFM)

Full size image
Fig. 10
figure 10

Presentation of LM-NN results with outputs of dataset for second case of scenario 5 of magnetohydrodynamics nanofluidic model (MHD-NFM)

Full size image
Fig. 11
figure 11

Error histogram dynamics for LM-NN results for second case of 4 scenarios of MHD-NFM

Full size image
Fig. 12
figure 12

Regression diagrams for LM-NN results of second case of scenario 1 of MHD-NFM

Full size image
Fig. 13
figure 13

Regression diagrams for LM-NN results of second case of scenario 2 of MHD-NFM

Full size image
Fig. 14
figure 14

Regression diagrams for LM-NN results of second case of scenario 3 of MHD-NFM

Full size image
Fig. 15
figure 15

Regression diagrams for LM-NN results of second case of scenario 5 of MHD-NFM

Full size image
Table 2 Outcomes of LM-NN of scenario 1 (variation of A for velocity parameter) of MHD-NFM
Full size table
Table 3 Outcomes of LM-NN scenario1 (variation of A for temperature parameter) of MHD-NFM
Full size table
Table 4 Outcomes of LM-NN of scenario 2 (variation of λ for temperature parameter) of MHD-NFM
Full size table
Table 5 Outcomes of LM-NN for scenario 3 (variation of k1 for temperature parameter) of MHD-NFM
Full size table
Table 6 Outcomes of LM-NN for scenario 3 (variation of k1 for velocity parameter) of MHD-NFM
Full size table
Table 7 Outcomes of LM-NN for scenario 4 (variation of Pr for temperature parameter) of MHD-NFM
Full size table
Table 8 Outcomes of LM-NN for scenario 5 (variation of M for temperature parameter) of MHD-NFM
Full size table
Table 9 Outcomes of LM-NN for scenario 5 (variation of M for velocity parameter) of magnetohydrodynamics nanofluidic model MHD-NFM
Full size table

In subfigures 5(a), 5(b), 5(c) and 5(d), convergence of mean square error for train, test and validation best curve is given for second case of scenarios 1, 2, 3 and 5 of magnetohydrodynamics nanofluidic model (MHD-NFM). One may witness that the most excellent and unified execution is accomplished at 355, 383, 360 and 357 epochs with MSE in the range 10–9, 10–9, 10–9, and 10–09, individually. The gradient and Mu parameters of Levenberg–Marquardt backpropagation are [9.94 × 10–08, 9.77 × 10–08, 9.951 × 10–08 and 9.92 × 10–08] and [10–07, 10–08, 10–07, 10–07] as shown in subfigures 6(a), 6(b), 6(c) and 6(d). The outputs prove correctness and convergent efficacy of LM-NN scheme for each case of MHD-NFM.

The efficacy of LM-NN-based calculated results is observed with matching outcomes of Adams numerical solver for scenarios 1, 2, 3 and 5 of MHD-NFM as shown in Figs. 7–10 and further endorsed by error plots. The maximum error for testing, training and validation inputs of the design LN-NN is around 2 × 10–04, 1 × 10–04, 10 × 10–04 and 1 × 10–04 for different cases of system MHD-NFM. The dynamics of the performance is further assessed by error histogram as given in subfigures 11(a), 11(b), 11(c) and 11(d) for scenarios 1, 2, 3 and 5, respectively, of MHD-NFM. The average error value closed to zero line or at 1.33 × 10–06, 3.5 × 10–06, -2 × 10–06 and -0.00018 for respective 1, 2, 3 and 5 scenarios of MHD-NFM. The investigation through regression trainings is carried out by means of co-relation studies. Figures 12, 13, 14, and 15 are the results of regression outputs of respective four variations of MHD-NFM given in Eqs. (17–19). One may witness that the values of correlation index R are closed to unity, i.e., perfect modeling scenario, in case of training, testing as well as validation, which certified the correctness of LM-NN methodology for MHD-NFM.

Furthermore, the respective numerical values listed in Tables 2, 3, 4, 5, 6, 7, 8 and 9 for scenarios 1–5 of both velocity and temperature parameter of MHD-NFM demonstrate that performance on MSE for proposed LM-NN procedure is around 10–09 to 10–07, 10–09, 10–10 to 10–09, 10–10 to 10–09, 10–09, 10–10 to 10–07, 10–09 and 10–10 to 10–09 for MHD-NFM. All numerical results and illustrations presented in Table 2, 3, 4, 5, 6, 7, 8, 9 and 10 authenticate the consistent, robust and accurate performance of LM-NN for solving the variants of MHD-NFM.

Besides the presentation of the analysis on first element of velocity component, i.e., \(f(\eta )\), the analysis should be extending for variation of velocity profile \(f^{\prime}(\eta )\) and temperature profile \(\theta (\eta )\). Therefore, the results of LMBNNs are calculated for \(f^{\prime}(\eta )\), \(\theta (\eta )\) for all five scenarios of MHD-NFM and are given in Figs. 16–19.

Fig. 16
figure 16

Presentation of designed LM-NN with outputs of dataset of scenario 1 of MHD-NFM

Full size image
Fig. 17
figure 17

Presentation of designed LM-NN with outputs of dataset of scenario 2 and 4 of MHD-NFM

Full size image
Fig. 18
figure 18

Presentation of designed LM-NN with outputs of dataset of scenario 3 of MHD-NFM

Full size image
Fig. 19
figure 19

Presentation of designed LM-NN with outputs of dataset of scenario 5 of MHD-NFM

Full size image

The outcomes of velocity profile \(f^{\prime}(\eta )\) for scenarios 1, 2, 4 and 5 are given in subfigures 16 (a), 18 (a) and 19 (a) of MHD-NFM. These results show the consistent and accurate overlapping of proposed and reference solutions. The respective values of AE are plotted in 16(b and d), 17(b and d) 18(b and d) and 19(b and d) in order to access the performance of LM-NN approach. Accordingly, the outcomes of temperature profile θ(η) are shown in subfigures 16 (c), 17 (a), 17 (b), 18 (c) and 19 (c) for scenarios 1, 2, 3, 4 and 5, respectively, of MHD-NFM. These results also show the consistent overlapping between proposed and reference results. The AE attain values for scenarios 1, 2 and 5 for velocity profile 10–06 to 10–02, 10–07 to 10–03 and 10–06 to 10–03, respectively. The AE attained for temperature profile is around 10–08 to 10–03, 10–07 to 10–04, 10–07 to 10–03, 10–07 to 10–04 and 10–07 to 10–04, for scenarios 1, 2, 3, 4 and 5 individually. The numerical and graphical diagrams validated accuracy, convergence and robustness of LM-NN methodology for the solution of MHD-NFM.

5 Conclusions

The integrated stochastic numerical computing solver is presented for finding the solution of fluid mechanics problem representing the dynamics of MHD-NFM along a stretchable surface with porous medium involving heat source or sink, as well as variable viscosity based on different scenarios for parameter of viscosity, parameter of heat source and sink, parameter of permeability, magnetic field parameter, and Prandtl number. The training (70%), validation (15%) and testing (15%) are exploited to develop the designed LM-NNs with 10 number of hidden neurons. The MSE level 10–09 to 10–04 authenticated the accuracy of the proposed structure based on LM-NNs. Additionally, the correctness is verified through numerical and graphical illustrations for the convergence plots on MSE index, regression dynamics as well as error histograms.