Optimal Strategy in a Two Resources Two Consumers Grazing Model

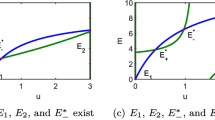
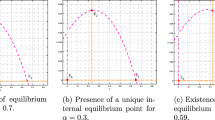
Abstract

In this paper, we consider a mathematical model of two herbivore groups and two available resources, described by a control system. The controls model how the herbivores feed on the two types of resources. The choice of these controls is based on the standard assumption of optimal feeding theory that requires each predator to maximize the net rate of energy intake during feeding. Qualitative analysis of the model highlights four resource thresholds, called resource switching densities. At these thresholds, herbivores can have pure dynamics, meaning that they consume only one type of resource, or adaptive dynamics, meaning that they consume both types of resources. Various equilibria, including the coexistence equilibrium and boundaries equilibria, are computed and their stability analysis are rigorously studied. A detailed description of the switching zones is made using Filippov’s solutions. Notably, we find that within the framework of adaptative dynamics, the system components may experience a long term sustainable coexistence where in the pure dynamics case, at least one component may go to extinction. Also, thanks to the adaptative dynamics, periodic behaviors in the system are observed. Finally, we provide some numerical simulations in order to illustrate our qualitative results.

Appendices

Appendix A. Proof of Lemma 3

• (1) Since the vector field defined by the right hand side of system (1) is tangential on the boundary of ${\mathbb {R}}^4_+$, therefore for any initial condition in ${\mathbb {R}}^4_+$ the solution of system (1) remains in ${\mathbb {R}}^4_+$.

• (2) Let us now prove that the set $\Omega$ is a positively invariant region and absorbing set for the system (1). From the first equation we have:

  $$\begin{aligned} R_1(t)\le \displaystyle \frac{K_1 R_1(0)}{R_1(0)+e^{-r_1t}(K_1-R_1(0))}. \end{aligned}$$

  Since $r_1> 0$, one has $\limsup \limits _{t \rightarrow \infty } R_1(t)\le K_1$. Similarly, one may deduce that $\limsup \limits _{t \rightarrow \infty } R_2(t)\le K_2$. Let us set

  $$\begin{aligned} \omega (t)=R_1(t)+R_2(t)+\left( \displaystyle \frac{1}{e_1}+\displaystyle \frac{1}{e_2}\right) H_1(t)+\left( \displaystyle \frac{1}{e_1'}+\displaystyle \frac{1}{e_2'}\right) H_2(t) \end{aligned}$$

  and $\eta >0$ be a constant, with $\eta <\min (\mu _1,\mu _2)$. Then

  $$\begin{aligned} {\dot{\omega }}+\eta \omega= & {} {\dot{R}}_1+{\dot{R}}_2+\left( \frac{1}{e_1}+\frac{1}{e_2}\right) {\dot{H}}_1+\left( \frac{1}{e_1'}+\frac{1}{e_2'}\right) {\dot{H}}_2\\+ & {} \eta \Big (R_1+R_2+\left( \frac{1}{e_1}+\frac{1}{e_2}\right) H_1+\left( \frac{1}{e_1'}+\frac{1}{e_2'}\right) H_2\Big )\\= & {} (r_1+\eta )R_1-\displaystyle \frac{r_1R_1^2}{K_1}+(r_2+\eta )R_2-\displaystyle \frac{r_2R_2^2}{K_2}-(\mu _1-\eta )H_1-(\mu _2-\eta )H_2 \end{aligned}$$

  Since $\eta <\min (\mu _1,\mu _2)$, we have

  $$\begin{aligned} {\dot{\omega }}+\eta \omega\le & {} (r_1+\eta )R_1-\displaystyle \frac{r_1R_1^2}{K_1}+(r_2+\eta )R_2-\displaystyle \frac{r_2R_2^2}{K_2}\\= & {} \frac{K_1}{4r_1}(r_1+\eta )^2-\frac{r_1}{K_1}\Big (R_1-\frac{K_1}{2r_1}(r_1+\eta )\Big )^2\\+ & {} \frac{K_2}{4r_2}(r_2+\eta )^2-\frac{r_2}{K_2}\Big (R_2-\frac{K_2}{2r_2}(r_2+\eta )\Big )^2\\\le & {} \frac{K_1}{4r_1}(r_1+\eta )^2+\frac{K_2}{4r_2}(r_2+\eta )^2=\nu . \end{aligned}$$

  Applying the theory of differential inequality (Birkoff and Rota [3]), we obtain

  $$\begin{aligned} 0<\omega \Big (R_1(t),R_2(t),H_1(t),H_2(t)\Big )\le \frac{\nu }{\eta }\Big (1-e^{-\eta t}\Big )+\Big (R_1(0),R_2(0),H_1(0),H_2(0)\Big )e^{-\eta t}. \end{aligned}$$

  Consequently, part 2 of Lemma 3 holds. This completes the proof.

Appendix B. Proof of Theorem 2

• (a) Stability of $E_{01}^*=(R_{11}^*,0,0,H_{21}^*)$. The characteristic polynomial of the Jacobian matrix of system (1) at equilibrium $E_{01}^*$ is given by

  $$\begin{aligned} P(\lambda )=(a_{22}-\lambda )(a_{33}-\lambda )(\lambda ^2-a_{11}\lambda -a_{14}a_{41}) \end{aligned}$$

  (19)

  where, $a_{33}=\displaystyle \frac{e_1p_1\ell _1R_{11}^*}{1+p_1h_1\ell _1R_{11}^*}-\mu _1$, $a_{22}=r_2-\displaystyle \frac{q_1\ell _1'H_{21}^*}{1+q_1h_1'\ell _1'R_{11}^*}$, $a_{11}=r_1(1-\frac{R_{11}^*}{K_1})-\displaystyle \frac{q_1\ell _1'H_{21}^*}{(1+q_1h_1'\ell _1'R_{11}^*)^2}$, $a_{14}=-\displaystyle \frac{q_1\ell _1'R_{11}^*}{1+q_1h_1'\ell _1'R_{11}^*}$ and $a_{41}=\displaystyle \frac{e_1'q_1\ell _1'H_{21}^*}{(1+q_1h_1'\ell _1'R_{11}^*)^2}$. Since $-a_{14}a_{41}>0$, then $E_{01}^*$ is locally asymptotically stable if $a_{33}<0$, $a_{22}<0$ and $a_{11}<0$ i.e., ${\mathcal {A}}_{01}<1$, ${\mathcal {A}}_{02}<1$ and ${\mathcal {A}}_{03}<1$, where ${\mathcal {A}}_{01}=\displaystyle \frac{e_1p_1\ell _1R_{11}^*}{\mu _1(1+h_1p_1\ell _1R_{11}^*)}$, ${\mathcal {A}}_{02}=\displaystyle \frac{r_2(1+h_1'q_1\ell _1'R_{11}^*)}{q_1\ell _1'H_{21}^*}$ and ${\mathcal {A}}_{03}=\displaystyle \frac{r_1\left( 1-\frac{R_{11}^*}{K_1}\right) (1+h_1'q_1\ell _1'R_{11}^*)^2}{q_1\ell _1'H_{21}^*}$.

• (b) Stability of $E_{02}^*=(R_{12}^*,0,H_{12}^*,0)$. The characteristic polynomial of Jacobian matrix of system (1) at equilibrium $E_{02}^*$ is given by

  $$\begin{aligned} P(\lambda )=(b_{22}-\lambda )(b_{44}-\lambda )(\lambda ^2-b_{11}\lambda -b_{13}b_{31}) \end{aligned}$$

  (20)

  where, $b_{44}=\displaystyle \frac{e_1'q_1\ell _1'R_{12}^*}{1+q_1h_1'\ell _1'R_{12}^*}-\mu _2$, $b_{22}=r_2-\displaystyle \frac{p_2\ell _2H_{12}^*}{1+p_1h_1\ell _1R_{12}^*}$, $b_{11}=-\displaystyle \frac{ r_1R_{12}^*}{K_1}+\displaystyle \frac{p_1\ell _1^2H_{12}^*}{1+p_1h_1\ell _1R_{12}^*}$, $b_{13}=-\displaystyle \frac{p_1\ell _1R_{12}^*}{1+p_1h_1\ell _1R_{12}^*}$ and $b_{31}=\displaystyle \frac{e_1p_1\ell _1H_{12}^*}{(1+p_1h_1\ell _1R_{12}^*)^2}$. Since $-b_{13}b_{31}>0$, then $E_{02}^*$ is locally asymptotically stable if $b_{44}<0$, $b_{22}<0$ and $b_{11}<0$ i.e ${\mathcal {A}}_{04}<1$, ${\mathcal {A}}_{05}<1$ and ${\mathcal {A}}_{06}<1$, where ${\mathcal {A}}_{04}=\displaystyle \frac{e_1'q_1\ell _1'R_{12}^*}{\mu _2(1+h_1'q_1\ell _1'R_{12}^*)}$, ${\mathcal {A}}_{05}=\displaystyle \frac{r_2(1+h_1p_1\ell _1R_{12}^*)}{p_2\ell _2H_{12}^*}$ and ${\mathcal {A}}_{06}=\displaystyle \frac{K_1p_1^2\ell _1^2H_{12}^*}{r_1R_{12}^*(1+h_1p_1\ell _1R_{12}^*)}$.

• (c) Stability of $E_{03}^*=(0,R_{23}^*,0,H_{23}^*)$. The characteristic polynomial of Jacobian matrix of system (1) at equilibrium $E_{03}^*$ is given by

  $$\begin{aligned} P(\lambda )=(c_{11}-\lambda )(c_{33}-\lambda )(\lambda ^2-c_{22}\lambda -c_{24}a_{42}) \end{aligned}$$

  (21)

  where, $c_{33}=\displaystyle \frac{e_2p_2\ell _2R_{23}^*}{1+h_2p_2\ell _2R_{23}^*}-\mu _1$, $c_{11}=r_1-\displaystyle \frac{q_2\ell _2'H_{23}^*}{1+h_2'q_2\ell _2'R_{23}^*}$, $c_{22}=r_2(1-\frac{R_{23}^*}{K_2})-\displaystyle \frac{q_2\ell _2'H_{23}^*}{(1+h_2'q_2\ell _2'R_{23}^*)^2}$, $c_{24}=-\displaystyle \frac{q_2\ell _2'R_{23}^*}{1+q_2h_2'\ell _2'R_{23}^*}$ and $c_{42}=\displaystyle \frac{e_2'q_2\ell _2'H_{23}^*}{(1+h_2'q_2\ell _2'R_{23}^*)^2}$. Since $-c_{24}c_{42}>0$, then $E_{03}^*$ is locally asymptotically stable if $c_{33}<0$, $c_{22}<0$ and $c_{11}<0$ i.e ${\mathcal {A}}_{07}<1$, ${\mathcal {A}}_{08}<1$ and ${\mathcal {A}}_{09}<1$, where ${\mathcal {A}}_{07}=\displaystyle \frac{e_2p_2\ell _2R_{23}^*}{\mu _1(1+h_2p_2\ell _2R_{23}^*)}$, ${\mathcal {A}}_{08}=\displaystyle \frac{r_1(1+h_2'q_2\ell _2'R_{23}^*)}{q_2\ell _2'H_{23}^*}$ and ${\mathcal {A}}_{09}=\displaystyle \frac{r_2(1-\frac{R_{23}^*}{K_2})(1+h_2'q_2\ell _2'R_{23}^*)^2}{q_2\ell _2'H_{23}^*}$.

• (d) Stability of $E_{04}^*=(0,R_{24}^*,H_{14}^*,0)$. The characteristic polynomial of Jacobian matrix of system (1) at equilibrium $E_{04}^*$ is given by

  $$\begin{aligned} P(\lambda )=(d_{11}-\lambda )(d_{44}-\lambda )(\lambda ^2-d_{22}\lambda -d_{23}d_{32}) \end{aligned}$$

  (22)

  where, $d_{44}=\displaystyle \frac{e_2'q_2\ell _2'R_{24}^*}{1+h_2'q_2\ell _2'R_{24}^*}-\mu _2$, $d_{11}=r_1-\displaystyle \frac{p_1\ell _1H_{14}^*}{1+h_2p_2\ell _2R_{24}^*}$, $d_{22}=-\displaystyle \frac{ r_2R_{24}^*}{K_2}+\displaystyle \frac{p_2^2\ell _2^2h_2H_{14}^*}{1+h_2p_2\ell _2R_{24}^*}$, $d_{23}=-\displaystyle \frac{p_2\ell _2R_{24}^*}{1+h_2p_2\ell _2R_{24}^*}$ and $d_{32}=\displaystyle \frac{e_2p_2\ell _2H_{14}^*}{(1+h_2p_2\ell _2R_{24}^*)^2}$. Since $-d_{23}d_{32}>0$, then $E_{04}^*$ is locally asymptotically stable if $d_{44}<0$, $d_{22}<0$ and $d_{11}<0$ i.e ${\mathcal {A}}_{10}<1$, ${\mathcal {A}}_{20}<1$ and ${\mathcal {A}}_{30}<1$, where ${\mathcal {A}}_{10}=\displaystyle \frac{e_2'q_2\ell _2'R_{24}^*}{\mu _2(1+h_2'q_2\ell _2'R_{24}^*)}$, ${\mathcal {A}}_{20}=\displaystyle \frac{r_1(1+h_2p_2\ell _2R_{24}^*)}{p_1\ell _1H_{14}^*}$ and ${\mathcal {A}}_{30}=\displaystyle \frac{K_2p_2^2\ell _2^2h_2H_{14}^*}{ r_2R_{24}^*(1+h_2p_2\ell _2R_{24}^*)}$.

• (e) The Jacobian of system (1) at equilibrium $E_{05}^*=(0,R_{25}^*,H_{15}^*,H_{25}^*)$ admits zero as a double eigenvalue while the others are $e_{11}$ and $e_{22}$. Hence, $E_{05}^*$ is unstable when $e_{11}>0$ or $e_{22}>0$.

• (f) The Jacobian of system (1) at equilibrium $E_{06}^*$ admits zero as a double eigenvalue while the others are $f_{11}$ and $f_{22}$. Hence, $E_{06}^*$ is unstable when $f_{11}>0$ or $f_{22}>0$.

• (g) Stability of $E_{07}^*=(R_{17}^*,R_{27}^*,0,H_{27}^*)$. The Jacobian matrix of system (1) at equilibrium $E_{07}^*$ is given by:

  $$\begin{aligned} J(E_{07}^*)=\left( \begin{array}{cccc} g_{11} &{} g_{12} &{} g_{13} &{} g_{14} \\ g_{21} &{} g_{22} &{} g_{23} &{} g_{24} \\ 0 &{} 0 &{} g_{33} &{} 0 \\ g_{41} &{} g_{42} &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

  where $g_{11}=r_1(1-\frac{2R_{17}^*}{K_1})-\displaystyle \frac{q_1\ell _1'H_{27}^*(1+q_2h_2'\ell _2'R_{27}^*)}{(1+q_1h_1'\ell _1'R_{17}^*+q_2h_2'\ell _2'R_{27}^*)^2}$; $g_{12}=\displaystyle \frac{q_1\ell _1'q_2h_2'\ell _2'R_{17}^*H_{27}^*}{(1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*)^2}$; $g_{13}=-\frac{p_1\ell _1R_{17}^*}{1+p_1\ell _1h_1R_{17}^*+p_2\ell _2h_2R_{27}^*}$; $g_{14}=-\frac{q_1\ell _1'R_{17}^*}{1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*}$; $g_{21}=\frac{q_1\ell _1'h_1'q_2\ell _2'R_{27}^*H_{27}^*}{(1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*)^2}$; $g_{22}=r_2(1-\frac{2R_{25}^*}{K_2})-\displaystyle \frac{q_2\ell _2'H_{27}^*(1+q_1h_1'\ell _1'R_{17}^*)}{(1+q_1h_1'\ell _1'R_{17}^*+q_2h_2'\ell _2'R_{27}^*)^2}$; $g_{23}=-\displaystyle \frac{q_2\ell _2'R_{27}^*}{1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*}$; $g_{24}=-\displaystyle \frac{q_2\ell _2'R_{17}^*}{1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*}$; $g_{41}=\displaystyle \frac{q_1\ell _1'H_{27}^*\Big (e_1'+q_2\ell _2'R_{27}^*(e_1'q_2h_2'-e_2'q_1h_1')\Big )}{(1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*)^2}$; $g_{42}=\displaystyle \frac{q_2\ell _2'H_{27}^*\Big (e_2'+q_1\ell _1'R_{17}^*(e_2'q_1h_1'-e_1'q_2h_2')\Big )}{(1+q_1\ell _1'h_1'R_{17}^*+q_2\ell _2'h_2'R_{27}^*)^2}$; $g_{33}=\displaystyle \frac{e_1p_1\ell _1R_{15}^*+e_2p_2\ell _2R_{27}^*}{1+p_1h_1\ell _1R_{17}^*+p_2h_2\ell _2R_{27}^*}-\mu _1$. The characteristic polynomial of Jacobian matrix of system (1) at equilibrium $E_{07}^*$ is given by

  $$\begin{aligned} P(\lambda )=(g_{33}-\lambda )(\lambda ^3+G_2\lambda ^2+G_1\lambda +G_0) \end{aligned}$$

  (23)

  where, $G_2=-(g_{11}+g_{22})$, $G_1=g_{11}g_{22}-g_{12}g_{21}-g_{42}g_{23}-g_{14}g_{41}$ and $G_0=g_{11}g_{42}g_{23}+g_{22}g_{14}g_{41}-g_{12}g_{41}g_{24}-g_{14}g_{21}g_{42}$. Equilibrium $E_{07}^*$ is locally asymptotically stable if $g_{33}<0$ and Routh-Hurwitz conditions

  $$\begin{aligned} G_2>0;\;\; G_0>0 \;\;and\;\; G_2G_1>G_0 \end{aligned}$$

  are satisfied.

• (h) Stability of $E_{08}^*=(R_{18}^*,R_{28}^*,H_{18}^*,0)$. The Jacobian of model system (1) at equilibrium $E_{08}^*$ is given by:

  $$\begin{aligned} J(E_{08}^*)=\left( \begin{array}{cccc} p_{11} &{} p_{12} &{} p_{13} &{} p_{14} \\ p_{21} &{} p_{22} &{} p_{23} &{} p_{24} \\ p_{31} &{} p_{32} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} p_{44} \end{array}\right) , \end{aligned}$$

  where, $p_{11}=r_1(1-\frac{2R_{16}^*}{K_1})-\displaystyle \frac{p_1\ell _1H_{18}^*(1+p_2h_2\ell _2R_{28}^*)}{(1+p_1h_1\ell _1R_{18}^*+p_2h_2\ell _2R_{28}^*)^2}$; $p_{12}=\displaystyle \frac{p_1\ell _1h_2p_2\ell _2R_{18}^*H_{18}^*}{(1+p_1\ell _1h_1R_{18}^*+p_2\ell _2h_2R_{28}^*)^2}$; $p_{13}=-\frac{p_1\ell _1R_{16}^*}{1+p_1\ell _1h_1R_{16}^*+p_2\ell _2h_2R_{26}^*}$; $p_{14}=-\frac{p_1\ell _1R_{18}^*}{1+p_1\ell _1h_1R_{18}^*+p_2\ell _2h_2R_{28}^*}$; $p_{21}=\frac{p_1\ell _1h_1p_2\ell _2R_{28}^*H_{18}^*}{(1+p_1\ell _1h_1R_{16}^*+p_2\ell _2h_2R_{28}^*)^2}$; $p_{22}=r_2(1-\frac{2R_{28}^*}{K_2})-\displaystyle \frac{p_2\ell _2H_{18}^*(1+p_1h_1\ell _1R_{18}^*)}{(1+p_1h_1\ell _1R_{18}^*+p_2h_2\ell _2R_{28}^*)^2}$; $p_{23}=-\displaystyle \frac{p_2\ell _2R_{28}^*}{1+p_1\ell _1h_1R_{28}^*+p_2\ell _2h_2R_{28}^*}$; $p_{24}=-\displaystyle \frac{q_2\ell _2'R_{18}^*}{1+q_1\ell _1'h_1'R_{18}^*+q_2\ell _2'h_2'R_{28}^*}$; $p_{44}=\displaystyle \frac{e_1'q_1\ell _1'R_{18}^*+e_2'q_2\ell _2'R_{28}^*}{1+q_1h_1'\ell _1'R_{18}^*+q_2h_2'\ell _2'R_{28}^*}-\mu _1$; $p_{31}=\displaystyle \frac{p_1\ell _1H_{18}^*\Big (e_1+p_2\ell _2R_{28}^*(e_1p_2h_2-e_2p_1h_1)\Big )}{(1+p_1\ell _1h_1R_{17}^*+p_2\ell _2h_2R_{28}^*)^2}$; $p_{32}=\displaystyle \frac{p_2\ell _2H_{18}^*\Big (e_1+p_1\ell _1R_{18}^*(e_2p_1h_1-e_1p_2h_2)\Big )}{(1+p_1\ell _1h_1R_{18}^*+p_2\ell _2h_2R_{28}^*)^2}$; The characteristic polynomial of Jacobian matrix of system (1) at equilibrium $E_{08}^*$ is given by

  $$\begin{aligned} P(\lambda )=(p_{44}-\lambda )(\lambda ^3+P_2\lambda ^2+P_1\lambda +P_0) \end{aligned}$$

  (24)

  where, $P_2=-(p_{11}+p_{22})$, $P_1=p_{11}p_{22}-p_{12}p_{21}-p_{32}p_{23}-p_{13}p_{31}$ and $P_0=p_{11}p_{32}p_{23}+p_{22}p_{13}p_{31}-p_{12}p_{31}p_{23}-p_{13}p_{21}p_{32}$. Equilibrium $E_{08}^*$ is locally asymptotically stable if $p_{33}<0$ and Routh-Hurwitz conditions

  $$\begin{aligned} P_2>0;\;\; P_0>0 \;\;and\;\; P_2P_1>P_0 \end{aligned}$$

  are satisfied.

• (i) The Jacobian of model system (1) at the coexisting equilibrium $E^*$ is given by:

  $$\begin{aligned} J(E^*)=\left( \begin{array}{cccc} a_{11} &{} a_{12} &{} a_{13} &{} a_{14} \\ a_{21} &{} a_{22} &{} a_{23} &{} a_{24} \\ a_{31} &{} a_{32} &{} 0 &{} 0 \\ a_{41} &{} a_{42} &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

  where, $a_{11}=\displaystyle \frac{p_1\ell _1^2h_1R_1^*H_1^*}{(1+\ell _1p_1h_1R_1^*+\ell _2p_2h_2R_2^*)^2}+ \displaystyle \frac{q_1\ell _1'^2h_1'R_1^*H_2^*}{(1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*)^2}-\displaystyle \frac{r_1R_1^*}{K_1}$; $a_{12}=\displaystyle \frac{p_1\ell _1p_2h_2\ell _2R_1^*H_1^*}{(1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*)^2}+ \displaystyle \frac{q_1\ell _1'q_2h_2'\ell _2'R_1^*H_2^*}{(1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*)^2}$; $a_{13}=-\displaystyle \frac{p_1\ell _1R_1^*}{1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*}$; $a_{14}=-\displaystyle \frac{q_1\ell _1'R_1^*}{1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*}$; $a_{21}=\displaystyle \frac{p_1\ell _1h_1\ell _2R_2^*H_1^*}{(1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*)^2}+ \displaystyle \frac{q_1\ell _1'h_1'\ell _2'R_2^*H_2^*}{(1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*)^2}$; $a_{22}=\displaystyle \frac{p_2\ell _2^2h_2R_2^*H_1^*}{(1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*)^2}+ \displaystyle \frac{q_2\ell _2'^2h_2'R_2^*H_2^*}{(1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*)^2}-\displaystyle \frac{r_2R_2^*}{K_2}$; $a_{23}=-\displaystyle \frac{p_2\ell _2R_2^*}{1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*}$; $a_{24}=-\displaystyle \frac{q_2\ell _2'R_2^*}{1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*}$; $a_{31}=\displaystyle \frac{p_1\ell _1H_1^*\Big (e_1+p_2\ell _2R_2^*(e_1p_2h_2-e_2p_1h_1)\Big )}{(1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*)^2}$; $a_{32}=\displaystyle \frac{p_2\ell _2H_1^*\Big (e_2+p_1\ell _1R_1^*(e_2p_1h_1-e_1p_2h_2)\Big )}{(1+p_1\ell _1h_1R_1^*+p_2\ell _2h_2R_2^*)^2}$; $a_{41}=\displaystyle \frac{q_1\ell _1'H_2^*\Big (e_1'+q_2\ell _2'R_2^*(e_1'q_2h_2'-e_2'q_1h_1')\Big )}{(1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*)^2}$; $a_{42}=\displaystyle \frac{q_2\ell _2'H_2^*\Big (e_2'+q_1\ell _1'R_1^*(e_2'q_1h_1'-e_1'q_2h_2')\Big )}{(1+q_1\ell _1'h_1'R_1^*+q_2\ell _2'h_2'R_2^*)^2}$. The characteristic polynomial is given by:

  $$\begin{aligned} P(\lambda )=\lambda ^4+A_3\lambda ^3+A_2\lambda ^2+A_1\lambda +A_0, \end{aligned}$$

  (25)

  where,

  $$\begin{aligned} A_3= & {} -(a_{11}+a_{22}); \\ A_2= & {} a_{11}a_{22}-a_{23}a_{32}-a_{12}a_{21}-a_{13}a_{31}-a_{24}a_{42}-a_{41}a_{14};\\ A_1= & {} a_{11}a_{23}a_{32}+a_{22}a_{13}a_{31}+a_{11}a_{42}a_{24}+a_{22}a_{41}a_{14}-a_{12}a_{31}a_{23}\\- & {} a_{13}a_{21}a_{32}-a_{14}a_{42}a_{21}-a_{41}a_{24}a_{12};\\ A_0= & {} a_{41}a_{32}a_{23}a_{14}+a_{42}a_{24}a_{13}a_{31}-a_{41}a_{32}a_{13}a_{24}-a_{42}a_{31}a_{14}a_{23}. \end{aligned}$$

  The coexisting equilibrium $E^*$ is locally asymptotically stable if the Routh-Hurwitz conditions

  $$\begin{aligned} A_3>0; \;\; A_2>0; \;\; A_0>0 \;\; and \;\; A_1(A_3A_2-A_1)>A_3^2A_0 \end{aligned}$$

  are satisfied.