Vaccination and isolation based control design of the COVID-19 pandemic based on adaptive neuro fuzzy inference system optimized with the genetic algorithm

Abstract

The study of the COVID-19 pandemic is of pivotal importance due to its tremendous global impacts. This paper aims to control this disease using an optimal strategy comprising two methods: isolation and vaccination. In this regard, an optimized Adaptive Neuro-Fuzzy Inference System (ANFIS) is developed using the Genetic Algorithm (GA) to control the dynamic model of the COVID-19 termed SIDARTHE (Susceptible, Infected, Diagnosed, Ailing, Recognized, Threatened, Healed, and Extinct). The number of diagnosed and recognized people is reduced by isolation, and the number of susceptible people is reduced by vaccination. The GA generates optimal control efforts related to the random initial number of each chosen group as the input data for ANFIS to train Takagi–Sugeno (T–S) fuzzy structure coefficients. Also, three theorems are presented to indicate the positivity, boundedness, and existence of the solutions in the presence of the controller. The performance of the proposed system is evaluated through the mean squared error (MSE) and the root-mean-square error (RMSE). The simulation results show a significant decrease in the number of diagnosed, recognized, and susceptible individuals by employing the proposed controller, even with a 70% increase in transmissibility caused by various variants.

1 Introduction

The novel coronavirus disease (COVID-19) was first identified in Wuhan, China, and spread to many other countries (Velavan and Meyer 2020). The COVID-19 prevalence has affected all aspects of humans' lives, from mental health to economic issues. Recent findings indicate that the new strains may be more contagious and spread more readily between people (World Health Organization (WHO) 2021). Therefore, mathematical modelling can be advantageous for investigating the pandemic's nature, predicting future trends, and evaluating strategies for control purposes (Diekmann and Heesterbeek 2000; Hethcote 2000; Brauer et al. 2012). Several epidemic models exist, from basic to developed ones with application to Ebola, Influenza (Amiri Mehra et al. 2019), HIV, and other epidemic diseases. These epidemic models can be stochastic, deterministic, discrete (Boutayeb et al. 2020), or continuous (Amiri Mehra et al. 2019), used for the COVID-19 pandemic by changing the parameters and adding or subtracting some states. There are also several epidemiological models (e.g., within-host type (Abbasi et al. 2022), SIR (Cooper et al. 2020), SEIAR (Chen et al. 2020), SQAIR (Amiri Mehra et al. 2020), SQEIAR (Abbasi et al. 2020), SIQHRE (Badfar et al. 2022), SEIAQRDT (Kumari et al. 2020), and SIDARTHE (Giordano et al. 2020)) being used to control and predict the evolution of COVID-19 in different countries across the world. In the present work, a comprehensive epidemic model, termed SIDARTHE (Giordano et al. 2020), is used as the study model, considering the discrimination between infected individuals depending on whether they have been diagnosed and on the severity of their symptoms, which is an important issue to prevent the COVID-19 pandemic from spreading.

The motivation of the present study arises from the necessity of controlling the dynamic model of COVID-19 strains with a high affinity to spread. Hence, this study focuses on an optimized ANFIS based controller design to prevent and control the ongoing COVID-19 outbreak. ANFIS is a kind of adaptive network functionally equal to fuzzy inference systems (Mamdani and Assilian 1975; Kasabov and Song 2002; Abbasi et al. 2021a) based on a T–S fuzzy inference system. ANFIS uses fuzzy logic and neural network in a single framework, taking advantage of the fuzzy system in an adaptive network structure (Jang 1993). It can also control and predict biological phenomena like epidemic models, especially the COVID-19 pandemic (Al-Qaness et al. 2021, 2020a). In this regard, in Ly (2021), an ANFIS structure is employed to estimate the number of COVID-19 cases in the United Kingdom, using data from Spain and Italy. Also, in Behnood et al. (2020); Chowdhury et al. (2021), the authors use ANFIS to forecast COVID-19. Moreover, (Deif et al. 2021) proposes the ANFIS approach to detect COVID-19 cases using available laboratory blood tests. Meanwhile, (Denai et al. 2004) shows the application of the neuro-fuzzy method for the modelling of nonlinear systems.

Reviewing studies shows an increment in the use of different artificial intelligence techniques. A marine predators algorithm (MPA) is employed in Al-Qaness et al. 2020b as an optimizer of ANFIS to forecast the number of infected people in four countries, including Iran, Korea, Italy, and the USA. Moreover, authors in Saif et al. (2021) have used Mutation-Based Bees Algorithms to optimize the performance of ANFIS, making a hybrid model. In (Paterlini and Krink 2006), the aim is to calibrate ANFIS parameters using PSO to forecast the trend of COVID-19. Thus, it is necessary to develop an optimized ANFIS to have better control efforts applied to society. The GA is one of the evolutionary algorithms with many scientific application fields, derived from Darwin's theory of evolution, based on the survival of the fittest or natural selection. Optimized ANFIS with GA has been extensively researched over the past few years (Harandizadeh and Armaghani 2021; Zhang et al. 2021). In this regard, a new ANFIS-polynomial neural network (PNN) optimized by the GA is introduced in Harandizadeh and Armaghani (2021) to predict air overpressure. The performance of the proposed system is evaluated through the correlation coefficient (R) and the mean squared error (MSE). The proposed algorithm is also used in Zhang et al. (2021) for a three-dimensional pulse image of the normal and string-like pulse. However, few ANFIS-GA algorithms were devoted to epidemic disease (Salgotra et al. 2020; Miralles-Pechuán et al. 2020; Yousefpour et al. 2020; Khoshbin et al. 2016; Azimi et al. 2017). Authors in Yousefpour et al. (2020) use a multi-objective GA to investigate the economic consequences of COVID-19. In order to use GA in ANFIS optimization, the authors in Khoshbin et al. (2016) optimized the ANFIS using the GA and the singular value decomposition (SVD) method. Also, the authors in Azimi et al. (2017) used the GA to optimize the membership function of ANFIS.

There are also different studies on the optimal control design for the COVID-19 pandemic (Cooper et al. 2020; Abbasi et al. 2020; Azar and Hassanien 2022). Authors in Abbasi et al. (2020) have presented an optimal control theory to prevent the spread of the COVID-19 pandemic using Pontryagin’s Maximum Principle, considering the control inputs for the whole duration of the treatment process. While in the present study, daily control efforts are based on the initial number of states at the beginning of each day (Khodaei-Mehr et al. 2018), which is more efficacious due to the significant daily growth of infected people. In addition, the GA has been used to train the ANFIS with different random values of states, and the optimal values of control inputs are collected to be used as the input data set for the ANFIS.

An optimized ANFIS-based controller is applied to the dynamic of the COVID-19 pandemic in two different situations: before and after vaccine development. The first strategy aims to isolate only detected infected people (asymptomatic and symptomatic) in the absence of the vaccine. The second strategy, however, seeks to continue the previous strategy in the presence of the vaccine. In this strategy, the susceptible people will get immune to the infectious by vaccination, and the diagnosed and recognized people will be isolated. It should be noted that the selected epidemic model (SIDARTHE) is a comprehensive model considering the acute infected needed ICU admission and all infected-type people groups categorized based on the possibility of recognition and appearance of symptoms.

The main aims, objectives, and goals of the present work are numbered as follows:

• Because of the social, mental, and economic problems of imposing the quarantine, this paper aims to control the COVID-19 pandemic without quarantine.

• The objective is to employ an optimal strategy that takes advantage of the fuzzy system in an adaptive network structure leading to optimized ANFIS with GA.

• The first goal is to apply an isolation strategy before vaccine development to reduce the number of diagnosed and recognized people and move them into isolated groups using the optimal isolation rate calculated by ANFIS optimized with the GA. After vaccine development, the second goal is to apply the vaccination in addition to the isolation strategy, which converts the susceptible people into vaccinated groups using the optimal vaccination rate calculated by ANFIS optimized with the GA along with isolating diagnosed and recognized people.

Furthermore, in the following, the principal contributions of this paper are summarized as:

• Dividing the main strategy into two parts: before and after vaccine development in the absence of quarantine.

• Using a dataset containing the random number of states from a statistical population to optimize control efforts with the aid of GA.

• Training the ANFIS using optimized values of control efforts.

• Validating the proposed model with the real dataset of South Korea, taken from the Korea Disease Control and Prevention Agency (KDCA).

• Controlling the different strains of the COVID-19 pandemic with the optimized ANFIS.

• Evaluating the performance of the proposed system through MSE and RMSE.

The rest of this paper is organized as follows. In Sect. 2, the mathematical model of the COVID-19 is presented, and all parameters and variables are described. Section 3 introduces the GA, and the optimal data selection, followed by the ANFIS structure and the learning methods described in Sect. 4. The controller design is obtained in Sect. 5, including two subsections; the first strategy is given in 5.1 and the second one in 5.2. The basic properties of the model in the presence of the controller, like positivity, boundedness, and existence, are discussed in Sect. 6. Numerical results are provided in Sect. 7. Finally, the discussion, threats to validity, and conclusion sections are stated in Sects. 8–10, respectively.

2 Mathematical model

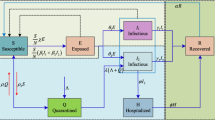
The SIDARTHE epidemic model taken from Giordano et al. (2020) is presented in this section. The model has used eight groups of people involved in COVID-19 in society (see Fig. 1). The groups are introduced as follows:

• $S\left(t\right)$: Uninfected (susceptible), the class of healthy individuals who can contract the disease.

• $I(t)$: Undetected infected without symptoms (infected), the class of individuals who have contracted the disease asymptomatically but are not detected yet.

• $D\left(t\right):$ Detected infected without symptoms (diagnosed), the class of individuals who have contracted the disease asymptomatically, detected and labeled as diagnosed.

• $A(t)$: Symptomatic undetected infected (ailing), the class of individuals who get infectious and have symptoms but are not detected yet.

• $R(t)$: Symptomatic detected infected (recognized), the class of individuals who get infectious and have symptoms and are also detected.

• $T\left(t\right):$ Detected acutely symptomatic infected (threatened), the class of individuals infected with life-threatening symptoms.

• $H(t)$: Recovered people (healed), the class of individuals treated in proper ICUs.

• $E(t)$: Extinct (dead) people, the class of individuals who are died of the disease.

Fig. 1

Conceptual flow diagram of the SIDARTHE dynamical model (Giordano et al. 2020)

The dynamical system is concertedly termed SIDARTHE and is mathematically described as:

$$\dot{S}(t)=-S(t)\left(\alpha I\left(t\right)+\beta D\left(t\right)+\gamma A\left(t\right)+\delta R(t)\right),$$

(1–a)

$$\dot{I}\left(t\right)=S\left(t\right)\left(\alpha I\left(t\right)+\beta D\left(t\right)+\gamma A\left(t\right)+\delta R\left(t\right)\right)-\left(\varepsilon +\zeta +\lambda \right)I\left(t\right),$$

(1–b)

$$\dot{D}\left(t\right)=\varepsilon I\left(t\right)-(\eta +\rho )D(t),$$

(1–c)

$$\dot{A}\left(t\right)=\zeta I\left(t\right)-(\theta +\mu +\kappa )A(t),$$

(1–d)

$$\dot{R}\left(t\right)=\eta D\left(t\right)+\theta A\left(t\right)-\left(\upsilon +\xi \right)R(t),$$

(1–e)

$$\dot{T}\left(t\right)=\mu \mathrm{A}\left(t\right)+\upsilon R\left(t\right)-(\sigma +\tau )T(t),$$

(1–f)

$$\dot{H}\left(t\right)=\lambda I\left(t\right)+\rho D\left(t\right)+\kappa A\left(t\right)+\xi R\left(t\right)+\sigma T\left(t\right),$$

(1–g)

$$\dot{E}\left(t\right)=\tau T\left(t\right),$$

(1–h)

where $N\left(t\right)=S\left(t\right)+I\left(t\right)+D\left(t\right)+A\left(t\right)+R\left(t\right)+T\left(t\right)+H(t)+E(t)$. The non-negative initial conditions are $\left(S\left(0\right),I\left(0\right),D\left(0\right),A\left(0\right),R\left(0\right),T\left(0\right),H\left(0\right),E(0\right))=\left({S}_{0},{I}_{0}{,{D}_{0},A}_{0},{R}_{0},{T}_{0},{H}_{0},{E}_{0}\right)$ and the state variables and parameters are also positive values (Giordano et al. 2020). In addition, $\alpha$, $\beta$, $\gamma$ and $\delta$ denote the transmission rates due to the contact between a susceptible and an infected, a diagnosed, an ailing, or a recognized individual, respectively. Supposed that people tend to eschew contacts with undetected symptomatic people; therefore, α is larger than $\gamma$ and, in the same way, larger than $\beta$ and $\delta .$ There is no contact between susceptible and threatened individuals that require ICU admission. $\varepsilon$ and $\theta$ are the detection rate of asymptomatic and symptomatic individuals, respectively. Since the symptomatic individuals are more likely to be tested, $\theta$ is larger than ε. Also, $\zeta$ and $\eta$ represent the rate of developing relevant symptoms in the detected and undetected asymptomatic infected individuals, respectively. The undetected and detected infected individuals develop life-threatening symptoms at rates $\mu$ and $\nu$, respectively. Threatened individuals die at a mortality rate $\tau$. The five infected groups will be recovered at rates $\lambda$, $\kappa$, $\xi$, $\rho$ and $\sigma$.

3 Genetic algorithm and optimal selection of the data set

Optimization is one of the basic tools to find the best possible solution to any objective function of a given problem. An optimization problem can be employed to minimize the objective function with an optimal solution. The GA, inspired by Darwinian evolutionary theory (survival of the fittest) to describe the way of natural selection (Mitchell 1998), was invented by John Holland in the 1960s and 1970s (Holland 1992; Yang 2020). Natural selection is a difference in reproductive output among replicating organisms created because of the differences in survival in a specific environment, increasing the ratio of advantageous characteristics, which can be passed down within a population from one generation to the next. The main idea of a nature-inspired GA is to find the best solution in the population of candidate solutions (called individuals) to a given optimization problem using selection and genetic variation operators induced by nature. Each possible solution has a set of features (its chromosomes or genotype) that can be mutated and altered (Jafari et al. 2018). The GA starts with an initial population of randomly generated individuals that happened over generations. All individuals merged, and every individual is validated using the cost function, then sorted from the smallest to the highest costs in each generation. Individuals with a lower cost are selected from the current population and modified to make a new generation, and the other will be truncated. This process will be continued in each generation until the algorithm terminates. The stop criterion is either a maximum number of generations produced or the desired fitness level reached for the population (Mitchell 1998). The flowchart of applied GA is presented in Fig. 2.

Fig. 2

GA flowchart

GA defines a function as an objective function (fitness function) that expresses the individual ability to select in the current population. The control objective is to minimize the number of diagnosed and recognized people and susceptible individuals using minimum control effort ${U}_{I}(t) ({0\le U}_{I}(t)\le 1)$ and ${U}_{V }\left(t\right) ({0\le U}_{V}(t)\le 1)$, respectively. ${U}_{I}$ is the control rate to isolate the diagnosed and recognized people, and ${U}_{V}$ is the susceptible vaccination rate. The control design is considered two strategies before and after vaccine development. In the first strategy, before developing an appropriate vaccine, recognized infected people (whether symptoms or asymptomatic) are isolated in dedicated quarantine centers, as was done partly in Italy (Giordano et al. 2020), confining infected people in individual hotel rooms to get them away from the other people to ensure they cannot transmit the virus. In the next strategy, the vaccine is developed. Therefore, susceptible people are vaccinated, and the isolation of the diagnosed and recognized ones is continued simultaneously. In this regard, two cost functions are introduced as follows.

$${J}_{1}=\sum_{i=1}^{N}{\int }_{{t}_{i-1}}^{{t}_{i}}\left[{H}_{1}D{\left(t\right)}^{2}+{H}_{2}R{\left(t\right)}^{2}+{G}_{1}{{U}_{I}(t)}^{2}\right]dt,$$

(2)

$${J}_{2}=\sum_{i=1}^{N}{\int }_{{t}_{i-1}}^{{t}_{i}}\left[{H}_{3}S{\left(t\right)}^{2}+{H}_{4}R{\left(t\right)}^{2}+{{H}_{5}D{\left(t\right)}^{2}+{G}_{2}{{U}_{I}(t)}^{2}+G}_{3}{{U}_{V}(t)}^{2}\right]dt,$$

(3)

In the above formulas, ${J}_{1}$ and ${J}_{2}$ are regarded as cost functions of the first and second strategies, respectively. Also, ${H}_{1},{H}_{2},{H}_{3},{H}_{4},{H}_{5},{G}_{1},{G}_{2}$ and ${B}_{3}$ are weighting coefficients determining the relative importance of each term and $N$ represents the number of days. The length of each integration interval $({t}_{i}$-${t}_{i-1})$ is equal to one day. The control input for each day is different from other days based on the initial numbers of each $R(t)$, $D(t)$, and $S(t)$ states at the beginning of that day. In order to produce the optimal data set to train the ANFIS (described in Sect. 4), the GA is employed. Two control efforts are defined as the GA variables and obtained such that the cost functions are minimized. In the isolation strategy (before vaccination), for each random number of diagnosed and recognized people ($R(t)$ and $D(t)$), each element of the optimal control input vector ${U}_{I}(t)$ is calculated by GA at the beginning of each day. It assumes 20 days for this process to generate a data set, as shown in Table 1. Similarly, for the second strategy, 20 random numbers of $S(t)$, $R(t)$, and $D(t)$ are selected to generate optimized ${U}_{I}(t)$ and ${U}_{V}(t)$ using GA, which is presented in Table 2.

Table 1 The optimal data set for first strategy

Table 2 The optimal data set for second strategy

In addition, Table 3 presents the GA controlling parameters used in solving optimization problems.

Table 3 GA parameters

4 Adaptive neuro fuzzy inference system (ANFIS)

ANFIS is a kind of artificial neural network developed in the 1990s. The technique is based on the T–S fuzzy inference system (Jang 1993; Takagi and Sugeno 1985; Jang and Sun 1995; Jang et al. 1997; Zamani and Zarif 2011). Due to the capability of fuzzy logic in approximating nonlinear functions and the learning ability of the neural networks, combining these instruments in a single framework approximates a nonlinear function by learning from the input data. The considered system has two inputs and one output for simplicity. The rule base contains the fuzzy if–then rules of Takagi and Sugeno’s type (Takagi and Sugeno 1983) as follows:

Rule 1: If $x$ is ${A}_{1}$ and $y$ is ${B}_{1}$ then ${f}_{1}={p}_{1}x+{q}_{1}y+{r}_{1}$

Rule 2: If $x$ is ${A}_{2}$ and $y$ is ${B}_{2}$ then ${f}_{2}={p}_{2}x+{q}_{2}y+{r}_{2}$where ${A}_{1}$, ${A}_{2}$, ${B}_{1}$ and ${B}_{2}$ are membership values of input variables $x$ and $y$, respectively. The parameters of the output functions ${f}_{1}$, and ${f}_{2}$ are ${p}_{1}$, ${q}_{1}$, ${r}_{1}$, ${p}_{2}$, ${q}_{2}$ and ${r}_{2}$, respectively. A basic T-S fuzzy inference system with triangular membership functions is illustrated schematically in Fig. 3.

Fig. 3

Takagi–Sugeno fuzzy inference system

Then, the output of the fuzzy inference system is defined as:

$$f=\frac{{w}_{1}}{{w}_{1}+{w}_{2}}{f}_{1}+\frac{{w}_{2}}{{w}_{1}+{w}_{2}}{f}_{2}=\overline{{w }_{1}}{f}_{1}+\overline{{w }_{2}}{f}_{2}=\left(\overline{{w }_{1}}x\right){p}_{1}+\left(\overline{{w }_{1}}y\right){q}_{1}+\left(\overline{{w }_{1}}\right){r}_{1}+\left(\overline{{w }_{2}}x\right){p}_{2}+\left(\overline{{w }_{2}}y\right){q}_{2}+\left(\overline{{w }_{2}}{r}_{2}\right),$$

(4)

where Eq. (4) is linear with respect to the consequent parameters $({p}_{1},{q}_{1},{r}_{1},{p}_{2},{q}_{2},{r}_{2})$. As illustrated in Fig. 4, there are five different layers in the ANFIS network. These five layers of this structure is explained as follows.

Fig. 4

ANFIS model with two input variables and two rules

Layer 1 $({{\varvec{L}}}_{1})$: Every node $i$ in this layer is adaptive with a node function and generates the membership grades of a linguistic label.

$${O}_{i}^{1}={\mu }_{{A}_{i}}\left(x\right),$$

(5)

in which, $x$ is the input to node $i$,${A}_{i}$ is the linguistic variable and ${\mu }_{{A}_{i}}$ is the membership function of ${A}_{i}$ that typically chosen as ${\mu }_{{A}_{i}}\left(x\right)=\frac{1}{1+{\left[{\left(\frac{x-{c}_{i}}{{a}_{i}}\right)}^{2}\right]}^{{b}_{i}}}$ or ${\mu }_{{A}_{i}}\left(x\right)=\mathrm{exp}\left\{-{\left(\frac{x-{c}_{i}}{{a}_{i}}\right)}^{2}\right\}$, where $\{{a}_{i}, {b}_{i}, {c}_{i}\}$ is the membership parameter set. As the values of the parameters change, the shape of the membership function varies, called premise parameters. Premise parameters are the coefficients of membership functions and their number varies based on the considered type and number of membership functions.

Layer 2 $({{\varvec{L}}}_{2})$: Each node in this layer is a fixed node which calculates the firing strength ${w}_{i}$ of each rule using the $min$ or $prod$ operator. Therefore, the production of all the incoming signals is used as the output of each node.

$${O}_{i}^{2}={w}_{i}={\mu }_{{A}_{i}}\left(x\right)\times {\mu }_{{B}_{i}}\left(y\right),$$

(6)

Layer 3 $\left({{\varvec{L}}}_{3}\right)$: The fixed nodes calculate the ratio of the $i$ th rule’s firing strength to the sum of firing strengths of all the rules. The result is a normalized firing strength given by,

$${O}_{i}^{3}=\overline{{w }_{i}}=\frac{{w}_{i}}{{w}_{1}+{w}_{2}},$$

(7)

Layer 4 $({{\varvec{L}}}_{4})$: The adaptive nodes compute a parameter function on the output of the layer 3.

$${O}_{i}^{4}=\overline{{w }_{i}}{f}_{i}=\overline{{w }_{i}}\left({p}_{i}x+{q}_{i}y+{r}_{i}\right),$$

(8)

where $\overline{{w }_{i}}$ is the output of Layer 3 and $\{{p}_{i}, {q}_{i}, {r}_{i}\}$ is the consequent parameter set.

Layer 5 $({{\varvec{L}}}_{5})$: This layer includes only one single fixed node that aggregates the overall outputs the summation of all incoming signals

$${O}_{i}^{5}=\sum_{i}\overline{{w }_{i}}{f}_{i}=\frac{\sum_{i}{w}_{i}{f}_{i}}{\sum_{i}{w}_{i}}. \left(9\right)$$

(9)

When the premise parameters are fixed, the overall output is a linear combination of the consequent parameters. A hybrid learning algorithm adjusts the consequent parameters in a forward pass and the premise parameters in a backward pass (Jantzen 1998). In the forward pass of the learning algorithm, the network inputs propagate forward until layer 4, where the least-squares method identifies the consequent parameters. In the backward pass, the error signals, the squared error derivatives for each node output, propagate backward from the output layer to the input one. The premise parameters are updated by the gradient descent algorithm (Haykin and Network 2004; Zurada 1992; Hagan et al. 1997). In addition, Table 4 highlights the information regarding the ANFIS structure. The available data is divided into training and testing, with 70% for training and 30% for testing purposes.

Table 4 Parameters setting for the selected ANFIS structure

5 Controller design

This section presents the control strategy employed to curb the COVID-19 pandemic. The premise and consequent parameters used to build the T–S fuzzy system are obtained from the ANFIS training process. The ANFIS utilizes the optimal dataset generated in Sect. 3 (Tables 1 and 2) for the training process. The combination of GA and ANFIS builds the controller of the present study shown in Fig. 5 using a block diagram.

Fig. 5

Schematic diagram of the control strategy

In order to explain the structure of the proposed controllers applied to Eq. 1, the dynamical system is mathematically described in Eqs. 10 and 11 for the first and second strategies, respectively. The process of vaccination and isolation is also illustrated in Fig. 6.

Fig. 6

Conceptual flow diagram of the COVID-19 SIDARTHE dynamics with the proposed controllers (Giordano et al. 2020)

5.1 First strategy (isolation)

As mentioned, this strategy is only based on the isolation of the detected infected people described as follows:

$$\dot{D}\left(t\right)=\varepsilon I\left(t\right)-\left(\eta +\rho \right)D\left(t\right)-D\left(t\right){U}_{{I}_{fit}}\left(R\left(t\right),D\left(t\right)\right),$$

(10a)

$$\dot{R}\left(t\right)=\eta D\left(t\right)+\theta A\left(t\right)-\left(\upsilon +\xi \right)R\left(t\right)-R\left(t\right){U}_{{I}_{fit}}\left(R\left(t\right),D\left(t\right)\right),$$

(10b)

in which ${U}_{{I}_{fit}}\left(\left(R\left(t\right),D\left(t\right)\right)\right)=\mathcal{A}+\mathcal{B}\mathrm{cos}\left(R\left(t\right)D\left(t\right)\pi \right)+\mathcal{C}\mathrm{sin}\left(\mathcal{D}R\left(t\right)D\left(t\right)\pi \right)$, where ${U}_{{I}_{fit}}\left(\left(R\left(t\right),D\left(t\right)\right)\right)$ is the mathematical function fitted to the output data set of ANFIS used to isolate detected infected people ($R$ and $D$), in which $\mathcal{A}=-0.6821, \mathcal{B}=0.8659, \mathcal{C}=-2.291,\mathcal{D}=-0.123$.

Remark 1

According to Eq. $(10-a)$ and the structure of the dynamic, it is assumed that $I\left(t\right)=Z\left(t\right)D(t)$, where $\left|Z\left(t\right)\right|\le 1$ and $Z\left(t\right)>0$. Then it can be concluded that $\dot{D}\left(t\right)\le \left(\varepsilon -\left(\eta +\rho \right)-{U}_{I}\left(R\left(t\right),D\left(t\right)\right)\right)D(t)$. By solving the ordinary differential equation: $D\left(t\right)\le {D}_{0}{e}^{-\underset{0}{\overset{t}{\int }}\left(\eta +\rho +{U}_{I}-\varepsilon \right)dt}={D}_{0}{e}^{(-\left(\eta +\rho +{U}_{I})+\varepsilon \right)t}$. Since $\eta +\rho +{U}_{I}>\varepsilon$, $D\left(t\right)$ converges to zero as $t\to \infty$. As a result, Eq. (10b) is written as $\dot{R}\left(t\right)=\theta A\left(t\right)-(\upsilon +\xi +{U}_{I}\left(R\left(t\right),D\left(t\right)\right)R(t)$. Similarly, it can be proved that $R\left(t\right)$ converges to zero. As a result, Eq. (1a) is written as $\dot{S}(t)=-S(t)\left(\alpha I\left(t\right)+\gamma A\left(t\right)\right)$. By solving the ordinary differential equation: $S\left(t\right)={S}_{0}{e}^{-\alpha \underset{0}{\overset{t}{\int }}I\left(t\right)dt}{e}^{-\gamma \underset{0}{\overset{t}{\int }}A\left(t\right)dt}$. The maximum value of the two groups $A(t)$ and $I(t)$ is equal to 1, therefore, $S\left(t\right)\le {S}_{0}{e}^{-\alpha t}{e}^{-\gamma t}$. Hence, $S\left(t\right)\to 0$ as $t \to \infty$ and $S\left(t\right)\left(\alpha I\left(t\right)+\beta D\left(t\right)+\gamma A\left(t\right)+\delta R\left(t\right)\right)\to 0$. Therefore, Equation (1b) can be written as $\dot{I}\left(t\right)=-\left(\varepsilon +\zeta +\lambda \right)I\left(t\right)$. In a similar way, solving the mentioned ordinary differential equation, $I(t)$ finally converges to zero. $A(t)$ and $T(t)$ converge to zero similarly. Finally, it can be concluded that two states, $E(t)$ and $H\left(t\right)$, reach their maximum values and remain stationary.

5.2 Second strategy (isolation and vaccination)

Similarly, in this strategy, both isolation and vaccination are applied to detected infected and susceptible people, respectively, to overcome the outbreak. The dynamic equations are presented as:

$$\dot{S}\left(t\right)=-S\left(t\right)\left(\alpha I\left(t\right)+\beta D\left(t\right)+\gamma A\left(t\right)+\delta R\left(t\right)\right)-S\left(t\right){U}_{{V}_{fit}}\left(mean\left(R\left(t\right),D\left(t\right)\right),S\left(t\right)\right),$$

(11a)

$$\dot{D}\left(t\right)=\varepsilon I\left(\mathrm{t}\right)-\left(\eta +\rho \right)D\left(t\right)-D\left(t\right){U}_{{I}_{fit}}\left(mean\left(R\left(t\right),D\left(t\right)\right),S\left(t\right)\right),$$

(11b)

$$\dot{R}\left(t\right)=\eta D\left(t\right)+\theta A\left(t\right)-\left(\upsilon +\xi \right)R\left(t\right)-R\left(t\right){U}_{{I}_{fit}}\left(mean\left(R\left(t\right),D\left(t\right)\right),S\left(t\right)\right),$$

(11c)

in which,

$${U}_{{V}_{fit}}\left(mean\left(R\left(t\right),D\left(t\right)\right),S\left(t\right)\right)=\mathcal{E}+\mathcal{F}\mathrm{cos}\left(mean\left(R\left(t\right),D\left(t\right)\right)S\left(t\right)\pi \right)+\mathcal{G}\mathrm{sin}\left(mean\left(R\left(t\right),D\left(t\right)\right)S\left(t\right)\pi \right)+{\mathrm{e}}^{\left(\mathcal{H}mean\left(R\left(t\right),D\left(t\right)\right)S\left(t\right)\right)}$$

and,

${U}_{{I}_{fit}}\left(mean\left(R\left(t\right),D\left(t\right)\right),S\left(t\right)\right)=\mathcal{I}+\mathcal{J}\mathrm{cos}\left(mean\left(R\left(t\right),D\left(t\right)\right)S\left(t\right)\pi \right)+\mathcal{K}\mathrm{sin}\left(mean\left(R\left(t\right),D\left(t\right)\right)S\left(t\right)\pi \right)$.

Similarly, ${U}_{{V}_{fit}}$ and ${U}_{{I}_{fit}}$ are control efforts to vaccinate the susceptible people and isolate diagnosed and recognized people, respectively, in which $\mathcal{E}=-1.3$, $\mathcal{F}=0.5921$, $\mathcal{G}=-0.3037$, $\mathcal{H}=1.408$, $\mathcal{I}=0.02754$, $\mathcal{J}=0.04352$, and $\mathcal{K}=0.08908.$

Remark 2

Similar to the proof of Remark 1, if $t \to \infty$, states $S\left(t\right), I\left(t\right), D\left(t\right), A\left(t\right), R(t)$ and $T(t)$ converge to zero. Also, $E(t)$ and $H(t)$ reach and remain at their maximum value.

6 Model basic properties in the presence of the controller

This section systematically discusses the basic properties of the model in the presence of the controller, like positivity, boundedness, and existence in 3 subsections, respectively (Kada et al. 2020; Birkhoff and Rota 1962).

6.1 Positivity of solutions

In the following, the positivity of solutions is investigated with Theorem 1.

Theorem 1

If ${S}_{0}\ge 0, {I}_{0}\ge 0, { D}_{0}\ge 0, {R}_{0}\ge 0, {T}_{0}\ge 0,{ H}_{0}\ge 0$, and ${E}_{0}\ge 0$, then solutions to the system in the presence of the controller are positive for all $t\ge 0.$

Proof

Since all the parameters of the model and control rates $({U}_{I},{U}_{v})$ are positive, Eq. (11a) can be written as $\dot{S}\left(t\right)=-{\rm M}_{1}\left(t\right)S(t)$, where ${M}_{1}\left(t\right)=\alpha I\left(t\right)+\beta D\left(t\right)+\xi A\left(t\right)+\sigma R\left(t\right)+{U}_{V}$. Therefore, $S\left(t\right)={S}_{0}{e}^{-{\int }_{0}^{t}{M}_{1}\left(r\right)dr}$, as a result, $S\left(t\right)\ge 0$ regardless of the sign of ${M}_{1}(t)$. In addition, Eq. (1b) can be written as

$$\dot{I}\left(t\right)=-{\rm M}_{2}S\left(t\right)+\left(S\left(t\right)-{M}_{3}\right)I\left(t\right),$$

(12)

in which ${M}_{2}={M}_{1}(t)-{U}_{V}$ and ${\rm M}_{3}=\varepsilon +\zeta +\lambda \ge 0$. On the one hand, if ${M}_{2}\ge 0$, Eq. (12) changed to be as

$$\dot{I}\left(t\right)\ge \left(S\left(t\right)-{M}_{3}\right)I\left(t\right).$$

(13)

According to Remarks 1 and 2, we have $S\left(t\right)-{M}_{3}\le 0$, as a result we get

$$\dot{I}\left(t\right)\ge -{M}_{4}I\left(t\right),$$

(14)

where ${M}_{4}=\left|S\left(t\right)-{M}_{3}\right|$. Then, left and right multiplying of Eq. (14) by ${e}^{{\int }_{0}^{t}{M}_{4}dr}$ leads to $\dot{I}\left(t\right){e}^{{\int }_{0}^{t}{M}_{4}dr}+{M}_{4}{e}^{{\int }_{0}^{t}{M}_{4}dr}I\left(t\right)\ge 0$ which equals $\frac{d}{dt}\left({e}^{{\int }_{0}^{t}{M}_{4}dr}I\left(t\right)\right)\ge 0$, and integrating this inequality from $0$ to $t$ gives $I\left(t\right)\ge {I}_{0}{e}^{-{\int }_{0}^{t}{M}_{4}dr}\ge 0$. On the other hand, if ${M}_{2}<0$, we have

$$\dot{I}\left(t\right)=\left(S\left(t\right)-{M}_{3}+{M}_{2}S\left(t\right)\right)I\left(t\right).$$

(15)

According to Remarks 1 and 2. The solution to this equation converges to zero and never becomes negative. Therefore $I\left(t\right)$ is positive $(I\left(t\right)\ge 0)$. Similarly, the other states $(D\left(t\right), A\left(t\right), R\left(t\right), T(t))$ are positive too.

$$D\left(t\right)\ge {D}_{0}{e}^{-{\int }_{0}^{t}{M}_{5}dr}\ge 0, {M}_{5}=\eta +\rho +{U}_{I}\ge 0,$$

(16a)

$$A\left(t\right)\ge {A}_{0}{e}^{-{\int }_{0}^{t}{M}_{6}dr}\ge 0, {M}_{6}=\theta +\mu +\kappa \ge 0,$$

(16b)

$$R\left(t\right)\ge {R}_{0}{e}^{-{\int }_{0}^{t}{M}_{7}dr}\ge 0, {M}_{7}=\upsilon +\xi +{U}_{I}\ge 0,$$

(16c)

$$T\left(t\right)\ge {T}_{0}{e}^{-{\int }_{0}^{t}{M}_{8}dr}\ge 0, {M}_{8}=\sigma +\tau \ge 0,$$

(16d)

Since $I\left(t\right), D\left(t\right), A\left(t\right)$ and $R(t)$ are positive. According to Eq. $\left(1-g\right)$ and considering $\left(I\left(t\right),D\left(t\right), A\left(t\right), R\left(t\right), T\left(t\right)\right)\ge 0$, the following equation is concluded,

$$\frac{d}{dt}\left(H\left(t\right)\right)\ge 0,$$

(17)

Integrating Eq. (17) from $0$ to $t$ gives $H\left(t\right)\ge {H}_{0}$, hence $H\left(t\right)\ge 0$ and similarly $E\left(t\right)\ge 0.$

6.2 Boundedness of solutions

In the following, the boundedness of solutions is investigated with Theorem 2.

Theorem 2

The set $\Omega = \left\{ \begin{gathered} \left( {S\left( t \right),I\left( t \right),D\left( t \right),A\left( t \right),R\left( t \right),T\left( t \right),H\left( t \right),E\left( t \right)} \right) \in \mathbb{R}_{ + }^{8} ;0 \le S\left( t \right) \hfill \\ + I\left( t \right) + D\left( t \right) + A\left( t \right) + R\left( t \right) + T\left( t \right) + H\left( t \right) + E\left( t \right) \le N_{0} + N_{2} \left( 0 \right) \hfill \\ \end{gathered} \right\}$ is positive invariants.

Proof

Since $\dot{N}\left(t\right)=\dot{S}\left(t\right)+\dot{I}\left(t\right)+\dot{D}\left(t\right)+\dot{A}\left(t\right)+\dot{R}\left(t\right)+\dot{T}\left(t\right)+\dot{H}(t)+\dot{E}(t)$, therefore $\dot{N}\left(t\right)=-{U}_{V}S(t)-{U}_{I}(D(t)+R(t))$. Also, $S\left(t\right)=N\left(t\right)-(I\left(t\right)+D\left(t\right)+A\left(t\right)+R\left(t\right)+T\left(t\right)+H\left(t\right)+E\left(t\right))$ and $D\left(t\right)+R(t)=N\left(t\right)-(S\left(t\right)+I\left(t\right)+A\left(t\right)+T\left(t\right)+H\left(t\right)+E\left(t\right))$ then, $\dot{N}\left(t\right)=-{N}_{1}N\left(t\right)+{N}_{2}(t)$, where, ${N}_{1}={U}_{V}+{U}_{I}\ge 0$ and according to Theorem 1, ${N}_{2}\left(t\right)={U}_{V}\left(I\left(t\right)+D\left(t\right)+A\left(t\right)+R\left(t\right)+T\left(t\right)+H\left(t\right)+E\left(t\right)\right)+{U}_{I}\left(S\left(t\right)+I\left(t\right)+A\left(t\right)+T\left(t\right)+H\left(t\right)+E\left(t\right)\right)\ge 0$. The both sides in $\dot{N}\left(t\right)=-{N}_{1}N\left(t\right)+{N}_{2}(t)$ are multiplied by ${e}^{{\int }_{0}^{t}{N}_{1}dr}$ gives $\dot{N}\left(t\right){e}^{{\int }_{0}^{t}{N}_{1}dr}=-{N}_{1}{e}^{{\int }_{0}^{t}{N}_{1}dr}N\left(t\right)+{N}_{2}(t){e}^{{\int }_{0}^{t}{N}_{1}dr}$. Then, $\frac{d}{dt}\left(N\left(t\right){e}^{{\int }_{0}^{t}{N}_{1}dr}\right)={N}_{2}(t){e}^{{\int }_{0}^{t}{N}_{1}dr}$, integrating this inequality from $0$ to $t$ gives $N\left(t\right)={N}_{0}{e}^{-{\int }_{0}^{t}{N}_{1}dr}+{N}_{2}(t)$, where ${N}_{0}={S}_{0}+{I}_{0}{+{D}_{0}+A}_{0}+{R}_{0}+{T}_{0}+{H}_{0}+{E}_{0}$, therefore $0\le N\left(t\right)\le {N}_{0}+{N}_{2}\left(0\right).$ Then all possible solutions enter the set $\Omega$. It implies that $\Omega$ is a positively invariant set for the controller-based model.

6.3 Existence of solutions

In the following, the existence of solutions is investigated with Theorem 3.

Theorem 3

The system with the initial conditions $S\left(0\right)\ge 0,I\left(0\right)\ge 0,D\left(0\right)\ge 0,A\left(0\right)\ge 0,R\left(0\right)\ge 0,T\left(0\right)\ge 0,H\left(0\right)\ge 0,$ and $E\left(0\right)\ge 0$ has a unique solution.

Proof

Let $X={[\begin{array}{ccc}S(t)& I(t)& D(t)\end{array} \begin{array}{ccc}A(t)& R(t)& T\left(t\right) \begin{array}{cc}H(t)& E(t)\end{array}\end{array}]}^{T}$. So, the model in the presence of the controller is rewritten as $f\left(X\right)=\mathcal{A}X+{f}_{1}(X)$ where $\mathcal{A}=$ diag $[\begin{array}{ccc}-{U}_{V},& -\left(\varepsilon +\zeta +\lambda \right),& -\left(\eta +\rho +{U}_{I}\right)\end{array}, \begin{array}{ccc}-\left(\theta +\mu +\kappa \right),& -\left(\upsilon +\xi +{U}_{I}\right),& -\left(\sigma +\tau \right)\end{array}, \begin{array}{cc}0,& 0\end{array}]$ and, ${f}_{1}\left(X\right)={[\begin{array}{ccc}-\Lambda \left(t\right)S\left(t\right)&\Lambda \left(t\right)S\left(t\right)& \varepsilon I\left(t\right)\end{array} \begin{array}{ccc}\zeta I(t)& \eta D\left(t\right)+\theta A(t)& \mu A\left(t\right)+\upsilon R(t) \begin{array}{cc}\lambda I\left(t\right)+\rho D\left(t\right)+\kappa A\left(t\right)+\xi R\left(t\right)+\sigma T(t)& \tau T(t)\end{array}\end{array}]}^{T}$ in which $\Lambda \left(t\right)=\alpha I\left(t\right)+\beta D\left(t\right)+\gamma A\left(t\right)+\delta R(t)$. The function ${f}_{1}(X)$ satisfies:

$$\left|{f}_{1}\left({X}_{1}\right)-{f}_{1}\left({X}_{2}\right)\right|=\left|2\left({\Lambda }_{1}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{2}(t)\right)+\varepsilon \left({I}_{1}\left(t\right)-{I}_{2}(t)\right)+\eta \left({D}_{1}\left(t\right)-{D}_{2}(t)\right)+\theta \left({A}_{1}\left(t\right)-{A}_{2}(t)\right)+\mu \left({A}_{1}\left(t\right)-{A}_{2}\left(t\right)\right)+\upsilon \left({R}_{1}\left(t\right)-{R}_{2}(t)\right)+\lambda \left({I}_{1}\left(t\right)-{I}_{2}\left(t\right)\right)+\rho \left({D}_{1}\left(t\right)-{D}_{2}\left(t\right)\right)+\kappa \left({A}_{1}\left(t\right)-{A}_{2}\left(t\right)\right)+\xi \left({R}_{1}\left(t\right)-{R}_{2}\left(t\right)\right)+\sigma \left({T}_{1}\left(t\right)-{T}_{2}(t)\right)+\tau \left({T}_{1}\left(t\right)-{T}_{2}(t)\right)\right|,$$

(18)

Assumed that all parameters have their maximum value and $\left|{y}_{1}+{y}_{2}\right|\le \left|{y}_{1}\right|+\left|{y}_{2}\right|$ then,

$$\left|{f}_{1}\left({X}_{1}\right)-{f}_{1}\left({X}_{2}\right)\right|\le 2\left|{\Lambda }_{1}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{2}\left(t\right)\right|+3\left|{I}_{1}\left(t\right)-{I}_{2}\left(t\right)\right|+2\left|{D}_{1}\left(t\right)-{D}_{2}\left(t\right)\right|+3\left|{A}_{1}\left(t\right)-{A}_{2}\left(t\right)\right|+2\left|{R}_{1}\left(t\right)-{R}_{2}\left(t\right)\right|+2\left|{T}_{1}\left(t\right)-{T}_{2}\left(t\right)\right|,$$

(19)

The $\left|{\Lambda }_{1}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{2}\left(t\right)\right|$ can be rewritten as the follows

$$\left|{\Lambda }_{1}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{2}\left(t\right)\right|=\left|{\Lambda }_{1}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{1}\left(t\right)+{\Lambda }_{2}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{2}\left(t\right)\right|=\left|{S}_{1}\left(t\right)\left({I}_{1}\left(t\right)-{I}_{2}\left(t\right)\right)+{S}_{1}\left(t\right)\left({D}_{1}\left(t\right)-{D}_{2}\left(t\right)\right)+{S}_{1}\left(t\right)\left({A}_{1}\left(t\right)-{A}_{2}\left(t\right)\right)+{S}_{1}\left(t\right)\left({R}_{1}\left(t\right)-{R}_{2}\left(t\right)\right)+{I}_{2}\left(t\right)\left({S}_{1}\left(t\right)-{S}_{2}\left(t\right)\right)+{D}_{2}\left(t\right)\left({S}_{1}\left(t\right)-{S}_{2}\left(t\right)\right)+{A}_{2}\left(t\right)\left({S}_{1}\left(t\right)-{S}_{2}\left(t\right)\right)+{R}_{2}(t)\left({S}_{1}\left(t\right)-{S}_{2}\left(t\right)\right)\right|,$$

(20)

The maximum value of normalized states is equal to 1 and $\left|{y}_{1}+{y}_{2}\right|\le \left|{y}_{1}\right|+\left|{y}_{2}\right|$, therefore,

$$\left|{\Lambda }_{1}\left(t\right){S}_{1}\left(t\right)-{\Lambda }_{2}\left(t\right){S}_{2}\left(t\right)\right|\le \left|{I}_{1}\left(t\right)-{I}_{2}\left(t\right)\right|+\left|{D}_{1}\left(t\right)-{D}_{2}\left(t\right)\right|+\left|{A}_{1}\left(t\right)-{A}_{2}\left(t\right)\right|+\left|{R}_{1}\left(t\right)-{R}_{2}\left(t\right)\right|+4\left|{S}_{1}\left(t\right)-{S}_{2}\left(t\right)\right|,$$

(21)

Substitution Eq. 21 in Eq. 19 gives

$$\left|{f}_{1}\left({X}_{1}\right)-{f}_{1}\left({X}_{2}\right)\right|\le 8\left|{S}_{1}\left(t\right)-{S}_{2}\left(t\right)\right|+5\left|{I}_{1}\left(t\right)-{I}_{2}\left(t\right)\right|+4\left|{D}_{1}\left(t\right)-{D}_{2}\left(t\right)\right|+5\left|{A}_{1}\left(t\right)-{A}_{2}\left(t\right)\right|+4\left|{R}_{1}\left(t\right)-{R}_{2}\left(t\right)\right|+2\left|{T}_{1}\left(t\right)-{T}_{2}\left(t\right)\right|,$$

(22)

Then, $\left|{f}_{1}\left({X}_{1}\right)-{f}_{1}\left({X}_{2}\right)\right|\le 8\left|{X}_{1}-{X}_{2}\right|$. It can be concluded that $\Vert {f}_{1}\left({X}_{1}\right)-{f}_{1}\left({X}_{2}\right)\Vert \le 8\Vert {X}_{1}-{X}_{2}\Vert$. Therefore, $\Vert f\left({X}_{1}\right)-f\left({X}_{2}\right)\Vert \le L\Vert {X}_{1}-{X}_{2}\Vert$ where $L=\mathrm{max}(8,\Vert \mathcal{A}\Vert )$. Thus, $f$ is uniformly Lipschitz continuous, and the solutions exist.

7 Simulation results

In this section, the performance of the proposed optimal ANFIS-based controller is evaluated using MATLAB software. The realistic model parameters were extracted from Giordano et al. (2020), as listed in Table 5. The simulations are performed for two situations: before and after vaccine development. The initial values of states are selected arbitrarily (Table 6). The population size $(N)$ in society is assumed to be 10,000.

Table 5 The values of parameters in the SIDARTHE epidemic model

Table 6 Initial values of the states in the SIDARTHE epidemic model

The results of applying the controller are divided into two subsections: the first strategy (Isolation) and the second one (Isolation and Vaccination), which are illustrated in the following.

7.1 First strategy (isolation)

This section investigates the isolation strategy's impact before developing an effective vaccine, and the theoretical results are compared. The evolution of all groups involved with COVID-19 is compared in two cases: with and without isolation. Before vaccine development, recognized and diagnosed people are isolated in places with zero contact probability with susceptible ones, which means there is no infectious transmission.

Figure 7$\mathrm{a}$ depicts the number of susceptible people with and without an isolation strategy. It should be noted that in the present study, the quarantine of susceptible people is ignored; therefore, there is no direct control to reduce their number. As is observed, after isolating recognized and diagnosed people, the reduction rate of the susceptible people is slightly decreased. Thus, it can be concluded that the contact of recognized and diagnosed people with the rest of the people in other groups will be dropped after isolation, and therefore, fewer susceptible people will be infected.

Fig. 7

The comparison of the number of the Susceptible and Infected individuals with and without the proposed controller

Figure 7$\mathrm{b}$ compares the number of infected people in the presence and absence of the employed controller. As an overall trend, isolation of recognized and diagnosed people indirectly reduces undetected ones. When recognized and diagnosed people get isolated, their contact with susceptible people decreases, and consequently, fewer susceptible people get infectious and move to the infected people groups.

Figure 8$\mathrm{a}$ shows a significant fall in the number of diagnosed people. Before applying the isolation strategy, their maximum number is approximately 4400. Whereas, after isolation, in the outbreak peak, their number drops by 2000 and reaches almost 2200. This fall starts at 2200 on the tenth day to reach zero in less than 40 days. In addition, the results illustrate that the proposed method could be effective in a real situation.

Fig. 8

The comparison of the number of the diagnosed and ailing individuals with and without the proposed controller

Figure 8$\mathrm{b}$ compares the number of ailing people in the presence and lack of the proposed controller. It can be seen that isolating recognized and diagnosed people leads to fewer people infected, the number of susceptible people grows, and fewer people show the disease symptoms and move to the ailing people group.

Figure 9$\mathrm{a}$ demonstrates a significant difference between the number of recognized people after and before isolation. If the recognized people go freely among the other people at the peak days of the outbreak, their number reaches 2000 in almost 25 days. In contrast, their peak number falls dramatically after applying the isolation and reaches about 420. This fall occurs in less than 50 days. As shown in Fig. 9$\mathrm{b}$, due to the decrement in the number of diagnosed and recognized people, the number of threatened people diminishes rapidly compared to pre-isolation. The maximum number of threatened people from just above 800 declines to 100 and reduces from 100 on the 25th day to zero on the 170th day, whereas without isolation, the threatened people have not been zero even until the 250th day.

Fig. 9

The comparison of the number of the recognized and threatened individuals with and without the proposed controller

Figure 10$\mathrm{a}$ shows the differences between the number of extinct (dead) people after and before the isolation. Before isolation, 80 people are extinct in only 25 days. In contrast, after isolation, the number of threatened people decreases; consequently, the number of extinct people falls. Therefore, only 80 people die in a population of 10,000 after 150 days and remain unchanged until the 250th day, demonstrating the efficiency of the proposed control. Also, isolation decreases the number of five groups involved with infectious ($I(t)$, $A(t)$, $D(t)$, $R(t)$, and $T(t)$); therefore, the number of recovered people reduces (Fig. 10$\mathrm{b}$). As shown, 3000 people get healed in less than 20 days, and this number remains steady until the 200th day. Whereas, without isolation, 9000 infected people, who are infected recover from the infection in 200 days.

Fig. 10

The comparison of the number of the Extinct and Healed individuals with and without the proposed controller

As illustrated in Fig. 11, the control effort value is between 0 and 0.23, satisfying ${0\le U}_{I}(t)\le 1$. The number of diagnosed and recognized people in the absence of the controller is shown in Figs. 8$a$ and 9$a$, respectively. The number of $R(t)$ and $D(t)$ reaches 2000 and just under 4500 in their maximum value, respectively. It is evident that the value of the control effort depends on the recognized and diagnosed people; as their number increases, the control effort grows to overcome their rise.

Fig. 11

The relationship between the isolation-based controller and the recognized and diagnosed individuals

Figure 12 shows that the number of detected infected people increases in the early days of the peak; therefore, the controller applies more control effort to overcome this increment. After that, the value of effort decreases and remains stationary by reducing the number of detected infected people.

Fig. 12

The control effort for isolation-based strategy

7.2 Second strategy (isolation and vaccination)

The population change depends on the presence and the absence of vaccination and isolation strategies. In this section, the impact of applying the isolation and vaccination is investigated simultaneously. After vaccine development, the susceptible people get immune against the infectious. An isolation strategy is also used to isolate the detected infected people. As shown in Fig. 13$\mathrm{a}$, after the vaccination campaign, the number of susceptible people converges to zero sooner because they get immune and move to the vaccinated group. Studies include (Ng and Gui 2020) reveal that the recovered people in the COVID-19 pandemic can get susceptible again, whereas the vaccinated people are immune against the virus; hence, the vaccinated people do not go to the healed people group with a possibility of resusceptibility or, in other words, ability to reinfect. Figure 13$\mathrm{b}$ shows that the number of infected people before using any controller is 4000. As seen in Fig. 7$\mathrm{b}$, their number decreases to approximately 3650 after the isolation strategy, whereas in the presence of vaccination and isolation, their number drops to 1500. Vaccination reduces the number of susceptible people; therefore, fewer ones get infected, and then there is a reduction of 2500 people in the peak time of the infectious.

Fig. 13

The comparison of the number of the Susceptible and Infected individuals with and without the proposed controller

As shown in Fig. 8$\mathrm{a}$, the number of diagnosed people reaches 2200 after applying only the isolation strategy. Figure 14$\mathrm{a}$ indicates that the proposed controller reduces the number of diagnosed people at the peak of the outbreak from just less than 4500 to about 1200 people. The number of diagnosed people converges to zero in almost 50 days in the presence of the controller, while without it, their number does not reach zero even until the 100th day. The number of ailing people controlled with the isolation strategy (Fig. 8$\mathrm{b}$) converges to zero in 30 days. While in the second strategy, their number reaches zero in 25 days without any peak. Figures 15$\mathrm{a}$ and $\mathrm{b}$ show that the number of recognized and threatened people decreases compared to the control-free case.

Fig. 14

The comparison of the number of the Diagnosed and Ailing individuals with and without the proposed controller

Fig. 15

The comparison of the number of the Recognized and Threatened individuals with and without the proposed controller

There is a reduction of about 900 people in mortality after applying the isolation-vaccination strategy compared to the control-free case (Fig. 16a). By comparing Figs. 10b and 16b, it is evident that combining vaccination and isolation reduces the number of healed people because susceptible people get vaccinated (moving to the vaccinated group). Thus, fewer get infected; as a result, fewer get to recover and move to the healed people group.

Fig. 16

The comparison of the number of the Extinct and Healed individuals with and without the proposed controller

In Figs. 17 and 18, the relation between the control rate and groups $R(t)$, $D(t)$, and $S(t)$ is presented. The more susceptible people are, the more effort is needed to vaccinate them. Also, the more susceptible people exist, the more they get infected; therefore, a higher isolation rate is required in order to isolate them.

Fig. 17

The relationship between the controller (vaccination) and the mean of recognized and diagnosed and susceptible individuals

Fig. 18

The relationship between the controller (isolation) and the mean of recognized and diagnosed and susceptible individuals

It can be concluded from Fig. 19 that in the early days of the outbreak, the number of susceptible people is large, then a considerable control effort is needed, which decreases over time.

Fig. 19

The control efforts for isolation and vaccination-based strategy

7.3 Evaluation of the controller for new SARS-Cov-2 variants

In this section, the parameters of the SIDARTHE epidemic model $(\alpha ,\beta , \delta$, and $\gamma )$ are changed to match the new transmissibility rate, which faced an estimated increase between 40 and 70%, as the preliminary reports show. All figures show the comparison between applying the controller (both strategies) on the original SIDARTHE Epidemic and the new SIDARTHE Epidemic with a 70% increase in transmissibility rate (the most transmissions) (World Health Organization (WHO) 2021).

7.3.1 Comparison first strategy for the original and new SIDARTHE epidemic model

Given that the current vaccines for the SARS-Cov-2 variants have not been accessible to everyone yet and the transferring of a safe and effective vaccine worldwide takes time, it can be assumed that there is no vaccination and the only control effort is isolation. Figures 20, 21, 22 and 23 show that since the transmission rate has dramatically increased, the controller can control the outbreak only by applying isolation.

Fig. 20

The comparison between the number of $S(t)$ and $H(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

Fig. 21

The comparison between the number of $I(t)$ and $A(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

Fig. 22

The comparison between the number of $D(t)$ and $R(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

Fig. 23

The comparison between the number of $T(t)$ and $E(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

As shown in Fig. 20, with a 70% increase in transmissibility rate, in the absence of an effective vaccine, more susceptible people get infected; therefore, their number decrease sooner in less than ten days. Also, although the transmissibility increases, the number of healed people in each situation is equal.

Figure 21 shows that the number of infected people increases with an increment in the transmissibility rate in the early days. Therefore, the control input applies more effort to decrease this growth; hence, their number drops sooner and converges to zero in less than 25 days. Similarly, an increase in the transmissibility rate leads to a peak in the number of ailing people in the early days of the outbreak. After that, the controller can reduce this increment. In Figs. 22 and 23, the controller controls the prevalence of pandemics and drives the number of detected infected people to converge to zero. Although the rapid-spreading coronavirus is developing quickly, there is no increment in the mortality rate by applying only the isolation strategy.

7.3.2 The impact of second strategy on the new model

In this section, the impact of the proposed controller (second strategy) on the original SIDARTHE epidemic model and the new one with a 70% increase in transmissibility are investigated and compared. Although the transmission rate is increased up to 70%, the controller can control the outbreak with very little difference and acceptable performance. Regardless of the disease peak in the infected group, the controller has increased in the outbreak’s early days and can still control and converge it to zero. As shown in Fig. 24, the number of susceptible people diminishes because of the vaccination strategy. Also, by comparing the number of healed people (70% increase in transmissibility) with their number in the case of with-controller in Fig. 20, it can be concluded that their number with a 70% increase reaches just less than 2500. In contrast, their number is more than 300 when the transmissibility rate is not so large. Similarly, in the other Figs. 25, 26 and 27, it is clear that the controller can control the effect of increment in the transmissibility rate well.

Fig. 24

The comparison between the number of $S(t)$ and $H(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

Fig. 25

The comparison between the number of $I(t)$ and $A(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

Fig. 26

The comparison between the number of $D(t)$ and $R(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

Fig. 27

The comparison between the number of $T(t)$ and $E(t)$ in the presence of proposed controllers applied on original and new SIDARTHE epidemic model

8 Discussion

The containment measures related to the COVID-19 pandemic, mainly physical distancing and quarantine applied to society in the early days of the outbreak, had damaging consequences on the economic and mental health of the general population worldwide in the long term. According to the vaccine design and development through to clinical applications, it can be emphasized that vaccination should be used as a control effort to control the outbreak. Also, in the absence of curative treatment, non-pharmaceutical interventions, such as infected isolation can be used to curb the pandemic. Therefore, this paper is focused only on vaccination and isolation without dealing with quarantine and its limitation that society faces. The vaccination strategy indirectly reduces the number of infected people; that is, a decrease in the number of susceptible people by vaccination leads to eradicating the pandemic. Also, infected isolation has fewer limitations than quarantine and is easier to apply. The prevalence of new COVID-19 caused by the variants with an increase in transmissibility is examined in this paper. The mentioned strategies are evaluated with a 70% increase and have overcome the pandemic.

In the present study, the simulation results show that, without vaccination, the susceptible people move to the infected people group; therefore, decrement in their number is more, and they reach zero in a shorter period compared to the free-control case. Besides, as the number of diagnosed, ailing, recognized, and acutely infected people grows, more people will die of the disease. Whereas vaccinating susceptible people with a vaccine reduces their number and moves them to the vaccinated group. Hence, fewer people get infected, and the mortality rate will be diminished. Moreover, Moreover, by isolating the infected people, the contact with the susceptible people will be reduced, preventing the cycle of transmission in society, and fewer people will die.

ANFIS usage in various research fields has been extensively researched over the past few years, but few were devoted to the COVID-19 pandemic (Moayedi et al. 2020; Alawad et al. 2020; Shokouhifar and Pilevari 2021; Mohadesi and Aghel 2020; Alameer et al. 2019; Abd Elaziz et al. 2020; Husein et al. 2019; Turabieh and Muhanna 2016). Authors in Moayedi et al. (2020) optimized the ANFIS with two optimization algorithms: first, Genetic Algorithm (GA) and, second, Particle Swarm Optimization (PSO) for the calculation of friction capacity ratio (α) in driven shafts in the area of pile engineering. Risk assessment of overcrowding levels in railway stations is also investigated using ANFIS (Alawad et al. 2020). In addition, (Shokouhifar and Pilevari 2021) assessed the resilience of e-learning in education systems using the combined model of GA-ANFIS. The GA-ANFIS strategy is also used for the prediction purposes such as inorganic indicators of water quality (Mohadesi and Aghel 2020), copper prices (Alameer et al. 2019), crude oil prices (Abd Elaziz et al. 2020), need for drugs based on disease population (Husein et al. 2019), the existence of breast cancer or not (Turabieh and Muhanna 2016). Furthermore, regarding COVID-19, ANFIS is used to predict epidemic peak and infected cases for COVID-19 in India (Kumar et al. 2021; Ly 2021). Authors in Eshaghi Chaleshtori and Aghaie (2021) proposed a novel prediction model (i.e., PSO-GA-ANFIS) to estimate and predict the total confirmed cases of COVID-19 assessed by Iran’s data to forecast the COVID-19 epidemic prevalence trend in Iran.

In the following, the present study is compared to some studies specifically to show the capability of the given controller. Authors in Cooper et al. (2020); Abbasi et al. 2021b) introduced an optimal technique to control the SEIR model for Influenza and COVID-19, respectively. Those papers aimed to reduce the number of susceptible and infected individuals and increase the number of recovered individuals using minimum vaccination and antiviral treatment rates. Several new groups should be added to the model introduced in Cooper et al. (2020) to make it more beneficial to investigate the COVID-19 features. Due to the rapid changes in the outbreak rate of the disease, another control effort can be applied in addition to vaccination. Therefore, as mentioned in the introduction, the authors in Abbasi et al. (2020) applied an optimal control strategy to the SQEIAR epidemic model with application to COVID-19. They controlled the outbreak using susceptible people quarantine and infected people treatment. A successful vaccine is developed to defeat the pandemic, and society faces economic and social constraints concerning quarantine. Therefore, it has become clear that we must go beyond and use new strategies to face the disease according to vaccine development. In this regard, the authors in Higazy (2020) used an optimal control strategy to control the SIDARTHE model using susceptible vaccination and infected treatment with four control efforts. They obtained the control efforts for the whole duration of the outbreak. However, as stated by the daily trend in the size of the COVID-19 infected population globally, it is necessary to control the pandemic on a daily basis. Hence, the present study uses the SIDARTHE model with a more detailed description of infection stages. The advantage of this work is using the daily control effort instead of the optimal control duration with only two control efforts. It is motivated by the daily changes in the number of people involved with the disease. The optimal ANFIS-based control is also applied to the SIDARTHE model, which has not been addressed in the literature before. Also, the impact of the proposed controller with a 70% increase in transmissibility is investigated, showing the capability of the presented controller to overcome the variants.

In following, Table 7 represents the performance of the proposed strategies using MSE and RMSE criteria. The available random dataset is divided into two subsets: training, and testing, with 70% for training and 30% for testing purposes (Tables 1 and 2), while the validation is done using the real data of South Korea, taken from the Korea Disease Control and Prevention Agency (KDCA), given in Amiri Mehra et al. (2020). According to the comparison results between the GA-ANFIS and ANFIS, it can be concluded that the proposed model (GA-ANFIS) had a better performance than the conventional ANFIS model, and the results ignore the limitations of the ANFIS model.

Table 7 The performance metric for each strategy and algorithm

9 Threats to validity

In this section, the threats related to the validation in Table 8 clarify the proposed research.

Table 8 The validity threats to the proposed method

10 Conclusion

In this work, a comprehensive SIDARTHE epidemic model was considered to investigate the trend of the COVID-19 outbreak. The objective of this study was: first, infected-isolation with the aid of minimum control effort in the lack of the vaccination campaign; second, susceptible-vaccination and infected-isolation simultaneously using minimum control efforts without difficulties in dealing with susceptible-quarantine. To this end, an ANFIS was optimized based on GA to be used as a controller to draw the states to reach the objective. In this regard, an optimized data set was obtained using two fitness functions to train the ANFIS. Hence, the proposed ANFIS-based optimal control was employed to reduce the number of diagnosed and recognized people via isolation and susceptible people via vaccination. Meanwhile, the basic properties of the model, such as positivity, boundedness, and existence, were discussed in the presence of the controller. Finally, numerical results showed that the controller had overcome the outbreak despite the new strains spreading rapidly in several countries.

Following are the potential directions that can be explored for future research:

• Since the COVID-19 pandemic spreading is on the rise and some new rapid-spread strains have been identified recently, the need to control the prevalence trend is the main concern for researchers. Therefore, it could be an excellent opportunity to develop a new controller according to the new features of the mutated coronavirus in future studies.

• Exploring the possibility of optimizing the ANFIS model with other evolutionary algorithms and comparing the results.

• Investigating other properties of the model, such as sensitivity and accuracy in the presence of the controller.