Pseudolites/repeaters infrastructure autopositioning approach—mathematics and first simulation-based results

Abstract

In the various infrastructure-based indoor positioning systems using Global Navigation Satellite System signals, i.e. pseudolites, repeaters, and repealites, there is the need for the terminal to know the positions of the various transmitters. Some techniques have been proposed for high accuracy pseudolite systems, but they require carrier phase measurements and a careful choice of some specific test locations. Other approaches consider that these data are simply available by any means: Of course, this can be achieved through manual distance measurements and the use of maps of the indoor environment. In this paper, we describe a new method that is based on a two-step approach. The first one consists in deploying the system. The second one is the calculation of the position of the transmitters through classic code measurements for a few specific chosen locations. Thus, the system can be deployed without any constraint and the locations of the transmitters calculated through a basic set of elementary measurements. The theoretical method is first described and the resulting accuracy of the position of the transmitters is then evaluated through theoretical calculations. In addition, electromagnetic simulations are carried out in order to estimate the pseudo-range errors of the proposed measurements: The accuracy of the determination of the position of the transmitters is then estimated (note that two receiver tracking loop implementations are considered). Thus, the accuracy of the proposed method is evaluated theoretically and through simulations.

1 Introduction

It is of uppermost importance to simplify the deployment phase of these “infrastructure-based” indoor positioning systems since this is clearly their major drawback. Works carried out so far are mainly based on two steps: installation and transmitter position estimations. All these works are related to high precision pseudolite systems, and the required accuracy of the positions must be in the centimeter range, leading to carried phase measurement techniques. In the case of repeater or repealite systems, where code measurements are carried out, the above-described techniques for calculating the location of the transmitters are no longer described, and the proposed method only needs to implement code phase measurements. For instance, an accuracy of a few tens of centimeters is probably sufficient.

Among some other specific problems of transmitter-based indoor positioning system, i.e., synchronization, near-far effects, and multipath, one can say that the determination of their locations must be solved. It is not compulsory to imagine an automatic procedure when the required accuracy is not so high. Thus, although such an automatic procedure is certainly required in the case of pseudolites, a “manual” procedure could be enough for repeaters. The case of repealites, a sort of mix between repeaters and pseudolites is probably in between. Thus, in the case of repeaters, it is probably more for ease of installation rather than for pure performance that such an autopositioning technique is required.

The approach used so far is to actually locate the positions of the transmitters by measurements of local distances (using a laser meter for instance) or to use the maps of the building. These techniques are not so bad but require a “specialized” intervention which is potentially time-consuming. In addition, it is quite often not possible to do this job before the real deployment since the locations of all indoor components (lights, panels, local furniture, etc.) are usually not available. An automatic method allows for a “light” specification (approximate) of the deployment, followed by a second phase of more accurate determination of the geometry of the transmitting system.

Here we propose an approach for automatic positioning through the use of code measurements: First, the method of calculation is described and the necessary assumption clearly explained (note that there is only one required). Then, evaluations of the sensitivity of the accuracy of the automatic positioning according to the imprecision of the pseudo-range measurements are conducted. The Ergospace ray tracing software is used to simulate “real cases” and to estimate the behaviors of two tracking loop implementations (the standard approach and the short multipath insensitive code loop (SMICL) approach).

2 State-of-the-art

In all these systems, based on Global Navigation Satellite Systems (GNSS)-like signal generators, there is the need for the receiver to know the location of the various transmitters (the same applies to the satellites for outdoor GNSS). In the literature, the most described approach is related to pseudolites and generally deals with high accuracy positioning. Note that the approach proposed in this paper is intended for code pseudolites (PL), repeaters (R), or repealites (RL) which are not implementing differential positioning: The accuracy target is no longer in the centimeter range, but rather in the sub-meter range. The constraint of the transmitter position in the present paper is thus not as high as described in previous papers.

In 1999 [1], a procedure for calibrating the PL system is proposed. It uses a user’s position set and proposes the optimization of this set. Thus, the paper deals with the determination of the number and the locations of the required test locations. Finally, the authors showed that a 1–2-cm accuracy of the PL locations is reachable with the optimized set (defined regarding some geometrical and algorithmic constraints concerning measurements). In this case, the double differenced measurements described are much more difficult to carry out than the proposed very natural code phase measurements but lead to better results: Compromise has to be made, as usual! Other works [2] dealt with all the potential errors in pseudolite-related systems, including location of the transmitters, and gave some order of magnitude of accuracies. In 2002 [3], a new paper, concerning the specific case of PL, showed that the positioning errors can potentially reach twice the location error of the PLs. In addition, an emphasis on geometrical factors (later called indoor dilution of precision, IDOP [4]) that link the PL location errors and the resulting indoor positioning error was discussed. In 2003, the first cited authors proposed the practical implementation of their works with a specific double differenced carrier phase measurement technique [5]. Convergence problems are related and some hints are given in order to successfully terminate the calibration procedure. In this paper, it is noted that estimating the location of the PL within 1 m can easily be achieved by eye. We believe this assertion is only true when all the PLs are in optical visibility from each other, which is clearly not the situation we are dealing with. In our case, R or RL can be separated by walls or even located on different floors. Thus, the “eye” estimation is not so easy to carry out.

A new review of the various errors in pseudolite systems was proposed in 2004 [6] highlighting once again the classical problems linked to near-far, multipath, synchronization, and of course errors due to the uncertainty of the location of the pseudolites. Once again, the discussion focused on centimeter accuracy systems and came back to the facts described in [3].

More recently, the Center for Remote Sensing, Inc., proposed some PLs. The transmitting GNSS signals lies in various bandwidths [7]. The way PL locations are obtained is briefly addressed stating that they can be obtained either from external sources (i.e., eye, distance measurements, or use of maps) or using built-in GNSS receivers in case they are outdoors. In our present case, i.e., indoors, it is just suggested to use another means to position the PL.

Works are also carried out [8] with Galileo signals: The idea here is in fact to use PL in order to simulate the future Galileo constellation in order to validate a few concepts and preliminary performance: The PLs are located outdoors. The locations of the PLs are thus known and sent to the receivers in a slightly different way GNSS satellites send their orbital parameters, through geographical terms [9]. Another interesting paper [10] dealt with the inversion of the pseudolite approach, considering a set of GPS receivers tracking a mobile pseudolite.

In conclusion, if one does not want to carry out carrier phase measurements, due to their complexity and to the important associated constraints, the way the location of the transmitters is obtained is usually not an automatic process. These “manual” approaches are nice but require a double human intervention and must follow an initial process that has to evaluate the optimal locations. Unfortunately, unless the technician who installs the transmitters is well aware of the first process, the above-mentioned locations have to be specified and real situations are likely to happen that force him to modify the initially planned locations. In this case, a new measurement campaign is required in environments that are not always of easy access (great hall height, difficulty to find representative places for reference measurements, etc.).

Finally, the accuracy of the positioning of the transmitters is not equivalent for the various systems. For instance, pseudolite-based systems that seek decimeter level accuracy require typically a centimeter accuracy of the location of the transmitters. In comparison, the meter accuracy goal of a repeater-based approach is not so stringent.

3 The autopositioning proposed approach

Let us consider the configuration given in Fig. 1 in which R ₁, R ₂, R ₃, and R ₄ are the various transmitters and (X, Y, Z) a local frame of reference. In order to simplify the calculations and the implementation of required measurements for the autopositioning, we propose in a first preliminary step to define a new local reference frame. It is centered on R ₁ and with the new Y′ axis oriented toward R ₂ (as shown in Fig. 2). The first (and unique) hypothesis that we have to make is that the Z′ (formerly Z) is directed upward and vertically (this will also be useful for the needed additional measurements of the proposed method, as discussed in the following pages). Note that verticality is the constraint of the method.

Fig. 1

Initial configuration

Fig. 2

New frame orientation

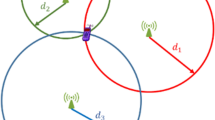
From this new configuration, we still need to find eight unknown variables of the problem, namely y ₂, z ₂, x ₃, y ₃, z ₃, x ₄, y ₄, and z ₄. Indeed, using this new reference frame allows us to get rid of four unknown variables of the initial problem, i.e., x ₁, y ₁, z ₁, and x ₂. This new frame helps us to transform the 12 unknown variable problems into a simpler eight unknown variable problems. The basic idea of the proposed approach (in order to solve this problem) will be to use a receiver R ₅ located at a generic (x ₅, y ₅, z ₅) position, as shown in Fig. 3.

Fig. 3

R ₅ positioning and d _ij definitions

Figure 3 also indicates the distances we will consider in the future calculations. The distance d _ij is the distance between R _i and R _j (and hence R _j and R _i as well) in the new local reference frame. In particular, the distances d ₁₅, d ₂₅, d ₃₅, and d ₄₅ are the distances from each transmitter to receiver R ₅.

Let us now consider what happens when we apply the transmitter-based positioning system to receiver R ₅, i.e., when on wants to locate R ₅ indoors. The transitions, denoted T _i , are given by the following equality:

$$ \matrix{{*{20}{c}} \begin{gathered} {T_1} = \sqrt {{{{\left( {{x_5} - {x_2}} \right)}^2} + {{\left( {{y_5} - {y_2}} \right)}^2} + {{\left( {{z_5} - {z_2}} \right)}^2}}} - \sqrt {{{{\left( {{x_5} - {x_1}} \right)}^2} + {{\left( {{y_5} - {y_1}} \right)}^2} + {{\left( {{z_5} - {z_1}} \right)}^2}}} \hfill \\ { } = \sqrt {{x_5^2 + {{\left( {{y_5} - {y_2}} \right)}^2} + {{\left( {{z_5} - {z_2}} \right)}^2}}} - \sqrt {{x_5^2 + y_5^2 + z_5^2}} \hfill \\ \end{gathered} \\ } $$

This transition corresponds to the pseudo-range skip from R ₁ to R ₂. Similarly, the following transitions, from R ₂ to R ₃, and finally from R ₃ and R ₄ are respectively as follows:

$$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \begin{gathered} {{\text{T}}_{{2}}}{ = }\sqrt {{{{\left( {{{\text{x}}_{{5}}} - {{\text{x}}_{{3}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{y}}_{{5}}} - {{\text{y}}_{{3}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{z}}_{{5}}} - {{\text{z}}_{{3}}}} \right)}^{{2}}}}} - \sqrt {{{{\left( {{{\text{x}}_{{5}}} - {{\text{x}}_{{2}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{y}}_{{5}}} - {{\text{y}}_{{2}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{z}}_{{5}}} - {{\text{z}}_{{2}}}} \right)}^{{2}}}}} \hfill \\ { = }\sqrt {{{{\left( {{{\text{x}}_{{5}}} - {{\text{x}}_{{3}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{y}}_{{5}}} - {{\text{y}}_{{3}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{z}}_{{5}}} - {{\text{z}}_{{3}}}} \right)}^{{2}}}}} - \sqrt {{{\text{x}}_{{5}}^{{2}}{ + }{{\left( {{{\text{y}}_{{5}}} - {{\text{y}}_{{2}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{z}}_{{5}}} - {{\text{z}}_{{2}}}} \right)}^{{2}}}}} \hfill \\ \end{gathered} \\ \end{array} } \hfill \\ {{{\text{T}}_{{3}}}{ = }\sqrt {{{{\left( {{{\text{x}}_{{5}}} - {{\text{x}}_{{4}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{y}}_{{5}}} - {{\text{y}}_{{4}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{z}}_{{5}}} - {{\text{z}}_{{4}}}} \right)}^{{2}}}}} - \sqrt {{{{\left( {{{\text{x}}_{{5}}} - {{\text{x}}_{{3}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{y}}_{{5}}} - {{\text{y}}_{{3}}}} \right)}^{{2}}}{ + }{{\left( {{{\text{z}}_{{5}}} - {{\text{z}}_{{3}}}} \right)}^{{2}}}}} } \hfill \\ \end{array} $$

Now we shall consider some specific cases for the location of R ₅. A first set of measurements is carried out placing R ₅ in the very close vicinity of R ₁ (typically a few centimeters apart). Practically, this could be achieved by having a dual antenna transmitter: the standard one that emits and the second one that is only used for this autopositioning phase that receives. In this case, the various transitions take the following values:

$$ \matrix{{*{20}{c}} {{T_{{1{R_1}}}} = \sqrt {{y_2^2 + z_2^2}} = {d_{{21}}}} \hfill \\ {{T_{{2{R_1}}}} = \sqrt {{x_3^2 + y_3^2 + z_3^2}} - \sqrt {{y_2^2 + z_2^2}} = {d_{{31}}} - {d_{{21}}}} \hfill \\ {{T_{{3{R_1}}}} = \sqrt {{x_4^2 + y_4^2 + z_4^2}} - \sqrt {{x_3^2 + y_3^2 + z_3^2}} = {d_{{41}}} - {d_{{31}}}} \hfill \\ } $$

In these expressions, T _iRj corresponds to the measured value of the transition T _i when the receiver is in R _j . In pursuing this logic, we perform a second set of measurements, R ₅ being located in R ₂.

The transitions become:

$$ \matrix{{*{20}{c}} {{T_{{1{R_2}}}} = - \sqrt {{y_2^2 + z_2^2}} = - {d_{{21}}}} \hfill \\ {{T_{{2{R_2}}}} = \sqrt {{x_3^2 + {{\left( {{y_2} - {y_3}} \right)}^2} + {{\left( {{z_2} - {z_3}} \right)}^2}}} = {d_{{32}}}} \hfill \\ {{T_{{3{R_2}}}} = \sqrt {{x_4^2 + {{\left( {{y_2} - {y_4}} \right)}^2} + {{\left( {{z_2} - {z_4}} \right)}^2}}} - \sqrt {{x_3^2 + {{\left( {{y_2} - {y_3}} \right)}^2} + {{\left( {{z_2} - {z_3}} \right)}^2}}} = {d_{{42}}} - {d_{{32}}}} \hfill \\ } $$

Then with R ₅ in R ₃:

$$ \matrix{{*{20}{c}} {{T_{{1{R_3}}}} = \sqrt {{x_3^2 + {{\left( {{y_3} - {y_2}} \right)}^2} + {{\left( {{z_3} - {z_2}} \right)}^2}}} - \sqrt {{x_3^2 + y_3^2 + z_3^2}} = {d_{{32}}} - {d_{{31}}}} \hfill \\ {{T_{{2{R_3}}}} = - \sqrt {{x_3^2 + {{\left( {{y_3} - {y_2}} \right)}^2} + {{\left( {{z_3} - {z_2}} \right)}^2}}} = - {d_{{32}}}} \hfill \\ {{T_{{3{R_3}}}} = \sqrt {{{{\left( {{x_4} - {x_3}} \right)}^2} + {{\left( {{y_4} - {y_3}} \right)}^2} + {{\left( {{z_4} - {z_3}} \right)}^2}}} = {d_{{43}}}} \hfill \\ } $$

And finally in R ₄:

$$ \matrix{{*{20}{c}} {{T_{{1{R_4}}}} = \sqrt {{{x_4}^2 + {{\left( {{y_4} - {y_2}} \right)}^2} + {{\left( {{z_4} - {z_2}} \right)}^2}}} - \sqrt {{{x_4}^2 + {y_4}^2 + {z_4}^2}} = {d_{{42}}} - {d_{{41}}}} \hfill \\ {{T_{{2{R_4}}}} = \sqrt {{{{\left( {{x_4} - {x_3}} \right)}^2} + {{\left( {{y_4} - {y_3}} \right)}^2} + {{\left( {{z_4} - {z_3}} \right)}^2}}} - \sqrt {{{x_4}^2 + {{\left( {{y_4} - {y_2}} \right)}^2} + {{\left( {{z_4} - {z_2}} \right)}^2}}} = {d_{{43}}} - {d_{{42}}}} \hfill \\ {{T_{{3{R_4}}}} = - \sqrt {{{{\left( {{x_4} - {x_3}} \right)}^2} + {{\left( {{y_4} - {y_3}} \right)}^2} + {{\left( {{z_4} - {z_3}} \right)}^2}}} = - {d_{{43}}}} \hfill \\ } $$

This allows us to write the system of independent equations that follows:

$$ \matrix{{*{20}{c}} {y_2^2 + z_2^2 = T_{{1{R_1}}}^2 = m_1^2} \hfill \\ {x_3^2 + y_3^2 + z_3^2 = {{\left( {{T_{{1{R_1}}}} + {T_{{2{R_1}}}}} \right)}^2} = m_2^2} \hfill \\ {x_4^2 + y_4^2 + z_4^2 = {{\left( {{T_{{1{R_1}}}} + {T_{{2{R_1}}}} + {T_{{3{R_1}}}}} \right)}^2} = m_3^2} \hfill \\ {x_3^2 + {{\left( {{y_2} - {y_3}} \right)}^2} + {{\left( {{z_2} - {z_3}} \right)}^2} = T_{{2{R_2}}}^2 = m_4^2} \hfill \\ {x_4^2 + {{\left( {{y_2} - {y_4}} \right)}^2} + {{\left( {{z_2} - {z_4}} \right)}^2} = {{\left( {{T_{{2{R_2}}}} + {T_{{3{R_2}}}}} \right)}^2} = m_5^2} \hfill \\ } $$

(1)

It is interesting to note that these measurements provide a certain redundancy which could certainly be useful in a real implementation in order to allow an averaging effect leading to a reduction of remaining errors. In particular, it is possible to rewrite Eq. 1 in the following new equivalent form:

$$ \matrix{{*{20}{c}} {y_2^2 + z_2^2 = {{\left( { - {T_{{1{R_2}}}}} \right)}^2} = m_1^{{\prime 2}}} \hfill \\ {x_3^2 + y_3^2 + z_3^2 = {{\left( {{T_{{1{R_3}}}} + {T_{{2{R_3}}}}} \right)}^2} = m_2^{{\prime 2}}} \hfill \\ {x_4^2 + y_4^2 + z_4^2 = {{\left( { - {T_{{1{R_4}}}} - {T_{{2{R_4}}}} - {T_{{3{R_4}}}}} \right)}^2} = m_3^{{\prime 2}}} \hfill \\ {x_3^2 + {{\left( {{y_2} - {y_3}} \right)}^2} + {{\left( {{z_2} - {z_3}} \right)}^2} = {{\left( {{T_{{1{R_3}}}} + {T_{{1{R_1}}}} + {T_{{2{R_1}}}}} \right)}^2} = m_4^{{\prime 2}}} \hfill \\ {x_4^2 + {{\left( {{y_2} - {y_4}} \right)}^2} + {{\left( {{z_2} - {z_4}} \right)}^2} = {{\left( {{T_{{1{R_4}}}} + {T_{{3{R_1}}}} + {T_{{1{R_1}}}} + {T_{{2{R_1}}}}} \right)}^2} = m_5^{{\prime 2}}} \hfill \\ } $$

It appears that it is possible to extract the five equations of Eq. 1 from all the measurements made previously. We shall now deal with the system given in Eq. 1, noting that the measurements obtained by positioning the receiver R ₅ in R ₄ are not critical, except in order to allow some redundancy. Since we still have to deal with eight unknowns, three equations remain missing. Here the unique assumption made so far takes its full meaning: The z axis is vertical, pointing upward. In this case, we can locate the receiver R ₅ on a position located z _1 m meters above one transmitter. We will obviously choose R ₁ whose coordinates are all zero. R ₅ coordinates are thus (0; 0; z _1 m), i.e., R ₅ lies on the Z′ axis.

The various transitions for this new location are given by:

$$ \matrix{{*{20}{c}} {{T_{{1{R_{{1\;{\text{m}}}}}}}} = \sqrt {{y_2^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_2}} \right)}^2}}} - \sqrt {{z_{{1\;{\text{m}}}}^2}} = d_{{21}}^{\prime } - {z_{{1\;{\text{m}}}}}} \hfill \\ {{T_{{2{R_{{1\;{\text{m}}}}}}}} = \sqrt {{x_3^2 + y_3^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_3}} \right)}^2}}} - \sqrt {{y_2^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_2}} \right)}^2}}} = d_{{31}}^{\prime } - d_{{21}}^{\prime }} \hfill \\ {{T_{{3{R_{{1\;{\text{m}}}}}}}} = \sqrt {{x_4^2 + y_4^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_4}} \right)}^2}}} - \sqrt {{x_3^2 + y_3^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_3}} \right)}^2}}} = d_{{41}}^{\prime } - d_{{31}}^{\prime }} \hfill \\ } $$

This allows us to add the following equations to Eq. 1:

$$ \matrix{{*{20}{c}} {y_2^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_2}} \right)}^2} = {{\left( {{T_{{1{R_{{1\;{\text{m}}}}}}}} + {z_{{1\;{\text{m}}}}}} \right)}^2} = m_6^2} \hfill \\ {x_3^2 + y_3^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_3}} \right)}^2} = {{\left( {{T_{{2{R_{{1\;{\text{m}}}}}}}} + {T_{{1{R_{{1\;{\text{m}}}}}}}} + {z_{{1\;{\text{m}}}}}} \right)}^2} = m_7^2} \hfill \\ {x_4^2 + y_4^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_4}} \right)}^2} = {{\left( {{T_{{3{R_{{1\;{\text{m}}}}}}}} + {T_{{2{R_{{1\;{\text{m}}}}}}}} + {T_{{1{R_{{1\;{\text{m}}}}}}}} + {z_{{1\;{\text{m}}}}}} \right)}^2} = m_8^2} \hfill \\ } $$

We obtain the final system 2 with eight equations. Note that these equations are typically of the second degree: It is clear that choices about the direction of the X and Y axes (remember that the orientation of Z has already been determined by the hypothesis) will be required when solving the complete set of equations. The system 2 is as follows (note that the order of equations is modified to group those that will be coupled in the resolution process and that a change of the names of the variables has also been carried out).

$$ \matrix{{*{20}{c}} {(1)\quad y_2^2 + z_2^2 = m_1^2 = M_1^2} \hfill \\ {(2)\quad y_2^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_2}} \right)}^2} = m_6^2 = M_2^2} \hfill \\ {(3)\quad x_3^2 + y_3^2 + z_3^2 = m_2^2 = M_3^2} \hfill \\ {(4)\quad x_3^2 + y_3^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_3}} \right)}^2} = m_7^2 = M_4^2} \hfill \\ {(5)\quad x_3^2 + {{\left( {{y_2} - {y_3}} \right)}^2} + {{\left( {{z_2} - {z_3}} \right)}^2} = m_4^2 = M_5^2} \hfill \\ {(6)\quad x_4^2 + y_4^2 + z_4^2 = m_3^2 = M_6^2} \hfill \\ {(7)\quad x_4^2 + y_4^2 + {{\left( {{z_{{1\;{\text{m}}}}} - {z_4}} \right)}^2} = m_8^2 = M_7^2} \hfill \\ {(8)\quad x_4^2 + {{\left( {{y_2} - {y_4}} \right)}^2} + {{\left( {{z_2} - {z_4}} \right)}^2} = m_5^2 = M_8^2} \hfill \\ } $$

(2)

In order to solve this system, we propose the following, rather simple, eight steps:

• 1. (1)–(2) gives z ₂:

$$ \begin{gathered} 2{z_{{1\;{\text{m}}}}}{z_2} - z_{{1\;{\text{m}}}}^2 = M_1^2 - M_2^2 \hfill \\ { } \to {z_2} = \frac{1}{{2{z_{{1\;{\text{m}}}}}}}\left[ {M_1^2 - M_2^2 + z_{{1\;{\text{m}}}}^2} \right] \hfill \\ \end{gathered} $$

• 2. Which is used in (1) in order to obtain y ₂:

$$ {y_2} = \sqrt {{M_1^2 - z_2^2}} $$

• 3. (3)–(4) gives z ₃:

$$ {z_3} = \frac{1}{{2{z_{{1\;{\text{m}}}}}}}\left[ {M_3^2 - M_4^2 + z_{{1\;{\text{m}}}}^2} \right] $$

• 4. (6)–(7) gives z ₄:

$$ {z_3} = \frac{1}{{2{z_{{1\;{\text{m}}}}}}}\left[ {M_6^2 - M_7^2 + z_{{1\;{\text{m}}}}^2} \right] $$

• 5. One obtains y ₃ through (1) + (3)–(5):

$$ \begin{gathered} 2{y_2}{y_3} + 2{z_2}{z_3} = M_1^2 + M_3^2 - M_5^2 \hfill \\ { } \to { }{y_3} = \frac{1}{{2{y_2}}}\left[ {{M_1}^2 + {M_3}^2 - {M_5}^2 - 2{z_2}{z_3}} \right] \hfill \\ \end{gathered} $$

• 6. One obtains y ₄ through (1) + (6)–(8)

$$ \begin{gathered} 2{y_2}{y_4} + 2{z_2}{z_4} = M_1^2 + M_6^2 - M_8^2 \hfill \\ { } \to {y_4} = \frac{1}{{2{y_2}}}\left[ {M_1^2 + M_6^2 - M_8^2 - 2{z_2}{z_4}} \right] \hfill \\ \end{gathered} $$

• 7. (3) leads to x ₃:

$$ {x_3} = \sqrt {{M_3^2 - y_3^2 - z_3^2}} $$

Indeed, since (3) gives $x_3^2$, it is possible to choose a positive or a negative value for x ₃. We have already chosen the orientation of Z′ (upward), and the orientation of Y′ was determined by the choice of y ₂ (in the direction of R ₂ from R ₁). The choice of X′ is now up to us, depending on whether one wants a direct or reverse (X′, Y′, Z′) reference frame. If one decides not to make the choice, it is then possible to choose x ₃ positive (for example) and thus one has completely defined the local reference frame.

• 8. (4) leads to x ₄

$$ {x_4} = \pm \sqrt {{M_6^2 - y_4^2 - z_4^2}} $$

Here we certainly have no more choice for x ₄, the frame being set up. To find the sign of x ₄, we could use the measurement of the third transition obtained when the receiver R ₅ was located in R ₄ and check, for the positive and negative values, the following equation:

$$ {\left( {{x_4} - {x_3}} \right)^2} = T_{{3{R_4}}}^2 - {\left( {{y_4} - {y_3}} \right)^2} - {\left( {{z_4} - {z_3}} \right)^2} $$

Only one of the two values will verify this last equation, except in the unlikely event where x ₃ is zero (when installing, it will be necessary to ensure that this is not the case; otherwise, it will be the choice of x ₄ that will define the orientation of the reference frame). Finally, note that it is also possible to make the same calculations through the third transition obtained when the receiver R ₅ was located in R ₃ as follows:

$$ {\left( {{x_3} - {x_4}} \right)^2} = T_{{3{R_3}}}^2 - {\left( {{y_3} - {y_4}} \right)^2} - {\left( {{z_3} - {z_4}} \right)^2} $$

We now have all the coordinates of the transmitters in a reference frame centered on R ₁, with the Y-axis oriented toward R ₂ and the X-axis defined according to R ₃. These calculations have of course been validated by simulations, as presented in the following sections. However, a preliminary question is raised: What is the impact of the precision of the measurements of the transitions on the accuracy of the positioning of the various transmitters? In order to achieve such a goal, we will run simulations by considering added noise on the various measurements (see next section).

4 Theoretical effect of measurement inaccuracies

To estimate the effect of the precision of the measurements on the precision of the automatic positioning method, we will consider a specific deployment. It is characterized by four transmitters with the following coordinates in the initial local reference frame:

$$ {R_1} = \left( {\matrix{{*{20}{c}} {29.5} \\ {0.5} \\ {4.0} \\ } } \right)\quad {R_2} = \left( {\matrix{{*{20}{c}} {0.5} \\ {0.5} \\ {4.5} \\ } } \right)\quad {R_3} = \left( {\matrix{{*{20}{c}} {0.5} \\ {59.5} \\ {3.5} \\ } } \right)\quad {R_4} = \left( {\matrix{{*{20}{c}} {29.5} \\ {59.5} \\ {3.0} \\ } } \right) $$

Following the procedure described in the preceding paragraph, we carried out some simulations. The basic principle of these simulations is to set a range of accuracies of raw measurements of the transitions (e.g., 2 m), then to generate a measurement that corresponds to the actual distance to which is added a random value between, say, +2 m and −2 m. As it is important to conduct a sufficient number of simulations to get a significant result, a simulation variable “NbMaes,” specifying the number of complete cycles to be achieved, is specified. Remember that a complete cycle is a set of eight measurements allowing the computation of the transmitter locations. A second variable is of course the accuracy of the measurement “ErrMeas” that varies between 0.1 and 10 m in the simulations presented below.

In Tables 1, 2, and 3, the theoretical results of the 12 coordinates of the transmitters R ₁ to R ₄ are recalled in the first line. Then, on each line, the following are given:

• The NbMeas parameter (used to evaluate the impact of the number of cycles it would be better to carry out)

• Parameter ErrMeas (described above)

• The 12 coordinates of the transmitters

• The number of calculations (for the NbMeas attempts) that do not provide any positioning of the transmitters (i.e., for which the algorithm does not converge)

• Errors in meters between the average positions (computed for the NbMeas calculations) and the actual positions of the transmitter (included in the first row of Table 1, 2, and 3)

Tables 1, 2, and 3 have been prepared for various values of z _1 m. Table 1 corresponds to a value of 1 m.

Table 1 Autopositioning result table for z _1 m = 1 m

Table 2 Autopositioning result table for z _1 m = 2 m

Table 3 Autopositioning result table for z _1 m = 5 m

The italicized values of the three columns on the right represent values greater than 2 m in accuracy for the position of the transmitter. This value is considered as the unacceptable limit value for our system. Values in bold have been chosen for accuracies between 1 and 2 m and in bold italic when the accuracy is below 1 m. This emphasis helps the reader to rapidly understand the results.

The results of this first test are not very encouraging, given the number of in italic. Let us now see what happens when we increase the value of z _1 m to 2 m for Table 2.

The results are significantly better but nonetheless reveal the need for the accurate measurements of distances. In this configuration, the measurements should be more accurate than 50 cm in order to obtain a satisfactory result. It is also noticeable that the number of cycles required to achieve this precision does not seem to be a fundamental criterion. Nevertheless, 50 cm of pseudo-ranges accuracy is not in the range of the repeater-based system and is at the limit of the expected accuracy of the repealite system. Thus, the above results, although better than those obtained for z _1 m equal to 1 m, are yet not good enough. Let us now consider z _1 m equal to 5 m.

As expected, the improvement is significant. Moreover, it seems that the increase in the number of cycles may improve the effect of averaging. Thus, performing more than 100 cycles with a typical transition accuracy of 2 m allows us to achieve a more than a meter automatic positioning of the transmitters. This result is perfectly acceptable, especially since it should be possible to further improve the approach: In particular, these various results are obtained by making a “choice” of the original transmitter positioned at (0; 0; 0). Another choice would lead to other results that should be useful for statistical purposes once again. This should be the subject of further works.

A final point concerns the way to verify in real time the validity of self-positioning. It seems that an indicator showing the number of positions that cannot be calculated (i.e., when the algorithm does not converge) allows us to specify the limit to 2 m that we considered. This should be very useful during a real deployment.

5 Simulation-based validation of the approach

In the previous chapters, calculations have been described and potential noise taken into account. In addition to this theoretical approach, one should consider the constraints of a real environment. In order to carry out an acceptable estimation of the proposed technique, we decided to simulate the method using ErgoSpace, an electromagnetic software that allows us to consider a real environment and to consider the “real” propagation conditions, i.e., transmission and reflection phenomenon. The environment considered is a large car park, as illustrated in Fig. 4, located in Turin in Italy.

Fig. 4

The Turin car park

The ErgoSpace simulation consists in describing the complete environments in terms of structures and materials, placing the various transmitters geographically and defining the location of the receiver. Once achieved, the simulations give the various paths, either direct or reflected (with a maximum number of three transmissions and three reflections considered for the present paper). Please note that the roof of the building has been removed in the figure for readability but is of course present in reality and in simulations. Figure 5 gives an example of the complexity taken into account for the propagation: Black rays are direct paths and green rays are reflected paths. The green circles are the transmitters and the receiver is somewhere in the middle of the car park, where all the rays converge. A very important point to understand is that propagation modeling is achieved in a deterministic way, thus making the evaluation of the effect of a statistical measurement error impossible.

Fig. 5

Typical rays indoors

In addition to these propagation simulations, we implemented two receiver code tracking loops in order to estimate the performance of the autopositioning method for standard receivers implementing a standard digital lock loop (SDLL) and for enhanced receivers implementing the SMICL [11]. The results given hereafter are thus the combination of the propagation and the receiver behavior to a real environment with a lot of reflected signals.

Let us now give a few details concerning the SMICL which has to be implemented in order to obtain the following results. Indoor environments are characterized by a very complex propagation of radio signals. Many multipath rays are usually present, and sometimes direct signals are not even available. In these environments, our transmitter-based system must cope efficiently with the multipath problem. Our approach, the SMICL, is based on previous works [11] which showed that the most important reflected paths are mainly short delay ones. This means that we must concentrate on techniques that are able to cope with small delay reflected paths. SDLL and narrow correlator do not propose an optimal approach for these paths. The main reason is that these paths mainly affect the right-hand side of the autocorrelation function (ACF): thus, the SMICL is based on a new discriminator that tries to cope with only the left-hand side of the ACF.

The formula of the discriminator of the SMICL is as follows (already described in detail in [11] for an infinite bandwidth):

$$ D = \left( {{\text{I}}{{\text{E}}^2} + {\text{Q}}{{\text{E}}^2}} \right) - \left[ {{{\left( {{\text{IP}} - \frac{\Delta }{{2 \cdot (2 - \alpha \cdot \Delta )}} \cdot \alpha \cdot \left( {{\text{IE}} + {\text{IL}}} \right)} \right)}^2} + {{\left( {{\text{QP}} - \frac{\Delta }{{2 \cdot (2 - \alpha \cdot \Delta )}} \cdot \alpha \cdot \left( {{\text{QE}} + {\text{QL}}} \right)} \right)}^2}} \right] $$

with:

D :

the discriminator

IE, QE:

the in-phase and in-quadrature replicas of the early correlator

IP, QP:

the in-phase and in-quadrature replicas of the prompt correlator

IL, QL:

the in-phase and in-quadrature replicas of the late correlator

Δ:

the phase difference, in chips, between the early and the late replicas, typically Δ = 1

α :

a correction factor which depends on the satellite PRN

We have also shown that α should be as follows, depending on the PRN used:

• α = 1,001 for PRN 1 to 6, 9 to 14, 16, 18 to 20, 23, 25 to 34

• α = 1,063 for PRN 8, 22, 35

• α = 0,937 for PRN 7, 15, 17, 21, 24, 36

In addition, the normalization considered for the SMICL has been chosen in order to reduce the sensitivity of this loop to thermal noise, which is the main limitation of the SMICL, which requires a rather high signal-to-noise ratio (higher than 44 dBHz) in order to propose an increased efficiency. The final discriminator expression is then:

$$ {D_{\text{SMICL}}} = \frac{{\sqrt {{\left( {{\text{I}}{{\text{E}}^2} + {\text{Q}}{{\text{E}}^2}} \right)}} - \sqrt {{{{\left( {{\text{IP}} - \frac{\Delta }{{2 \cdot (2 - \alpha \cdot \Delta )}} \cdot \alpha \cdot \left( {{\text{IE}} + {\text{IL}}} \right)} \right)}^2} + {{\left( {{\text{QP}} - \frac{\Delta }{{2 \cdot (2 - \alpha \cdot \Delta )}} \cdot \alpha \cdot \left( {{\text{QE}} + {\text{QL}}} \right)} \right)}^2}}} }}{{\sqrt {{\left( {{\text{I}}{{\text{E}}^2} + {\text{Q}}{{\text{E}}^2}} \right)}} + \sqrt {{\left( {{\text{I}}{{\text{L}}^2} + {\text{Q}}{{\text{L}}^2}} \right)}} }} $$

This approach is used for all the following simulated results that mix both the electromagnetic simulation and the receiver loop. The theoretical errors due to the presence of a single multipath on the pseudo-range measurement are given in Fig. 6. Note that the SMICL is efficient only for reflected rays of a delay that is less than 0.5 chips (typically 147 m), whose effects are the most disturbing ones.

Fig. 6

Theoretical envelopes of various discriminators

Many experimental results are available and allow us to draw the real error curve for a few discriminators (see Fig. 7), and this confirms the very efficient way the SMICL deals with multipath. Using the notations of Section 3, the comparative results obtained from the simulations are given in Table 4. Note that only 1 and 2 m have been considered in this real case simulation (for z _1 m) since 5 and 10 m give locations outside the building, hence impossible to use experimentally.

Fig. 7

Experimental envelopes of various discriminators (note that Δ = 0.1 for the narrow correlator)

Table 4 Transition measurement errors for the SDLL and the SMICL

From these starting values, it is possible to carry out the calculations provided in Section 3 in order to obtain the estimated locations of the various transmitters. Results and obtained accuracies are provided in Table 5. Note that no location can be calculated when using the SDLL or the SMICL with z _1 m = 1 m due to transition errors which are too large: This fact highlights the need for specific treatments to reduce the effect of multipath in indoor environments (but we all know about this).

Table 5 Autopositioning result table for z _{1 m} = 2 m

As expected from the theoretical results given in Section 4, as soon as the transition errors are greater than a few meters, the resulting calculating position of the transmitters is much degraded. In many cases (all the cases presented here for the SDLL), the calculation is not even possible.

In the present case, z _1 m values have been limited to the size of the structure and 5 or 10 m were not envisaged. A point that will be investigated in future works is the impact of the choice of the numbering of the transmitters (i.e., what happens if one chooses transmitter #2 as the origin of the new reference frame with coordinates (0; 0; 0)). In order to evaluate the proposed method thoroughly, we decided to create an artificial car park and considering its roof to be no longer at 7 m, but now at 17 m high. In this new configuration (but considering real structures, see Fig. 8), all measurements are possible and are summarized in Tables 6, 7, 8, 9, and 10.

Fig. 8

The new configuration with the roof at 17 m high

Table 6 Transition measurement errors for the new car park

Table 7 Autopositioning result table for z _1 m = 1 m

Table 8 Autopositioning result table for z _1 m = 2 m

Table 9 Autopositioning result table for z _1 m = 5 m

Table 10 Autopositioning result table for z _1 m = 10 m

From these starting values, it is possible to carry out the calculations provided in Section 3 in order to obtain the estimated locations of the various transmitters. Results and obtained accuracies are in Tables 7, 8, 9, and 10. Note that a few locations can now be calculated when using the SDLL, even if the difference with the SMICL is obvious.

As can be seen in the previous tables, 2D values are quite good with the SMICL, even for z _1 m equal to 1 m. However, values are not so good with the SDLL, as expected: It is clear that multipath mitigation is absolutely compulsory for indoor positioning. 3D values are not good enough for the “less than 1 m” accuracy being sought, even with the SMICL when z _1 m is 1 m. For 2 m, the results (Table 8) are too close to 1 m to be judged as acceptable. Thus, there really is the need for 5 m or even better 10 m. These results confirm the theoretical expectations given in previous sections.

Let us now consider another indoor environment where it is actually possible to put the test receiver above transmitter #1 with z _1 m = 10 m. This new environment is indeed a large warehouse made of concrete walls, a classical roof (with no metal) and a soil made of concrete. Its dimensions are 100 m long × 60 m wide with a height of 20 m. The transmitters are located respectively at (2; 2; 0.2), (2; 58; 18), (98; 58; 18), and (98; 2; 15) allowing for an acceptable IDOP for 3D positioning. Note that this requires that one transmitter has to be located close to the ground (transmitter #1 here). In the present case, we have considered that the warehouse is empty because this autopositioning phase is achieved at the moment of the construction of the building. In addition, some walls are also present indoors (made of plaster), as shown in Fig. 9. In a similar way to Fig. 8, Fig. 9 also shows the transmitter locations (the red circles) of this new building.

Fig. 9

The warehouse model

Once again, both the SDLL and the SMICL have been implemented and coupled to the propagation simulations. Using the notations of Section 3, the comparative results obtained from the simulations are given in Table 11.

Table 11 Transition measurement errors for the warehouse (good HDOP)

From these starting values, it is possible to carry out the calculations provided in Section 3 in order to obtain the estimated locations of the various transmitters. Results and obtained accuracies are as follows in Tables 12, 13, 14, and 15. Note that a few locations can now be calculated when using the SDLL, even if the difference with the SMICL is obvious.

Table 12 Autopositioning result table for z _1 m = 1 m

Table 13 Autopositioning result table for z _1 m = 2 m

Table 14 Autopositioning result table for z _1 m = 5 m

Table 15 Autopositioning result table for z _1 m = 10 m

It appears once again quite clearly that the proposed autopositioning approach is only viable if the transition measurements are of acceptable quality, i.e., with a less than 1-m accuracy. For the SDLL, this is clearly never the case, hence very poor performance of the method. For the SMICL, things are a lot better but, as can be extracted from Tables 11, 12, 13, 14, and 15, a single transition that is accurate to1.1 m (T3 typically) is enough to push the resulting transmitter position accuracy out of the 1-m limit.

Another interesting point to be evaluated is the sensitivity of the proposed approach to the distribution of the transmitters, i.e., the horizontal dilution of precision (HDOP). We carried out several simulations with various configurations, summarized in Table 16 (note that the HDOP are given for a receiver being located 1 m above the ground). With comparison to the reference configuration presented in Tables 11, 12, 13, 14, and 15, obtained with an average HDOP of 3.5 (configuration #1), the main autopositioning results are provided in Table 17.

Table 16 Various HDOP configurations considered

Table 17 Comparison of autopositioning results

As expected, the HDOP of the transmitters has a huge impact: When the DOP values increase from 3.5 to 7 (configuration #2) and then to more than 20 (configuration #3), the resulting autopositioning technique reaches its limit. Note that this impact is bound to occur also in the indoor positioning results: Of course, in a similar way as outdoors, the DOP values are very important in the resulting accuracy estimation. Nevertheless, the SMICL has shown that it can allow us to obtain a positioning where the standard DLL is often unable to provide us with any results.

As a summary and in accord with theory, in the case of acceptable DOP values (which is a must for indoor positioning anyway), results are better with higher values of z _1 m. It is also obvious, also in accord with theory, that transition uncertainties are directly linked to the accuracy of the autopositioning proposed approach. A multipath mitigation technique is thus absolutely compulsory. In the case of z _1 m equal to 5 or 10 m, it is possible to consider that the autopositioning technique proposed in this paper is almost acceptable for GNSS indoor positioning system using code-based measurements (i.e., typically repeaters and repealites) and bound to provide positioning accuracy in the meter range (for the indoor receiver).

The warehouse simulations have shown that remaining transition errors are of great importance. Future works are planned toward the determination of the impact of the choice of the reference transmitter. Furthermore, the real constraint of the proposed technique is that we need to be able to locate a transmitter 5 or 10 m above the location considered for one of the transmitters. This feature limits the use of this technique to large warehouses, large halls, or high buildings. As a matter of fact, this is clearly our target. We believe that society is currently searching for a real continuity of the positioning service and that industry and operators do not want to have to deploy any additional infrastructure. Unfortunately, the required positioning accuracy, typically in the meter range for mass market applications, is not easily reachable without any local infrastructure. Nevertheless, this infrastructure should be reduced to its minimum in order to have a real chance to be implemented in real life. Our point of view is then to make the best use of various techniques (this is a classical opinion today): Our choice is currently oriented toward the combination of the proposed transmitter-based approach, which uses radio signals, that will be deployed in large halls and buildings where only a reduced number of transmitters are required, with an inertial system that can be regularly calibrated through the use of this radio system and that provides the terminal with positioning in more confined areas. Note that this kind of system is also of great help outdoors in order to complement the well-known limitations of the GNSS. Thus, the limitation of the proposed autopositioning technique is reduced by the fact that the technique will only be deployed in relatively large areas.

In addition, another question is: What kind of autopositioning do we obtain if transmitter 2 or transmitter 3 is chosen as reference of the new frame? Theoretically, with no measurement error, the difference is zero. But, due to transition measurement errors that mainly depend on multipath distribution, the reality is clearly different. In order to improve the proposed technique, new investigations are thus envisaged.

Another interesting future work is clearly the investigation of a multiple measurement approach, on a basis close to the proposed works of [1]. Finally, a mix between the choice of the reference transmitter and additional calibration points is probably a nice direction for forthcoming works.

6 Synthesis

The proposed autopositioning technique has shown to be viable in large environments where it is possible to locate a receiver 5 or 10 m above one chosen transmitter. As seen with the Turin car park, this is not always possible, and this is clearly a real limitation of the proposed approach. On the other hand, in order to be able to achieve acceptable 3D accuracy indoors, previous works have shown the need for one transmitter to be located near the ground (or even below when possible): In this case, the above-mentioned constraint is slightly reduced to the need for a roof of 5 m of height. Where there is a need for autopositioning, i.e., in rather large structures, this constraint is probably reached quite often.

The remaining question concerns the operational way these various measurements could be carried out. In our minds, there are two different steps: measurements very close to the transmitters and measurements at 1 m (or more) from the transmitters. This second kind of measurement would be carried out through an autonomous “test” antenna, which should be properly located (this is probably not such a problem). For the close measurements, one has to imagine a sort of dual antenna for each transmitter, where the principal antenna will serve to transmit the GNSS-like signal, while the second one is dedicated to the specific receiving step of the autopositioning method. Note that this increased antenna transmitter complexity is counterbalanced by the autopositioning advantages (no need for accurate and specialized installation, capability to check the proper installation, reduction of time required for the setup of the indoor system, etc.). It is also noticeable that when in the receiving mode, the transmitter is switched off: Thus, no interference problems are foreseen. As usual, the next step is clearly to test this technique in operational and real-world environments …