Abstract
Reservation wages are part of the transmission mechanism between minimum wages and unemployment via the labour force participation decision. The limited available empirical evidence on the relationship between reservation wages and legal minimum wages suggest that individuals use minimum wages as benchmarks against which their reservation wages are set. This has a profound behavioural effect that may encourage individuals to either enter the labour force or price themselves out of potential employment. We employ a fuzzy regression discontinuity design to explore the influence of minimum wages on reservation wages. Our findings suggest that the behavioural response is too small to be extracted from the variability of the reservation wage data. For policy makers this finding is important. While minimum wages raise earnings and living standards, they can push some workers out of the labour force by increasing their reservation wage beyond the minimum. We do not find any evidence of such a response of the reservation wage of jobseekers to the minimum wage in the UK.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The effect of operating minimum wage laws on individuals’ labour supply decisions is an under-researched area despite the extensive, theoretical and empirical, literature on the role of legal wage floors on labour demand (Belman and Wolfson 2014; Neumark and Wascher 2008). Economic theory predicts that in competitive markets, minimum wages lead to employment losses, higher equilibrium wages and higher unemployment. In imperfect markets, employment gains can be observed provided firms have enough monopsony (oligopsony) power, the minimum wage is set above what the firm (monopsonist) would pay in its absence, and the minimum wage remains below the competitive wage level. Even if labour markets are broadly competitive, firms can still benefit from some monopsony power if search frictions are present, for example if worker relocation costs are large enough or if hiring costs are substantial (Manning 2003). Under such conditions, setting a minimum wage can lead to increases in employment, particularly if individuals’ participation to the labour market is sensitive enough to the wage offered (Boeri and van Ours 2008).
In the presence of frictions, higher minimum wages induce some workers (back) into the labour force (supply effect) if the minimum wage is set above their reservation wage. Given that the reservation wage determines the participation rate, it is effectively part of a transmission channel on the supply side, that links minimum wages to employment. It is the interaction of this supply-side mechanism with the, better understood, demand-side transmission mechanism of the minimum wage to employment which determines the overall effect of the minimum wage on unemploymentFootnote 1. A higher reservation wage contributes to non participation in less direct ways. For example in an environment where individuals search for work, it results in longer spells devoted to job seeking. This would contribute further to higher (voluntary) unemployment.
The impact of minimum wages on reservation wages has been largely overlooked in the labour supply literature mainly due to the lack of appropriate data. This gap is partially filled by Falk et al. 2006) and more recently (Fedorets et al. 2018). Using laboratory experiments, (Falk et al. 2006), show that minimum wages have a strong and positive influence on reservation wages. The authors argue that a government mandated wage is not only a legal minimum but acts as a benchmark for what workers come to perceive as a “fair” wage, giving rise to so called entitlement effects. Reservation wages are subsequently adjusted in tandem with the legal minimum. (Fedorets et al. 2018) use the German Socio-Economic Panel and present evidence that minimum wages have significant effects on both the observed and reservation wage distributions. The authors estimate an around 4% increase in reservation wages in the lower percentiles of the reservation wage distribution following the introduction of a minimum wage.
Koenig et al. (2021) consider minimum wages as a “reference” point in the determination of reservation wages in the context of their model explaining the “wage flexibility puzzle” - the disproportionate volatility of unemployment and wages over the business cycle. The direct impact of minimum wages on reservation wages is consistent with the authors’ “backward-looking” individuals’ decision making proposition. The interpretations of (Koenig et al. 2021) and (Falk et al. 2006) of minimum wages are similar despite arising from different vantage points. Both studies view the minimum wage as a behaviour-changing external influence – whether the minimum is understood as an entitlement or a threshold wage value. In either case, the empirical questions concern the existence of an effect on the reservation wage of an increase to the minimum wage and the magnitude of that effect. Falk et al. (2006) suggest that labour market behaviour ought to confirm experimental findings. The present study follows in (Falk et al. 2006) line of enquiry using, however, observational field data to explore the role of minimum wages on individuals’ reservation wage formation.
We use individual-level data drawn from the British Household Panel Survey (BHPS) from 1998 to 2008 and we focus our analysis on workers who are looking for work in a low-pay occupation. The BHPS data contains information which allows us to construct a credible measure of the reservation wage for these workers similarly to (Brown and Taylor 2013). We can then describe the association between the reservation wage and the regular up-rating of the UK National Minimum Wage. Formally we use a regression discontinuity (RD) design where the difference between last period’s reservation wage and the current period minimum wage act as the scoring variable and the current reservation wage is the outcome of interest. We then exploit the premise that individuals in the neighbourhood of the threshold are otherwise comparable in terms of observed and unobserved characteristics so any differences in the reservation wage in the current period can be attributed to the effect of the National Minimum Wage. We find a positive and significant effect of the National Minimum Wage on reservation wages in the lower part of the skills distribution. In particular, individuals with reservation wages below the minimum increase their reservation wages by approximately 6%, compared to individuals whose reservation wages are above.
The contribution of our study is twofold. First, it confirms the theoretical insights which describe the effect of minimum wages on reservation wages and it explores the validity of existing laboratory results using observational data. Secondly, it contributes to the limited literature on the effects of minimum wages on reservation wages, and the determinants of the latter, by presenting empirical estimates of the relationship between the national minimum wage and reservation wages in the UK. Recent studies by (Krueger et al. 2011), (Krueger and Mueller 2012, 2014) and (Barbanchon et al. 2017) explore the effect of institutional factors on reservation wages but do not explicitly consider the effect of minimum wages. The effect of minimum wage laws on labour supply via the reservation wage matters both at the macro and micro levels. While minimum wages seek to raise living standards of those in low-pay employment, they should ensure that jobseekers do not price themselves out of employment at the same time.
The paper is organised as follows. The next two sections describe the data used and our modelling strategy, respectively. The following section presents a graphical analysis and our estimates of the main effects of interest with a discussion of the latter. The final section concludes.
Data
The National Minimum Wage (NMW) was formally introduced in 1999, however, the adjustment process is likely to have started a year earlier following the announcement of the impending policy reform, hence we use 1998 as the beginning of the period when the NMW is in effect. The level and changes to the National Minimum Wage, since its introduction by the Labour government in 1999, is the decision of the UK government, in consultation with the Low Pay Commission. The Low Pay Commission is an independent body that submits a report to the government in October each year, making recommendations on the future level of the National Minimum Wage rates, and related mattersFootnote 2. Table 1 below, summarises the UK National Minimum Wage rates for the sample period. The yearly percentage changes may be small in magnitude, especially in later years, however, we believe they are significant enough to induce a response change among survey participants. Arguably, it is the announcement of the uprating rather than the absolute NMW change that entices a revision of one’s reservation wage. In that respect, even seemingly small increases generate significant responses.
We draw individual-level data from the British Household Panel Survey (BHPS), from 1998 to 2008Footnote 3. Individual respondents (job seekers) are asked, firstly, what is the lowest net payment they would consider for taking up a job, and secondly, how many hours per week they would expect to work for that payment. From these two responses we construct a simple measure of individuals’ reservation wage. We divide the lowest net payment required by the expected number of hours for that payment and convert the data to a 40-hour working week following Blackaby et al. (2007).
Our sample consist of 18-65 year old individuals who are looking for work in a low-pay occupation (personal and protective services, sales, plant and machine operatives and other occupations), and who further satisfy the Lancaster and Chesher (1983) rationality restriction, which requires that reservation wages are greater than or equal to unemployment benefit payments and less than or equal to expected wages. We exclude individuals who report wages or reservation wages less than £1 (0.04% of the sample) on the basis that such a low figure ought to be erroneous. We also exclude those who are in work (either employed or self-employed) yet their records show a reservation wage (0.25% of the sample). Only individual respondents who do not have a job, and are actively looking for one, were asked the relevant questions and hence this information must be recorded in error. A measure of the respondents’ expected wage is constructed using responses to two questions on the expected weekly net pay and hours committed for the job sought.
Following Brown and Taylor (2013), we include economically inactive individuals who report a reservation wage. Table 2 below reports the response rates to the relevant questions in our sample. In line with similar surveys (e.g. NLSY79), there is a low response rate raising concerns over sample selection issues. In Table 7 we report summary descriptive statistics for the response and non-response samples. The two groups are comparable in all key characteristics such as age, gender composition, educational attainment, and non-labour income among others.
Figures 1 and 2 present the distributions of the wage and reservation wage over the sample periodFootnote 4 for 22+ and 18-21 year old adults, respectively.
From Fig. 1 we see that the reservation wage distribution follows the wage distribution closely in all years suggesting that people are mindful of average wages in the economy. After 1998, while the two distributions never deviate greatly, the reservation wage distribution is clearly anchored to the NMW rate. Flinn (2006) makes the interesting theoretical prediction that “a binding minimum wage results in a (positive-valued) wedge between the minimal acceptable wage imposed by the policy maker and the wage offer that a searcher would be willing to take” (Flinn 2006 p. 1021). The evidence appears to support this prediction. This is clearly seen for years 1999 to 2003 in Fig. 1 and for years 1999 to 2008 in Fig. 2. For years 2004 to 2008 in Fig. 1, we could interpret the observed reservation wage distribution as an indication that reservation wages either do not adjust upwards with each uprating or they are slow to do so. If we understand an individual’s reservation wage as a function of the discounted future stream of earnings (from employment), as in the context of a standard search model, then it becomes an implicit function of the wage offer distribution and the job offer arrival rate. The minimum wage affects the reservation wage positively through a right shift in the wage distribution and/or negatively through a reduction in the job offer arrival rate – the overall effect is a priori indeterminate and thus an empirical question.
Figure 2 shows a similar picture for the 18-21 year old jobseekers in so far as the alignment of the wage and reservation wage distributions is concerned. However, the reservation wage distribution is consistently centered to the right of the sub-minimum rate in line with the theoretical proposition of Flinn (2006) model. It may reflect the older jobseekers’ greater need for labour income and/or young jobseekers’ greater valuation of non-labour time – younger people will value non-labour time higher if it can be devoted to education and/or training (the opportunity cost of which is lower to them).
Overall, the empirical distributions of the reservation and actual wages are aligned. Since the introduction of the legal minimum, the reservation wage distribution is centered to the left of the wage distribution and closer to the minimum wage value. The NMW rates appear to act as an anchor or reference point (also in line with Koenig et al. (2021) proposition) for the determination of the reservation wage. To reinforce the proposition that minimum wages act as a benchmark for reservation wages, Fig. 3 plots the median reservation wage against the minimum wage over time. The former clearly converges to the legal minimum for both the 18-21 and 22+ year old jobseekers.
Empirical Strategy
If jobseekers use the NMW as a reference point or as an anchor for their reservation wage formation, then the NMW matters. However, it will matter only (or more) for those individuals whose reservation wage in period \(t-1\), \(w^{r}_{t-1}\), is below the NMW in period t, i.e., whenever \(w^{r}_{t-1} < \underline{w}_{t}\), where \(w^{r}\) and \(\underline{w}\) denote the reservation and minimum wage, respectively. If we understand \(x_{t-1} \equiv \underline{w}_{t} -w^{r}_{t-1}\) as a non-random “scoring” variable and define a threshold value (in this context 0), we could assign individuals into two groups, a first group where the binary variable T is \(T=1\) whenever \(x_{t-1}=\underline{w}_{t}-w^{r}_{t-1} \ge 0\) and a second group such that \(T=0\) whenever \(x_{t-1}=\underline{w}_{t}-w^{r}_{t-1} < 0\), and in period t, we would expect the reservation wage of individuals in the first group to be different from the reservation wage of individuals in the second group. Because the scoring variable is predetermined and can not be manipulated, around the threshold value of 0 the difference in reservation wage between the two groups measures the reservation wage increase in the current period in response to an increase of the national minimum wage such that \(x_{t-1}\) takes its values close to 0.
This is the essence of the Regression Discontinuity (RD) design, which works similarly to a randomised experiment but where the assignment to the control or treatment groups is now based on a non-random variable. In the RD case, assignment is exogenous conditional on the scoring (other common names are forcing or running) variable. RD exploits the premise that individuals in the neighborhood of the threshold are otherwise comparable in terms of observed and unobserved characteristics so any differences in outcomes can be attributed to the effect of the “treatment” Dunning (2012).
There are several factors that affect the reservation wageFootnote 5 and that are not captured by the NMW rate. If a job-seeker’s reservation wage is below next period’s minimum, she is likely to (but not compelled to) increase her/his reservation wage to or above the minimum – the reservation wage question asks for the lowest acceptable wage rather than the lowest expected wageFootnote 6. Similarly, workers with a reservation wage at time \(t-1\) greater than the minimum wage in period t, are likely to respond less, if at all, to the NMW increaseFootnote 7. To capture this possibility we consider that the group of interest, the treated group, is the group of individuals with a reservation wage above the NMW. This defines the binary variable \(D_{t}\) which is such that \(D_{t} = 1\) if \(\underline{w}(t)>w^{r}(t)\), and 0 otherwise. Our interest is then to measure the reservation wage increase among those who set their reservation value below the current minimum wage.
Unlike in situations where “treatment” can be effectively monitored (and implemented), in this context some individuals with reservation wages below next period’s NMW may not subsequently adjust their wage demands and/or individuals with reservation wages above next period’s NMW may doFootnote 8. When the probability of being in the “affected” or “treated” groupFootnote 9 does not deterministically change from 1 to 0 at the threshold, \(x_{t-1}=0\) where \(w^{r}_{t-1} = \underline{w}_{t}\), the discontinuity is referred to as fuzzy and the design is called fuzzy RD. In a fuzzy RD design, the exogeneity of assignment created by the running (or scoring) variable and its threshold, is maintained.
Angrist and Pischke (2008) formalise this idea and present the general fuzzy RD set up, which we adapt here. Considering that the assignment to “treatment” or control group is no longer clear cut – in the fuzzy RD design, it is not receipt of treatment that changes at the threshold but rather the probability of receiving the treatment – we can define a potential “treatment” receipt indicator as (note that we drop the implied i subscript to index individuals throughout):
where \(x_{t-1} = w^{r}_{t-1} - \underline{w}_{t}\). The relationship between receiving the “treatment” and the scoring (running) variable, \(x_{t-1}\), can be described by:
where \(T_{t}\) is the binary variable which indicates the location of the individual relative to the threshold, \(T_{t}=1(x_{t-1}>0)\). \(T_{t}\) can be understood as an “intent-to-treat” indicator.
If we further define potential outcomes as
where \(g_0\) is a continuous function, we can specify a regression model such as
where \(\delta\) is the causal effect of interest, which cannot, however, be directly uncovered by Eq. 5 since \(D_{t}\) is a deterministic function of \(x_{t-1}\). Angrist and Pischke (2008) show that \(T_{t}\) can be used as an instrumental variable for \(D_{t}\) to obtain consistent and unbiased estimates of \(\delta\), using a Two Stage Least Squares (2SLS) Instrumental Variable (IV) estimator.
Assuming that \(f_i (x_{t-1})\) can be adequately described by polynomials of some orderFootnote 10 (to be determined empirically), we can describe Eq. 2 with a series of polynomial terms and their interactions with \(T_{t}\), which can all be used as instruments for \(D_{t}\) in a regression model such as Eq. 5 Angrist and Pischke (2008).
The RDD estimator will be unbiased as long as the functional form of the relationship between the outcome and the scoring variables is correctly specified. In the current set up, we expect the relationship between the reservation wage and the scoring variable to vary systematically with scores (values of \(x_{t-1}\)). Individuals with higher scores i.e. jobseekers with reservation wages ’far’ (to the left) from the current minimum, are expected to adjust their reservation wages more or be more likely to respond to the NMW uprating. Accordingly, we expect those with reservation wages close (to the left or right) to the minimum i.e. low scores, not to adjust their reservation wages much, if at allFootnote 11. This gives rise to a nonlinear relationship between \(w^{r}_{t}\) and \(x_{t-1}\).
In the absence of any theoretical justification for such a relationship or guidance as to the true shape of the relationship, the choice of functional form is an empirical question. Gelman and Imbens (2018) recommend that local linear or quadratic polynomials are used for the functional form of \(f_i(x_{t-1})\). We test the appropriate form of function \(f_i(x_{t-1})\) following Lee and Lemieux (2009). We conduct F-tests for a series of model specifications to determine which best fits the data. We conclude that a second-order polynomial specification that includes interaction terms with the treatment variable is adequately describing the relationship between the outcome and scoring variablesFootnote 12.
The model we therefore estimate is given by the first-stage equation:
and the fuzzy RD reduced-form, which we get by substituting Eqs. 6 into Eqs. 5:
where \(\gamma _i = \beta _i +\delta \zeta _i\), and \(\theta _i = \delta \tau _i\). Identification rests in the ability to distinguish between the (continuous) trend relationship described by the polynomial approximation and the discontinuous \(T_{t}=1(x_{t-1}>0)\) step function.
Estimation is carried out using the 1998-2008 sample accounting for within-individual correlation of the errors over time using clustered standard errors following Lee and Lemieux (2009). Whenever additional controls are included in the specification, we follow (Koenig et al. 2021 p. 21) and include available variables pertinent to reservation wage determination. Table 8, in the Appendix, provides summary measures of the estimation sample.
Results and Discussion
Graphical Analysis
Lee and Lemieux (2009) argue for the importance of graphical exploration and representation of RD designs and (Calonico et al. 2015 p. 1754) suggest appropriate RD plots to be used. In particular, a graph can (a) reveal discontinuities away from the cut-off point, which would invalidate the RD design and (b) describe the data variability. Such data features could be concealed by a simple scatterplot of raw data. Figure 4 is a typical RD plot and has two elements. The first depicts a smooth approximation of the conditional expectation of the outcome variable (the natural logarithm of \(w^{r}_{t}\)) given the scoring variable, \(x_{t-1} = \underline{w}_{t} - w^{r}_{t-1}\), for the control and ’treatment’ groups separately. The second element is a set of means of sub-samples, defined by a specified bin width. Calonico et al. (2015, 2014) describe in detail different approaches in the construction of these bins and suggest optimal data-driven procedures, which we follow hereFootnote 13. What we are looking for is clear evidence of a discontinuity (jump) in the conditional mean of the outcome variable around the cut-off point. Figure 4 shows a (relatively) small yet clear discontinuity at the threshold and confirms that there are no other jumps in the conditional expectation of \(w^{r}_{t} | x_{t-1}\), which implies that the discontinuity can be understood as the causal effect of the “intended treatment.”
Conditional expectation of the outcome variable, the natural logarithm of \(w^{r}_{t}\), given the scoring variable \(x_{t-1} = \underline{w}_{t} - w^{r}_{t-1}\) for the control (to the right of the cut-off, \(n_{+}= 612\)) and treatment (to the left of the cut-off, \(n_{-}= 540\)) groups. The support of \(x_{t-1}\) is restricted to \([-2, 2]\) for clarity. The solid grey circles (dots) represent means of sub-samples of variable sizes, defined by the optimal bin widths 0.082 (to the left of the cut-off point) and 0.067 (to the right of the cut-off point). The data comes from the estimation sample (1998-2008), which consists of 18-65 year old individuals who are looking for work in a low-pay occupation and who further satisfy the Lancaster and Chesher (1983) rationality restriction
Figure 5 illustrates the observed association between the scoring variable \(x_{t-1}\) and \(D_{t}\). The discontinuity (jump) of the conditional mean of the binary variable \(D_{t}\) around the cut-off point is clearly visible. This indicates that in the Fuzzy discontinuity design, \(T_{t}\) will have substantial explanatory power for \(D_{t}\), i.e. it is not a weak instrument. Finally, from Fig. 6 we see that there is no discontinuity in the distribution of the scoring variable at the threshold value. McCrary (2008) suggests that in some instances, individuals may “manipulate” the forcing variable, if the threshold is known, which would invalidate the RDD. In the current setting this is highly unlikely since we do not expect individuals to report reservation wages this period below next period’s NMW rate on purpose. As expected, Fig. 6 confirms our belief.
Conditional expectation of the treatment indicator variable, \(D_{t}\), given the scoring variable \(x_{t-1} = \underline{w}_{t} - w^{r}_{t-1}\) for the control (to the right of the cut-off, \(n_{+}= 616\)) and treatment (to the left of the cut-off, \(n_{-}= 547\)) groups. The support of \(x_{t-1}\) is restricted to \([-2, 2]\) for clarity. The solid grey circles (dots) represent means of sub-samples of variable sizes, defined by the optimal bin widths 0.082 (to the left of the cut-off point) and 0.091 (to the right of the cut-off point). The data comes from the estimation sample (1998-2008), which consists of 18-65 year old individuals who are looking for work in a low-pay occupation and who further satisfy the Lancaster and Chesher (1983) rationality restriction
Density of the scoring variable, \(x_{t-1}\), using data from the estimation sample (1998-2008), which consists of 18-65 year old individuals who are looking for work in a low-pay occupation and who further satisfy the Lancaster and Chesher (1983) rationality restriction. A Gaussian kernel function is used for the kernel density estimate. The number of bins is set to 90
Estimates
In this section we present the estimates of the ‘sharp’ regression discontinuity design and the estimates of the ‘fuzzy’ regression discontinuity design we describe in the previous section. In Table 3, column (1), we present the sharp RD estimation results for the whole sample in the absence of any additional controls. We then proceed and present the results for the data near the threshold value for \(x_{t-1}\) in columns (2) and (3), within a distance of 0.2, resp. 0.5, from 0 . Next we focus on the whole data controlling for individual characteristics, column (4), adding time fixed effects, column (5). In principle the absence of control variables does not affect the ability of the sharp design to identify the effect of the treatment at the threshold. Adding controls however can improve the precision of the RD estimator if the controls contribute to increasing the signal to noise ratio.
The last six columns present the estimation results, without or with some or all controls, for the sub-sample of individuals covered by the national minimum wage rules for those aged less than 21 and for the sub-sample of individuals older than 22. The point estimates are systematically small (in absolute value they are always less than 0.08) and given the estimated standard error they are not precise enough to distinguish them from the value of 0. Adding controls has the expected effect of reducing the estimated standard errors. This is not sufficient for us to modify the conclusion that according to the sharp RD design an increase to the NMW does not have a measurable effect on the individual reservation wage.
The estimates based on local-polynomial regressions, see Table 4, provide a similar picture. The estimates are in general too imprecise to conclude for a noticeable effect of the NMW on the reservation wage except if we restrict our attention to observations within 0.5 of the threshold or if we focus on the younger sub-sample. In the former case the effect increases from \(15\%\) to \(34\%\) with the use of bias correction. The use of a robust version of the estimator based on local-polynomial regressions does not change the conclusion. The estimates based on the younger sub-sample show large effects of the NMW on the reservation wage, around \(30\%\), in the absence of controls. Adding demographic controls reduces the estimated effect to about \(19\%\), and increases the estimated standard errors. Controlling both for demographic and time specific effects reduces the estimated value further and suggests that the estimated effect is not measured precisely enough to draw a clear cut conclusion about its value or its sign.
Given our definition of \(D_{t}\) , i.e. \(D_{t}=1\) if \(\underline{w}_{t} \ge w^{r}(t)\), we estimate model Eqs. 5 using 2SLS as discussed in the previous section. Table 5 presents our findings in the same manner we presented the results for the sharp RD design. Hence we present estimates with or without controls, as well as estimates obtained on the sub-sample of observation such that the scoring variables are close to the threshold (resp. within 0.2 or 0.5 of the threshold), or the sub-sample of individuals younger than 21 or older than 22. Overall, the estimated values for \(\delta\) are too imprecisely estimated to be able to draw any sharp conclusion concerning the absolute magnitude or sign. Table 6 presents estimates of \(\delta\) based on local polynomial regressions. Again these estimates are characterised by large standard errors (in some cases extremely so) which suggest that the effect of the NMW on the reservation wage is close to zero. We further estimate all specification with an alternative (placebo) discontinuity threshold set arbitrarily at the NMW level + £2. With the exception of the ∓0.5 sample in the restricted (no additional controls) specification using 2SLS, all other estimates of δ are statistically insignificant as expected. These estimates confirm the validity of the discontinuity threshold defined by the actual NMW level. We do not include the full set of results at the placebo threshold, but these are available from the authors upon request.
Because of their lack of precision and despite not being directly comparable, our findings do not contradict the very limited available empirical evidence in the literature. Experimental findings reported by Falk et al. (2006) support the proposition that the introduction of minimum wages leads to an upward revision of reservation wages. Fedorets et al. (2018) find that minimum wages cause a \(4\%\) increase in reservation wages in the lower end of the distribution. Falk et al. (2006) interpret their estimates as evidence of a behavioural effect of economic policy. Our findings suggest that the behavioural response is too small to be extracted from the variability of the reservation wage data. For policy makers this finding is important. While minimum wages intend to raise earnings and living standards, they can push some workers out of the labour force by increasing their reservation wage beyond the minimum. We do not find any evidence of such a response of the reservation wage of jobseekers to the minimum wage in the UK.
Conclusion
Although the effect of operating minimum wage laws on labour demand has been extensively researched in the literature, their influence on the decision to enter the labour market has remained largely unexplored due to the unavailability of direct data on reservation wages. Our study tests inferences from theory about the effect of minimum wages on reservation wages and explores the validity of existing laboratory results using observational data. It also contributes to the very scant literature of the influence of minimum wages on job seekers’ reservation wages. Our results suggest that minimum wages and their periodic increases do not have a positive effect on reservation wages. We motivate this result by the work of Falk et al. (2006) who through experiments, support the proposition that the introduction of minimum wages leads to an upward revision of significant effect on reservation wages. Our estimates suggest that a positive and statistically significant effect can be identified only near the discontinuity threshold.
Despite statistically insignificant, the estimated effect is greater in magnitude for 18-21 year old job seekers suggesting that younger job seekers align their reservation wage with the NMW more than older ones do. This is not surprising if we consider that younger people would have less labour market experience and thus use the NMW as a “reference” point. Older adults while influenced by the NMW are more likely to take into account a variety of factors when deciding on their reservation wage. For policy makers this means that job seekers may well use the NMW as a way of obtaining labour market and wage information (particularly younger ones), hence the NMW becomes/is an expectation forming “reference” point.
Data Availability
The datasets generated during and/or analysed during the current study are available in the UK Data Archive repository, https://doi.org/10.5255/UKDA-SN-5151-2
Notes
There are 9 Low Pay Commissioners drawn from a range of employee, employer and academic backgrounds Low Pay Commission (2019)
In 2009 the BHPS sample was absorbed into the UK Household Longitudinal Study and the questions relevant to our study were discontinued.
We go back to 1993 until 1997 for a comparison sample solely for descriptive purposes. For the comparison sample (when the NMW was not in effect), we could set the period to coincide with the start of the BHPS survey sample in 1991; however, we choose 1993 as the start following Butcher (2005) who argues for using 1993 as the start of the comparison period since Wage Councils were still in operation in 1992 and that year marks the end of the early 1990s recession.
The reservation wage can be understood as the marginal rate of substitution between consumption and labour supply at the non participation corner solution to an individual’s utility maximisation problem.
This line of reasoning appears at odds with Flinn (2006) theoretical prediction, however, his model does not allow for compensation other than the wage, which could arguably affect individuals’ reservation wage.
We could expect that some effects ripple up the reservation wage distribution mainly in response to employers maintaining a differential in the actual wages.
This can also be understood as “imperfect compliance” Lee and Lemieux (2009).
By “treatment” or being in the “treated” group we mean reporting a reservation wage at period t, greater than that reported in period \(t-1\).
Angrist and Pischke (2008) show the general case of a \(p-\)th order polynomial.
If the NMW acts as a benchmark, individuals (closely) above the threshold my increase their reservation wage in order to maintain their relative distance from it. Table 9, in the appendix, provides descriptive statistics for those respondents \(\pm 0.5\) from the cutoff value of the scoring variable. These summary measures reassure us that respondents on either side of the threshold are similar in most key characteristics
We don’t report details of the tests here for brevity but these are available from the authors upon request.
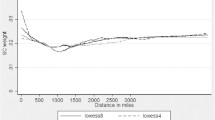
Figure 7, in the appendix, plots the outcome against the scoring variable for different bin sizes.
References
Angrist JD, Pischke J-S (2008) Mostly harmless econometrics: An Empiricist’s Companion. Princeton University Press
Barbanchon TL, Rathelot R, Roulet A (2017) Unemployment insurance and reservation wages: Evidence from administrative data. Journal of Public Economics
Belman D, Wolfson PJ (2014) What does the minimum wage do? W.E. Upjohn Institute for Employment Research, Kalamazoo, MI
Blackaby D, Latreille P, Murphy P, O’Leary N, Sloane P (2007) An analysis of reservation wages for the economically inactive. Economics Letters 97(1):1–5
Boeri T, van Ours J (2008) The economics of imperfect labor markets (STU - Student edition ed.). Princeton University Press
Brown S, Taylor K (2011) Reservation wages, market wages and unemployment: Analysis of individual level panel data. Economic Modelling 28(3):1317–1327
Brown S, Taylor K (2013) Reservation wages, expected wages and unemployment. Economics Letters 119(3):276–279
Butcher T (2005) The hourly earnings distribution before and after the national minimum wage. Labour Market Trends 113(10):427–35
Calonico S, Cattaneo MD, Titiunik R (2014) Robust nonparametric confidence intervals for regression-discontinuity designs. Econometrica 82(6):2295–2326
Calonico S, Cattaneo MD, Titiunik R (2015) Optimal data-driven regression discontinuity plots. Journal of the American Statistical Association 110(512):1753–1769
Dunning T (2012) Natural experiments in the social sciences: a design-based approach. Cambridge University Press, Strategies for Social Inquiry
Falk A, Fehr E, Zehnder C (2006) Fairness perceptions and reservation wages: The behavioral effects of minimum wage laws. The Quarterly Journal of Economics 121(4):1347–1381
Fedorets A, Filatov A, Shupe C (2018) Great expectations: reservation wages and the minimum wage reform. DIW, SOEPpapers No, p 968
Flinn CJ (2006) Minimum wage effects on labor market outcomes under search, matching, and endogenous contact rates. Econometrica 74(4):1013–1062
Gavrel F, Lebon I, Rebière T (2010) Wages, selectivity, and vacancies: Evaluating the short-term and long-term impact of the minimum wage on unemployment. Economic Modelling 27(5):1274–1281
Gelman A, Imbens G (2018) Why high-order polynomials should not be used in regression discontinuity designs. Journal of Business & Economic Statistics 0(0),1–10
Koenig F, Manning A, Petrongolo B (2021). Reservation wages and the wage flexibility puzzle. CEP Discussion Papers dp1406, Centre for Economic Performance, LSE
Krueger AB, Mueller A, Davis SJ, Sahin A (2011) Job search, emotional well-being, and job finding in a period of mass unemployment: Evidence from high frequency longitudinal data [with comments and discussion]. Brookings Papers on Economic Activity, 1–81
Krueger AB, Mueller AI (2012) Time use, emotional well-being, and unemployment: Evidence from longitudinal data. The American Economic Review 102(3):594–599
Krueger AB, Mueller AI (2014). A contribution to the empirics of reservation wages. Working Paper 19870, National Bureau of Economic Research
Lancaster T, Chesher A (1983) An econometric analysis of reservation wages. Econometrica 51(6):1661–1676
Lee DS, Lemieux T (2009) Regression discontinuity designs in economics. NBER Working Papers 14723, National Bureau of Economic Research, Inc
Low Pay Commission (2019) 20 years of the national minimum wage a history of the uk minimum wage and its effects. Technical report
Manning A (2003) Monopsony in motion: imperfect competition in labor markets. Princeton University Press
McCrary J (2008) Manipulation of the running variable in the regression discontinuity design: A density test. Journal of Econometrics 142(2), 698 – 714. The regression discontinuity design: Theory and applications
Neumark D, Wascher WL (2008) Minimum wages. Mit Press
Funding
No funding was received to assist with the preparation of this manuscript
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Panos Sousounis and Gauthier Lanot. The first draft of the manuscript was written by Panos Sousounis and Gauthier Lanot and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflicts of Interest
All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.
Ethical Approval
Not applicable.
Informed Consent
Not applicable.
Appendix
Appendix
Smoothed plots of decreasing bin width. The \(x-\)axis is the average of the scoring variable, \(x_{t-1}\) based on the respective bin size. Each circle represents the mean of each bin, which is weighted by the number of observations in the bin, so the size of the circle represents the number of observations in that bin. A lowess line is superimposed as a visualisation aid. The number of bins to the left and to the right of the cutoff point is indicated at the bottom of each panel. The average bin length is 0.4 when J=5 bins are used, 0.2 for J=10, 0.13 for J=15, 0.1 for J=20, 0.08 for J=25, and 0.067 for J=30
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sousounis, P., Lanot, G. Minimum Wage Effects on Reservation Wages. J Labor Res 43, 415–439 (2022). https://doi.org/10.1007/s12122-022-09337-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12122-022-09337-y
Keywords
- Minimum wages
- Reservation wages
- Fuzzy regression discontinuity
- Participation rate
- Unemployment
- Employment