Introduction

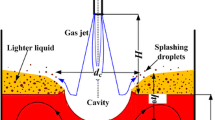
Kaldo furnaces, also known as top blown rotary furnaces, are widely used as the preferred smelting equipment for extracting gold, silver, selenium, tellurium and other precious metals from copper anode slime because of their strong raw material adaptability levels, high valuable metal recovery rates, low energy consumption levels, short process times and low waste gas emissions.1,2,3,4 The smelting process of copper anode slime by a Kaldo furnace involves multiphase physical and chemical behaviors of gas-slag-metal, in which the fluctuation behavior of a gas–liquid interface (cavity, splash, etc.) directly affects the smelting energy efficiency, furnace life and precious metal yield.2,5 During the smelting process, the compressed gas ejected from the oxygen lance interacts with the molten pool surface to form a cavity; it forms a strong turbulent vortex with the rotation of the furnace, thus improving the heat and mass transfer efficiencies in the molten pool and accelerating various physical and chemical reactions in the furnace. The shape of the cavity is an important parameter reflecting the flow characteristics of molten metal and lean slag in the Kaldo furnace, and it is closely related to factors such as the gas flow velocity and rotation speed of the furnace. The penetration depth of the cavity mainly affects the oxygen utilization rate of the injection lance and the gas blowing process; the area of the cavity affects the refining of the slag phase and the multiphase emulsification process of gas-slag-metal. Therefore, maintaining a reasonable liquid level fluctuation is of great significance for slag entrapment and the quality of the Dore alloy.

The behavior of the gas–liquid-solid interface, which couples mass transfer, heat transfer and chemical reaction, is of great importance and exists in many high-temperature metallurgical processes. Examples include copper smelting by oxygen bottom blowing and side blowing, high-manganese molten iron by conversion with a converter and anode slime by conversion with a Kaldo furnace.5,6,7,8,9,10,11,12 The three-phase interface behavior of gas–liquid-solid formed by the interaction between the blowing gas flow and the molten pool is a basic phenomenon in metallurgical converting equipment. Scientific and reasonable mixing performance control in furnaces has always been a key problem that needs to be solved in the metallurgical field, and it has been widely considered by many scholars.13,14,15,16,17 To date, research on this aspect has mainly focused on cold physical experiments and computational fluid dynamics (CFD) numerical simulations. For example, Zhao et al.12 studied gas–liquid mass transfer and flow characteristics in a Peirce-Smith converter by a water model experiment and obtained the optimal gas flow rate and blow angle. Shui et al.18,19,20 studied the mixing characteristics of water and an oil–water double phase using a water model and revealed the behavior of the surficial longitudinal wave formed on the surface of the molten pool in a bottom-blown copper smelting furnace. Maia et al.21 studied the influences of blow parameters on jet penetration through a 1/6 geometric scale for a physical model of a BOF converter. Their work can provide guidance for the selection of various parameters, such as lance height and flow rate, and for the optimized design of furnace structures in industrial practice. Zhao et al.22 studied the mixing characteristics of fluids in an Isa smelting furnace based on a 1:10 cold model that was scaled down geometrically and proposed a new standard for determining the mixing time. Li et al.23 studied the cratering process due to the impingement of the top-blown gas jets on the single or two-layer liquid bath (oil and water), and the cavity dimensions with respect to lance height, gas flow rate, inclination angle of jet and volume of the upper immiscible liquid were analyzed. Quiyoom et al.6 studied the gas–liquid two-phase mixing behavior in basic oxygen furnace (BOF) steel making process based on a water model and CFD simulation technology and proposed a feasible scheme to improve its mixing efficiency. Barron et al.10 researched the decarburization process in a BOF for steelmaking by establishing an improved mathematical model and discussed the influences of the oxygen flow rate and lance height on the decarburization rate. Li et al.24 carried out a numerical study of the interaction between the multiple jets and slag-metal bath in a BOF by means of the three-phase volume of fluid model. Ersson et al.25 presented a novel modeling for achieving a dynamic coupling of computational fluid dynamics and thermodynamics software to simulate certain metallurgical processes, such as top blown converters. Cao et al.26 summarized the latest achievements in a study of multiphase flows in the converter steelmaking process based on physical and mathematical models, such as supersonic oxygen jet, stirring and mixing, splashing and droplet generation, and energy transfer; this work provided a theoretical basis for realizing intelligent manufacturing in the steelmaking process. Li et al.27 studied the cavity oscillation and splashing distribution with excitation by bottom gas blowing in a combined-blown steelmaking converter using a numerical model in combination with a theoretical model. In addition, they also carried out other relevant research using numerical simulation methods, such as the splashing phenomenon induced by the impingement of multiple supersonic jets onto a molten slag-metal bath,28 the transferring characteristics of momentum/energy during oxygen jetting into the molten bath in BOFs29 and the swirling supersonic jets generated through a nozzle-twisted lance.30 The above research can provide technical and theoretical references for the study of multiphase flow behavior in Kaldo furnaces.

To date, there are few studies on the water model of mixing behavior in Kaldo furnaces; this model is mainly represented by the research of Pérez-Tello et al.2 In this work, a 1:7 scale water model of a Kaldo furnace was established. Colored oil and water were selected to represent the slag phase and a Dore alloy, respectively. The influences of different parameters, such as the rotation speed and inclination angle, on the maximum penetration distance of the injection lance d* and the free fluctuation of the liquid surface caused by the oblique airflow were preliminarily explored; the dimensionless mathematical expression between d* and its influencing factors was obtained. This work provided us with meaningful guidance and help for the study of gas–liquid interface behavior in the Kaldo furnace. Besides d*, the area of the cavity formed by the jet flow is also an important factor affecting gas–liquid interface behavior. In addition, during the blowing process, the viscosity of the slag phase has a certain influence on the interaction between the blowing gas flow and the molten pool. However, this research did not involve the experimental design of a water model according to the actual changes in slag viscosity in industrial reactors, which needs further consideration.16,31

In this work, a 1:4.5 cold water experimental model is built by geometrically scaling down an industrial Kaldo furnace based on the similarity principle. The effects of certain process parameters, such as the gas flow rate, rotation speed, liquid volume fraction and dynamic viscosity, of slag on the cavity shape of the gas–liquid two-phase interface in the Kaldo furnace are observed by computer image processing technology and dimensional analysis. Our findings are expected to provide a theoretical basis for the efficient smelting and optimal design of Kaldo furnaces.

Experiment

Principles

By taking the industrial Kaldo furnace as the prototype, the water model experiment is carried out based on the principle of geometric similarity, which is described as follows:

$$ \lambda = \frac{{l_{m} }}{{l_{p} }} $$
(1)

where λ is the geometric similarity ratio and lm and lp are the dimensions of the physical model and prototype, respectively.

In addition, it is necessary to ensure that the Froude number Fr, the Reynolds number Re and other similar criteria of fluid flow in the experimental model and prototype are equal. However, it is difficult to find a solution system with the same Re and Fr values during the actual experiment. Therefore, the modified Froude number Fr′ is selected as the decisive similarity number according to the characteristics of the top blowing smelting process of the Kaldo furnace based on dynamics similarity.32,33 The gas flow parameters during physical simulation are determined as follows:

$$ Fr_{{}}^{^{\prime}} = \frac{{\rho_{g} u^{2} }}{{g\left( {\rho_{l} - \rho_{g} } \right)D}} $$
(2)
$$ u = \frac{4Q}{{\pi d^{2} }} $$
(3)
$$ Fr_{m}^{^{\prime}} = Fr_{p}^{^{\prime}} = \frac{{16\rho_{gm} Q_{m}^{2} }}{{g\pi^{2} \left( {\rho_{lm} - \rho_{gm} } \right)D_{m} d_{m}^{4} }} = \frac{{16\rho_{gp} Q_{p}^{2} }}{{g\pi^{2} \left( {\rho_{lp} - \rho_{gp} } \right)D_{p} d_{p}^{4} }} $$
(4)
$$ Q_{m} = \left( {\frac{{\rho_{gp} }}{{\rho_{gm} }} \cdot \left( {\frac{{d_{m} }}{{d_{p} }}} \right)^{4} \cdot \frac{{D_{m} }}{{D_{p} }} \cdot \frac{{\rho_{lm} - \rho_{gm} }}{{\rho_{lp} - \rho_{gp} }}} \right)^{1/2} \cdot Q_{p} $$
(5)

where u is the characteristic velocity, D is the inner diameter of the furnace, g is the gravitational acceleration, ρg is the gas density, ρl is the liquid density, Q is the volume flow of gas, d is the inner diameter of the oxygen lance nozzle, and m and p are subscripts that represent the water model and industrial reactors, respectively.

Experimental Setup and Image Processing Method

The physical simulation experiment of the Kaldo furnace is carried out on a cold model made of acrylic tubes with a geometric similarity ratio of 1:4.5. This model is mainly composed of three parts: (1) a physical simulation injection system composed of the Kaldo furnace model, an inclinometer, a sliding support and an injection lance; (2) a gas supply and flow adjustment system consisting of a pressure reducing meter, a flow meter (MF5712-250, Siargo, Ltd., USA) and a compressed gas cylinder; (3) a parameter adjustment and data recording system consisting of a computer, a noncontact tachometer (TA8146C, Suzhou TASI Electronics Co., Ltd., China) and a high-speed camera (Photon FASTCAM Mini UX 50, Japan). The experimental device is shown in Fig. 1a and b, and the size parameters of each component are shown in Table I.

Fig. 1
figure 1

Schematic diagram of the water model experimental device for the Kaldo furnace. (a) Water model structure, (b) physical model structure, (c) schematic diagram of the cavity morphology (Hp and Sp).

Full size image
Table I Geometric parameters of the water model and physical Kaldo furnace
Full size table

In the converting process of the Kaldo furnace, the interaction between the top blowing compressed oxygen jet and the molten pool forms a cavity with a certain penetration depth and area. Relevant research has shown that a good cavity morphology can guarantee the smooth and uniform movement of the molten pool in the smelting process and increase the smelting efficiency.34,35 Therefore, it is necessary to systematically measure and analyze the shapes of cavities. In this experiment, a ruler is set at the bottom of the furnace for the convenience of measurement, as shown in Fig. 1c. The penetration depth of cavity Hp refers to the vertical distance from the lowest point of the cavity to the liquid level, and the oxygen lance height h refers to the vertical distance from the oxygen lance to the liquid surface. Sp represents the area of the cavity, as depicted in Fig. 1c. Notably, the jet from the lance is not vertical, and the angle of inclination to the liquid surface is 60°. Before the experiment, the viscosity and density of slag in the industrial Kaldo furnace are measured by a molten salt physical property comprehensive tester (RT-4, produced by Northeast University, China). The measured average value of the dynamic viscosity of slag is 0.512 Pa·s, and the average value of slag density is 4700 kg/m3. During the experiment, the dynamic viscosity of the aqueous solution is adjusted through sodium carboxymethyl cellulose (FVH9, produced by Henan Enmiao Food Co., Ltd., China) to endow it with the same kinematic viscosity as the slag. The values of various physical parameters used in the industrial reactor and water model experiment are listed in Table II.

Table II Input variables and physical properties of the fluids used in this work
Full size table

In this work, the penetration depth Hp and area of the cavity Sp are analyzed and measured through an image analysis method, and the specific processing steps are shown in Fig. 2. First, based on OpenCV computer vision and a machine learning software library, the images taken by a high-speed camera are processed by image subtraction, median filtering and morphological processing (image erosion, dilate, open operation, close operation of image and edge detection); liquid level line division operation is carried out to eliminate irrelevant interference data. Second, the mapping relationship between the pixel points and the size of the captured image is realized through a ruler pasted on the side of the water model. Finally, the penetration depth Hp and area of the cavity Sp are obtained through image feature calculation.

Fig. 2
figure 2

Schematic diagram of the data extraction of a captured image.

Full size image

Experimental Design

This experiment is designed to explore the influences of various process parameters, such as the gas flow rate, rotation speed, liquid volume, injection lance height and dynamic viscosity of slag, on the shape of the cavity in the molten pool.

The single-factor experimental design used in this work is listed in Table III. Each experiment is repeated three times, and the average values of Hp and Sp are taken as the final measurement results to ensure the accuracy of the experimental results. The basic working conditions of this experiment are as follows: the gas flow rate Q is 161 L/min, the injection lance height h is 50 mm, the inclination angle is 28°, the rotation speed ω is 10 rpm, the liquid phase volume V is 7.0 L, and the viscosity of the slag phase μ is 110.0 mPa·s.

Table III Single-factor experimental design in this work
Full size table

Dimensional Analysis of the Penetration Depth H p and Area of the Cavity S p

During the smelting process of anode slime in the Kaldo furnace, the cavity morphology of the liquid level in the molten pool is affected by the simultaneous action of multiple parameters, such as the rotation speed (ω), melt volume fraction (φ), injection lance height (h), gas outlet velocity (u), inner diameter of the furnace (D), density (ρ), dynamic viscosity of the slag (μ) and inner diameter of the nozzle (d). The variable dimensions are listed in Table IV.

Table IV Variable dimensions
Full size table

According to the principle of dimensional consistency and the Π theorem,36 the functional relationship between the penetration depth of the cavity Hp and each dimensionless parameter is determined:37,38

$$ H_{{\text{p}}} = f\left( {\omega ,\varphi ,h,u,d,D,g,\rho_{g} ,\rho_{l} ,\mu_{l} } \right) $$
(6)

The above equation involves 11 variables with 3 basic dimensions (mass M, length L and time T). The density ρl, acceleration of gravity g and inner diameter of the furnace D are selected as repeated variables; a set of dimensionless group numbers with dimension 1 is constructed according to the dimensional analysis method:

$$ \begin{gathered} \pi_{1} = \rho_{l}^{{a_{1} }} D^{{\beta_{1} }} g^{{\gamma_{1} }} H_{p} \hfill \\ \pi_{2} = \rho_{l}^{{a_{2} }} D^{{\beta_{2} }} {\text{g}}^{{\gamma_{2} }} \omega \hfill \\ \pi_{3} = \rho_{l}^{{a_{3} }} D^{{\beta_{3} }} g^{{\gamma_{3} }} \varphi \hfill \\ \pi_{4} = \rho_{l}^{{a_{4} }} D^{{\beta_{4} }} {\text{g}}^{{\gamma_{4} }} h \hfill \\ \pi_{5} = \rho_{l}^{{a_{5} }} D^{{\beta_{5} }} g^{{\gamma_{5} }} u \hfill \\ \pi_{6} = \rho_{l}^{{a_{5} }} D^{{\beta_{5} }} g^{{\gamma_{5} }} d \hfill \\ \pi_{7} = \rho_{l}^{{a_{6} }} D^{{\beta_{6} }} {\text{g}}^{{\gamma_{6} }} \rho_{g} \hfill \\ \pi_{8} = \rho_{l}^{{a_{8} }} D^{{\beta_{8} }} {\text{g}}^{{\gamma_{8} }} \mu_{l} \hfill \\ \end{gathered} $$
(7)

Equation 8 is obtained by solving each dimensional relation, and it is rewritten as Eq. 9.

$$ \begin{gathered} \pi_{1} = \frac{{H_{{\text{p}}} }}{D},\;\pi_{2} = \frac{{\omega^{2} D}}{g},\,\pi_{3} = \varphi ,\;\pi_{4} = \frac{h}{D} \hfill \\ \pi_{5} = \frac{{u^{2} }}{gD},\,\pi_{6} = \frac{d}{D},\,\pi_{7} = \frac{{\rho_{g} }}{{\rho_{l} }},\,\pi_{8} = \frac{{\mu_{l}^{2} }}{{gD^{3} }} \hfill \\ \end{gathered} $$
(8)
$$ f\left( {\frac{{H_{{\text{p}}} }}{D},\frac{{\omega^{2} D}}{g},\varphi ,\frac{h}{D},\frac{{u^{2} }}{gD},\frac{d}{D},\frac{{\rho_{g} }}{{\rho_{l} }},\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right) = 0 $$
(9)

where D, d, ρg and ρl are known as constants throughout the experiment; thus, Eq. 9 is further transformed:

$$ f\left( {\frac{{H_{{\text{p}}} }}{D},\frac{{\omega^{2} D}}{g},\varphi ,\frac{h}{D},Fr^{^{\prime}} ,\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right) = 0 $$
(10)

Then, the dimensionless expression of the penetration depth Hp/D of the cavity is obtained as shown in Eq. 11. The same method may be easily adapted to obtain the dimensionless expression of Sp/D2 as described by Eq. 12.

$$ \frac{{H_{{\text{p}}} }}{D} = f\left( {\frac{{\omega^{2} D}}{g},\varphi ,\frac{h}{D},Fr^{^{\prime}} ,\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right) $$
(11)
$$ \frac{{S_{{\text{p}}} }}{{D^{2} }} = f\left( {\frac{{\omega^{2} D}}{g},\varphi ,\frac{h}{D},Fr^{^{\prime}} ,\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right) $$
(12)

Results and Discussion

Effect of Gas Flow Rate Q

The penetration depth Hp/D and area of the cavity Sp/D2 versus gas flow rate Q represented by Fr' are shown in Fig. 3. Figure 3 shows that increasing the gas flow rate Q generally leads to an increase in Hp/D and the area of the cavity Sp/D2. When Fr' = 11.6 (corresponding to Q = 161 L/min in the experiment and 1200 Nm3/h under industrial conditions), Hp/D and Sp/D2 are 0.276 (Hp = 66.25 mm) and 0.088 (Sp = 5064.53 mm2), respectively. When Fr' = 20.6 (corresponding to Q = 215 L/min in the experiment and 1600 Nm3/h under industrial conditions), Hp/D and Sp/D2 reach 0.345 (Hp = 82.72 mm) and 0.12 (Sp = 6731.14 mm2), respectively, increasing to values that are 125% and 136.4% of the initial level (Fr' = 5.1). This phenomenon occurs because the increase in gas flow increases the kinetic energy of the injected gas and enhances its impact on the free surface of the molten pool. However, the phenomenon is not that the greater the gas flow rate is, the better the mixing performance of the molten pool in actual production. Excessive oxygen jets may penetrate the metal molten pool, causing severe disturbance, and may cause splashing in serious cases.39

Fig. 3
figure 3

Penetration depth Hp/D and area of the cavity Sp/D2 versus the gas flow rate Q represented by Fr′.

Full size image

Effect of Injection Lance Height h

Figure 4 shows the effects of the injection lance height h represented by h/D on the penetration depth Hp/D and the area of the cavity Sp/D2. As shown in Fig. 4, both Hp/D and Sp/D2 decrease with increasing injection lance height. When the injection lance height h/D increases from 0.04 (h = 10 mm) to 0.08 (h = 90 mm), Hp/D decreases by 60% from 0.418 (Hp = 100.31 mm) to 0.167 (Hp = 40.19 mm), and Sp/D2 decreases by 70% from 0.138 (Sp = 7946.67 mm2) to 0.0414 (Sp = 2385.17 mm2). This phenomenon occurs because when the height of the injection lance is low, the kinetic energy of the oxygen jet is concentrated on penetrating the molten pool; thus, the impact penetration depth on the molten pool is large. With the continuous increase in the injection lance height, the energy attenuation of the oxygen jet above the molten pool increases; simultaneously, the kinetic energy acting on the interface of the molten pool decreases, resulting in a smaller penetration depth of the cavity. Relevant research has shown that both overly high and low h values are not conducive to the stirring and mixing of the molten pool.16 Therefore, in actual production, the height of the injection lance should be systematically controlled to ensure good mixing and a good mixing effect of the fluid in the molten pool.

Fig. 4
figure 4

Penetration depth Hp/D and area of the cavity Sp/D2 versus injection lance height h represented by h/D.

Full size image

Effect of Rotation Speed ω

Figure 5 shows the penetration depth Hp/D and the area of the cavity Sp/D2 versus the rotation speed ω, which is represented by ω2D/g. As ω2D/g increases from 2.45 × 10–4 (ω = 6 rpm) to 1.33 × 10–3 (ω = 14 rpm), Hp/D tends to increase first and then decrease, while Sp/D2 tends to decrease first, then increase and finally decrease. When the rotation speed ω2D/g is 6.80 × 10–4 (ω = 10 rpm), Hp/D and Sp/D2 reach maximum values of 0.319 (Hp = 66.25 mm) and 0.106 (Sp = 5064.53 mm2), respectively. This is because as the rotational speed increases, the turbulence degree of the gas–liquid two phases increases, leading to a generally increasing trend in the depth and area of the cavity. This increases the interaction area of the two phases and increases the surface renewal rate, thereby accelerating the reaction. Research has shown that properly increasing the rotation speed is conducive to increasing the reaction area and the concentration differences of reactants at the reaction interface to improve the overall reaction rate.40 By further increasing the rotation speed to 9.97 × 10–4 (ω = 12 rpm), the penetration depth Hp/D and the area of the cavity Sp/D2 decrease significantly. When the rotation speed increases to 1.33 × 10–3 (ω = 14 rpm), both Hp/D and Sp/D2 decrease slightly. However, there should be a limit to the increase in rotational speed. For a certain gas flow rate, it usually corresponds to a maximum rotational speed value. Excessive rotational speed can cause serious splashing and consume additional energy, leading to a reduction in the depth and area of cavity. In addition, a too fast rotation speed consumes more power, accelerates the abrasion between the lining and the melt and shortens the service life of the furnace lining.40 Therefore, to promote the full implementation of physical and chemical reactions in the pool and ensure stable and normal blowing operation, the rotation speed should be controlled within a reasonable range of 10–12 rpm.

Fig. 5
figure 5

Penetration depth Hp/D and area of the cavity Sp/D2 versus rotation speed ω represented by ω2D/g.

Full size image

Effect of Liquid Volume Fraction φ

The influence of liquid volume fraction φ on the penetration depth Hp/D and the area of the cavity Sp/D2 is shown in Fig. 6. When the liquid volume fraction φ increases from 0.27 (corresponding to V = 3.0 L in the experiment and 0.27 m3 under industrial conditions) to 1.00 (corresponding to V = 11.0 L in the experiment and 1.0 m3 under industrial conditions), the penetration depth Hp/D of the cavity shows a decreasing trend, while the area Sp/D2 shows a trend of first increasing and then decreasing. This is because when the liquid volume fraction φ is 0.27 (V = 3.0 L), the liquid level is very low, and the cavity formed by the gas jet is relatively close to the wall. In this event, the cavity collided with the wall, resulting in a smaller area of the cavity. At the same time, due to the wall effect, the resistance of the gas jet to expand laterally along the cavity increases, and the longitudinal flow intensifies, resulting in a large depth of the cavity. When the liquid volume fraction φ is between 0.27 and 0.64, Hp/D and Sp/D2 have high values, which are conducive to maintaining a high reaction efficiency in the molten pool. When φ increases to 1.00, Hp/D and Sp/D2 decrease significantly. This is because as the liquid volume fraction increases, the liquid level continuously increases, and the cavity formed by the gas jet is farther from the wall, resulting in a weakening of the wall effect. Therefore, an overly high liquid level of the molten pool is not conducive to the full stirring and mixing of the molten pool by the gas jet and even causes serious splash problems.

Fig. 6
figure 6

Influences of the liquid volume fraction on the penetration depth Hp/D and area of the cavity Sp/D2.

Full size image

Effect of the Dynamic Viscosity of Slag μ

The dynamic viscosity of slag μ reflects the internal friction between layers during the relative movement of the slag, which directly affects the physical and chemical reaction rates of each phase in the molten pool and the flow and heat transfer capabilities of the fluid. Figure 7 shows the penetration depth Hp/D and the area of the cavity Sp/D2 versus the dynamic viscosity of the slag phase μ represented by μl2/(g/D3). When the dynamic viscosity of the slag phase μl2/(g/D3) is in the range of 0.036–0.166 (μ = 70–150 mPa·s), with the increase in the dynamic viscosity of the slag, both Hp/D and Sp/D2 show a trend of first decreasing, then increasing, then decreasing and finally increasing. However, the changes in values are not large. When μ2/(g/D3) is 0.125 (μ = 130 mPa·s), Hp/D and Sp/D2 have minimum values of 0.27 (Hp = 64.97 mm) and 0.0786 (Sp = 4529.04 mm2), respectively. In general, the influences of liquid viscosity on the penetration depth and area of the cavity are not significant. Relevant studies show that the slag viscosity mainly affects the mixing time and the stirring effect of the molten pool.41

Fig. 7
figure 7

Penetration depth Hp/D and area of the cavity Sp/D2 versus the dynamic viscosity of slag phase μl represented by μl2/(g/D3).

Full size image

Mathematical Correlation Analysis of H p/D and S p/D 2

Under a fixed similarity ratio of the feature size of the furnace and injection lance, the dimensionless feature sizes θ and d/D are regarded as constants, and Eqs. 11 and 12 are expressed as follows:

$$ \frac{{H_{{\text{p}}} }}{D} = a\left( {\frac{{\omega^{2} D}}{g}} \right)^{b} \varphi^{c} \left( \frac{h}{D} \right)^{d} \left( {{\text{Fr}}^{{\prime }} } \right)^{e} \left( {\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right)^{f} $$
(13)
$$ \frac{{S_{{\text{p}}} }}{{D^{2} }} = a\left( {\frac{{\omega^{2} D}}{g}} \right)^{b} \varphi^{c} \left( \frac{h}{D} \right)^{d} \left( {{\text{Fr}}^{{\prime }} } \right)^{e} \left( {\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right)^{f} $$
(14)

In this work, the penetration depth and area of the cavity are calculated according to Eqs. 13 and 14, respectively. The above mathematical expressions are solved by nonlinear generalized reduced gradient (GRG) algorithms, and then Eqs. 15 and 16 are obtained.

$$ \frac{{H_{{\text{p}}} }}{D} = 0.041\left( {\frac{{\omega^{2} D}}{g}} \right)^{ - 0.026} \varphi^{ - 0.206} \left( \frac{h}{D} \right)^{ - 0.304} \left( {{\text{Fr}}^{^{\prime}} } \right)^{0.438} \left( {\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right)^{ - 0.013} $$
(15)
$$ \frac{{S_{{\text{p}}} }}{{D^{2} }} = 0.006\left( {\frac{{\omega^{2} D}}{g}} \right)^{ - 0.007} \varphi^{ - 0.122} \left( \frac{h}{D} \right)^{ - 0.384} \left( {{\text{Fr}}^{^{\prime}} } \right)^{0.748} \left( {\frac{{\mu_{l}^{2} }}{{gD^{3} }}} \right)^{ - 0.038} $$
(16)

Figure 8 shows the comparison of the calculated and experimental values of Hp/D and Sp/D2 for all the experimental conditions tested in this work. Figure 8a and b shows that the calculated value is in good agreement with the experimental value, indicating that Eqs. 15 and 16 have a high accuracy. Of course, there is an inevitable deviation between the calculated value and the experimental value. The error between the calculated results by the dimensionless formulas and the experimental data is basically controlled within 10% and 20%. However, some data points with large deviations are found in the statistical process. This phenomenon mainly occurs under the working condition of a high injection lance height (90 mm). The calculated value of Hp/D is 0.222, and the deviation from the experimental value is 32.4%. The calculated value of Sp/D2 is 0.062 with a deviation of 50.2%. The reason for this phenomenon is preliminarily believed to be that the injection lance height is overly high; thus, the impact force reaching the liquid level is small, resulting in small liquid level fluctuation, which leads to a poor stirring effect on the molten pool. In general, the error is within an acceptable range; thus, the dimensionless formulas of Hp/D and Sp/D2 obtained can be used in production practice and provide a reference for the efficient smelting and optimal design of Kaldo furnaces.

Fig. 8
figure 8

Comparison of the calculated and experimental values of Hp/D and Sp/D2 for all the experimental conditions tested in this work. (a) Penetration distance Hp/D, (b) area of the cavity Sp/D2.

Full size image

Conclusion

A water model experimentation and dimensional analysis have been conducted to determine the influences of different process parameters on the gas–liquid interface behavior (represented by the shape of the cavity) in a Kaldo furnace. The main conclusions are as follows:

  1. 1.

    The influences of various parameters, such as the gas flow rate Q, injection lance height h, rotation speed ω, liquid volume fraction φ and liquid viscosity μ, on the shape of the cavity in the Kaldo furnace are revealed. The results show that with increasing Q and h, the shape of the cavity regarding the penetration depth Hp/D and area Sp/D2 in the molten pool increases and decreases, respectively. With increasing ω, Hp/D tends to increase first and then decrease, while Sp/D2 tends to decrease first, then increase and finally decrease. With increasing φ, Hp/D shows a decreasing trend, while Sp/D2 shows a trend of first increasing and then decreasing. In addition, the liquid viscosity μ has an insignificant impact on the penetration depth Hp/D and area of the cavity Sp/D2.

  2. 2.

    A dimensionless mathematical correlation for the penetration depth Hp/D and area of the cavity Sp/D2 as a function of ω, φ, h, μ and Fr′ in the molten pool of the Kaldo furnace is developed through data fitting and programming. The mathematical expressions for Hp/D and Sp/D2 are \({{H_{{\text{p}}} } \mathord{\left/ {\vphantom {{H_{{\text{p}}} } D}} \right. \kern-0pt} D} = 0.041\left( {{{\omega^{2} D} \mathord{\left/ {\vphantom {{\omega^{2} D} g}} \right. \kern-0pt} g}} \right)^{ - 0.026} \varphi^{ - 0.206} \left( {{h \mathord{\left/ {\vphantom {h D}} \right. \kern-0pt} D}} \right)^{ - 0.304} \left( {{\text{Fr}}^{^{\prime}} } \right)^{0.438} \left( {{{\mu^{2} } \mathord{\left/ {\vphantom {{\mu^{2} } {\left( {gD^{3} } \right)}}} \right. \kern-0pt} {\left( {gD^{3} } \right)}}} \right)^{ - 0.013}\) and \({{S_{{\text{p}}} } \mathord{\left/ {\vphantom {{S_{{\text{p}}} } {D^{2} }}} \right. \kern-0pt} {D^{2} }} = 0.006\left( {{{\omega^{2} D} \mathord{\left/ {\vphantom {{\omega^{2} D} g}} \right. \kern-0pt} g}} \right)^{ - 0.007} \varphi^{ - 0.122} \left( {{h \mathord{\left/ {\vphantom {h D}} \right. \kern-0pt} D}} \right)^{ - 0.384} \left( {{\text{Fr}}^{^{\prime}} } \right)^{0.748} \left( {{{\mu^{2} } \mathord{\left/ {\vphantom {{\mu^{2} } {\left( {gD^{3} } \right)}}} \right. \kern-0pt} {\left( {gD^{3} } \right)}}} \right)^{ - 0.038}\), respectively. By comparing the calculated value of the mathematical formula with the experimental value, the results show that the relative errors are < 10% and 20%, respectively, and they are within an acceptable range; this finding indicates that the dimensionless formula has meaningful reference value for production practice.