Skip to main content
SpringerLink
Log in

Vibration Prediction of Bladed Disks Coupled by Friction Joints

  • Original Paper
  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

Abstract

The present review article addresses the vibration behavior of bladed disks encountered e.g. in aircraft engines as well as industrial gas and steam turbines. The utilization of the dissipative effects of dry friction in mechanical joints is a common means of the passive mitigation of structural vibrations caused by aeroelastic excitation mechanisms. The prediction of the vibration behavior is a scientific challenge due to (a) the strongly nonlinear contact interactions involving local sticking, sliding and liftoff, (b) the model order required to accurately describe the dynamic behavior of the assembly, and (c) the multi-disciplinary character of the problem associated with the need to account for structural mechanical as well as fluid dynamical effects. The purpose of this article is the overview and discussion the current state of the art of vibration prediction approaches. The modeling approaches in this work embrace the description of the rotating bladed disk, the contact modeling, the consideration of aeroelastic effects, appropriate model order reduction techniques and the exploitation of the rotationally periodic nature of the problem. The simulation approaches cover the direct computation of periodic, steady-state externally forced and self-excited vibrations using the high-order harmonic balance method, the formulation of the contact problem in the frequency domain, methods for the solution of the governing algebraic equations and advanced simulation approaches, including the concept of nonlinear modes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. Note that the actual values of \({}^{\,(n)}_{{\mathrm{fe}}}{\varvec{f}}_{{\mathrm{c}}}\) and \({}^{\,(n)}_{{\mathrm{fe}}}{\varvec{f}}_{{\mathrm{a}}}\) still depend on the independent displacement vectors \({}^{\,(n)}_{{\mathrm{fe}}}{\varvec{u}}\) and are, of course, generally not equal to each other.

  2. Hence, the part \({}_{\,\mathrm{fe}}{\varvec{K}}\) related to elastic forces is sometimes referred to as ‘tangent’ stiffness matrix.

  3. Sometimes also referred to as cyclic or nodal diameter coordinates.

  4. The actual Mortar method does not only involve the discretization by means of contact segments, but is commonly associated with an augmented Lagrangian formulation of the contact laws. Here, ‘Mortar-like’ only refers to the discretization using contact segments.

  5. \({\varvec{u}}\) is a vector of generalized displacements of dimension \(n_{{\mathrm{d}}}\times 1\). In particular, it can stand for \({}_{\,\mathrm{fe}}{\varvec{u}}\) or \({}_{\,\mathrm{tw}}{\varvec{u}}\).

  6. This coordinate transform may also involve reduced descriptions of subdomains in terms of component modes, see Sect. 2.3, in which case \({\varvec{u}}\) refers to generalized coordinates instead of nodal coordinates. This also includes the special case where one or both of the contacting surfaces belongs to a rigid body, where \({\varvec{B}}\) takes into account rigid body kinematics.

  7. The actual reduction depends on the discretizaton. In accordance with the notation introduced in the previous subsection, for the variant (a), the number of coupling coordinates equals the number of rows of \({\varvec{B}}\) containing non-zero elements. For variant (b), the number of coupling coordinates is \(3n_{{\mathrm{c}}}\), that is, the dimension of the vector of contact gaps \({}_{\,\mathrm{c}}{\varvec{g}}\).

  8. For more information and an illustration of such traveling waves, see ‘Appendix 1’.

  9. Note that one approach to formally derive Eq. (17) is the principle of virtual work.

  10. Since this matrix is formulated in the modal space, it is often referred to as modal aerodynamical influence matrix, and its entries are referred to as modal aerodynamical influence coefficients.

  11. Note that for assessing the aeroelastic stability, an alternative to the energy method is to carry out a fluid-structure simulation of the whole annulus, starting from an initial perturbation, and analyzing whether the vibrations grow or decay [166].

  12. As discussed in Sect. 2.1.2, this is the case if the sector-to-sector deviations of (geometrical, material and contact) properties are sufficiently small or the inter-sector coupling is sufficiently strong.

  13. For enlightening illustrations of this rule, the reader is referred to [114].

  14. It appears to be a common belief that the equations of motion can be solved exactly if piecewise linear contact laws are considered. Indeed, the set of ordinary differential equations becomes piecewise integrable. However, the transition times between the different contact states (stick, slip, liftoff) are generally not a priori known and need to be determined from the transition conditions. The latter are usually transcendental equations in the unknown transition times, rendering an exact solution impossible.

  15. In the literature, other widely used names for the method described here are the ‘Describing Function method’ and the ‘Krylov–Bogoliubov–Mitropolsky method’. Moreover, the prefixes ‘multi’ or ‘high-order’ are often used for the harmonic balance method in order to clarify the difference to the single-term variant which only considers the fundamental harmonic.

  16. Hence, this procedure is considered a pure frequency-domain method, since there is no need to switch to the time domain, in contrast to the alternating frequency–time scheme presented in the following paragraph.

  17. cf. discussion in paragraph ‘Tangential contact’ in Sect. 2.2.3.

  18. Note that the normal preload is sometimes also referred to as initial normal load, which emphasizes that the actual normal load may change due to vibrations. In fact, even the static component (or average value) of the normal load is generally influenced by the dynamic contact interactions.

  19. The task of finding such an appropriate guess is addressed in Sect. 3.4.4.

  20. In the literature, the name ‘Newton–Raphson’ method is also commonly used for the method described here.

  21. This method is sometimes referred to as the Riks method.

  22. In fact, in the case of the horizontal tangent condition, it cannot even be ensured that the traced point is a maximum, but a local minimum or a saddle node might be traced ‘by mistake’.

  23. In literature, the term Nonlinear Normal Mode (NNM) is quite common. However, the term ‘normal’ may lead to the wrong conclusion that nonlinear modes are orthogonal to each other. Apparently this term goes back to Rosenberg [137], who defined nonlinear modes as vibrations in unison, i. e. where all material points cross their equilibrium points and their extremum points simultaneously. For this type of vibration, the motions take place on so-called modal curves in the generalized displacement space which are normal to the surface of maximum potential energy [167]. However, this property is only valid for symmetric conservative systems, whereas non-trivial phase lags among the oscillations of the coordinates may exist in general. Hence the term ‘normal’ in this context is avoided in this article.

  24. In the literature, this number is also referred to as ‘harmonic index’. To avoid confusion with (temporal) harmonics in the context of frequency domain methods, this terms is avoided in this work. Moreover, the term ‘nodal diameter number’ is also common for this number.

  25. Here, ‘left’ and ‘right’ is meant with respect to the rotation axis (and, consequently, the numbering of the sectors).

  26. Note that \({\varvec{B}}^{\mathrm{T}}{\varvec{u}}= \left[ {\begin{array}{cc} {\varvec{B}}^{\mathrm{T}}\left( {\varvec{B}}^{\mathrm{T}}\right) ^{+}&{} {\varvec{B}}^{\mathrm{T}}{\varvec{N}}_{{\varvec{B}}^{\mathrm{T}}}\\ \end{array}}\right] \left[ {\begin{array}{c} {}_{\,\mathrm{c}}{\varvec{g}}\\ {\varvec{u}}_{{\mathrm{rem}}}\\ \end{array}}\right] = {}_{\,\mathrm{c}}{\varvec{g}}\), in full accordance with Eq. (6).

Abbreviations

\(N_0\) :

Initial normal load

\(g_{{\mathrm{n}},0}\) :

Initial normal gap

\({\mathcal{H}}\) :

Set of (temporal) harmonics

\(m\) :

Engine order

\(m_0\) :

Fundamental engine order

\({\mathcal{M}}\) :

Set of relevant engine orders

\(\epsilon _{{\mathrm{DL}}}\) :

Dynamic Lagrangian penalty coefficient

\(\varOmega _{{\mathrm{rot}}}\) :

Rotational speed

\(\theta\) :

Inter-blade phase angle

\({\varvec{f}}_{{\mathrm{a}}}\) :

Aerodynamical forces

\({\varvec{f}}_{{\mathrm{ae}}},{\varvec{F}}_{{\mathrm{ae}}}\) :

Aerodynamical external forces (time domain, frequency domain)

\({\varvec{f}}_{{\mathrm{ai}}}\) :

Aerodynamical interaction forces

\({\varvec{f}}_{{\mathrm{c}}},{\varvec{F}}_{{\mathrm{c}}}\) :

Global contact forces (time domain, frequency domain)

\({\varvec{g}}\) :

Contact gaps

\({\varvec{\lambda }},{\varvec{\varLambda }}\) :

Local contact forces (time domain, frequency domain)

\({\varvec{u}},{\varvec{U}}\) :

Vector of (generalized) coordinates (time domain, frequency domain)

\({\varvec{p}}\) :

Pressure

\({\varvec{B}}\) :

Interface coupling matrix

\({\varvec{D}}\) :

Damping matrix

\({\varvec{G}}_{{\mathrm{ai}}}\) :

Aerodynamic influence matrix

\({\varvec{H}}\) :

Dynamic compliance matrix

\({\varvec{I}}\) :

Identity matrix

\({\varvec{K}}\) :

Matrix of velocity proportional forces

\({\varvec{M}}\) :

Mass matrix

\({\varvec{S}}\) :

Dynamic stiffness matrix

\({\varvec{T}}\) :

Matrix of component modes

\({\varvec{W}}_{n_{{\mathrm{s}}}}\) :

Discrete Fourier matrix for \(n_{{\mathrm{s}}}\) samples

\({\varvec{\nabla }}\) :

Frequency domain derivative matrix

\(n_{{\mathrm{c}}}\) :

Number of contact points

\(n_{{\mathrm{d}}}\) :

Number of (generalized) coordinates

\(n_{{\mathrm{fe}}}\) :

Number of finite element nodal degrees of freedom

\(n_{{\mathrm{fe,s}}}\) :

… per sector

\(n_{{\mathrm{if}}}\) :

Number of interfaces

\(n_{{\mathrm{r}}}\) :

Number of component modes

\(n_{{\mathrm{s}}}\) :

Number of sectors

\((\,)_{{\mathrm{n}}}\) :

Associated to the normal direction

\((\,)_{{\mathrm{t}}}\) :

Associated to the tangential direction

\({}^{(n)}(\,)\) :

Associated to sector n

\({}_{{\mathcal{C}}}(\,)\) :

In the coordinates of the continuous contact interface

\({}_{{\mathrm{c}}}(\,)\) :

In the coordinates of the discrete contact interface

\({}_{{\mathrm{fe}}}(\,)\) :

In the physical degrees of freedom of the finite element model

\({}_{\,\mathrm{r}}(\,)\) :

In the generalized coordinates of the component modes

\({}_{\,\mathrm{tw}}(\,)\) :

In traveling wave coordinates

\({(\,)}^*\) :

Complex conjugate

\({\mathfrak {I}}\left\{ (\,) \right\}\) :

Imaginary part

\({\mathfrak {R}}\left\{ (\,) \right\}\) :

Real part

\((\,)^{+}\) :

Pseudo inverse

\((\,)^{\mathrm{H}}\) :

Hermitian transpose

\((\,)^{\mathrm{T}}\) :

Transpose

\({\varvec{N}}_{\varvec{A}}\) :

Null space of matrix \({\varvec{A}}\)

References

  1. Acary V, Brogliato B (2008) Numeerical methods for nonsmooth dynamical systems: applications in mechanics and electronics. Springer, Berlin

    MATH  Google Scholar 

  2. Batailly A, Legrand M, Cartraud P, Pierre C, Lombard JP (2007) Study of component mode synthesis methods in a rotor–stator interaction case. In: Proceedings of the ASME international design engineering technical conferences & computers and information in engineering conference, September 4–7, Las Vegas, NV, USA, pp 1–8

  3. Berthillier M, Dupont C, Mondal R, Barrau JJ (1998) Blades forced response analysis with friction dampers. J Vib Acoust 120(2):468–474

    Article  Google Scholar 

  4. Bhaumik SK, Sujata M, Venkataswamy MA, Parameswara MA (2006) Failure of a low pressure turbine rotor blade of an aeroengine. Eng Fail Anal 13(8):1202–1219

    Article  Google Scholar 

  5. Bladh JR (2001) Efficient predictions of the vibratory response of mistuned bladed disks by reduced order modeling. Dissertation, The University of Michigan, Michigan. http://tel.archives-ouvertes.fr/tel-00358168/en/

  6. Bladh R, Castanier MP, Pierre C (2003) Effects of multistage coupling and disk flexibility on mistuned bladed disk dynamics. J Eng Gas Turbines Power 125(1):121–130

    Article  Google Scholar 

  7. Bonhage M, Pohle L, Panning-von Scheidt L, Wallaschek J (2015) Transient amplitude amplification of mistuned blisks. J Eng Gas Turbines Power 137(11):112502

    Article  Google Scholar 

  8. Borrajo JM, Zucca S, Gola MM (2006) Analytical formulation of the Jacobian matrix for non-linear calculation of the forced response of turbine blade assemblies with wedge friction dampers. Int J Non-Linear Mech 41(10):1118–1127

    Article  Google Scholar 

  9. Cameron TM, Griffin JH (1989) An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic systems. J Appl Mech 56(1):149–154

    Article  MathSciNet  MATH  Google Scholar 

  10. Cardona A, Coune T, Lerusse A, Geradin M (1994) A multiharmonic method for non-linear vibration analysis. Int J Numer Methods Eng 37(9):1593–1608

    Article  MATH  Google Scholar 

  11. Castanier MP, Pierre C (1997) Consideration of the benefits of intentional blade mistuning for the forced response of turbomachinery rotors. In: Proceedings of the 1997 ASME international mechanical engineering congress and exposition, Nov. 16–21, Dallas, TX

  12. Castanier MP, Pierre C (1998) Investigation of the combined effects of intentional and random mistuning on the forced response of bladed disks. Paper AIAA-98-3720, Proceedings of the 34th AIAA/ASME/SAE/ASEE joint propulsion conference & exhibit, Cleveland, OH, July 13–15

  13. Castanier MP, Pierre C (2006) Modeling and analysis of mistuned bladed disk vibration: current status and emerging directions. J Propuls Power 22(2):384–396

    Article  Google Scholar 

  14. Cesari L (1963) Functional analysis and periodic solutions of nonlinear differential equations. Contrib Differ Equ 1:149–187

    MathSciNet  MATH  Google Scholar 

  15. Charleux D (2006) Étude des effets de la friction en pied d’aube sur la dynamique des roues aubagées. Dissertation, L’École Centrale de Lyon, Lyon

  16. Charleux D, Gibert C, Thouverez F, Dupeux J (2006) Numerical and experimental study of friction damping in blade attachments of rotating bladed disks. Int J Rotat Mach 2006:1–13

    Article  Google Scholar 

  17. Charleux D, Thouverez F, Lombard J (2004) Three-dimensional multiharmonic analysis of contact and friction in dovetail joints. In: Proceedings of the 22nd international modal analysis conference, January 26–29, Dearborn, MI, USA, pp 1–9

  18. Chen JJ, Menq CH (2001) Periodic response of blades having three-dimensional nonlinear shroud constraints. J Eng Gas Turbines Power 123(4):901–909

    Article  Google Scholar 

  19. Chen JJ, Yang BD, Menq CH (2000) Periodic forced response of structures having three-dimensional frictional constraints. J Sound Vib 229(4):775–792

    Article  Google Scholar 

  20. Cigeroglu E, An N, Menq CH (2007) A microslip friction model with normal load variation induced by normal motion. Nonlinear Dyn 50(3):609–626

    Article  MathSciNet  MATH  Google Scholar 

  21. Claeys M, Sinou JJ, Lambelin JP, Todeschini R (2015) Experiments and numerical simulations of nonlinear vibration responses of an assembly with friction joints—application on a test structure named ‘Harmony’. Mech Syst Signal Process 70–71:1097–1116

    Google Scholar 

  22. Cochelin B, Medale M (2013) Power series analysis as a major breakthrough to improve the efficiency of asymptotic numerical method in the vicinity of bifurcations. J Comput Phys 236(1):594–607

    Article  MathSciNet  Google Scholar 

  23. Cochelin B, Vergez C (2009) A high order purely frequency-based harmonic balance formulation for continuation of periodic solutions. J Sound Vib 324(1–2):243–262

    Article  Google Scholar 

  24. Cook RD (2002) Concepts and applications of finite element analysis, 4th edn. Wiley, New York

    Google Scholar 

  25. Coorevits P, Hild P, Hjiaj M (2001) A posteriori error control of finite element approximations for Coulomb’s frictional contact. SIAM J Sci Comput 23(3):976–999

    Article  MathSciNet  MATH  Google Scholar 

  26. Corral R, Gallardo JM, Ivaturi R (2013) Conceptual analysis of the non-linear forced response of aerodynamically unstable bladed-discs. In: Proceedings of the ASME Turbo Expo, June 3–7, San Antonio, TX, USA, pp 1–14

  27. Coudeyras N, Sinou JJ, Nacivet S (2009) A new treatment for predicting the self-excited vibrations of nonlinear systems with frictional interfaces: the constrained harmonic balance method, with application to disc brake squeal. J Sound Vib 319(3–5):1175–1199

    Article  Google Scholar 

  28. Craig RR (2000) Coupling of substructures for dynamic analysis: an overview. In: Collection of technical papers—AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics and materials conference, April 3–6, Atlanta, GA, USA, pp 1–12

  29. Dahl PR (1976) Solid friction damping of mechanical vibrations. AIAA J 14:1675–1682

    Article  Google Scholar 

  30. Didier J, Sinou JJ, Faverjon B (2013) Nonlinear vibrations of a mechanical system with non-regular nonlinearities and uncertainties. Commun Nonlinear Sci Numer Simul 18(11):3250–3270

    Article  MathSciNet  MATH  Google Scholar 

  31. Donders S, Hadjit R, Hermans L, Brughmans M, Desmet W (2006) A wave-based substructuring approach for fast modification predictions and industrial vehicle optimization. In: Proceedings of the ISMA2006

  32. Dowell EH, Hall KC (2001) Modeling of fluid-structure interaction. Annu Rev Fluid Mech 33:445–490

    Article  MATH  Google Scholar 

  33. de Klerk D, Rixen DJ, Voormeeren SN (2008) General framework for dynamic substructuring: history, review and classification of techniques. AIAA J 46(5):1169–1181

    Article  Google Scholar 

  34. de Wit CC, Olsson H, Astrom KJ, Lischinsky P (1995) New model for control of systems with friction. IEEE Trans Autom Control 40(3):419–425

    Article  MathSciNet  MATH  Google Scholar 

  35. Earles SW, Williams EJ (1972) A linearized analysis for frictionally damped systems. J Sound Vib 24(4):445–458

    Article  Google Scholar 

  36. Ewins DJ (1995) Modal testing: theory and practice. Research Studies Press Ltd., Taunton

    Google Scholar 

  37. Feeny B, Moon FC (1994) Chaos in a forced dry-friction oscillator: experiments and numerical modelling. J Sound Vib 170(3):303–323

    Article  MATH  Google Scholar 

  38. Ferri AA, Dowell EH (1988) Frequency domain solutions to multi-degree-of-freedom, dry friction damped systems. J Sound Vib 124(2):207–224

    Article  MathSciNet  MATH  Google Scholar 

  39. Filsinger D, Szwedowicz J, Schäfer O (2002) Approach to unidirectional coupled CFD-FEM analysis of axial turbocharger turbine blades. J Turbomach 124(1):125–131

    Article  Google Scholar 

  40. Firrone CM, Zucca S (2009) Underplatform dampers for turbine blades: the effect of damper static balance on the blade dynamics. Mech Res Commun 36(4):515–522

    Article  MATH  Google Scholar 

  41. Firrone CM, Zucca S (2011) Modelling friction contacts in structural dynamics and its application to turbine bladed disks. In: Awrejcewicz J (Ed) Numerical Analysis - Theory and Application, chap 14. Intech, pp 301–334. http://www.intechopen.com/books/numerical-analysis-theory-and-application/modellingfriction-contacts-in-structural-dynamics-and-its-application-to-turbine-bladed-disks

  42. Firrone CM, Zucca S, Gola MM (2011) The effect of underplatform dampers on the forced response of bladed disks by a coupled static/dynamic harmonic balance method. Int J Non-Linear Mech 46(2):363–375

    Article  Google Scholar 

  43. Gasch R, Knothe K (1987) Strukturdynamik. Band 1: Diskrete Systeme, Strukturdynamik, vol 1. Springer, Berlin

    Book  MATH  Google Scholar 

  44. Gasch R, Knothe K (1989) Strukturdynamik. Band 2: Kontinua und ihre Diskretisierung, Strukturdynamik, vol 2. Springer, Berlin

    Book  MATH  Google Scholar 

  45. Georgiades F, Peeters M, Kerschen G, Golinval JC, Ruzzene M (2008) Nonlinear modal analysis and energy localization in a bladed disk assembly. In: Proceedings of the ASME Turbo Expo, June 9–13, Berlin, Germany, pp 1–8

  46. Géradin M, Rixen DJ (2014) Mechanical vibrations: theory and application to structural dynamics. Wiley, New York

    Google Scholar 

  47. Glocker C (2001) Set-valued force laws: dynamics of non-smooth systems. Springer, Berlin

    Book  MATH  Google Scholar 

  48. Green JS, Fransson TH (2006) Scaling of turbine blade unsteady pressures for rapid forced response assessment. Paper GT2006-90613, Proceedings of the GT2006, ASME Turbo Expo 2006: power for land, sea and air, May 8–11, Barcelona, Spain

  49. Greenwood JA, Williamson JBP (1966) Contact of nominally flat surfaces. Proc R Soc Proc A 295(1442):300–319

    Article  Google Scholar 

  50. Grolet A, Thouverez F (2011) Vibration analysis of a nonlinear system with cyclic symmetry. J Eng Gas Turbines Power 133(2):022,502–022,509

    Article  Google Scholar 

  51. Grolet A, Thouverez F (2012) Free and forced vibration analysis of a nonlinear system with cyclic symmetry: application to a simplified model. J Sound Vib 331(12):2911–2928

    Article  Google Scholar 

  52. Grolet A, Thouverez F (2012) On a new harmonic selection technique for harmonic balance method. Mech Syst Signal Process 30:43–60

    Article  Google Scholar 

  53. Grolet A, Thouverez F (2015) Computing multiple periodic solutions of nonlinear vibration problems using the harmonic balance method and Groebner bases. Mech Syst Signal Process 52–53:529–547

    Article  Google Scholar 

  54. Groll Gv, Ewins DJ (2001) The harmonic balance method with arc-length continuation in rotor/stator contact problems. J Sound Vib 241(2):223–233

    Article  Google Scholar 

  55. Gruin M, Thouverez F, Blanc L, Jean P (2011) Nonlinear dynamics of a bladed dual-shaft. Eur J Comput Mech 20(1–4):207–225

    Google Scholar 

  56. Gu W, Xu Z, Wang S (2010) Advanced modelling of frictional contact in three-dimensional motion when analysing the forced response of a shrouded blade. Proc Inst Mech Eng Part A J Power Energy 224(4):573–582

    Article  Google Scholar 

  57. Guskov M, Thouverez F (2012) Harmonic balance-based approach for quasi-periodic motions and stability analysis. J Vib Acoust 134(3):031,003/1–031,003/11

    Article  Google Scholar 

  58. He Z, Epureanu BI, Pierre C (2007) Fluid-structural coupling effects on the dynamics of mistuned bladed disks. AIAA J 45(3):552–561

    Article  Google Scholar 

  59. Hesthaven JS, Gottlieb S, Gottlieb D (2007) Spectral methods for time-dependent problems, vol 21. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  60. Hohl A, Neubauer M, Schwarzendahl SM, Panning L, Wallaschek J (2009) Active and semiactive vibration damping of turbine blades with piezoceramics. In: Proceedings of the SPIE, vol 7288. Active and Passive Smart Structures and Integrated Systems 2009, San Diego, CA, March 8–12. 72881H

  61. Iranzad M, Ahmadian H (2012) Identification of nonlinear bolted lap joint models. Comput Struct 96–97:1–8

    Article  Google Scholar 

  62. Ivancic F, Palazotto A (2005) Experimental considerations for determining the damping coefficients of hard coatings. J Aerosp Eng 18(1):8–17

    Article  Google Scholar 

  63. Jacquet-Richardet G, Torkhani M, Cartraud P, Thouverez F, Nouri Baranger T, Herran M, Gibert C, Baguet S, Almeida P, Peletan L (2013) Rotor to stator contacts in turbomachines. Review and application. Mech Syst Signal Process 40(2):401–420

    Article  Google Scholar 

  64. Jaumouillé V, Sinou JJ, Petitjean B (2010) An adaptive harmonic balance method for predicting the nonlinear dynamic responses of mechanical systems—application to bolted structures. J Sound Vib 329(19):4048–4067

    Article  Google Scholar 

  65. Ji BH, Zhang GH, Wang LT, Yuan Q, Meng QJ, Liu DY (1998) Experimental investigation of the dynamic characteristics of the damped blade. J Sound Vib 213(2):223–234

    Article  Google Scholar 

  66. Johnson KL (1989) Contact mechanics. Cambridge University Press, Cambridge

    Google Scholar 

  67. Kamakoti R, Shyy W (2004) Fluid-structure interaction for aeroelastic applications. Prog Aerosp Sci 40(8):535–558

    Article  MATH  Google Scholar 

  68. Karkar S, Cochelin B, Vergez C (2013) A high-order, purely frequency based harmonic balance formulation for continuation of periodic solutions: the case of non-polynomial nonlinearities. J Sound Vib 332(4):968–977

    Article  Google Scholar 

  69. Kenyon JA, Griffin JH (2003) Forced response of turbine engine bladed disks and sensitivity to harmonic mistuning. J Eng Gas Turbines Power 125(1):113–120

    Article  Google Scholar 

  70. Kenyon JA, Griffin JH, Feiner DM (2003) Maximum bladed disk forced response from distortion of a structural mode. J Turbomach 125(2):352–363

    Article  Google Scholar 

  71. Kerschen G, Peeters M, Golinval JC, Vakakis AF (2009) Nonlinear normal modes, part I: a useful framework for the structural dynamicist: special issue: non-linear structural dynamics. Mech Syst Signal Process 23(1):170–194

    Article  Google Scholar 

  72. Kersken H, Frey C, Voigt C, Ashcroft G (2012) Time-linearized and time-accurate 3D RANS methods for aeroelastic analysis in turbomachinery. J Turbomach 134(5):425–433

    Article  Google Scholar 

  73. Khenous HB, Laborde P, Renard Y (2008) Mass redistribution method for finite element contact problems in elastodynamics. Eur J Mech A/Solids 27(5):918–932

    Article  MathSciNet  MATH  Google Scholar 

  74. Kielb RE, Kaza KR (1983) Aeroelastic characteristics of a cascade of mistuned blades in subsonic and supersonic flows. J Vib Acoust Stress reliab Des 105:425–433

    Article  Google Scholar 

  75. Kim TC, Rook TE, Singh R (2003) Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity. J Sound Vib 263(3):665–678

    Article  MathSciNet  MATH  Google Scholar 

  76. Kim TC, Rook TE, Singh R (2005) Super- and sub-harmonic response calculations for a torsional system with clearance nonlinearity using the harmonicbalanc e method. J Sound Vib 281(3–5):965–993

    Article  Google Scholar 

  77. Kim YB, Noah ST, Choi YS (1991) Periodic response of multi-disk rotors with bearing clearances. J Sound Vib 144(3):381–395

    Article  Google Scholar 

  78. King ME, Vakakis AF (1995) A very complicated structure of resonances in a nonlinear system with cyclic symmetry: nonlinear forced localization. Nonlinear Dyn 7(1):85–104

    MathSciNet  Google Scholar 

  79. Knoll DA, Keyes DE (2004) Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J Comput Phys 193(2):357–397

    Article  MathSciNet  MATH  Google Scholar 

  80. Krack M (2015) Nonlinear modal analysis of nonconservative systems: extension of the periodic motion concept. Comput Struct 154:59–71

    Article  Google Scholar 

  81. Krack M, Bergman LA, Vakakis AF (2016) On the efficacy of friction damping in the presence of nonlinear modal interactions. J Sound Vib 370:209–220

    Article  Google Scholar 

  82. Krack M, Herzog A, Panning-von Scheidt L, Wallaschek J, Siewert C, Hartung A (2012) Multiharmonic analysis and design of shroud friction joints of bladed disks subject to microslip. In: Proceedings of the ASME international design engineering technical conferences& computers and information in engineering conference, August 12–15, Chicago, IL, USA, pp 1–10. doi:10.1115/DETC2012-70184

  83. Krack M, Panning-von Scheidt L, Wallaschek J (2013) A high-order harmonic balance method for systems with distinct states. J Sound Vib 332(21):5476–5488

    Article  Google Scholar 

  84. Krack M, Panning-von Scheidt L, Wallaschek J (2013) A method for nonlinear modal analysis and synthesis: application to harmonically forced and self-excited mechanical systems. J Sound Vib 332(25):6798–6814

    Article  Google Scholar 

  85. Krack M, Panning-von Scheidt L, Wallaschek J (2016) On the interaction of multiple traveling wave modes in the flutter vibrations of friction-damped tuned bladed disks. In: Proceedings of the ASME Turbo Expo, Seoul, South Korea, GT2016-56126, pp 1–11

  86. Krack M, Tatzko S, Panning-von Scheidt L, Wallaschek J (2014) Reliability optimization of friction-damped systems using nonlinear modes. J Sound Vib 333:2699–2712

    Article  Google Scholar 

  87. Kuether RJ, Renson L, Detroux T, Grappasonni C, Kerschen G, Allen MS (2015) Nonlinear normal modes, modal interactions and isolated resonance curves. doi:10.1016/j.jsv.2015.04.035

  88. Laborenz J, Krack M, Panning L, Wallaschek J, Denk M, Masserey P (2012) Eddy current damper for turbine blading: electromagnetic finite element analysis and measurement results. J Eng Gas Turbines Power 134(4):052505

    Article  Google Scholar 

  89. Laborenz J, Siewert C, Panning L, Wallaschek J, Gerber C, Masserey PA (2010) Eddy current damping: a concept study for steam turbine blading. J Eng Gas Turbines Power 132(5):052505-1–052505-7

  90. Laxalde D, Legrand M (2011) Nonlinear modal analysis of mechanical systems with frictionless contact interfaces. Comput Mech 47(4):469–478

    Article  MathSciNet  MATH  Google Scholar 

  91. Laxalde D, Pierre C (2011) Modelling and analysis of multi-stage systems of mistuned bladed disks. Comput Struct 89(3–4):316–324

    Article  Google Scholar 

  92. Laxalde D, Thouverez F (2007) Non-linear vibrations of multi-stage bladed disks systems with friction ring dampers. In: Proceedings of the ASME international design engineering technichal conferences and computers and information in engineering conference, September 4–7, Las Vegas, NE, USA, pp 3–10

  93. Laxalde D, Thouverez F (2009) Complex non-linear modal analysis for mechanical systems application to turbomachinery bladings with friction interfaces. J Sound Vib 322(4–5):1009–1025

    Article  Google Scholar 

  94. Laxalde D, Thouverez F, Lombard JP (2007) Dynamical analysis of multi-stage cyclic structures. Mech Res Commun 34(4):379–384

    Article  MATH  Google Scholar 

  95. Laxalde D, Thouverez F, Lombard JP (2007) Vibration control for integrally bladed disks using friction ring dampers. In: Proceedings of the ASME Turbo Expo, May 14–17, Montreal, Canada, pp 1–11

  96. Lazarus A, Thomas O (2010) A harmonic-based method for computing the stability of periodic solutions of dynamical systems. Comptes Rendus Mécanique 338(9):510–517

    Article  MATH  Google Scholar 

  97. Lechner C, Seume J (eds) (2003) Stationäre Gasturbinen, nachdr edn. VDI-Buch. Springer, Berlin

  98. Lim SH, Bladh R, Castanier MP, Pierre C (2003) A compact, generalized component mode mistuning representation for modeling bladed disk vibration. Paper AIAA 2003-1545, Proceedings of the 44th AIAA/ASME/ASCE/AHS structures, structural dynamics, and materials conference, 7–10 April, Norfolk, Virginia

  99. Lim SH, Castanier MP, Pierre C (2004) Intentional mistuning design space reduction based on vibration energy flow in bladed disks. Paper GT2004-53873, Proceedings of ASME Turbo Expo 2004, power for land, sea, and air, June 14–17, Vienna, Austria

  100. Ling FH (1991) Quasi-periodic solutions calculated with the simple shooting technique. J Sound Vib 144(2):293–304

    Article  Google Scholar 

  101. Lv F, Fu G, Cai Z, Zhang D (2009) Failure analysis of components in compressor vane. Eng Fail Anal 16(5):1703–1710

    Article  Google Scholar 

  102. Marshall JG, Imregun M (1996) A review of aeroelasticity methods with emphasis on turbomachinery applications. J Fluids Struct 10(3):237–267

    Article  Google Scholar 

  103. Martel C, Corral R (2013) Fluttter amplitude saturation by nonlinear friction forces: an asymptotic approach. In: Proceedings of the ASME Turbo Expo 2013, June 3–7, San Antonio, TX, USA, pp 1–9

  104. Martel C, Corral R, Ivaturi R (2014) Flutter amplitude saturation by nonlinear friction forces: reduced model verification. J Turbomach 137(4):041,004

    Article  Google Scholar 

  105. McMullen M, Jameson A, Alonso J (2006) Demonstration of nonlinear frequency domain methods. AIAA J 44(7):1428–1435

    Article  Google Scholar 

  106. Miyakozawa T, Kielb RE, Hall KC (2009) The effects of aerodynamic asymmetric perturbations on forced response of bladed disks. J Turbomach 131(4):1–8

    Article  Google Scholar 

  107. Moffatt S, He L (2005) On decoupled and fully-coupled methods for blade forced response prediction. J Fluids Struct 20(2):217–234

    Article  Google Scholar 

  108. Moreau JJ (1970) Sur les lois de frottement, de plasticité et de viscosité. Comptes Rendus de l’Académie des Sciences 271:608–611

    Google Scholar 

  109. Moreau JJ (1974) New variational techniques in mathematical physics. CISM course, vol 52. Springer, Berlin, p 53

  110. Moussi E, Bellizzi S, Cochelin B, Nistor I (2013) Nonlinear normal modes of a two degrees-of-freedom piecewise linear system. Mech Syst Signal Process 64–65:1–26

  111. Nacivet S, Pierre C, Thouverez F, Jezequel L (2003) A dynamic Lagrangian frequency–time method for the vibration of dry-friction-damped systems. J Sound Vib 265(1):201–219

    Article  MathSciNet  MATH  Google Scholar 

  112. Nayfeh AH, Mook DT (1979) Nonlinear oscillations. Wiley, New York

    MATH  Google Scholar 

  113. Nikolic M, Petrov EP, Ewins DJ (2007) Coriolis forces in forced response analysis of mistuned bladed disks. J Turbomach 129(4):730–739

    Article  Google Scholar 

  114. Olson BJ, Shaw SW, Shi C, Pierre C, Parker RG (2014) Circulant matrices and their application to vibration analysis. Appl Mech Rev 66(4):040803

    Article  Google Scholar 

  115. Padmanabhan C, Singh R (1995) Analysis of periodically excited non-linear systems by a parametric continuation technique. J Sound Vib 184(1):35–58

    Article  Google Scholar 

  116. Panning L (2005) Auslegung von Reibelementen zur Schwingungsdämpfung von Turbinenschaufeln. Dissertation, Universität Hannover, Hannover

  117. Panning L, Sextro W, Popp K (2003) Spatial dynamics of tuned and mistuned bladed disks with cylindrical and wedge-shaped friction dampers. Int J Rotat Mach 9(3):219–228

    Article  MATH  Google Scholar 

  118. Panunzio AM, Schwingshackl C, Salles L, Gola M (2015) Asymptotic numerical method and polynomial chaos expansion for the study of stochastic non-linear normal modes. In: ASME (ed) Proceedings of the Turbo Expo

  119. Peletan L, Baguet S, Torkhani M, Jacquet-Richardet G (2013) A comparison of stability computational methods for periodic solution of nonlinear problems with application to rotordynamics. Nonlinear Dyn 72(3):671–682

    Article  MathSciNet  Google Scholar 

  120. Peradotto E, Salles L, Panunzio AM, Schwingshackl C (2015) Stochastic methods for nonlinear rotordynamics with uncertainties. In: ASME (ed) Proceedings of the Turbo Expo

  121. Petrov EP (2006) Direct parametric analysis of resonance regimes for nonlinear vibrations of bladed discs. J Turbomach 129(3):495–502

    Article  Google Scholar 

  122. Petrov EP (2009) Analysis of sensitivity and robustness of forced response for nonlinear dynamic structures. Mech Syst Signal Process 23(1):68–86

    Article  Google Scholar 

  123. Petrov EP (2010) A high-accuracy model reduction for analysis of nonlinear vibrations in structures with contact interfaces. J Eng Gas Turbines Power 133(10):102,503/1–102,503/10

    Google Scholar 

  124. Petrov EP (2012) Analysis of flutter-induced limit cycle oscillations in gas-turbine structures with friction, gap, and other nonlinear contact interfaces. J Turbomach 134(6):061,018/1–061,018/13

    Article  Google Scholar 

  125. Petrov EP, Ewins DJ (2003) Analytical formulation of friction interface elements for analysis of nonlinear multi-harmonic vibrations of bladed disks. J Turbomach 125(2):364–371

    Article  Google Scholar 

  126. Petrov EP, Ewins DJ (2004) Generic friction models for time-domain vibration analysis of bladed disks. J Turbomach 126(1):184–192

    Article  Google Scholar 

  127. Petrov EP, Ewins DJ (2004) State-of-the-art dynamic analysis for non-linear gas turbine structures. Proc Inst Mech Eng Part G J Aerosp Eng 218(3):199–211

    Article  Google Scholar 

  128. Petrov EP, Ewins DJ (2005) Method for analysis of nonlinear multiharmonic vibrations of mistuned bladed disks with scatter of contact interface characteristics. J Turbomach 127(1):128–136

    Article  Google Scholar 

  129. Pfaffrath M, Wever U (2012) Stochastic integration methods: comparison and application to reliability analysis. Paper GT2012-68973, Proceedings of the ASME Turbo Expo 2012, June 11–15, 2012, Copenhagen, Denmark

  130. Pfeiffer F, Hajek M (1992) Stick-slip motion of turbine blade dampers. Philos Trans R Soc A Math Phys Eng Sci 338(1651):503–517

    Article  Google Scholar 

  131. Phadke R, Berger EJ (2008) Friction damping analysis in turbine blades using a user-programmed function in Ansys. Paper ISROMAC12-2008-20176, Proceedings of the 12th international symposium on transport phenomena and dynamics of rotating machinery, Honolulu Hawaii, February 17–22

  132. Poudou O, Pierre C, Reisser B (2004) A new hybrid frequency–time domain method for the forced vibration of elastic structures with friction and intermittent contact. In: Proceedings of the 10th international symposium on transport phenomena and dynamics of rotating machinery, March 7–11, Honolulu, HI, USA, pp 1–14

  133. Poudou OJ (2007) Modeling and analysis of the dynamics of dry-friction-damped structural systems. Dissertation, The University of Michigan, Michigan

  134. Press WH (1992) Numerical recipes in FORTRAN: the art of scientific computing, 2nd edn. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  135. Ribeiro P, Petyt M (2000) Non-linear free vibration of isotropic plates with internal resonance. Int J Non-Linear Mech 35(2):263–278

    Article  MATH  Google Scholar 

  136. Rizvi A, Smith CW, Rajasekaran R, Evans KE (2016) Dynamics of dry friction damping in gas turbines: literature survey. J Vib Control 22(1):296–305

    Article  Google Scholar 

  137. Rosenberg RM (1960) Normal modes of nonlinear dual-mode systems. J Appl Mech 27:263–268

    Article  MathSciNet  MATH  Google Scholar 

  138. Salles L, Blanc L, Thouverez F, Gouskov AM (2008) Dynamic analysis of fretting-wear in friction contact interfaces. Paper GT2008-51112, Proceedings of the GT2008, ASME Turbo Expo 2008: power for land, sea and air, June 9–13, Berlin, Germany

  139. Salles L, Blanc L, Thouverez F, Gouskov AM, Jean P (2011) Dual time stepping algorithms with the high order harmonic balance method for contact interfaces with fretting-wear. Paper GT2011-46488, Proceedings of the GT2011, ASME Turbo Expo 2011: advancing clean and efficient turbine technology, June 7–10, Vancouver, Canada

  140. Salles L, Schwingshackl C, Green J (2013) Modelling friction contacts in nonlinear vibration of bladed disks. In: Proceedings of the world tribology congress, September 8–13, Torino, Italy, pp 1–1

  141. Sanliturk KY, Ewins DJ (1996) Modelling two-dimensional friction contact and its application using harmonic balance method. J Sound Vib 193(2):511–523

    Article  MATH  Google Scholar 

  142. Sarrouy E, Grolet A, Thouverez F (2011) Global and bifurcation analysis of a structure with cyclic symmetry. Int J Non-Linear Mech 46(5):727–737

    Article  Google Scholar 

  143. Schilder F, Vogt W, Schreiber S, Osinga HM (2006) Fourier methods for quasi-periodic oscillations. Int J Numer Methods Eng 67(5):629–671

    Article  MathSciNet  MATH  Google Scholar 

  144. Schurzig D (2016) Development of a numerically efficient model for the dynamics of revolute clearance joints in adjustable stator cascades. Dissertation. University of Hannover, Germany

    Google Scholar 

  145. Segalman DJ (2005) A four-parameter Iwan model for lap-type joints. J Appl Mech 72(5):752–760

    Article  MATH  Google Scholar 

  146. Segalman DJ (2007) Model reduction of systems with localized nonlinearities. J Comput Nonlinear Dyn 2(3):249–266

    Article  Google Scholar 

  147. Sextro W (2000) The calculation of the forced response of shrouded blades with friction contacts and its experimental verification. In: Proceedings of the ASME Turbo Expo, May 8–11, Munich, Germany, pp 1–8

  148. Sextro W, Popp K, Krzyzynski T (2001) Localization in nonlinear mistuned systems with cyclic symmetry. Nonlinear Dyn 25(4):207–220

    Article  MATH  Google Scholar 

  149. Seydel R (1994) Practical bifurcation and atability analysis: from equilibrium to chaos. Springer, New York

    MATH  Google Scholar 

  150. Shapiro B (1999) Passive control of flutter and forced response in bladed disks via mistuning. Dissertation, California Institute of Technology, Pasadena

  151. Siewert C, Panning L, Wallaschek J, Richter C (2010) Multiharmonic forced response analysis of a turbine blading coupled by nonlinear contact forces. J Eng Gas Turbines Power 132(8):082501/1–082501/9

    Article  Google Scholar 

  152. Slater JC, Minkiewicz GR, Blair AJ (1998) Forced response of bladed disk assemblies—A survey. PAPER 98-3743

  153. Srinivasan AV (1997) Flutter and resonant vibration characteristics of engine blades. J Eng Gas Turbines Power 119(4):742–775

    Article  Google Scholar 

  154. Sternchuss A, Balmes E (eds) (2006) On the reduction of quasi-cyclic disk models with variable rotation speeds, vol 7

  155. Stromberg N (1997) Augmented Lagrangian method for fretting problems. Eur J Mech A/Solids 16(4):573–593

    MathSciNet  MATH  Google Scholar 

  156. Strömberg N (1999) Finite element treatment of two-dimensional thermoelastic wear problems. Comput Methods Appl Mech Eng 177(3–4):441–455

    Article  MathSciNet  MATH  Google Scholar 

  157. Strömberg N, Johansson L, Klarbring A (1996) Derivation and analysis of a generalized standard model for contact, friction and wear. Int J Solids Struct 33(13):1817–1836

    Article  MathSciNet  MATH  Google Scholar 

  158. Sundararajan P, Noah ST (1997) Dynamics of forced nonlinear systems using shooting/arc-length continuation method-application to rotor systems. J Vib Acoust 119(1):9–20

    Article  Google Scholar 

  159. Sundararajan P, Noah ST (1998) An algorithm for response and stability of large order non-linear systems-application to rotor systems. J Sound Vib 214(4):695–723

    Article  Google Scholar 

  160. Szwedowicz J, Kissel M, Ravindra B, Kellerer R (2001) Estimation of contact stiffness and its role in the design of a friction damper. In: Proceedings of the ASME Turbo Expo, June 4–7, New Orleans, LA, USA, pp 1–8

  161. Thompson JMT, Stewart HB (2002) Nonlinear dynamics and chaos. Wiley, New York

    MATH  Google Scholar 

  162. Tran DM (2001) Component mode synthesis methods using interface modes. Application to structures with cyclic symmetry. Comput Struct 79(2):209–222

    Article  Google Scholar 

  163. Urabe M (1965) Galerkin’s procedure for nonlinear periodic systems. Arch Ration Mech Anal 20(2):120–152

    Article  MathSciNet  MATH  Google Scholar 

  164. Vahdati M, Breard C, Simpson G, Imregun M (2008) Forced response assessment using modal force based indicator functions. Paper GT2008-50306, Proceedings of the ASME Turbo Expo 2008: power for land, sea and air, GT2008, June 9–13, Berlin, Germany

  165. Vahdati M, Salles L (2015) The effects of mistuning on Fan flutter. In: ISUAAAT 2015. http://hdl.handle.net/10044/1/27294

  166. Vahdati M, Sayma AI, Marshall JG, Imregun M (2001) Mechanisms and prediction methods for fan blade stall flutter. J Propuls Power 17(5):1100–1108

    Article  Google Scholar 

  167. Vakakis A, Manevitch L, Mikhlin Y, Pilipchuk V, Zevin A (2008) Normal modes and localization in nonlinear systems. Wiley, New York

    MATH  Google Scholar 

  168. Vakakis AF, Nayfeh T, King M (1993) A multiple-scales analysis of nonlinear, localized modes in a cyclic periodic system. J Appl Mech 60(2):388–397

    Article  MathSciNet  MATH  Google Scholar 

  169. Visintin A (1994) Differential models of hysteresis. Springer, Berlin

    Book  MATH  Google Scholar 

  170. Wen YK (1976) Method for random vibration of hysteretic systems. J Eng Mech Div 102(2):249–263

    Google Scholar 

  171. Whiteman WE, Ferri AA (1997) Multi-mode analysis of beam-like structures subjected to displacement-dependent dry friction damping. J Sound Vib 207(3):403–418

    Article  Google Scholar 

  172. Wildheim SJ (1981) Excitation of rotating circumferentially periodic structures. J Sound Vib 75(3):397–416

    Article  MATH  Google Scholar 

  173. Willner K (2003) Kontinuums-und Kontaktmechanik: Synthetische und Analytische Darstellung. Springer, Berlin

    Book  Google Scholar 

  174. Wriggers P (2006) Computational contact mechanics. Springer, Berlin

    Book  MATH  Google Scholar 

  175. Yang BD, Menq CH (1998) Characterization of 3D contact kinematics and prediction of resonant response of structures having 3D frictional constraint. J Sound Vib 217(5):909–925

    Article  Google Scholar 

  176. Yastrebov VA, Anciaux G, Molinari JFc (2015) From infinitesimal to full contact between rough surfaces: evolution of the contact area. Int J Solids Struct 52:83–102

    Article  Google Scholar 

  177. Yen HY, Shen MHH (2001) Passive vibration suppression of beams and blades using magnetomechanical coating. J Sound Vib 245(4):701–714

    Article  Google Scholar 

  178. Zhou B, Thouverez F, Lenoir D (2014) Essentially nonlinear piezoelectric shunt circuits applied to mistuned bladed disks. J Sound Vib 333(9):2520–2542

    Article  Google Scholar 

  179. Zucca S, Epureanu BI (2014) Bi-linear reduced-order models of structures with friction intermittent contacts. Nonlinear Dyn 77(3):1055–1067

    Article  Google Scholar 

  180. Zucca S, Firrone CM, Gola MM (2013) Modeling underplatform dampers for turbine blades: a refined approach in the frequency domain. J Vib Control 19(7):1087–1102

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Aircraft Propulsion Systems, University of Stuttgart, Pfaffenwaldring 6, 70569, Stuttgart, Germany

    Malte Krack

  2. Department of Mechanical Engineering, Vibration University Technology Centre, Imperial College London, Exhibition Road, London, SW7 2AZ, UK

    Loic Salles

  3. Laboratoire de Tribologie et Dynamique des Systmes, École Centrale de Lyon, 36 Avenue Guy de Collongue, 69134, Ecully Cedex, France

    Fabrice Thouverez

Authors
  1. Malte Krack
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Loic Salles
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fabrice Thouverez
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Malte Krack.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Appendices

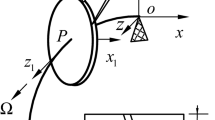
Appendix 1: The Traveling Wave Coordinate System

In this appendix, we define the traveling wave coordinate system and illustrate the notion of traveling waves. The traveling wave coordinates are related to the physical coordinates by the (inverse) discrete Fourier transform. The transformation can be applied to any physical quantity (displacement, force, etc.). For the displacement, this transform reads

$${}_{\,\mathrm{tw}}{\varvec{u}}_j(t)= \frac{1}{\sqrt{n_{{\mathrm{s}}}}}\sum \limits _{n=0}^{n_{{\mathrm{s}}}-1}{\mathrm{e}}^{-{\mathrm{i}}\frac{2\pi j n}{n_{{\mathrm{s}}}}}\,{}^{\,(n)}_{{\mathrm{fe}}}{\varvec{u}}(t),\quad j\in \left[ 0,n_{{\mathrm{s}}}-1\right] ,$$
(39)
$${}^{\,(n)}_{{\mathrm{fe}}}{\varvec{u}}(t)= \frac{1}{\sqrt{n_{{\mathrm{s}}}}}\sum \limits _{j=0}^{n_{{\mathrm{s}}}-1}{\mathrm{e}}^{{\mathrm{i}}\frac{2\pi j n}{n_{{\mathrm{s}}}}}{}_{\,\mathrm{tw}}{\varvec{u}}_j(t),\quad n\in \left[ 0,n_{{\mathrm{s}}}-1\right] ,$$
(40)
$$\begin{aligned} {}_{\,\mathrm{tw}}{\varvec{u}}(t) &= \left( {\varvec{W}}_{n_{{\mathrm{s}}}}^{\mathrm{H}}\otimes {\varvec{I}}_{n_{{\mathrm{fe,s}}}}\right) {}_{\,\mathrm{fe}}{\varvec{u}}(t)\,\, \Leftrightarrow \nonumber \\ {}_{\,\mathrm{fe}}{\varvec{u}}(t) &= \left( {\varvec{W}}_{n_{{\mathrm{s}}}}\otimes {\varvec{I}}_{n_{{\mathrm{fe,s}}}}\right) {}_{\,\mathrm{tw}}{\varvec{u}}(t). \end{aligned}$$
(41)

Herein, \({}_{\,\mathrm{tw}}{\varvec{u}}_j\) denotes the displacement vector associated with the (spatial) wave numberFootnote 24 j, and \({}^{\mathrm{H}}\) denotes the Hermitian transpose. A congruent discretization and ordering is here assumed for each sector, such that the physical displacement vector \({}^{\,(n)}_{{\mathrm{fe}}}{\varvec{u}}\) comprises the same number of degrees of freedom, \(n_{{\mathrm{fe}},n}=n_{{\mathrm{fe,s}}}\) for each sector \(n\in \left[ 0,n_{{\mathrm{s}}}-1\right]\). The vector \({}_{\,\mathrm{tw}}{\varvec{u}}_j\) has the same number of coordinates as the physical displacement vector \({}^{\,(n)}_{{\mathrm{fe}}}{\varvec{u}}\). The more compact notation in Eq. (41) involves the Fourier matrix \({\varvec{W}}_{n_{{\mathrm{s}}}}\), defined in Eq. (47).

Remark

At this point, it is important to note that both \({}_{\,\mathrm{fe}}{\varvec{u}}(t)\) and \({}_{\,\mathrm{tw}}{\varvec{u}}(t)\) are complex-valued quantities in general. The complex arithmetic is very convenient for the mathematical derivations. Of course, eventually we are interested only in the physical part, that is, the real component.

Fig. 17
figure 17

Illustration of the spatiotemporal nature of a traveling wave: a \(q\) as a function of the sector number and the temporal phase similar to [114], b temporal phase as a bijective function of time

Full size image

To illustrate the traveling wave character of the coordinate system, regard the k-th wave component, \({}_{\,\mathrm{tw}}{\varvec{q}}_k\), of a physical quantity \({\varvec{q}}\) (displacement, force, etc.), and consider the case of an oscillation with

$${}_{\,\mathrm{tw}}{\varvec{q}}_k(t) = {\sqrt{n_{{\mathrm{s}}}}}{\varvec{Q}}{\mathrm{e}}^{{\mathrm{i}}\phi (t)}.$$
(42)

Herein, \({\varvec{Q}}\in {\mathbb {C}}^{n_{{\mathrm{fe,s}}}}\) is a complex-valued amplitude vector and \(\phi (t)\) is the phase, which is assumed to be strictly monotonous in time with \(\dot{\phi }(t)>0\) in the considered time span, see Fig. 17b. As a consequence, the relation between phase and time is bijective. All other wave components are assumed to be zero, \({}_{\,\mathrm{tw}}{\varvec{q}}_j={\mathbf{0}}\quad\forall j\in \left[ 0,n_{{\mathrm{s}}}-1\right] \backslash k\). Taking into account the transform defined in Eqs. (39)–(41), the response of sector n reads

$$\begin{aligned} {}^{(n)}{\varvec{q}}\left( \phi \left( t\right) \right) &= \frac{1}{{\sqrt{n_{{\mathrm{s}}}}}}{\mathrm{e}}^{{\mathrm{i}}\frac{2\pi kn}{n_{{\mathrm{s}}}}}{}_{\,\mathrm{tw}}{\varvec{q}}_k\left( \phi \left( t\right) \right) \nonumber \\ &={ \varvec{Q}}{\mathrm{e}}^{{\mathrm{i}}\left( \phi (t)+\frac{2\pi kn}{n_{{\mathrm{s}}}}\right) }={}^{(0)}q\left( \phi (t)+n\theta _k\right) .\end{aligned}$$
(43)

Herein, the abbreviation \(\theta _k\) is used, with

$$\theta _k=\frac{2\pi }{n_{{\mathrm{s}}}}k.$$
(44)

\(\theta _k\) is the phase lag between neighboring sectors and is hence often referred to as inter-blade phase angle (IBPA). Since the relation between phase and time is assumed as bijective, Eq. (43) defines a unique time lag \(\varDelta t\) with \({}^{(n)}{\varvec{q}}(t)={}^{(0)}q(t+\varDelta t)\). Moreover, \({\varvec{q}}(t)\) is spatially periodic; i.e.,\({}^{(n+n_{{\mathrm{s}}})}{\varvec{q}}(t) = {}^{(n)}{\varvec{q}}(t)\), which can be easily verified from Eq. (43). Hence, the spatiotemporal form of the quantity \({\varvec{q}}(t)\) can be identified as a traveling wave, discrete in space and continuous in time, as illustrated in Fig. 17a. Since \(\dot{\phi }\) is allowed to be time-dependent, the time lag \(\varDelta t\) generally varies with time t and sector number n. This means that the wave does not have to propagate with constant speed. However, the case of constant wave speed is of particular practical relevance, which coincides with a harmonic oscillation of constant angular frequency \(\varOmega , \dot{\phi }(t)=\varOmega\). In this case, the constant wave speed is \(\varOmega /k\) (in \({\hbox {rad}}\,\hbox {s}^{-1}\)).

Table 3 Correspondence between wave number k, IBPA \(\theta _k\), nature of the apparent wave form and the short name (FTW: forward traveling wave, BTW: backward traveling wave, SW: standing wave, ND: nodal diameter)
Full size table

It should be noted that Eq. (43) defines a strict backward traveling wave. However, the traveling wave nature is seen to alias relative to \(n_{{\mathrm{s}}}\), depending on the wave number k. The ranges of k and \(\theta _k\) that correspond to apparent forward and backward traveling waves (FTW and BTW, respectively), and the special cases of standing waves (SW), are given in Table 3. Herein, \(s^-_{n_{{\mathrm{s}}}}\) and \(s^+_{n_{{\mathrm{s}}}}\) depend on \(n_{{\mathrm{s}}}\), with

$$s^-_{n_{{\mathrm{s}}}}= {\left\{ \begin{array}{ll} \frac{n_{{\mathrm{s}}}}{2}-1 &{} n_{{\mathrm{s}}}\,\,{\mathrm{even}}\\ \frac{n_{{\mathrm{s}}}-1}{2} &{} n_{{\mathrm{s}}}\,\,{\mathrm{odd}} \end{array}\right. }$$
(45)
$$s^+_{n_{{\mathrm{s}}}}= {\left\{ \begin{array}{ll} \frac{n_{{\mathrm{s}}}}{2}+1 &{} n_{{\mathrm{s}}}\,\,{\mathrm{even}}\\ \frac{n_{{\mathrm{s}}}+1}{2} &{} n_{{\mathrm{s}}}\,\,{\mathrm{odd}} \end{array}\right. }$$
(46)

In this sense, the columns of the Fourier matrix \({\varvec{W}}_{n_{{\mathrm{s}}}}\) in Eq. (41) can be interpreted as discrete unit traveling waves, such that \({}_{\,\mathrm{tw}}{\varvec{u}}_k\) corresponds to a wave form with wave number k and IBPA \(\theta _k\).

Remark

It should be emphasized that wave numbers and nodal diameter numbers are only illustrative expressions for strictly mathematical concepts. The physical number of waves or nodal diameters can deviate from the mathematical one. Consider the example of a rotationally symmetric disk. We can divide the disk into a finite number of \(n_{{\mathrm{s}}}\) sectors. The highest possible wave number is then bounded by \(n_{{\mathrm{s}}}-1\) in accordance with our definition. But, of course, the disk can carry an infinite number of waves. The higher wave forms are generally not lost by the dissection into a finite number of sectors, but represent higher modes of vibration for a specific mathematical wave number.

In the above considerations, the complex-valued amplitude vector \({\varvec{Q}}\) is assumed to be constant in time. If \({\varvec{Q}}(t)\) depends on time, the strict relation \({}^{(n)}{\varvec{q}}(t)={}^{(0)}q(t+\varDelta t)\) between time and sector number is no longer satisfied. However, it still holds that \({}^{(n)}{\varvec{q}}(t) = {}^{(0)}q(t){\mathrm{e}}^{{\mathrm{i}}n\theta _k}\); that is, there is a constant phase lag between the individual sectors for a given k. The corresponding motion for time-dependent \({\varvec{Q}}(t)\) can thus be interpreted as a pseudo-traveling wave. This notion can be useful to describe vibration phenomena during run-up or run-down of a rotating machine. In this case, the oscillation frequency and the amplitudes vary with time, but excitation and vibration response might still exhibit a characteristic traveling wave form. For instance, in the case of constant acceleration, the phase \(\phi\) would be defined as \({\ddot{\phi }}(t)=\alpha\).

The discrete Fourier matrix \({\varvec{W}}_{n_{{\mathrm{s}}}}\) for a number of \(n_{{\mathrm{s}}}\) sectors (or samples in general) is defined as,

$${\varvec{W}}_{n_{{\mathrm{s}}}}= \left[ W_{ab}\right] = \left[ {\begin{array}{ccc} {\varvec{w}}_{1}&{} \cdots &{} {\varvec{w}}_{n_{{\mathrm{s}}}}\\ \end{array}}\right] ,\,\,\text {with}\, W_{ab} = w_{n_{{\mathrm{s}}}}^{\left( a-1\right) \left( b-1\right) }.$$
(47)

where \(w_{n_{{\mathrm{s}}}} = {\mathrm{e}}^{{\mathrm{i}}\frac{2\pi }{n_{{\mathrm{s}}}}}\) is the \(n_{{\mathrm{s}}}\)-th root of unity.

Appendix 2: Traveling Wave Structural Matrices

In this appendix, we describe how the structural matrices in traveling wave coordinates \({}_{\,\mathrm{tw}}{\varvec{K}}_k, {}_{\,\mathrm{tw}}{\varvec{D}}_k\) and \({}_{\,\mathrm{tw}}{\varvec{M}}_k\) can be obtained from the structural matrices of a reference sector. Suppose that a finite element model of the reference sector is given. The sector spans an angular region of \(2\pi /n_{{\mathrm{s}}}\), and can be divided into an inner volume, and left and right boundary.Footnote 25 Typically, the finite element model spans the whole sector, including left and right boundaries, making the description of the reference sector somewhat redundant. The sector’s displacement vector in physical coordinates can be permuted and partitioned as \(\left[ {\begin{array}{ccc} {\varvec{u}}_{{\mathrm{l}}}^{\mathrm{T}}&{} {\varvec{u}}_{{\mathrm{i}}}&{} {\varvec{u}}_{{\mathrm{r}}}^{\mathrm{T}}\\ \end{array}}\right] ^{\mathrm{T}}\), where \({\varvec{u}}_{{\mathrm{l}}}\) and \({\varvec{u}}_{{\mathrm{r}}}\) are degrees of freedom associated with left and right boundaries and \({\varvec{u}}_{{\mathrm{i}}}\) are the inner degrees of freedom. \({\varvec{u}}_{{\mathrm{l}}}\) and \({\varvec{u}}_{{\mathrm{r}}}\) shall have the dimension \(n_{{\mathrm{b}}}\) and \({\varvec{u}}_{{\mathrm{i}}}\) shall have the dimension \(n_{{\mathrm{i}}}\). Because of the redundancy, the total number of degrees of freedom of the sector (without constraints on left and right boundaries) is \(2n_{{\mathrm{b}}}+n_{{\mathrm{i}}}\) and exceeds the number \(n_{{\mathrm{fe,s}}}=n_{{\mathrm{fe}}}/n_{{\mathrm{s}}}\) of degrees of freedom per sector (of the full model) by the number of degrees of freedom of one boundary, \(n_{{\mathrm{b}}}\). The accordingly ordered structural matrices (in physical coordinates) without any constraints on left and right boundaries are denoted \({}_{\,\mathrm{fe}}^{(0)}{\varvec{K}}, {}_{\,\mathrm{fe}}^{(0)}{\varvec{D}}\) and \({}_{\,\mathrm{fe}}^{(0)}{\varvec{M}}\), and they take the form

$${\varvec{A}}= \left[ {\begin{array}{ccc} {\varvec{A}}_{{\mathrm{ll}}}&{} {\varvec{A}}_{{\mathrm{li}}}&{} {\mathbf{0}}\\ {\varvec{A}}_{{\mathrm{li}}}^{\mathrm{T}}&{} {\varvec{A}}_{{\mathrm{ii}}}&{}{\varvec{A}}_{{\mathrm{ri}}}^{\mathrm{T}}\\ {\mathbf{0}} &{} {\varvec{A}}_{{\mathrm{ri}}}&{} {\varvec{A}}_{{\mathrm{rr}}}\\ \end{array}}\right] ,\,\quad{\varvec{A}}\in \lbrace {}_{\,\mathrm{fe}}^{(0)}{\varvec{K}}, {}_{\,\mathrm{fe}}^{(0)}{\varvec{D}}, {}_{\,\mathrm{fe}}^{(0)}{\varvec{M}}\rbrace ,$$
(48)

where \({\varvec{A}}_{{\mathrm{ll}}}, {\varvec{A}}_{{\mathrm{rr}}}\) and \({\varvec{A}}_{{\mathrm{ii}}}\) account for the coupling within each boundary and inner volume, and the matrices \({\varvec{A}}_{{\mathrm{li}}}\) and \({\varvec{A}}_{{\mathrm{ri}}}\) account for the coupling between boundaries and inner volume. It is here assumed that left and right boundaries are disjunct, so that no coupling exists between them.

The matrices \({}_{\,\mathrm{tw}}{\varvec{A}}_k\) for each IBPA \(\theta _k\) can be obtained as [5],

$${}_{\,\mathrm{tw}}{\varvec{A}}_k= {\varvec{P}}_{k}^{\mathrm{H}}{}_{\,\mathrm{fe}}^{(0)}{\varvec{A}}{\varvec{P}}_{k},\,\quad{\varvec{A}}\in \lbrace {\varvec{K}}, {\varvec{D}}, {\varvec{M}}\rbrace ,$$
(49)

with the matrix \({\varvec{P}}_{k}\)

$${\varvec{P}}_{k}= \left[ {\begin{array}{cc} {\varvec{I}}_{n_{{\mathrm{b}}}} {\mathrm{e}}^{{\mathrm{i}}\theta _k} &{} {\mathbf{0}}\\ {\mathbf{0}} &{} {\varvec{I}}_{n_{{\mathrm{i}}}}\\ {\varvec{I}}_{n_{{\mathrm{b}}}} &{} {\mathbf{0}}\\ \end{array}}\right] .$$
(50)

The resulting matrices \({}_{\,\mathrm{tw}}{\varvec{A}}_k\) then have the proper size \(n_{{\mathrm{fe,s}}}\times n_{{\mathrm{fe,s}}}\).

It is assumed in the above formulations that left and right boundary have matching nodes and the local coordinate systems are conform after rotation by the sector angle. If this is not the case, Eq. (50) has to be adjusted by accounting for the coupling of non-conforming meshes and coordinate transformation. Note that the formal relation \({}_{\,\mathrm{tw}}{\overline{{\varvec{A}}}}_k= \left( {\varvec{W}}_{n_{{\mathrm{s}}}}^{\mathrm{H}}\otimes {\varvec{I}}_{n_{{\mathrm{fe,s}}}}\right) {\overline{\varvec{A}}}\left( {\varvec{W}}_{n_{{\mathrm{s}}}}\otimes {\varvec{I}}_{n_{{\mathrm{fe,s}}}}\right)\) could also be utilized to obtain these matrices. However, the method described in this appendix is much more efficient, since it involves only a single sector.

Appendix 3: Transformation to Relative Coordinates at the Contact Interface

In this appendix, we describe how the transformation to relative coordinates discussed in Sect. 2.3.1 is applied. To this end, the global displacement vector \({\varvec{u}}\) is expressed in terms of relative coordinates \({}_{\,\mathrm{c}}{\varvec{g}}\) at the contact interface and remaining coordinates \({\varvec{u}}_{{\mathrm{rem}}}\),

$${\varvec{u}}=\left[ {\begin{array}{cc} \left( {\varvec{B}}^{\mathrm{T}}\right) ^{+}&{} {\varvec{N}}_{{\varvec{B}}^{\mathrm{T}}}\\ \end{array}}\right] \left[ {\begin{array}{c} {}_{\,\mathrm{c}}{\varvec{g}}\\ {\varvec{u}}_{{\mathrm{rem}}}\\ \end{array}}\right] = {\varvec{L}}{\varvec{u}}^{(b)}.$$
(51)

Herein, \({}^{+}\) denotes the pseudo-inverse, and \({\varvec{N}}_{{\varvec{A}}}= {\text {Null}}\left( {\varvec{A}}\right)\) denotes the nullspace of matrix \({\varvec{A}}\), and (b) refers to the variant (b) for the definition of the coupling coordinates, as introduced in Sect. 2.3.1.Footnote 26

In general, the transformation matrix \({\varvec{L}}\) could be expensive to compute, since it involves the computation of the pseudo-inverse and the null space of the comparatively large matrix \({\varvec{B}}^{\mathrm{T}}\) (dimension \(n_{{\mathrm{d}}}\times 3n_{{\mathrm{c}}}\), where \(n_{{\mathrm{d}}}\) could be \(n_{{\mathrm{fe,s}}}\) or \(n_{{\mathrm{fe}}}\)). The computational cost can be considerably reduced by taking advantage of the local nature of the problem, i.e., by computing the sub-matrices of \({\varvec{L}}\) separately for each interface. For convenience, the coordinate vector \({\varvec{u}}\) is rearranged in such a way that the nodal DOFs associated with a particular interface are grouped together. The matrix \({\varvec{B}}\) then takes the form \({\varvec{B}}={\mathbf{bdiag}}\lbrace {\varvec{B}}_{1},\ldots ,{\varvec{B}}_{n_{{\mathrm{if}}}}\rbrace\) where \({\varvec{B}}_{n}\) is the local coupling matrix of interface n and \(n_{{\mathrm{if}}}\) is the number of interfaces. The \(n_{{\mathrm{int}}}\) interior DOFs are not associated with any of the interfaces and form the rear part of the re-ordered vector \({\varvec{u}}\), where typically \(n_{{\mathrm{int}}}\gg 3n_{{\mathrm{c}}}\). The null space associated to the interior DOFs is trivial and does not have to be computed explicitly. The matrix \({\varvec{L}}\) can then be assembled as

$${\varvec{L}}= \left[ {\begin{array}{ccccccc} \left( {\varvec{B}}_1^{\mathrm{T}}\right) ^{+}&{} \cdots &{} {\mathbf{0}} &{} {\varvec{N}}_{{\varvec{B}}_1^{\mathrm{T}}}&{} \cdots &{} {\mathbf{0}}&{} {\mathbf{0}}\\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ {\mathbf{0}} &{} \cdots &{} \left( {\varvec{B}}_{n_{{\mathrm{if}}}}^{\mathrm{T}}\right) ^{+}&{} {\mathbf{0}} &{} \cdots &{} {\varvec{N}}_{{\varvec{B}}_{n_{{\mathrm{if}}}}^{\mathrm{T}}}&{} {\mathbf{0}}\\ {\mathbf{0}} &{} \cdots &{} {\mathbf{0}} &{} {\mathbf{0}} &{} \cdots &{} {\mathbf{0}}&{} {\varvec{I}}_{n_{{\mathrm{int}}}}\\ \end{array}}\right] .$$
(52)

The coordinate transform is applied by substituting Eq. (51) into the equations of motion and left-multiplication by \({\varvec{L}}^{\mathrm{T}}\). It should be noted that the matrix \({\varvec{L}}\) defined in Eq. (52) has full rank, and, thus, Eq. (51) defines an invertible coordinate transform.

Resulting structure of the contact force vector The structure of the contact force vector depends on the variant pursued for the definition of the coupling DOFs. If the conventional variant (a) is used, the contact force vector \({\varvec{f}}_{{\mathrm{c}}}\) takes the form,

$${\varvec{f}}_{{\mathrm{c}}}^{(a)}\left[ {\varvec{u}}\right] = {\varvec{B}}{\varvec{\lambda }}\left[ {\varvec{B}}^{\mathrm{T}}{\varvec{u}}\right] ,$$
(53)

where \({\varvec{\lambda}}[\cdot]\) represents the actual contact force law formulated in terms of the contact gaps (and/or velocities). The gaps are determined by means of the transform \({\varvec{B}}^{\mathrm{T}}{\varvec{u}}\), every time when the contact force vector \({\varvec{\lambda}}\) is evaluated, and a multiplication by \({\varvec{B}}\) is formally necessary to determine the force vector \({\varvec{f}}_{{\mathrm{c}}}\) acting on the global displacement vector \({\varvec{u}}\). In the case of variant (b), this transformation is applied, once and for all, during the dynamic substructuring procedure. The contact force vector thus becomes

$$\begin{aligned} {\varvec{f}}_{{\mathrm{c}}}^{(b)}\left[ {\varvec{u}}^{(b)}\right]&= {\varvec{L}}^{\mathrm{T}}{\varvec{f}}_{{\mathrm{c}}}^{(a)}\left[ {\varvec{L}}{\varvec{u}}\right] \nonumber \\ &= {\varvec{L}}^{\mathrm{T}}{\varvec{B}}{\varvec{\lambda }}\left[ {\varvec{B}}^{\mathrm{T}}{\varvec{L}}{\varvec{u}}^{(b)}\right] \nonumber \\ &= \left[ {\begin{array}{c} {\varvec{I}}_{3n_{{\mathrm{c}}}}\\ {\mathbf{0}}\\ \end{array}}\right] {\varvec{\lambda }}\left[ \left[ {\begin{array}{cc} {\varvec{I}}_{3n_{{\mathrm{c}}}} &{} {\mathbf{0}}\\ \end{array}}\right] {\varvec{u}}^{(b)}\right] \nonumber \\ &= \left[ {\begin{array}{c} {\varvec{\lambda }}\left[ {}_{\,\mathrm{c}}{\varvec{g}}\right] \\ {\mathbf{0}}\\ \end{array}}\right] .\end{aligned}$$
(54)

Owing to the preliminary coordinate transformation, the global contact vector depends and acts on only the first \(3n_{{\mathrm{c}}}\) components of the coordinate vector. Hence, no transformation is necessary during the nonlinear dynamic analysis.

Appendix 4: Craig-Bampton and MacNeal-Rubin Method

In this appendix, explicit expressions are given for the matrix \({\varvec{T}}\) of component modes for the well-known CB and MR methods, see e.g. [28]. Consider an initial model with a hermitian, positive-definite stiffness matrix \({\varvec{K}}={\varvec{K}}^{\mathrm{H}}>{\mathbf{0}}\) and a hermitian, positive-definite mass matrix. The associated vector of coordinates \({\varvec{u}}\) is of the form \({\varvec{u}}= \left[ {\begin{array}{cc} {\varvec{u}}_{{\mathrm{ret}}}^{\mathrm{T}}&{} {\varvec{u}}_{{\mathrm{del}}}^{\mathrm{T}}\\ \end{array}}\right] ^{\mathrm{T}}\) where \({\varvec{u}}_{{\mathrm{ret}}}\) and \({\varvec{u}}_{{\mathrm{del}}}\) denote the coordinates to be retained in the reduced model and those that are (deleted and) replaced by generalized coordinates, respectively.

In the case of the CB method, the reduction basis is spanned by constraint modes and a set of fixed interface normal modes,

$${\varvec{T}}_{{\mathrm{cb}}}= \left[ {\begin{array}{cc} {\varvec{I}}_{n_{{\mathrm{ret}}}} &{} {\mathbf{0}}_{n_{{\mathrm{ret}}}\times n_{{\mathrm{del}}}} \\ {\varvec{\varPsi }}&{} {\varvec{\varPhi }}^{{\mathrm{fixed}}}\\ \end{array}}\right] .$$
(55)

The first hyper-column represents the constraint modes, which are static deformation shapes for a unit displacement applied to one of the coupling DOFs, while the remaining coupling DOFs are kept fixed,

$${\varvec{K}}_{{\mathrm{del}},\mathrm{del}}{\varvec{\varPsi }}= -{\varvec{K}}_{{\mathrm{del}},\mathrm{ret}},$$
(56)

where \({\varvec{K}}_{{\mathrm{del}},\mathrm{ret}}\) refers to the restriction of \({\varvec{K}}\) to the rows associated with \({\varvec{u}}_{{\mathrm{del}}}\) and the columns associated with \({\varvec{u}}_{{\mathrm{ret}}}\) and so on. The fixed interface normal modes, assembled in the matrix \({\varvec{\varPhi }}^{{\mathrm{fixed}}}\) in Eq. (55), are obtained from modal analysis of the system with all coupling DOFs fixed,

$$\begin{aligned} {\varvec{\varPhi }}^{{\mathrm{fixed}}} &= \left[ {\begin{array}{c} {{\varvec{\phi} }^{{\mathrm{fixed}}}_1 \cdots {\varvec{\phi} }^{{\mathrm{fixed}}}_{n_{{\mathrm{mod}}}}} \end{array}}\right] ,\nonumber \\ &\quad \left( {\varvec{K}}_{{\mathrm{del}},\mathrm{del}} - {\omega ^{{\mathrm{fixed}}}_{j}}^2 {\varvec{M}}_{{\mathrm{del}},\mathrm{del}} \right) {\varvec{\phi }}^{{\mathrm{fixed}}}_{j} = {\mathbf{0}},\nonumber \\ &\quad\omega ^{{\mathrm{fixed}}}_{1}\le \ldots \le \omega ^{{\mathrm{fixed}}}_{n_{{\mathrm{mod}}}}.\end{aligned}$$
(57)

It should be emphasized that the coupling DOFs are either the nodal or the relative DOFs at the interface, as explained in Sect. 2.3.1.

The MR method is the complement of the CB method with free interface normal modes. In the case of the MR method, the reduction basis is, thus, spanned by the residual attachment modes and a set of free interface normal mode shapes \({\varvec{\varPhi }}^{{\mathrm{free}}}\),

$${\varvec{T}}_{{\mathrm{mr}}}= \left[ {\begin{array}{cc} {\varvec{I}}_{n_{{\mathrm{ret}}}} &{} {\mathbf{0}}_{n_{{\mathrm{ret}}}\times n_{{\mathrm{del}}}} \\ {\varvec{\varDelta }}&{} {\varvec{\varPhi }}^{{\mathrm{free}}}_{{\mathrm{del}}} - {\varvec{\varDelta }}{\varvec{\varPhi }}^{{\mathrm{free}}}_{{\mathrm{ret}}} \end{array}}\right] .$$
(58)

The residual attachment modes essentially represent the static deformation shapes for a unit force applied to one of the coupling DOFs, while the remaining DOFs are not loaded.

$$\begin{aligned} {\varvec{\varDelta }} &= {\varvec{R}}_{{\mathrm{del}}}{\varvec{R}}_{{\mathrm{ret}}}^{-1},\nonumber \\ \left[ {\begin{array}{c} {\varvec{R}}_{{\mathrm{ret}}}\\ {\varvec{R}}_{{\mathrm{del}}}\\ \end{array}}\right] &= \left[ {\begin{array}{c} \left( {\varvec{K}}^{-1}\right) _{{\mathrm{ret}},{\mathrm{ret}}}\\ \left( {\varvec{K}}^{-1}\right) _{{\mathrm{del}},\mathrm{ret}}\\ \end{array}}\right] -\sum \limits _{j=1}^{n_{{\mathrm{mod}}}} \left[ {\begin{array}{c} {\varvec{\varPhi }}^{{\mathrm{free}}}_{{\mathrm{ret}}}\\ {\varvec{\varPhi }}^{{\mathrm{free}}}_{{\mathrm{del}}}\\ \end{array}}\right] \frac{{{\varvec{\varPhi }}^{{\mathrm{free}}}_{{\mathrm{ret}}}}^{\mathrm{H}}}{\omega ^{{\mathrm{free}}}_j}.\end{aligned}$$
(59)

Herein, \({\varvec{R}}\) denotes the residual static flexibility associated with loading of the retained coordinates. The presence of rigid body modes requires special attention [28]; however, this case is not further discussed in this work. The free interface normal modes are defined as

$$\begin{aligned} &{\varvec{\varPhi }}^{{\mathrm{free}}} = \left[ {\begin{array}{ccc} {\varvec{\phi }}^{{\mathrm{free}}}_{1} &{} \cdots & {\varvec{\phi }}^{{\mathrm{free}}}_{n_{{\mathrm{mod}}}}\\ \end{array}}\right] ,\nonumber \\ & \left( {\varvec{K}} - {\omega ^{{\mathrm{free}}}_{j}}^2 {\varvec{M}} \right) {\varvec{\phi }}^{{\mathrm{free}}}_{j} = {\mathbf{0}},\,\,\omega ^{{\mathrm{free}}}_{1}\le \cdots \le \omega ^{{\mathrm{free}}}_{n_{{\mathrm{mod}}}}.\end{aligned}$$
(60)

Appendix 5: Exact Condensation Procedure

In this appendix, an exact procedure is presented for the condensation of the harmonic balance equations, which takes advantage of the sparsity of the nonlinear terms. To this end, it is convenient to arrange the equations of motion in such a manner that the nonlinear force and generalized coordinates vectors have the form

$${\varvec{f}}_{{\mathrm{c}}}\left[ {\varvec{u}}\right] = \left[ {\begin{array}{c} {\varvec{\lambda }}\left[ {}_{\,\mathrm{c}}{\varvec{g}}\right] \\ {\mathbf{0}}\\ \end{array}}\right] ,\quad {\varvec{u}}= \left[ {\begin{array}{c} {}_{\,\mathrm{c}}{\varvec{g}}\\ {\varvec{u}}_{{\mathrm{rem}}}\\ \end{array}}\right] .$$
(61)

Herein, \({\varvec{f}}_{{\mathrm{c}}}\) and \({\varvec{u}}\) have the dimension \(n_{{\mathrm{d}}}\), whereas \({\varvec{\lambda }}\) and \({}_{\,\mathrm{c}}{\varvec{g}}\) have the dimension \(3n_{{\mathrm{c}}}\). We refer to \({}_{\,\mathrm{c}}{\varvec{g}}\) as nonlinear coordinates, and to \({\varvec{u}}_{{\mathrm{rem}}}\) as linear coordinates, since for given \({}_{\,\mathrm{c}}{\varvec{g}}(t)\) a linear ODE governs \({\varvec{u}}_{{\mathrm{rem}}}(t)\). The vector of nonlinear forces is considered as sparse, if \(3n_{{\mathrm{c}}}\ll n_{{\mathrm{d}}}\). This sparsity is inherited by the harmonics \({\varvec{\varLambda }}\) and the associated gradients. The extent of this sparsity depends on the choice of the generalized coordinates. If the physical coordinates \({}_{\,\mathrm{c}}{\varvec{g}}\), that describe the (relative) interface motions, are not retained, the sparsity is generally lost. In the simplest case, \({}_{\,\mathrm{c}}{\varvec{g}}\) represents the local relative deformation at the contact points.

Taking advantage of this sparsity during the numerical solution process is a common procedure in conjunction with harmonic balance, see e.g. [3, 18, 54, 77]. To this end, one condenses the set of \(n_{{\mathrm{d}}}\) nonlinear algebraic equations for each harmonic to a set of \(3n_{{\mathrm{c}}}\) equations. This can significantly reduce the number of explicit unknowns and thus reduce the computational effort required for the iterative solution process.

The procedure is exemplified for the balance of generalized displacements given in Eq. (28), but a fully analogous procedure is available for the balance of generalized forces given in Eq. (27), see e.g. [133]. To this end, Eq. (28) is split into the individual harmonics,

$${\varvec{U}}_n+ {\varvec{H}}_{n}\left( \varOmega \right) {\varvec{F}}_{{\mathrm{c,n}}}\left( {\varvec{U}}_{0},\ldots ,{\varvec{U}}_{H}\right) = {\varvec{U}}_{{\mathrm{ae}},n}\quad \forall n\in {\mathcal {H}}.$$
(62)

The matrices \({\varvec{H}}_{k}\) are also partitioned as in Eq. (61),

$${\varvec{H}}_{k}= \left[ {\begin{array}{cc} {\varvec{H}}_k^{\mathrm{nl,nl}}&{} {\varvec{H}}_k^{\mathrm{nl,l}}\\ {\varvec{H}}_k^{\mathrm{l,nl}}&{} {\varvec{H}}_k^{\mathrm{l,l}}\\ \end{array}}\right].$$
(63)

With this, the first hyper-row of Eq. (62) reads

$${\varvec{G}}_{k}+ {\varvec{H}}_k^{\mathrm{nl,nl}}(\varOmega ){\varvec{\varLambda }}_{k}\left( {\varvec{G}}_0,\ldots ,{\varvec{G}}_{n_{{\mathrm{h}}}}\right) = {\mathbf{0}}\quad\forall \,n\in {\mathcal {H}},$$
(64)

where \({\varvec{H}}_k^{\mathrm{nl,nl}}\) is a portion of the matrix \({\varvec{H}}_{k}\). Equation (64) only depends on the harmonic components \({\varvec{G}}_0,\ldots ,{\varvec{G}}_{n_{{\mathrm{h}}}}\) of the nonlinear coordinates, but not on \({\varvec{U}}_{{\mathrm{rem}},k}\), the harmonic components of the linear coordinates. It is thus sufficient to solve Eq. (64), which is of much smaller dimension than Eq. (62) if \(3n_{{\mathrm{c}}}\ll n_{{\mathrm{d}}}\). Upon solution of Eq. (64) for \({\varvec{G}}_{k}\), the remaining portion of the generalized coordinates can be determined using the explicit formulation \({\varvec{U}}_{{\mathrm{rem}},k}= -{\varvec{H}}_k^{\mathrm{l,nl}}{\varvec{\varLambda }}_{k}\). It should be noted that this dynamic condensation procedure is mathematically exact, so that it does not suffer from poor accuracy like, e.g., the static (Guyan) condensation procedure.

Note that the dynamic compliance matrix is defined as the inverse of the dynamic stiffness matrix. Computing \({\varvec{H}}_{n}\) by matrix inversion, however, would be time consuming. This is particularly true since \({\varvec{H}}_{n}\) depends on \(\varOmega\) and, thus, typically has to be re-computed in every iteration. As long as the dynamic stiffness matrix can be expressed as a polynomial in \(\varOmega\) with constant coefficient matrices, the matrix inversion can be replaced by a small number of matrix multiplications and the trivial inversion of a diagonal matrix, see e.g. [84, 133].

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Krack, M., Salles, L. & Thouverez, F. Vibration Prediction of Bladed Disks Coupled by Friction Joints. Arch Computat Methods Eng 24, 589–636 (2017). https://doi.org/10.1007/s11831-016-9183-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-016-9183-2

Search

Navigation