Nonconforming Dirichlet boundary conditions in implicit material point method by means of penalty augmentation

Abstract

In many geomechanics applications, material boundaries are subjected to large displacements and deformation. Under these circumstances, the application of boundary conditions using particle methods, such as the material point method (MPM), becomes a challenging task since material boundaries do not coincide with the background mesh. This paper presents a formulation of penalty augmentation to impose nonhomogeneous, nonconforming Dirichlet boundary conditions in implicit MPM. The penalty augmentation is implemented utilizing boundary particles, which can move either according to or independently from the material deformation. Furthermore, releasing contact boundary condition, as well as the capability to accommodate slip boundaries, is introduced in the current work. The accuracy of the proposed method is assessed in both 2D and 3D cases, by convergence analysis reaching the analytical solution and by comparing the results of nonconforming and classical grid-conforming simulations.

1 Introduction

In recent years, continuum-based particle methods, including, among others, the smoothed particle hydrodynamics (SPH) [1], the particle finite element method (PFEM) [2], the reproducing kernel particle method [3], the element-free Galerkin method [4], and the moving particle semi-implicit method (MPS) [5], are the natural choice when simulating large deformation solid dynamics problems. While classical mesh-based approaches, such as the finite element method (FEM) [6], have been proven to be very powerful and accurate to model materials under small deformation, they are likely to suffer from mesh distortion and entanglement. When the material deformation becomes too large, mesh-based methods generally require remeshing and remapping of variables, which do not only introduce an error but are also computationally costly. Particle-based methods on the other side overcome this drawback by switching to either meshless or hybrid approach. SPH, MPS, and meshless methods in general discretize the problem domain into moving particles governed solely by the interaction between the neighboring particles. Even though remeshing processes can be avoided in this case, searching procedures and the usage of high-order basis functions are necessary to obtain accurate results [7]. Moreover, the difficulty to enforce Dirichlet boundary conditions (i.e., due to the absence of the Kronecker delta property) should be addressed properly, on top of the presence of tensile instability caused by an insufficient number of neighbor particles. Even though many attempts have been continuously proposed to overcome these issues [8], a valuable alternative could be represented by the hybrid approaches, combining the strengths of mesh-based and meshless techniques while simultaneously minimizing their drawbacks.

The material point method (MPM), belonging to the hybrid techniques, was originally proposed by Sulsky et al. [9] as an extension of the particle-in-cell (PIC) [10] and fluid-implicit-particle (FLIP) [11] method for treating solid dynamics problems. The key difference between MPM and its preceding methods is that MPM performs the integration of constitutive stress at the Lagrangian moving particles, while keeping the fixed “background” mesh in order to approximate continuous fields and their spatial gradients. MPM can be interpreted as a modified updated-Lagrangian finite element technique with moving integration points and a final mesh reset at each time step. MPM can simulate history-dependent materials with considerably large deformation avoiding mesh-distortion issue since the material properties are stored within the particles, called material points. The method since then has been successfully employed for the simulation of a variety of problems that are not easily addressed with mesh-based approaches. We can mention, for instance, hyper-velocity impact [12, 13], explosions [14], failure [15], and multi-phase geomechanical problems [16,17,18]. Some applications of the MPM are listed as a general review in the books published by Zhang et al. [19] and Fern et al. [20].

The use of MPM and its extended variants, such as the generalized interpolation material point (GIMP) method [21] or the convected particle domain interpolation (CPDI) [22, 23], to simulate large deformation solid dynamics problems, indeed, provides tremendous advantages, as it successfully tackles and solves the problem with mesh entanglement. Nevertheless, the method still suffers from some major difficulties. One open issue to be addressed is related to the nonconforming boundary conditions. In MPM, differently from other Lagrangian mesh-based approaches, boundary conditions often need to be applied on boundaries which does not match with the background mesh. Similar problems appears in the unfitted methods for computational fluid dynamics (CFD) problems [24,25,26,27,28].

This MPM problem has been addressed by few other authors. One possibility is to move the background fixed mesh according to the material displacements and deformation [29,30,31]. By doing this, the material boundary always coincides with the mesh edges in 2D or surface in 3D and boundary conditions can be applied in a FEM fashion to the mesh nodes. However, the accuracy of this method is strongly limited by the boundary shape and motion, i.e., the material boundary has to maintain its surface description and be subjected to small deformation movements without severe rotations. Otherwise, remeshing should be performed, losing the main motivation behind the choice of MPM instead of the standard FEM. Furthermore, the moving-mesh technique is also observed to produce numerical noises [32] due to the cell-crossing instabilities, which occur when material points cross the computational mesh boundaries [21]. In alternative the desired boundary conditions can be applied to the boundary particles. This can be done either by identifying the outer layer of material points [33] or by building a layer of mass-less boundary particles which track the deformation of material boundaries. In both cases the carried information is mapped onto the connectivity’s nodes through the element shape functions. The main disadvantage of this approach is that the applied boundary condition is not exactly lying on the material boundary, but across a boundary band, which therefore, results in an increase of the thickness of the actual boundary. This leads to significant errors and element size dependency as pointed out by Beuth [33] and Kafaji [29].

Another potential method was proposed by Mast et al. [34], assuming a dual-grid approach. Essentially, this method introduces an additional grid which follows the geometry of the material boundary, and the communication between the additional grids and the original background grids is performed to enforce the nonconforming essential boundary conditions. However, as explained by Bing et al. [35], the dual-grid configuration is problematic even for simple 1D problems, since it is sensitive to different boundary cell size and location. Mast’s colleague, Yang [36], proposed a scheme for handling nonconforming Dirichlet boundaries by giving a specific boundary force field. This technique defines an influence region nearby the boundary, divided into three zones: constrained, decay, and free. Within the decay zone, the magnitude of boundary forces is reduced by a prescribed decay function to reflect a decreasing influence to the material. It should be noted here that the choice of assumed decay function will influence the quality of the numerical results.

An interesting alternative work to address moving Neumann boundary conditions has been proposed by Remmerswall et al. [37]. In their work, Remmerswall and colleagues introduced a boundary detection algorithm using the proximity field method (PFM), which is based on the concept derived from free surface boundary detection used in CFD. However, the PFM approach is reported to be computationally costly, highly mesh dependent, and its accuracy, at present, is still questionable [37].

Last but not least, most recently, Bing and colleagues [35, 38, 39] have proposed a more general way to track the evolution of physical boundary by utilizing a cubic B-spline interpolation method. By using this technique, the integration of surface traction for Neumann boundary can be done directly along the B-spline surface by incorporating Gauss quadrature. The B-spline surface can also be combined with a Dirichlet boundary imposition using the implicit boundary method (IBM) adopted from FEM [40,41,42,43]. The key idea of the IBM is to enforce essential boundary conditions by introducing extra stiffness terms in the system of equations, which can be calculated through a “Dirichlet function” that depends on the signed-distance function measured from the material boundaries. Bing et al. [35, 38] extended it to MPM to include the roller boundary conditions on inclined boundaries and the treatment of nonhomogeneous boundaries. However, since the definition of the B-spline surface has to be established from the beginning of the simulation, this approach is still doubted to work for large deformation cases involving crack, fragmentation, and new surface reconstruction.

IBM has been proven to be suitable for imposing homogeneous and nonhomogeneous Dirichlet boundary conditions for 2D quasi-static linear-elastic problems in MPM with structured quadrilateral elements [35, 38, 39]. Yet, so far, implementation for 3D cases, with unstructured background mesh, and for nonlinear dynamic problems involving elastoplastic materials is not yet presented. Within their method, there are some limitations observed rooted from the undertaken assumptions. First, the IBM enforces the Dirichlet imposition by modification of the trial and test function spaces. Here, the approximated displacement field is modified by including the influence of diagonal Dirichlet matrix as well as the boundary condition to be imposed. This may lead to the violation of continuity requirements between elements, i.e., between cut and regular elements, which, by further, may potentially cause numerical instability. Secondly, the method also utilizes the material constitutive matrix $\mathbf{D}$ within its boundary enforcement formulation; this particularly may be difficult to represent when complex mixture of elastoplastic materials are involved.

While the application of Neumann boundary conditions has its paramount importance in many solid dynamics simulations, which have been discussed thoroughly in many prior works [35, 37, 44, 45], the current paper solely focuses in developing methods to handle the application of Dirichlet boundary conditions, which are needed in many problems of transient dynamics. The discussion on Neumann boundary conditions will be kept as a future work. This paper offers an alternative approach of implicit boundary imposition. Instead of modifying the interpolation shape functions or field parameterization as in the IBM [35, 38, 39], a modification of the weak form is adopted by appending an extra term derived from the penalty formulation.

The penalty formulation in general has been well established in FEM to impose constraint conditions of nonconforming elements [46], as well as in isogeometric B-Rep analysis (IBRA) [47, 48] to couple boundary conditions between patches. Compared to methods such as the Lagrange multiplier [49], where additional degrees of freedom (DOF) are required, the penalty method is significantly less expensive in computational cost. Furthermore, for similar imposition purposes, this approach has also been extended to meshfree methods [50,51,52] and other continuum-based methods, such as in the CutFEM [53] and the finite cell methods (FCM) [54]. In the present paper, the adaption of the penalty method to MPM is presented. The penalty augmentation is adopted using boundary particles, which can be fixed or can move not only according to the material deformation, but also following prescribed field values, independently from the deformation.

The objective of this work is to introduce a penalty augmentation to impose nonhomogeneous, nonconforming boundary conditions in MPM. The proposed approach can work independent of background meshes (e.g., triangular, quadrilateral, tetrahedral, hexahedral), all type of materials, in both small and large strain regimes, and in both 2D and 3D problems. An extension to accommodate inclined roller support and frictionless contact (detaching) condition is also added to the formulation. The developed MPM code employed in the current work utilizes implicit integration scheme [55,56,57] and has been developed by the authors within the Kratos Multiphysics open-source platform [58]. The code proposed is available in GitHub¹ under a BSD license.

The paper is structured as follows. First, Sect. 2 introduces the governing equations needed, including a summary of procedure to perform an implicit MPM simulation. Section 3 provides some numerical details on how the boundary conditions are treated in implicit MPM, for both the grid-conforming and the proposed nonconforming boundary imposition. In Sect. 4, some numerical tests are simulated and discussed to assess the capabilities of the proposed approach. Finally, Sect. 5 presents the conclusions and suggestions for future works.

2 Displacement-based implicit MPM formulation

This section presents an overview of the displacement-based implicit MPM formulation used in the current work. The reader is strongly recommended to refer to [55, 56, 59] for more detailed information on the algorithm.

2.1 Balance equations and weak formulation

Consider a body $\mathcal {B}$, which occupies an initial domain $\Omega$ of the three-dimensional Euclidean space $\mathcal {E}$, with a regular boundary $\partial \Omega$ in its reference configuration. A deformation of $\mathcal {B}$ at a given time t is defined by a one-to-one mapping $\varphi$,

$$\begin{aligned} {\varphi }:\Omega \rightarrow \mathcal {E}. \end{aligned}$$

(1)

The deformation gradient $\mathbf{F}$ is defined as

$$\begin{aligned} \mathbf{F} \left( \mathbf{X}, t \right) = \nabla _{\mathbf{X}} {\varphi } \left( \mathbf{X}, t \right) = \frac{\partial \mathbf{x}}{\partial \mathbf{X}}, \end{aligned}$$

(2)

where $\mathbf{x}$ and $\mathbf{X}$ denote the current and the reference configurations, respectively.

Continuity equation reads

$$\begin{aligned} \frac{\mathrm{d}\rho }{\mathrm{d}t} + \rho \nabla \cdot \mathbf{v} = 0 \quad \mathrm{in} \quad \varphi (\Omega ), \end{aligned}$$

(3)

where $\rho$ and $\mathbf{v}$ are the density and velocity vector and $\varvec{\rho } / \mathrm{d}{t}$ indicates the total derivative of $\rho$. The conservation of linear momentum of $\mathcal {B}$ is given by:

$$\begin{aligned} \rho \ddot{\mathbf{u}} = \nabla \cdot \varvec{\sigma } + \rho \mathbf{b} \quad \mathrm{in} \quad \varphi (\Omega ), \end{aligned}$$

(4)

where $\ddot{\mathbf{u}}$ represents the acceleration vector, $\varvec{\sigma }$ is the symmetric Cauchy stress tensor and $\mathbf{b}$ denotes the volume acceleration.

The governing Eqs. (3) and (4) have to be solved numerically in a three-dimensional field $\Omega \subseteq \mathbb {R}^3$, within the time range $t \in [0,T]$, considering the following boundary conditions:

$$\begin{aligned} \mathbf{u}= & {} \bar{\mathbf{u}} \quad \mathrm{on} \quad \varphi \left( \partial \Omega _D \right) , \end{aligned}$$

(5)

$$\begin{aligned} \varvec{\sigma }\cdot \mathbf{n}= & {} \bar{\mathbf{t}} \quad \mathrm{on} \quad \varphi \left( \partial \Omega _N \right) , \end{aligned}$$

(6)

where $\mathbf{n}$ is the outward unit normal vector, while $\bar{\mathbf{u}}$ and $\bar{\mathbf{t}}$ are the Dirichlet prescribed displacement and the Neumann traction on $\partial \Omega _D$ and $\partial \Omega _N$, respectively.

Assuming the following constitutive stress–strain relation:

$$\begin{aligned} \varvec{\sigma } = \varvec{\sigma } (\varvec{\varepsilon }) = \varvec{\sigma } (\varvec{\varepsilon }(\mathbf{u})), \end{aligned}$$

(7)

where $\varvec{\varepsilon }$ is the strain tensor, and calling $\mathcal {V} \subset \mathbb {R}^3$ the space of the solution $\mathbf{u}$, we can derive the corresponding weak formulation. The problem is, hence, reduced to find a kinematically admissible displacement field $\mathbf{u} \in \mathcal {V}$ at each time t which satisfies:

$$\begin{aligned} R(\mathbf{u},\mathbf{w})= & {} \int _{\varphi (\Omega )} \varvec{\sigma }(\varvec{\varepsilon }(\mathbf{u})) : \nabla ^s \mathbf{w} \mathrm{d}v \nonumber \\&- \int _{\varphi (\Omega )} \rho \left( \mathbf{b} - \ddot{\mathbf{u}} \right) \cdot \mathbf{w} \mathrm{d}v \nonumber \\&- \int _{\varphi (\partial \Omega _{N})} \bar{\mathbf{t}} \cdot \mathbf{w} \mathrm{d}a = 0 \quad \forall \mathbf{w} \in \mathcal {V}, \end{aligned}$$

(8)

where $\mathbf{w} \in \mathcal {V}$ is an arbitrary test function.

2.2 Linearization of the weak formulation

Equation (8) is valid for any kind of strain definitions, including the large strain definitions. Since, in the current work, we attempt to solve problems involving strong material and geometric nonlinearities, a linearization of the weak form is necessary to solve the associated nonlinear boundary value problems (BVP). By utilizing the Newton–Raphson’s method, the approximation of the solution can be obtained iteratively by means of directional derivatives.

The linearization of the residual weak form following a Taylor’s expansion yields to the following linear system matrix to be solved at every time step t:

$$\begin{aligned} \mathbf{K}^{\mathrm{tan}} \delta \mathbf{u} = - \mathbf{R}. \end{aligned}$$

(9)

where $\mathbf{R}$ is the residual vector expressed by Eq. (8), whereas $\mathbf{K}^{\mathrm{tan}}$ is the corresponding tangent matrix associated to the directional derivative of $\mathbf{R}$. The displacement $\mathbf{u}$ is continuously updated during the Newton–Raphson’s iterations by adding the previously unknown increment $\delta \mathbf{u}$ to its previous converged values.

The tangent stiffness matrix can be split into several sub-matrices given by:

$$\begin{aligned} \mathbf{K}^{\mathrm{tan}} = \mathbf{K}^{\mathrm{geo}} + \mathbf{K}^{\mathrm{mat}} +\mathbf{K}^{\mathrm{dyn}}. \end{aligned}$$

(10)

The first two sub-matrices represent the static part of $\mathbf{K}$ and are known as the geometric and material stiffness matrices, respectively:

$$\begin{aligned} \mathbf{K}^{\mathrm{geo}}:= & {} \int _{\varphi (\Omega )} \nabla _x \delta \mathbf{u} \cdot \varvec{\sigma } \cdot \nabla _x \mathbf{w} \mathrm{d}v, \end{aligned}$$

(11)

$$\begin{aligned} \mathbf{K}^{\mathrm{mat}}:= & {} \int _{\varphi (\Omega )} \nabla ^s_x \mathbf{w} \cdot \mathbf{D} \cdot \nabla ^s_x \delta \mathbf{u} \mathrm{d}{v}. \end{aligned}$$

(12)

Here, $\mathbf{D}$ is the tangent stiffness matrix defined for the used constitutive equation and $\nabla _x$ denotes the spatial gradient at the current configuration, $\nabla _x= \partial /\partial \mathbf{x}$.

Moreover, the dynamic component of the stiffness matrix can be computed as:

$$\begin{aligned} \mathbf{K}^{\mathrm{dyn}} = \int _{\varphi (\Omega )} \left( \rho \, \alpha \, \mathbf{w} \cdot \delta \mathbf{u} \right) \mathrm{d}v, \end{aligned}$$

(13)

where the value of $\alpha$ depends on the time integration scheme used. For instance, $\alpha = 1 / \beta _N \Delta t^2$ in Newmark integration scheme, where $\beta _N$ is typically equal to 0.25.

2.3 Spatial discretization

The integrals written in Eqs. (9)–(13) need to be approximated spatially by discretization techniques. In MPM, as the continuous geometry and domain are approximated by finite number of material points and background grids, the field quantities presented in the weak forms, e.g., stresses, displacements, etc., can be approximated through extrapolation and interpolation methods. In the following formulations, the variables at the mesh nodes will be identified with subscript I and J, while the properties associated with material points will be identified with subscript p. Moreover, the superscript n and $n+1$ indicate the current (known) and next (unknown) time step, respectively. All the variables with subscript h are nothing but the approximation of the variables themselves in the discretized geometry.

Following the standard nonlinear finite element discretization [60], Eq. (9) is discretized as:

$$\begin{aligned} \mathbf{K}^{\mathrm{tan}} \Delta \mathbf{u} = - \mathbf{R}, \end{aligned}$$

(14)

where $\Delta \mathbf{u}$ is the increment of the discrete solution of the problem (i.e., the discrete counterpart of the incremental displacement $\delta \mathbf{u}$ used in Eq. 9). The elemental tangent stiffness matrix $\mathbf{K}^{\mathrm{tan}}$ and residual vector $\mathbf{R}$ are expressed as,

$$\begin{aligned} \mathbf{R}_{I}= & {} \bigcup _{p=1}^{n_p} \left( \mathbf{B}_I \varvec{\sigma } - \rho \mathbf{b}N_I + \sum _{J=1}^{n_n} N_I \rho N_J \mathbf{a}_J \right) v_p \nonumber \\&- \bigcup _{a=1}^{n_a} N_I\bar{\mathbf{t}}A_a, \end{aligned}$$

(15)

$$\begin{aligned} \mathbf{K}^{\mathrm{tan}}_{IJ}= & {} \bigcup _{p=1}^{n_p} \left( (\nabla _x N_I)^T \varvec{\sigma } (\nabla _x N_J) + \mathbf{B}_I^T \mathbf{D} \mathbf{B}_J \right. \nonumber \\&\left. + N_I \rho \alpha N_J \mathbf{I} \right) v_p. \end{aligned}$$

(16)

where $v_p$ and $A_a$ are the current volume of a single material point and the area weight of surface boundary, respectively. $\mathbf{D}$ is the constitutive matrix and $\mathbf{B}_I$ is the deformation matrix related to each node I in the element. $N_{I}$ is corresponding shape function value associated with grid node I, whereas $n_n$ is the total number of computational node. Operator $\bigcup$ is used in Eqs. (15) and (16), instead of $\sum$ over all $n_p$, as the assembly procedure is not only adding up each of the material point contributions but also addressing the kinematic compatibility between the points.

2.4 Implicit MPM

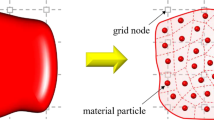
The material point method (MPM) was originally proposed by [9] as an extension of the particle-in-cell (PIC) and fluid-implicit-particle (FLIP) method for treating solid dynamics problems. The method has been developed over the last two decades especially for solids undergoing large deformation [61], including many other multiphase, multi-physics, and multi-scale problems. MPM uses a fixed background mesh and a set of moving material points. While the mesh is used for calculation purpose in a FEM fashion and is reset at the end of each time step, all historical information is stored inside the material points which are moving in a Lagrangian way and employed as moving integration nodes (Fig. 1).

Fig. 1

The three phases of MPM: a initialization phase, b Lagrangian phase, and c convective phase. Square markers and capital letters identify the mesh nodes, while round markers and small letters indicate the material points

While MPM algorithms are generally written using an explicit time integration [62, 63], recently, implicit formulations [64,65,66] are often preferred as they are more accurate and robust to simulate cases with small rate of deformation, or static and quasi-static problems. On top of that, the stability of the method (for properly chosen dissipative approaches) does not depend on the wave propagation speed within the media and, thus, allows the usage of a relatively larger time steps. Finally, implicit formulations are advantageous to solve multi-physics coupling problems, especially if MPM should be coupled with other implicit-based methods such as FEM [67]. A more recent extension of the implicit MPM to GIMP has been proposed and showed to work well for large deformation elastoplastic materials by [68, 69]. The three main phases of the classical implicit MPM are graphically summarized in Fig. 1.

• (a) Initialization phase

  • The material point-mesh connectivity is first defined by searching the element where each material point is located;

  • The kinematic information obtained at the previous time step n is mapped by means of mass projection from each material point p to the connectivity nodes as initial conditions.

    $$\begin{aligned} m_{I}^n= & {} \sum _{p=1}^{n_p} m_p N_{I}(\varvec{\xi }_{p}^n), \end{aligned}$$

    (17)
    $$\begin{aligned} \mathbf{q}_{I}^n= & {} \sum _{p=1}^{n_p} m_p \mathbf{v}_{p}^n N_{I}(\varvec{\xi }_{p}^n), \end{aligned}$$

    (18)
    $$\begin{aligned} \mathbf{f}_{I}^n= & {} \sum _{p=1}^{n_p} m_p \mathbf{a}_{p}^n N_{I}(\varvec{\xi }_{p}^n), \end{aligned}$$

    (19)

    where $n_p$ and $\varvec{\xi }_p$ are the total number of material points inside one element and local coordinate of the material point p inside the connectivity. Here, $\mathbf{f},\, \mathbf{q},\, \mathbf{v}$, and $\mathbf{a}$ denote the force, momentum, velocity, and acceleration vectors, respectively.

  • The corresponding initial nodal velocity and acceleration can be computed as:

    $$\begin{aligned} \tilde{\mathbf{v}}_{I}^n= & {} \frac{\mathbf{q}_{I}^n}{m_{I}^n}, \end{aligned}$$

    (20)
    $$\begin{aligned} \tilde{\mathbf{a}}_{I}^n= & {} \frac{ \mathbf{f}_{I}^n}{ m_{I}^n}. \end{aligned}$$

    (21)

• (b) Lagrangian phase

  • The discretized form of the governing equations (Eq. (14)) is solved on the active background mesh—those which contain material points—according to the scheme used.

• (c) Convective phase

  • The obtained solutions are interpolated back to the material points following:

    $$\begin{aligned} \mathbf{u}_{p}^{n+1}= & {} \sum _{I=1}^{n_n} N_{I}(\varvec{\xi }_{p}^n) \mathbf{u}_{I}^{n+1}, \end{aligned}$$

    (22)
    $$\begin{aligned} \mathbf{a}_{p}^{n+1}= & {} \sum _{I=1}^{n_n} N_{I}(\varvec{\xi }_{p}^n) \mathbf{a}_{I}^{n+1}, \end{aligned}$$

    (23)
    $$\begin{aligned} \mathbf{v}_{p}^{n+1}= & {} \mathbf{v}_{p}^n + \frac{1}{2} \Delta t \left( \mathbf{a}_{p}^n + \mathbf{a}_{p}^{n+1} \right) , \end{aligned}$$

    (24)

    where $n_n$ is the total number of nodes per geometrical element.

  • The position of the material points can be updated as:

    $$\begin{aligned} \mathbf{x}_{p}^{n+1} = \mathbf{x}_{p}^{n} + \mathbf{u}_{p}^{n+1}. \end{aligned}$$

    (25)

  • The background mesh is recovered to their initial undeformed configuration, and all the nodal variables are cleared.

The implicit approach implemented in this paper is an extension of the displacement-based formulation, which was originally proposed by Guilkey and Weiss [64]. Further details of the used algorithm, such as the prediction–correction scheme derived from Newmark integration scheme and its extension to incorporate mixed formulation, can be found in [55, 56, 59].

3 Treatment of Dirichlet boundary conditions

The treatment of boundary conditions in MPM, for both the Neumann and Dirichlet boundaries, is not always straightforward, since the material surface boundary $\Gamma = \partial \Omega$, most of the time, does not coincide with the mesh boundary. As discussed in Sect. 1, a number of different strategies have been adopted to overcome this problem in the past. From hereon, the boundary coinciding with the background mesh will be called grid-conforming boundary, while the nonconforming boundary will describe the boundary which does not coincide with the background element boundary (i.e., its nodes), see Fig. 2 for illustrative description. The current section will present the general formulation to apply grid-conforming boundary conditions in implicit MPM, followed by the proposed nonconforming boundary enforcement by means of the penalty method.

Fig. 2

Types of boundary conditions in MPM: grid-conforming (left) and nonconforming (right) boundary conditions

3.1 Grid-conforming boundary conditions

As commonly done in FEM, degrees of freedom (dofs) can be ordered such that the unknown dofs come first and the Dirichlet nodes afterward. The algebraic solution system now reads:

$$\begin{aligned} \begin{bmatrix} \mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}} &{} \mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}_{\Gamma _D}} \\ \mathbf{K}^{\mathrm{tan}}_{\mathbf{u}_{\Gamma _D} \mathbf{u}} &{} \mathbf{K}^{\mathrm{tan}}_{\mathbf{u}_{\Gamma _D}\mathbf{u}_{\Gamma _D}} \end{bmatrix} \begin{bmatrix} \Delta \mathbf{u} \\ \Delta \mathbf{u}_{\Gamma _D} \end{bmatrix} = - \begin{bmatrix} \mathbf{R}_{\mathbf{u}} \\ \mathbf{R}_{\mathbf{u}_{\Gamma _D}} \end{bmatrix}, \end{aligned}$$

(26)

where $\Delta \mathbf{u}$ is the increment of displacement evaluated at each time step such that, $\mathbf{u}^{n+1} = \mathbf{u}^{n} + \Delta \mathbf{u}$. The sub-matrices $\mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}}$ and $\mathbf{K}^{\mathrm{tan}}_{\mathbf{u}_{\Gamma _D}\mathbf{u}_{\Gamma _D}}$ are the stiffness matrix components which solely correspond to the regular displacement to solve $\mathbf{u}$ and the known displacement $\mathbf{u}_{\Gamma _D}$, whereas $\mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}_{\Gamma _D}}$ and $\mathbf{K}^{\mathrm{tan}}_{\mathbf{u}_{\Gamma _D} \mathbf{u}}$ are the off-diagonal components connecting the solved and prescribed displacements. In general, the tangent stiffness matrix is symmetric, and thus, $\mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}_{\Gamma _D}} = \left( \mathbf{K}^{\mathrm{tan}}_{\mathbf{u}_{\Gamma _D} \mathbf{u}}\right) ^T$. In addition to that, the residual right-hand-side vector $\mathbf{R}$ can also be split into two components related to $\mathbf{u}$ and $\mathbf{u}_{\Gamma _D}$, i.e., $\mathbf{R}_{\mathbf{u}}$ and $\mathbf{R}_{\mathbf{u}_{\Gamma _D}}$, respectively.

Hence, the goal is to obtain $\Delta \mathbf{u}_{\Gamma _D} = 0$, as if the following predictor–corrector scheme was used:

$$\begin{aligned} (\mathbf{predictor}\,\mathrm{on}\, \partial \Omega _D):\quad \mathbf{u}^{n+1,0}_{\Gamma _D}= & {} \bar{\mathbf{u}}, \end{aligned}$$

(27)

$$\begin{aligned} (\mathbf{corrector}\,\mathrm{on}\, \partial \Omega _D):\quad \mathbf{u}^{n+1,k}_{\Gamma _D}= & {} \mathbf{u}^{n+1,k-1}_{I} + \Delta \mathbf{u}^{k}_{\Gamma _D}\nonumber \\= & {} \bar{\mathbf{u}}, \end{aligned}$$

(28)

the Dirichlet boundary Eq. (5) is enforced automatically. The superscript k is used to denote iteration of the Newton–Raphson’s method. This can be accomplished by setting the off-diagonal elements of the tangent stiffness matrix, $\mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}_{\Gamma _D}}$ and $\mathbf{K}^{\mathrm{tan}}_{ \mathbf{u}_{\Gamma _D} \mathbf{u}}$, to zero, and assigning the diagonal components as identity, $\mathbf{K}^{\mathrm{tan}}_{ \mathbf{u}_{\Gamma _D} \mathbf{u}_{\Gamma _D}} = \mathbf{I}$. Meanwhile, the right-hand-side components corresponding to the Dirichlet conditions are also modified as $\mathbf{R}_{\mathbf{u}_{\Gamma _D}} = \mathbf{0}$. Equation (26) can, therefore, be rewritten as:

$$\begin{aligned} \begin{bmatrix} \mathbf{K}^{\mathrm{tan}}_{\mathbf{u} \mathbf{u}} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{I} \end{bmatrix} \begin{bmatrix} \Delta \mathbf{u} \\ \Delta \mathbf{u}_{\Gamma _D} \end{bmatrix} = - \begin{bmatrix} \mathbf{R}_{\mathbf{u}} \\ \mathbf{0} \end{bmatrix}. \end{aligned}$$

(29)

Solving the modified system yields the solution set $[\mathbf{u}^{n+1}, \bar{\mathbf{u}}]$, and the Dirichlet boundary conditions are automatically enforced.

Equation (29) works for both homogeneous and nonhomogeneous boundaries, as well as for roller supports if the boundary conditions are described in the direction of Cartesian coordinate bases, i.e., $\mathbf{e}_i$. However, this will not work for roller boundaries with an arbitrary inclination (Fig. 3). To accommodate the roller boundary conditions in an inclined configuration, a rotation matrix $\mathbf{Q}$ is introduced:

$$\begin{aligned} \mathbf{Q} = \begin{bmatrix} \hat{n}_x &{} \hat{n}_y &{} \hat{n}_z \\ \hat{t}_x &{} \hat{t}_y &{} \hat{t}_z \\ \hat{q}_x &{} \hat{q}_y &{} \hat{q}_z \\ \end{bmatrix}, \end{aligned}$$

(30)

where $\hat{\mathbf{n}}$, $\hat{\mathbf{t}}$, and $\hat{\mathbf{q}}$ are the unit normal vector perpendicular to the inclined surface and the two unit tangent vectors parallel to the surface, respectively. Note that, $\mathbf{Q}$ is orthogonal, and therefore, $\mathbf{Q}^T = \mathbf{Q}^{-1}$. The mapping between (n, t, q) and (x, y, z) can be performed as:

$$\begin{aligned} \mathbf{u}^\theta = \mathbf{Q} \mathbf{u} = [u_n \,\, u_t \,\, u_q ]^T, \end{aligned}$$

(31)

where $\mathbf{u}^\theta$ is the displacement described in the axis-aligned configuration.

Fig. 3

Grid-conforming slip or roller support with arbitrary inclination

We then use a similar approach to compute a partially axis-aligned system by multiplying Eq. (26) with a modified rotation matrix $\widehat{\mathbf{Q}}$ as:

$$\begin{aligned} \widehat{\mathbf{Q}} \mathbf{K}^{\mathrm{tan}} \left( \widehat{\mathbf{Q}}^T \widehat{\mathbf{Q}} \right) \Delta \mathbf{u}= & {} - \widehat{\mathbf{Q}} \mathbf{R} \\ \left( \widehat{\mathbf{Q}} \mathbf{K}^{\mathrm{tan}} \widehat{\mathbf{Q}}^T \right) \widehat{\mathbf{Q}} \Delta \mathbf{u}= & {} - \widehat{\mathbf{Q}} \mathbf{R} \\ \mathbf{K}^\theta \Delta \mathbf{u}^\theta= & {} - \mathbf{R}^\theta . \end{aligned}$$

(32)

$\widehat{\mathbf{Q}}$ is a block matrix with the following structure:

$$\begin{aligned} \widehat{\mathbf{Q}} = \begin{bmatrix} \left[ \mathbf{I} \right] &{} \left[ \mathbf{0} \right] \\ \left[ \mathbf{0} \right] &{} \left[ \mathbf{Q} \right] \end{bmatrix}, \end{aligned}$$

(33)

where the unsupported system is kept as it is, while the Dirichlet boundary is rotated by multiplying it with the rotation matrix $\mathbf{Q}$. Equation (32) can be expanded as:

(34)

As the partially rotated system has been obtained, we can then enforce support only in the normal direction, similar to the one in Eq. (29). This yields the following system:

(35)

Solving Eq. (35) will give:

$$\begin{aligned} \Delta \mathbf{u}^\theta _{\Gamma _D} = [0 \,\, \Delta u_{\Gamma _D,t} \,\, \Delta u_{\Gamma _D,q}]^T, \end{aligned}$$

(36)

which has to be rotated back to the original configuration before being added to the solution step. This modifies the predictor–corrector scheme specified by Eqs. (27) and (28) to:

$$\begin{aligned}&(\mathbf{predictor}\,\mathrm{on}\, \partial \Omega _D):\quad \mathbf{u}^{n+1,0}_{\Gamma _D} = \bar{u}_n \hat{\mathbf{n}}, \end{aligned}$$

(37)

$$\begin{aligned}&(\mathbf{corrector}\,\mathrm{on}\, \partial \Omega _D):\quad \mathbf{u}^{n+1,k}_{\Gamma _D} = \mathbf{u}^{n+1,k-1}_{I} + \mathbf{Q}^T \Delta \mathbf{u}^\theta _{\Gamma _D}, \end{aligned}$$

(38)

which results in a slip boundary condition that supports the normal direction but allows the tangential directions to move freely for arbitrary inclination.

3.2 Nonconforming boundary enforcement

The imposition of nonconforming Dirichlet boundary conditions in MPM should be as general and simple as possible, so that it can be used in practice, without the necessity of modifying the underlying parameterization. This is the main motivation behind the choice of implicit boundary imposition by means of penalty method proposed in the current work. The penalty method has been previously used just for contact algorithm in explicit [70, 71] and implicit [72] MPM. The method works seamlessly within the nonlinear implicit MPM framework established earlier for Dirichlet boundary enforcement. Furthermore, this work proposes and extends the usage of the method to include slip and releasing contact boundaries, which formulation will be elaborated in the current section and summarized in Algorithm 1 provided in Appendix A. While the following section will present an applicability of penalty method to implicit MPM, the technique has never been used in explicit MPM. However, it was used to couple trimmed B-Rep patches through weak enforcement in explicit IBRA by [73]. The formulation of penalty method in explicit MPM should not differ substantially from the current work, but the usage of smaller time step might be necessary to provide stability of the boundary imposition. The extension of the proposed implementation towards implicit GIMP [68, 69] or other variants of implicit MPM can be done with minimum modifications, although more comprehensive assessment of the accuracy and the feasibility of the penalty augmentation should be investigated further and is left for future works.

3.2.1 Penalty approach

The basic concept of the penalty method is introduced in this section, which can be used to impose Dirichlet boundary condition in two nonconforming discretizations. First, let’s assume two coupling boundary edges $\Gamma _1$ and $\Gamma _2$, which can be discretized by using any methods, e.g., as surface meshes, B-spline surfaces, or even as particles. Each of the boundary edge contains a corresponding displacement field $\mathbf{u}_1=\mathbf{u}_1(\mathbf{x}_1)$ and $\mathbf{u}_2=\mathbf{u}_2(\mathbf{x}_2)$, respectively. The penalty approach formulation to couple the displacement between the two surfaces starts with the following virtual work formulation:

$$\begin{aligned} \begin{aligned} \delta W^{\mathrm{penalty}}= & {} \beta \int _{\Gamma _1} \left( \mathbf{u}_1 - \mathbf{u}_2 \right) \cdot \left( \delta \mathbf{u}_1 - \delta \mathbf{u}_2 \right) \mathrm{d}\Gamma _1,\\= & {} \beta \int _{\Gamma _2} \left( \mathbf{u}_2 - \mathbf{u}_1 \right) \cdot \left( \delta \mathbf{u}_2 - \delta \mathbf{u}_1 \right) \mathrm{d}\Gamma _2, \end{aligned} \end{aligned}$$

(39)

where $\beta$ is the user-defined penalty factor. Here, $\delta W^{\mathrm{penalty}}$ corresponds to the coupling between the displacement (i.e., the position) of two coupling surfaces, written in a weak sense. Notice that the subscripts 1 and 2 are interchangeable, which should result in the same virtual work formulation independently whether the integral is computed along $\Gamma _1$ or along $\Gamma _2$. If the discretization of the surface $\Gamma _1$ is matching and consistent with the discretization of $\Gamma _2$, which means that the displacement is conforming $\mathbf{u}_1 = \mathbf{u}_2$, Eq. (39) vanishes and the coupling is inherently satisfied.

Dirichlet boundary imposition actually can be seen as a special type of surface coupling, with a prescribed displacement $\bar{\mathbf{u}}$, instead of the displacement fields $\mathbf{u}_2$ in $\Gamma _2$. We can then rewrite Eq. (39), assuming $\mathbf{u}=\mathbf{u}_1$, as:

$$\begin{aligned} \delta W^{\mathrm{penalty}} = \beta \int _{\Gamma _D} \left( \mathbf{u} - \bar{\mathbf{u}} \right) \cdot \delta \mathbf{u}_D \,\, \mathrm{d}\Gamma _D, \end{aligned}$$

(40)

where $\Gamma _D = \Gamma _1$ indicates the boundaries to be enforced.

Appending Eqs. (40) to (8), the modified system of equations can be written as:

$$\begin{aligned} \left( {\mathbf{K}}^{\mathrm{tan}} + {\mathbf{K}}^{\mathrm{penalty}} \right) \Delta \mathbf{u} = - \left( \mathbf{R} + {\mathbf{R}}^{\mathrm{penalty}} \right) , \end{aligned}$$

(41)

where ${\mathbf{K}}^{\mathrm{tan}}$ and $\mathbf{R}$ are the regular local tangent stiffness matrix and residual vector without the imposition (Eq. (10)). The additional penalty terms in the system matrix are given as:

$$\begin{aligned} {\mathbf{K}}^{\mathrm{penalty}} = \beta \int _{\Gamma _D} \mathbf{H}^T \cdot \mathbf{H} \,\, \mathrm{d}\Gamma _D, \end{aligned}$$

(42)

while the additional residual term is:

$$\begin{aligned} \begin{aligned} \mathbf{R}^{\mathrm{penalty}}&= \beta \int _{\Gamma _D} \mathbf{H}^T \cdot \left( \mathbf{u} - \bar{\mathbf{u}} \right) \,\, \mathrm{d}\Gamma _D\\&= \left[ \beta \int _{\Gamma _D} \mathbf{H}^T \cdot \mathbf{H} \,\, \mathrm{d}\Gamma _D \right] \left( \mathbf{u}_I - \bar{\mathbf{u}}_I \right) \\&= {\mathbf{K}}^{\mathrm{penalty}} \left( \mathbf{u}_I - \bar{\mathbf{u}}_I \right) \end{aligned} \end{aligned}$$

(43)

with matrix $\mathbf{H}$ being defined as follows:

$$\begin{aligned} \mathbf{H} = \begin{bmatrix} N_1 &{} 0 &{} 0 &{} \cdots &{} N_n &{} 0 &{} 0 \\ 0 &{} N_1 &{} 0 &{} \cdots &{} 0 &{} N_n &{} 0 \\ 0 &{} 0 &{} N_1 &{} \cdots &{} 0 &{} 0 &{} N_n \\ \end{bmatrix}. \end{aligned}$$

(44)

Here, the subscript n denotes the number of nodes for each element.

3.2.2 Extension to inclined roller boundary

An extension to the regular penalty imposition is to include the inclined roller (or slip) boundary condition, similar to what explained in Sect. 3.1 for grid-conforming boundary conditions (Eqs. (32)–(38)). However, instead of modifying the matrix and vector elements in the normal direction, the modification will interest only the tangential components.

Initially, the new linear system of equation including the penalty term should be rotated to the partially axis-aligned configuration as in Eq. (32).

Therefore, applying the modified block matrix to Eq. (41) yields:

$$\begin{aligned} \left( \widehat{\mathbf{Q}} \left[ \mathbf{K}^{\mathrm{tan}} + \mathbf{K}^{\mathrm{penalty}} \right] \widehat{\mathbf{Q}}^T \right) \widehat{\mathbf{Q}} \Delta \mathbf{u} = - \widehat{\mathbf{Q}} \left( \mathbf{R} + \mathbf{R}^{\mathrm{penalty}} \right) \end{aligned}$$

(45)

which can be rewritten as:

$$\begin{aligned} \left( \widehat{\mathbf{Q}} \mathbf{K}^{\mathrm{tan}} \widehat{\mathbf{Q}}^T + \widehat{\mathbf{Q}} \mathbf{K}^{\mathrm{penalty}} \widehat{\mathbf{Q}}^T \right) \widehat{\mathbf{Q}} \Delta \mathbf{u} = - \left( \widehat{\mathbf{Q}}\mathbf{R} + \widehat{\mathbf{Q}}\mathbf{R}^{\mathrm{penalty}} \right) . \end{aligned}$$

(46)

Calling

$$\begin{aligned} \mathbf{K}^{\theta }:= & {} \widehat{\mathbf{Q}} \mathbf{K}^{\mathrm{tan}} \widehat{\mathbf{Q}}^T,\\ \mathbf{K}^{\mathrm{penalty,\theta }}:= & {} \widehat{\mathbf{Q}} \mathbf{K}^{\mathrm{penalty}} \widehat{\mathbf{Q}}^T,\\ \mathbf{R}^\theta:= & {} \widehat{\mathbf{Q}}\mathbf{R},\\ \mathbf{R}^{\mathrm{penalty,\theta }}:= & {} \widehat{\mathbf{Q}}\mathbf{R}^{\mathrm{penalty}}, \end{aligned}$$

Equation (46) becomes:

$$\begin{aligned} \left( \mathbf{K}^{\theta } + \mathbf{K}^{\mathrm{penalty},\,\theta } \right) \Delta \mathbf{u}^\theta = - \left( \mathbf{R}^\theta + \mathbf{R}^{\mathrm{penalty},\,\theta } \right) \end{aligned}$$

(47)

Since Dirichlet constraint only interests $\mathbf{R}^{\mathrm{penalty},\,\theta }$ and $\mathbf{K}^{\mathrm{penalty},\,\theta }$, the other terms should remain untouched. The main idea of the following steps is to enforce the normal displacement by penalty terms, whereas the tangential directions are kept as it is (free to deform and not restricted by the additional penalty terms). The modified penalty stiffness and residual vector can be expanded as:

(48)

(49)

Finally, we can obtain the imposed rotated system with slip support as:

$$\begin{aligned} \left( \mathbf{K}^{\theta } + \mathbf{K}^{\mathrm{penalty},\,\theta }_{\mathrm{modified}} \right) \Delta \mathbf{u}^\theta = - \left( \mathbf{R}^\theta + \mathbf{R}^{\mathrm{penalty},\,\theta }_{\mathrm{modified}} \right) . \end{aligned}$$

(50)

Solving this modified system of equation will yield the Dirichlet imposition that is working for nonconforming boundaries with arbitrary inclination.

3.2.3 Imposing penalty conditions in MPM through boundary particles

Notice that the surface integrals in Eqs. (42) and (43) can be approximated through various approaches, which depend on how the surface topology is represented. In this work, a particle discretization technique is used to represent the continuous surface $\Gamma _D$ with a discrete number of boundary particles b. Hence, if this is the case, the continuous surface integral can be approximated as:

$$\begin{aligned} \int _{\Gamma _D} (\cdots ) \mathrm{d}\Gamma _D\approx & {} \int _{\Gamma _{D_h}} (\cdots ) \mathrm{d}\Gamma _{D_h} \nonumber \\= & {} \bigcup _{b=1}^{n_b} \int _{\Gamma _b} (\cdots ) \mathrm{d}\Gamma _b = \bigcup _{b=1}^{n_b} (\cdots ) A_b, \end{aligned}$$

(51)

where the last term can be written assuming that all the quantities inside the surface integral are independent of the surface.

The surface particle discretization is performed at the beginning of the simulation to generate boundary particles from an initial surface mesh, where the penalty conditions are imposed to the MPM. Here, the surface unit normal vector is also initially defined at each particle, which is needed when a contact boundary is considered (please refer to Sect. 3.2.4 for further discussion on the topic). The boundary particles are mass-less and only carry some necessary kinematic variables, as well as the boundary variables for imposition. Each of the generated boundary particle is assigned with a corresponding area which is needed to approximate surface integrals as in (51). The surface area of the particles can be initiated by a simple division operation in 2D and 3D cases as:

$$\begin{aligned} A_b = \frac{A^{\mathrm{3D}}_{\mathrm{mesh}}}{\bar{n}_{b}} = \frac{L^{\mathrm{2D}}_{\mathrm{mesh}}}{\bar{n}_{b}} \cdot t_{\mathrm{mesh}}, \end{aligned}$$

(52)

where $A_b$ indicates the area of particle condition (or boundary) b. Meanwhile, $A_{\mathrm{mesh}}$, $L_{\mathrm{mesh}}$, $t_{\mathrm{mesh}}$, and $\bar{n}_{b}$ are the area, length, thickness, and the number of boundary particle per initial mesh, which is an input parameter. An illustrative example of the associated boundary area in 3D assigned in the particle boundary is shown in Fig. 4. Boundary particles can be initiated similarly in 2D from line segments with length $L_{\mathrm{mesh}}$ and unit thickness $t_{\mathrm{mesh}}=1$. It is worth to note that, according to our experience, the number of boundary particles per line segment in 2D or a surface element in 3D should be more than, or at least equal to, the considered number of material point per cell.

Fig. 4

Surface discretization and boundary particle generation: (left) initial triangle surface mesh and (right) generated boundary particle with its integration weight contour

Numerical instability could appear when the nonconforming boundary intersects the background mesh very close to one of its edges. This instability is commonly known as the “small-cut” instability, very common also in FEM-based unfitted approaches [28, 74]. To overcome this issue a simple modification to the shape function values is performed while constructing matrix $\mathbf{H}$ in Eq. (44). The modified shape function value $\bar{N}_{Ib}$ for background node I at boundary particle b can be obtained as:

$$\begin{aligned} \bar{N}_{Ib}= & {} \frac{N_{Ib}^*}{ \sum _{I}^{n_n} N_{Ib}^*} \quad \mathrm{where}, \quad N_{Ib}^* = {\left\{ \begin{array}{ll} \epsilon ,&{} \text {if}\quad N_{Ib}\le \epsilon \\ N_{Ib},&{} \text {otherwise} \end{array}\right. }, \end{aligned}$$

(53)

where $\epsilon$ is the stabilization tolerance, which is often set to be $\epsilon = 0.01$, and $N_{Ib}= N_I(\mathbf{\xi }_b)$ is the original shape function value. Notice that, to ensure the partition of unity, the weighting procedure is necessary.

Another aspect which is worth to be noticed, especially in the presence of inclined roller support, is the definition of the unit normal vector, i.e., of the outward normal direction of the imposed boundary. First, the normal vector needs to be defined on each boundary particle b, $\hat{\mathbf{n}}_b$ when creating the boundary particles. Hence, the value of the $\hat{\mathbf{n}}_b$ is mapped (Fig. 5) at the beginning of each time step n to the background grid nodes I as:

$$\begin{aligned} \hat{\mathbf{n}}_{I}^n = \frac{ \sum _{b=1}^{n_b} \hat{\mathbf{n}}_{b}^n {{A}}_{b}^n {N}_{I}(\mathbf{\xi }_{b}^n)}{ \left\| \sum _{b=1}^{n_b} \hat{\mathbf{n}}_{b}^n {{A}}_{b}^n {N}_{I}(\mathbf{\xi }_{b}^n) \right\| }. \end{aligned}$$

(54)

The $\hbox {L}_2$ normalized unit normal vector of the background nodes, $\hat{\mathbf{n}}_I$, is required here to compute the tangential directions and to construct the rotation matrix $\mathbf{Q}_I$ (Eq. (30)). With this matrix in hand, the transformation of the global system is straightforward as described in (47). Please note that $\hat{\mathbf{n}}_b$ should be updated according to the boundary particle deformation.

Fig. 5

Illustrative figure describing unit normal vector of the imposed boundary particles and the background nodes

3.2.4 Contact consideration

One further extension feature of the nonconforming boundary conditions is to consider a releasing contact, which is exceptionally useful in many large deformation transient problems. Here, if nonsticking contact condition is assumed, a gap function g can be evaluated to describe the relative normal displacement between the kinematic fields and the imposed values. The gap function is normally evaluated at a certain boundary particle b, which is also assumed as the contact point, and expressed as:

$$\begin{aligned} g_b = \hat{\mathbf{n}}_b \cdot \left[ \mathbf{u}(\mathbf{x}_b) - \bar{\mathbf{u}}_b \right] = \hat{\mathbf{n}}_b \cdot \left[\sum _{j=1}^{n_n} N_j(\mathbf{\xi }_b) \mathbf{u}_j - \bar{\mathbf{u}}_b \right] , \end{aligned}$$

(55)

where $\hat{\mathbf{n}}_b$ indicates the unit normal vector pointing outwards and $u_p$ the prescribed displacement. The gap function g indicates whether the boundary condition should be imposed or not, i.e., if $g<0$, the continuum field nearby the boundary is penetrating the interface, and hence, the penalty imposition (Eq. (40)) should be appended to the system of equations. However, if $g \ge 0$, no further treatment is needed, and the particles at the vicinity of the contact area are allowed to separate.

By including the contact consideration using the aforementioned gap function, we can model a nonsticking contact condition for both nonslip and slip conditions. Moreover, this allows more accurate imposition of Dirichlet boundary conditions as it reduces the element band where the boundary condition is enforced. However, it requires smaller time increment for problems with high relative velocity towards the boundary, as otherwise, the boundary enforcement will be too late and the incoming material points may penetrate the nonconforming boundary surfaces.

4 Numerical examples

This section aims at assessing the quality of the numerical solutions achieved with the proposed MPM formulation with nonconforming penalty boundary condition. Four validation tests have been studied and will be presented in the following subsections. Here, the original MPM linear basis function with a Dirac delta characteristic function of MP volume is assumed for all cases.

• 1. A static hyperelastic cantilever beam under self-weight is used to investigate quantitatively the convergence of Dirichlet boundary imposition by changing the penalty factor $\beta$, the size of the background mesh, and material parameters.

• 2. The collapse of a granular column with nonconforming side walls is simulated to demonstrate the capability of the proposed boundary imposition in elastoplastic dynamic problems.

• 3. A rolling cylinder on an inclined slope is simulated in 2D and 3D to analyze the accuracy of the penalty-based contact and slip condition in comparison to analytical results.

• 4. A granular mixing problem in a rotating drum is addressed to demonstrate the applicability of a nonconforming (round) wall with prescribed displacement and detaching condition.

4.1 Static hyperelastic cantilever beam under self-weight

A two-dimensional static analysis of a hyperelastic cantilever beam is simulated to investigate quantitatively the convergence of the penalty boundary imposition by modifying numerical, geometrical, and material properties. The cantilever beam considered in this case has a length of $l=8\,\hbox {m}$ and a square cross section with unit area of $A = 1\times 1\,\hbox {m}^2$ as sketched in Fig. 6. The material model is assumed to be neo-Hookean hyperelastic. Initially, the material parameters are set as follows: density $\rho =1000\,\hbox {kg}/\hbox {m}^3$, Young’s modulus $E=90\,\hbox {MPa}$, and Poisson’s ratio $\nu =0.0$.

Fig. 6

Static hyperelastic beam: geometry, boundary conditions, and initial material parameters. The constrained left boundary is nonconforming with the background mesh

Three convergence studies were conducted to quantify the performance of the proposed method with respect to different numerical conditions. In this study, four material points per cell were considered for all simulations, whereas seven boundary particles per initial boundary segment were assumed. First, the influence of the penalty factor is measured by comparing the displacement obtained in the observation point A (Fig. 6) with the reference results conducted with direct enforcement of the boundary conditions on the nodes, as done in [55]. Both the absolute and the relative errors are evaluated according to

$$\begin{aligned} e_a= & {} \vert \delta _A - \delta _A^{\mathrm{ref}} \vert , \end{aligned}$$

(56)

$$\begin{aligned} e_r= & {} \left| \frac{ \delta _A - \delta _A^{\mathrm{ref}} }{ \delta _A^{\mathrm{ref}}} \right| , \end{aligned}$$

(57)

where the reference vertical displacement is denoted by $\delta _A^{\mathrm{ref}}$, which is equal to the following expression according to [75]:

$$\begin{aligned} \delta _A^{\mathrm{ref}} = - \left( \frac{\rho g (bhl) l^3}{8EI} + \frac{\rho g l^2}{2GA_s} \right) . \end{aligned}$$

(58)

where g is the gravity acceleration, $I = bh^3/12$ is the inertia of the beam section, and $A_s = 5/6 A$ is the reduced cross section area due to the shear effect. G is the beam shear modulus, which is equal to $G=\frac{E}{2(1+\nu )}$.

Figure 7 (left) shows that both errors are converging linearly as the penalty factor $\beta$ increases. It is observed that this linearly decreasing tendency is only valid up to a certain threshold. After passing a certain magnitude of penalty factor, the obtained results show a nonchanging behavior; this can be observed by the change of convergence slope around $\beta =10^{15}$. Moreover, Fig. 7 (right) demonstrates the converging tendency with respect to background mesh size, which is linear for very coarse meshes and quadratic at smaller element size. At larger element size, the error is observed to be governed by the choice of penalty factor, in this case $\beta =10^{15}$ is kept constant during the convergence study, whereas, at smaller element size, the error returns back to quadratic as the accuracy gained by reducing the element size is more dominant. However, this means that nonconforming imposition of boundary conditions in very coarse meshes exhibits lower accuracy than the standard grid-conforming approach which has a quadratic convergence rate as shown by [55].

Fig. 7

Static hyperelastic beam: convergence analysis: (left) varying the penalty factor $\beta$ and (right) varying the background element size

Last but not least, Fig. 8 shows the convergence analysis for different values of the Young’s modulus. As the Young’s modulus influences the condition number of the tangent stiffness matrix, the effective value of penalty factor is inherently influenced by the value of the material Young’s modulus. In Fig. 8 (left), the convergence lines, varying the penalty factor $\beta$ for four different values the of Young’s modulus, are plotted. There linear convergence is reached; this is expected and is previously shown in Fig. 7 (left). This is the motivation behind the convergence study shown in Fig. 8 (right). This convergence study gives an insight on how to choose the suitable value of penalty factor $\beta$ given a material’s Young’s modulus and the intended relative error. From the author’s experience, a ratio of $\frac{\beta }{E}=10^3-10^4$ is normally suitable to achieve a considerable accuracy for engineering analysis.

Fig. 8

Static hyperelastic beam: convergence analysis varying the Young’s modulus E for (left) regular and (right) weighted result

4.2 Granular column collapse with nonconforming side walls

A 2D granular column collapse simulation of noncohesive soil was simulated according to the two-dimensional experiment conducted by Bui [76]. In this validation case, the soil is modeled using a nonassociated elastoplastic model, assuming Mohr–Coulomb yield criterion as specified by Clausen [77]. However, the implementation of the model has been adapted to the finite strain assumption to handle relatively larger deformation at every time step. Here, the elastic material parameters of the granular soil are set to be: $E=840\,\hbox {kPa}$, $\nu =0.3$, and $\rho =2650\,\hbox {kg}/\hbox {m}^3$, for the material Young’s modulus, Poisson’s ratio, and density, respectively, whereas the plastic variables, such as the angle of internal friction, cohesion, and the angle of dilation are $\phi '=19.8^\circ$, $c'=0.0\,\hbox {kPa}$, and $\psi =0.0^\circ$, respectively, which describe a noncohesive, nondilative granular material.

In this example, the left and bottom side walls are assumed to be nonslip and implemented either as grid-conforming boundaries [57] or as nonconforming boundaries. The detailed simulation model can be seen in Fig. 9 with a zoomed region indicating the nonconforming boundary. Linear structured triangular elements with mesh size $h=0.002\,\hbox {m}$ are used as background mesh. Here, three material points per cell and six boundary particles per line segment are considered. The simulations are run until reaching the final runout ($t_{\mathrm{end}} = 2.0\,\hbox {s}$).

Fig. 9

Granular flow: simulation model with nonconforming Dirichlet boundaries

In Fig. 10, the obtained granular soil configurations, for both grid-conforming and nonconforming boundary conditions, are compared with the experimental data and the simulation results conducted by [76] using the smoothed particle hydrodynamics (SPH) method. One can observe, as indicated in Fig. 10c, that the obtained surface configuration and the failure line show a good agreement with the experimental measurement as well as the simulations conducted by other methods. As discussed before, the quality of penalty boundary imposition strongly depends on the input value of the penalty factor $\beta$. For this validation test, the penalty factor is chosen to be $\beta =10^{11}$. All in all, the nonconforming Dirichlet boundary imposition by penalty method can also be confirmed to work well with elastoplastic granular material model.

Fig. 10

Granular flow: simulation results obtained with a grid-conforming (default) and b nonconforming left and bottom walls; and c comparison of final surface configuration and failure with results obtained by [76]

4.3 Cylinder on an inclined slope

A cylinder rolling down an inclined slope of $60^{\circ }$ is simulated in both 2D and 3D. As the cylinder is solely driven by gravitational force, the achieved calculation results can be compared to the analytical solution as proposed by [78] for both rolling without slip and friction-less sliding conditions, which are enforced by the proposed Penalty Method. Figure 11 shows the geometry of the cylinder and the plane in 3D, where the diameter and height of the cylinder are both 100 cm. The 2D geometry is nothing but the cross section cut of the 3D model presented in Fig. 11.

Fig. 11

Cylinder on an inclined slope: geometry and boundary conditions

The material model is considered to be linear elastic with a very large stiffness and a density of $\rho =3000\,\hbox {kg}/\hbox {m}^3$. For the numerical model, an unstructured tetrahedral mesh is utilized having a mesh size of 8 cm. The cylinder itself is discretized initially by three material points located within each element. The condition is imposed by introducing nine boundary particles for each surface element, each of them having a penalty factor of $10^{18}$. The time step for the implicit calculation is chosen to be $10^{-3}$. The evolution of the position of the center axis of the cylinder in time is plotted in Fig. 12 and compared with the analytical solution for 2D and 3D case. One can observe that the obtained results match very well to the analytical solution for both the rolling and sliding conditions. This confirms the proposed method to being applicable for arbitrarily inclined slip conditions independently of the considered background mesh.

Fig. 12

Cylinder on an inclined slope: simulation results for frictionless slip condition in comparison to the analytical solution

It is worth noticing that in this numerical example the implemented contact algorithm, essential for rolling condition without slip, generally requires higher mesh resolution in comparison to the slip condition only. For instance, in 2D rolling condition, the solution plotted in Fig. 12 can be achieved by assuming mesh size of $h=1.25\,\hbox {cm}$, whereas, for the slip condition, the mesh size can be $h=8\,\hbox {cm}$, which is more than 6 times larger. This leads to the need of a significantly larger number of particles, especially for 3D case, increasing sensibly the computational cost and calling for distributed memory calculation capability.

4.4 Granular mixing in a rotating drum

To show the performance of the moving boundaries including the releasing contact algorithm, the example of the rotating drum proposed by Zuo et al. [79] is chosen. They compared the experimental data to the simulations obtained using the discrete element method as well as MPM and GIMP. It is worth noticing that, while this is a classical example to study the mixing of granular materials, in this paper it was chosen for the challenging imposition of boundary conditions: there is a circular, moving boundary, which requires releasing contact treatment. The mixing procedure itself is out of scope for the current work and will not be analyzed in detail.

The considered rotating drum, partially filled with dry granular material, has a diameter of 0.1 m and a height of 0.05 m. The three-dimensional geometry is reduced to a 2D plane strain model, represented in Fig. 13.

Fig. 13

Rotating drum: geometry and boundary conditions (left) and discretized simulations model (right)

The rotating speed of the drum is $\omega =10\,\hbox {rpm}$, while the gravitational acceleration is set as $9.81\,\hbox {m}/\hbox {s}^2$. The material model chosen for this example is the Mohr–Coulomb model, whereas Zuo et al. [79] used a Drucker–Prager yield surface with an equivalent set of parameters. The material parameters are set to be: $E=2700\,\hbox {Pa}$, $\nu =0.2$, and $\rho =920\,\hbox {kg}/\hbox {m}^3$, for the Young’s modulus, Poisson’s ratio, and density of the material, respectively. The plastic variables, such as the angle of internal friction, cohesion, and the angle of dilation, are $\phi '=27^\circ$, $c'=0.0\,\hbox {kPa}$, and $\psi =0.0^\circ$, respectively, which describe a noncohesive, nondilative granular material.

While a quadrilateral background mesh with element size of 3 mm is used for the simulation, an unstructured triangular mesh is employed for the discretization of the material points. The latter mesh size is set as 2 mm, and three material points per element are generated. Three mass-less boundary particles are located within each boundary segment, getting the corresponding information of the normal direction and the prescribed angular velocity which are updated during the calculation process by means of unit quaternions. For the implicit calculation scheme a time step of $5\times 10^{-4}$ is used.

Figure 14 presents the results of the simulation at time step $t = 0\,\hbox {s}$ and $t =3.5\,\hbox {s}$ in comparison to [79]. It can be observed that the obtained results show less mixing of the two materials. This is due to the fact that in the present simulation a contact model between the material points which allows relative sliding and separation between elements is not considered, while [79] considers friction contact condition between the granular material and drum particles. Nevertheless, the simulation results are in good agreement with the results by [79]. Furthermore, focusing on the boundary imposition two main achievements can be observed. First, the imposition of the nonconforming curved moving boundary can be imposed accurately without modeling the rotating drum as done by [79]. This may significantly reduce the computational cost. Secondly, even more important, by imposing the Dirichlet boundary condition using the proposed Penalty method, the problem of material points penetrating through the boundary layer, as observed in [79], can be resolved. Future works to include frictional contact boundary are necessary to improve the quality of the mixing.

Fig. 14

Rotating drum: comparison of the flow patterns from [79] (a–d) and results using penalty method (e)

5 Conclusions

The proposed penalty method, specially designed for an implicit MPM formulation, allows the imposition of Dirichlet boundary conditions on nonconforming, arbitrarily inclined and moving boundaries both in two and three dimensions. This is obtained by introducing moving boundary particles carrying an appended stiffness term determined by the penalty factor $\beta$. Hence, the implementation of the proposed method is straightforward as it solely requires an extra stiffness term as well as the corresponding residual force term to be appended to the global systems of equations, without modifying the discretization assumptions of the MPM algorithm. Furthermore, using the proposed approach, nonhomogeneous boundary conditions on top of the slip condition for arbitrary inclined boundary and releasing contact feature can be imposed without solving any additional equation.

However, the accuracy of the method has the classical limitations of the penalty approaches: it strongly depends on the value of the penalty factor $\beta$. While $\beta$ is required to be large enough to enforce the prescribed boundary condition, too large value of $\beta$ may result in an ill-conditioned tangent stiffness matrix. The penalty factor is influenced by various simulation parameters, such as, among others, the Young’s Modulus of the material and the element size of the background mesh, as well as by the prescribed Neumann boundary condition and other external loading. Hence, $\beta$ needs to be calibrated by the user. Nevertheless, this is inherent for the penalty method and not related to its adaption to MPM.

It is worth noting that the current implementation requires a predefined set of boundary particles to enforce the nonconforming boundary condition. The extension of the method to track and handle dynamic evolution of boundary particles will be left for future works since it may provide a tremendous benefits in simulating many hydro-geomechanical problems such as erosion and fracture problems. Nevertheless, as long as the boundary particles can be identified and reconstructed, the proposed technique can be applied straightforwardly to the newly constructed surface.

Several numerical examples have been simulated to assess the quality of the proposed work. The comparison of the results with the analytical solution proves the accuracy and expected convergence rate of the proposed method in two- as well as three-dimensional models. The method shows good agreement with experimental data available in the literature also in elastoplastic regimes. On top of that, the example of the granular mixing in a rotating drum shows the robustness and broad applicability of this method, as curved, moving nonconforming Dirichlet boundary conditions including a releasing contact formulation can be imposed in MPM using the proposed penalty method.

To conclude, the proposed enhancements make MPM more complete for the simulation of large deformation problems of granular and geomaterials and are of paramount importance for the predictive simulation and assessment of the effects caused by environmental phenomena like mud flow and avalanches.

Appendix A: Implicit MPM algorithm

The proposed formulation described in Sects. 2 and 3 is summarized in this appendix within Algorithm 1, which implementation is accessible in GitHub² under the Kratos-Multiphysics Particle Mechanics Application.