Skip to main content

Advertisement

SpringerLink
Log in

Joint probability analysis of streamflow and sediment load based on hybrid copula

  • Research Article
  • Published:
Environmental Science and Pollution Research Aims and scope Submit manuscript

Abstract

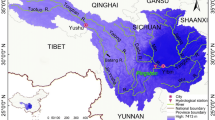
Statistical analysis of streamflow and sediment is very important for integrated watershed management and the design of water infrastructure, especially in silt-rich rivers. Here, we propose a bivariate joint distribution framework based on nonparametric kernel density estimation (KDE) and a hybrid copula function to describe the complex streamflow-sediment dependent structure. In this framework, the non-parametric KDE is used to fit the marginal distribution function of streamflow and sediment variables, and then the hybrid copula function is constructed by using the linear combination of Clayton, Frank, and Gumbel copulas, and compared with five commonly used single copulas (Clayton, Frank, Gumbel, Gaussian, and t). We use the Jinsha River Basin (JRB) in the Yangtze River’s (JR) upper reaches to verify the proposed method. The results show the following: (1) Compared with the gamma distribution (Gamma) and generalized extreme value (GEV) distribution of parameters, the marginal distribution function of streamflow and sediment variables can be effectively obtained based on nonparametric KDE. (2) Compared with the single copula, the hybrid copula function more fully reflects the complex dependent structure of streamflow and sediment variables. (3) Compared with the best single copula, the precision of return period based on hybrid copula can be increased by 7.41%. In addition, the synchronous probability of streamflow and sediment in JRB is 0.553, and the asynchronous probability of streamflow and sediment is 0.447. This study can not only improve the accuracy of streamflow and sediment statistical analysis in JRB, but also provide a useful framework for other bivariate joint probability analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

The data used in this study can be requested by the corresponding authors.

References

  • Aissia MAB, Chebana F, Ouarda TBMJ (2017) Multivariate missing data in hydrology – review and applications. Adv Water Resour 110:299–309

    Google Scholar 

  • Ayantobo OO, Li Y, Song S (2019) Multivariate drought frequency analysis using four-variate symmetric and asymmetric Archimedean copula functions. Water Resour Manage 33:103–127

    Google Scholar 

  • Abdollahi S, Akhoond-Ali A, Mirabbasi R, Adamowski JF (2019) Probabilistic event based rainfall-runoff modeling using copula functions. Water Resour Manage 33:3799–3814

    Google Scholar 

  • Bacchi B, Becciu G, Kottegoda NT (1994) Bivariate exponential model applied to intensities and durations of extreme rainfall. J Hydrol 155(1–2):225–236

    Google Scholar 

  • Bownan KO, Shenton LR (1982) Properties of estimators for the gamma distribution. Commun Stat Simul Comput 11(4):377–519

    Google Scholar 

  • Chen L, Guo S (2019) Flood coincidence risk analysis using multivariate copula functions. In: Copulas and its application in hydrology and water resources. Springer Water. Springer, Singapore

  • Coles S (2001) An introduction to statistical modeling of extreme values. Springer-Verlag, London

    Google Scholar 

  • Fang QS, Chen ZH, Zheng JP, Zhu ZH (2020) Comparison of pb (ii) and cd (ii) micro-interfacial adsorption on fine sediment in the pearl river basin, china. Int J Sedim Res 3:401–418

    Google Scholar 

  • Goel NK, Kurothe RS, Mathur BS, Vogel RM (1997) A derived flood frequency distribution for correlated rainfall intensity and duration. Water Resour Res 228(1–2):56–67

    Google Scholar 

  • Huang SZ, Li P, Huang Q, Leng GY (2017) Copula-based identification of the non-stationarity of the relation between runoff and sediment load. Int J Sediment Res 02(v.32):89–98

    Google Scholar 

  • Hu JF, Zhao GJ, Mu XM, Tian P, Gao P, Sun WY (2019) Quantifying the impacts of human activities on runoff and sediment load changes in a Loess Plateau catchment, China. J Soils Sediments 19:3866–3880

    Google Scholar 

  • Hu L (2006) Dependence patterns across financial markets: a mixed copula approach. Appl Financ Econ 16:717–729

    Google Scholar 

  • Huang KD, Chen L, Zhou JZ, Zhang JH, Singh VP (2018) Flood hydrograph coincidence analysis for mainstream and its tributaries. J Hydrol 565:341–353

    Google Scholar 

  • Huang L, Gao QF, Fang HW, He GJ, Reible D, Wang DC, Wu XH (2022) Effects of bedform migration on nutrient fluxes at the sediment–water interface: a theoretical analysis. Environ Fluid Mech 22:447–466

    Google Scholar 

  • Jiang C, Xiong LH, Yan L, Dong J, Xu CY (2019) Multivariate hydrologic design methods under nonstationary conditions and application to engineering practice. Hydrol Earth Syst Sci 23:1683–1704

    Google Scholar 

  • Ji YD, Li Y, Yao N, Biswas A, Chen XG, Li L, Pulatov A, Liu FG (2022) Multivariate global agricultural drought frequency analysis using kernel density estimation. Ecol Eng 177:106550

    Google Scholar 

  • Karmakar S, Simonovic SP (2008) Bivariate flood frequency analysis: part 1. determination of marginals by parametric and nonparametric techniques. J Flood Risk Manag 1(4):190–200

    Google Scholar 

  • Kim M, Yhang YB, Lim CM (2018) Gaussian copula method for bias correction of daily precipitation generated by a dynamical model. J Appl Meteorol Climatol

  • Lu CH, Dong XY, Tang JL, Liu GC (2019) Spatio-temporal trends and causes of variations in runoff and sediment load of the Jinsha river in china. J Mt Sci 16(10):2361–2378

    Google Scholar 

  • Li D, Lu XX, Yang X, Chen L, Lin L (2018) Sediment load responses to climate variation and cascade reservoirs in the Yangtze river: a case study of the Jinsha river. Geomorphology 322(DEC.1):41–52

    Google Scholar 

  • Li YT, Cai YP, Li Z, Wang X, Fu Q, Liu D, Sun L, Xu RH (2020a) An approach for runoff and sediment nexus analysis under multi-flow conditions in a hyper-concentrated sediment river, southwest china. J Contam Hydrol 103702

  • Li T, Wang S, Fu B, Feng XM (2020b) Frequency analyses of peak discharge and suspended sediment concentration in the United States. Journal of Soils Sediments 20:1157–1168

    Google Scholar 

  • Nourani V, Behfar N (2021) Multi-station runoff-sediment modeling using seasonal LSTM models. J Hydrol 1:126672

    Google Scholar 

  • Li H, Wang D, Singh VP, Wang Y, Wu J, Wu JC, Liu JF, Zou Y, He RM, Zhang JY (2019) Non-stationary frequency analysis of annual extreme rainfall volume and intensity using Archimedean copulas: a case study in eastern China. J Hydrol 571:114–131

    Google Scholar 

  • Li L, Ni JR, Chang F, Yu Y, Frolova N, Magritsky D, Borthwick AGL, Ciais P, Wang YC, Zheng CM, Walling D (2020c) Global trends in water and sediment fluxes of the world’s large rivers. Science Bulletin 65(1):62–69

    Google Scholar 

  • Nelsen RB (2006) An Introduction to Copulas, 2nd edn. Springer-Verlag, New York

    Google Scholar 

  • Nasr IB, Chebana F (2019) Homogeneity testing of multivariate hydrological records, using multivariate copula l-moments. Adv Water Resour 134(Dec):103449.1–103449.14

  • Peng Y, Shi Y, Yan H, Zhang JP (2020a) Multivariate frequency analysis of annual maxima suspended sediment concentrations and floods in the Jinsha river. China Journal of Hydrologic Engineering 25(9):05020029

    Google Scholar 

  • Peng Y, Yu XL, Yan HX, Zhang JP (2020b) Stochastic simulation of daily suspended sediment concentration using multivariate Copulas. Water Resour Manage 34:3913–3932

    Google Scholar 

  • Qian LX, Dang SZ, Bai CZ, Wang HR (2021) Variation in the dependence structure between runoff and sediment discharge using an improved copula. Theoret Appl Climatol 145:285–293

    Google Scholar 

  • Rüschendorf L (2009) On the distributional transform, Sklar’s theorem, and the empirical copula process. Journal of Statistical Planning & Inference 139(11):3921–3927

    Google Scholar 

  • Requena AI, Mediero L, Garrote L (2013) Bivariate return period based on copulas for hydrologic dam design: comparison of theoretical and empirical approach. Hydrol Earth Syst Sci Discuss 10:557–596

    Google Scholar 

  • Santhosh D, Srinivas V (2013) Bivariate frequency analysis of floods using a diffusion based kernel density estimator. Water Resour Res 49(12):8328–8343

  • Sedighi MP, Ramezani Y, Tahroudi MN, Taghian M (2022) Joint frequency analysis of river flow rate and suspended sediment load using conditional density of copula functions. Acta Geophys. https://doi.org/10.1007/s11600-022-00894-5

    Article  Google Scholar 

  • Shojaeezadeh SA, Nikoo MR, Mcnamara JP, Aghakouchak A, Sadegh M (2018) Stochastic modeling of suspended sediment load in alluvial rivers. Adv Water Resour 119(SEP):188–196

  • Shiau JT (2021) Lien YC (2021) Copula-based infilling methods for daily suspended sediment loads. Water 13(12):1701

    Google Scholar 

  • Silverman BW (1986) Density estimation for statistics and data analysis. Chapman and Hall, London

    Google Scholar 

  • Tootoonchi F, Sadegh M, Haerter JO, Rty O, Grabs T, Teutschbein C (2022) Copulas for hydroclimatic analysis: a practice‐oriented overview. Wiley Interdisciplinary Reviews: Water (9–2)

  • Tarn D (2004) Bandwidth selectors for multivariate kernel density estimation. University of Western Australia, Perth

    Google Scholar 

  • Vahidi MJ (2022) Bivariate analysis of river flow and suspended sediment load in Aharchai Basin, Iran. Arab J Geosci 0.15:1268

  • Walling DE, Fang D (2003) Recent trends in the suspended sediment loads of the world’s rivers. Global Planet Change 39(1–2):111–126

    Google Scholar 

  • Wu Y, Fang H, Huang L, Ouyang W (2019) Changing runoff due to temperature and precipitation variations in the dammed Jinsha river. J Hydrol 582:124500

    Google Scholar 

  • Wang C, Chang NB, Yeh GT (2010) Copula-based flood frequency (COFF) analysis at the confluences of river systems. Hydrol Process 23(10):1471–1486

    Google Scholar 

  • Wu JF, Yao HX, Chen XH, Wang GX, Bai XY, Zhang DJ (2022) A framework for assessing compound drought events from a drought propagation perspective. J Hydrol 2022:127228

    Google Scholar 

  • Yadav A, Chatterjee S, Equeenuddin SM (2021) Suspended sediment yield modeling in Mahanadi River, India by multi-objective optimization hybridizing artificial intelligence algorithms. Int J Sedim Res 36(1):76–91

    Google Scholar 

  • Yue S (2000) A bivariate gamma distribution for use in multivariate food frequency analysis. Hydrology Processes 15:1033–1045

    Google Scholar 

  • Yue S (2002) The bivariate lognormal distribution for describing joint statistical properties of a multivariate storm event. Environmetrics 13:811–819

    Google Scholar 

  • Yin JB, Guo SL, He SK, Guo JL, Hong XJ, Liu ZJ (2018) A copula-based analysis of projected climate changes to bivariate flood quantiles. J Hydrol 566

  • Zhang F, Shi XN, Zeng C, Wang L, Xiao X, Wang GX, Chen Y, Zhang HB, Lu XX, Immerzeel W (2020) Recent stepwise sediment flux increase with climate change in the Tuotuo river in the central Tibetan plateau. Science Bulletin 65(5):410–418

    Google Scholar 

  • Zhang JH, Sun MK, Deng ZM, Lu J, Wang DW, Chen L, Liu XY (2017) Runoff and sediment response to cascade hydropower exploitation in the middle and lower Han river, China. Math Problems Eng Theory Methods Appl 1–15

  • Zhang JP, Ding ZH, You JJ (2014) The joint probability distribution of runoff and sediment and its change characteristics with multi-time scales. J Hydrol Hydromech 62(3):218–225

  • Zhang L, Singh VP (2007) Bivariate rainfall frequency distributions using Archimedean copulas. J Hydrol 332(1–2):93–109

    Google Scholar 

  • Zhang PP, Cai YP, Xie YL, Yi YJ, Yang W, Li Z (2022) Effects of a cascade reservoir system on runoff and sediment yields in a River Basin of southwestern China. Ecol Eng 179:106616

    Google Scholar 

  • Zucchini W (2000) An introduction to model selection. J Math Psychol 44(1):41–61

    CAS  Google Scholar 

Download references

Funding

The research is financially supported by the National Natural Science Foundation of China (Grant No. 51879291).

Author information

Authors and Affiliations

  1. School of Civil Engineering, Sun Yat-Sen University, Guangzhou, 510275, China

    Xi Yang, Zhihe Chen & Min Qin

  2. Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai, 519000, China

    Zhihe Chen

  3. Guangdong Research Institute of Water Resources and Hydropower, Guangzhou, 510635, China

    Min Qin

Authors
  1. Xi Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhihe Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Min Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Xi Yang: data collection, conceptualization, methodology, writing-original draft. Zhihe Chen: writing-review and editing, funding acquisition. Min Qin: data collection, writing-review and editing.

Corresponding author

Correspondence to Zhihe Chen.

Ethics declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Responsible Editor: Marcus Schulz

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, X., Chen, Z. & Qin, M. Joint probability analysis of streamflow and sediment load based on hybrid copula. Environ Sci Pollut Res 30, 46489–46502 (2023). https://doi.org/10.1007/s11356-023-25344-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11356-023-25344-7

Keywords

Search

Navigation