A game-theoretic approach for pricing in a closed-loop supply chain considering product exchange program and a full-refund return policy: a case study of Iran

Abstract

The increasing rate of manufacturers and consequently the production of the products gave rise to an increase in used products. The growth in old goods, as well as their negative environmental and social consequences, prompted supply chain operators to focus more on reverse logistics for collecting and reusing these items. However, there are a few key issues that should be handled in this manner, covering how to implement an effective collecting plan. What categories of used items should be collected? And how should they be handled for the aim of reusing them? To address these questions, the pricing issues are investigated in a CLSC with a manufacturer and two retailers. As an effective collection strategy, the first retailer, along with selling new products, benefits from the product exchange program (PEP). In this program, the retailer, by offering two types of discounts on a new product’s price, is able to collect two types of products, including those without and with useful lifetime left as the first- and second-category products, respectively. In terms of used products management, the first-category products are sent to the manufacturer for recycling, and the second-category ones are sold as second-hand products by the first retailer. Besides, the first retailer exercises a full refund return policy, where the returned defective products, after being remanufactured by the manufacturer, are sold to customers by the second retailer in the secondary market. With respect to buy back price of first-category products from the first retailer, two scenarios are considered: 1) the manufacturer pays as much as the difference between the original retail price and discounted retail price in order to encourage the retailer to offer exercise the PEP for returned used items, or 2) by considering the discount on wholesale price, the manufacturer pays as much as the difference between the original wholesale price and discounted wholesale price. In this study, a real-world case study is considered based on an Iranian automotive industry to understand the issue better and obtain practical results. The findings show that the second scenario is more profitable due to lower selling prices and greater demand rates. It is proved that the PEP along with providing environmental benefits can improve supply chain financial profit even for the first or the second-category products.

Introduction

Nowadays, supply chains are coming across serious environmental challenges with the increasing rate of manufacturers. A large number of manufacturers lead to a higher amount of used or waste products and, consequently, the demand for sustainable and cost-effective solutions to protect the environment and prevent economic losses (Mondal and Giri 2020b). As a result, by taking into account the importance of logistics in the economic growth of countries (Suki et al. 2021), companies like Kodak, Xerox, and Caterpillar adopt a closed-loop supply chain (CLSC ) in order to collect wastes and used products to reduce their destructive effects and diminish production costs by recycling and reusing them (Rezayat et al. 2020). Closed-loop supply chain management (CLSCM) includes all forward-looking logistics such as raw material preparation, product production, and distribution (Sahebi et al. 2021). Along with all these factors, it can encompass reverse logistics for the collection and process of products (used or unused), including reuse, repair, recycling, and even disposal of materials, especially electronics, in terms of environmental requirements and socio-economic sustainability (Liu et al. 2021). Therefore, the first and general motivation of this study is incorporating CLSC since it helps sustainability in many ways, including reducing energy usage, material consumption, and discarded old items, and it is regarded as the greatest solution for used products by collecting and reusing them in the forward direction.

It should be taken into account that the desire of customers to return old goods is an important aspect of reverse logistics performance (Jolai et al. 2020). However, few individuals with adequate social responsibility return old products to collection facilities. As a result, collecting centers underperform. However, a collecting process’ efficiency is required for a CLSC network’s efficiency (Govindan et al. 2015). Consequently, incentives are required to encourage customers to return old goods. Thus, one of the goals of this research is to create an efficient incentive-based collection strategy called a Product Exchange Program (PEP). As can be understood from its name, an exchange involves exchanging a person’s staff for that of others that are almost the same in quality and value. The PEP can be used in various ways; for instance, resources needed or wanted by individuals or organizations can be exchanged through barter; this method can increase the product’s value, and it also can give a higher value to abolished or old items (Chang et al. 2019). In another way, companies like Apple use a strategy called “Trade In” as an exchange policy, making it easy to exchange any qualified smartphone for immediate credit to a new iPhone. This strategy provides a trade-in value of the used product to lower the price of a new iPhone (Apple 2021). Exchanging the old products with new or even remanufactured products at a discounted price is widely used in developing countries like India or China (Das and Dutta 2012).

Although the PEP could be a beneficial way to encourage people to return their used products, managing these products is the next challenge that supply chain managers come across due to a large number of returns (Bhatia and Kumar Srivastava 2019). The most common environmentally friendly way to deal with this issue is recycling. Recycling is not only an eco-friendly process, but it also reduces production costs and escalates the supply chain’s overall profit (Parsaeifar et al. 2019).

However, based on the supply chain owner’s policy, the returned used products are not always the EOL ones; the large proportion of returned products could be those with a useful lifetime left (Hosseini et al. 2019). Returned goods with varying useful lifetimes need different preparation. Most research on reverse logistics does not prepare for the lifetime of returned items. So, all gathered goods are believed to be remanufactured or recycled. This led this study to classify returned items depending on their remaining usable life, resulting in a new pricing concept for second-hand products.

During the past decades, the second-hand product market has gained more popularity since the new products are expensive and benefit from a longer useful lifetime thanks to the highly developed technologies (Dehghanbaghi and Dabbaghi 2021). Individuals prefer to utilize second-hand products not only because of the quality, value, and function, which are almost the same as new ones, but also because purchasing price of second-hand items categorized in “good-as-new” ones is significantly lower than new items (Chang et al. 2019).

The contents provided above refer only to the services which can be provided on sold goods. Although these services play a prominent role in customer satisfaction, especially in the case of being eco-friendly, some services can be offered on new products to increase customer loyalty and satisfaction.

Giving services like return policy allows any firm that wants to establish loyalty by surpassing consumers’ expectations to become a powerful repeat buy company rather than a one-time purchase one. Return policies allow consumers to return products easily and get all or part of their payment back (Jin et al. 2020). This policy is mostly used to increase demand, although increasing demand also increases return (Tao et al. 2021). In general, the use of return policies has increased customers’ satisfaction, ensured their loyalty, and improved product sales (Assarzadegan and Rasti-Barzoki 2020).

Therefore, another objective of this study is to consider return policy which not only made this study so comprehensive on reverse logistics and gave an opportunity to study the impact of used products and defective new product’s reverse logistics on each other, but it also let this study to incorporate services which are of great importance in customer’s loyalty and satisfaction.

Most past research on pricing problems has seldom employed the PEP, which enhances sales and customer satisfaction while also creating a collection mechanism for old items and an ecologically friendly supply chain as an incentive to collect used products. Furthermore, practically all prior research employed CLSC collection techniques to gather EOL items, with just a few focusing on products with various useful lifetimes left. As a result, managing these collected items is also a subject that has received little attention.

To fill this research need, this study looks at pricing issues in a CLSC, which includes a manufacturer and two retailers. The PEP is utilized for the first time as an incentive to collect old items with varying useful lifetimes, which is investigated in two situations. The gathered goods are handled in one of two ways: the retailer sells them as secondhand items or sends them to the manufacturer for recycling. As another novelty, in terms of providing service for new items, the model gets a full-refund return policy to recover defective new products as part of a comprehensive supply chain that also considers the reverse channel for used products. The Iranian automobile industry is explored as a real-world example. The below-mentioned questions are some of the important ones answered in this study:

• 1- Which payment strategies does the manufacturer use to pay for returned products under scenarios one and two are the most favorable for the retailer? What about the whole supply chain?

• 2- How is PEP suitable for the supply chain as well as the society?

• 3- What motivates a manufacturer to take necessary steps to reduce the number of defective new products?

• 4- In which process should the manufacturer invest first to be improved? Remanufacturing or recycling?

It is worth mentioning that this study added some contributions to the existing literature listed below:

• 1 This paper extends previous studies on product pricing using a game-theoretic approach in CLSC by simultaneously conducting an incentive-based collection strategy called PEP and return policy.

• 2 To be closer to real-world applications, the used product’s useful lifetime left is considered in collection and management.

• 3 As one of the pioneer studies, a second-hand product’s pricing is studied along with new ones.

• 4 A PEP for collecting used products and a full-refund return policy to collect new defective products are studied simultaneously in an integrated CLSC.

• 5 Finally, under two scenarios, decision variables are calculated, and results and managerial insights based on a case study are provided.

The rest of the paper is arranged in the following way. In the “Literature review” section, for reviewing related literature, firstly, the research background of key elements, including Closed-Loop Supply Chain (CLSC), product exchange, second-hand products, and the return policy, is investigated. The methodology, including a list of symbols, model description, assumptions, formulation as well as solving method, is presented in the “Methodology” section. The “Analysis” section, as the section of analysis and findings, contains scenarios comparison, numerical analyses considering a real case study from the automation industry are presented, some valuable managerial insights are gained, and policies are recommended. In the “Results and insights” section, the results based on important question asked in the “Introduction” section are provided. Conclusions and guidance for future research are presented in the “Conclusions” section. Table 1 refers to the acronyms used in this paper.

Table 1 Acronym list

Literature review

The reverse supply chain, in contrast to the classic one known as the forward supply chain, tries to take into account defective or End-of-life (EOL) products in an eco-friendly manner. The combination of classic and reverse supply chains resulted in a CLSC (Fu et al. 2021). In other words, CLSC is made up of two different cycles: forward and reverse logistics. Forward logistics is the process of creating and delivering a new product, while reverse logistics occurs after the product has fulfilled its function. Reverse logistics might include repairing, reselling, and dismantling items for reuse and recycling (Ritola et al. 2022), which attracted a great deal of attention among researchers. For instance, Jian et al. (2021) designed green CLSC considering fairness in the profit-sharing contract coordination to investigate the supply chain members’ decision-making. Under the Stackelberg game, Wu et al. (2020) developed quantitative models of two-level CLSCs that are environmentally friendly to examine investment decisions about environmental responsibility, pricing, and collection rates. Gorji et al. (2021) studied vehicles CLSC, where the government pays the take-back centers to deliver their used vehicles. In another study, Wen et al. (2020) investigated game models to examine the rate of collection as well as price decisions by taking into account environmentally responsible heterogeneous consumers. The authors in (Mondal and Giri 2020a) studied a multi-period CLSC model including a single manufacturer as well as a retailer to investigate the effects of marketing, product collection, and green innovation on supply chain decisions. Amirian et al. (2022) suggested a mathematical model in a heavy tires CLSC by examining the economic price of its goods under unpredictable situations.

Consumer returns play a significant part in CLSCs since successful collection techniques are specified in terms of them (Ritola et al. 2022). Consequently, many studies in the field of CLSC try to explore practical strategies to collect used products (Aminipour et al. 2021). In this regard, a PEP can be defined as one strategy that encourages customers to participate in the CLSCs sustainability process (Shekarian 2020). PEP could be defined as exchanging any used qualified products for immediate credit or a discount for a new one. This strategy provides value to the used product to lower the price of a new product. As a non-linear discount offer function, Das and Dutta (2019) investigated product exchange offer (PEO) in order to motivate customers to return used products and their willingness to accept this offer. In a study by Taleizadeh et al. (2019b), in the multi-period, multi-echelon CLSC, which was sustainable, planning discounts were used as incentives to return used products. Ray et al. (2021) investigated the profitability of “exchange offer” and “incentive offer” collection strategies for original equipment manufacturers as well as independent remanufacturers. In a two-echelon CLSC, Maiti and Giri (2017) studied two collection policies, wherein the first one, the collected, used products were considered as a fraction of new sold products, and in the second one, used products were collected via a product exchange offer by a retailer. Frequently, consumers evaluate the discount received as well as the new product’s price before deciding to participate in PEPs. Therefore, most of the time amount of collected products is considered under two types of discounts, including variable and fixed discounts. In this regard, the authors in (Genc and De Giovanni 2018) searched for the optimal discount mechanism in the PEP.

The way to manage collected used products is the next challenge that supply chain owners are coming across. The most often used techniques for managing these items are recycling, landfilling, and waste combustion (Hantoko et al. 2021). But selling these products as second-hand ones can be considered as another way which has an increasing trend in recent years. For instance, Fig. 1 shows the sale of new and second-hand vehicles in the USA from 1990 to 2019. In 2019 1,477,000 vehicles were sold, where 841,000 were second-hand compared to new ones, which were only 636,000 (BTS 2021).

Fig. 1

New and used cars sales in the USA

In general, the term “second-hand goods” refers to any new or used object that has been sold, traded, or swapped by its original owner, and he or she is not its owner anymore. In other words, products that do not belong to their first owners could be considered second-hand ones. Reviewing the literature on second-hand products, Turunen et al. (2020) examined values and meanings related to a way of selling second-hand luxury products. As a result, they presented the ways selling second-hand luxury products challenges the common meaning of the luxuriness. In terms of buying second-hand automobiles, Habib and Sarwar (2021) aimed to examine the concept of customers’ willingness and brand equity. The results showed a direct correlation between brand loyalty and equity with customers’ willingness to purchase second-hand automobiles. To measure online second-hand shopping motivation, Padmavathy et al. (2019) tried to model, improve and validate a scale. Results revealed that attitude and repurchase intentions could be positively predicted by online second-hand shopping motivation. Cianni (2020), for the first time, presented a pricing theory for almost all types of second-hand products. In this study, they built a framework and introduced cohort-specific model to explain used products’ price evolution. In the US automobile industry, as a buyback program, used rental cars are repurchased from rental agencies by manufacturers and redistributed through dealers. In this regard, Esenduran et al. (2020) investigated the effect of buyback pricing timing of second-hand cars on ordering decisions of intermediaries and the manufacturer’s profit.

A return policy can be considered a strategy that can play a prominent role in motivating customers to return their new defective products in a CLSC. A return policy is a policy by which, for any reason, a consumer has given the right to return a previously bought product to the merchant and refund it in the original method of payment (fully or partially), exchange it for another item, or receives shop credit (Wu et al. 2022). Reviewing the history of the return policy and its application in the supply chain reveals the widespread use of this policy in recent years. For example, Batarfi et al. (2017) studied generation, renovation, collection, and disposal procedures in a supply chain network. Also, a return policy was used in this model, where a refund is considered for returned purchased products. The authors in (Taleizadeh et al. 2019a) studied three stimuli: reduced carbon emissions, return policies, and efforts to improve quality and their effect on each other in a supply chain. Rokonuzzaman et al. (2021) examined the critical importance of a retailer's return policy in customers’ purchasing decisions. Assarzadegan and Rasti-Barzoki (2020), for the first time, introduced a return policy where buyers are allowed to return defective or healthy products. The retailer uses a full refund policy for defective products and also offers a partial refund for healthy returned products. In a mathematical model for the three-echelon supply chain, Dabaghian et al. (2022) examined the influence of the return method on profit margins as well as the best ratio of wholesale-retail pricing.

Table 2 summarizes the research backgrounds presented in various fields and the research conducted to fill the study gap. Also, Table 3 presents the most relevant papers and their gaps

Table 2 Comparison of the related articles

Table 3 The most relevant previous studies and the related research gaps

In this regard, to fill the study gaps, in this paper, a pricing issue in a CLSC containing a manufacturer and first and second retailers is considered. This model benefits from a return policy with a full refund in which defective products have a chance to be remanufactured by the manufacturer and sold to customers in another market by the second retailer. As an innovation, a PEP has been used as an incentive to collect old products to meet environmental requirements. All collected products are categorized into two categories based on their useful lifetime left and managed in two ways: second-hand and recyclable products that can be sold and recycled.

Methodology

List of symbols

The list of symbols is provided in Table 4.

Table 4 List of symbols

Model description

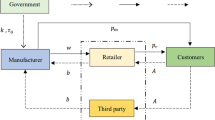
As shown in Fig. 2, in this study, the model includes one manufacturer along with the first and second retailers. The first retailer benefits from PEP to collect used products categorized into two categories by offering different discounts on new products. The first and second-categories include old products without and with a useful lifetime left. The exchange program is widely used by famous companies like Mercedes Benz or Apple, where customers enter the specifications of their used cars or mobile phones on the website. After estimating their prices by companies, if customers wish, they will be exchanged for new products (Apple 2021; Mercedes-Benz 2021). Or in Amazon Company customers may earn an Amazon gift card in exchange for qualified Amazon devices from different brands in more than 20 countries via the Amazon Trade-In program (Amazon 2022).

Fig. 2

A schematic representation of the suggested model

In this model, the collected products are managed in two ways. First-category products, as EOL ones, are sent by the retailer to the manufacturer for recycling purposes by receiving payment for each one. The second-category products are sold as second-hand products by the first retailer, just like what Amazon Company does in the Amazon warehouse project (Amazon 2021). The model also benefits from a return policy in which customers can get a full refund by taking back the defective new products. These products are sent to a manufacturer to remanufacture, and then they are sent to the second retailer to sell. The companies, including Wal-Mart, Hudson’s Bay, and Sear, offer full-refund on the wide range of the items they sell (Chen and Grewal 2013).

The manufacturer generates new products at the cost of ${c}_{m}$. The produced products are sold to the first retailer at a price of ${w}_{n}$ (${w}_{n}>{c}_{m}$), and the retailer offers them to customers at the price of ${p}_{n}$ which is higher than ${w}_{n}$.

The useful lifetime of products is indicated by $u,$ and their age is indicated by $z$. Customers who intend to participate in the PEP will benefit from a discount percentage of ${\lambda }_{1}$ on the price of new products if their old products meet the condition in Eq. (1), as first-category products. Other customers whose old products meet the condition in Eq. (2), as second-category products, will receive a discount percentage of ${\lambda }_{2}$ on the price of new products through PEP.

$$u-z\le 0$$

(1)

$$u-z>0$$

(2)

Considering various types of customers, the demand for new products (${D}_{n}$) consists of three proportions: $1) {\theta }_{1}:$ the proportion of demand for new products, including customers who do not have old products, 2) ${\theta }_{2}:$ the proportion of demand for new products, including customers who have first-category products, and 3) ${\theta }_{3}:$ the proportion of demand for new products, including customers who have second-category products where $0<{\theta }_{1},{\theta }_{2},{\theta }_{3}<1$, and ${\theta }_{1}+{\theta }_{2}+{\theta }_{3}=1$.

The first-category products, after being collected by the first retailer, are purchased by the manufacturer at a price of ${b}_{r}$ per product according to a study of (Savaskan and Van Wassenhove 2006). These products are recycled by the manufacturer and, assuming that their quality is the same as the new products made from raw materials (Savaskan et al. 2004), are sold to the first retailer as new products. The cost of production from raw materials (${c}_{m}$) is higher than from recycled materials (${c}_{c}$) (Savaskan et al. 2004). Therefore, the cost saved by the production from recycled materials for each unit based on Eq. (3) is ${\partial }_{1}$ which is a positive value (Zu-Jun et al. 2016).

$${c}_{m}-{c}_{c}={\partial }_{1}$$

(3)

Second-category products, after being collected by the first retailer, are prepared at the cost of ${c}_{s}$ to sell as second-hand products. The preparation includes all actions like cleaning, which make used products ready to sell again. The second-hand products are offered at a price of ${p}_{s}$ to the customers with the demand of ${D}_{s}$.

A return policy with a full refund is considered for new defective products. It means that if a defective product is returned, the full payment (${p}_{n}$) will be paid back, even to those who bought the product with a discount. It is assumed that the rate of return is equal to ${\theta }_{0}$, which is $0<{\theta }_{0}<1$. The first retailer sends back the returned products to the manufacturer in exchange for receiving ${w}_{n}$ per product (Assarzadegan and Rasti-Barzoki 2020). After remanufacturing, the manufacturer sells remanufactured items to the second retailer at a price of ${w}_{r}$ less than ${w}_{n}$. The second retailer sells these products at a price of ${p}_{r}$, which is less than ${p}_{n}$ (Souza 2013), and more than ${w}_{r}$. Demand for remanufactured products ${(D}_{r})$ is positive as all demands, and prices are used in this study.

In this paper, based on the payment, which the manufacturer pays to the first retailer for each unit of first-category products (${b}_{r}$), two scenarios are considered. 1) The manufacturer pays as much as the difference between the original retail price and discounted retail price (${\lambda }_{1}{p}_{n}$), or 2) by considering the discount on wholesale price, the manufacturer pays as much as the difference between the original wholesale price and discounted wholesale price (${\lambda }_{1}{w}_{n}$). It is clear that the payment in the first scenario is higher than in the second one, and this is the difference between the two scenarios. The only reason for paying more in the first scenario is to motivate the retailer to execute the PEP for used products.

Assumptions

This section contains five main assumptions that are considered in this model.

• 1) The new product’s price is higher than the second-hand ones (${p}_{n}>{p}_{s})$.

• 2) Given the operating cost of second-hand products ${(c}_{s})$, the first retailer’s profit from the sale of this type of product must be guaranteed; ${p}_{s}>{{\lambda }_{2}p}_{n}+{c}_{s}$.

• 3) The remanufacturing and recycling costs are fixed (Savaskan et al. 2004).

• 4) Due to the high maintenance cost for the first retailer, all returned used products in PEP with useful lifetime left (second-category products) must be sold as second-hand products; ${D}_{s}={\theta }_{3}{D}_{n}.$

• 5) Due to the high maintenance cost for the manufacturer, all products remanufactured must be sold; ${D}_{r}={\theta }_{0}{D}_{n}$ (Assarzadegan and Rasti-Barzoki 2020).

Formulation

The problem formulation is categorized into two categories, including 1) demand and 2) profit functions, and presented as follows.

Demand functions

In this model, price-dependent linear demand functions are provided in Eqs. (4)–(6). The demand function in this type has been used extensively in academic backgrounds (Sinayi and Rasti-Barzoki 2018; Kumar et al. 2018), where demand declines as product prices rise.

$${D}_{n}={\alpha }_{n}-{\upbeta }_{\mathrm{n}}{p}_{n}$$

(4)

$${D}_{s}={\alpha }_{s}-{\upbeta }_{\mathrm{s}}{p}_{s}$$

(5)

$${D}_{r}={\alpha }_{r}-{\upbeta }_{\mathrm{r}}{p}_{r}$$

(6)

where ${\alpha }_{n}$,${\alpha }_{s}$ and ${\alpha }_{r}$ as well as ${\upbeta }_{\mathrm{n}}$,${\upbeta }_{\mathrm{s}}$, and ${\upbeta }_{\mathrm{r}}$ are the market-based demands and the self-price elasticities, respectively for new, second-hand, and remanufactured products, respectively.

The profit functions

Scenario one

Consistent with the model description and assumptions, the profit functions of the manufacturer (${\pi }_{m}$) and retailers (${\pi }_{r1},$ and ${\pi }_{r2}$) in the first scenario are presented in Eqs. (7)–(9).

$${\pi }_{m}=\left({w}_{n}-{c}_{m}\left(1-{\theta }_{2}\right)-{c}_{c}{\theta }_{2}-{\theta }_{2}{{\lambda }_{1}p}_{n}\right){D}_{n}+\left({w}_{r}-{c}_{r}-{w}_{n}\right){\theta }_{0}{D}_{n}$$

(7)

$${\pi }_{r1}=\left({p}_{n}-{w}_{n}\right){\theta }_{1}{D}_{n}+\left({\left(1-{\lambda }_{1}\right)p}_{n}-{w}_{n}+{{\lambda }_{1}p}_{n}\right){\theta }_{2}{D}_{n}+\left({\left(1-{\lambda }_{2}\right)p}_{n}-{w}_{n}\right){\theta }_{3}{D}_{n}+ \left({w}_{n}-{p}_{n}\right){\theta }_{0}{D}_{n}+\left({p}_{s}-{c}_{s}\right){D}_{s}$$

(8)

$${\pi }_{r2}=\left({p}_{r}-{w}_{r}\right){D}_{r}$$

(9)

Based on Eqs. (7)–(9),${\pi }_{m}, {\pi }_{r1} \mathrm{\;and\;} {\pi }_{r2}$ consist of two, five, and one part, respectively, which are explained after Eq. (12).

Scenario two

In the second scenario, considering model description and assumptions, the manufacturer’s profit functions (${\pi }_{m}$) along with the profit function of retailers (${\pi }_{r1},$ and ${\pi }_{r2}$) are provided in Eqs. (10)–(12).

$${\pi }_{m}=\left({w}_{n}-{c}_{m}\left(1-{\theta }_{2}\right)-{c}_{c}{\theta }_{2}-{\theta }_{2}{{\lambda }_{1}w}_{n}\right){D}_{n}+({w}_{r}-{c}_{r}-{w}_{n}){\theta }_{0}{D}_{n}$$

(10)

$${\pi }_{r1}=\left({p}_{n}-{w}_{n}\right){\theta }_{1}{D}_{n}+\left({\left(1-{\lambda }_{1}\right)p}_{n}-{w}_{n}+{{\lambda }_{1}w}_{n}\right){\theta }_{2}{D}_{n}+\left({\left(1-{\lambda }_{2}\right)p}_{n}-{w}_{n}\right){\theta }_{3}{D}_{n}+ \left({w}_{n}-{p}_{n}\right){\theta }_{0}{D}_{n}+\left({p}_{s}-{c}_{s}\right){D}_{s}$$

(11)

$${\pi }_{r2}=\left({p}_{r}-{w}_{r}\right){D}_{r}$$

(12)

In the manufacturer’s profit function (${\pi }_{m}$), the first component in both scenarios expresses the income that the manufacturer gains from selling new products to the first retailer. Manufacture’s income from selling remanufactured defective products to second retailers is presented in the second part.

The profit function of the first retailer (${\pi }_{r1}$) in scenarios one and two consist of five components. The first, second, and third components represent the retailer’s revenue per product sale to ${\theta }_{1},{\theta }_{2},\mathrm{and\;}{\theta }_{3}$ proportions of new product’s demand, respectively. The second component also includes the retailer’s income in exchange for the return of first-category products to a manufacturer. The fourth component shows the revenue from sending back the returned products. The fifth part represents the retailer’s revenue from selling second-hand products. The profit function of the second retailer (${\pi }_{r2}$) in both scenarios represents its revenue from the sale of remanufactured products.

Solving method

Consistent with studies (Xu et al. 2018), the manufacturer is considered the leader, and retailers as followers. As depicted in Fig. 3, decisions are made to solve the problem in three stages; in the first stage, the new product’s wholesale price (${w}_{n}$) is determined by the manufacturer. Secondly, based on ${w}_{n}$, the manufacturer and the first retailer announce their price of remanufactured (${w}_{r}$) and new product’s (${p}_{n}$) prices, respectively. In the third stage, based on the prices determined in the first two stages, the first and the second retailers decide on their second-hand (${p}_{s}$) and remanufactured products (${p}_{r}$) prices, respectively. The problem is solved backward based on game theory principles (Aumann 2019).

Fig. 3

Decision-making sequence

The best values of decision variables in Scenario 1 

Based on Fig. 3, the best answers of decision variables in each step for the first scenario are derived.

Proposition 1

The best price of each unit of remanufactured (${p}_{r}^{*}$) and second-hand products $({p}_{s}^{*})$ is shown in Eqs. (13) and (14), respectively.

$${p}_{r}^{*}=\frac{{\theta }_{0}{\upbeta }_{\mathrm{n}}{p}_{n}{-\theta }_{0}{\alpha }_{n}+{\alpha }_{r}}{{\upbeta }_{\mathrm{r}}}$$

(13)

$${p}_{s}^{*}=\frac{{{\theta }_{3}{\upbeta }_{\mathrm{n}}{p}_{n}-\theta }_{3}{\alpha }_{n}+{\alpha }_{s}}{{\upbeta }_{\mathrm{s}}}$$

(14)

Proposition 2

The concavity of the first retailer’s profit function (${\pi }_{r1}$) in the new product’s selling price (${p}_{n}$) is proved. The ideal answer for the price of each new product (${p}_{n}^{*}$) based on the Karush–Kuhn–Tucker (KKT) method can be presented as Eq. (15).

$${p}_{n}^{*}=\frac{1}{2}\left(\frac{{{{(\upbeta }_{\mathrm{s}}(\upbeta }_{\mathrm{n}}\left({w}_{n}-{w}_{n}{\theta }_{0}+{\theta }_{3}{c}_{\mathrm{s}}\right)-{{\alpha }_{n}(\theta }_{0}-1+\theta }_{3}{\lambda }_{2}))+{\upbeta }_{\mathrm{n}}{\theta }_{3}(2{\theta }_{3}{\alpha }_{n}-{\alpha }_{s})}{{\upbeta }_{\mathrm{n}}\left({\upbeta }_{\mathrm{s}}(1-{\theta }_{0}-{\theta }_{3}{\lambda }_{2}\right)+{\theta }_{3}^{2}{\upbeta }_{\mathrm{n}})}\right)$$

(15)

Proposition 3

The ideal value of the wholesale price of each remanufactured item (${w}_{r}^{*}$) is provided in Eq. (16).

$${w}_{r}^{*}=\frac{{p}_{r}^{*}+{c}_{r}}{2}=\frac{1}{4}\left(\frac{\begin{array}{c}{2A}_{1}\left({\alpha }_{r}+{c}_{r}{\upbeta }_{r}-{\theta }_{0}{\alpha }_{n}\right)+{\theta }_{0}{A}_{3}{w}_{n}+{\theta }_{0}{A}_{2}\end{array}}{{\upbeta }_{r}{A}_{1}}\right)$$

(16)

Proposition 4

The concavity of manufacturer's profit function (${\pi }_{m}$) in new product’s wholesale price (${w}_{n}$) is proved, and the best value of the wholesale price of each new product (${w}_{n}^{*}$) is as Eq. (17).

$${w}_{n}^{*}=\frac{1}{2}\left(\frac{{A}_{4}}{{A}_{3}\left({{A}_{3}(2{\upbeta }_{\mathrm{r}}{\lambda }_{1}\theta }_{2}-{\theta }_{0}^{2}{\upbeta }_{n})-4{{A}_{1}\upbeta }_{r}{\upbeta }_{n}(1-{\theta }_{0})\right)}\right)$$

(17)

All proofs and the values of ${A}_{1},{A}_{2},{A}_{3}, and{A}_{4}$ are given in Appendix A.

The best values of decision variables in Scenario 2

Based on Fig. 3, the optimal answers of decision variables in each step for the second scenario are derived:

Proposition 5

The optimal price of each unit of remanufactured products (${p}_{r}^{*}$) and second-hand products (${p}_{s}^{*}$) is illustrated in Eqs. (18) and (19) respectively.

$${p}_{r}^{*}=\frac{{{\alpha }_{r}-\theta }_{0}{\alpha }_{n}+{\theta }_{0}{\upbeta }_{\mathrm{n}}{p}_{n}}{{\upbeta }_{\mathrm{r}}}$$

(18)

$${p}_{s}^{*}=\frac{{{\alpha }_{s}-\theta }_{3}{\alpha }_{n}+{\theta }_{3}{\upbeta }_{\mathrm{n}}{p}_{n}}{{\upbeta }_{\mathrm{s}}}$$

(19)

Proposition 6

The concavity of the first retailer’s profit function (${\pi }_{r1}$) in the new product’s selling price (${p}_{n}$) is proved. The best value of the price of each new product (${p}_{n}^{*}$) based on the Karush–Kuhn–Tucker (KKT) method can be presented as Eq. (20).

$${p}_{n}^{*}=\frac{1}{2}\left(\frac{{{{(\upbeta }_{\mathrm{s}}(\upbeta }_{\mathrm{n}}\left({w}_{n}-{w}_{n}{\theta }_{0}+{\theta }_{3}{c}_{\mathrm{s}}-{\theta }_{2}{\lambda }_{1}{w}_{n}\right)-{{\alpha }_{n}(\theta }_{0}-1+{\theta }_{2}{\lambda }_{1}+\theta }_{3}{\lambda }_{2}))+{\upbeta }_{\mathrm{n}}{\theta }_{3}(2{\theta }_{3}{\alpha }_{n}-{\alpha }_{s})}{{\upbeta }_{\mathrm{n}}\left({\upbeta }_{\mathrm{s}}(1-{\theta }_{0}-{\theta }_{3}{\lambda }_{2}\right)+{\theta }_{3}^{2}{\upbeta }_{\mathrm{n}})}\right)$$

(20)

Proposition 7

The best value of remanufactured product’s wholesale price (${w}_{r}^{*}$) is as Eq. (21).

$${w}_{r}^{*}=\frac{{p}_{r}^{*}+{c}_{r}}{2}=\frac{1}{4}\left(\frac{\begin{array}{c}{2B}_{1}\left({\alpha }_{r}+{c}_{r}{\upbeta }_{r}-{\theta }_{0}{\alpha }_{n}\right)+{\theta }_{0}{B}_{3}{w}_{n}+{\theta }_{0}{B}_{2}\end{array}}{{\upbeta }_{r}{B}_{1}}\right)$$

(21)

Proposition 8

The concavity of the manufacturer's profit function (${\pi }_{m}$) in the new product’s wholesale price (${w}_{n}$) is proved, and the optimal value of the wholesale price of each new product $({w}_{n}^{*})$ is presented in Eq. (22).

$${w}_{n}^{*}=\frac{1}{2}\left(\frac{{B}_{4}}{{B}_{3}\left(-{B}_{3}{\theta }_{0}^{2}-4{{B}_{1}\upbeta }_{r}(1-{{\theta }_{2}{\lambda }_{1}-\theta }_{0})\right)}\right)$$

(22)

All proofs and the values of ${B}_{1},{B}_{2},{B}_{3},\mathrm{\;and\;}{B}_{4}$ are given in appendix A.

Analysis

Various types of analyses, including scenarios comparison, and numerical analysis based on a real-world case study are investigated, and findings as well as managerial insights are presented.

Scenarios comparison

The first-category products, after being collected by the first retailer, are bought back by the manufacturer from the first retailer for recycling purposes. The buy-back price (${b}_{r}$) in scenario one is as the difference between the original retail price (${p}_{n}$) and discounted retail price (${(1-\lambda }_{1}){p}_{n}$) which equals to ${\lambda }_{1}{p}_{n}$.

On the other hand, by considering the discount on wholesale price, the buy-back price (${b}_{r}$) is as much as the difference between the original wholesale price (${w}_{n}$) and discounted wholesale price (${(1-\lambda }_{1}){w}_{n}$) which equals to ${\lambda }_{1}{w}_{n}$. The manufacturer’s payment is higher in scenario one (${\lambda }_{1}{p}_{n}$) than two (${\lambda }_{1}{w}_{n}$) due to the fact that it wants to encourage the retailer to participate in the PEP program.

According to the profit functions of the first retailer (${\pi }_{r1}$) and the manufacturer (${\pi }_{m}$), the manufacturer’s payment per unit of first-category products (${b}_{r}$) directly affects the second and first parts of ${\pi }_{r1}$ and the ${\pi }_{m}$, respectively. In the first scenario, when the first retailer collected products without a useful lifetime left (first category) and delivered them to the manufacturer, the first part of ${\pi }_{m}$ is as shown in Eq. (23).

$${w}_{n}-{c}_{c}-{{\lambda }_{1}p}_{n}$$

(23)

and the second part of ${\pi }_{r1}$ is equal to Eq. (24).

$${\left(1-{\lambda }_{1}\right)p}_{n}-{w}_{n}+{{\lambda }_{1}p}_{n}$$

(24)

In the same situation in scenario two, the first part of ${\pi }_{m}$ is as provided in Eq. (25).

$${w}_{n}-{c}_{c}-{\lambda }_{1}{w}_{n}$$

(25)

and the second part of ${\pi }_{r1}$ is equal to Eq. (26).

$${\left(1-{\lambda }_{1}\right)p}_{n}-{w}_{n}+{{\lambda }_{1}w}_{n}$$

(26)

It can be concluded that the first component of the manufacturer’s profit function in the second scenario is much more profitable than the first scenario based on Eqs. (23) and (25). On the other hand, considering Eqs. (24) and (26), the first scenario in comparison to the second one is profitable for the second part of the first retailer’s profit function. It is worth mentioning that these comparisons only show the differences between the first and the second scenarios profits based on the components of profit functions that the manufacturer’s payment per unit of first-category products directly affects. Therefore, the effect of each scenario on other parts of the manufacturer and first retailer’s profit functions may vary.

In this regard, the next section is provided to compare the effect of the scenarios on the whole components (directly and indirectly affected parts) of the first retailer (${\pi }_{r1}$) as well as the manufacturer’s (${\pi }_{m}$) profit functions. Besides, the difference between the values of the decision variables as well as demands in both scenarios is investigated based on Fig. 4.

Fig. 4

The difference between the values in scenarios one and two

The comparison shows that, although based on Eqs. (24) and (26), in scenario one, the second part of the first retailer’s profit function is more profitable than in scenario two, ${\pi }_{r1}$ in scenario two is higher than one.

In the first scenario, the manufacturer pays more per first-category products than in the second scenario (${\lambda }_{1}{p}_{n}>{\lambda }_{1}{w}_{n}$), which increases the manufacturer’s wholesale price (${w}_{n}$) and escalates the new product’s price (${p}_{n}$) based on Eq. (15). According to assumption 2, the price of second-hand products (${p}_{s}$) also increases. Due to Eqs. (4) and (5), the demand for new products (${D}_{n}$) same as the second-hand products (${D}_{s}$) decreases, which leads to the first retailer and the manufacturer ‘s profits (${\pi }_{r1} \mathrm{\;and\;} {\pi }_{m}, \mathrm{\;respectively}$) fall.

In this case, the remanufactured product’s wholesale price (${w}_{r}$) increases according to Eq. (16). This increment causes to rise in remanufactured product’s price (${p}_{r}$), ending in a drop in demand for remanufactured products (${D}_{r}$). Lower ${D}_{r}$ leads to lower ${\pi }_{r2} \mathrm{\;and\;} {\pi }_{m}.$  

From this sub-section, it can be concluded that in terms of higher profit level for whole members of the presented CLSC, the second scenario is better than the first one.

Numerical analysis: a case study

This section contains a real-world case study based on an Iranian automotive industry to understand the issue better and obtain practical results.

Iran’s automobile industry is the largest in Iran after the oil industry (Bahar 2008). Iran benefits from many car companies, the largest of which are the two state-owned companies Iran Khodrdo and Saipa. From January till June of 2020, Iran has produced a total of 473,461 vehicles, which is a growth of 20.2% compared to the same period last year, which was about 393,882 vehicles. A comparison between Iran’s car production statistics with other countries in the first half of 2020 shows that Iran is known as the 15th largest car producer in the world during this period due to a sharp decline in production in other countries and sanctions (OICA 2020). Iran’s automotive industry is trying to increase its production to 3 million units per year by 2025 (IVMA 2015).

Statistics released by the Global Carbon Project show that Iran is the seventh-largest air polluter in the world, with an annual emission of 648 million tons of carbon dioxide. These statistics show that Iran almost accounts for 2% of the world’s carbon dioxide emissions (GCP 2020). According to the latest report from the Communication and International Affairs Center of Tehran Municipality about the main polluters in the capital of Iran, Tehran, the share of vehicles in air pollution is about 83%. Among them, the largest share is related to private vehicles, with about 38% (CCIA 2019).

To reduce environmental pollution, the Iranian Fuel Conservation Company in cooperation with two Iranian car companies, including Iran Khodro and Saipa, has presented a plan for 2020 (IFCO 2020). In this plan, the owners of old cars will receive a new product with a discount by delivering their old vehicles. Saipa Company offers its product called Tiba in exchange for delivering old personal cars (Emdad 2020). In this study, the data of this car available on the website of Saipa Automotive Company (Saipa 2020) is used. The study of Saeedi et al. (2010) has been used to estimate the price elasticity and demand for cars in Iran.

The impacts of changes in important parameters on the decision variables and functions are investigated in this section. The parameters’ values for both scenarios are prepared in Table 5. The data provided is from the Iranian automotive industry; however, some data is an estimate of actual data.

Table 5 Parameters’ values for case study

Discount on the new products in exchange for first-category products (${{{\lambda}}}_{1}$)

In this subsection, the effect of discount on the new products in exchange for first-category products (${\lambda }_{1}$) on selected decision variables as well as demands and profit functions is examined as shown in Fig. 5.

Fig. 5

The impact of ${\lambda }_{1}$ on selected decision variables, demands, and profit functions

Figure 5 clearly shows that, in general, increasing ${\lambda }_{1}$ causes a fall in total supply chain’s profit like the results in (Heydari et al. 2017). Therefore, the best value for the ${\lambda }_{1}$ could be zero but it is impossible because of PEP and environmental concerns.

This shrank in the supply chain’s profit happens because as ${\lambda }_{1}$ increases the ${b}_{\mathrm{r}}$, due to its amounts ${\lambda }_{1}{p}_{\mathrm{n}}$ and ${\lambda }_{1}{w}_{\mathrm{n}}$ in the first and the second scenarios, it increases as well. It means that a higher amount of ${\lambda }_{1}$ makes the manufacturer pay more to the retailer for each first-category products. Therefore, to reduce loss, the manufacturer chooses two ways simultaneously and rises both the new product’s wholesale price (${w}_{\mathrm{n}}$), Fig. 5(b), as well as the wholesale price of remanufactured products (${w}_{\mathrm{r}}$), Fig. 5(c).

On the one hand, the rise in ${w}_{\mathrm{n}}$ gives rise to the increase in the new products price (${p}_{\mathrm{n}}$), Fig. 5(d), which decreases the demand (${D}_{\mathrm{n}}$) for these types of products, Fig. 5(f). Also, a fall in ${D}_{\mathrm{n}}$ causes a drop in the return rate of first-category products. It means that based on Eq. (3), manufacturer’s production cost increases due to lower recycled materials. On the other hand, higher ${w}_{\mathrm{r}}$ results in higher remanufactured product’s price (${p}_{\mathrm{r}}$),Fig. 5(e), and drop in demand (${D}_{\mathrm{r}}$), Fig. 5(g). The decreased ${D}_{\mathrm{n}}$ and${D}_{\mathrm{r}}$, and the lower amount of EOL products for recycling cause a drop in retailer’s as well as manufacturer’s profits (${\pi }_{r1}, {\pi }_{r2} ,\mathrm{\;and\;} {\pi }_{m}$)(Fig. 5(h, i and j)).

Comparing the first and the second scenarios, it can be concluded that the loss in the profit of supply chain members in scenario two is far less than in scenario one. This happens for the sake of the difference between the payment per unit of first-category products in the first and the second scenarios, ${\lambda }_{1}{p}_{\mathrm{n}}$ and ${\lambda }_{1}{w}_{\mathrm{n}}$, respectively. Considering that the ${p}_{\mathrm{n}}$ is higher than ${w}_{\mathrm{n}}$, the payment in the second scenario is less than in the first scenario, which causes less profit loss for the manufacturer and a slight increase in ${w}_{\mathrm{n}}$ and ${w}_{\mathrm{r}}$.

An interesting point in Fig. 5 is that the increment rates in the first retailer’s profit (${\pi }_{r1}$) in scenario one and two are almost equal, and there is no noticeable difference between them. By considering the second component of the profit function of retailer one, Eq. (27), in both scenarios, it can be seen that in the first scenario, the first retailer’s received payment from the manufacturer for each first-category product (${{\lambda }_{1}p}_{n}$) is equal to its discounted selling price (${{\lambda }_{1}p}_{n}$).

$${\left(1-{\lambda }_{1}\right)p}_{n}-{w}_{n}+{{\lambda }_{1}p}_{n}={p}_{n}-{w}_{n}$$

(27)

As a result, with increasing ${\lambda }_{1}$ the first retailer suffers only from higher ${w}_{\mathrm{n}}$, which causes to rise in${p}_{\mathrm{n}}$. But, in the second scenario, with increasing${\lambda }_{1}$, the first retailer is not only suffering from the higher ${w}_{\mathrm{n}}$ but it also struggles with more profit loss from higher discounted selling prices (${{\lambda }_{1}p}_{n}$) and lower payments from the manufacturer ${({\lambda }_{1}w}_{n})$ as the Eq. (28).

$${\left(1-{\lambda }_{1}\right)p}_{n}-{w}_{n}+{{\lambda }_{1}w}_{n}={p}_{n}-{{\lambda }_{1}p}_{n}-{w}_{n}+{{\lambda }_{1}w}_{n}$$

(28)

It can be concluded that the rise in a discount on the new products in exchange for first-category products (${\lambda }_{1}$) causes a fall in the total supply chain’s profit in both scenarios. However, the supply chain comes across less profit loss if it chooses the second scenario. Although in the whole supply chain’s point of view, the second scenario is better, for the first retailer, there is no significant difference between scenarios since its profit loss in both scenarios is almost the same.

Discount on the new products in exchange for second-category products (${{{\lambda}}}_{2}$)

In this subsection, the effect of discount on the new products in exchange for second-category products (${\lambda }_{2}$) on all decision variables as well as demands and profit functions in both scenarios is examined as shown in Fig. 6.

Fig. 6

The impact of ${\lambda }_{2}$ on selected decision variables, demands, and profit functions

As can be deduced from Fig. 6, by increasing ${\lambda }_{2}$ the total profit of the supply chain drops, which means that approaching ${\lambda }_{2}$ to zero makes the supply chain more profitable. This is consistent with and consistent with the study of (Saha et al. 2016) in which it was shown that an increase in discounts drops the manufacturer’s profit as a discount provider as well as the whole supply chain. However, a decrease in ${\lambda }_{2}$ makes the first retailer lose demand for new products in exchange for second-category products (${\theta }_{3}{D}_{n}$) as a part of PEP.

The main reason for the falling supply chain’s profit with increasing ${\lambda }_{2}$ is that, based on assumption 2, higher ${\lambda }_{2}$ leads to higher price of second-hand products (${p}_{s}$), Fig. 6(b). This falls the demand for second-hand products $({D}_{s})$, Fig. 6(f), which causes a drop in the first retailer’s profit in selling second-hand products as well, Fig. 6(g). To reduce the profit loss, the first retailer tends to increase the new products price (${p}_{n}$), Fig. 6(a). But considering the devastating effect of higher retail price on new product’s demand (${D}_{n}$), Fig. 6(e), and the first-category product’s return rate, the manufacturer tries to help the first retailer by decreasing the new product’s wholesale price (${w}_{n}$) Fig. 6(c). The results show that the impact of profit loss in selling second-hand products on the first retailer is higher than the lower wholesale price (${w}_{n}$) which makes the first retailer rise the new products price (${p}_{n}$), Fig. 6(a). Therefore, the demand (${D}_{n}$) and the profit of the first retailer $({\pi }_{r1})$ drop, Fig. 6(e and g), respectively.

On the other hand, the manufacturer tries to reduce the loss by increasing the remanufactured product’s wholesale price (${w}_{r}$), Fig. 6(d), but it gives rise to a drop in remanufactured product’s demand (${D}_{r}$) as well as the second retailer’s profit $({\pi }_{r2})$, Fig. 6(i), making the manufacturer’s profit $({\pi }_{m})$ decline more than before, Fig. 6(h).

Comparing two scenarios, increase in ${\lambda }_{2}$ leads to the significant difference between ${p}_{n}$ in the first and second scenarios leading to a noticeable difference in ${D}_{n}$ as well. This makes the second scenario much more profitable than the first one. But for the first retailer, the amount of profit $({\pi }_{r1})$ and its reduction rate are almost equal in both scenarios. There is one explanation in this regard. Based on Eq. (27) in the first scenario, as ${p}_{n}$ increase and ${w}_{n}$ decrease, the first retailer receives much more payment for each returned first-category products ${(\lambda }_{1}{ p}_{\mathrm{n}})$ and reduces its profit loss.But in the second scenario, based on Eq. (28), the first retailer receives less payment ${(\lambda }_{1}{ w}_{\mathrm{n}})$ which rises its profit loss. It means that, although in whole supply chain’s point of view, with increasing ${\lambda }_{2}$ the second scenario is more profitable than the first one due to the lower ${w}_{n}$,and ${p}_{n}$ leading to higher ${D}_{n}$, for the first retailer, this is vice-versa.

It can be inferred that just like the ${\lambda }_{1}$, the increase in ${\lambda }_{2}$ causes a drop in the total profit of the supply chain, which is sharper in the first scenario than in the second. And it is worth mentioning that the manufacturer tries to reduce the devastating effect of the rise in ${\lambda }_{2}$ by decreasing ${w}_{\mathrm{n}}$, since higher ${\lambda }_{2}$ drops the demand for new products leading to the fall in the return rate of first-category products which manufacturer recycles.

The effect of the product exchange program (PEP) on the supply chain’s profit (${{{\pi}}}_{{{t}}}$)

Based on the previous analysis, it is concluded that an increase in ${\lambda }_{1 }\mathrm{and} {\lambda }_{2}$ as the PEP drops the supply chain’s profit. Therefore, this may raise the question that except for the environmental benefits that using PEP in the supply chain brings by collecting and recycling, and reusing old products, does this program bring any financial benefit?

To answer this question, the supply chain’s total profit (${\pi }_{t}={\pi }_{m}+{\pi }_{r1}+{\pi }_{r2}$) is compared in four modes, including 1) the supply chain with a full PEP (exchange program for the first and second-category products) (${\theta }_{2}\ne 0$ and ${\theta }_{3}\ne 0$), 2), the supply chain with PEP for customers with first-category products only (${\theta }_{2}\ne 0$ and ${\theta }_{3}=0$), 3) the supply chain with PEP for customers with second-category products only (${\theta }_{2}=0$ and ${\theta }_{3}\ne 0$), and 4) the supply chain without PEP (${\theta }_{2}=0$ and ${\theta }_{3}=0$). To compare the profits of different modes in the equal condition, it assumed that ${\theta }_{2}={\theta }_{3}=0.25$

The comparison between modes shows that the supply chain with a full PEP (Mode 1) in both scenarios is far profitable than without it (Mode 4). Table 6 can lead to the conclusion that even the supply chain with partial PEPs (Modes 2 and 3) is profitable compared to Mode1. The reason is with PEP, the total demand (${D}_{\mathrm{n}}$) is not limited to the customers without having new products, and people with the first- and second-category products are attracted to update their old products, which causes a surge in ${D}_{\mathrm{n}}$. Consequently, the PEP not only is environmentally friendly but also extends the supply chain’s market and increases its profit (${\pi }_{t}$).

Table 6 Total profit values in different modes

Another result that can be obtained from Table 6 is that in both scenarios, the PEP regarding second-category products only (Mode 3) brings higher benefit (${\pi }_{t}$) in comparison to the PEP for the first-category products only (Mode2) while the full PEP (Mode 1) stays on top.

From the analyses presented in this section, it can be concluded that the PEP not only brings environmental benefits to the supply chain by encouraging customers to return back their old products, but it also can help the supply chain to be much more profitable. This happens since the PEP creates more demand by attracting customers with old products. Besides, the PEP in the second scenario leads to a higher profit level for the supply chain (${\pi }_{t}$) compared to the first one.

The simultaneous effect of ${{{\lambda}}}_{1}$ and ${{{\lambda}}}_{2}$ on the profit of the second retailer (${{{\pi}}}_{{{r}}2}$)

Based on Fig. 7 in both scenarios, the increase in ${\lambda }_{1}$ and ${\lambda }_{2}$ makes the second retailer’s profit (${\pi }_{r2}$) drop. This happens due to the fact that an increase in ${\lambda }_{1}$ and ${\lambda }_{2}$ reduces manufacturer’s profit (${\pi }_{m}$) as stated in subsections 4.2.1 and 0. Therefore, to reduce the profit loss, it rises the wholesale price of remanufactured products (${w}_{r}$), which leads to higher remanufactured products price (${p}_{r}$), and drop in second retailer’s profit (${\pi }_{r2}$).

Fig. 7

The simultaneous effect of ${\lambda }_{1}$ and ${\lambda }_{2}$ on ${\pi }_{r2}$

In both scenarios, ${\lambda }_{1}$ has a greater impact on falling second retailer’s profit (${\pi }_{r2}$) than ${\lambda }_{2}$.with increasing ${\lambda }_{1}$ the manufacturer loses the profit more since along with paying more to the first retailer for each returned first-category product (${b}_{r}$), in the first and the second scenarios (${\lambda }_{1}{p}_{\mathrm{n}}$ and ${\lambda }_{1}{w}_{\mathrm{n}},\mathrm{ respectively}$) the return rate of first-category products falls. This drop reduces the recycled materials and increases the production cost. Hence, the manufacturer rises the ${w}_{r}$ more.

The decline in profit of the second retailer (${\pi }_{r2}$) is less in scenario two than the one because, in scenario two, the manufacturer has to pay ${b}_{r}=$ ${\lambda }_{1}{w}_{\mathrm{n}}$ to the first retailer, which is less than ${b}_{r}=$ ${\lambda }_{1}{p}_{\mathrm{n}}$. As a result, the rise in ${w}_{r}$ to reduce the profit loss is minor in the second scenario than the first one.

It can be concluded that an increase in ${\lambda }_{1}$ and ${\lambda }_{2}$ makes the second retailer’s profit (${\pi }_{r2}$) drop. In lower rates of ${\lambda }_{1}$ and ${\lambda }_{2}$, the difference between the scenarios is slight, but as they increase ${\pi }_{r2}$ falls, which is sharper in the first scenario than the second one.

The return rate of defective new products (${{{\theta}}}_{0}$)

The impact of increasing return rate of defective products (${\theta }_{0}$) on selected decision variables as well as demands and profit functions in both scenarios is investigated in this subsection as shown in Fig. 8.

Fig. 8

The impact of ${\theta }_{0}$ on selected decision variables, demands, and profit functions

Although for some values of ${\theta }_{0}$ the manufacturer and second retailer’s profit $({\pi }_{m} \mathrm{and} {\pi }_{r2},\mathrm{ respectively})$ increase, consistent with (Assarzadegan and Rasti-Barzoki 2019) generally, a rise in ${\theta }_{0}$ drops the supply chain’s overall profit due to the full-refund return policy.

Based on Fig. 8(d), with increasing ${\theta }_{0}$ the manufacturer’s profit (${\pi }_{m}$) shrinks since not only it has to pay for returned defective products (${w}_{n}$), but it also has to remanufacture and sell at a price $({w}_{r})$ lower than the new products wholesale price (${w}_{n}$). Therefore, it tries to reduce its profit loss by increasing ${w}_{n}$ slightly, which results in a rise in new products price (${p}_{n}$), Fig. 8(a and b), and gradual fall in demand (${D}_{n}$), Fig. 8(c). On the other hand, although ${D}_{n}$ decreases due to the sharper increment in ${\theta }_{0}$, based on Fig. 8(g) the amount of returned defective products (${{\theta }_{0}D}_{n}$) increase, which gives an opportunity to the manufacturer to reduce profit loss. Therefore, the manufacturer reduced the wholesale price of remanufactured products (${w}_{r}$), which makes remanufactured product’s price drop (${p}_{r}$) and as a result, demand for remanufactured products (${D}_{r}$), Fig. 8(e and f) as well as second retailer’s profit increase (${\pi }_{r2}$), Fig. 8(h).

But in higher ${\theta }_{0}$, the situation changes. After reaching ${\theta }_{0}$ to the peak in Fig. 8(g) in both scenarios, which can be called the maximum allowed rate of return, 0.67 in the first scenario and 0.7 in the second scenario, the increasing rate of defective products production and the new products price (${p}_{n}$) make even loyal customers unwilling to buy. This causes a sharp drop in new product’s demand (${D}_{n}$), Fig. 8(c). Consequently, lower returned defective products (${{\theta }_{0}D}_{n}$) are inevitable, which makes the manufacturer increase the ${w}_{r}$ to reduce its profit loss. But higher ${w}_{r}$ makes a fall in demand for remanufactured products (${D}_{r}$) and second retailer’s profit (${\pi }_{r2}$), Fig. 8(h), which can bankrupt the supply chain due to the sharp approach of the ${D}_{n}$ and ${D}_{r}$ to zero. This clearly shows the importance of controlling the production process.

Comparing the two scenarios, the manufacturer’s maximum allowed return rate in the second scenario (0.7) is higher than the first one (0.67). This is because of the lower wholesale price (${w}_{n}$) in the second scenario results in the lower new products price (${p}_{n}$) and higher demand (${D}_{n}$) in comparison to the first scenario. Therefore, with increasing ${\theta }_{0}$ which results in a drop in ${D}_{n}$, the manufacturer reaches to maximum allowed return rate later in the second scenario than in the first one.

There is a point in the chart related to the manufacturer’s profit (${\pi }_{m}$) in both scenarios. As can be seen, although in terms of manufacturer, the second scenario is profitable than the first one, in both scenarios, its profit reached zero at one point (${\theta }_{0}=0.9$). The main reason for that is shown in the charts related to the wholesale (${w}_{n}$) and new products price (${p}_{n}$) in both scenarios. In point ${\theta }_{0}=0.9$, the wholesale price reaches the new products price (${w}_{\mathrm{n}}={p}_{\mathrm{n}}$), which means that at this point, there is no difference between the first and the second scenarios based on equal pay (${b}_{\mathrm{r}}$) for each returned first-category product.

In conclusion, the rise in the return rate of defective products (${\theta }_{0}$) increases the second retailer’s profit (${\pi }_{r2}$) before starting to fall at the ${\theta }_{0}=$ 0.67 and 0.7, the manufacturer’s maximum allowed return rates in the first scenario in the second scenario, respectively. The higher manufacturer’s maximum allowed return rate can show the customers' loyalty to the new products in both scenarios, which is higher in the second scenario than the first one because of affordable ${w}_{n}$ and ${p}_{n}.$ also, at ${\theta }_{0}=0.9$ there is no difference between scenarios since ${w}_{n}$ = ${p}_{n}$.

The simultaneous effect of ${{{c}}}_{{{c}}}$ and ${{{c}}}_{{{r}}}$ on the profit of the manufacturer (${{{\pi}}}_{{{m}}}$)

To analyze the simultaneous impact of the cost of new products production by recycled materials (${c}_{\mathrm{c}}$), and the returned products remanufacturing cost (${c}_{\mathrm{r}}$) on the manufacturer’s profit (${\pi }_{m}$) in fair condition, the return rate of defective new products (${\theta }_{0}$) and demand rate of new products with having first-category products (${\theta }_{2}$) are assumed equal (${\theta }_{0}={\theta }_{2}=0.35)$.

Based on Fig. 9 and in accordance with results obtained in the study related to Gu et al. (2018), the simultaneous increase in ${c}_{\mathrm{c}}$ and${c}_{\mathrm{r}}$, according to Eqs. (7) and (10), reduces the manufacturer’s profit (${\pi }_{m}$) in both scenarios. Although an increase in both ${c}_{\mathrm{c}}$ and ${c}_{\mathrm{r}}$ make ${\pi }_{m}$ shrink, the impact of changes in ${c}_{\mathrm{c}}$ on ${\pi }_{m}$ is far more significant than changes in${c}_{\mathrm{r}}$.This is because the increase in ${c}_{\mathrm{c}}$ cause to rise in the wholesale price (${w}_{\mathrm{n}}$) and drop in demand for new products (${D}_{\mathrm{n}}$) which affects the drop in ${\pi }_{m}$ far more than the grow in ${c}_{\mathrm{r}}$.The grow in ${c}_{\mathrm{r}}$ chiefly influences the wholesale price of remanufactured products (${w}_{\mathrm{r}}$) and their demand (${D}_{\mathrm{r}}$).

Fig. 9

The simultaneous effect of ${c}_{c}$ and ${c}_{r}$ on ${\pi }_{m}$

In conclusion, the rise in ${c}_{\mathrm{c}}$ and ${c}_{\mathrm{r}}$ makes ${\pi }_{m}$ drop, but the manufacturer should pay much attention to ${c}_{\mathrm{c}}$ than ${c}_{\mathrm{r}}$ since the change in ${c}_{\mathrm{c}}$ have a noticeable impact on ${\pi }_{m}$ compared to the change in ${c}_{\mathrm{r}}.$

Results and insights

In this section, the main results of this research are presented based on the research questions provided in the introduction section. Also, some insights and policies are provided for the managers of the considered supply chain members.

The main results

Based on the research questions posed in the introduction, the results are summarized as follows.

• 1- Which payment strategies does the manufacturer use to pay for returned products under scenarios one and two are the most favorable for the retailer? What about the whole supply chain? It is indicated that, although in the first scenario, the first retailer receives higher payment for every first-category product (${b}_{\mathrm{r}}$), the new product’s demand (${D}_{\mathrm{n}}$) is lower because of the higher wholesale prices (${w}_{\mathrm{n}}$) leading to higher retail prices (${p}_{\mathrm{n}}$). Consequently, the supply chain is much profitable in the second scenario than in the first.

• 2- How is PEP suitable for the supply chain as well as the society? Except for the environmental benefits PEP brings by collecting and recycling, and reusing old products, it has been proved that the PEP as an incentive-based collection strategy can attract more customers and increase demand. The increased demand can lead to higher profit levels for the host supply chain (${\pi }_{t}$).

• 3- What motivates a manufacturer to take necessary steps to reduce the number of defective new products? It is shown that the increasing rate of defective new products (${\theta }_{0}$) can even bankrupt the supply chain if it passes the maximum allowed return rate. Therefore, the manufacturer must take some actions to control and improve the production line to reduce defective products production before reaching the maximum allowed return rate point

• 4- In which process should the manufacturer invest first to be improved? Remanufacturing or recycling? Analyzing the simultaneous impact of the cost of new products production by recycled materials (${c}_{\mathrm{c}}$), and the returned products remanufacturing cost (${c}_{\mathrm{r}}$), it is found that increase in ${c}_{c}$ makes the manufacturer lose profit far more than the time the ${c}_{r}$ increases. Therefore, improving the recycling process can make the manufacturer much profitable.

Managerial insights and policy recommendations

Insight 1

On the one hand, raising the discount on new items in return for first-category products (${\lambda }_{1})$ raises the payment for each collected first-category product (${b}_{\mathrm{r}})$, resulting in greater profit levels for the first retailer (${\pi }_{r1}$). The rise in ${\lambda }_{1}$, on the other hand, has a negative impact on the demand for new items (${D}_{\mathrm{n}}$). As a result, the first retailer must discover the best condition of equilibrium between ${D}_{\mathrm{n}}$ and ${b}_{\mathrm{r}}$ by lowering the percentage of ${\lambda }_{1}$ in order to maximize profit (${\pi }_{r1}$). The vitality of taking this action in COVID-19 pandemic is more than ever since consumer demand for both physical and immaterial things falls precipitously under these constraints related to the pandemic (Yu et al. 2021).

Insight 2

The increase in the discount on new items in exchange for second-category products (${\lambda }_{2}$) results in an increase in the price of new products (${p}_{\mathrm{n}}$), and a decrease in the profit of the first retailer (${\pi }_{r1}$). The manufacturer should contribute to the increase in ${\lambda }_{2}$ by assisting the first retailer in minimizing its loss. The primary reason for this is that when the ${\lambda }_{2}$ increases, used goods grow as well. As a result, the number of prospective customers who own items in the first-category increases in subsequent periods. This indicates that by promoting the growth in ${\lambda }_{2}$, the manufacturer contributes to future increases in recyclable goods, resulting in reduced manufacturing costs from recycled materials. Besides, the growth in ${\lambda }_{2}$ raises demand for second-hand products at reduced prices.This would benefit consumers, particularly during the COVID-19 epidemic, when the typical person’s buying power has fallen to an all-time low, as seen during the historic global economic crisis (Khan et al. 2021).

Insight 3

While an increase in the return rate of faulty new items (${\theta }_{0})$ may result in an increase in the second retailer’s and manufacturer’s profit (${\pi }_{r2}, \mathrm{and} {\pi }_{m}, \mathrm{respectively})$, the profit gained by the manufacturer by selling new non-defective products is far greater. Thus, the manufacturer’s ideal situation is when ${\theta }_{0}=0$. Unfortunately, unexpected events like a COVID-19 pandemic, contaminated workers and limitations, human errors, and machine or production line problems make this impossible. As a result, the manufacturer should optimize production to reduce ${\theta }_{0}$. Otherwise, if a problem arises that pushes the ${\theta }_{0}$ beyond the limit, bankruptcy is a certain consequence.

Insight 4

It is shown that decreasing the wholesale price of new goods (${w}_{n}$) results in decreased new product prices (${p}_{n}$) and increased demand (${D}_{n}$), which increases not only the supply chain's total profit (${\pi }_{t}$), but also the maximum allowed return rate (see Fig. 8). This provides the manufacturer with more time to enhance the manufacturing line, as mentioned in the “The return rate of defective new products (θ₀)” section. As a result of the comparison established in the “The return rate of defective new products (θ₀)” section between two scenarios, selecting the optimal scenario is critical to the supply chain’s profitability and survival.

Insight 5

It has been shown that increasing the discount on new items in exchange for first and second-category products (${\lambda }_{1}$ and ${\lambda }_{2 },$ respectively) reduces the manufacturer's and first retailer’s profits (${\pi }_{m}, \mathrm{and} {\pi }_{r1}, \mathrm{respectively})$, as well as the second retailer’s profit (${\pi }_{r2}$). Given the PEP’s importance in collecting old items and addressing environmental difficulties, the government should provide subsidies or financial assistance to make it more successful. Such assistance should be utilized to help the supply chain grow ${\lambda }_{1}$ and ${\lambda }_{2}$. This may help customers purchase things at lower costs in COVID-19 pandemic owing to economic slowdown and poor purchasing power (Khan et al. 2021).

Insight 6

While the PEP, which is dependent on discounts (${\lambda }_{1 },{\lambda }_{2}$), can expand the supply chain market and increase demand, setting inappropriate discount rates has the potential to destroy not only the attracted demands (${\theta }_{2}{D}_{\mathrm{n}},{\theta }_{3}{D}_{\mathrm{n}}$), but also to have a devastating effect on other types of demand (${\theta }_{1}{D}_{\mathrm{n}}$) through a decline in overall demand (${D}_{\mathrm{n}}$). As a result, the first retailer should set the discounts (${\lambda }_{1 },{\lambda }_{2}$) prudently in order to maximize the total profit (${\pi }_{t}$).

Insight 7

It was shown that the cost of producing new items using recycled materials (${c}_{c}$) has a significant influence on the manufacturer’s profit (${\pi }_{m}$) when compared to the cost of remanufacturing returned products (${c}_{r}$). Therefore, when it comes to cost-cutting measures, the manufacturer should prioritize improving the recycling process above improving the remanufacturing process for returned items.

Conclusions

The importance of the problem and the model description

Undoubtedly, CLSC is one of the main factors of sustainability and is defined as one of the influential factors in achieving sustainable operations as well as coming across environmental concerns (Shekarian 2020). Besides, factors including return policies and incentive-based collection strategies attracting more attention among academic researchers could play a prominent role in customer satisfaction and providing environmentally friendly supply chain (Sadjadi et al. 2018). To address all these factors in a comprehensive and innovative way, the CLSC provided in this paper comprises a manufacturer, first and the second retailers. As an innovative collection method, the first retailer benefits from a PEP for old products with and without useful lifetime left. The retailer sells products with useful lifetime left in another segment as second-hand products and returns products without useful lifetime left to the manufacturer to recycle. The recycled products return to the chain as new ones.

The manufacturer benefits from two policies to pay for each unit of first-category products discussed under the first and second scenarios. In the first scenario, the buy-back price is as the difference between the original retail price and discounted retail price. On the other hand, by considering the discount on wholesale price, the buy-back price in the second scenario is as much as the difference between the original wholesale price and discounted wholesale price. The manufacturer’s payment is higher in scenario one than two due to the fact that it wants to encourage the first retailer to participate in the PEP program.

Some results and insights

The results showed that, although in the first scenario, the manufacturer pays more to the retailer for each unit of first-category products, the wholesale price, and consequently, the retail price of new products, are higher than in the second scenario. As a result, demand for the new products, as well as overall profits of the first retailer and the manufacturer, is less than in the second scenario, which shows that the second scenario is profitable and better. Also, it is concluded that discounts directly impact the wholesale price of remanufactured products, which gives the first retailer more channel power.

On the other hand, higher discounts on new products exchange for the first- and second-category products lead to lower profit levels for the first retailer, and as a result, appropriate measures should be taken by the first retailer to stay profitable. In terms of defective products, the maximum return rate of defective products which manufacturer is allowed to produce derived to provide insight to stay profitable and take appropriate measures to improve production line before entering the loss zone.

Future research

In this model, one manufacturer and two retailers are considered. Future studies can consider two or more manufacturers with different products and locations (internal and external) considering disruption risk in supply with a third-party collector. In order to pay more attention to environmental requirements, products with different green degrees and government subsidies can be taken into account.

Appendix (A)

$${A}_1={\upbeta}_s\left({\theta}_0+{\theta}_3{\lambda}_2-1\right)-{\theta}_3^2{\upbeta}_n$$

$${A}_2={\upbeta}_s\left({\lambda}_2{\theta}_3{\alpha}_n+{\theta}_0{\alpha}_n{\theta}_1{\alpha}_n-{\alpha}_n-{\upbeta}_n{\theta}_3{c}_s\right)-2{\alpha}_n{\upbeta}_n{\theta}_3^2+{\alpha}_s{\upbeta}_n{\theta}_3$$

$${A}_3={\upbeta}_s{\upbeta}_n\left({\theta}_0-1\right)$$

$${A}_4=4{\alpha}_n{\upbeta}_n{\upbeta}_r{A}_1^2\left({\theta}_0-1\right)+((2{A}_3{\theta}_2{\lambda}_1{\alpha}_n+2{\upbeta}_n{A}_2\left(1-{\theta}_0\right)+\left(2{c}_{\mathrm{m}}{\theta}_2-2{c}_{\mathrm{c}}{\theta}_2-2{c}_{\mathrm{m}}-{c}_{\mathrm{r}}{\theta}_0\right){\upbeta}_n{A}_3){\upbeta}_r-2{A}_3{\alpha}_n{\upbeta}_n{\theta}_0^2+{\theta}_0{A}_3{\alpha}_r{\upbeta}_n){A}_1-{A}_3{A}_2\left(2{\theta}_2{\lambda}_1{\alpha}_r-{\upbeta}_n{\theta}_0^2\right)$$

$${B}_1={A}_1+{\lambda}_1{\theta}_2{\upbeta}_s$$

$${B}_2={A}_2+{\lambda}_1{\theta}_2{\upbeta}_s{\alpha}_n$$

$${B}_3={A}_3+{\lambda}_1{\theta}_2{\upbeta}_s{\upbeta}_n$$

$${B}_4={\alpha}_n\left(4{\upbeta}_r{B}_1^2\left({\lambda}_1{\theta}_2-1+{\theta}_0\right)-2{\theta}_0^2{B}_1{B}_3\right)+{B}_2\left({\theta}_0^2{B}_3+2{\upbeta}_r{B}_1\left(1-{\theta}_0-{\lambda}_1{\theta}_2\right)\right)+{B}_1{B}_3\left({\upbeta}_r\left(2{c}_{\mathrm{m}}{\theta}_2-2{c}_{\mathrm{c}}{\theta}_2-2{c}_{\mathrm{m}}-{c}_{\mathrm{r}}{\theta}_0\right)+{\theta}_0{\alpha}_r\right)$$

Proof of proposition 1

According to the method used in the study of Assarzadegan and Rasti-Barzoki (2020) and assumption (5), the demand for remanufactured products (D_r) should be equal to returned defective products (θ₀D_n). Replacing Eqs (4) and (6) in D_r = θ₀D_n yields Eq (13), which is the optimal price of each remanufactured product (p_r). Besides, according to assumption (4), the demand for second-hand products (D_s) should be equal to the demand for new products, which have the second category products (θ₃D_n). Replacing Eqs (4) and (5) in the D_s = θ₃D_n , yields Eq (14) which is the optimal price of each unit of second-hand product (p_s).

Proof of proposition 2

As shown in (A.1) the first retailer's hessian is negative and concave in the new product’s selling price (p_n)based on the model’s assumptions.

$$\frac{{\partial \pi}_{r1}}{\partial {p}_n^2}=\left[-\frac{2{\upbeta}_{\mathrm{n}}{\upbeta}_{\mathrm{s}}\left(1-{\theta}_3{\lambda}_2-{\theta}_0\right)+{\theta}_3^2{\beta}_n^2}{\upbeta_{\mathrm{s}}}\right]$$

(A.1)

The K.K.T. conditions for Eq (8) are as follows:

$$\nabla {\pi}_{r1}\left({p}_n\right)=\sum_i{T}_i{g}_i\left({p}_n\right).$$

$${\displaystyle \begin{array}{c}{\theta}_1\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left({p}_n-{w}_n\right){\theta}_1{\upbeta}_n+\left(1-{\lambda}_2\right){\theta}_3\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left(\left(1-{\lambda}_2\right){p}_n-{w}_n\right){\theta}_3{\upbeta}_n+\\ {}{\theta}_2\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left(\left(1-{\lambda}_1\right){p}_n-{w}_n\right){\theta}_2{\upbeta}_n-{\theta}_0\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left({w}_n-{p}_n\right){\theta}_0{\upbeta}_n+\kern4em \\ {}\frac{\theta_3{\upbeta}_{\mathrm{n}}\left({\theta}_3{\alpha}_n-{\theta}_3{\upbeta}_{\mathrm{n}}{p}_n\right)}{\upbeta_{\mathrm{s}}}-{\theta}_3{\upbeta}_{\mathrm{n}}\left(\frac{\theta_3{\upbeta}_{\mathrm{n}}{p}_n-{\theta}_3{\alpha}_n+{\alpha}_s}{\upbeta_{\mathrm{s}}}\right)={T}_1\left({\lambda}_2-\frac{\theta_3{\upbeta}_n}{\upbeta_{\mathrm{s}}}\right)-{T}_2\kern11em \end{array}}$$

(A.2)

$${T}_1\left(-\left(\frac{-{\theta}_3{\upbeta}_n+{\theta}_3{\upbeta}_n{p}_n+{\alpha}_s}{\upbeta_{\mathrm{s}}}\right)+{\lambda}_2{p}_n+{c}_s\right)=0$$

(A.3)

$${T}_2\left(-{p}_n\right)=0$$

(A.4)

$$-\left(\frac{-{\theta}_3{\upbeta}_n+{\theta}_3{\upbeta}_n{p}_n+{\alpha}_s}{\upbeta_{\mathrm{s}}}\right)+{\lambda}_2{p}_n+{c}_s\le 0.$$

(A.5)

$$-{p}_n\le 0,$$

(A.6)

$${T}_i\ge 0\kern2.25em i=1,2,3$$

(A.7)

The answer obtained from the Karush-Kuhn-Tucker (K.K.T), Eq (13), covers all the constraints and assumptions of the model.

Proof of proposition 3

The second derivative of Eq (7) with respect to w_r is equal to zero and the first derivative is equal to θ₀D_n, which is a positive value. In this study, an approach similar to the one used in SeyedEsfahani et al. (2011); Xie and Neyret (2009) is conducted to calculate the optimal value of w_r, which is as follows:

$${p}_r-{w}_r\ge {w}_r-{c}_r\to 2{w}_r\le {p}_r+{c}_r\to {w}_r\le \frac{p_r+{c}_r}{2}.$$

From the above equation, it can be concluded that the best value for w_r is equal to: $\frac{p_r+{c}_r}{2}$

Proof of proposition 4

After replacing the optimal values of ${p}_{r\mathrm{n}}^{\ast }\ \mathrm{and}\ {w}_r^{\ast },$Eqs (13) and (14), in the supplier's profit function (π_m), the hessian with respect to w_nis calculated as follows:

$$\frac{{\partial \pi}_m}{\partial {w}_n^2}=\left[\frac{1}{4}\frac{A_3\left(-4{\upbeta}_{\mathrm{r}}{A}_1{\upbeta}_{\mathrm{n}}+2{\upbeta}_{\mathrm{r}}{\theta}_2{\lambda}_1{A}_3-{\theta}_0^2{\upbeta}_{\mathrm{n}}{A}_3+4{\theta}_0{\upbeta}_{\mathrm{r}}{A}_1{\upbeta}_{\mathrm{n}}\right)}{A_1^2{\upbeta}_{\mathrm{n}}{\upbeta}_{\mathrm{r}}}\right]$$

(A.8)

The above equation is negative for all assumptions and the concavity condition is established. The optimal value of the supplier's wholesale price $\Big({w}_n^{\ast }$), Eq (17), is obtained through the first derivative of the supplier's profit function (π_m) with respect to w_n.

Proof of proposition 5

According to the method used in the study of Assarzadegan and Rasti-Barzoki (2020) and assumption (5), the demand for remanufactured products (D_r) should be equal to returned defective products (θ₀D_n). Replacing Eqs (4) and (6) in D_r = θ₀D_n, yields Eq (18) which is the optimal price of each remanufactured product (p_r). Besides, according to assumption (4), demand for second-hand products (D_s) should be equal to the demand for new products that have second category products (θ₃D_n). Replacing the Eqs (4) and (5) in D_s = θ₃D_n, yields Eq (14) which is the optimal price of each unit of second-hand product (p_s).

Proof of proposition 6

As shown in (A.9) first part of the first retailer's hessian is negative and concave in the new product’s selling price(p_n) based on the model’s assumptions.

$$\frac{{\partial \pi}_{r1}}{\partial {p}_n^2}=\left[-\frac{2{\upbeta}_{\mathrm{n}}{\upbeta}_{\mathrm{s}}\left(1-{\theta}_3{\lambda}_2-{\theta}_2{\lambda}_1-{\theta}_0\right)+{\theta}_3^2{\beta}_n^2}{\upbeta_{\mathrm{s}}}\right]$$

(A.9)

The K.K.T. conditions for Eq (11) are as follows:

$$\nabla {\pi}_{r1}\left({p}_n\right)=\sum_i{T}_i{g}_i\left({p}_n\right).$$

$${\theta}_1\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left({p}_n-{w}_n\right){\theta}_1{\upbeta}_n+\left(1-{\lambda}_2\right){\theta}_3\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left(\left(1-{\lambda}_2\right){p}_n-{w}_n\right){\theta}_3{\upbeta}_n+\left(1-{\lambda}_1\right){\theta}_2\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left(\left(1-{\lambda}_1\right){p}_n-{w}_n\right){\theta}_2{\upbeta}_n-{\theta}_0\left({\alpha}_n-{\upbeta}_{\mathrm{n}}{p}_n\right)-\left({w}_n-{p}_n\right){\theta}_0{\upbeta}_n+\frac{\theta_3{\upbeta}_{\mathrm{n}}\left({\theta}_3{\alpha}_n-{\theta}_3{\upbeta}_{\mathrm{n}}{p}_n\right)}{\upbeta_{\mathrm{s}}}-{\theta}_3{\upbeta}_{\mathrm{n}}\left(\frac{\theta_3{\upbeta}_{\mathrm{n}}{p}_n-{\theta}_3{\alpha}_n+{\alpha}_s}{\upbeta_{\mathrm{s}}}\right)={T}_1\left({\lambda}_2-\frac{\theta_3{\upbeta}_n}{\upbeta_{\mathrm{s}}}\right)-{T}_2$$

(A.10)

$${T}_1\left(-\left(\frac{-{\theta}_3{\upbeta}_n+{\theta}_3{\upbeta}_n{p}_n+{\alpha}_s}{\upbeta_{\mathrm{s}}}\right)+{\lambda}_2{p}_n+{c}_s\right)=0.$$

(A.11)

$${T}_2\left(-{p}_n\right)=0.$$

(A.12)

$$-\left(\frac{-{\theta}_3{\upbeta}_n+{\theta}_3{\upbeta}_n{p}_n+{\alpha}_s}{\upbeta_{\mathrm{s}}}\right)+{\lambda}_2{p}_n+{c}_s\le 0.$$

(A.13)

$$-{p}_n\le 0.$$

(A.14)

$${T}_i\ge 0\kern2.25em i=1,2,3$$

(A.15)

The answer obtained from the Karush-Kuhn-Tucker (K.K.T), Eq (20), covers all the constraints and assumptions of the model.

Proof of proposition 7

The second derivative of Eq (10) with respect to w_r is equal to zero and the first derivative is equal to θ₀D_n, which is a positive value. In this study, an approach similar to the one used in SeyedEsfahani et al. (2011); Xie and Neyret (2009) is conducted to calculate the optimal value of w_r, which is as follows:

$${p}_r-{w}_r\ge {w}_r-{c}_r\to 2{w}_r\le {p}_r+{c}_r\to {w}_r\le \frac{p_r+{c}_r}{2}.$$

From the above equation, it can be concluded that the best value for w_r is equal to: $\frac{p_r+{c}_r}{2}.$

Proof of proposition 8

After replacing the optimal values of ${p}_n^{\ast}\kern0.50em \mathrm{and}\ {w}_r^{\ast }$, Eqs (20) and (21), in the supplier's profit function (π_m), Eq (10), the hessian with respect to w_nis calculated as follows:

$$\frac{{\partial \pi}_m}{\partial {w}_n^2}=\left[\frac{1}{4}\frac{B_3\left(-4{\upbeta}_{\mathrm{r}}{B}_1+4{\upbeta}_{\mathrm{r}}{\theta}_2{\lambda}_1{B}_1-{\theta}_0^2{B}_3+4{\theta}_0{\upbeta}_{\mathrm{r}}{B}_1\right)}{B_1^2{\upbeta}_{\mathrm{r}}}\right]$$

(A.16)

The above equation is negative for all assumptions and the concavity condition is established. The optimal value of the supplier's wholesale price ${w}_n^{\ast }$, Eq (22), is obtained through the first derivative of the supplier's profit function (π_m) with respect to (w_n).