The spatial distribution dynamic and convergence of CO₂ emissions in Iran’s provinces

Abstract

It is essential to study CO₂ emissions intensity as the most critical factor affecting temperature increase and climate change in a country like Iran, which ranked seven regarding CO₂ emissions intensity. Investigating the convergence of CO₂ emissions intensity is essential in recognizing its dynamics in identifying the effectiveness of government environmental policies. In this paper, using the Markov chain and spatial Markov chain methods, the convergence of CO₂ emissions intensity from fossil-fuel consumption has been investigated in 28 provinces of Iran from 2002 to 2016. The empirical results showed that convergence clubs and neighbors significantly influenced the transition probability of regions to clubs with high and low CO₂ emissions. Therefore, if a province had a neighbor with low (high) CO₂ emissions intensity, the transition probability of this province to the club with low (high) CO₂ intensity increased. Therefore, in provinces that have neighbors with low (high) CO₂ emissions intensity, the transition probability to the club with low (high) CO₂ intensity increases.

Introduction

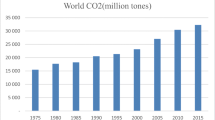
CO₂ emissions increased from 22 billion tons in 1990 to more than 36 billion tons in 2019 (ourworldindata.org). However, in 2020, with the COVID 19 pandemic, which reduced energy demand by 4%, the global CO₂ emissions related to energy fell by 5.8% to about 2 billion tons per year, unprecedented in human history (www.iea.org). However, energy consumption and CO₂ emissions are expected to return to normal with the prevention of the COVID 19 pandemic. Figure 1 shows the highest CO₂ intensity (CO₂-I) countries in the world. South Africa, Kazakhstan, Taiwan, Russia, and Ukraine have the highest CO₂-I. Iran ranks seventh in the world regarding CO₂-I. A comparison of the trend of CO₂-I between Iran and the global average showed that although CO₂-I in the world has been decreasing from 1990 to 2018, this trend is increasing in Iran (Fig. 2). This is in the context that Iran has the second-largest gas reserves after Russia and the fourth-largest oil reserves after Venezuela, Saudi Arabia, and Canada (Dudley, 2020).

Fig. 1

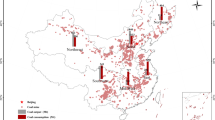
CO₂ intensity breakdown by country (kCO2/$2015p). Source: https://yearbook.enerdata.net

Fig. 2

CO₂ intensity (kCO2/$2015p). Source: https://yearbook.enerdata.net

One of the most critical effects of CO₂ emissions is climate change and global warming. This is essential for survival on earth because “Every bit of warming matters” (IPCC, 2018). Figure 3 shows the effect of emissions on heating imbalance, in watts per square meter, caused by all major artificial greenhouse gases. It is known that the highest share and highest growth of greenhouse gases are related to CO₂ emissions. As a result, the absorbed heat per watt per square meter had almost doubled from 1980 to 2019. Given the high effects of CO₂ emissions on climate change and temperature, it is essential to identify the factors affecting CO₂ emissions. Many studies, including Wang et al. (2018), Kang et al. (2019), Chen et al. (2019), and Shahnazi and Shabani (2021), have been done in this regard. One of the factors related to CO₂ emissions is CO₂ emissions convergence.

Fig. 3

Combined heating influence of greenhouse gases. Source: https://www.climate.gov

This research aims to investigate the convergence of CO₂ emissions intensity in Iranian provinces. The convergence of CO₂ emissions can be explained theoretically based on three foundations, i.e., environmental Kuznets theory, the orientation of global environmental treaties, and economic growth convergence.

The environmental Kuznets theory is one of the most important models used to explain CO₂ emissions. Accordingly, the relationship between economic development and environmental quality is an inverse-U relationship. According to Grossman and Krueger (1991), economic development affects environment in three ways: (i) scale effect in the sense that increasing the scale of the economy leads to more destruction of natural resources and more emissions; (ii) composition effect: with the increasing development, production structures change and move towards cleaner activities with less pollution; (iii) technological effect resulting from increasing research and development costs in the development process which leads to new clean technologies. Therefore, considering these effects, economic growth has negative environmental effects in the short run and leads to increase pollution. However, in the long run, with the growth of clean technology development, the quality of environment improves, and different regions converge in CO₂ emissions. The second explanation for the convergence of CO₂ emissions is related to international environmental treaties such as the Kyoto Protocol or the Paris Agreement (Haider and Akram 2019). International environmental treaties can be the basis for CO₂ emissions convergence to provide unified policies for improving environmental conditions in different countries. Regarding the treaties of universal laws and regulations from 1850 up to now, current content includes 1368 Multilateral environment agreements (MEAs), 2264 bilateral environment agreements (BEAs), and 250 other environmental agreements (https://iea.uoregon.edu). It should be noted that Iran is present in 320 of the agreements described in Table 1. The third basis for explaining the convergence of CO₂ emissions is related to the principles of convergence of economic growth. The concept of convergence is stemming from economic growth literature (Barro, 1991). Due to the fact that part of CO₂ emissions is related to energy consumption for economic growth, as convergence in economic growth, CO₂ emissions associated with economic growth also converge.

Table 1 Iran has taken steps in 320 agreements

This study has two significant contributions: first, a non-parametric method that considers the spatial effects was used to assess CO₂ emission convergence. Although parametric methods have been used in different studies, which may provide misleading results as multimodality and distribution dynamics are ignored (Quah, 1993, 1997). On the other hand, if research deals with spatial data with locational information, spatial effects must be considered in data analysis as ignoring the spatial effects may lead to biased results. Second, as far as researchers examined, it is the first study examining CO₂-I convergence in Iran. Previous studies investigated CO₂ emissions in Iran (e.g., Mirzaei and Bekri 2017, Hajilary et al. 2018, Hosseini et al. 2019), but CO₂-I convergence was not investigated in Iran. It is important to examine CO₂-I convergence in Iran regarding international environmental goals to fulfill Iran’s commitments in international environmental treaties and agreements such as the Kyoto Protocol and the Paris Agreement.

This study has the following sections: literature review is provided in “Literature review.” “Methodology and data” presents methodology. The empirical results are reported in “Empirical results.” Conclusion and policy implications are drawn in “Conclusion and policy implications.”

Literature review

Many studies explored the convergence of CO₂ emissions is shown in Table 2. These studies differ in the areas, duration, method, and type of convergence. Some studies such as Yu et al. (2018) and Boussemart et al. (2015) focused on studying the convergence of CO₂ emissions in the interior of a country, and some like Romero-Avila (2008), Yan et al. (2017), and Li et al. (2020) examined the convergence between countries. The single country study focuses mainly on the study of the USA and China. In multi-country studies, some have examined countries located in a region, mainly including EU and OECD countries. And some articles have reviewed a large number of countries in more than 100 countries. The study period ranges from 11 years (Li et al., 2017) to more than 100 years (Presno et al., 2018).

Table 2 Summary of studies on CO₂-I convergence

Previous studies differed in terms of the method used. For example, Romero-Ávila (2008) used the bootstrap methods, Van (2005) used the Kernel density estimates, Li et al. (2017) applied the spatial panel data models, Lee et al. (2008) used the panel unit root stationarity analysis, Huang and Meng (2013) employed the spatial panel data, and Morales-Lage et al. (2019) applied the nonlinear dynamic factor model to investigate the convergence of CO₂-I. Another difference between the studies was related to the type of convergence. Accordingly, some studies such as Boussemart et al. (2015) showed the existence of non-club convergences, and others such as Kounetas (2018), Morales-Lage et al. (2019), and Tiwari et al. (2021) showed the existence of club convergences. Although most studies conclude that there is convergence in emission intensity, in some studies, such as Yan et al. (2017), convergence is not confirmed.

A review of previous studies indicates the existence of two research gaps that the purpose of this article is to fill two. First, previous studies have mostly been performed with parametric methods or have not seen spatial effects. And second, CO₂-I convergence has not been studied in Iran.

Some previous studies have used parametric methods that may provide misleading results as multimodality and distribution dynamics are ignored (Quah, 1993, 1997). On the other hand, Van (2005) and Kounetas (2018) investigated the convergence of CO₂-I using a non-parametric method while not considering the spatial or neighbor effects on CO₂-I convergence; ignoring the spatial effects may lead to biased results. This paper uses a non-parametric method of spatial effects to fill this research gap. As Table 2 shows, there is no study on CO₂-I convergence in Iran. Although Iran has seventh place globally, CO₂ emissions intensity and the trend of CO₂-I are increasing in Iran, contrary to the global trend from 1990 to 2018 (https://yearbook.enerdata.net); identifying CO₂-I convergence is very important for Iran in terms of policies to reduce emissions.

Methodology and data

Theoretical models

The concept of convergence was first introduced in the economic growth literature in 1991 and is now being used in other fields such as carbon dioxide emissions. Three concepts of beta, sigma, and random convergence can be used to check convergence. Sigma convergence examines the decreased difference in carbon dioxide emissions between regions over time. The increased difference in carbon dioxide emissions between regions means divergence. The sigma convergence is investigated using the standard deviation of carbon dioxide between regions or using the kernel density function. Beta convergence is divided into unconditional and conditional convergence. The convergence of CO₂ emissions of all regions into a common and stable steady state is called unconditional beta convergence. Their convergence to the steady-state conditions in proportion to the initial level of factors in each region is called conditional beta convergence. Based on the conditional beta convergence, each region converges to its own specific steady state, and regions farther from their equilibrium point converge more rapidly to their steady state. This type of convergence led to forming a new concept called club convergence or multiple equilibrium models. In this case, regions with similar carbon dioxide emissions (e.g., high carbon dioxide emissions and low carbon dioxide emissions) converge to a steady state. Thus, in the long run, not only the difference between the regions does not disappear, but the carbon dioxide emissions of the regions converge towards similar peaks, and carbon dioxide emissions distribution of the regions moves towards two or more peaks. In this case, homogeneity between regions or countries increases, and differences between groups increase (Le Gallo, 2004). An examination of economic literature showed that the concept of club convergence was first proposed by Baumol (1986) and then was completed by Durlauf and Johnson (1992, 1995). Next, Quah (1997) developed it in other ways. Kova argued that the econometric methods, a common method for examining beta convergence, often have misleading results, produce Galton’s problem, and do not describe distribution behavior and movements. Hence, he introduces the Markov chain as a powerful tool for studying and identifying convergence clubs (Quah, 1993). Stochastic convergence indicates that shocks to carbon dioxide emissions are temporary (Fallahi, 2017). A randomness unit root test is used to investigate random convergence.

In this paper, due to limited information, it was not possible to investigate Stochastic convergence. Moreover, since the provinces of Iran are not homogeneous and similar in terms of economic and geographical factors, conditional beta convergence (club convergence) should be considered. According to Quah (1993), the use of measurement methods to investigate the conditional beta convergence (club convergence) leads to misleading results. Hence, in this paper, the Markov chain method was used to investigate club convergence. In addition, the kernel density function has also been used to investigate Sigma convergence.

Empirical models

Kernel density

The kernel density estimator is a weighted moving average of the sample frequency distribution. The function K is the kernel if it is as follows:

$${\int}_{-\infty}^{+\infty }K(x) dx=1$$

(1)

In most cases, K is a symmetric probability density function. The kernel density estimator at point x with K is as follows:

$$\hat{f}(x)=\frac{1}{nh}{\sum}_{i=1}^nK\left\{\frac{x-{X}_i}{h}\right\}$$

(2)

where n is the number of observations, x_i is the observation of i, and h is the smoothing parameter or bandwidth.

Markov chain

A random process with a set of finite values x_{r, t + 1}, x_{r, t}, x_{r, t − 1}, …, x_{r, 0} is called a Markov chain, if this process is in state i at time t (x_{r, t} = i) and the probability P_ij is in state j at time t + 1(x_{r, t + 1} = j). So, for all values t ≥ 0 and all states,j, i₋₁, i₋₂, …, i₀, we can write:

$$P\left({x}_{r,t+1}=j|{x}_{r,t}=i,{x}_{r,t-1}={i}_{-1},\dots, {x}_{r,0}={i}_0\right)=P\left({x}_{r,t+1}=j|{x}_{r,t}=i\right)={P}_{ij}$$

(3)

P _ij is the probability of transition of the process from state i now to state j in the next time (Bickenbach and Bode 2003). If the Markov process is time-independent, the Markov chain is completely defined by the Markov transfer matrix (M). M is called the transition probability matrix; each of its values in row i and column j is P_ij, which is the probability of moving from state i to j. Assuming the number of states is 2, the Markov transition probability matrix is a 2×2 matrix as follow:

The number of states in the Markov chain must be chosen so that the initial distribution of data in the different states is approximately the same (Quah 1993). The initial distribution of the data is explained by the initial vector (Monfort 2008). If the Markov chain is irreducible and periodical, the process reaches a steady-state or stationary-state vector. The steady-state vector is called the ergodic distribution vector and calculated using an eigenvector associated with the eigenvalues of 1 in the transpose of transition probability matrix (Ibe 2009). The ergodic vector is used for considering convergence in the literature (Liddle 2012, Li et al. 2019). If the data concentration is in one state in the ergodic vector, there is absolute convergence. If the data is divided between different states with equal frequency, there is a divergence. Convergence clubs exist when the data are concentrated in some states (Le Gallo, 2004). According to transition probability matrix, we can calculate stability and half-life index. The stability index is as follows:

$$S=\frac{Tr(M)}{N}$$

(4)

where N is the number of states, and Tr(M) is the trace of the matrix M (Monfort 2008). The half-life index shows the speed of convergence toward the ergodic vector and calculates the years to cover the half distance to the ergodic vector. This index is as follows:

$$H=\left(\frac{-\mathrm{Log}\ (2)}{\mathrm{Log}\left|{\alpha}_2\right|}\right)\ast T$$

(5)

where α₂ is the largest eigenvalue after 1 of transpose M, T is year interval (Shorrocks 1978). In this study, the year interval is 1. Matrix M presents the transition probability matrix but does not take into account spatial autocorrelation between observations of regions.

The Moran’s I statistic (1950) is the common method to investigate spatial autocorrelation of regions as follow:

$$I=\frac{n\sum_{i=1}^n\sum_{j=1}^n{W}_{ij}\left({C}_i-\overline{C}\right)\left({C}_j-\overline{C}\right)}{\sum_{i=1}^n\sum_{j=1}^n{W}_{ij}{\left({C}_i-\overline{C}\right)}^2}$$

(6)

where C_i is the variable of region i,$\overline{C}$ presents the average of variable, n is the number of regions, and W_ij is i^th and j^th components of the spatial weights matrix.

For considering the effect of neighbors on the transition probability matrix, Rey (2001) proposed spatial Markov transition probability. In this matrix, the transition probabilities depended on the state of neighbors (spatial lag). If the number of states is 2, the spatial Markov matrix is a 2×2×2 matrix (Rey 2001).

Table 3 presents the spatial Markov transition probability with two states. Spatial lags are determined based on the average CO₂ in the neighboring provinces in the starting year (e.g., 2002). For example, provinces are in state one according to spatial lag when the average CO₂ of neighbors is in a state of 1 in 2002. In Table 3, p_ij/k is the probability shifting from state i to j when the neighboring provinces are in k state. The spatial effects can be understood by comparing the elements of matrix M with the corresponding elements in Table 2. If the transition probabilities are as follows:

$${P}_{ij/1}={P}_{ij/2}={P}_{ij}\kern0.5em \forall i,j=1,2$$

(7)

Table 3 Spatial transition probability matrix (K=2)

There is no spatial effect. Spatial effects exist when, for example, P_12/1 < P₁₂, meaning that if the neighbors of a province are in state 1, then the province moves from state 1 to state 2 with a lower probability.

Data

Data of CO₂-I for 28 Iranian provinces in the period of 2002 to 2016 was used in this study. To calculate the CO₂-I, first, energy consumption was extracted from different energy carriers. Second, the CO₂ emissions was calculated based on the carbon dioxide coefficient for each energy carrier documented in the Iranian energy balance sheet. Third, CO₂ emissions for each province is divided into the real GDP to calculate CO₂-I. The data of GDP was collected from the statistical yearbook of provinces (www.amar.org.ir). The real GDP was calculated using the provincial consumer price index.

In the Markov chain method, relative variables are used and the relative CO₂-I is applied. To do this, CO₂-I in each province was divided into the average CO₂-I in Iran. Table 4 shows the descriptive statistics of CO₂-I, GDP, and the relative CO₂-I in Iranian provinces.

Table 4 descriptive statistics of relative co₂ emissions Intensity

Empirical results

The kernel density in Fig. 4 shows how CO₂-I in 2002 evolves into 2016. The probability density function was not symmetric and was left-skewed and had a positive kurtosis. The positive kurtosis indicates that the distribution is peaked and has thick tails relative to normal distribution. As shown in Fig. 4, the distribution of the relative CO₂-I of Iranian provinces in 2002 was not normal and was in 105% of the country’s mean. Therefore, evidence suggested that the CO₂-I of most provinces in Iran was higher than the country’s average. In addition, kurtosis of distribution showed more data at this point than the normal state. Figure 4 shows that the concentration of provincial CO₂-I was 120% of the country’s average in 2016. Moreover, the negative skewness of distribution has increased, which shows that the CO₂-I of some provinces has been decreased compared to 2002.

Fig. 4

Kernel density of relative CO₂-I

A comparison of the four density distributions in 2002, 2007, 2012, and 2016 showed that the distribution kurtosis increased in 2016, and the skewness shifted more to the left than in 2002, 2007, and 2012. Thus, over the 15 year, two peaks became apparent, one small peak was formed at around 30% of the country’s average, and a major peak was formed above the average. So, there are individual convergence clubs in CO₂ emissions. The reason for this can be inequality in GDP per capita (Padilla and Duro 2013), and different energy mix and efficiency (Barassi et al. 2008; Wang et al. 2005), different industrial structures (Talukdar and Meisner 2001), and demographic variation (Knapp and Mookerjee 1996) among the provinces of Iran.

Although the distribution density function showed the shape of the distribution and formation of the convergence clubs, it cannot explain the intra-distribution movements and the evolution of distribution. Therefore, to investigate the intra-distribution dynamics, steady state, club convergence, and convergence speed of CO₂-I, the first-order static Markov chain model, can be used.

In this study, the number of observations was 420, classified into four states. State 1 includes observations whose CO₂-I was 0 to 75% of Iran’s average CO₂-I, which is called low CO₂-I. In state 2, observations whose relative CO₂-I were between 75 and 100% of average are called medium-low CO₂-I. The relative CO₂-I is between 100 and 120% of Iran’s CO₂-I average in state 3, a medium CO₂-I state. Finally, observations with CO₂-I above 120% of the average are in state 4. This state is called high CO₂-I. The initial distribution of observations between different states using the initial distribution vector showed that 24% of the observations were in state 1, 25% of the data were in state 2, 25% of the observations were in state 3, and 26% were in state 4 (Table 5). In this study, four states are considered, so the transition probability matrix was a 4×4. The transition probabilities matrix is presented in Table 5, the elements of which indicate the probability of transfer from one state to another. As the results in Table 5 show the element on the main diagonal of the transition matrix were high and, on average, 80%. Therefore, the stability index was 80%. Moreover, the probability of movements outside the main diagonal was 7% on average. Therefore, according to the stability index and mobility outside the main diagonal, as well as the high probabilities staying in the states 1 (95%) and 4 (80%), it can be concluded that the provinces with high and low relative CO₂-I do not see changes in their relative position over time.

Table 5 Transition probability matrix for Iran-relative CO₂-I

Table 5 showed that 87 observations were in state 1 during 15 years which remained in state 1 with a 95% probability the next year and will shift up to states 2 and 3 with a probability of 4% and 1%, respectively. Therefore, provinces with low CO₂-I are very unlikely to leave the low CO₂ emissions club. According to the data (Appendix Table 10 in appendix), Ilam, Tehran, Khuzestan, Kohkiluyeh, and Boyer-Ahmad provinces have been in the state 1 in 15 years. Golestan has been in state 1 for 8 years and then has moved to state 2; Lorestan has been in state 1 for 7 years. Moreover, Ardabil province has been in state 1 for 1 year and has shifted to state 2. Furthermore, 95 observations were in state 2, of which 78% remained in state 2 in the next year, and the highest probability of movement was 17% into state 3. Chaharmahal Bakhtiari province for 15 years; Ardabil and Zanjan for 12 years; Azerbaijan Sharghei, Kerman, and Lorestan for 8 years; Semnan, Fars, and Golestan for 6 years; Khorasan for 5 years; Kurdistan for 3 years; Gilan for 2 years; Bushehr, Mazandaran, and Markazi for 1 year were in state 2. Most observations (120 observations) were in state 3, which had a CO₂-I of 100 to 120% of Iran’s average. According to Table 5, the observations in state 3 will remain in this state with a probability of 66% in the next year. The probability of shifting down to state 2 is 12%, and the probability of shifting up to state 4 is 22%. Azerbaijan Gharbei, Khorasan, Gilan, and Mazandaran have been in state 2 for more than 10 years.

As shown in Table 5, 118 observations were in state 4, with a probability of 80% remaining in state 4 in the next year and with a probability of 18% and 2% moving down to states 2 and 3 in the next year, respectively. Isfahan, Sistan and Baluchistan, and Qazvin provinces have been in state 4 for 15 years; Hormozgan for 14 years; Hamedan for 10 years, Markazi for 9 years; Kurdistan for 8 years; Yazd, Kermanshah, and Qom for 6 years; Azerbaijan Gharbei for 4 years; Bushehr, Semnan, and Gilan provinces for 2 years; and Mazandaran, Kerman, Zanjan, and Azerbaijan Sharghei provinces for 1 year. The ergodic distribution vector is presented in Table 5. The results of this vector were used to investigate the convergence. The results of ergodic vectors showed that in the long run, 87% of the observations are in states 1 and 2. The number of regions in state 1 or low CO₂-I club will increase from 24% in the initial vector to 27% in the ergodic vector. Moreover, the observations in state 2, i.e., in the medium-low CO₂-I club, will increase from 25 to 59%. According to the results of the ergodic vector, the observations in state 3, i.e., the medium CO₂-I club, will decrease from 25 to 12%, and the number of observations in state 4 will decrease from 26 to 2%. However, the results indicate that there is club convergence. This finding was contradicted Boussemart et al. (2015) and Huang and Meng (2013) that support convergence in CO₂ emissions across provinces in a country, and consistent with Rios and Gianmoena (2018), Kounetas (2018), Apergis and Payne (2017), and Tiwari et al. (2021) that predict the club convergence of CO₂ emissions. A possible explanation can be attributed to the fact that the provinces of Iran have different climatic conditions and structures of economies. Therefore, provinces with similar climates, production composition, fuel consumption, and energy efficiency will converge towards the same provinces.

The half-life index was 14 years, indicating that 14 years are needed to cover the half distance between the initial vector to the ergodic vector. The results of half-life and stability indices indicated that the move towards long-run equilibrium was very slow and stability of the process was high. The results of Table 5 examined the evolution and dynamics of CO₂-I distribution without considering the neighborhood effects.

However, the data used in this study were spatial data containing the locational information, so the spatial effects should be considered in the data analysis. Figure 5 shows the continuous state in which each province is located from 2002 to 2016. As Fig. 5 shows, most of the provinces that had a similar continuous state were located next to each other. A spatial correlation test must confirm this visual impression of spatial correlation.

Fig. 5

Continuous state of Iranian provinces (2002–2016)

The common test for the spatial autocorrelation was Moran’s I statistic. According to the results of Table 6, the Moran value was positive and was statistically significant in all years except 2009, showing that there was a positive spatial autocorrelation between CO₂-I in Iranian provinces. As a result, provinces with high (low) CO₂-I were adjacent to each other. This finding is consistence with Shahnazi and Shabani 2019, 2021, Liu et al. 2019, You and Lv 2018.

Table 6 Global Moran’s I statistics for CO₂-I

Table 7 shows two transition probability matrices. The first matrix was constructed using the neighbor-relative CO₂-I distribution, in which CO₂-I of each province is normalized to the average CO₂-I of the neighboring provinces. The second matrix included the probability of transition between Iran-relative CO₂-I distribution and the neighbor-relative CO₂-I distribution. This matrix showed probability transition between two different distributions at a given time. If there are no spatial effects, the first matrix in Table 7 is similar to the matrix in Table 5, and the second matrix in Table 7 is a unity matrix. The results of Table 6 showed that the first matrix is not similar to the matrix in Table 5, and the second matrix is not a unity matrix.

Table 7 Transition probability matrix for neighbor-relative and Iran to neighbor-relative CO₂-I

N, number of observations, upper endpoint is a ratio of the province to the national average CO₂-I

Table 8 shows the spatial transition probability matrix, which is conditioned on the spatial lag in 2002. The spatial lag indicates the state of the average CO₂-I of neighbors. It seems that the spatial lag of a province affects the transition probability of a province between different states. For example, provinces with low CO₂-I are negatively affected by the provinces with high CO₂-I. In fact, by increasing the CO₂-I of neighbors, the transition probability of moving up to the high states increase. According to Table 5, provinces with low CO₂-I (state 1) with an average probability of 5% of this state shift up to states 2 and 3. However, according to Table 8, if the neighboring provinces with low CO₂-I (state 1 in spatial lag) surrounded these provinces, the probability of transition upwards is only 4%. But, if the neighboring provinces had a medium-low CO₂-I (state 2 in spatial lag), the probability increases to 6%, and if the neighboring provinces were in state 3, the probability increases to 13%.

Table 8 Spatial Markov transition probability matrix (spatial lag in 2002)

If the province is in state 2, as shown in Table 5, the probability of moving to states 3 and 4 is 18%. But if this province has neighbors with low CO₂-I, then the probability of moving upwards will be 0%. Moreover, if the neighbors are in low-medium CO₂-I, the probability of moving upwards increases to 12%, and if it has neighbors with medium CO₂-I, the probability of moving upwards is 24%, and if the neighbors are in high CO₂-I, then, the probability of moving upwards will be 100%. Furthermore, provinces in state 3 have been affected by the neighbors. As seen in Table 5, if a province is in state 3, the probability of transition to state 4 is 22%. But, according to the results of Table 8, this province will not have neighbors with low CO₂-I. If this province is surrounded by the provinces that are in state 2, the probability of moving upwards is 17%, and if it has neighbors with the medium CO₂-I (state 3), the probability of moving up is 20%, and in the presence of neighbors that they are in state 4, the probability of moving upwards is 38%. The results of Table-8 indicated that the provinces with high CO₂-I had not been affected by their neighbors. The results of ergodic distribution vectors of spatial lag are presented in Table 8. The results showed that if neighbors are in low or medium-low CO₂-I states, the frequencies of observations in state 1 were 53% and 46%, respectively. When neighbors were in state 3, the concentration of observations in state 3 was 42%, and when neighbors were in state 4, the data concentration in state 4 was 100%. As a result, the results of the ergodic vectors indicated that their neighbors influenced the provinces.

Finally, we can summarize the information of the Markov spatial chain by considering the relationship between the probability of a specific transition (down, none, or up) and the CO₂-I of neighbors (spatial lag). Table 9 showed that neighbors had an important effect on the probability of moving down or up. For example, when a province was surrounded by provinces with low CO₂-I, the probability of moving downward was higher than moving upward. Moreover, if the provinces had neighbors with the high CO₂-I, then the probability of shifting upwards was higher than downwards. From the perspective of interregional convergence, all these results highlighted that the geographical environment affected interregional convergence. In this way, the neighbors affected the location of each province in the convergence clubs. This finding can be considered a result of spatial or social interactions in the provinces. These interaction processes can be considered to result from economic linkages, knowledge spillovers, policy copying among provinces, and trade (Huang and Meng 2013).

Table 9 Transition probabilities conditioned on spatial lag of CO₂-I

Table 10 The states of relative CO₂-I in 28 provinces during 2002 to 2016

This result contradicts Huang and Meng 2013, who state that spatial autocorrelation will lead to convergence. Also, our finding is consistent with Li et al. (2017) and Rios, V., and Gianmoena, L. (2018). In these studies, spatial autocorrelation has caused divergence and convergence clubs.

Conclusion and policy implications

Iran is one of the countries with the highest CO₂-I globally, making it essential to study CO₂-I convergence to encourage the government’s CO₂ policies to decrease the external effects of CO₂ emissions. On the other hand, assessing CO₂-I convergence is essential as the CO₂-I gap between provinces (or regions) can assist policymakers design and implementing effective policies to decrease CO₂-I and the loss of the environment. As a result, the Markov chain and spatial Markov chain methods examined the CO₂-I convergence in 28 Iranian provinces from 2002 to 2016. The results indicate convergence clubs in CO₂ emissions in Iranian provinces. Therefore, the results emphasized that the geographical environment affects interregional convergence. In this way, each province’s location in the convergence clubs is influenced by its neighbors.

Figure 6 presented a conditional map of CO₂-I. These figures demonstrated the CO₂-I of provinces in 2016 compared to 2002. Accordingly, the dynamics of CO₂-I are different in different provinces. While the provinces of Ardabil, Zanjan, West Azerbaijan, Kurdistan, and Yazd have improved, in Fars, Chaharmahal and Bakhtiari, Khorasan, Semnan, and Qom provinces, the situation has worsened. The intensity of CO₂ emissions in Iran is increasing. Also, the results showed that there was a fundamental difference in the overall CO₂-I and dynamics of CO₂-I in Iranian provinces.

Fig. 6

Conditional map of CO₂-I

These findings have policy implications for emissions reduction targets, as recognizing differences in convergence patterns in Iranian provinces helps design and implement emission reduction policies.

The amount and intensity of carbon dioxide emissions in Iran are high for two main reasons: macro and micro. In both categories, based on the results obtained in this paper, it is important to pay attention to regional spillover effects. At the macro level, the high CO₂-I in Iran is related to national and regional reasons. Factors such as the low price of fossil fuels are important at the national level. A different and unequal technology pattern between regions can lead to the high CO₂-I and CO₂-I divergence at the regional level. So, the spillover effects of CO₂ emissions should be considered by the policymakers, and paragraph 3 of Article 6 of the Sixth Development Plan of Iran (2017–2021), in which the distribution of funds obtained from pollution tax is limited to population proportion should be changed by considering the spillover effects of CO₂ emissions for neighboring cities or provinces. At the micro-level, the main factors of high energy intensity and subsequent increase in CO₂ emissions in Iran are the following: low and out-of-date power plants (Iranian parliament research center, 2015a). About 1.5 times higher electricity transmission and distribution losses in Iran compared to the global average (data.worldbank.org), vehicles with old technologies and high energy consumption, more in low-income areas, weakness of rail transportation system, disadvantages of intercity and intercity road networks and heavy traffic loads, a high share of old technology industries and low share of high-tech industries in GDP (Iranian parliament research center, 2015b; Shahnazi 2021), and imbalance in the type of industry in different provinces of Iran.

In order to promote regional convergence, the adoption of new technologies and greater use of renewable energy, making older equipment more efficient, and changing consumer behavior are effective to achieve long-term convergence. Therefore, the Iranian government must provide policy tools to introduce and disseminate technologies throughout the provinces. At the same time, the provinces, especially those that use inefficient technologies and have the high CO₂ emission density (including Hormozgan, Qazvin, Hamadan, Isfahan, Kermanshah, Sistan and Baluchestan, Qom, Gilan, and South Khorasan), must be active in promoting energy-intensive and low-emission technologies. Of course, adopting new technologies must consider local characteristics and regional compatibility. Providing incentives for technological development and innovation, efficient energy production, and distribution is also effective in convergence. Hence, as a complementary policy, supportive fiscal policy can be effective. The government can reduce taxes on purchasing new, energy-intensive, and low-emission technologies or provide financial subsidies to adopt efficient technologies.

Appendix

www.amar.org.ir

https://www.climate.gov

https://www.iea.org/articles/global-energy-review-co2-emissions-in-2020

https://iea.uoregon.edu/base-agreement-list?page=56

https://ourworldindata.org

https://yearbook.enerdata.net