1 Introduction

The main aims of measuring irrigation water flowing in main channels and laterals are to guarantee its proper distribution and beneficial and economical use. The weir is the most basic device used in the measurement of small water supplies and is very accurate when properly constructed and operated under standard controlled conditions.

Bautista-Capetillo et al. (2014) defined weirs as elevated structures, usually arranged perpendicular to the main flow direction, which force the flow to rise above the barrier going through a regular-shaped opening. Weirs are constructed, as an example, to measure discharge in irrigation networks and structures, or to channelize the surplus water over the dams caused by the floods (Nafchi et al. 2021), even if the specific application and their characteristics are related to the weir type (Borghei et al. 2003).

Previous research was developed to deduce a comprehensive stage-discharge relationship modeling the weir outflow process for a wide range of flows and geometrical weir types (Aydin et al. 2011; Bijankhan and Ferro 2017; Bijankhan et al. 2014; Ferro 2012; Hager and Schwalt 1994; Nicosia et al. 2023; Swamee 1988).

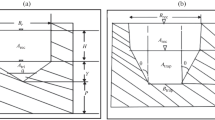
Weirs are classified considering their cross-sectional shape, plan view, and crest length L. In particular, according to h/L ratio (where h is the water depth measured from the reference horizontal plane localized at the weir crest having an height p), the weirs of a finite crest length are categorized into four groups (Azimi et al. 2013; Hager and Schwalt 1994): long-crested (0 < h/L ≤ 0.1), broad-crested (0.1 < h/L ≤ 0.4), short-crested (0.4 < h/L ≤ 2), and sharp-crested weir (h/L > 2).

Often, the problem of deducing flow stage-discharge relationship of weirs is solved determining the discharge coefficient Cd, which allows for considering the effects (i.e., viscosity, surface tension, velocity distribution in the approach channel, and streamline curvature due to weir contraction) that are not considered deriving the equations used for estimating discharge from flow depth (Aydin et al. 2011).

For a rectangular normal sharp-crested or broad-crested weir, the following stage-discharge relationship is derived following energy considerations (Aydin et al. 2002, 2011; Gharahjeh et al. 2015; Herschy 1999):

$$Q= \frac{2}{3} {C}_{d} b \sqrt{2 g} {h}^{3/2}$$
(1)

in which Q is the discharge of the free flow over the weir, b is the crest width, h is the water depth measured at a distance from the weir equal to 2–3 h, and g is the acceleration due to gravity.

Rearranging Eq. (1), Ferro (2012) obtained the following expression:

$$\frac{{Q}^{2/3}}{{p b}^{2/3} {g}^{1/3}}= {\left(\frac{8 {C}_{d}^{2}}{9}\right)}^{1/3} \left(\frac{h}{p}\right)$$
(2)

Setting

$$K= \frac{{Q}^{2/3}}{{ b}^{2/3} {g}^{1/3}}$$
(3)

and

$$a= {\left(\frac{8 {C}_{d}^{2}}{9}\right)}^{1/3}$$
(4)

Equation (1) can be rewritten as:

$$\frac{K}{p}=a \left(\frac{h}{p}\right)$$
(5)

Dimensional analysis can be usefully applied to study the flow over the weirs (Bijankhan and Ferro 2017). The starting point of the application of dimensional analysis to the study of a physical process is only to establish the “quantities which characterize the phenomenon being studied” (Barenblatt 1987). Moreover, Barenblatt (1987) suggested to combine the original dimensionless groups to obtain new similarity parameters Π generally applied in Hydraulics.

The stage-discharge relationship for a rectangular weir, with a width b equal to the channel one, B, and a height p, can be expressed by the following functional relationship:

$$\varphi \left(h, Q, B, p, g, \mu , \rho , \sigma \right)=0$$
(6)

where φ is a functional symbol, μ is the water viscosity, ρ is the water density, and σ is the water surface tension.

Using the Π-Theorem of dimensional analysis, Ferro (2012) deduced the following functional relationship:

$$f\left(\frac{K}{p}, \frac{h}{p}, Re, We\right)=0$$
(7)

in which f is a functional symbol, K is the critical depth defined by Eq. (3), Re and We are the Reynolds and Weber numbers, respectively. Except for very low values of the water depth h, the effects of the Reynolds and Weber numbers are generally negligible (De Martino and Ragone 1984; Ranga Raju and Asawa 1977; Rao and Shukla 1971; Sargison 1972). Consequently, Eq. (5) becomes:

$$\frac{K}{p}= \phi \left( \frac{h}{p}\right)$$
(8)

where φ is a functional symbol.

The functional relationship (Eq. 8), applying the incomplete self-similarity theory (Barenblatt 1979, 1987), assumes the following mathematical form:

$$\frac{K}{p}= a{\left( \frac{h}{p} \right)}^{n}$$
(9)

where a and n are numerical constants that should be determined experimentally.

Thereby, Eq. (9), which is theoretically obtained by the dimensional analysis and the self-similarity condition, reduces to Eq. (5) by setting n = 1.

The flow conveyance reduction due to flexible vegetation on the weir crest is a poorly investigated topic. Recently, Bai et al. (2023) carried out some experimental runs using rectangular weirs having a sharp-edged crest covered by artificial vegetation. The effects of equivalent roughness height ks of the vegetation on the weir discharge capacity were investigated, and the following empirical equations for predicting the discharge coefficient Cd of Eq. (1), considering the vegetation resistance effects, were proposed:

$${C}_{d}= \frac{3}{2} 0.36\;\mathrm{tanh}\,\left[3.5 {\left(\frac{h}{L}\right)}^{0.1} {\left(\frac{h}{{k}_{s}}\right)}^{0.4} {\left(\frac{p}{L}\right)}^{0.8} \right]\;\mathrm{for}\;0.1 < h/L < 0.4$$
(10)
$${C}_{d}= \frac{3}{2} 0.39\;{\left[ {\left(\frac{h}{L}\right)}^{2} {\left(\frac{h}{{k}_{s}}\right)}^{0.85} {\left(\frac{p}{{k}_{s}}\right)}^{-0.58} \right]}^{0.09}\;\mathrm{for}\;0.4 < h/L < 1.5$$
(11)

The developed analysis demonstrated that a noticeable reduction of the discharge coefficient corresponds to high roughness height ks as consequence of the weir discharge capacity due to the flow resistance associated with vegetation. Furthermore, the estimate of Cd, and the relative discharge Q, obtained by Eq. (1), is characterized by errors less than or equal to ± 15% for 96.9% of the investigated cases and less than or equal to ± 10% for 90.7% of the investigated cases (i.e., slightly over the accuracy limit of ± 5% suggested by Boiten (2000)).

In this paper, the outflow process of vegetated weirs is investigated applying the Π-Theorem of dimensional analysis and the incomplete self-similarity theory. A new theoretical stage-discharge relationship is presented, and its applicability is verified by measurements recently carried out by Bai et al. (2023). The main advantage of the proposed relationships is supplying a single stage-discharge relationship characterized by errors of the discharge estimate less than those obtained by the equations of Bai et al. (2023). Moreover, the main novel element is obtaining a stage-discharge relationship valid for vegetated weirs and operating regardless of the discharge coefficient estimate.

2 Applying Dimensional Analysis for Deducing the Stage-Discharge Relationship

Following Azimi et al. (2013), who indicated that the crest length L should be introduced in the functional stage-discharge relationship (Ferro 2012), Bijankhan et al. (2014) proposed the following functional relationship:

$$\Phi \left(h, Q, B, L, p, g, \mu , \rho , \sigma \right)=0$$
(12)

where Φ is a functional symbol.

Using p, g, and ρ as dimensional independent variables, the following dimensionless groups are deduced:

$${\Pi }_{1}=\frac{h}{p}$$
(13)
$${\Pi }_{2}=\frac{Q}{{g}^{1/2} {p}^{5/2}}$$
(14)
$${\Pi }_{3}=\frac{B}{p}$$
(15)
$${\Pi }_{4}=\frac{L}{p}$$
(16)
$${\Pi }_{5}=\frac{\mu }{{p}^{3/2}{ g}^{1/2} \rho }$$
(17)
$${\Pi }_{6}=\frac{\mu }{{p}^{2} g \rho }$$
(18)

Combining the groups Π1 and Π4 yields:

$${\Pi }_{\mathrm{1,4}}=\frac{{\Pi }_{1}}{{\Pi }_{4}}= \frac{h}{p} \frac{p}{L}= \frac{h}{L}$$
(19)

Considering Eqs. (14) and (15), the following dimensionless group is obtained:

$${\Pi }_{\mathrm{2,3}}=\frac{{\Pi }_{2}^{2/3}}{{\Pi }_{3}^{2/3}}=\frac{{Q}^{2/3}}{{g}^{1/3} {p}^{5/3}} \frac{{p}^{2/3}}{{B}^{2/3}}= \frac{K}{p}$$
(20)

Combining Eqs. (14), (15) and (17), the following dimensionless group is obtained:

$${\Pi }_{\mathrm{5,3},2}=\frac{{\Pi }_{2}}{{\Pi }_{5} {\Pi }_{3}}=\frac{Q}{{g}^{1/2} {p}^{5/2}} \frac{{p}^{3/2} {g}^{1/2} \rho }{\mu } \frac{p}{B}= \frac{\rho Q}{\mu B}=Re$$
(21)

where Re is the Reynolds number.

Considering the definitions of Π1 and Π6, the following dimensionless group is obtained:

$${\Pi }_{\mathrm{1,6}}=\frac{{\Pi }_{1}^{2}}{{\Pi }_{6}}= \frac{{h}^{2}}{{p}^{2}} \frac{{p}^{2} g \rho }{\sigma }= \frac{\rho g {h}^{2}}{\sigma }=We$$
(22)

in which We is the Weber number.

For the Buckingham’s Theorem, the dimensionless groups commonly used in hydraulics can be combined, and the functional relationship (Eq. 12) can be rewritten as follows:

$${\Pi }_{\mathrm{2,3}}=f\left({\Pi }_{\mathrm{1,4}}, {\Pi }_{4}, {\Pi }_{\mathrm{5,3},2}, {\Pi }_{\mathrm{1,6}}\right)$$
(23)

where f is a functional symbol.

Introducing the dimensionless groups into Eq. (23), the functional relationship can be rewritten in the following form:

$$\frac{K}{p}=f\left(\frac{h}{L}, \frac{L}{p}, Re, We\right)$$
(24)

Neglecting the effects of Re and We, Eq. (24) becomes:

$$\frac{K}{p}=\omega \left(\frac{h}{L}, \frac{L}{p}\right)$$
(25)

where ω is a functional symbol.

The mathematical shape of the functional relationship (Eq. 25) can be deduced using the incomplete self-similarity theory (Barenblatt 1979, 1987). For a given L/p value, when \(\frac{h}{L}\to 0\), then \(\frac{K}{p}\to 0\), and when \(\frac{h}{L}\to \infty\), then \(\frac{K}{p}\to \infty\), and consequently the ISS occurs. Therefore, for a given L/p value, Eq. (25) becomes:

$$\frac{K}{p}=a{\left(\frac{h}{L}\right)}^{n}$$
(26)

where the coefficient a is a function of L/p that should be obtained experimentally.

3 Available Experimental Data

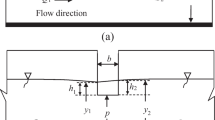
For testing the applicability of the stage-discharge relationship Eq. (26), the data by Bai et al. (2023) were used. The experiments were performed in a horizontal rectangular glass flume, 7.0 m long, 0.4 m wide, and 0.5 m high. Three weir crest lengths L (0.2 m, 0.5 m, and 1.0 m) were investigated.

These authors tested seven crest roughness configurations, including a smooth case, a vegetated weir crest covered by artificial turf, and five vegetated crests covered by artificial plants with different densities. The vegetation was uniformly distributed in the weir crest area. For each investigated condition, the equivalent sand roughness height ks was defined (ks = 1, 18, 22, 41, 78, 147, 318 mm) by fitting the measured velocity profiles to the universal equation of the wall for steady uniform flows.

Further details on the experimental lay-out and the used measurement techniques are reported in Bai et al. (2023).

4 Results and Discussion

for each ks/p value.

At first, each investigated experimental series, characterized by a single value of the crest length L (0.2, 0.5, and 1 m), was used to calibrate Eq. (26). As an example for L = 0.2 m, Fig. 1 shows the comparison between the measured pairs (h/L, K/p) and Eq. (26).

Fig. 1
figure 1

Comparison, as an example for L = 0.2 m, between the measured pairs (h/L, K/p) and Eq. (26)

Full size image

For each investigated weir length L, Table 1 lists the coefficients a and n corresponding to each roughness height ks and the mean value nm of the coefficient n for each crest length. This last value can be used under the hypothesis that, for each weir length, the exponent n of Eq. (26) can be assumed independent of roughness height.

Table 1 Values of the coefficients a and n of Eq. (26) obtained for each pair (L, ks/p)
Full size table

For each L value, considering the small variability of n, the mean value nm was assumed representative of each investigated weir and the following stage-discharge relationship was applied:

$$\frac{K}{p}=a{\left(\frac{h}{L}\right)}^{{n}_{m}}$$
(27)

in which the coefficient a was estimated for each roughness height (Table 2).

Table 2 Values of the coefficient a of Eq. (27) obtained for each pair (L, ks/p)
Full size table

As an example for L = 0.5 m, Fig. 2 shows the comparison between the measured pairs (h/L, K/p) and Eq. (27).

Fig. 2
figure 2

Comparison, as an example for L = 0.5 m, between the measured pairs (h/L, K/p) and Eq. (27)

Full size image

for each ks/p value.

The a values listed in Table 2 were related to the ratio ks/p according to the following relationships:

$$a=0.7173-0.0413\;\frac{{k}_{s}}{p}\quad\mathrm{for}\;L = 0.2\mathrm{ m}$$
(28a)
$$a=1.7949-0.1923\;\frac{{k}_{s}}{p}\quad\mathrm{for}\;L = 0.5\mathrm{ m}$$
(28b)
$$a=4.1500-0.6861\;\frac{{k}_{s}}{p}\quad\mathrm{for}\;L = 1.0\mathrm{ m}$$
(28c)

For comparing the errors in the discharge estimate E obtained by different equations, Table 3 lists the percentage of cases in which the errors are less than or equal to a given threshold value (± 15%, ± 10%, and ± 5%). In particular, for each investigated L value, Table 3 lists the errors corresponding to the discharge Q estimated by (i) Eq. (1), coupled with Eqs. (10) and (11), (ii) Eq. (26) with the coefficients a and n listed in Table 1, and (iii) Eq. (27) with the coefficient a estimated by Eqs. (28a), (28b) and (28c). Furthermore, Eq. (27), which uses an exponent nm dependent on the weir length, is characterized (Table 3) by errors that are comparable or less than those obtained by Eq. (1). For each investigated L value, Table 3 demonstrates that the errors in discharge estimate by Eq. (26) are always less than or equal to ± 10% and less than or equal to ± 5% for 97–100% of cases. In other words, the performances in estimating discharge by Eq. (26) are always better than those obtained by Eq. (1), coupled with Eqs. (10) and (11), proposed by Bai et al. (2023).

Table 3 Percentage of cases in which the errors of discharge estimated by Eqs. (1), (26) and (27) are less than or equal to a given value (± 15%, ± 10%, and ± 5%)
Full size table

Table 3 also shows that Eq. (27), with the coefficient a estimated by Eqs. (28a), (28b) and (28c), notwithstanding for each L, a single value of the exponent nm is applied, is characterized by \ errors in discharge estimate that, for a threshold value of 15%, are always less than or equal to those obtained by Eq. (1).

Considering the limited variability of nm range (1.10–1.17), the mean value (1.1471) of the exponent nm was considered, and the following stage-discharge relationship was also tested:

$$\frac{K}{p}=a{\left(\frac{h}{L}\right)}^{1.1471}$$
(29)

in which the values of a coefficient were estimated by the available data (Table 4).

Table 4 Values of the coefficient a of Eq. (29) obtained for each pair (L, ks/p)
Full size table

The a values listed in Table 4 were related to the ratio ks/p according to the following relationship (Fig. 3):

$$a=b-c\;\frac{{k}_{s}}{p}$$
(30)

in which b = 0.7175 and c = 0.0414 for L = 0.2 m, b = 1.8675 and c = 0.1989 for L = 0.5 m, and b = 3.9893 and c = 0.6589 for L = 1 m.

Fig. 3
figure 3

Relationship between the a values, listed in Table 4, and the ratio ks/p for each L investigated value

Full size image

The coefficients b and c of Eq. (30) are related to the ratio L/B according to the following relationships (Fig. 4):

Fig. 4
figure 4

Relationships between b (a) and c (b) coefficients and the L/B ratio

Full size image
$$b=1.571\;\frac{L}{B}$$
(31a)
$$c=0.136\;{\left(\frac{L}{B}\right)}^{1.7191}$$
(31a)

The developed analysis demonstrated that the stage-discharge relationship (Eq. 29), coupled with Eq. (30), is characterized by errors less than or equal to 15% for 94.4% of the investigated cases, while errors in discharge estimate by Eq. (1), coupled with Eqs. (10) and (11), are less than or equal to ± 15% for 95.4% of cases; in other words, similar performances in discharge estimate are obtained by the last proposed approach and that by Bai et al. (2023).

For the investigated weirs, the comparison between Eq. (29) and Eq. (1) was also developed by the empirical cumulative distribution of the errors E (%) in discharge estimate. The statistical data of the errors associated with Eqs. (29) and (1) are listed in Table 5.

Table 5 Statistical data of the errors associated with Eqs. (29) and (1)
Full size table

For Eq. (29), Fig. 5 highlights that the errors E are normally distributed, as also demonstrated by the Kolmogorov–Smirnov test, having a significance level of 5%. This result ensures that the applied Eq. (29) is a complete model, which does not need any other dimensionless groups.

Fig. 5
figure 5

Empirical frequency distribution of the errors E

Full size image

The proposed approach, based on the dimensional analysis, always guaranteed an accuracy better than the threshold of ± 5% suggested by Boiten (2000). Anyway, even the procedure leading to the worst results (i.e., Eq. 29 coupled with Eq. 30) has an accuracy similar to that obtained by Bai et al. (2023). Consequently, the aim of obtaining a relationship, excluding the use of discharge coefficient, characterized by better performances than the equations reported in the literature was achieved.

5 Conclusions

The developed analysis allowed for concluding that a power equation can be used to establish a stage-discharge equation (Eq. 26) with the exponent n varying with the crest length, and the coefficient a depending on the roughness height. The obtained relationship (Eq. 26) improves the performances estimating the discharge if compared with those proposed by Bai et al. (2023). For each weir length, hypothesizing that the exponent n is independent of roughness height, and the coefficient a is estimated by Eqs. (28a), (28b) and (28c), the proposed relationship (Eq. 27) leads to errors in discharge estimate always less than or equal to those obtained by using the discharge coefficient (Eq. 1). Finally, also applying the relationship with a single value of the exponent (1.1471) and the coefficient a estimated by Eq. (30), gives performances in discharge estimate similar to those by Bai et al. (2023).

In conclusion, the proposed approach, which excludes the discharge coefficient, also guarantees a better estimate of the relationship available in the literature for vegetated weirs.