1 Introduction

Water distribution systems are part of the critical economic networks on which modern-day societies depend, and it is widely accepted that there is considerable uncertainty associated with their planning, design and operation. The uncertainty arises from many factors, for example, the deterioration in the structural integrity and hydraulic capacity, unpredictable demands for fire-fighting and random fluctuations in the demands in addition to the underlying temporal and spatial variations, to name but a few. Hence, it is widely accepted that, ideally, explicit criteria for hydraulic capacity reliability and failure tolerance should be included in the design specifications for water distribution systems.

However, it is often difficult to set such performance criteria. Moreover, quantified reliability measures for water distribution systems are particularly difficult to define and evaluate (Wagner et al. 1988). It is even more challenging to incorporate reliability in the procedures used to optimize the design of water distribution systems. Consequently, some surrogate reliability measures such as flow entropy and resilience index have been adopted as they are computationally less demanding (Templeman 1982; Yates et al. 1984).

Flow entropy has been suggested as a surrogate measure of reliability and failure tolerance for water distribution systems. Flow entropy has the advantages that it is relatively easy to calculate and the data it requires are minimal. Also, it lends itself to direct incorporation into formal optimization procedures. Flow entropy is an extension of Shannon’s statistical entropy that is a measure of the amount of uncertainty that a probability distribution represents (Shannon 1948).

In the context of water distribution systems, uncertainty may arise due to a variety of reasons including incomplete or imprecise data, future demand requirements and the network’s structural integrity and hydraulic capacity that cannot be described or predicted with sufficient accuracy due to incomplete knowledge or understanding of the relevant factors or processes. Furthermore, the uncertainty due to randomness is unavoidable. Examples include the pipe and other component failures that may be related to extraneous factors also, and random fluctuations in demand.

Many different approaches have been developed including stochastic and reliability-based methods that address aleatoric uncertainty due to randomness (Gupta and Bhave 1996; Xu and Goulter 1999a; Laguna et al. 2000; Tolson et al. 2004; Afshar et al. 2005; Kapelan et al. 2005; Giustolisi et al. 2009; Saleh and Tanyimboh 2013) and fuzzy sets for epistemic uncertainty due to incomplete or imprecise information (Xu and Goulter 1999b; Revelli and Ridolfi 2002; Bhave and Gupta 2004; Vamvakeridou-Lyroudia et al. 2005; Gupta and Bhave 2007; Branisavljević et al. 2009; Fu and Kapelan 2011; Shibu and Reddy 2011; Spiliotis and Tsakiris 2012; Sivakumar et al. 2015).

Also, scenario-based robust optimization approaches that address the uncertainty associated with the various scenarios seek solutions that provide the best compromise with respect to the scenarios considered (Watkins and McKinney 1997; Afonso and Cunha 2007; Cunha and Sousa 2010; Napolitano et al. 2016).

Other surrogate measures in the literature include: Tsallis entropy (Singh and Oh 2015), diameter-sensitive flow entropy (Liu et al. 2016), resilience indices (Todini 2000; Prasad and Park 2004; Jayaram and Srinivasan 2008; Liu et al. 2016) and surplus power factor (Vaabel et al. 2006). The results to date seem to indicate that flow entropy (Tanyimboh and Templeman 1993a) yields the most consistent results (Gheisi and Naser 2015; Tanyimboh et al. 2016; Liu et al. 2016). Recent reviews and comparisons include Liu et al. (2014, 2016), Tanyimboh et al. (2016), Gheisi and Naser (2015), Atkinson et al. (2014) and Greco et al. (2012). In particular, Gheisi and Naser (2015) emphasized the importance of failure tolerance while Tanyimboh et al. (2016) highlighted the need for more consistency in future comparisons.

Flow entropy was tested on different networks over the years and the function proposed in Tanyimboh and Templeman (1993a) was consistently satisfactory. Nevertheless, most of the work focused on networks with a single operating condition based on steady-state simulation that assumes that nodal demands are constant. It is common practice to use the maximum daily demand and steady-state modelling in designing water distribution networks.

In reality, however, the demands vary with the time of the day and other loading conditions including fire flows that have to be satisfied by the network (Cunha and Sousa 2010; Simpson et al. 1994; Walski et al. 1987; Tanyimboh and Seyoum 2016). Alperovits and Shamir (1977) suggested that, in addition to the maximum daily demand and fire flows, the minimum demand periods should be considered also. Furthermore, Prasad (2010) has shown that even if a network satisfies the peak demands it does not follow that other operating conditions will be satisfied as a result. Prasad (2010) also demonstrated that designs that consider multiple operating conditions are more reliable than those based on a single operating condition. Similarly, maximum entropy designs achieve higher levels of reliability and redundancy by being maximally noncommittal to other operating conditions besides those that are designed for explicitly.

Evolutionary optimization algorithms that rely on simulation models are very popular in many disciplines including water resources (Mora-Melia et al. 2015; Borah and Bhattacharjya 2016; Chang et al. 2016; Masoumi et al. 2016; Shokoohi et al. 2016; Steffelbauer and Fuchs-Hanusch 2016). Simulation models make the inclusion of multiple operating conditions in optimization models relatively straightforward. On the other hand, the flow entropy in systems with multiple operating conditions has not been investigated hitherto.This paper describes a multi-objective genetic algorithm that maximizes the flow entropy for multiple operating conditions for any given network (Czajkowska 2016). The new methodology proposed is consistent with the maximum entropy formalism (Jaynes 1957) that requires active consideration of “whatever is known”. An alternative flow entropy function is presented that considers the relative uniformity of the nodal demands, as opposed to the relative uniformity of the source supplies, and its equivalence to the existing function is established. Also, the flow entropy function for multiple operating conditions is discussed with reference to the joint entropy of a combination of probability schemes to provide the theoretical foundation for the optimization model proposed.

2 The Flow Entropy Function

Shannon (1948) developed the informational entropy function as a statistical measure of the amount of uncertainty that a probability distribution represents. Shannon’s entropy function for a single probability space is

$$ S=-\sum_{i=1}^n{p}_i \ln {p}_i $$
(1)

in which S is the entropy; p i is the probability of the ith outcome; and n is the number of outcomes. Tanyimboh and Templeman (1993a, b) developed the framework that enabled the pipe flow rates in a water distribution network to be cast as probabilities. Given the pipe flow rates, the entropy function is

$$ S={S}_0+\sum_{i=1}^{nn}{P}_i{S}_i $$
(2)

where S is the entropy; S 0 is the entropy that accounts for the relative contributions of the supply nodes; S i is the entropy at node i; P i  ≡ T i /T is the fraction of the total flow through the network that reaches node i; T i is the total flow that reaches node i; T is the sum of the nodal demands; nn is the number of nodes in the network. The entropy for the relative contributions of the supply nodes is

$$ {S}_0=-\sum_{i\in I}\frac{Q_{0 i}}{T} \ln \left(\frac{Q_{0 i}}{T}\right) $$
(3)

where Q 0i is the inflow at supply node i; I represents the set of supply nodes. Similarly, the entropy at demand node i is

$$ {S}_i=-\frac{Q_{i0}}{T_i} \ln \left(\frac{Q_{i0}}{T_i}\right)\kern1em -\sum_{i j\in {ND}_i}\frac{Q_{i j}}{T_i} \ln \left(\frac{Q_{i j}}{T_i}\right);\kern2em i=1,\kern1em \dots, \kern1em nn $$
(4)

where Q i0 is the demand at node i; Q ij is the flow rate in pipe ij with node i and j as the upstream and downstream nodes, respectively; the set ND i represents the pipe flows from node i. The entropy reflects the number of paths supplying the various demand nodes and the relative uniformity of the flows in the respective supply paths. The greater the uniformity in the path flows and the number of supply paths, the greater the entropy (Tanyimboh 1993; Yassin-Kassab et al. 1999). Awumah et al. (1990, 1991) proposed several alternatives, but they did not account for the interdependencies in the various processes involved in a satisfactory way (Tanyimboh 1993).

The entropy also depends on the flow directions in the pipes. The problem of identifying the optimal or most suitable set of flow directions is a complex nonlinear optimization problem (Saleh and Tanyimboh 2014, 2016). Furthermore, previous results suggest that efficient sets of flow directions in networks generally result in high maximum entropy values (Tanyimboh and Setiadi 2008). To clarify further, each feasible set of flow directions has a maximum entropy value and thus a network may have many different maximum entropy values due to the multiplicity of flow directions.

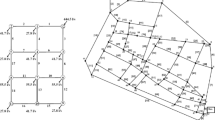
The first term S 0 in Eq. (2) relates to the relative contributions of the supply nodes. For systems with multiple sources, S0 may change continuously. For example, the network shown in Fig. 1 has five variable head supply nodes and three demand categories with demand patterns that change with time (Tanyimboh and Seyoum 2016). In addition to these practical considerations, the S 0 term arises because the underlying model comprises multiple inter-related probability spaces and the flow entropy function stems from the conditional entropy concept (Tanyimboh 1993; Khinchin 1953, 1957).

Fig. 1
figure 1

A water distribution network with five variable head supply nodes (R1 to R5)

Full size image

It may appear, at first glance, that there is an imbalance between the supply nodes and the demand node in Eq. (2). However, a water distribution network combines and/or separates the flows in the various paths in the network repeatedly at successive nodes and junctions. A closer examination reveals that Eq. (2) involves only the flow separation points in the network. In fact, there is an analogous function for the flow collection points that may be summarised briefly as follows (Tanyimboh 1993: 106–111).

$$ {S}^{\prime }={S}_0^{\prime }+\sum_{i=1}^{nn}{P}_i^{\prime }{S}_i^{\prime } $$
(5)
$$ {S}_0^{\prime }=-\sum_{i\in D}\frac{Q_{i0}}{T} \ln \left(\frac{Q_{i0}}{T}\right) $$
(6)
$$ {S}_i^{\prime }=-\frac{Q_{0 i}}{T_i} \ln \left(\frac{Q_{0 i}}{T_i}\right)\kern1em -\sum_{i j\in {NU}_i}\frac{Q_{i j}}{T_i} \ln \left(\frac{Q_{i j}}{T_i}\right);\kern2em i=1,\kern1em \dots, \kern1em nn $$
(7)

where S ′ is the entropy of the network and \( {S}_0^{\prime } \) is the entropy or uncertainty that arises due to the distribution, or relative contributions, of the nodal demands. \( {S}_i^{\prime } \) is the entropy at node i, based on the inflows at node i. The inflows include any source supplies as the first term in Eq. (7) shows. NU i refers to the set of pipes upstream of node i that supply node i directly. T i is the total flow that reaches node i and T is the sum of the demands. \( {P}_i^{\prime}\equiv {P}_i={T}_i/ T \) is the fraction of the total flow through the network that reaches node i.

As one might expect, S ′ ≡ S. In other words, the total amount of uncertainty associated with the path flow separation and collection processes is the same. However, in general \( {S}_i^{\prime}\ne {S}_i \) and \( {S}_0^{\prime}\ne {S}_0. \)

3 Maximum Entropy Flows in Networks

Flow entropy is often used as a practical and computationally efficient surrogate measure for reliability and redundancy. It has been shown previously that on average reliability and redundancy increase as flow entropy increases in water distribution networks (Gheisi and Naser 2015). However, flow entropy is a relative measure for which there is no absolute scale.

Hence, it is frequently necessary to ascertain the maximum entropy value for any network under consideration. It its simplest form, the problem involves maximizing the entropy subject to the continuity of flow at the nodes and junctions, given the topology of the network and direction of flow in the pipes as follows.

$$ \underset{\forall {Q}_{i j}}{Maximize}\kern1em S={S}_0+\sum_{i=1}^{nn}{P}_i{S}_i $$
(8)

Subject to:

$$ \sum_{j\in {N}_i}{Q}_{i j}+{Q}_{0 i}=0;\kern2em \forall i\in I $$
(9)
$$ \sum_{j\in {N}_i}{Q}_{i j}+{Q}_{i0}=0;\kern2em \forall i\in D $$
(10)
$$ {Q}_{ij}\ge 0;\kern2em \forall ij $$
(11)

Q 0i and Q i0 are supplies and demands at the supply and demand nodes, respectively. The sets I and D represent the supply and demand nodes, respectively. The pipe flow rates Q ij are the decision variables; the set N i comprises the upstream or downstream nodes of the pipes connected to node i.

The model in Eqs. (8) to (11) is nonlinear and convex; i.e. it has a unique maximum entropy value for any given topology and set of flow directions (Tanyimboh 1993: 128). The computational solution of the optimization problem requires numerical nonlinear optimization. Efficient algorithms that avoid numerical optimization have been developed that are quick and non-iterative (Tanyimboh and Templeman 1993b; Walters et al. 1995; Yassin-Kassab et al. 1999; Ang and Jowitt 2005a, b). More specifically, Yassin-Kassab et al. (1999) described the fundamental property of maximum entropy flows that underpins the α-method they developed. Whereas Yassin-Kassab et al. (1999) carried out numerical experiments, Ang and Jowitt (2005a, b) provided a rigorous mathematical proof that they then used to develop path entropy methods.

The α and path entropy methods relate to a single operating condition, in other words, one set of demands under steady state conditions. They also require the flow directions in the pipes to be specified in advance. In the case of water distribution systems, in general the flow directions may not be available. For example, at the planning or design stages the topology and/or pipe diameters may not be available initially.

The global maximum entropy approach formulated recently by Saleh and Tanyimboh (2014, 2016) shows how the topology and/or flow directions along with the pipe diameters and flow rates may be optimized simultaneously. This is a key contribution in the development of flow entropy as it addresses a complex issue in practical applications.

4 Flow Entropy under Multiple Operating Conditions

In practice water distribution systems do not operate under steady state conditions. There are other loading conditions besides the daily demand variations e.g. fire-fighting flows. Every operating condition has an entropy value and an appropriate methodology for maximizing the entropy is required. Maximizing the entropy for every operating condition may result in too many objectives. Optimization problems with many objectives are extremely difficult to solve; as the proportion of solutions that are nondominated increases very rapidly and disproportionately as the objectives increase in number (Yuan et al. 2016).

An important property of informational entropy is that the joint entropy of a combination of independent probability schemes is the sum of their entropies (Tanyimboh 1993: 73–77, Shannon 1948). Furthermore, Jaynes (1957) stated that “in making inference on the basis of partial information, we must use that probability distribution that has maximum entropy subject to whatever is known”. In other words, maximizing the entropy results in the least biased solution. Thus the formal definition of the joint entropy and the requirement to include whatever is known suggest that the flow entropy under multiple operating conditions is the sum of the entropies. An illustrative example in Section 5 includes results that appear to support this hypothesis.

5 Network Design under Multiple Operating Conditions

Results in the literature (e.g. Gheisi and Naser 2015, etc.) show that flow entropy is an effective surrogate measure of hydraulic reliability and failure tolerance. However, most of the research to date has focussed on a single operating condition and it is common practice to use the maximum daily demand based on steady state analysis. In reality the nodal demands follow a diurnal pattern and other loading patterns have to be satisfied also. Alperovits and Shamir (1977) suggested that the minimum daily demand be considered in addition to the maximum daily demand and fire-fighting flows.

A multi-objective evolutionary algorithm that handles multiple operating conditions seamlessly for any given network was developed and applied to three well-known networks in the literature. The results showed that solutions that considered multiple operating conditions outperformed solutions based on a single operating condition (Czajkowska 2016).

5.1 Formulation of the Optimization Model

The objectives are the initial construction cost that is to be minimized and flow entropy that is to be maximized subject to adequate flow and pressure at the demand nodes. The nodal mass balance and energy conservation constraints were satisfied externally using the EPANET 2 hydraulic solver (Rossman 2000). Pipe diameters were selected from a set of commercially available discrete pipe sizes. A solution is considered feasible if the residual pressures at all the demand nodes are greater than or equal to the required pressures for the respective operating conditions.

The minimum node pressure constraints were transformed into an infeasibility objective that was minimized. In this way the constrained optimization problem was converted and solved as an unconstrained problem without introducing any constraint violation penalties as penalty-free genetic algorithms have achieved better results than other algorithms in the literature consistently (Saleh and Tanyimboh 2013; Siew et al. 2014, 2016).

The optimization problem may be summarized as follows.

$$ \mathrm{Minimize}\ \mathrm{the}\ \mathrm{total}\ \mathrm{cost}:{f}_1=\sum_{i=1}^{np}{C}_i\left({D}_i,{L}_i\right) $$
(12)
$$ \mathrm{Minimize}\ \mathrm{the}\ \mathrm{largest}\ \mathrm{node}\ \mathrm{pressure}\ \mathrm{deficit}:{f}_2=\mathit{\operatorname{Max}}\left\{\mathit{\max}\left[0,\left({H}_i^{des}-{H}_i\right)\right];\forall i\right\} $$
(13)
$$ \mathrm{Maximize}\ \mathrm{the}\ \mathrm{flow}\ \mathrm{entropy}:{f}_3={S}_{MOC} $$
(14)

where S MOC is the flow entropy based on all the operating conditions considered and is to be established in this research; C i (D i , L i ) is the cost associated with pipe i of diameter D i and length L i ; np represents number of pipes; H i is the available head at node i; and \( {H}_i^{des} \) is the required residual head at node i. The required residual head at a node is the head above which the demand is satisfied in full. The infeasibility function f 2 in Eq. (13) represents the largest node pressure deficit.

Three alternatives were considered for the entropy S MOC as follows:

  1. Case I.

    To maximize the maximum entropy, the highest entropy value achieved was chosen, considering all the operating conditions. This option seeks feasible solutions with high entropy values in any operating condition, without attaching any weight to the rest of the entropy values. This option seems unduly optimistic and may be costly in certain circumstances.

  2. Case II.

    If the smallest entropy value achieved in any operating conditions is maximized, then it would alleviate the adverse effects of the worst-case failures. This option seems unduly pessimistic.

  3. Case III.

    By contrast, maximizing the sum of the entropies would consider all entropy values with an expectation that the resulting solutions would be the most robust or failure tolerant in all the operating conditions considered.

5.2 Solution Methodology

5.2.1 Description of the Optimization Algorithm

The non-dominated sorting genetic algorithm NSGA II (Deb et al. 2002) has been used widely by many researchers in various disciplines. It is an efficient evolutionary algorithm based on Pareto-dominance and global elitism. The general purpose binary coded NSGA II algorithm written in the C++ language was modified and coupled with the hydraulic simulation model EPANET 2 (Rossman 2000). A subprogram that calculates the flow entropy for any given layout was developed, tested and incorporated in the optimization algorithm. The multiobjective genetic algorithm thus developed can handle multiple operating conditions for any network configuration (Czajkowska 2016).

It was observed that many infeasible solutions were present in the Pareto-optimal fronts achieved. This was expected as the algorithm did not prioritize any of the objective functions and, provided they were nondominated, even infeasible solutions with low cost and high entropy survived until the end of the optimization. This could be beneficial for the decision maker as solutions with a small shortfall in the residual pressure may be worth considering due to budgetary or other reasons.

Furthermore, it is widely known that evolutionary algorithms that deploy both feasible and infeasible solutions in the optimization outperform those that penalise infeasible solutions unduly (Woldesenbet et al. 2009; Saleh and Tanyimboh 2013; Siew et al. 2016). At the end of the optimization, after removing the infeasible solutions in the Pareto-optimal front, a program developed in the Perl language was used to select and sort all the feasible solutions, including those from all the preceding generations, based on Pareto-dominance considering entropy and cost.

5.2.2 Reliability and Failure Tolerance Evaluation

The nondominated feasible solutions were evaluated further by calculating the hydraulic reliability and pipe failure tolerance, using a pressure-driven analysis program (PRAAWDS) (Tanyimboh et al. 2003; Tanyimboh and Templeman 2010). The program is robust, computationally efficient, and has been tested and used extensively (Czajkowska 2016; Czajkowska and Tanyimboh 2013). An extension developed in the Perl language allows seamless pipe failure simulations for the reliability calculations (Czajkowska 2016).

For a water distribution system, the reliability may be considered a probabilistic measure of the ability to satisfy the required nodal demands at adequate pressure under normal and abnormal operating conditions. The pipe failure tolerance is a complementary measure that provides a probabilistic estimate of the demand that can be satisfied when one or more components are out of service. Accordingly, the hydraulic reliability and failure tolerance were calculated as in Tanyimboh and Templeman (2000).

5.3 Details of the Network Investigated

The network is shown in Fig. 2 and was based on Simpson et al. (1994). The peak demand and two fire flows were considered. Each fire flow comprised the peak demand plus a fire flow at one node, i.e. nodes 7 and 12, for fire flows 1 and 2, respectively (Table 1). Consequently, the minimum nodal head was higher for the peak demand than the fire flows (Walski et al. 1987; Farmani et al. 2006; Cunha and Sousa 2010). The properties of the pipes are shown in Table 2.

Fig. 2
figure 2

Pipe network topology and diameter options

Full size image
Table 1 Nodal demands and required residual heads for the network investigated
Full size table
Table 2 Pipe properties for the network investigated
Full size table

The original design problem (Simpson et al. 1994) was to determine the pipe diameters to upgrade and expand an existing network. For the purposes of the present research, all the pipe diameters were optimized. The network comprises 10 demand nodes, 14 pipes and 2 reservoirs. A Hazen-Williams roughness coefficient (Rossman 2000) of 120 was assumed for all the pipes (Table 2). The network is partially branched; demand node 12 has only one incident pipe. The water levels at supply nodes 1 and 5 were 365.76 m and 371.86 m, respectively.

With 8 pipe diameter options and 14 pipes to size, the solution space comprised a total of 814 = 4.398 × 1012 feasible and infeasible solutions. A 3-bit binary substring was used. Thus there were 23 = 8 substrings, an exact match for the 8 diameter options with no redundant codes. A single-point crossover operator was used to produce two offspring from two parents. A bitwise mutation operator was used to change the bit from 0 to 1 or vice versa. For each entropy option in Case I to III, 30 GA runs were performed; i.e. 90 GA runs in total. The average CPU time for a single execution of the optimization algorithm was approximately 17 min on a PC (Intel Core 2 Duo @ 3.5GHz and RAM of 3GB).

Extensive testing and sensitivity analysis were carried out to determine suitable values for the parameters used in the optimization algorithm (Czajkowska 2016). The crossover probability was 1.0. The mutation probability was 1/42 = 0.0238 based on a chromosome length of 42, i.e. a 2.38% chance that any single bit would mutate. The population size was 200. In each optimization run 200,000 function evaluations (i.e. 1000 generations) were allowed.

5.4 Results and Discussion

It was observed that the ranges of the entropy values achieved by the various flow entropy options (Case I to III) were different. Also, the Pareto-optimal fronts had slightly different shapes. With three different operating conditions having three different sets of nodal demands and residual pressure requirements, this outcome was not entirely surprising and, indeed, the result seems to support the hypothesis that the entropy should include all the operating conditions, i.e. Case III.

It was observed that a large number of solutions for which the increase in cost was very high but the improvement in entropy was insignificant were at the upper ends of the entropy ranges. This is consistent with previous research in the literature on the trade-off between cost and reliability. In other words, after the improvements taper off, any further improvements become insignificant while the cost increases excessively (Vamvakeridou-Lyroudia et al. 2005, Czajkowska 2016, etc.). Therefore, cut-off points for entropy were set at 99% of the respective maximum entropy values. The resulting performance indicators are summarised in Table 3. The peak demands were used to evaluate the hydraulic reliability and failure tolerance. Unlike the fire flows that are extreme situations, the peak loading would be expected to occur frequently.

Table 3 Coefficient of determination for the relationships indicated
Full size table

Previous research has shown that both the mean and uniformity of the pipe diameters increase as the flow entropy increases. Larger and more uniform pipe diameters improve the hydraulic reliability by providing lower pipe failure rates and larger flow re-routing capacities (Czajkowska and Tanyimboh 2013; Tanyimboh and Setiadi 2008). The correlation between entropy and the mean pipe diameter was high for all the entropy options (Case I to III), with the total entropy having the highest value of 0.952.

Figure 3 shows the relationship between the hydraulic reliability and entropy for Case II that maximized the minimum entropy, for solutions that are nondominated based on the trade-off between cost and flow entropy (CEND), of which the solutions that are nondominated based on the trade-offs between cost and reliability (CRND) and between cost and failure tolerance (CFTND) have been identified also. Table 3 shows the corresponding coefficients of determination.

Fig. 3
figure 3

Hydraulic reliability vs. entropy for the minimum entropy maximization option

Full size image

The minimum entropy maximization option (Case II) generated the largest number of feasible solutions (Table 3). However, for the cost-vs-entropy nondominated solutions (CEND), the coefficient of determination of 0.007 for this option (Case II) suggests there is practically no correlation. In fact negative correlation can be seen in Fig. 3 between entropy values of about 2.8 and 3.0. A general pattern of negative correlation can be seen also in the bottom right corner. Overall, the results seem to show that maximization of the minimum entropy (Case II) improves the reliability somewhat, but does not lead to the most effective solutions compared to Case I and III.

It may be noted, however, that the entropy values in Fig. 3 from around 3.0 and above seem to belong to a separate cluster with good correlation as can be seen in the graph. Indeed, it was observed that all the entropy maximization options had clusters of solutions located around the highest entropy values. This could be due to the NSGA II optimization algorithm or the optimization model itself (Eqs. 12–14). Despite using solutions up to 99% of the respective maximum entropy values, the majority of the solutions, with entropy values of more than about 3.0 were close to the highest entropy values. This may have influenced the reliability-entropy relationship achieved and may be an area for further research in the future. Also, reintroducing the nondominated feasible solutions from all the previous generations may have altered the distribution of solutions in the final nondominated set. Additional investigations may be needed to verify this.

Furthermore, the observed preponderance of high entropy solutions is consistent with previous comments by Saleh and Tanyimboh (2014, 2016) who found that the high entropy solutions were over-represented if the entropy was maximized on its own as a separate objective function rather than within the hydraulic performance objective function they used. Hence, they developed a multi-directional approach to maximize the global and local maximum entropy values simultaneously. A more even distribution of the entropy values was achieved as a result. The local maximum entropy values are associated with the various alternative sets of feasible flow directions in the network.

Finally, Table 3 shows that maximization of the sum of the entropies achieved better results than maximization of the maximum entropy; it can be seen that the correlations were consistently stronger for the total entropy option (Case III). Maximization of the total entropy therefore seems to be the most robust approach among the three options investigated and reinforces the hypothesis put forward here, that it is essential to take the entropy values from all the operating conditions into consideration.

6 Conclusions

A penalty-free maximum entropy based multi-objective evolutionary optimization approach for water distribution networks under multiple operating conditions has been presented and evaluated. The novelty of this research in the context of entropy maximization is that the optimization works under many loading conditions for any given network. Sensitivity analysis was carried out to assess the robustness of the algorithm and to identify efficient input data values relating to the population size, mutation and crossover rates, and the allocation of redundant binary codes.

Maximization of the sum of the entropies produced the best results, i.e. the most robust or failure-tolerant solutions. The significant advantage of the total entropy option (Case III) is that it takes into consideration all the operating conditions. Jaynes (1957) stated that the probability distribution that has maximum entropy subject to whatever is known should be used as it is the least biased. Only the total entropy option is consistent with the maximum entropy principle (Jaynes 1957). Self-evidently, maximization of the maximum entropy or maximization of minimum entropy would place unjustified weight on one operating condition at the expense of all the others and thus would introduce bias.

Finally, it is worth noting that the majority of the solutions achieved were relatively close to the highest entropy values. This may have influenced the reliability-entropy relationship achieved and may be an area for further research in the future. Similarly, Saleh and Tanyimboh (2014, 2016) observed that the high-entropy solutions were over-represented if the entropy was maximized on its own as a separate objective. Hence the global maximum entropy approach they developed may be worth considering in the future as it provided a more even distribution of the entropy values.