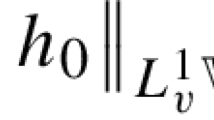Abstract
We analyze the asymptotic behavior of linear Fokker-Planck equations with time-dependent coefficients. Relaxation towards a Maxwellian distribution with time-dependent temperature is shown under explicitly computable conditions. We apply this result to the study of Brownian motion in granular gases by showing that the Homogenous Cooling State attracts any solution at an algebraic rate.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
H. Risken, The Fokker-Planck Equation. Methods of Solution and Applications, Springer, Berlin (1989).
W. T. Coffey, Yu. P. Kalmikov, and J. T. Waldron, The Langevin Equation with Applications in Physics Chemistry and Electrical Engineering, World Scientific, 1996.
A. Arnold, P. Markowich, G. Toscani, and A. Unterreiter, “On convex Sobolev inequalities and the rate of convergence to equilibrium for Fokker-Planck type equations,” Commun. Partial Different. Equat., 26, 43–100 (2001).
J. A. Carrillo and G. Toscani, “Exponential convergence toward equilibrium for homogeneous Fokker-Planck-type equations,” Math. Meth. Appl. Sci., 21, 1269–1286 (1998).
A. Arnold, J. A. Carrillo, L. Desvillettes, J. Dolbeault, A. Jungel, C. Lederman, P. A. Markowich, G. Toscani, and C. Villani, “Entropies and equilibria of many-particle systems: an essay on recent research,” Monatsh. Math., 142, 35–43 (2004).
P. Alpatov and L. E. Reichl, “Spectral properties of a time-periodic Fokker-Planck equation,” Phys. Rev. E, 49, 2630–2638 (1994).
J. Luczka and B. Zaborek, Brownian Motion: a Case of Temperature Fluctuations, Preprint arxiv: cond-mat/0406708v1 (2004).
J. J. Brey, J. W. Dufty, and A. Santos, “Kinetic models for granular flow,” J. Statist. Phys., 97, 281–322 (1999).
J. L. Vazquez, “Asymptotic behaviour for the porous medium equation posed in the whole space,” J. Evol. Equat., 3, 67–118 (2003).
A. V. Bobylev, C. Cercignani, and G. Toscani, “Proof of an asymptotic property of self-similar solutions of the Boltzmann equation for granular materials,” J. Statist. Phys., 111, 403–417 (2003).
J. J. Brey, J. W. Dufty, and A. Santos, “Dissipative dynamics for hard spheres,” J. Statist. Phys., 87, 1051–1066 (1997).
I. Goldhirsch, “Scales and kinetics of granular flows,” Chaos, 9, 659–672 (1999).
M. H. Ernst and R. Brito, “High energy tails for inelastic Maxwell models,” Europhys. Lett., 43, 497–502 (2002).
P. K. Haff, “Grain flow as a fluid-mechanical phenomenon,” J. Fluid Mech., 134, 401–430 (1983).
C. Cercignani, The Boltzmann equation and its applications, Springer, New York (1988).
B. Lods and G. Toscani, “The dissipative linear Boltzmann equation for hard spheres,” J. Statist. Phys., 117, No.3, 635–664 (2004).
M. H. Ernst and R. Brito, “Scaling solutions of inelastic Boltzmann equation with over-populated high energy tails,” J. Statist. Phys., 109, 407–432 (2002).
S. McNamara and W. R. Young, “Kinetics of a one-dimensional granular medium in the quasielastic limit,” Phys. Fluids A, 5, 34–45 (1993).
G. Toscani, “One-dimensional kinetic models of granular flows,” MMAN Math. Model. Numer. Anal., 34, 1277–1291 (2000).
E. Caglioti and C. Villani, “Homogeneous cooling states are not always good approximations to granular flows,” Arch. Ration. Mech. and Anal., 163, 329–343 (2002).
Li Hailang and G. Toscani, “Long-time asymptotics of kinetic models of granular flows,” Arch. Ration. Mech. and Anal., 172, 407–428 (2004).
Author information
Authors and Affiliations
Additional information
__________
Published in Ukrains'kyi Matematychnyi Zhurnal, Vol. 57, No. 6, pp. 778–789, June, 2005.
Rights and permissions
About this article
Cite this article
Lods, B., Toscani, G. Long-Time Behavior of Nonautonomous Fokker-Planck Equations and Cooling of Granular Gases. Ukr Math J 57, 923–935 (2005). https://doi.org/10.1007/s11253-005-0240-5
Received:
Issue Date:
DOI: https://doi.org/10.1007/s11253-005-0240-5