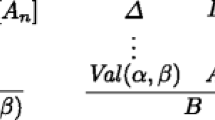Abstract
This note motivates a logic for a theory that can express its own notion of logical consequence—a ‘syntactically closed’ theory of naive validity. The main issue for such a logic is Curry’s paradox, which is averted by the failure of contraction. The logic features two related, but different, implication connectives. A Hilbert system is proposed that is complete and non-trivial.
Similar content being viewed by others
Notes
To see that this is revenge, consider the similar structure of solutions to the problem: ‘stratification’ approaches to the validity paradox, e.g. (Myhill 1975), fail to satisfy closure, since they do not allow expression of all that is expressible; e.g. a stratified validity predicate cannot deal with intuitive data, such as Dean/Nixon circles (Kripke 1975):
-
Dean: All of Nixon’s arguments are valid.
-
Nixon: Everything Dean says is true. Therefore, we are doomed!
This pair of sentences produces a circular Validity-Curry paradox (see Sect. 1.2, Weber 2014). One could say that attempts to mitigate what is effectively Gödel’s first incompleteness theorem with non-classicality all founder on what is effectively the second incompleteness theorem.
-
In all of our examples, strings of the form \(A_1,\ldots,A_n\vdash B\) are inferences, horizontal lines are rules that putatively preserve the validity of inferences which we sometimes call meta-inferences, capital Roman letters are schematic for sentences, and capital Greek letters are schematic for multisets of sentences.
Ripley and others have recently proposed non-transitive approaches (Ripley 2013); nothing we say here is an argument against that approach; non-contractive solutions are, at this stage, an alternative.
As a referee points out, that substructural logics admit distinct implication connectives is itself important, since connectives that (i) express meaning equivalence, and (ii) satisfy the deduction theorem, collapse in classical logic (Spinks and Veroff 2008).
For an object lesson in what happens if a biconditional like ⇔ is allowed to be sufficient for identity, see (Restall 2013).
And all of this remains true if a posit of Shapiro (2011) is right, viz. that the validity predicate merely serves to generalize over a certain kind of validity connective.
Reductio is the rule that if \(\Upgamma,A\vdash\neg A\) then \(\Upgamma\vdash\neg A. \) It implies an instance of contraction: If \(A,A\vdash\neg A\) then \(A\vdash\neg A. \) But rejecting contraction in full generality still allows some instances to hold.
One direct way to make these nice negation facts official is to commit our naive validity theory to the direction of paraconsistency—but we leave such future choice-points open for now.
To make this more precise, we could appeal to the plausible idea that propositional content is closed under entailment—what Stephen Read calls calls Bradwardine’s Postulate (Read 2002). This principle entails that any ‘self-oppositional’ sentence expresses its own truth as part of its content. Roughly, since C expresses that T(C), and T(C) entails \(T(C) \to \bot, \) then C expresses \(\bot. \) But, as above, the VCurry sentence has non-trivial content! Therefore, the non-triviality of C might force us to say that propositional content is not closed under conjunction. Maybe in ‘familiar’ cases we have this kind of closure, but not as a general principle. If we think of conjunction as ‘compossibility’ a la Routley-Meyer (1973), we can say that the VCurry sentence expresses two non-compossible things; if we think of conjunction as ‘information combination’ a la Slaney (1990), we can say that the VCurry sentence expresses two non-combinable contents (on pain of triviality). For the present paper, we take no particular stand on conjunction.
If m is the name \(\ulcorner V(x, \ulcorner B \urcorner) \urcorner, \) then \(V(m, \ulcorner B \urcorner)\) is the diagonalization of \(V(x, \ulcorner B \urcorner)\). Then if n is the name \(\ulcorner V(m, \ulcorner B \urcorner) \urcorner, \) write d(m) for n. A very specific instance of Gödel’s diagonal lemma then follows: for any A, there is a sentence G 0 such that
$$ \vdash_{{\sf NV}} G_0 \qquad \hbox{iff} \qquad \vdash_{{\sf NV}} {\rm V}({\ulcorner{G_0}\urcorner},{\ulcorner{B}\urcorner}) $$Just consider \(V(d(x), \ulcorner B \urcorner)\). Suppose m is \(\ulcorner V(d(x), \ulcorner B \urcorner)\urcorner\). Then let n be \(\ulcorner V(d(m), \ulcorner B \urcorner)\urcorner\). Since d(m) is n, the formula \(V(d(m), \ulcorner B \urcorner)\) is the witness. Proof that for any B there is a G 1 such that G 1 is a theorem iff \({\rm V}({\ulcorner{A}\urcorner},{\ulcorner{G_1}\urcorner})\) is, is the same. Whether there are also fixed point sentences \(\vdash_{{\sf NVT}} G \leftrightarrow (G \Rightarrow B)\) depends on the success of the program in Sect.3.2.2.
Thanks to an anonymous referee for pressing us to clarify this point.
References
Anderson AR, Belnap ND (1962) The pure calculus of entailment. J Symbol Logic 27(1):19–52
Avron A (1991) Simple consequence relations. Inform Comput 92:105–139
Beall JC, (eds) (2008) Revenge of the Liar: new essays on the paradox. Oxford University Press, Oxford
Beall J (2009) Spandrels of truth. Oxford University Press, Oxford
Beall J, Murzi J (2013) Two flavors of curry’s paradox. J Philos CX(3):143–165
Brady R (2006) Universal logic. CSLI Publications, Stanford
Field H (2008) Saving truth from paradox. Oxford University Press, Oxford
Field Hartry (2009) What is the normative role of logic?. Aristot Soc Suppl Vol 83(1):251–268
Fitch F.B. (1964) Universal metalanguages for philosophy. Rev Metaphys 17(3):396–402
Halbach V, Horsten L (2006) Axiomatizing kripke’s theory of truth. J Symb Logic 71:677–712
Kripke Saul (1975) Outline of a theory of truth. J Philos 72(19):690–716
Mares E, Paoli F (forthcoming) Logical consequence and the paradoxes. J Philos Logic
Meadows T (forthcoming) Fixed points for consequence relations. Logique et Analyse
Myhill J (1975) Levels of implication. In: Anderson AR, Marcus RC, Martin RM (eds) The logical enterprise. Yale University Press, New Haven
Priest G (1987) In Contradiction. Dordrecht: Martinus Nijhoff,
Quine WVO (1969) Set theory and its logic. Belknap Press, Harvard
Read S (2002) The liar paradox from john buridan back to thomas bradwardine. Vivarium 40(2)
Restall G (2005) Multiple Conclusions. In: Hájek P, Valdés-Villanueva L, Westerståhl D (eds) Logic, methodology and philosophy of science: proceedings of the twelfth international congress. King’s College Publications, London
Restall G (2013) Assertion, denial and non-classical theories. In: Tanaka K, Berto F, Mares E, Paoli F (eds) Paraconsistency: logic and applications. Springer, Berlin, pp 81–100
Ripley D (2012) Conservatively extending classical logic with transparent truth. Rev Symbol Logic 5(2):354–378
Ripley D (2013) Paradoxes and failures of cut. Aus J Philos 91(1):139–164
Routley R, Loparić A (1978) Semantical Analysis of Arruda da Costa P systems and adjacent non-replacement relevant systems. Studia Logica 37:301–320
Routley R, Meyer R (1973) The semantics of entailment. In: LeBlanc H (eds) Truth, syntax, and modality. North-Holland Publishing Co., Amsterdam
Routley R, Plumwood V, Meyer RK, Brady RT (1982) Relevant logics and their rivals. Ridgeview, Atascadero
Shapiro L (2011) Deflating logical consequence. Philos Quart 61:320–342
Slaney JK (1990) A General Logic. Aus J Philos 68:74–88
Spinks M, Veroff R (2008) Constructive logic with strong negation is a substructural logic i and ii. Studia Logica, 88 and 89:325 – 348 and 401–425
Weber Z (2014) Naive validity. Philos Quart 64(254):99–114
Acknowledgments
Thanks to two anonymous referees for very helpful feedback, and to the editors of the special issue.
Author information
Authors and Affiliations
Corresponding author
Appendix: Derivations of Key Theorems
Appendix: Derivations of Key Theorems
We first derive a useful subordinate theorem (ST): \(1\vdash B\to((A\Rightarrow(B\Rightarrow C))\Rightarrow(A\Rightarrow C)\).

Using this, we can derive the permutation theorem (T1): \(1\vdash (A\Rightarrow(B\Rightarrow C))\to(B\Rightarrow(A\Rightarrow C))\).
For readability, we let X stand for A⇒(B⇒ C), and Y for the instance B⇒((A⇒(B⇒ C))⇒(A⇒ C)) of the above ST.

It is then a simple matter to derive the suffixing theorem (T2): \(1\vdash (A\Rightarrow B)\to((B\Rightarrow C)\Rightarrow(A\Rightarrow C))\).

We derive both directions of the contraposition theorem (T3): \(1\vdash (A\to B)\leftrightarrow(\neg B\to\neg A)\)

We derive both directions of the following associativity theorem: \(1\vdash ((A\land B)\land C)\leftrightarrow(A\land(B\land C))\)

We derive the second extensional identity theorem as follows: \(1\vdash B\Rightarrow(B\land(A\to A))\)

We derive the fourth inversion theorem as follows: \(1\vdash \neg(A\Rightarrow B)\Rightarrow\neg(A\to\neg\neg B). \)

Rights and permissions
About this article
Cite this article
Caret, C.R., Weber, Z. A Note on Contraction-Free Logic for Validity. Topoi 34, 63–74 (2015). https://doi.org/10.1007/s11245-014-9241-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11245-014-9241-z