A Single-Pole Approximation to Interfacial Mass Transfer in Porous Media Augmented with Bulk Reactions

Abstract

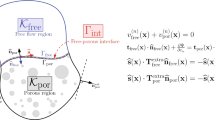
We study interfacial mass transfer between two immiscible fluids in porous media augmented with bulk reactions. A closed-form analytic approximation derived through Laplace transformation is represented for Darcy–Brinkman flow in the presence of first-order bulk reactions represented by the Damköhler number (Da). By comparing the residues of all the singularities, it is shown that the main contributor to the solution is the simple pole of the equations. We show that the solution holds for a range of $Da.Pe<2.5\times 10^{5}$, where Pe is the Péclet number. By determining the bulk flow mass transfer coefficient, we verify our approximation compared to the previous studies and show acceptable conformity of the solutions. We find that the results are applicable for potential bulk reactions, such as biodegradation, in a typical groundwater system.

Appendix

“Lemma 1” section shows that $\nu$ does not take nonzero integers in our study. “Lemma 2” section proves the problem has a simple pole at $s=0$ and a number of identified singularities. “Lemma 3” section shows that except for the pole, the effect of residues of other singularities is negligible in inverse Laplace transformation.

1.1 Lemma 1

Lemma 1

For the range of Da . Pe in the study, the index of Bessel function defined by Eq. (28) does not take nonzero integers. That is, $\nu (s) \notin \{\ldots ,-3,-2,-1,1,2,3,\ldots \}$.

Proof

Suppose $\nu =\frac{2 \sqrt{-\alpha }}{\tau } \in \{ \ldots ,-3,-2,-1,1,2,3,\ldots \}$. We know that $Da.Pe=\frac{\tau ^2 \nu ^2}{4}-Pe.\acute{P_2}.s$ (Eq. 28). Considering $P_2 < 0$ (Sookhak Lari et al. 2015), the term $Pe.\acute{P_2}.s$ is negative, which leads to $Da.Pe > \frac{1}{4}\tau ^2 \nu ^2$. For this study, we suppose the upper bound of $Da . Pe < \tau ^2 / 4$. This indicates that $-1<\nu <1$, and therefore, $\nu$ $\notin \{ \ldots ,-3,-2,-1,1,2,3,\ldots \}$. Considering the most limiting range of parameters in Sookhak Lari et al. (2015) (i.e. $\eta = 10^3$), our study then holds for $Da. Pe < 2.5 \times 10^5$.

1.2 Lemma 2

Lemma 2

The singularities of $\tilde{c}$ are the pole $s=0$, the removable singularity $s=-\frac{Da}{\acute{P_2}}$ and the roots of function $K(s)=e^{\frac{1}{2}\tau \nu }(1+\frac{1}{\nu +1}\frac{\beta }{\tau ^2})+e^{\frac{-1}{2}\tau \nu }(1+\frac{1}{-\nu +1}\frac{\beta }{\tau ^2})$. Except for these singularities, $\tilde{c}$ is holomorphic.

Proof

Since s is a factor in the denominator of Eq. (35) and $s.\tilde{c}$ is bounded in the neighbourhood of $s=0$ (see Fig. 8), $s=0$ is a first-order pole (Krantz 2008, p. 116).

We now consider the generalized Bessel function $w_p$

$$\begin{aligned} w_p(z)=\frac{z^p }{2^p \varGamma (p+\frac{b+1}{2})}u_p(z^2); \quad \forall z \in \mathbb {C}, \end{aligned}$$

(45)

where

$$\begin{aligned} u_p(z)=\sum _{n\ge 0} \frac{(-\frac{c}{4})^n z^n \varGamma (p+\frac{b+1}{2})}{n!\varGamma (p+\frac{b+1}{2}+n) };\quad p+\frac{b+1}{2}\ne 0,-1,-2,\ldots . \end{aligned}$$

(46)

is the generalized and normalized Bessel function of first kind and is analytic in $\mathbb {C}$ (Baricz 1994, p. 11). $\Gamma$ is also the Gamma function. By letting $b=1$ and $c=1$, the generalized Bessel function in Eq. (45) reduces to $J_p (z)$ (Baricz 1994, p. 10). Therefore, the only possible non-analytic points for $J_p (z)$ are the roots of the denominator of $w_p(z)$, i.e. $(p+1) \in \{0,-1,,-2,\ldots \}$ (properties of the Gamma function) (Hildebrand 1962, p. 80).

As a result of this, by referring to the transformed solute concentration defined in Eq. (35), all possible non-analytic points (except for the roots of denominator) occur when $(\pm \nu (s) \vee \pm \nu (s) \pm 1) \in \{0,-1,-2,\ldots \}$. This is equal to $\nu (s) \in \mathbb {Z}$. However, we know $\nu (s)\notin \mathbb {Z}-\{0\}$ (see Lemma 1). For the case of $\nu (s)=0$, Eq. (28) gives $s=-\frac{Da}{\acute{P_2}}$. Figure 9 shows that $\tilde{c}$ remains bounded at the neighbourhood of this point, and therefore, it is a removable singularity (Krantz 2008, p. 116).

Fig. 8

Bounded behaviour of $s.\tilde{c}$ near $s=0$

Another set of singular points is the roots for denominator of $\tilde{c}$ (the part without the factor s). In order to obtain a better interpretation of how the roots are distributed and where their locations are, we first denote $J_{\nu (s)}(Z(s,0)) f(\nu (s) , Z(s,-1))+J_{-\nu (s)}(Z(s,0))g(\nu , Z(s,-1))$ (in the denominator of Eq. 35) by $J_\nu f+J_{-\nu } g$ for convenience. We then assume $Z(s,-1)$ is a small argument for Bessel function of first kind. Indeed, this assumption is valid since $\tau$ is a large quantity and makes $Z(s,-1)=\frac{2\sqrt{\beta }}{\tau }e^{\frac{-1}{2}\tau }$ small enough to perform the approximation $J_\nu (Z(s,-1)) \sim \frac{ Z(s,-1)^\nu }{2^\nu \varGamma (\nu +1)}$ (Hildebrand 1962, p. 151). Therefore,

$$\begin{aligned} J_\nu f+J_{-\nu } g= & {} \left( \frac{1}{2^{-\nu -1} \varGamma (-\nu )}Z(s,-1)^{-\nu -1}\!-\!\frac{1}{2^{-\nu +1}\varGamma (-\nu \!+\!2)}Z(s,-1)^{-\nu +1}\right) J_{\nu }(Z(s,0)\nonumber \\&+\left( \frac{1}{2^{\nu +1} \varGamma (\nu +2)}Z(s,-1)^{\nu +1}-\frac{1}{2^{\nu -1}\varGamma (\nu )}Z(s,-1)^{\nu -1}\right) J_{-\nu }(Z(s,0)).\nonumber \\ \end{aligned}$$

(47)

With the aid of asymptotic notation for Bessel function of first kind (by letting $b=c=1$ in Eqs. 45 and 46) and substituting $Z(s,-1)$ for $\frac{2\sqrt{\beta }}{\tau }e^{\frac{-1}{2}\tau }$, Eq. (47) gets the form

$$\begin{aligned} J_\nu f+J_{-\nu } g= & {} e^{\frac{1}{2}\tau \nu }u_{\nu }\left( \frac{4\beta }{\tau ^2}\right) \left( \frac{\tau . e^{\frac{1}{2}\tau }}{\sqrt{\beta }.\varGamma (-\nu )\varGamma (\nu +1)}-\frac{\sqrt{\beta } }{\tau . e^{\frac{1}{2}\tau } \varGamma (-\nu +2)\varGamma (\nu +1)}\right) \nonumber \\&+\,e^{\frac{-1}{2}\tau \nu }u_{-\nu }\left( \frac{4\beta }{\tau ^2}\right) \left( -\frac{\tau . e^{\frac{1}{2}\tau }}{\sqrt{\beta }.\varGamma (\nu )\varGamma (-\nu +1)}+\frac{\sqrt{\beta } }{\tau . e^{\frac{1}{2}\tau } \varGamma (\nu +2)\varGamma (-\nu +1)}\right) .\nonumber \\ \end{aligned}$$

(48)

The second terms in the two parentheses above can be neglected since $\tau$ is large and Gamma functions are bounded (note that $\nu (s)\notin \mathbb {Z}$). Moreover, application of reflection relationship between Gamma functions defined as $\varGamma (\nu +1) \varGamma (-\nu )=\frac{-\pi }{\sin {\pi \nu }}$ $(\nu \notin \{0,\pm 1,\pm 2,\ldots \})$ (Hildebrand 1962, p. 80) and the recurrence formula $\varGamma (\nu +1 )= \nu \varGamma (\nu )$ (Hildebrand 1962, p. 78) changes Eq. (48) into

$$\begin{aligned} J_\nu f+J_{-\nu } g=e^{\frac{1}{2}\tau \nu }u_{\nu }\left( \frac{4\beta }{\tau ^2}\right) \times \frac{\tau }{\sqrt{\beta }} \frac{e^{\frac{1}{2}\tau }}{\frac{- \pi }{\sin {\pi \nu }}}+ e^{\frac{-1}{2}\tau \nu }u_{-\nu }\left( \frac{4\beta }{\tau ^2}\right) \times \frac{-\tau }{\sqrt{\beta }} \frac{e^{\frac{1}{2}\tau }}{\frac{ \pi }{\sin {\pi \nu }}}. \end{aligned}$$

(49)

Fig. 9

Sketch of the Laplace-transformed function near the removable singularity $s=\frac{-Da}{\acute{p_2}}$. For $Da.Pe=0.01$, $\frac{-Da}{\acute{p_2}}=1.02\times 10^{-12}$ and for $Da.Pe=100$, $\frac{-Da}{\acute{p_2}}=1.02\times 10^{-8}$

We are now willing to find the roots of function (49). Since $\frac{\tau }{\sqrt{\beta }} \frac{e^{\frac{1}{2}\tau }}{\frac{ \pi }{\sin {\pi \nu }}}$ is not zero, then we solve equation $e^{\frac{1}{2}\tau \nu }u_{\nu }(\frac{4\beta }{\tau ^2})+ e^{\frac{-1}{2}\tau \nu }u_{-\nu }(\frac{4\beta }{\tau ^2})=0$ instead. Lets denote $K(s)=e^{\frac{1}{2}\tau \nu }u_{\nu }(\frac{4\beta }{\tau ^2})+ e^{\frac{-1}{2}\tau \nu }u_{-\nu }(\frac{4\beta }{\tau ^2})$ for convenience. The roots for this function cannot be found explicitly, so we continue to approximate K(s) in order to clarify the distribution and location of the roots.

Considering the asymptotic representation $u_p(z)=\sum _{n\ge 0} \frac{(-\frac{1}{4})^n z^n \varGamma (p+1)}{n!\varGamma (p+1+n) }$ (Eq. 46 by letting $b=c=1$) and replacing in K(s) gives

$$\begin{aligned} K(s)=\sum _{n\ge 0}{\frac{\left( \frac{1}{4}\right) ^n \left( \frac{4\beta }{\tau ^2}\right) ^n}{n!}}\left( \frac{e^{\frac{1}{2}\tau \nu }\varGamma (\nu +1)}{\varGamma (n+\nu +1)}+\frac{e^{-\frac{1}{2}\tau \nu }\varGamma (-\nu +1)}{\varGamma (n-\nu +1)}\right) . \end{aligned}$$

(50)

Again, by applying repetitive reflection and recurrence formula to the product of Gamma functions defined as $\varGamma (\nu +1)\varGamma (n-\nu +1)=\nu \frac{\pi }{\sin {\pi \nu }}(-\nu +1)(-\nu +2)\ldots (-\nu +n)$, $\varGamma (-\nu +1)\varGamma (n+\nu +1)=-\nu \frac{-\pi }{\sin {\pi \nu }}(\nu +1)(\nu +2)\ldots (\nu +n)$ and $\varGamma (n+\nu +1)\varGamma (n-\nu +1)=\nu \frac{\pi }{\sin {\pi \nu }}\{(\nu +1)(\nu +2)\ldots (\nu +n)\}\{(-\nu +1)(-\nu +2)\ldots (-\nu +n)\}$, K(s) can be written as

$$\begin{aligned} K(s)=\sum _{n\ge 0}{\frac{\left( \frac{1}{4}\right) ^n \left( \frac{4\beta }{\tau ^2}\right) ^n}{n!}}\left( \frac{e^{\frac{1}{2}\tau \nu }}{\prod \limits _{i=1}^{n}(\nu +i)}+\frac{e^{-\frac{1}{2}\tau \nu }}{\prod \limits _{i=1}^{n}(-\nu +i)}\right) . \end{aligned}$$

(51)

We then approximate the summation into its two main terms corresponding to $n=0$ and $n=1$. The result is

$$\begin{aligned} K(s)=e^{\frac{1}{2}\tau \nu }\left( 1+\frac{1}{\nu +1}\frac{\beta }{\tau ^2}\right) +e^{\frac{-1}{2}\tau \nu }\left( 1+\frac{1}{-\nu +1}\frac{\beta }{\tau ^2}\right) . \end{aligned}$$

(52)

Figure 10 shows an acceptable conformity between the roots of K(s) and the poles of the transformed function $\tilde{c}$. Equation 52 suggests that there is an infinite number of roots that occur periodically. They do not make a continuous set, but there is the smallest root (greater than zero). This enables us to consider paths of integration in the complex plane which surrounds separately each singular point, and as a result, the reduction in complex integral (36) to the summation (37) is possible. Except for $s=0$, $s=\frac{-Da}{\acute{p_2}}$, and the roots of K(s), $\tilde{c}$ is holomorphic (analytic) elsewhere. $\square$

Fig. 10

Coincidence between the roots of K(s) and the poles of $\tilde{c}$ for $Da.Pe=0.01$ and 100

1.3 Lemma 3

Lemma 3

The residue truncation is acceptably small.

Proof

Let $Res_0$ be the residue of $e^{s\bar{x}}\tilde{c}(s)$ at s=0 and $Res_i$ be the residue at singularity $s=s_i$. Then,

$$\begin{aligned} \frac{Res_0}{Res_i}= & {} \frac{\lim _{s \rightarrow 0}(s-0)\tilde{c}(s)e^{s\bar{x}}}{\lim _{s \rightarrow s_i}(s-s_i)\tilde{c}(s)e^{s\bar{x}}}=\frac{\lim _{s \rightarrow 0}(s)\tilde{c}(s)e^{s\bar{x}}}{\lim _{t \rightarrow 0}(t)\tilde{c}(s_i+t)e^{(s_i+t)\bar{x}}}\nonumber \\= & {} \frac{\lim _{s \rightarrow 0}(s)\tilde{c}(s)e^{s\bar{x}}}{\lim _{s \rightarrow 0}(s)\tilde{c}(s_i+s)e^{(s_i+s)\bar{x}}}, \end{aligned}$$

(53)

where $t=s-s_i$. We now take the limit sign out and rewrite Eq. (53) as

$$\begin{aligned} \frac{Res_0}{Res_i}=e^{-s_i\bar{x}}\lim _{s \rightarrow 0}\frac{\tilde{c}(s)}{\tilde{c}(s+s_i)}. \end{aligned}$$

(54)

Fig. 11

Behaviour of the function $\frac{\tilde{c}(s,\bar{y})}{\tilde{c}(s+s_i,\bar{y})}$ near $s=0$ and $s_i \in (10^{-12},10^{-7})$, for $Da.Pe=0.01$

Fig. 12

Behaviour of the function $\frac{\tilde{c}(s,\bar{y})}{\tilde{c}(s+s_i,\bar{y})}$ near $s=0$ and $s_i\in (10^{-10},10^{-7})$, for $Da.Pe=100$

We plotted the ratio $\frac{\tilde{c}(s)}{\tilde{c}(s+s_i)}$ for $Da.Pe=0.01$ and 100 in Figs. 11 and 12, respectively. It is observed that near $s=0$, this ratio tends to infinity. Therefore, $\frac{Res_0}{Res_i}$ is large enough to let us consider the residue of the simple pole $s=0$ as the main contributor. It must be mentioned that for $Da.Pe=0.01$, $s_i \in (10^{-12},10^{-7})$ (to cover all other singularities) while this range is $s_i \in (10^{-10},10^{-7})$ for $Da.Pe=100$. $\square$