Skip to main content
SpringerLink
Log in

An enhanced decomposition-based multiobjective evolutionary algorithm with adaptive neighborhood operator and extended distance-based environmental selection

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

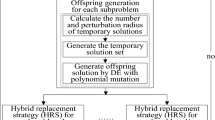
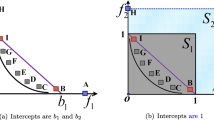
The multiobjective evolutionary algorithm based on decomposition (MOEA/D) proposed in 2007 has shown to be effective in solving multiobjective optimization problems. However, the fixed neighborhood size prevents MOEA/D series algorithm from effective exploring and exploiting. Meanwhile, since the newly generated offspring can replace the parent solutions in the neighborhood without any constraints, the current solutions of multiple subproblems may converge to a certain region or even a certain point. Obviously, the population diversity is significantly deteriorate. To alleviate these problems, this paper proposes an enhanced MOEA/D with adaptive neighborhood operator and extended distance-based environmental selection (MOEA/D-ANED) to solve many-objective optimization problems (MaOPs). The basic idea is that the adaptive neighborhood operator based on utility assignment is helpful for the algorithm to select a more promising solution, thereby enhancing the search performance in many-objective optimization. In addition, the extended distance-based environmental selection strategy is developed to considerably improve the accuracy and effectiveness of updating the parent solutions of different subproblems. Experimental results on two widely used test suits demonstrate the competitiveness of the proposed algorithm in terms of solution accuracy compared with eight state-of-the-art multiobjective optimization algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Data availability

The experimental data used to support the findings of this study are included within the article.

References

  1. Trivedi A, Srinivasan D, Sanyal K, Ghosh A (2017) A survey of multiobjective evolutionary algorithms based on decomposition. IEEE Trans Evol Comput 21(3):440–462

    Google Scholar 

  2. Liu Y, Hu Y, Zhu N, Li K, Zou J, Li M (2021) A decomposition-based multiobjective evolutionary algorithm with weights updated adaptively. Inf Sci 572:343–377

    MathSciNet  Google Scholar 

  3. Miettinen K (1998) Nonlinear multiobjective optimization (international series in operations research & management science). Springer, USA, p 12

    Google Scholar 

  4. Zhang M, Wang L, Guo W, Li W, Pang J, Min J, Liu H, Wu Q (2021) Many-objective evolutionary algorithm based on dominance degree. Appl Soft Comput 113:107869

    Google Scholar 

  5. Giagkiozis I, Fleming PJ (2015) Methods for multi-objective optimization: an analysis. Inf Sci 293:338–350

    MathSciNet  MATH  Google Scholar 

  6. Qiao J, Zhou H, Yang C, Yang S (2019) A decomposition-based multiobjective evolutionary algorithm with angle-based adaptive penalty. Appl Soft Comput 74:190–205

    Google Scholar 

  7. Zhou A, Zhang Q (2016) Are all the subproblems equally important? resource allocation in decomposition-based multiobjective evolutionary algorithms. IEEE Trans Evol Comput 20(1):52–64

    Google Scholar 

  8. Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197

    Google Scholar 

  9. Zitzler E, Laumanns M, Thiele L (2002) SPEA2: improving the strength Pareto evolutionary algorithm for multi-objective optimization. In: Proceedings of the Evolutionary Methods for Design, Optimisation, and Control, Barcelona, CIMNE, Spain, pp. 95–100

  10. Li M, Yang S, Liu X (2014) Shift-based density estimation for Pareto-based algorithms in many-objective optimization. IEEE Trans Evol Comput 18(3):348–365

    Google Scholar 

  11. Yang S, Li M, Liu X, Zheng J (2013) A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 17(5):721–736

    Google Scholar 

  12. Liu S, Yu Q, Lin Q, Tan KC (2020) An adaptive clustering-based evolutionary algorithm for many-objective optimization problems. Inf Sci 537:261–283

    MathSciNet  MATH  Google Scholar 

  13. Wang R, Purshouse RC, Giagkiozis I, Fleming PJ (2015) The iPICEA-g: a new hybrid evolutionary multi-criteria decision making approach using the brushing technique. Eur J Oper Res 243(2):442–453

    MathSciNet  MATH  Google Scholar 

  14. Zhou X, Wang X, Gu X (2021) A decomposition-based multiobjective evolutionary algorithm with weight vector adaptation. Swarm Evol Comput 61:1–17

    Google Scholar 

  15. Zitzler E, Künzli S (2004) Indicator-based selection in multiobjective search. Springer, Heidelberg, pp 832–842

    Google Scholar 

  16. Bader J, Zitzler E (2011) HypE: an algorithm for fast hypervolume-based many-objective optimization. Evol Comput 19(1):45–76

    Google Scholar 

  17. Beume N, Naujoks B, Emmerich M (2007) SMS-EMOA: multiobjective selection based on dominated hypervolume. Eur J Oper Res 181(3):1653–1669

    MATH  Google Scholar 

  18. Bringmann K, Friedrich T (2010) Approximating the volume of unions and intersections of high-dimensional geometric objects. Comput Geom 43(6–7):601–610

    MathSciNet  MATH  Google Scholar 

  19. Emmerich M, Beume N, Naujoks B (2005) An EMO algorithm using the hypervolume measure as selection criterion. In: International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, pp. 62–76

  20. Zhang Q, Li H (2007) MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 11(6):712–731

    Google Scholar 

  21. Schaffer JD (1985) Multiple objective optimization with vector evaluated genetic algorithms. In: Proceedings of the 1st International Conference on Genetic Algorithms, pp. 93–100

  22. Deb K, Jain H (2014) An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: solving problems with box constraints. IEEE Trans Evol Comput 18(4):577–601

    Google Scholar 

  23. Li M, Yao X (2020) What weights work for you? Adapting weights for any pareto front shape in decomposition-based evolutionary multiobjective optimization. Evol Comput 28(2):227–253

    Google Scholar 

  24. Derbel B, Liefooghe A, Zhang Q, Aguirre H, Tanaka K (2016) Multi-objective local search based on decomposition. In: Handl J, Hart E, Lewis P, López-Ibáñez M, Ochoa G, Paechter B (eds) Parallel problem solving from nature – PPSN XIV PPSN 2016. Lecture notes in computer science, vol 9921. Springer, Cham

    Google Scholar 

  25. Li H, Zhang Q (2009) Multiobjective optimization problems with complicated pareto sets, MOEA/D and NSGA-II. IEEE Trans Evol Comput 13(2):284–302

    Google Scholar 

  26. Zhao S, Suganthan PN, Zhang Q (2012) Decomposition-based multiobjective evolutionary algorithm with an ensemble of neighborhood sizes. IEEE Trans Evol Comput 16(3):442–446

    Google Scholar 

  27. Zhang A, Sun G, Ren J, Li X, Wang Z, Jia X (2018) A dynamic neighborhood learning-based gravitational search algorithm. IEEE Trans Cybern 48(1):436–447

    Google Scholar 

  28. Wang L, Wu F, Zhang M, Qiu F (2017) Decomposition multi-objective evolutionary algorithm based on differentiated neighborhood strategy. Pattern Recognit Artif Intell 30(12):1069–1082

    Google Scholar 

  29. Wang R, Zhang Q, Zhang T (2016) Decomposition-based algorithms using pareto adaptive scalarizing methods. IEEE Trans Evol Comput 20(6):821–837

    Google Scholar 

  30. Deb K, Thiele L, Laumanns M, Zitzler E (2005) Scalable test problems for evolutionary multiobjective optimization. Evolutionary multiobjective optimization (theoretical advances and applications). Springer, Berlin, pp 105–145

    MATH  Google Scholar 

  31. Huband S, Hingston P, Barone L, While L (2006) A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans Evol Comput 10(5):477–506

    MATH  Google Scholar 

  32. Li K, Zhang Q, Kwong S, Li M, Wang R (2014) Stable matching-based selection in evolutionary multiobjective optimization. IEEE Trans Evol Comput 18(6):909–923

    Google Scholar 

  33. Li K, Kwong S, Zhang Q, Deb K (2015) Interrelationship-based selection for decomposition multiobjective optimization. IEEE Trans Cybern 45(10):2076–2088

    Google Scholar 

  34. Wu M, Kwong S, Jia Y, Li K, Zhang Q (2017) Adaptive weights generation for decomposition-based multi-objective optimization using gaussian process regression. In: Proceedings of the 2017 Genetic and Evolutionary Computation Conference. Berlin, Germany, 641–648

  35. Ishibuchi H, Sakane Y, Tsukamoto N, Nojima Y (2009) Effects of using two neighborhood structures on the performance of cellular evolutionary algorithms for many-objective optimization. IEEE congress on evolutionary computation. Trondheim, Norway, pp 2508–2515

    Google Scholar 

  36. Ishibuchi H, Akedo N, Nojima Y (2013) Relation between neighborhood size and MOEA/D performance on many-objective problems. Evolutionary multi-criterion optimization (EMO) (LNCS 7811). Springer, Berlin, pp 459–474

    Google Scholar 

  37. Jiang S, Yang S (2016) An improved multiobjective optimization evolutionary algorithm based on decomposition for complex pareto fronts. IEEE Trans Cybern 46(2):421–437

    Google Scholar 

  38. Wang Z, Zhang Q, Zhou A, Gong M, Jiao L (2016) Adaptive replacement strategies for MOEA/D. IEEE Trans Cybern 46(2):474–486

    Google Scholar 

  39. Zhou H, Wang L (2017) Decomposition multiobjective evolutionary algorithm of dynamic neighborhood. J Chin Comput Syst 38(9):2039–2044

    Google Scholar 

  40. Wang L, Xu M, Yu W, Qiu Q, Wu F (2020) Decomposition multi-objective evolutionary algorithm based on adaptive neighborhood adjustment strategy. IEEE Access 8:78639–78651

    Google Scholar 

  41. Li K, Fialho Á, Kwong S, Zhang Q (2014) Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 18(1):114–130

    Google Scholar 

  42. Zhang K, Shen C, Liu X, Yen G (2020) Multiobjective evolution strategy for dynamic multiobjective optimization. IEEE Trans Evol Comput 24(5):974–988

    Google Scholar 

  43. Farias LRC, and Araújol AFR (2019) Many-objective evolutionary algorithm based on decomposition with random and adaptive weights. In: IEEE International Conference on Systems, Man and Cybernetics (SMC), pp. 3746–3751

  44. Wang P, Liao B, Zhu W, Cai L, Ren S, Chen M, Li Z, Li K (2018) Adaptive region adjustment to improve the balance of convergence and diversity in MOEA/D. Appl Soft Comput 70:797–813

    Google Scholar 

  45. Cheng R, Jin Y, Olhofer M, Sendhoff B (2016) A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 20(5):773–791

    Google Scholar 

  46. Jiang S, He X, Zhou Y (2019) Many-objective evolutionary algorithm based on adaptive weighted decomposition. Appl Soft Comput 84(105731):1–11

    Google Scholar 

  47. Li H, Zhang Q, Deng J (2017) Biased multi-objective optimization and decomposition algorithm. IEEE Trans Cybern 47(1):52–66

    Google Scholar 

  48. Zhang Q, Liu W, Li H (2009) The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances. In: IEEE Congress on Evolutionary Computation, pp. 203–208

  49. Liu H, Gu F, Zhang Q (2014) Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans Evol Comput 18(3):450–455

    Google Scholar 

  50. Tian Y, Cheng R, Zhang X, Jin Y (2017) PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput Intell Mag 12(4):73–87

    Google Scholar 

  51. Wang Y, Cai Z, Zhang Q (2011) Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans Evol Comput 15(1):55–66

    Google Scholar 

  52. Zitzler E, Thiele L, Laumanns M, Fonseca CM, da Fonseca VG (2003) Performance assessment of multiobjective optimizers: an analysis and review. IEEE Trans Evol Comput 7(2):117–132

    Google Scholar 

  53. Schutze O, Esquivel X, Lara A, Coello CAC (2012) Using the averaged hausdorff distance as a performance measure in evolutionary multiobjective optimization. IEEE Trans Evol Comput 16(4):504–522

    Google Scholar 

  54. Zhang Q, Zhou A, Jin Y (2008) A RM-MED, a regularity model-based multiobjective estimation of distribution algorithm. IEEE Trans Evolut Comput 12(1):41–63

    Google Scholar 

  55. Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength pareto approach. IEEE Trans Evol Comput 3(4):257–271

    Google Scholar 

  56. Li K, Wang R, Zhang T, Ishibuchi H (2018) Evolutionary many-objective optimization: a comparative study of the state-of-the-art. IEEE Access 6(26):194–214

    Google Scholar 

  57. Tan KC, Chew YH, Lee LH (2006) A hybrid multi-objective evolutionary algorithm for solving vehicle routing problem with time windows. Comput Optim Appl 34(1):115–151

    MathSciNet  MATH  Google Scholar 

  58. Solomon MM (1987) Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper Res 35(2):254–265

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research is partly supported by the National Natural Science Foundation of China under Project Code (62176146, 61773314), and the Special project of Education Department of Shaanxi Provincial Government for Local Services (Program No. 21JC026).

Author information

Authors and Affiliations

  1. School of Computer Science and Engineering, Xi’an University of Technology, Xi’an, 710048, China

    Wei Li, Junqing Yuan & Lei Wang

  2. Shaanxi Key Laboratory for Network Computing and Security Technology, Xi’an, 710048, China

    Wei Li & Lei Wang

Authors
  1. Wei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junqing Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. The algorithm design and implementation were performed by WL. Experiment and analysis were performed by JY. LW revised the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Junqing Yuan.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, W., Yuan, J. & Wang, L. An enhanced decomposition-based multiobjective evolutionary algorithm with adaptive neighborhood operator and extended distance-based environmental selection. J Supercomput 79, 12341–12393 (2023). https://doi.org/10.1007/s11227-023-05118-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-023-05118-1

Keywords

Search

Navigation