The framing of nothing and the psychology of choice

Abstract

Zero outcomes are inconsequential in most models of choice. However, when disclosing zero outcomes they must be designated. It has been shown that a gamble is judged to be more attractive when its zero outcome is designated as “losing $0” rather than “winning $0,” an instance of what we refer to as the mutable-zero effect. Drawing on norm theory, we argue that “losing $0” or “paying $0” evokes counterfactual losses, with which the zero outcome compares favorably (a good zero), and thus acquires positive value, whereas “winning $0” or “receiving $0” evokes counterfactual gains, with which the zero outcome compares unfavorably (a bad zero), and thus acquires negative value. Moreover, we propose that the acquired value of zero outcomes operates just as the intrinsic value of nonzero outcomes in the course of decision making. We derive testable implications from prospect theory for mutable-zero effects in risky choice, and from the double-entry mental accounting model for mutable-zero effects in intertemporal choice. The testable implications are consistently confirmed. We conclude that prevalent theories of choice can explain how decisions are influenced by mutable zeroes, on the shared understanding that nothing can have value, just like everything else.

Tversky and Kahneman (1981) introduced the notion of framing to the analysis of judgment and choice. Framing is no stranger to everyday life, for instance, when we say that optimists see half a glass of wine as a glass half full, whereas pessimists see it as a glass half empty. An empty glass of wine, however, would seem less divisive in nature: Nothing is nothing. Tversky and Kahneman (1981) examined framing effects from the prism of prospect theory (Kahneman and Tversky 1979), in which outcomes are evaluated as positive deviations (gains) or negative deviations (losses) from a neutral reference point. If the neutral reference point is the status quo, denoted W, then a zero outcome is evaluated as (W + 0) – W = 0, and this zero deviation receives value v(0) = 0. The zeroness of zeroes cannot be stated more unambiguously than this.

Prospects, however, have to be communicated to decision makers. In doing that, we can either leave the zero outcome implicit or make it explicit:

Implicit: “$x with probability p.”

Explicit $0: “$x with probability p, and $0 with probability 1 – p.”

These presentations ignore, however, that the sign of $x has to be communicated as well, and, if that is to be done, we have a choice of how to “describe” the zero outcome. Consider the following possibilities of communicating a gamble with a positive and a zero outcome:

Implicit: Win $x with probability p.

Explicit “nothing”: Win $x with probability p, and nothing otherwise.

Explicit “win $0”: Win $x with probability p, and win $0 with probability 1 – p.

Explicit “lose $0”: Win $x with probability p, and lose $0 with probability 1 – p.

Leaving the zero outcome implicit is perhaps the best way of achieving that it preserves its neutral value of zero. If we make the zero outcome explicit, however, it is unlikely it will do so. If we add “and nothing otherwise,” decision makers are likely to infer “and winning nothing otherwise.” We would thus achieve essentially the same result as when we add “and win $0 with probability 1 – p.” But, logically, “win $0” is the same as “lose $0,” so these two descriptions should also yield the same result. Bateman et al. (2007) showed, however, that “winning $0” is different from “losing $0.” They asked two different groups of participants to rate the attractiveness of the following gambles:

L A 7 in 36 chance of winning $9, and a 29 in 36 chance of losing $0.

W A 7 in 36 chance of winning $9, and a 29 in 36 chance of winning $0.

The only difference between L and W is whether the zero outcome is described as a loss or a gain. Gamble L, in which $0 is described as a loss, was rated as much more attractive than gamble W, in which $0 is described as a gain. Presumably, “losing $0” brings to mind other losses that might have occurred, among which $0 is the best possible one, and thus feels good, while “winning $0” brings to mind other wins that might have occurred, among which $0 is the worst possible one, and thus feels bad. This interpretation is consistent with norm theory (Kahneman and Miller 1986).¹ In norm theory, the counterfactuals evoked by a stimulus share the “immutable features of the evoking stimulus” (p. 139), but differ in other, “mutable” features. We suggest that, when the stimulus is “losing $0” or “winning $0,” the feature of losing and winning is less mutable than the amount. If you lose $0, it is easy to imagine that you might have lost $5, but hard to imagine that you might have won $0; similarly, if you win $0, it is easy to imagine that you might have won $5, but hard to imagine that you might have lost $0. Drawing on the terminology of norm theory, we refer to the phenomenon that an option with a zero outcome fares better or worse depending on how its zero outcome is described as the mutable-zero effect.

If zero outcomes acquire value in the process of communication about prospects, then current models are flawed in denying that acquired value. We advance the proposition that the acquired value of zero outcomes operates just as the intrinsic value of nonzero outcomes in the course of decision making. Thus, although the value of zero outcomes is not invariant with respect to their description, decision making is invariant with respect to the nature of value, whether acquired or intrinsic. Drawing on this proposition, we derive testable implications from prospect theory (Kahneman and Tversky 1979) for mutable-zero effects in risky choice, and from the double-entry mental accounting model (Prelec and Loewenstein 1998) for mutable-zero effects in intertemporal choice. Both models receive consistent support.

At this point, however, the mutable-zero effect itself is not very well established as an empirical phenomenon. Bateman et al. (2007) observed it in judgment under risk with win gambles, so we check whether the mutable-zero effect extends from judgment under risk to risky choice, and from win gambles to loss gambles, robustness checks it survives. The mutable-zero effect exists in choice, but it is small, so we check whether it extends from unincentivized risky choice to incentivized risky choice, a robustness check it survives as well. Finally, we check whether the mutable-zero effect extends from risky choice to intertemporal choice, which it does. With the mutable-zero effect established as a small but reliable effect in choice, we show that prospect theory and the double-entry mental accounting model can accommodate the effects of zero-outcome framing in risky choice and intertemporal choice if they grant zero outcomes acquired value, which then operates just as the intrinsic value of nonzero outcomes in the formal structure of these models.

1 Experiment 1: The mutable-zero effect in risky choice

Mutable-zero effects in choice constitute violations of descriptive invariance (Tversky and Kahneman 1986), because preference between objectively the same options depends on how the options are described. The goal of Experiment 1 is to establish the mutable-zero effect as a violation of descriptive invariance in risky choice.

It is not possible to examine the mutable-zero effect in direct choice between a gamble affording a possibility of “losing $0” and an equivalent gamble entailing a possibility of “winning $0.” So the method is to have each zero-outcome framing compared with a common standard. We use a sure thing as that common standard. Illustrating this with the gambles used by Bateman et al. (2007), the options could be as follows:

L_P A 7 in 36 chance of winning $9, and a 29 in 36 chance of losing $0.

W_P A 7 in 36 chance of winning $9, and a 29 in 36 chance of winning $0.

S_P Receiving $2 for sure.

One group chooses between L_P and S_P, another group chooses between W_P and S_P. The mutable-zero effect occurs when L_P is chosen more frequently than W_P. We will examine this in unincentivized risky choice (Experiment 1a) and in incentivized risky choice (Experiment 1b). Upon reversing the sign of the nonzero outcomes, the options would be as follows:

L_N A 7 in 36 chance of losing $9, and a 29 in 36 chance of losing $0.

W_N A 7 in 36 chance of losing $9, and a 29 in 36 chance of winning $0.

S_N Paying $2 for sure.

The mutable-zero effect occurs when L_N is chosen more frequently than W_N. We will examine this only in unincentivized risky choice (Experiment 1a).

1.1 Experiment 1a: Unincentivized risky choice

1.1.1 Stimuli

The stimuli are shown in Table 1. Each choice is between a Gamble (G) and a Sure thing (S). The zero outcome of G is described either as “winning £0” or “losing £0.” The stimuli were adapted from Bateman et al. (2007), changing the currency from dollars to pounds. With an eye on the incentivized experiment, we magnified both nonzero outcomes by a factor of 10, in order to make it more interesting to receive either amount if eligible, and we rounded the probabilities to 1/5 and 4/5, in order to make the risk more transparent.

Table 1 Stimuli for risky choices, proportions (p) choosing Risky, limits of 95% confidence intervals (95% CI_d), and effect sizes (ES_d’) for the difference in choice proportions between Lose and Win conditions, in Experiment 1a (unincentivized) and Experiment 1b (incentivized)

1.1.2 Participants and procedure

Participants were 602 British residents, recruited through Maximiles, an Internet service that awards its members points for completing online surveys. The sample was 34% male, with an average age of 38. Most were employed (66%, among whom 45% worked full time), and some had an academic degree (38%, among whom 26% had a bachelors, 10% masters, and 2% PhD) or were still studying (3%). The zero outcome was described as “losing £0” for half the sample (n = 297), and as “winning £0” for the other half (n = 305). Within each subsample, the order of the choices, and the order of the options within each choice, was randomized across participants.

1.1.3 Statistics

We obtain a choice probability, denoted p₁, when a zero event is described as “winning” or “receiving” £0, and, from an independent sample, a choice probability, denoted p₂, when the zero event is described as “losing” or “paying” £0. We report the 95% confidence interval for the difference between the two proportions as described by Agresti and Min (2005), i.e., d = p₂ – p₁, and CI_d = $\left({p}_2-{p}_1\right)\pm {Z}_{\alpha /2}\sqrt{p_1\left(1-{p}_1\right)/{n}_1+{p}_2\left(1-{p}_2\right)/{n}_2}$, where α = .05, and the corresponding effect size as described by Kline (2004), i.e., ES_d’ = logit(d´) / ($\pi /\sqrt{3}$), where logit(d´) = ln(p₂ / (1 – p₂)) – ln(p₁ / (1 – p₁)). For instance, the difference between proportions .9–.6 = .3 would emerge as the same effect size as the difference between proportions .6–.2 = .4, because the former is closer to the upper bound of 1 than the latter is to the lower bound of 0. The effects that we obtain are generally smaller than 0.20, which, by informal standards (Cohen 1988), are small effects.

1.1.4 Results

Table 1 shows the results. Small minorities choose the gamble, but, consistent with prospect theory’s reflection effect (Kahneman and Tversky 1979), choice of the gamble is more likely for losses than for gains. Moreover, there is a reliable mutable-zero effect for both gains and losses: In both outcome domains (gains and losses), choice of the gamble is more likely when the zero outcome is described as “lose £0” rather than “win £0,” although the effect is smaller for losses than for gains.

To submit the main effect and the moderating effect of outcome domain to an inferential test, we ran a multi-level logistic regression analysis, using choice of the gamble (yes-no) as the dependent variable, and using as independent variables: Outcome domain (losses [1] versus gains [−1]), zero-outcome framing (“lose £0” [1] versus “win £0” [−1]), and their interaction (the moderating effect). Choice of the gamble was more likely for losses than for gains, p < .0001, 95% CI_b = [0.57; 0.86; 1.15], and more likely when the zero outcome was described as “lose £0” rather than “win £0,” p < .0001, 95% CI_b = [0.31; 0.66; 1.01]. The effect of zero-outcome framing (which is the mutable-zero effect) was smaller for losses than for gains, but the moderating effect of outcome domain was not reliable, p > .20, 95% CI_b = [−0.45; −0.16; 0.14]. Altogether, the mutable-zero effect is reliable for both gains and losses, and although the effect is smaller for losses than for gains, the moderating effect of outcome domain is not reliable. In Experiment 2, we will find that the mutable-zero effect is reliable for gains, but unreliable for losses, and that this difference between outcome domains (the moderating effect of outcome domain) is reliable. Furthermore, we will derive from prospect theory that both realities are perfectly well possible.

1.2 Experiment 1b: Incentivized risky choice

The mutable-zero effect proved subtle in Experiment 1a, and one may wonder whether it can withstand incentivization. For economists, the rationale of incentives is that judgment and choice require cognitive effort, a scarce resource that people allocate strategically. If participants in an experiment are not paid contingent on their performance, they may not invest the necessary effort to avoid making judgment or decision errors, whereas contingent payoffs would move judgment and choice closer to the economic model, and help to remove errors (e.g., see Camerer and Hogarth 1999; Hertwig and Ortmann 2001; Read 2005). Therefore, as a robustness check, we conducted an incentivized experiment on the mutable-zero effect in risky choice. It is a single-shot choice experiment, with the zero outcome described as “win £0” for some, and as “lose £0” for others, and the single choice is incentivized by randomly selecting one participant to receive the sure amount (£10 for sure) or to play out the gamble (a 20% chance of £90, and £0 otherwise) for real, depending on the choice made. The chances of being the winner were very low, but the effort required by the experiment was as well. As a matter of fact, the Expected Value of participating in the experiment varies between EV_S = (1 / N) × £10, if all participants were to choose the sure amount, and EV_R = (1 / N) × 0.20 × £90, if all participants were to choose the gamble. Thus, with the sample size being N = 761, the Expected Value varies between £0.0131406 and £0.023653, which, if reading the instructions and making the single choice takes 15 seconds, amounts to a net hourly wage between £3.15 and £5.68, when the minimum wage in the United Kingdom is, at the moment of writing, £3.70.

1.2.1 Stimuli

Table 1 shows the stimuli. Relative to Experiment 1a, the magnitude of the sure outcome was decreased, from £20 to £10, to increase the likelihood of choosing the gamble, which was very low in Experiment 1a.

1.2.2 Participants and procedure

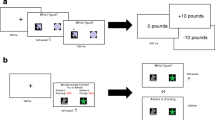
Participants, 761 in total, were recruited through Prolific Academic. Each participant made a single choice. Before doing so, they read the following: “When the whole experiment is finished, we will be selecting one person to play for real and, if that is you, you could win a lot of money.” They were then reminded that, at the end of the experiment, one participant would be randomly chosen to play his or her choice for real. This was concretized with the options on offer: “If you are selected and you have chosen Option A, you have a 1 in 5 chance to win £90 and a 4 in 5 chance to [win / lose] £0. If you are selected and you have chosen Option B, you will receive £10.” The participants then made their choice, and left the survey. No demographic information was collected.

1.2.3 Results

Table 1 shows the results. As intended, the gamble is more likely to be chosen than in Experiment 1a, but still only small minorities chose it. We do, however, obtain a reliable mutable-zero effect, in that the gamble is more likely to be chosen when the zero outcome is described as “lose £0” rather than “win £0.” The mutable-zero effect therefore extends from unincentivized to incentivized risky choice.

2 Experiment 2: Prospect theory and mutable zeroes

In Experiment 1a, we extended the mutable-zero effect from win gambles to loss gambles. There was a mutable-zero effect for losses as well as gains, and, although the effect was smaller for losses than for gains, the moderating effect of outcome domain was not reliable. In this section, we formally deduce from prospect theory that the mutable-zero effect should occur for gains, and that it may occur for losses. Thus, the mutable-zero effect for losses, and therefore the moderating effect of outcome domain, cannot be taken for granted, for reasons that can be provided by prospect theory.²

2.1 Theory

Original prospect theory (Kahneman and Tversky 1979) can serve as a descriptive account of elementary choices between a sure thing and a two-outcome gamble. Prospect theory invokes reference dependence, by which “the carriers of value are gains and losses defined relative to a reference point” (Tversky and Kahneman 1991, p. 1039), and loss aversion (Kahneman and Tversky 1984), which is that “losses loom larger than gains” (Kahneman and Tversky 1979, p. 279), or that losses “have a greater impact on preferences” than gains (Tversky and Kahneman 1991, p. 1039). By loss aversion, −v(−x) > v(x) > 0 or 0 > −v(x) > v(−x). By reference dependence, v(0) = 0, but the mutable-zero effect is that it matters how the zero outcome is being framed. As suggested earlier, “losing $0” is a good zero, because it brings to mind other losses that might have occurred, among which $0 is the best possible one. Letting –z < 0 be the central tendency of the counterfactual losses, the zero loss is, by reference dependence, evaluated as 0 – (−z) = z, and thus acquires the value v(z) > 0. Analogously, “winning $0” is a bad zero, because it brings to mind other gains that might have occurred, among which $0 is the worst possible one. Letting z > 0 be the central tendency of the counterfactual gains, the zero gain is, by reference dependence, evaluated as 0 – z = −z, and thus acquires the value v(−z) < 0.

Furthermore, loss aversion has been shown to operate only in judgments and decisions that require a direct comparison between losses and gains. McGraw et al. (2010) investigated loss aversion in judged feelings about mixed gambles of the form (x, .5; −x, .5). In joint evaluation, participants rated whether winning $x would have more, the same, or less influence on their feelings than losing $x. In separate evaluation, they rated how they would feel upon winning $x, and how they would feel upon losing $x. Loss aversion manifested itself in joint evaluation, but not in separate evaluation. Therefore, in deriving testable implications from prospect theory, we assume that loss aversion only operates in the presence of mixed prospects. Formally, we let v be a value function that exhibits loss aversion, i.e., −v(−x) > v(x), and u be a corresponding value function that exhibits no loss aversion, i.e., −u(−x) = u(x) = v(x) for x > 0.

Finally, choice probabilities must derive from subtractive prospect comparison, by which the probability of choosing the Gamble (G) over the Sure thing (S) is given by the Fechnerian choice rule P(G; S) = F[V(G) – V(S)], where V(G) and V(S) are the values of the respective options. An alternative to such subtractive would be ratio prospect comparison, by which the probability of choosing G over S is given as P(G; S) = L[V(G) / V(S)], often associated with Luce (1959). In the presence of mixed prospects, however, choice probabilities must derive from subtractive prospect comparison, because V(G) may be positive or negative, and may therefore not have the same sign as V(S), in which case choice probabilities would not be defined under ratio prospect comparison.

2.2 Derivation of predictions

2.2.1 The gain domain

The options in the gain domain will be as follows:

L_P A 7 in 36 chance of winning $9, and a 29 in 36 chance of losing $0.

W_P A 7 in 36 chance of winning $9, and a 29 in 36 chance of winning $0.

N_P A 7 in 36 chance of winning $9.

S_P Receiving $2 for sure.

Three different groups of participants choose between one of the three gambles (L_P, W_P, or N_P) and the sure thing (S_P). The zero outcome is a good zero in L_P, and a bad zero in W_P, whereas it is left implicit in N_P, and is therefore a neutral zero.³ The mutable-zero effect is that choice of L_P instead of S_P is more likely than choice of W_P instead of S_P, and it could logically arise (1) because L_P has a good zero, so that it compares better with S_P than N_P does, (2) because W_P has a bad zero, so that it compares worse with S_P than N_P does, or (3) because of both, which is what prospect theory predicts, with the added precision that the impact of the bad zero (“winning $0”) should be greater than the impact of the good zero (“losing $0”).

Winning nothing is a bad zero, and it has a negative effect. Since W_P states a potential gain along with a bad zero, it is a mixed prospect. Therefore, loss aversion applies to the comparison of W_P with S_P, and their outcomes are evaluated under v. Meanwhile, N_P only states a potential gain. Thus, loss aversion is not even an issue for the comparison of N_P with S_P, and their outcomes are evaluated under u. Then, W_P will compare worse with S_P than N_P does if:

$$ V\left({W}_P\right)\hbox{--} V\left({S}_P\right)<U\left({N}_P\right)\hbox{--} U\left({S}_P\right),\left\{w\left(7/36\right)v(9)+w\left(29/36\right)v\left(\hbox{--} z\right)\right\}\hbox{--} v(2)<w\left(7/36\right)u(9)\hbox{--} u(2), $$

which, considering that v(x) = u(x) for x > 0, reduces to

$$ w\left(29/36\right)v\left(-z\right)<0, $$

(1)

which is a negative effect.

Losing nothing is a good zero, and it has a positive effect. Since L_P states a potential gain along with a good zero, it is an unmixed prospect. Therefore, loss aversion does not apply to the comparison of L_P with S_P, and their outcomes are evaluated under u, as are the outcomes in the comparison of N_P with S_P. Then, L_P will compare better with S_P than N_P does if:

$$ U\left({L}_P\right)\hbox{--} U\left({S}_P\right)>U\left({N}_P\right)\hbox{--} U\left({S}_P\right),\left\{w\left(7/36\right)u(9)+w\left(29/36\right)u(z)\right\}\hbox{--} u(2)>w\left(7/36\right)u(9)\hbox{--} u(2),w\left(29/36\right)u(z)>0 $$

(2)

which is a positive effect.

Bad is stronger than good By loss aversion, −v(−z) > v(z) = u(z) > 0, so that the impact of “winning $0” (Inequality 1) should be greater than the impact of “losing $0” (Inequality 2) in the creation of the mutable-zero effect.

2.2.2 The loss domain

The options in the loss domain will be as follows:

L_N A 7 in 36 chance of losing $9, and a 29 in 36 chance of losing $0.

W_N A 7 in 36 chance of losing $9, and a 29 in 36 chance of winning $0.

N_N A 7 in 36 chance of losing $9.

S_N Paying $2 for sure.

Three different groups of participants choose between one of the three gambles (L_N, W_N, or N_N) and the sure thing (S_N). The zero outcome is a good zero in L_N, and a bad zero in W_N, whereas it is left implicit in N_N, and is therefore a neutral zero. The mutable-zero effect is that choice of L_N instead of S_N is more likely than choice of W_N instead of S_N. Prospect theory predicts that W_N compares worse with S_N than N_N does, which contributes to a mutable-zero effect. However, the mutable-zero effect may not occur, because prospect theory concludes that (1) L_N may compare better with S_N than N_N does, (2) L_N and N_N may compare equally well with S_N, or (3) L_N may compare worse with S_N than N_N does. Under conditions 1 and 2, there will be a mutable-zero effect, either carried by L_N as well as W_N (condition 1) or carried only by W_N (condition 2). Under condition 3, the mutable-zero effect is reduced by L_N, and may be eroded or even reversed.

Winning nothing is a bad zero, and it has a negative effect. Since W_N states a potential loss along with a bad zero, it is an unmixed prospect. Therefore, loss aversion does not apply to the comparison of W_N with S_N, and their outcomes are evaluated under u. Meanwhile, N_N only states a potential loss. Thus, loss aversion also does not apply to the comparison of N_N with S_N, and their outcomes are also evaluated under u. Then, W_N will compare worse with S_N than N_N does if:

$$ {\displaystyle \begin{array}{c}U\left({W}_N\right)-U\left({S}_N\right)<U\left({N}_N\right)-U\left({S}_N\right),\left\{w\left(7/36\right)u\left(-9\right)+w\left(29/36\right)u\left(-z\right)\right\}-u\left(-2\right)<w\left(7/36\right)u\left(-9\right)-u\left(-2\right),\\ {}\kern0ex w\left(29/36\right)u\left(-z\right)<0,\end{array}} $$

which is a negative effect. Inequalities 1 and 3 are identical up to the steepness of the value function, in that v exhibits loss aversion, whereas u does not, i.e., v(−z) < u(−z) < 0. Thus, the negative effect of the bad zero should be smaller for losses than for gains.

Losing nothing is a good zero, but it may have a negative effect Since L_N states a potential loss along with a good zero, it is a mixed prospect. Therefore, loss aversion applies to the comparison of L_N with S_N, and their outcomes are evaluated under v. Meanwhile, loss aversion continues not to apply to the comparison of N_N with S_N, the outcomes of which are evaluated under u. Then, L_N will compare better or worse with S_N than N_N does if:

The value of the zero loss works in favor of L_N, in that w(29 / 36)v(z) > 0. The difference in value between the safe losses also works in favor of L_N, in that (v(-2) u(-2)) > 0. However, the difference in value between the risky losses works against L_N, in that w(7 / 36)(v(-9) u(-9)) < 0. If the advantages of L_N outweigh its disadvantage, then L_N will compare better with S_N than N_N does, so there will be a mutable-zero effect. However, if the advantages of L_N are outweighed by its disadvantage, then L_N will compare worse with S_N than N_N does; if the adverse effect of the good zero on the popularity of L_N outweighs the adverse effect of the bad zero on the popularity of W_N, the mutable-zero effect will reverse in sign, such that choice of L_N instead of S_N is less likely than choice of W_N instead of S_N.

2.3 Summary of predictions

The predictions for Experiment 2 are as follows: (H₁) There should be a mutable-zero effect for gains, i.e., a win gamble should become more popular when the zero outcome is described as “lose $0” rather than “win $0;” underlying the mutable-zero effect for gains, there should be (H₂) a negative effect of describing the zero outcome as “win $0,” and (H₃) a positive effect of describing the zero outcome as “lose $0;” (H₄) the negative effect of “winning $0” should be larger than the positive effect of “losing $0;” (H₅) for losses, there should be a negative effect of describing the zero outcome as “win $0;” and (H₆) the negative effect of “winning $0” should be smaller for losses than for gains.

2.4 Method

The participants were 1299 British residents, recruited through Prolific Academic. The sample was 36% male, with an average age of 39. Most were employed (82%, among whom 48% full time), and most had an academic degree (61%, among whom 43% had a bachelors, 15% masters, and 3% PhD). Each participant made two choices, one in each domain (gain or losses). The zero outcome was described as “losing £0” in a third of the sample (n = 424), described as “winning £0” in another third of the sample (n = 427), and suppressed in the remaining third of the sample (n = 448). Within each subsample, the order of the choices, and the order of the options within each choice, was randomized across participants.

2.5 Results

2.5.1 The mutable-zero effect

Table 2 shows the results. (Note that each choice proportion is repeated across two pairwise comparisons between choice proportions.) Small minorities choose the gamble, but, consistent with prospect theory’s reflection effect, choice of the gamble is more likely for losses than for gains. There is a reliable mutable-zero effect for gains (confirmation of H₁): Choice of a win gamble is more likely when the zero outcome is described as “lose £0” rather than “win £0.” The mutable-zero effect is smaller, and not reliable, for losses.

Table 2 Stimuli for risky choices, proportions (p) choosing Risky, limits of 95% confidence intervals (95% CI_d), and effect sizes (ES_d’) for the difference in choice proportions between Lose, Win, and None conditions, in Experiment 2

To submit the main effect and the moderating effect of outcome domain to an inferential test, we ran a multi-level logistic regression analysis, using choice of the gamble as the dependent variable, and using as independent variables: Outcome domain, zero-outcome framing, and their interaction (the moderating effect). Choice of the gamble was more likely for losses than for gains, p < .05, 95% CI_b = [0.02; 0.24; 0.46], and more likely when the zero outcome was described as “lose £0” rather than “win £0,” p < .0001, 95% CI_b = [0.26; 0.50; 0.75]. The effect of zero-outcome framing (which is the mutable-zero effect) was smaller for losses than for gains, p < .01, 95% CI_b = [−0.52; −0.30; −0.08]. Altogether, the results were directionally the same as in Experiment 1a, but the mutable-zero effect was no longer reliable in losses, and, accordingly, the effect of outcome domain in moderating the strength of the mutable-zero effect was now reliable.

2.5.2 Behind the mutable-zero effect in the gain domain

There is a negative effect of describing the zero outcome as “win £0,” and this effect is reliable (confirmation of H₂). Furthermore, in support of H₃, there is a positive effect of describing the zero outcome as “lose £0,” but this effect is not reliable. Finally, the negative effect of “winning £0” is larger than the positive effect of “losing £0.” According to H₄, that should indeed be the case. Letting Ω be the odds of choosing the gamble over the sure thing, the hypothesis states that log(Ω_N) – log(Ω_W) > log(Ω_L) – log(Ω_N), or 2log(Ω_N) – log(Ω_W) – log(Ω_L) > 0. To submit this hypothesis to an inferential test, we ran a logistic regression using choice of the gamble as the dependent variable, and using outcome framing (neutral [2] versus “winning $0” [−1] and “losing $0” [−1]) as the independent variable. In support of H₄, outcome framing had a positive effect on choice of the gamble, but this effect was not reliable, p > .20, 95% CI_b [−0.03; 0.06; 0.15].

2.5.3 Behind the mutable-zero effect in the loss domain

There is a negative effect of describing the zero outcome as “win £0,” and this effect is reliable (confirmation of H₅).

2.5.4 Behind the mutable-zero effect: Comparison between domains

As can be seen in Table 2, the negative effect of describing the zero outcome as “win £0” is smaller for losses than for gains. Under H₆, that should indeed be the case, but it can also be seen that it is only a minor difference. Nonetheless, to submit the hypothesis to an inferential test, we ran a multi-level logistic regression analysis using choice of the gamble as the dependent variable, and using outcome domain, zero-outcome framing (“win £0” [1] versus suppressed zero [−1]), and their interaction, as independent variables. Choice of the gamble was more likely for losses than for gains, p < .0001, 95% CI_b = [0.21; 0.44; 0.66], and less likely when the zero outcome was described as “win £0” than when it was suppressed, p < .0001, 95% CI_b = [−0.75; −0.52; −0.28]. In support of H₆, the negative effect of describing the zero outcome as “win £0” was smaller for losses than for gains, but this effect was not reliable, p > .30, 95% CI_b = [−0.12; 0.11; 0.33].

2.6 Conclusion

Prospect theory accurately predicted how risky choice is influenced by mutable zeroes. The hypothesized effects all went in the right direction, but, as concluded from Experiments 1a and 1b, the effects of mutable zeroes are subtle, and, in Experiment 2, three out of six hypothesized effects were too subtle to be reliable. All three reliable effects were main effects, whereas two out of the three unreliable effects were moderating effects.

Importantly, prospect theory has an indefinite conclusion: What is the effect that “losing nothing” will have on the choice of a loss gamble? By norm theory, it should have a positive effect, but, when evaluated within the framework of prospect theory, as we did in the introduction to this experiment, the positive effect may be eradicated, or even reversed into a negative effect, for loss gambles. We did find that it reversed into a negative effect.

3 Experiment 3: The double-entry mental accounting model and mutable zeroes

We investigated the mutable-zero effect with risky prospects in which the zero outcome was one of two outcomes that might occur. Analogously, we will investigate the mutable-zero effect with temporal prospects in which the zero outcome is one of two outcomes that will occur.⁴ The options featuring the zero outcome will be paired with options that exchange a gain and a loss over time. These are either saving schedules, in which a sooner loss (depositing or investing money) is exchanged for a larger-later gain (the investment plus return), e.g., “Pay $100 today and receive $400 in 1 year” (Y_S) or borrowing schedules, in which a sooner gain (the loan) is exchanged for a larger-later loss (the repayment), e.g., “Receive $100 today and pay $400 in 1 year” (X_B). If the alternative to the saving schedule is “Pay $200 today” (X_S) and if the alternative to the borrowing schedule is “Receive $200 today” (Y_B), the interest rate implied by each option pair is 33.33% over the one-year period. Should one be unwilling to borrow, then one should also be willing to save. However, rejection rates of borrowing schedules tend to be higher than acceptance rates of saving schedules (see Meissner 2016; Prelec and Loewenstein 1998), which may be referred to as the borrowing-saving asymmetry. As a result of this asymmetry, one might be unwilling to borrow and unwilling to save.

3.1 Theory

The disparity between borrowing and saving is the focal point of the double-entry mental accounting model (Prelec and Loewenstein 1998), which we extend from consumption decisions (i.e., intertemporal exchanges of money for consumption) to income decisions (i.e., intertemporal exchanges of money for money). This model proposes (1) that later positive outcomes buffer the pain of sooner negative outcomes, while later negative outcomes attenuate the pleasure of sooner positive outcomes, (2) that, by loss aversion, pain is experienced as “more intense” than pleasure (Tversky and Kahneman 1991, p. 1055), and (3) that, by delay discounting, delayed experiences have less weight than immediate experiences. If we assume, as we will do throughout our analysis, that buffering and attenuation are not pronounced enough for pain to be reversed into an experience of pleasure, or for pleasure to be reversed into an experience of pain, then the experience of the above saving schedule is:

$$ V\left({Y}_S\right)=\lambda \left(-100+\beta 400\right)+\delta 400, $$

where 0 ≤ β ≤ 0.25 is buffering, λ > 1 is constant loss aversion (Tversky and Kahneman 1991), and 0 < δ < 1 is delay discounting.⁵ A hedonic reversal from pain to pleasure of paying would occur if 0.25 < β ≤ 1, a possibility that we exclude. In a similar vein, the experience of the borrowing schedule is:

$$ V\left({X}_B\right)=\left(100+\alpha \left(-400\right)\right)+\delta \lambda \left(-400\right), $$

where 0 ≤ α ≤ 0.25 is attenuation. A hedonic reversal from pleasure to pain of receiving would occur if 0.25 < α ≤ 1, a possibility that we exclude. In deriving testable implications from the double-entry mental accounting model, we add two working assumptions to the one of excluding hedonic reversals: Outcomes are not discounted over the one-year period, i.e., δ = 1 (an assumption that we relax in the Appendix), and attenuation is as pronounced as buffering, i.e., α = β (see also Prelec and Loewenstein 1998, sections 3.8 and 4.2). If it is not for differences in attenuation and buffering, loss aversion is necessary and sufficient for generating the saving-borrowing asymmetry.

Double-entry mental accounting only operates in the presence of mixed prospects, but the process is indifferent to whether value is acquired (zero outcomes) or intrinsic (nonzero outcomes). Thus, for instance, the positive experience of receiving $200 now is attenuated by the negative experience of “receiving $0” later (a bad zero, denoted –z), and the positive experience of receiving $200 later buffers the negative experience of “receiving $0” now. Conversely, the negative experience of paying $200 now is buffered by the positive experience of “paying $0” later (a good zero, denoted z), and the negative experience of paying $200 later attenuates the positive experience of “paying $0” now. In the absence of mixed prospects, double-entry mental accounting is inoperative: Receiving $200 now and “paying $0” later are both positive experiences, whereas paying $200 now and “receiving $0” later are both negative experiences, so that no buffering or attenuation takes place in the evaluation of these prospects. We next derive predictions about how decisions about saving and borrowing are influenced by the framing of zero outcomes.

3.2 Derivation of predictions

3.2.1 Borrowing versus saving

Consider the following option pairs, contrasting a borrowing decision and a saving decision with zero outcomes located in the future:

BORROW, ZFUTURE	XB	Receive $100 today and pay $400 in 1 year.
	YB	Pay $200 today and [receive / pay] $0 in 1 year.
SAVE, ZFUTURE	XS	Receive $200 today and [receive / pay] $0 in 1 year.
	YS	Pay $100 today and receive $400 in 1 year.

The mutable-zero effect will be stronger in the borrowing decision than in the saving when:

$$ \left(V\left({Y}_{B,\mathrm{pay}\kern0.15em \$0}\right)-V\left({X}_B\right)\right)-\left(V\left({Y}_{B,\mathrm{receive}\kern0.34em \$0}\right)-V\left({X}_B\right)\right)>\left(V\left({X}_{S,\mathrm{pay}\kern0.15em \$0}\right)-V\left({Y}_S\right)\right)-\left(V\left({X}_{S,\mathrm{receive}\kern0.34em \$0}\right)-V\left({Y}_S\right)\right),V\left({Y}_{B,\mathrm{pay}\kern0.15em \$0}\right)-V\left({Y}_{B,\mathrm{receive}\kern0.34em \$0}\right)>V\left({X}_{S,\mathrm{pay}\kern0.15em \$0}\right)-V\left({X}_{S,\mathrm{receive}\kern0.34em \$0}\right),\left\{\lambda \left(\left(-200\right)+\beta z\right)+z\right\}-\left\{\lambda \left(-200\right)+\lambda \left(-z\right)\right\}>\left\{200+z\Big\},-,\Big\{\left(200+\alpha \left(-z\right)\right)+\lambda \left(-z\right)\right\}, $$

where z < 800 so as to preclude hedonic reversals. This reduces to:

λβ > α,

which, under the assumption that buffering is as pronounced as attenuation (β = α > 0), requires loss aversion (λ > 1). Alternatively, consider the following option pairs, contrasting a borrowing decision and a saving decision with zero outcomes located in the present:

BORROW, ZPRESENT	XB	Receive £300 today and pay £500 in 1 year.
	YB	[Receive / pay] £0 today and pay £100 in 1 year.
SAVE, ZPRESENT	XS	[Receive / pay] £0 today and receive £100 in 1 year.
	YS	Pay £300 today and receive £500 in 1 year.

By a derivation analogous to the one for future zero outcomes, the mutable-zero effect will be stronger in the borrowing decision than in the saving decision when:

λβ > α,

which, under the assumption that buffering is as pronounced as attenuation (β = α > 0), requires loss aversion (λ > 1).

3.2.2 Future versus present zeroes

Consider the following option pairs, contrasting a borrowing decision with a future zero outcome and a borrowing decision with a present zero outcome:

BORROW, ZFUTURE	XF	Receive $100 today and pay $400 in 1 year.
	YF	Pay $200 today and [receive / pay] $0 in 1 year.
BORROW, ZPRESENT	XP	Receive $300 today and pay $500 in 1 year.
	YP	[Receive / pay] $0 today and pay $100 in 1 year.

The mutable-zero effect will be stronger in the borrowing decision with a future zero outcome than in the borrowing decision with a present zero outcome when:

$$ \left(V\left({Y}_{F,\mathrm{pay}\kern0.15em \$0}\right)-V\left({X}_F\right)\right)-\left(V\left({Y}_{F,\mathrm{receive}\kern0.34em \$0}\right)-V\left({X}_F\right)\right)>\left(V\left({X}_{P,\mathrm{pay}\kern0.15em \$0}\right)-V\left({Y}_P\right)\right)-\left(V\left({X}_{P,\mathrm{receive}\kern0.34em \$0}\right)-V\left({Y}_P\right)\right),V\left({Y}_{F,\mathrm{pay}\kern0.15em \$0}\right)-V\left({Y}_{F,\mathrm{receive}\kern0.34em \$0}\right)>V\left({X}_{P,\mathrm{pay}\kern0.15em \$0}\right)-V\left({X}_{P,\mathrm{receive}\kern0.34em \$0}\right),\left\{\lambda \left(\left(-200\right)+\beta z\right)+z\right\}-\left\{\lambda \left(-200\right)+\lambda \left(-z\right)\right\}>\left\{\left(z+\alpha \left(-100\right)\right)+\lambda \left(-100\right)\Big\},-,\Big\{\lambda \left(-z\right)+\lambda \left(-100\right)\right\}, $$

where 25 < z < 800 so as to preclude hedonic reversals. This reduces to:

λβz + α100 > 0,

which holds. Alternatively, consider the following option pairs, contrasting a saving decision with a future zero outcome and a saving decision with a present zero outcome:

SAVE, ZFUTURE	XF	Receive £200 today and [receive / pay] £0 in 1 year.
	YF	Pay £100 today and receive £400 in 1 year.
SAVE, ZPRESENT	XP	[Receive / pay] £0 today and receive £100 in 1 year.
	YP	Pay £300 today and receive £500 in 1 year.

By a derivation analogous to the one for borrowing decisions, the mutable-zero effect will be stronger in the saving decision with a future zero outcome than in the saving decision with a present zero outcome when:

λβ100 + αz > 0,

which holds.

3.3 Summary of predictions

We deduced that the mutable-zero effect should be stronger in decisions about borrowing than in decisions about saving, and stronger in decisions with a future zero outcome than in decisions with a present zero outcome. Letting Z_PAY be the mutable-zero factor (1 = pay zero; 0 = receive zero), BORROW be the borrowing-saving factor (1 = borrow decision; 0 = saving decision), and Z_FUTURE be the movable-zero factor (1 = future zero; 0 = present zero), and letting the dependent variable be choice of the option with the zero outcome, we expect a positive Z_PAY main effect (which is the mutable-zero effect), a positive Z_PAY × BORROW interaction effect (a stronger mutable-zero effect in borrowing decisions than in saving decisions), and a positive Z_PAY × Z_FUTURE interaction effect (a stronger mutable-zero effect in decisions with a future zero outcome than in decisions with a present zero outcome).

3.4 Method

3.4.1 Stimuli

Table 3 shows the stimuli. The experimental interest rate, as implied by the four option pairs, is held constant at 33.33%. In both the top and the bottom panel, the options in the third row, where Y is a saving schedule, are obtained from those in the first row, where is X is a borrowing schedule, by swapping the outcomes between the options and changing their sign, and the options in the fourth row are obtained from those in the second row by doing the same. This is the borrowing-saving factor (BORROW). The zero outcome occurs in the future in the first and third row, and in the present in the second and fourth row. This is the movable-zero factor (Z_FUTURE).

Table 3 Stimuli for intertemporal choices, proportions (p) choosing Better, limits of 95% confidence intervals (95% CI_d), and effect sizes (ES_d’) for the difference in choice proportions between Pay and Receive conditions, in the UK and USA samples of Experiment 3

3.4.2 Participants and procedure

We recruited a British sample (N = 609) and an American sample (N = 718). The British sample (UK), recruited through Maximiles, was 37% male, with an average age of 41. Most were employed (69%, among whom 44% worked full time), and some had an academic degree (35%, among whom 24% had a bachelors, 9% masters, 2% PhD) or were still studying (4%). The American sample (USA), recruited through MTurk and earning $0.25, was 64% male, with an average age of 30. Most were employed (72%, among whom 42% worked full time), and most had an academic degree (53%, among whom 46% had a bachelors, 6% masters, 1% PhD) or were still studying (17%). The zero outcomes were described as “paying zero” (in appropriate currency) for half the sample (n_UK = 308, n_USA = 366), and as “receiving zero” for the other half (n_UK = 301, n_USA = 352). Within each sample, the order of the choices, and the order of the options within each choice, was randomized across participants.

The USA sample was recruited to check on the robustness of the results obtained from the UK sample. The samples differ markedly in their demographics, in that the USA sample has more males, and is younger and better educated. We will see that the results, while directionally consistent across samples, are generally weaker in the USA sample than in the UK sample.

3.5 Results

Table 3 shows the results. Generally, an option fares better when the zero outcome is described as a “pay £0” rather than “receive £0.” As expected, the mutable-zero effect is stronger in the borrowing decisions than in the saving decisions, and stronger in decisions with future zero outcomes than in decisions with the present zero outcomes, although the effects are smaller, and less reliable, in the USA sample than in the UK sample.

We ran a multi-level logistic regression analysis, treating the four choice trials as nested within participant, using choice of the option with the mutable zero (yes-no) as the dependent variable, and using as independent variables: The mutable-zero factor (Z_PAY, whether the zero outcome is described as “pay £0” rather than “receive £0”), the borrowing-saving factor (BORROW, whether the decision is about borrowing rather than saving), the movable-zero factor (Z_FUTURE, whether the zero outcome is located in the future rather than the present), the two-way interactions between these three factors, and the two-way interactions between all foregoing independent variables and sample (USA, whether the sample was from the USA rather than the UK). Table 4 shows the results.

Table 4 Estimates from a hierarchical (multi-level) logistic model in Experiment 3, treating the four choice trials as nested within participant, and using choice of the option with the zero outcome (yes-no) as the dependent variable, including z-tests and 95% confidence intervals (95% CI_b) of regression coefficients

Among all effects estimated, second-largest is the mutable-zero effect (Z_PAY). As expected, the mutable-zero effect is larger in borrowing decisions than in saving decisions (Z_PAY × BORROW), and larger in decisions with future zero outcomes than in decisions with present zero outcomes (Z_PAY × Z_FUTURE). Furthermore, the mutable-zero effect is weaker in the USA sample than in the UK sample (USA × Z_PAY).

The largest effect is observed for the borrowing-saving factor (BORROW): The probability of rejecting a borrowing schedule (p) is higher than the probability of rejecting a saving schedule (q), or, equivalently, saving is more likely than borrowing. This confirms, in decisions about monetary costs and benefits, a preference for improvement over decline, as identified earlier for decisions about consumption (Loewenstein and Prelec 1993). The main effect of the borrowing-saving factor is not the borrowing-saving asymmetry, which is that the probability of rejecting a borrowing schedule is higher than the probability of accepting a saving schedule, i.e., p > 1 – q, or p + q > 1. This inequality was also observed, in that .70 + .50 = 1.21, 95% CI [1.19; 1.23].

Finally, there was an interaction between the borrowing-saving factor and the movable-zero factor (BORROW × Z_FUTURE): Table 5 shows that (1) rejecting the borrowing schedule was more likely when its future loss contrasted unfavorably with the future zero outcome of not borrowing than when its present gain contrasted favorably with the present zero outcome of not borrowing, and (2) accepting the saving schedule was more likely when its future gain contrasted favorably with the future zero outcome of not saving than when its present loss contrasted unfavorably with the present zero outcome of not saving. It therefore appears that, when choice involves sequences, people make direct comparisons between the outcomes occurring at the same point in time, as has been given treatment by the cumulative tradeoff model of intertemporal choice (Scholten et al. 2016). We return to this topic in the general discussion.

Table 5 Stimuli for intertemporal choices, and 95% confidence intervals of proportions (p) choosing Better, in Experiment 3. Proportions aggregated across Pay and Receive conditions

3.6 Conclusion

We obtained the mutable-zero effect in intertemporal choice, indicating that it is not specific to risky choice. Moreover, the strength of the mutable-zero effect varies, in ways predicted by the double-entry mental accounting model, across option pairs: It is stronger in borrowing decisions than in saving decisions, and it is stronger with future zero outcomes than with present zero outcomes. Meanwhile, the overriding result is that saving is more likely than borrowing.

4 General discussion

The valence of a zero event depends on its “irrelevant” description: It “feels better” to lose or pay nothing than to win or receive nothing. A negative wording (lose, pay) sets up a norm of negative events, with which the zero event compares favorably, while a positive wording (win, receive) sets up a norm of positive events, with which the zero event compares unfavorably, so that a negative wording acquires a more positive tone than a positive wording. Descriptive invariance requires from us that this should not affect our decisions, but we have shown that it does, among a fair number of us at least. To others among us, the framing of zero events may actually be irrelevant. The mutable-zero effect is indeed small; yet, it is a reliable phenomenon. And if one thinks of the alternative descriptions of a zero outcome as a minimal manipulation, the small effect may actually be considered quite impressive (Prentice and Miller 1992).

Descriptive invariance, along with dominance, is an essential condition of rational choice (Tversky and Kahneman 1986), and it has seen a number of violations, commonly referred to as framing effects. A stylized example of framing is the adage that optimists see a glass of wine as half full, while pessimists see it as half empty. And if the wine glass is half full, and therefore half empty, then these are complementary descriptions of the same state of the world, so that, normatively, using one or the other should not matter for judgment and choice (Mandel 2001)—but it does.

4.1 Counterfactuals versus expectations

Life often confronts us with zero events. A bookstore may offer us “free shipping.” Our employer may grant us “no bonus.” We are pleased to pay $0 to the bookstore, and this may be because we expected to pay something but did not. We are not pleased to receive $0 from our employer, and this may be because we expected to receive something but did not (Rick and Loewenstein 2008). In norm theory, Kahneman and Miller (1986) suggested that reasoning may not only flow forward, “from anticipation and hypothesis to confirmation or revision,” but also backward, “from the experience to what it reminds us of or makes us think about” (p. 137). In the latter case, “objects or events generate their own norms by retrieval of similar experiences stored in memory or by construction of counterfactual alternatives” (p. 136). Thus, “free shipping” may sound pleasant because it reminds us of occasions on which we were charged shipping fees, and “no bonus” may sound unpleasant because it reminds us of occasions on which we were granted bonuses; not so much because we expected to pay or receive something. Of course, both norms and expectations may influence our feelings, and may be difficult to disentangle in many real-life situations. Kahneman and Miller’s (1986) intention with norm theory was “not to deny the existence of anticipation and expectation but to encourage the consideration of alternative accounts for some of the observations that are routinely explained in terms of forward processing” (p. 137, emphasis added). Our intention was to compile a set of observations that cannot reasonably be explained in terms of forward processing, which therefore constitute the clearest exposure of norms.

4.2 Expectations in decision theory

We have incorporated counterfactuals into theories of choice, so as to predict the effects of mutable zeroes when people face risk and when people face time. Traditionally, decision theory has ignored counterfactuals, but expectations play a role in most theories of decision under risk. While prospect theory sacrifices the expectation principle from EU, by assigning a decision weight w(p) to probability p of an outcome occurring, other formulations have maintained the expectation principle but modified the utility function. For instance, the utility function has been expanded with anticipated regret and rejoicing as they result from comparisons between the possible outcomes of a gamble and those that would occur if one were to choose differently (Bell 1982, 1983; Loomes and Sugden 1982). Similarly, the utility function has been expanded with anticipated emotions as they result from comparisons between the possible outcomes of a gamble with the expected value of the gamble: Anticipated disappointment when “it could come out better,” and anticipated elation when “it could come out worse” (Bell 1985; Loomes and Sugden 1986). Zero outcomes acquire value in the same way as nonzero outcomes do: Either from between-gamble or within-gamble comparisons. Thus, a zero outcome acquires negative value (by regret or disappointment) if the comparison is with a gain, and positive value (by rejoicing or elation) if the comparison is with a loss. In our analysis, however, zero outcomes are unique, in that only they elicit counterfactual gains and losses, which will then serve as a reference point for evaluating the zero outcomes themselves. Nonetheless, in Experiment 3, dealing with zero outcomes in intertemporal choice, we obtained a result suggesting that between-prospect comparisons of zero and nonzero outcomes also affected choice.

4.3 The framing of something, the framing of nothing

The investigation of framing effects in judgment and decision making began with Tversky and Kahneman’s (1981) Asian Disease Problem, in which the lives of 600 people are threatened, and life-saving programs are examined. One group of participants preferred a program that would save 200 people for sure over a program that would save 600 people with a 1/3 probability, but save no people with a 2/3 probability. Another group of participants preferred a program that would let nobody die with a probability of 1/3, but let 600 people die with a 2/3 probability, over a program that would let 400 people die for sure. Prospect theory ascribes this result to reference dependence, i.e., v(0) = 0, and diminishing sensitivity, i.e., v is concave over gains, so that v(600) < 3v(200), which works against the gamble, and convex over losses, so that v(−600) > 3v(−200), which works in favor of the gamble.

Our interpretation is that some of the action may lie in the zero outcomes, rather than the nonzero outcomes. Specifically, “save no people” brings to mind saving some people, with which saving no people compares unfavorably, thus working against the gamble. Similarly, “let nobody die” brings to mind letting somebody die, with which letting nobody die compares favorably, thus working in favor of the gamble. Reference dependence is fine, but designating zero outcomes means that v(0) ≠ 0, because the reference point is no longer the status quo, but rather something imagined.

There is no shortage of competing views on framing effects (for one of many discussions, see Mandel 2014), and our norm-theory approach to the Asian Disease Problem is a partial explanation at best. Indeed, the reversal from an ample majority (72%) choosing the safe option in the positive frame (saving lives) to an ample majority (78%) choosing the risky option in the negative frame (giving up lives) is a large effect, whereas the mutable-zero effect is a small effect, unlikely to be the sole responsible for Tversky and Kahneman’s (1981) result. However, judgments and decisions are influenced by the framing of zero outcomes, and we have shown that prevalent theories of choice, Kahneman and Tversky’s (1979) prospect theory and Prelec and Loewenstein’s (1998) double-entry mental accounting model, can explain how decisions are influenced by mutable zeroes, on the shared understanding that nothing can have value, just like everything else.

Appendix

In this Appendix, we establish the boundary conditions for our predictions in Experiment 3 by removing the assumption of “no discounting,” thus allowing outcomes that are delayed by one year to receive the same weight as, or less weight than, immediate outcomes, i.e., 0 < δ ≤ 1. We continue to assume that buffering is as pronounced as attenuation, i.e., α = β = γ > 0, where γ will henceforth be referred to as “hedonic interaction.” We also continue to assume that hedonic interaction does not result in hedonic reversals, i.e., pleasure turning into pain, or pain turning into pleasure, as ensured by 0 < γ ≤ 0.25.

With zero outcomes located in the future, the mutable-zero effect will be stronger in the borrowing decision than in the saving decision if:

$$ \left(\lambda -1\right)\gamma >1-\delta, $$

(4)

i.e., if loss aversion and hedonic interaction outweigh discounting. Heuristically setting λ at 2.5 (Thaler et al. 1997), and δ at 0.9 (Prelec and Loewenstein 1998, section 4.2), the inequality holds if γ > 0.0667. With zero outcomes located in the present, discounting is irrelevant for the strength of the mutable-zero effect across choice tasks, in that the mutable-zero effect will be stronger in the borrowing decision than in the saving decision if:

$$ \lambda >1, $$

i.e., as long as there is loss aversion. As to the borrowing decisions, the mutable-zero effect will be stronger with future zero outcomes than with present zero outcomes if:

$$ \gamma \frac{\lambda z+100}{\lambda z+z}>1-\delta $$

(5)

Heuristically setting λ at 2.5, δ at 0.9, γ at 0.0667 (the minimum required by the foregoing simulation), and z at 25 (its minimum to preclude hedonic reversals), the inequality becomes 0.1238 > 0.1, which holds true. Finally, as to the saving decisions, the mutable-zero effect will be stronger with future zero outcomes than with present zero outcomes if:

$$ \gamma \frac{z+\lambda 100}{z+\lambda z}>1-\delta $$

(6)

This, with the settings used in the foregoing simulations, becomes 0.2095 > 0.1, which holds true.

Because the option pairs in our investigation imply an interest rate of r = 0.333, and considering that r = (1 – δ) / δ, we may redo our simulations with δ = 0.75. That is, we set δ at the value with which an individual, if governed solely by delay discounting, would be pairwise indifferent between the options. Substituting λ = 2.5 and δ = 0.75 into Inequality 4, we get γ > 0.1667. Further substituting the values of λ and δ, along with γ = 0.1667 and z = 25, into Inequalities 5 and 6, we get 0.3095 > 0.25 and 0.5238 > 0.25, respectively, both of which hold true.

We may also consider setting γ at its highest permissible value of 0.25 in our analysis. Substituting this value, along with λ = 2.5, into Inequality 4, we get δ > 0.625. Further substituting the values of γ and λ, along with δ = 0.625 and z = 25, into Inequalities 5 and 6, we get 0.4643 > 0.375 and 0.7857 > 0.375, both of which hold true. Thus, although discounting countervails hedonic interaction and loss aversion, our predictions will stand up in most realistic parameterizations of the double-entry mental accounting model.