Skip to main content
SpringerLink
Log in

Exact and asymptotic analysis of infinite server batch service queues with random batch sizes

  • Published:
Queueing Systems Aims and scope Submit manuscript

Abstract

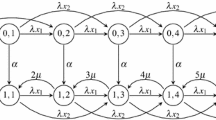
Batch service queueing systems are basically classified into two types: a time-based system in which the service facilities depart according to inter-departure times that follows a given distribution, such as the conventional bus system, and a demand-responsive system in which the vehicles start traveling provided that a certain number of customers gather at the waiting space, such as ride-sharing and on-demand bus. Motivated by the recent spreading of demand-responsive transportation, this study examines the M/M\(^{\textit{X}}\)/\(\infty \) queue. In this model, whenever the number of waiting customers reaches a capacity set by a discrete random variable \(\textit{X}\), customers are served by a group. We formulate the M/M\(^{\textit{X}}\)/\(\infty \) queue as a three-dimensional Markov chain whose dimensions are all unbounded and depict a book-type transition diagram. The joint stationary distribution for the number of busy servers, number of waiting customers, and batch size is derived by applying the method of factorial moment generating function. The central limit theorem is proved for the case that \(\textit{X}\) has finite support under heavy traffic using the exact expressions of the first two moments of the number of busy servers. Moreover, we show that the M/M\(^\textit{X}\)/\(\infty \) queue encompasses the time-based infinite server batch service queue (M/M\(^{G(x)}\)/\(\infty \) queue), which corresponds to the conventional bus system, under a specific heavy traffic regime. In this model, the transportation facility departs periodically according to a given distribution, \(\textit{G(x)}\), and collects all the waiting customers for a batch service for an exponentially distributed time corresponding to the traveling time on the road. We show a random variable version of Little’s law for the number of waiting customers for the M/M\(^{G(x)}\)/\(\infty \) queue. Furthermore, we present a moment approach to obtain the distribution and moments of the number of busy servers in a GI/M/\(\infty \) queue by utilizing the M/M\(^{G(x)}\)/\(\infty \) queue. Finally, we provide some numerical results and discuss their possible applications on transportation systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Arora, K.L.: Two-server bulk-service queuing process. Oper. Res. 12(2), 286–294 (1964)

    Article  MathSciNet  Google Scholar 

  2. Banerjee, A., Gupta, U.C., Sikdar, K.: Analysis of finite-buffer bulk-arrival bulk-service queue with variable service capacity and batch-size-dependent service. Int. J. Math. Op. Res. 5(3), 358–386 (2013)

    Article  MathSciNet  Google Scholar 

  3. Blom, J., De Turck, K., Mandjes, M.: Analysis of Markov-modulated infinite-server queues in the central-limit regime. Probab. Eng. Inf. Sci. 29(3), 433–459 (2015)

    Article  MathSciNet  Google Scholar 

  4. Bruneel, H., Wittevrongel, S., Claeys, D., Walraevens, J.: Discrete-time queues with variable service capacity: a basic model and its analysis. Ann. Oper. Res. 239(2), 359–380 (2016)

    Article  MathSciNet  Google Scholar 

  5. Cordeau, J.L., Chaudhry, M.L.: A simple and complete solution to the stationary queue-length probabilities of a bulk-arrival bulk-service queue. INFOR: Inform. Syst. Op. Res. 47(4), 283–288 (2009)

    MathSciNet  Google Scholar 

  6. Cosmetatos, G.P.: Closed-form equilibrium results for the M/M\((a, \infty )\)/n queue. Eur. J. Oper. Res. 12(2), 203–204 (1983)

    Article  Google Scholar 

  7. Durrett, R.: Probability: Theory and Examples. Cambridge University Press, Cambridge (2019)

    Book  Google Scholar 

  8. Ghare, P.M.: Letter to the editor - multichannel queuing system with bulk service. Oper. Res. 16(1), 189–192 (1968)

    Article  Google Scholar 

  9. Hassin, R., Haviv, M.: To Queue or not to Queue: Equilibrium Behavior in Queueing Systems. Springer, Berlin (2003)

    Book  Google Scholar 

  10. Ho Chang, S., Won Choi, D.: Modeling and performance analysis of a finite-buffer queue with batch arrivals, batch services, and setup times: The M\(^{X}\)/G\(^{Y}\)/\(1\)/\({K}+ {B}\) queue with setup times. INFORMS J. Comput. 18(2), 218–228 (2006)

    Article  MathSciNet  Google Scholar 

  11. Ho Chang, S., Won Choi, D., Kim, T.S.: Performance analysis of a finite-buffer bulk-arrival and bulk-service queue with variable server capacity. Stoch. Anal. Appl. 22(5), 1151–1173 (2004)

    Article  MathSciNet  Google Scholar 

  12. Kapodistria, S., Phung-Duc, T., Resing, J.: Linear birth/immigration-death process with binomial catastrophes. Probab. Eng. Inf. Sci. 30(1), 79–111 (2016)

    Article  MathSciNet  Google Scholar 

  13. Liu, L., Kashyap, B.R.K., Templeton, J.G.C.: The service system M/M\(^{R}\)/\(\infty \) with impatient customers. Queueing Syst. 2(4), 353–372 (1987)

    Article  MathSciNet  Google Scholar 

  14. Liu, L., Kashyap, B.R.K., Templeton, J.G.C.: Queue lengths in the GI\(^{X}\)/M\(^{R}\)/\(\infty \) service system. Queueing Syst. 22(1), 129–144 (1996)

    Article  MathSciNet  Google Scholar 

  15. Nain, P., Panigrahy, N.K., Basu, P., Towsley, D.: One-dimensional service networks and batch service queues. Queueing Syst. 98(1), 181–207 (2021)

    Article  MathSciNet  Google Scholar 

  16. Nakamura, A., Phung-Duc, T.: Stationary analysis of infinite server queue with batch service. Lect. Notes Comput. Sci. 13104, 411–424 (2022)

    Article  Google Scholar 

  17. Nakamura, A., Phung-Duc, T.: A moment approach for a conditional central limit theorem of infinite-server queue: A case of M/M\(^{X}\)/\(\infty \) queue. Mathematics 11(9), 2088 (2023)

    Article  Google Scholar 

  18. Sasikala, S., Indhira, K.: Bulk service queueing models - a survey. Int. J. Pure Appl. Math. 106(6), 43–56 (2016)

    Google Scholar 

  19. Sikdar, K., Gupta, U.C.: On the batch arrival batch service queue with finite buffer under server’s vacation: M\(^{X}\)/G\(^{Y}\)/\(1\)/\({N}\) queue. Comput. Math. Appl. 56(11), 2861–2873 (2008)

    Article  MathSciNet  Google Scholar 

  20. Sim, S.H., Templeton, J.G.C.: Computational procedures for steady-state characteristics of unscheduled multi-carrier shuttle systems. Eur. J. Oper. Res. 12(2), 190–202 (1983)

    Article  Google Scholar 

  21. Sim, S.H., Templeton, J.G.C.: Further results for the M/M\((a, \infty )\)/N batch-service system. Queueing Syst. 6, 277–286 (1990)

    Article  MathSciNet  Google Scholar 

  22. Takács, L.: Introduction to the Theory of Queues. Oxford University Press, New York (1962)

    Google Scholar 

  23. Takács, L.: A moment convergence theorem. Am. Math. Mon. 98(8), 742–746 (1991)

    Article  MathSciNet  Google Scholar 

  24. Ushakumari, P.V., Krishnamoorthy, A.: On a bulk arrival bulk service infinite service queue. Stoch. Anal. Appl. 16(3), 585–595 (1998)

    Article  Google Scholar 

  25. Ushakumari, P.V., Krishnamoorthy, A.: The queueing system M/M\(^{X(R)}\)/\(\infty \). Asia-Pacific J. Oper. Res. 15(1), 17–28 (1998)

    MathSciNet  Google Scholar 

  26. Whitt, W.: On the heavy-traffic limit theorem for GI/G/\(\infty \) queues. Adv. Appl. Probab. 14(1), 171–190 (1982)

    Article  MathSciNet  Google Scholar 

  27. Wolf, D.: Approximation of the invariant probability measure of an infinite stochastic matrix. Adv. Appl. Probab. 12(3), 710–726 (1980)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We deeply thank two anonymous reviewers and associate editor for their useful comments which improved the presentation of the paper. This work was supported by JSPS KAKENHI Nos. 21K11765, 18K18006, 23KJ0249, and JST SPRING No. JPMJSP2124. In addition, this study was supported by F-MIRAI: R &D Center for Frontiers of MIRAI in Policy and Technology, the University of Tsukuba and Toyota Motor Corporation Collaborative R &D center. The authors also would like to sincerely thank Yuichi Takano for his discussion on the model of Sect. 3.

Author information

Authors and Affiliations

  1. Graduate School of Science and Technology, University of Tsukuba, Tennoudai1-1-1, Tsukuba, Ibaraki, 305-8573, Japan

    Ayane Nakamura

  2. Institute of Systems and Information Engineering, University of Tsukuba, Tennoudai1-1-1, Tsukuba, Ibaraki, 305-8573, Japan

    Tuan Phung-Duc

Authors
  1. Ayane Nakamura
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tuan Phung-Duc
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tuan Phung-Duc.

Ethics declarations

Conflict of interest

The authors have no conflicts of interest.

Human and animal rights

This article does not contain any studies with human participants performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Ayane Nakamura and Tuan Phung-Duc have contributed equally to this work.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nakamura, A., Phung-Duc, T. Exact and asymptotic analysis of infinite server batch service queues with random batch sizes. Queueing Syst 106, 129–158 (2024). https://doi.org/10.1007/s11134-023-09898-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11134-023-09898-4

Keywords

Mathematics Subject Classification

Search

Navigation