Managing capacity and inventory jointly for multi-server make-to-stock queues

Abstract

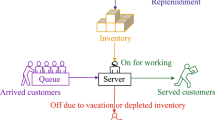
We consider joint capacity–inventory management for multi-server make-to-stock queues operating under a base stock policy. The number of servers corresponds to the capacity decision, and the base stock level is the inventory decision. Our goal is to minimize a combination of capacity, inventory, and backordering costs. We develop a square-root rule for the joint decision and justify the rule analytically in a many-server queue asymptotic framework. We demonstrate the accuracy of the square-root rule, first via our derivation and numerical assessment of a novel corrected diffusion approximation and then more directly by conducting extensive numerical experiments. Finally, we provide operational insights into the trade-offs involved in such joint management problems, through various analysis based on the square-root rule as well as a comparison with analogous results for single-server make-to-stock queues.

Appendices

Appendix 1: Preliminary results

In the appendices, we provide the proofs of the results found in the paper. We begin with some preliminary results with regard to the analytic continuation of various performance functions. As discussed in Sect. 3.2, we consider the continuous extension of each performance function, allowing c and s to take on any nonnegative real value. The same approach is taken in [24, 44] and is based on results from earlier work such as [23].

First, the continuation of the steady-state shortfall distribution to real-valued arguments is given by the following lemma.

Lemma 2

For any $c\in \mathbb {Z}_{+}\cup (R,\infty )$ and $s\in \mathbb {Z}_{+}$, $D(c,s,R)=\mathbb P_{c}\{Q(\infty )\le s\}$, where D(c, s, R) is defined for all $c\in (R,\infty )$ and $s\in [0,\infty )$:

$$\begin{aligned} D(c,s,R):=\left\{ \begin{array}{ll} [1-C(c,R)]\cdot R^{s-c+1}B(c-1,R)\varGamma (c)/[B(s,R)\varGamma (s+1)],&{} \quad \mathrm{if}~ s\le c,\\ {[}1-C(c,R)]\cdot \left[ 1+\rho (1-\rho ^{s-c+1})B(c-1,R)/(1-\rho )\right] ,&{} \quad \mathrm{if}~s>c, \end{array}\right. \end{aligned}$$

(43)

with

$$\begin{aligned} C(c,R):= & {} \left[ R\int _{0}^{\infty }t\mathrm{e}^{-Rt}(1+t)^{c-1}\mathrm{d}t\right] ^{-1},\quad \mathrm{for\ all}~{c\in (R,\infty )},\nonumber \\ B(x,R):= & {} \left[ R\int _{0}^{\infty }\mathrm{e}^{-Rt}(1+t)^{x}\mathrm{d}t\right] ^{-1},\quad \mathrm{for\ all}~{x\in [0,\infty )}. \end{aligned}$$

(44)

Proof

For any integer $c>R$, the analytic continuation of the Erlang C formula reads (see [24]):

$$\begin{aligned} \mathbb P_{c}\{Q(\infty )\ge c\}=C(c,R), \end{aligned}$$

(45)

and therefore

$$\begin{aligned} \mathbb P_{c}\{Q(\infty )\le c-1\}=1-C(c,R). \end{aligned}$$

(46)

For any $s\in \mathbb {Z}_{+}\cup [0,c]$, it follows from the exact formula for the distribution of $Q(\infty )$ that

$$\begin{aligned} \frac{\mathbb P_{c}\{Q(\infty )\le s\}}{\mathbb P_{c}\{Q(\infty )\le c-1\}}=\frac{\sum _{i=0}^{s}R^{i}/i!}{\sum _{i=0}^{c-1}R^{i}/i!}=\frac{R^{s-c+1}B(c-1,R)\varGamma (c)}{B(s,R)\varGamma (s+1)}. \end{aligned}$$

(47)

Multiplying (46) by (47) yields the desired result for $s\le c$. In the case of $s>c$, we have that

$$\begin{aligned} \frac{\mathbb P_{c}\{Q(\infty )\le s\}}{\mathbb P_{c}\{Q(\infty )\le c-1\}}=&\,1+\frac{\sum _{i=c}^{s}\mathbb P_{c}\{Q(\infty )=i\}}{\mathbb P_{c}\{Q(\infty )\le c-1\}}=1+\frac{c^{c}\sum _{i=c}^{s}\rho ^{i}/c!}{\sum _{i=0}^{c-1}R^{i}/i!}\nonumber \\ =&\,1+\frac{\rho (1-\rho ^{s-c+1})B(c-1,R)}{(1-\rho )}, \end{aligned}$$

(48)

which combined with (46) completes the proof. $\square$

We next show that a recursive relation that is known to hold for the Erlang B loss formula (see [39]) remains valid for its analytic continuation.

Lemma 3

For any $x>0$,

$$\begin{aligned} \frac{1}{B(x,R)}=\frac{R}{(x+1)B(x+1,R)}-\frac{R}{x+1}. \end{aligned}$$

Proof

The recursion follows from

$$\begin{aligned} B(x,R)=\frac{\mathrm{e}^{-R}R^{x}}{\varGamma (x+1,R)},~~\text {for all }{x>0}, \end{aligned}$$

and a recursive relation for the incomplete gamma function (see [40]):

$$\begin{aligned} \varGamma (x+1,R)=x\varGamma (x,R)+R^{x}\mathrm{e}^{-R}. \end{aligned}$$

$\square$

Our third preliminary result is the continuation for the two performance functions that determine the inventory holding cost and backorder cost.

Lemma 4

If $c\ge s$, $\mathbb E_{c}[(s-Q(\infty ))^{+}]=L_{1}(c,s,R)$, and if $c\le s$, $\mathbb E_{c}[(Q(\infty )-s)^{+}]=L_{2}(c,s,R)$, where

$$\begin{aligned}&L_{1}(c,s,R):=D(c,s,R)\cdot [s-R(1-B(s,R))], \end{aligned}$$

(49)

$$\begin{aligned}&L_{2}(c,s,R):=[1-C(c,R)]\cdot B(c-1,R)\cdot \rho ^{s-c}\cdot \frac{\rho ^{2}}{(1-\rho )^{2}}, \end{aligned}$$

(50)

and both functions are defined for all $c\in (R,\infty )$ and $s\in [0,\infty )$.

Proof

First, by examining the state transition rates in the underlying birth-death process of the total number of customers in the M / M / c queue, we observe that, if $c\ge s$, $Q(\infty )|Q(\infty )\le s$ is equal in distribution to $Q_{B}$, where $Q_{B}$ denotes the steady-state number of customers in the M / M / s / s loss queue with offered load R, and if $c\le s$, $Q(\infty )-s|Q(\infty )\ge s$ equal in distribution to $Q_{\mathrm{M/M/1}}$, where $Q_{\mathrm{M/M/1}}$ denotes the steady-state number of customers in the M / M / 1 queue with traffic intensity $\rho$.

If $c\ge s$, we condition to obtain that

$$\begin{aligned} \mathbb E_{c}[(s-Q(\infty ))^{+}]=\mathbb P_{c}\{Q(\infty )\le s\}\cdot \left( s-\mathbb E_{c}[Q(\infty )|Q(\infty )\le s]\right) . \end{aligned}$$

(51)

Substituting the formula for the expected steady-state queue-length in the M / M / s / s queue,

$$\begin{aligned} \mathbb E[Q_{B}]=R(1-B(s,R)), \end{aligned}$$

(52)

into (51) then yields (49).

In the case of $c\le s$,

$$\begin{aligned} \mathbb E_{c}[(Q(\infty )-s)^{+}]&=\mathbb P_{c}\{Q(\infty )\ge s\}\cdot \mathbb E_{c}[Q(\infty )-s|Q(\infty )\ge s]\nonumber \\&=\mathbb P_{c}\{Q(\infty )\ge s\}\cdot \mathbb E[Q_{\mathrm{{M/M/1}}}]\nonumber \\&=\frac{\mathbb P_{c}\{Q(\infty )=c\}\rho ^{s-c}}{1-\rho }\cdot \frac{\rho }{1-\rho }\nonumber \\&=L_{2}(c,s,R), \end{aligned}$$

(53)

because

$$\begin{aligned} \nonumber \mathbb P_{c}\{Q(\infty )=c\}=[1-C(c,R)]\cdot B(c-1,R)\rho , \end{aligned}$$

due to

$$\begin{aligned} \nonumber \frac{\mathbb P_{c}\{Q(\infty )=c\}}{\mathbb P_{c}\{Q(\infty )\le c-1\}}=\frac{R^{c}/c!}{\sum _{i=0}^{c-1}R^{i}/i!}=B(c-1,R)\rho . \end{aligned}$$

$\square$

We further note that

$$\begin{aligned} \nonumber \mathbb E_{c}[(Q(\infty )-s)^{+}]-\mathbb E_{c}[(s-Q(\infty ))^{+}]=\mathbb E_{c}[Q(\infty )]-s. \end{aligned}$$

Also, since

$$\begin{aligned} \nonumber \mathbb E_{c}[Q(\infty )]=C(c,R)\cdot \frac{\rho }{1-\rho }+R, \end{aligned}$$

we then have

$$\begin{aligned} \mathbb E_{c}[(Q(\infty )-s)^{+}]-\mathbb E_{c}[(s-Q(\infty ))^{+}]=C(c,R)\cdot \frac{\rho }{1-\rho }+R-s. \end{aligned}$$

(54)

Therefore, combining (54) and Lemma 4, we can have the continuation function for $\mathbb E_{c}[(s-Q(\infty ))^{+}]$ and $\mathbb E_{c}[(Q(\infty )-s)^{+}]$, regardless of whether c is greater than or less than s, and this eventually leads to the continued expression of $\varOmega (c,s,R)$.

Proposition 2

For any $c\in \mathbb {Z}_{+}\cup (R,\infty )$ and $s\in \mathbb {Z}_{+}$, $\varOmega (c,s,R)=\varPi (c,s,R)$, where

$$\begin{aligned}&\varPi (c,s,R):=(d+w)R+R^{1/2}K(c,s,R), \end{aligned}$$

(55)

$$\begin{aligned}&K(c,s,R):=\left\{ \begin{array}{ll} d\cdot \frac{c-R}{\sqrt{R}}-p\cdot \frac{s-R}{\sqrt{R}}+\frac{(w+p)\sqrt{R}}{c-R}\cdot C(c,R)+(p+h)L_{1}(c,s,R)\cdot R^{-1/2},\quad \mathrm{if}~s\le c,\\ d\cdot \frac{c-R}{\sqrt{R}}+h\cdot \frac{s-R}{\sqrt{R}}+\frac{(w-h)\sqrt{R}}{c-R}\cdot C(c,R)+(p+h)L_{2}(c,s,R)\cdot R^{-1/2},\quad \mathrm{if}~s>c. \end{array}\right. \nonumber \\ \end{aligned}$$

(56)

Proof

The representation simply follows by applying (54) and Lemma 4 to (4). We provide the details below.

$$\begin{aligned} \varPi (c,s,R)=\left\{ \begin{array}{ll} d\cdot c+(w+p)\cdot \mathbb E_{c}[Q(\infty )]+(p+h)\cdot L_{1}(c,s,R)-p\cdot s,~~~~ \text {if }s\le c,\\ d\cdot c+(w-h)\cdot \mathbb E_{c}[Q(\infty )]+(p+h)\cdot L_{2}(c,s,R)+h\cdot s,~~~~ \text {if }s>c. \end{array}\right. \end{aligned}$$

(57)

If $s\le c$,

$$\begin{aligned} \varPi (c,s,R) =&\,d\cdot \left( R+\frac{c-R}{\sqrt{R}}R^{1/2}\right) +(w+p)\cdot \left( C(c,R)\cdot \frac{\rho }{1-\rho }+R\right) \nonumber \\&+\,(p+h)\cdot L_{1}(c,s,R)-p\cdot \left( R+\frac{s-R}{\sqrt{R}}R^{1/2}\right) \nonumber \\ =&\,(d+w)R+\left( d\cdot \frac{c-R}{\sqrt{R}}-p\cdot \frac{s-R}{\sqrt{R}}\right) R^{1/2}\nonumber \\&+\frac{(w+p)\sqrt{R}}{c-R}\cdot C(c,R)R^{1/2}+(p+h)\cdot L_{1}(c,s,R)\nonumber \\ =&\,(d+w)R+R^{1/2}\left[ d\cdot \frac{c-R}{\sqrt{R}}-p\cdot \frac{s-R}{\sqrt{R}}\right. \nonumber \\&\left. +\frac{(w+p)\sqrt{R}}{c-R}\cdot C(c,R)+(p+h)L_{1}(c,s,R)\cdot R^{-1/2}\right] , \end{aligned}$$

(58)

and if $s>c$,

$$\begin{aligned} \varPi (c,s,R) =&\,d\cdot \left( R+\frac{c-R}{\sqrt{R}}R^{1/2}\right) +(w-h)\cdot \left( C(c,R)\cdot \frac{\rho }{1-\rho }+R\right) \nonumber \\&+\,(p+h)\cdot L_{2}(c,s,R)+h\cdot \left( R+\frac{s-R}{\sqrt{R}}R^{1/2}\right) \nonumber \\ =&\,(d+w)R+\left( d\cdot \frac{c-R}{\sqrt{R}}+h\cdot \frac{s-R}{\sqrt{R}}\right) R^{1/2}\nonumber \\&+\frac{(w-h)\sqrt{R}}{c-R}\cdot C(c,R)R^{1/2}+(p+h)\cdot L_{2}(c,s,R)\nonumber \\ =&\,(d+w)R+R^{1/2}\left[ d\cdot \frac{c-R}{\sqrt{R}}+h\cdot \frac{s-R}{\sqrt{R}}\right. \nonumber \\&\left. +\frac{(w-h)\sqrt{R}}{c-R}\cdot C(c,R)+(p+h)L_{2}(c,s,R)\cdot R^{-1/2}\right] . \end{aligned}$$

(59)

$\square$

Appendix 2: Diffusion approximation for the average cost function

In this section we provide the proof of Theorem 1.

Proof of Theorem 1

Throughout the proof, let $c:=R+\beta \sqrt{R}$ and $s:=R+b\sqrt{R}$. Due to Proposition 2, the desired result is equivalent to

$$\begin{aligned} K(c,s,R)=K_{*}(\beta ,b)+\mathcal {O}(R^{-1/2}). \end{aligned}$$

(60)

First, [24] shows that

$$\begin{aligned} C(c,R)=C_{*}(\beta )+\mathcal {O}(R^{-1/2}), \end{aligned}$$

(61)

and

$$\begin{aligned} B(s,R)^{-1}=\frac{\varPhi (\alpha _{s})}{\phi (\alpha _{s})}s^{1/2}+\mathcal {O}(1), \end{aligned}$$

(62)

where

$$\begin{aligned} \alpha _{s}=\sqrt{-2s(1-R/s+\ln (R/s))},\quad \mathrm{sign}(\alpha _{s})=\mathrm{sign}(1-R/s), \end{aligned}$$

(63)

a simple function of R and s with $\alpha _{s}\rightarrow b$ as $s\rightarrow \infty$. Inverting (62) yields

$$\begin{aligned} B(s,R)=\frac{\phi (\alpha _{s})}{\varPhi (\alpha _{s})}s^{-1/2}+\mathcal {O}(s^{-1}). \end{aligned}$$

(64)

Simple calculations show that

$$\begin{aligned} s^{-1/2}=R^{-1/2}+\mathcal {O}(R^{-1}), \end{aligned}$$

(65)

and

$$\begin{aligned} \frac{\phi (\alpha _{s})}{\varPhi (\alpha _{s})}=\frac{\phi (b)}{\varPhi (b)}+\mathcal {O}(R^{-1/2}). \end{aligned}$$

(66)

Applying (65) and (66) to (64), we have that

$$\begin{aligned} B(s,R)=\frac{\phi (b)}{\varPhi (b)}R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(67)

We then apply (67) and Proposition 1 to (49) and get that

$$\begin{aligned} L_{1}(c,s,R)&=D(c,s,R)\cdot [bR^{1/2}+R\cdot B(s,R)] \end{aligned}$$

(68)

$$\begin{aligned}&=D_{*}(\beta ,b)\left[ b+\frac{\phi (b)}{\varPhi (b)}\right] R^{1/2}+\mathcal {O}(1). \end{aligned}$$

(69)

On the other hand, expression (67) implies

$$\begin{aligned} B(c-1,R)= \frac{\phi (\beta )}{\varPhi (\beta )}R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(70)

Also,

$$\begin{aligned} \rho ^{s-c}=[1+\beta R^{-1/2}]^{(\beta -b)\sqrt{R}}=\mathrm{e}^{-\beta (b-\beta )}+\mathcal {O}(R^{-1/2}). \end{aligned}$$

(71)

Applying (70), (71), (61), and $\rho (1-\rho )^{-1}=\beta ^{-1}R^{1/2}$ to (50), we can obtain that

$$\begin{aligned} L_{2}(c,s,R)=[1-C_{*}(\beta )]\frac{\phi (\beta )}{\beta ^{2}\varPhi (\beta )}\cdot \mathrm{e}^{-\beta (b-\beta )}R^{1/2}+\mathcal {O}(1). \end{aligned}$$

(72)

Finally, substituting (61), (69), and (72) into (58) and (59) leads to (60). $\square$

Appendix 3: Asymptotic optimality of square-root rule

This section is mainly devoted to the proof of Theorem 2. We also provide the proof of Lemma 1.

Proof of Theorem 2

Since the cost function $\varPi$ is continuous, the asymptotic optimality of the cost objective function (21) follows directly from that of the decision variables (20). Therefore, it suffices to prove (20). We first note that by Proposition 2, the exact optimal solution pair $(c_{\mathrm{opt}},s_{\mathrm{opt}})$ must satisfy

$$\begin{aligned} \left( \frac{\partial K(c_{\mathrm{opt}},s_{\mathrm{opt}},R)}{\partial c},\frac{\partial K(c_{\mathrm{opt}},s_{\mathrm{opt}},R)}{\partial s}\right) =(0,0), \end{aligned}$$

(73)

in which the second component is equivalent to

$$\begin{aligned} D(c_{\mathrm{opt}},s_{\mathrm{opt}},R)=p/(p+h). \end{aligned}$$

(74)

From (73), (74), (60), and Proposition 1, we have that

$$\begin{aligned} \frac{p}{p+h}= & {} D(R+\beta _{\mathrm{opt}}\sqrt{R},R+b_{\mathrm{opt}}\sqrt{R},R)=D_{*}(\beta _{\mathrm{opt}},b_{\mathrm{opt}})+\mathcal {O}(R^{-1/2}), \end{aligned}$$

(75)

$$\begin{aligned} 0= & {} \frac{\partial K(R+\beta _{\mathrm{opt}}\sqrt{R},R+b_{\mathrm{opt}}\sqrt{R},R)}{\partial \beta }=\frac{\partial K_{*}(\beta _{\mathrm{opt}},b_{\mathrm{opt}})}{\partial \beta }+\mathcal {O}(R^{-1/2}).\nonumber \\ \end{aligned}$$

(76)

Let $g_{1,*}(R):=\beta _{\mathrm{opt}}-\beta _{*}$ and $g_{2,*}(R):=b_{\mathrm{opt}}-b_{*}$. Then applying a first-order Taylor expansion to (75), we obtain that

$$\begin{aligned} \frac{p}{p+h}=D_{*}(\beta _{*},b_{*})+\mathcal {O}(\max \{g_{1,*}(R),g_{2,*}(R)\})+\mathcal {O}(R^{-1/2}). \end{aligned}$$

(77)

Finally, substituting $D_{*}(\beta _{*},b_{*})=\frac{p}{p+h}$ into (77), we find that $\max \{g_{1,*}(R),g_{2,*}(R)\}=\mathcal {O}({R}^{-1/2})$, and therefore (19) holds, which immediately yields (20) in light of the definition of $(c_*,s_*)$ and that of $(\beta _{\mathrm{opt}},b_{\mathrm{opt}})$. $\square$

Proof of Lemma 1

The first part of the lemma simply follows by applying to (10) the result $\lim _{\beta \rightarrow \infty }\beta [\phi (\beta )+\beta \varPhi (\beta )]^{-1}=1$, which can be easily verified algebraically. For the second part, setting to $\delta$ the expression (10) for $\beta <b$, we solve for b and obtain that

$$\begin{aligned} b_{\delta }(\beta ) = \frac{\ln (C_{*}(\beta )) - \ln (1-\delta ) }{\beta } + \beta . \end{aligned}$$

(78)

Then note that

$$\begin{aligned} C_*(\beta )=1-\frac{\sqrt{2\pi }}{2}\beta +o(\beta ), \end{aligned}$$

(79)

where a function $f(\beta )$ is said to be $o(\beta )$ if $\lim _{\beta \rightarrow 0}f(\beta )/\beta =0$. Finally, the second part of the lemma follows after first applying (79) to (78) and then subsequently using the fact that $\ln (1+x)=x+o(x)$ for $|x| < 1$ (with x corresponding to $-\frac{\sqrt{2\pi }}{2}\beta +o(\beta )$ in this case). $\square$

Appendix 4: Corrected diffusion approximation

In this section we prove Theorem 3, i.e., the corrected diffusion approximation for the steady-state shortfall distribution, which is equivalent to the steady-state queue-length distribution in the elementary M / M / c queue. This corrected diffusion approximation refines the celebrated diffusion approximation first developed in Propositions 1 and 2 of [22] and may be of independent interest.

Proof of Theorem 3

Throughout the proof, let $c:=R+\beta \sqrt{R}$ and $s:=R+b\sqrt{R}$. By Theorem 2 in [24],

$$\begin{aligned} 1-C(c,R)=1-C_{*}(\beta )-C_{\bullet }(\beta )R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(80)

We first consider the case of $s\le c$ or $b\le \beta$. Due to (43) and (80), it is sufficient to prove

$$\begin{aligned} \frac{R^{s}/[B(s,R)\varGamma (s+1)]}{R^{c-1}/[B(c-1,R)\varGamma (c)]}=\varPhi (b)\varPhi (\beta )^{-1}+g_{1}(\beta ,b)R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(81)

In [24], it is shown that

$$\begin{aligned} B(s,R)^{-1}=\frac{\varPhi (\alpha _{s})}{\phi (\alpha _{s})}s^{1/2}+\frac{2}{3}+\mathcal {O}(s^{-1/2}), \end{aligned}$$

(82)

where

$$\begin{aligned} \alpha _{s}=\sqrt{-2s(1-R/s+\ln (R/s))},\quad \mathrm{sign}(\alpha _{s})=\mathrm{sign}(1-R/s), \end{aligned}$$

(83)

a simple function of R and s with $\alpha _{s}\rightarrow b$ as $s\rightarrow \infty$. By letting $p(s):=s^{s}\mathrm{e}^{-s}\sqrt{2\pi s}~\varGamma (s+1)^{-1}$, we have

$$\begin{aligned} \frac{\mathrm{e}^{-R}R^{s}}{\varGamma (s+1)}=\phi (\alpha _{s})p(s)s^{-1/2}. \end{aligned}$$

(84)

Multiplying (82) by (84) yields

$$\begin{aligned} \frac{\mathrm{e}^{-R}R^{s}}{\varGamma (s+1)B(s,R)}=p(s)\varPhi (\alpha _{s})+\frac{2}{3}\phi (\alpha _{s})p(s)s^{-1/2}+\mathcal {O}(s^{-1}). \end{aligned}$$

(85)

To expand the first term in (85), we note from the proof of Theorem 2 in [24] that

$$\begin{aligned} \nonumber \frac{\varPhi (\alpha _{s})}{\phi (b)}=\frac{\varPhi (b)}{\phi (b)}-\frac{1}{6}b^{2}R^{-1/2}+\mathcal {O}(R^{-1}), \end{aligned}$$

and thus

$$\begin{aligned} \varPhi (\alpha _{s})=\varPhi (b)-\frac{1}{6}b^{2}\phi (b)R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(86)

By Stirling’s approximation for the Gamma function (see p. 257 of [1]),

$$\begin{aligned} p(s)=1+\mathcal {O}(s^{-1})=1+\mathcal {O}(R^{-1}). \end{aligned}$$

(87)

We then multiply (86) by (87) and arrive at

$$\begin{aligned} p(s)\varPhi (\alpha _{s})=\varPhi (b)-\frac{1}{6}b^{2}\phi (b)R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(88)

Next, we expand the second term in (85). Simple computations show that

$$\begin{aligned} \nonumber \phi (\alpha _{s})=\phi (b)+\mathcal {O}(R^{-1/2}), \end{aligned}$$

and

$$\begin{aligned} \nonumber s^{-1/2}p(s)=s^{-1/2}+\mathcal {O}(s^{-3/2})=R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

It then follows that

$$\begin{aligned} \frac{2}{3}\phi (\alpha _{s})p(s)s^{-1/2}=\frac{2}{3}\phi (b)R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(89)

Substituting (88) and (89) into (85) yields

$$\begin{aligned} \frac{\mathrm{e}^{-R}R^{s}}{\varGamma (s+1)B(s,R)}=\varPhi (b)+\left[ \frac{2}{3}\phi (b)-\frac{1}{6}b^{2}\phi (b)\right] R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(90)

This provides a power series expansion of the numerator in (81) times $\mathrm{e}^{-R}$. We then turn to expanding the denominator of expression (81) times $\mathrm{e}^{-R}$. By Lemma 3,

$$\begin{aligned} \nonumber \frac{1}{B(c-1,R)}=\frac{R}{cB(c,R)}-\frac{R}{c}, \end{aligned}$$

and therefore

$$\begin{aligned} \frac{\mathrm{e}^{-R}R^{c-1}}{\varGamma (c)B(c-1,R)}=\frac{\mathrm{e}^{-R}R^{c}}{\varGamma (c+1)B(c,R)}-\frac{\mathrm{e}^{-R}R^{c}}{\varGamma (c+1)}. \end{aligned}$$

(91)

The expansion of the first term of (91) is just the same as (90), with b replaced by $\beta$:

$$\begin{aligned} \frac{\mathrm{e}^{-R}R^{c}}{\varGamma (c+1)B(c,R)}=\varPhi (\beta )+\left[ \frac{2}{3}\phi (\beta )-\frac{1}{6}\beta ^{2}\phi (\beta )\right] R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(92)

For the second term of (91), following the same procedure as above [i.e., from (84) to (89)], we obtain that

$$\begin{aligned} \frac{\mathrm{e}^{-R}R^{c}}{\varGamma (c+1)}=\phi (\beta )R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(93)

Substituting (92) and (93) into (91) yields

$$\begin{aligned} \nonumber \frac{\mathrm{e}^{-R}R^{c-1}}{\varGamma (c)B(c-1,R)}=\varPhi (\beta )-\left[ \frac{1}{3}\phi (\beta )+\frac{1}{6}\beta ^{2}\phi (\beta )\right] R^{-1/2}+\mathcal {O}(R^{-1}), \end{aligned}$$

which upon inversion becomes

$$\begin{aligned} \left[ \frac{\mathrm{e}^{-R}R^{c-1}}{\varGamma (c)B(c-1,R)}\right] ^{-1}=\varPhi (\beta )^{-1}+\varPhi (\beta )^{-2}\left[ \frac{1}{3}\phi (\beta )+\frac{1}{6}\beta ^{2}\phi (\beta )\right] R^{-1/2}\!+\!\mathcal {O}(R^{-1}). \end{aligned}$$

(94)

Finally, we multiply (90) by (94) to get (81). This completes the proof for the case of $b\le \beta$. We now turn to proving the theorem in the case of $b>\beta$. First, by Lemma 3 and (82) (with s replaced by c),

$$\begin{aligned} B(c-1,R)^{-1}&=\rho (B(c,R)^{-1}-1) \end{aligned}$$

(95)

$$\begin{aligned}&=\frac{\varPhi (\alpha _{c})}{\phi (\alpha _{c})}\cdot \rho c^{1/2}-\frac{1}{3}\rho +\mathcal {O}(c^{-1/2}), \end{aligned}$$

(96)

which upon inversion becomes

$$\begin{aligned} B(c-1,R)=\frac{1}{\rho }\cdot \frac{\phi (\alpha _{c})}{\varPhi (\alpha _{c})}\left( c^{-1/2}+\frac{1}{3}\cdot \frac{\phi (\alpha _{c})}{\varPhi (\alpha _{c})}c^{-1}\right) +\mathcal {O}(c^{-3/2}). \end{aligned}$$

(97)

Simple computations show that

$$\begin{aligned} \rho ^{-1}= & {} 1+\beta R^{-1/2}, \end{aligned}$$

(98)

$$\begin{aligned} c^{-1/2}= & {} R^{-1/2}-\frac{1}{2}\beta R^{-1}+\mathcal {O}(R^{-3/2}), \end{aligned}$$

(99)

and

$$\begin{aligned} \frac{\phi (\alpha _{c})}{\varPhi (\alpha _{c})}=\frac{\phi (\beta )}{\varPhi (\beta )}+\frac{1}{6}\beta ^{2}\left[ \left( \frac{\phi (\beta )}{\varPhi (\beta )}\right) ^{2}+\beta \frac{\phi (\beta )}{\varPhi (\beta )}\right] R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(100)

Applying (98)–(100) to (97), we have that

$$\begin{aligned} B(c-1,R)=\frac{\phi (\beta )}{\varPhi (\beta )}R^{-1/2}+g_{3}(\beta )R^{-1}+\mathcal {O}(R^{-3/2}). \end{aligned}$$

(101)

Next, we derive a refined approximation for $\rho ^{s-c+1}$. We shall need the following result (see [9]): for any $x<-1$,

$$\begin{aligned} \left( 1+\frac{1}{x}\right) ^{x}=e-\frac{e}{2}x^{-1}+\mathcal {O}(x^{-2}). \end{aligned}$$

(102)

Also, we can express the traffic intensity as

$$\begin{aligned} \rho =1+\frac{1}{-(\beta ^{-1}R^{1/2}+1)}=1-\beta R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(103)

Applying (102) and the two expressions in (103), we have that

$$\begin{aligned} \rho ^{s-c}&=\left[ \left( 1+\frac{1}{-(\beta ^{-1}R^{1/2}+1)}\right) ^{-(\beta ^{-1}R^{1/2}+1)}\cdot (1-\beta R^{-1/2}+\mathcal {O}(R^{-1}))\right] ^{-\beta (b-\beta )}\nonumber \\&=\left[ \left( e+\frac{e}{2}(\beta ^{-1}R^{1/2}+1)^{-1}+\mathcal {O}((\beta ^{-1}R^{1/2}+1)^{-2})\right) \right. \nonumber \\&\quad \left. \cdot (1-\beta R^{-1/2}+\mathcal {O}(R^{-1}))\right] ^{-\beta (b-\beta )}\nonumber \\&=\left[ \left( e+\frac{e}{2}\beta R^{-1/2}+\mathcal {O}(R^{-1})\right) \cdot (1-\beta R^{-1/2}+\mathcal {O}(R^{-1}))\right] ^{-\beta (b-\beta )}\nonumber \\&=\left( e-\frac{e}{2}\beta R^{-1/2}+\mathcal {O}(R^{-1})\right) ^{-\beta (b-\beta )}\nonumber \\&=\left( \mathrm{e}^{-1}+\frac{1}{2}\mathrm{e}^{-1}\beta R^{-1/2}+\mathcal {O}(R^{-1})\right) ^{\beta (b-\beta )}\nonumber \\&=\mathrm{e}^{-\beta (b-\beta )}\left( 1+\frac{1}{2}\beta R^{-1/2}+\mathcal {O}(R^{-1})\right) ^{\beta (b-\beta )}\nonumber \\&=\mathrm{e}^{-\beta (b-\beta )}\left( 1+\frac{1}{2}\beta ^{2}(b-\beta )R^{-1/2}+\mathcal {O}(R^{-1})\right) . \end{aligned}$$

(104)

Combining (104) with (103) yields

$$\begin{aligned} \rho ^{s-c+1}=\mathrm{e}^{-\beta (b-\beta )}+\left( \frac{1}{2}\beta ^{2}(b-\beta )-\beta \right) \mathrm{e}^{-\beta (b-\beta )}R^{-1/2}+\mathcal {O}(R^{-1}). \end{aligned}$$

(105)

Finally, substituting (80), (101), (105) and $\rho (1-\rho )^{-1}=\beta ^{-1}R^{1/2}$ into (43), we obtain the desired series expression in the case of $b>\beta$ and complete the proof of the theorem. $\square$