Empirical performance bounds for quantum approximate optimization

Abstract

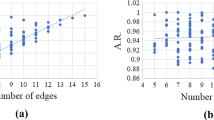
The quantum approximate optimization algorithm (QAOA) has been put forth as a method for near-term quantum computers to solve optimization problems. However, assessments of QAOA performance have mostly focused on small structured problem instances while performance on more general instances is less clear. Here, we numerically simulate QAOA pure state dynamics for every instance of MaxCut on non-isomorphic unweighted graphs with nine or fewer vertices with depth parameters $p\le 3$. We find the approximation ratios and optimized circuit parameters concentrate across graphs of a given size and empirically show increases in concentration as graph size increases. The parameter concentration leads to two median-angle heuristics that overcome difficulties in QAOA parameter optimization and obtain mean approximation ratios within 3% and 0.2% of the optimal. We also analyze the probability to measure an optimal solution and find increasing variations between graphs as depth increases, in stark contrast to the approximation ratios which concentrate as depth increases. The resulting benchmark data set gives empirical bounds for on-going experimental realizations and lays groundwork for theoretical extensions to greater problem sizes and depths where QAOA may prove important for practically relevant problems.

Angle symmetries

In this appendix, we discuss details of the angle symmetries from Sect. 3.3. Most of the symmetries have been described previously by Zhou et al. [7], although we note two of the symmetries they described for regular graphs apply more broadly to graphs where every vertex has even degree or every vertex has odd degree. Each symmetry relates different sets of angles $(\varvec{\gamma }, \varvec{\beta })$ and $(\varvec{\gamma }', \varvec{\beta }')$ that give the same approximation ratio in Eq. (11),

$$\begin{aligned} \langle {\hat{C}}(\varvec{\gamma },\varvec{\beta }) \rangle = \langle {\hat{C}}(\varvec{\gamma }', \varvec{\beta }')\rangle , \end{aligned}$$

(27)

where

$$\begin{aligned} \varvec{\gamma }&= (\gamma _1,\ldots ,\gamma _{q-1},\gamma _q,\gamma _{q+1},\ldots ,\gamma _p), \nonumber \\ \varvec{\beta }&= (\beta _1,\ldots ,\beta _{q-1},\beta _q,\beta _{q+1},\ldots ,\beta _p), \end{aligned}$$

(28)

with $(\varvec{\gamma }', \varvec{\beta }')$ related to $(\varvec{\gamma }, \varvec{\beta })$ in different ways for the different symmetries. An example is periodic behavior of the $\beta _q$ angles over intervals of $\pi /2$, we use this to restrict every $\beta _q$ component to the interval $-\pi /4 \le \beta _q \le \pi /4$, as described by Zhou et al. There are a variety of additional symmetries we describe below, with derivations in subsequent subsections.

The first type of symmetry applies to graphs where every vertex has even degree. In this case the $\gamma _q$ angles are periodic over intervals of $\pi$ since all the eigenvalues of ${\hat{C}}$ are even, as shown in detail in the next subsection. Thus the symmetry of Eq. (27) holds for any pair of angles with $\varvec{\beta } = \varvec{\beta }'$ and

$$\begin{aligned} \varvec{\gamma }' = (\gamma _1,\ldots ,\gamma _{q-1},\gamma _q \pm \pi ,\gamma _{q+1},\ldots ,\gamma _p), \end{aligned}$$

(29)

where $\varvec{\gamma }'$ differs from $\varvec{\gamma }$ by a shift $\gamma _q' = \gamma _q \pm \pi$ for any q. We use this symmetry to organize the angle distributions so $|\gamma _q| \le \pi /2$ for all q for graphs where every vertex degree is even. We search for generic optimized angles in our implementation of the BFGS algorithm from Sect. 3.2, but if we find a $|\gamma _q| > \pi /2$ then we add or subtract $\pi$ to get a $|\gamma _q'| \le \pi /2$.

The second type of symmetry applies to graphs where every vertex has odd degree. This gives a joint symmetry in both sets of angles in Eq. (27),

$$\begin{aligned} \varvec{\gamma }'&= (\gamma _1,\ldots ,\gamma _{q-1},\gamma _q \pm \pi ,\gamma _{q+1},\ldots ,\gamma _p)\nonumber \\ \varvec{\beta }'&= (\beta _1,\ldots ,\beta _{q-1},-\beta _q,-\beta _{q+1},\ldots ,-\beta _p). \end{aligned}$$

(30)

In Eq. (30), $\varvec{\gamma }'$ differs from $\varvec{\gamma }$ in the qth component, $\gamma _q' = \gamma _q \pm \pi$ for any q, and $\varvec{\beta }'$ differs from $\varvec{\beta }$ in the sign of all subsequent components, $\beta _r'= -\beta _r$ for all $r \ge q$. The proof follows from Pauli operator commutation relations applied to the two unitary operators of Eqs. (7)–(8), as shown in detail later. In our calculations, we use this symmetry to organize the angles so $|\gamma _q| \le \pi /2$ for all q for graphs where every vertex degree is odd, similar to how we organize the angles when all the vertex degrees are even.

The third analytic symmetry we use is the “time-reversal” symmetry [7]

$$\begin{aligned} (\varvec{\gamma }',\varvec{\beta }') = (-\varvec{\gamma }, -\varvec{\beta }). \end{aligned}$$

(31)

The symmetry is related to the ${\hat{B}}$ and ${\hat{C}}$ operators in Eqs. (7)–(8) and the initial state $\vert \psi _0\rangle$ of Eq. (5), which have real-valued matrix elements and coefficients in the computational basis. We give a proof at the end of “Appendix.” We use this symmetry to always transform to angles with $\beta _1 \le 0$. The $\beta _q$ for $q > 1$ can be positive or negative.

We find additional symmetries in the optimized angles for a small subset of graphs. For these, we report the angles with the most component-pairs $(\gamma _i,\beta _i) \in (\varGamma , {\mathrm {B}})$ from Eq. (22). Using the angles with the most components in $(\varGamma , {\mathrm {B}})$ is designed to emphasize the angle patterns in Sect. 4.3. The number of graphs M(p) we used the $(\varGamma , {\mathrm {B}})$ symmetry on is shown for each n and p in Table 10. The symmetry was used most often when a graph became fully optimized. For example, we found two sets of angles for an $n=3$ graph that optimized the cost function $\langle {\hat{C}} \rangle = C_\mathrm{max}$; we saved the angles with the most components in $(\varGamma ,{\mathrm {B}})$. Asterisks in the table denote each graph which we used the rule on for that n and p was fully optimized. Note when graphs are optimized at some p we do not simulate them at depths $p' > p$, so they do not carry over to columns for greater depths in the table. Overall, the rule is applied to a very limited subset of the graphs we study.

Table 10 Numbers of graphs M(p) where we found degeneracies and used the rule of saving the angles with the most components in $(\varGamma ,{\mathrm {B}})$ following Eq. (22), for various depths p

1.1 Symmetry when all vertices have even degree

When all the vertices have even degree, the angle components $\gamma _q$ are periodic over intervals of $\pi$, as discussed around Eq. (29). To demonstrate equivalence of $\langle {\hat{C}} \rangle$ in Eq. (27) for the angles $\varvec{\gamma }'$ from Eq. (29) and $\varvec{\gamma }$ from Eq. (28), in the next paragraph we show ${\hat{C}}$ of Eq. (17) has only even eigenvalues when each vertex has even degree. Then $C(z) = 2m_z$ for all z, where $m_z$ is an integer. The periodicity over $\pi$ follows since the matrix elements from the unitary operator ${\hat{U}}({\hat{C}},\gamma _q)$ of Eq. (7) are invariant under changes $\gamma _q \rightarrow \gamma _q \pm \pi$, since

$$\begin{aligned} \langle z \vert {\hat{U}}({\hat{C}},\gamma _q)\vert z \rangle= & {} \exp (\mp i2m_z\pi )\exp (-i 2m_z \gamma _q) \nonumber \\= & {} \langle z \vert {\hat{U}}({\hat{C}},\gamma _q \pm \pi )\vert z \rangle , \end{aligned}$$

(32)

where the factor $1 = \exp (\mp i2m_z\pi )$ connects the two expressions.

To show the eigenvalues C(z) are all even when all the vertex degrees are even, we begin by showing there exists a single bitstring $z^{(0)}$ for which $C(z^{(0)})$ is even. Then we show that if C(z) is even for any z and all the vertex degrees are even, then modifying any bit $z_k$ in the bitstring z to get a new bitstring $z'$ will give a $C(z')$ that is also even. Together these imply that every bitstring has even C(z) when all the vertex degrees are even, since any bitstring can be made from a series of modifications to $z^{(0)}$ and every modification gives an even C(z).

First consider the zero bitstring $z^{(0)} = (0,0,\ldots ,0)$. From Eqs. (15)–(16), this has $C(z^{(0)}) = 0$ which is even. Next consider an arbitrary bitstring $z = (z_{n-1}, z_{n-2}, \ldots , z_k, \ldots , z_0)$ for which C(z) is even. Suppose we flip a bit $z_k$ to make a new bitstring $z' = (z_{n-1}, z_{n-2}, \ldots , z_k', \ldots , z_0)$ where $z_k' \ne z_k$ but the $z_{j \ne k}$ are the same. The change $z_k \rightarrow z_k'$ will change the value of each $C_{\langle j,k\rangle }$ from Eq. (16) that is associated with $z_k$, so that if $C_{\langle j,k\rangle }(z)$ = 1 then $C_{\langle j,k\rangle }(z') = 0$ and vice-versa. The total number of edge terms $C_{\langle j,k\rangle }$ can be separated into $\kappa$ terms that increase in value and $\delta$ terms that decrease in value when $z \rightarrow z'$. The value of the cost function for $z'$ can then be expressed as $C(z') = C(z) + \kappa - \delta$. The number of edge components $C_{\langle j,k\rangle }$ that depend on $z_k$ is even when each vertex degree is even, so $\delta + \kappa = 2m$ for some integer m. This implies that $\kappa$ and $\delta$ are either both even or both odd; either way, the difference $\kappa -\delta$ is even. Since C(z) is even by assumption, $C(z') = C(z) + \kappa - \delta$ is also even.

We have shown there is a bitstring $z^{(0)}$ for which $C(z^{(0)})$ is even and we have shown changing any such bitstring gives a new $C(z')$ which is also even. This implies C(z) is even for all z for every graph where each vertex degree is even. By Eq. (32), the angle components $\gamma _q$ are periodic over intervals of $\pi$ for these graphs.

1.2 Symmetry when all vertices have odd degree

When all the vertices have odd degree, there is a symmetry Eq. (27) for angle-pairs $(\varvec{\gamma }, \varvec{\beta })$ and $(\varvec{\gamma }',\varvec{\beta }')$ from Eqs. (28) and (30), respectively. Only graphs with an even number of vertices can have this symmetry since it is impossible to have a graph with an odd number of vertices where every vertex has odd degree. We prove the symmetry holds in a simple case with $p=1$, the extension to $p>1$ uses similar reasoning. We begin by considering the relations between the unitary operators with $(\varvec{\gamma }, \varvec{\beta })$ and $(\varvec{\gamma }',\varvec{\beta }')$, then use the analysis to relate the time evolution and probabilities P(z) for states with the different angles.

Let $\gamma _1' = \gamma _1 \pm \pi$. The unitary operator ${\hat{U}}({\hat{C}}, \gamma _1)$ from Eq. (7) is a product of unitary-operator components for each edge, a single component can be expressed as

$$\begin{aligned} \exp (-i \gamma _1 {\hat{C}}_{\langle j,k\rangle })&= \exp \left( -i \frac{\gamma _1}{2}(\hat{\mathbb {1}} - {\hat{Z}}_j {\hat{Z}}_k)\right) \nonumber \\&= \exp \left( -i \frac{\gamma _1' \mp \pi }{2}\right) \exp \left( i \frac{\gamma _1' \mp \pi }{2}{\hat{Z}}_j {\hat{Z}}_k\right) . \end{aligned}$$

(33)

Separate out a term $\exp \left( \mp i (\pi /2){\hat{Z}}_j {\hat{Z}}_k\right) = \mp i {\hat{Z}}_j {\hat{Z}}_k$ to obtain

$$\begin{aligned} \exp (-i \gamma _1 {\hat{C}}_{\langle j,k\rangle }) = e^{i\delta } {\hat{Z}}_k {\hat{Z}}_j \exp (-i \gamma _1' {\hat{C}}_{\langle j,k\rangle }), \end{aligned}$$

(34)

where $e^{i\delta }$ is an overall phase.

Now consider the unitary operator ${\hat{U}}({\hat{C}}, \gamma _1)$ of Eq. (7). Using Eq. (34), we have

$$\begin{aligned} {\hat{U}}({\hat{C}}, \gamma _1)&= \prod _{\langle j,k\rangle } \exp (-i \gamma _1 {\hat{C}}_{\langle j,k\rangle }) \nonumber \\&= e^{i\eta }\left( \prod _{j=0}^{n-1} {\hat{Z}}_j\right) {\hat{U}}({\hat{C}}, \gamma _1'), \end{aligned}$$

(35)

where $e^{i\eta }$ is a phase factor. The term $\prod _{j=0}^{n-1} {\hat{Z}}_j$ comes from the product of ${\hat{Z}}_j {\hat{Z}}_k$ for all the edges—each ${\hat{Z}}_j$ is raised to an odd power in the product since each vertex degree is odd and using $({\hat{Z}}_j)^2 = \hat{\mathbb {1}}$ reduces this to $\prod _{j=0}^{n-1} {\hat{Z}}_j$.

We will use Eq. (35) to simplify the time evolution of $\vert \psi _p(\gamma _1,\beta _1)\rangle$ in Eq. (6). This includes the unitary operator ${\hat{U}}({\hat{B}}, \beta _1)$ from Eq. (8), which shows up in the product ${\hat{U}}({\hat{B}}, \beta _1) {\hat{U}}({\hat{C}}, \gamma _1)$. Our next goal will be to use commutation relations to move the $\prod _{j=0}^{n-1} {\hat{Z}}_j$ to the left side of the product.

Express the ${\hat{U}}({\hat{B}},\beta _1)$ from Eq. (8) as

$$\begin{aligned} {\hat{U}}({\hat{B}}, \beta _1) = \prod _{j=0}^{n-1}\left( \cos (\beta _1)\hat{\mathbb {1}} - i \sin (\beta _1){\hat{X}}_j\right) . \end{aligned}$$

(36)

Now consider the product of the unitary operators

$$\begin{aligned} {\hat{U}}({\hat{B}}, \beta _1) {\hat{U}}({\hat{C}}, \gamma _1)&= e^{i\eta }\prod _{j=0}^{n-1}\left( \cos (\beta _1)\hat{\mathbb {1}} - i \sin (\beta _1){\hat{X}}_j\right) \nonumber \\&\quad \times \left( \prod _{j=0}^{n-1} {\hat{Z}}_j \right) {\hat{U}}({\hat{C}}, \gamma _1'). \end{aligned}$$

(37)

The Pauli operators anticommute so

$$\begin{aligned} {\hat{U}}({\hat{B}}, \beta _1) {\hat{U}}({\hat{C}}, \gamma _1) = e^{i\eta }\left( \prod _{j=0}^{n-1} {\hat{Z}}_j \right) {\hat{U}}({\hat{B}}, -\beta _1) {\hat{U}}({\hat{C}}, \gamma _1'). \end{aligned}$$

(38)

We are now ready to show the angles $(\gamma _1, \beta _1)$ and $(\gamma _1',\beta _1')$ give equivalent $\langle {\hat{C}} \rangle$ in Eq. (11), where $\gamma _1' = \gamma _1 \pm \pi$ and $\beta _1' = - \beta _1$. To demonstrate the equivalence we show the computational basis state probabilities P(z) are the same for both $(\gamma _1, \beta _1)$ and $(\gamma _1',\beta _1')$.

The probability amplitude for a basis state $\vert z \rangle$ is

$$\begin{aligned} \langle z \vert \psi (\gamma _1,\beta _1)\rangle = \langle z \vert {\hat{U}}({\hat{B}}, \beta _1) {\hat{U}}({\hat{C}},\gamma _1) \vert \psi _0\rangle . \end{aligned}$$

(39)

Using Eq. (38), this can be expressed as

$$\begin{aligned} \langle z \vert \psi (\gamma _1,\beta _1) \rangle&=\langle z \vert e^{i\eta }\left( \prod _{j=0}^{n-1} {\hat{Z}}_j \right) {\hat{U}}({\hat{B}}, \beta _1') {\hat{U}}({\hat{C}}, \gamma _1') \vert \psi _0\rangle \nonumber \\&= e^{i\eta }\langle z \vert \left( \prod _{j=0}^{n-1}{\hat{Z}}_j \right) \vert \psi (\gamma _1',\beta _1')\rangle \end{aligned}$$

(40)

Squaring the amplitudes, we obtain

$$\begin{aligned} \vert \langle z \vert \psi (\gamma _1,\beta _1) \rangle |^2&= \langle \psi (\gamma _1',\beta _1') \vert \left( \prod _{j=0}^{n-1} {{\hat{Z}}_j}^{\dag } \right) \vert z \rangle \langle z \vert \nonumber \\&\quad \times \left( \prod _{j=0}^{n-1} {{\hat{Z}}_j} \right) \vert \psi (\gamma _1',\beta _1')\rangle . \end{aligned}$$

(41)

The $\left( \prod _{j=0}^{n-1} {{\hat{Z}}_j} \right)$ can be moved to the left since it commutes with $\vert z \rangle \langle z \vert$, then using $\left( \prod _{j=0}^{n-1} {{\hat{Z}}_j}^\dag \right) \left( \prod _{j=0}^{n-1} {{\hat{Z}}_j} \right) = \hat{\mathbb {1}}$ gives

$$\begin{aligned} P(z) = \vert \langle z \vert \psi (\gamma _1,\beta _1) \rangle |^2 = \vert \langle z \vert \psi (\gamma _1',\beta _1') \rangle |^2, \end{aligned}$$

(42)

where P(z) is the probability of $\vert z \rangle$ from Eq. (10). The P(z) are the same for $(\gamma _1, \beta _1)$ and $(\gamma _1',\beta _1')$ so $\langle {\hat{C}}(\gamma _1,\beta _1)\rangle = \langle {\hat{C}}(\gamma _1',\beta _1')\rangle$ in Eq. (11), which is the desired symmetry.

1.3 Time-reversal symmetry

We finally consider the “time-reversal” symmetry with the angles of Eqs. (28) and (31) in the symmetry relation Eq. (27) [7]. The symmetry is related to structures of the ${\hat{B}}$ and ${\hat{C}}$ operators, which have real-valued matrix elements in the computational basis in Eqs. (9) and (17), and the structure of the initial state $\vert \psi _0\rangle$, which has real-valued coefficients in the computational basis in Eq. (5). To demonstrate the symmetry we calculate generic computational basis probabilities P(z) for states with both sets of angles and show they are equal, thus the $\langle {\hat{C}} \rangle$ are equal following Eq. (11).

Consider the probability amplitude $\langle z \vert \psi _p(\varvec{\gamma },\varvec{\beta })\rangle$ for a single basis state $\vert z \rangle$. From Eqs. (5)–(8) this is

$$\begin{aligned} \langle z \vert \psi _p(\varvec{\gamma },\varvec{\beta })\rangle = \frac{1}{\sqrt{2^n}} \sum _{z'} \langle z \vert \left( \prod _{q=1}^p e^{-i\beta _q{\hat{B}}} e^{-i\gamma _q{\hat{C}}} \right) \vert z'\rangle . \end{aligned}$$

(43)

Taking the complex conjugate of Eq. (43) only changes the sign of the angle terms since the ${\hat{B}}$ and ${\hat{C}}$ matrices have real-valued matrix elements in the computational basis, thus

$$\begin{aligned} \langle z \vert \psi _p(\varvec{\gamma },\varvec{\beta })\rangle ^* = \langle z \vert \psi _p(-\varvec{\gamma },-\varvec{\beta })\rangle . \end{aligned}$$

(44)

The Born probabilities P(z) from Eq. (10) are the same for both states since

$$\begin{aligned} P(z)= \vert \langle z \vert \psi _p(\varvec{\gamma },\varvec{\beta })\rangle \vert ^2&= \vert \langle z \vert \psi _p(\varvec{\gamma },\varvec{\beta })\rangle ^*\vert ^2 \nonumber \\&= \vert \langle z \vert \psi _p(-\varvec{\gamma },-\varvec{\beta })\rangle \vert ^2, \end{aligned}$$

(45)

so the $\langle {\hat{C}} \rangle$ are the same in Eq. (11).